Introduction

The ultra-low-permeability shale gas reservoir has a lot of well-developed natural fractures. On the one hand, from the mechanical viewpoint, hydraulic fracture network can be created because the natural fractures will be activated and opened during the process of hydraulic fracturing in shale reservoir. On the other hand, production performance analysis shows that the shale gas production can be improved greatly by creating a connected fracture network with a certain conductivity around the hydraulic fracture (Hu et al. 2016), and it is also found that the gas production has a good correlation with the fracture network size and conductivity, as well as the fracture network complexity (Mayerhofer et al. 2010). Thus, the goal of hydraulic fracturing in shale gas reservoir is to activate and open natural fractures and create a fracture network, which is called stimulated reservoir volume (SRV). Therefore, it is important to predict the SRV based on actual geological reservoir and treatment parameters so as to evaluate production performance accurately and optimize hydraulic fracturing parameters in shale gas reservoirs.

Micro-seismic monitoring is the main method to be applied to analyze the hydraulic fracture propagation pattern. It has been found that a complex fracture network was created rather than a single planar crack in hydraulic fracturing of shale gas reservoir according to the micro-seismic monitoring map of typical Barnett-shale slickwater fracturing (Cipolla 2009). It is also believed that the complex fracture networks are caused by shear slippage and tensile failure of natural fractures. Palmer et al. (2007, 2009) considered that the complex fracture network is resulted from shear and tensile failures of natural fractures in the process of fluid injection. They also believed that shear slippage of natural fractures could increase the permeability of shale gas reservoir and improve the shale gas production, and they proposed an analytical model to evaluate the shear failure zone. Later, Palmer et al. (2013) developed a geomechanical model to predict the shear failure extend of a fractured well and obtained the porosity and permeability of the stimulation region by fitting the micro-seismic data. Shahid et al. (2015) presented a coupled flow fluid and geomechanical model to simulate the activation phenomenon of natural fractures in hydraulic fracturing of shale gas reservoirs. Nassir et al. (2012, 2014) established a fully coupled geomechanical model based on continuum method and adopted tensile/shear failure criteria to determine SRV. In their paper, the stimulated region is represented by an enhancement permeability area. Ge and Ghassemi (2012) used the analytic solution of the fluid diffusion equation and the Mohr–Coulomb failure criterion to predict the shear slippage zone and matched the permeability enhancement of the slippage zone with the micro-seismic data. Ghassemi et al. (2013) evaluated the tensile/shear failure zones according to the three-dimensional stress field and pore pressure field around the hydraulic fracture. However, they assumed that the hydraulic fracture length is stationary so that it could not simulate the SRV growth process. Ji et al. (2009) established a coupled flow and geomechanical model to simulate a single fracture propagation by modifying the transmissibility and porosity of the matrix grid block. Wang et al. (2016) developed a coupled fluid flow, stress and rock damage model to evaluate shear stimulation effect of shale gas reservoirs and performed a parameter sensitivity analysis. Yu and Aguilera (2012) calibrated the SRV development model according to 3D pressure diffusivity equation by adjusting the diffusivity coefficient with micro-seismic cloud data. Warpinski et al. (2001) put forward an analytic model to calculate the stress and pore pressure near the main crack plane and predicted the micro-seismic events induced by natural fracture slippage in hydraulic fracturing treatment. Ren et al. (2015) proposed critical net pressure conditions of tensile and shear failures for natural fractures after the intersection between hydraulic fractures and natural fractures. Based on the tensile and shear failure criteria and using effective stress, injection volume and other reservoir parameters, Maulianda et al. (2014) proposed an analytical model to predict the SRV.

Weng et al. (2011) considered natural fractures as random discrete cracks and presented an unconventional fracture model to simulate complex fracture network propagation based on pseudo-3D model. In this model, many factors incorporating interaction between hydraulic fracture and natural fractures, stress shadow effect and proppant transport were considered. However, it requires to know the actual distribution of natural fractures and cannot simulate tensile and shear failure phenomena. Xu et al. (2009, 2010) proposed a wire mesh model to simulate fracture network propagation, but the impacts of shear slippage effect and fracture orientation are not taken into consideration since they assumed that the natural fractures are two sets of orthogonal and parallel fractures. Ren et al. (2016) adopted pseudo-3D model to simulate the growth of fracture network according to the actual distribution of natural fractures. Zou et al. (2016) analyzed the impacts of relevant treatment and reservoir parameters on the SRV based on discrete element method with consideration of the length and orientation distribution of natural fractures.

It has been proven that complex fracture network can be created by breaking the rock and activating the natural fractures in hydraulic fracturing of shale gas reservoir with well-developed natural fractures and high-brittle mineral content. As shown in Fig. 1a, for engineering application, a single-stage case with three cluster fractures of horizontal multistage fracturing was researched in this simulation. During the process of fluid injection, the main fractures will propagate and intersect natural fractures. Then the natural fractures are activated by shear or tensile failure, and the reservoir pressure will be elevated. Finally, the increase in reservoir pore pressure may create a failed region, which is the so-called SRV zone, as shown in Fig. 1b. In order to describe the SRV growth process, a SRV prediction model is proposed based on full tensor permeability, continuum method and fluid mass conservation equation. In this model, the actual distribution of natural fractures is simplified as two groups of conjugate fractures, and tensile/shear failure criterions are employed to determine the SRV. The model has a much higher computational efficiency than the discrete fracture method since it does not require to describe the complex natural fracture distribution. Hence, this model provides a good tool for hydraulic fracturing treatment design.

Fig. 1
figure 1

a Propagation of hydraulic fractures in shale gas reservoir; b the simplified sketch map

Full size image

Mathematical models

The reservoir pore pressure will increase sharply when fracturing fluid is injected into the formation, causing the natural fracture failure or creating new fractures, and triggering micro-seismic events. In addition, the failure of natural fractures will rapidly increase the reservoir permeability and further expand the SRV. Thus, the spatial distribution of micro-seismic cloud data is used to estimate the SRV. Accordingly, the mathematical models of simulating SRV development mainly include the fluid flow equation, the natural fracture failure criterion and permeability change model.

Rock failure criterion

Natural fractures are well developed in shale and tight gas reservoirs. For these low-permeability reservoirs, fluid injection will rapidly enhance reservoir pore pressure, which may lead to tensile and shear failure of natural fractures or generation of new cracks. During the process of fluid injection, when the minimum effective stress in one grid block reaches the tensile strength of the rock, tensile fracture occurs, and it requires:

$$ \sigma_{ 3}^{'} = - T $$
(1)

where \( \sigma_{ 3}^{'} \) is the effective stress in minimum principal direction (MPa), and T is the tensile strength (MPa). According to the Mohr–Coulomb criterion, the shear failure occurs when the shear stress acting on the fracture plane exceeds the shear strength:

$$ \tau_{\text{n}} \ge C + \left( {\sigma_{\text{n}} - P} \right)\tan \left( {\varphi_{\text{basic}} } \right) $$
(2)

where τ n is the shear stress (MPa), C is the cohesive force of natural fracture (MPa), σ n is the normal stress on natural fracture surface (MPa), P is the reservoir pressure (MPa), and φ basic is the basic friction angle (°). With the further increase in pore fluid pressure, the tensile failure occurs and the natural fractures will be fully opened when the pore pressure is greater than the normal stress on the natural fracture plane:

$$ P \ge \sigma_{\text{n}} $$
(3)

According to the two-dimensional linear elastic theory, the normal stress and shear stress acting on natural fracture surface are expressed as (Potluri et al. 2005):

$$ \sigma_{\text{n}} = \frac{{\sigma_{\text{H}} + \sigma_{\text{h}} }}{2} - \frac{{\sigma_{\text{H}} - \sigma_{\text{h}} }}{2}\cos \left( {2\theta } \right) $$
(4)
$$ \tau_{\text{n}} = \frac{{\sigma_{\text{H}} - \sigma_{\text{h}} }}{2}\sin \left( {2\theta } \right) $$
(5)

where σ H and σ h are the maximum principal stress and minimum principal stress (MPa), respectively, and θ is the angle between the maximum principal stress and the natural fractures (°).

Fracture deformation and reservoir permeability

The increase in fracture aperture resulted from shear and tensile failures has a great effect on reservoir permeability. The shear dilation effect has been verified by experiment results (Fredd et al. 2001; Zhang et al. 2013). The stimulated aperture a s caused by shear slippage is defined according to the following formula (Hossain et al. 2002):

$$ a_{\text{s}} = \frac{{\tau_{\text{n}} }}{{K_{\text{s}} }}\tan \left( {\varphi_{\text{dil}} } \right) $$
(6)

where K s is the fracture shear stiffness (MPa/m), a s is the stimulated aperture because of shear slippage (m), and φ dil is the shear dilation angle (°).

After the occurrence of tensile failure for natural fractures, the fracture normal deformation has a relationship with the fluid pressure in the crack, the normal stress acting on the fracture surface and the fracture normal stiffness. The following equation can be used to represent the fracture normal deformation (Guo and Liu 2014a, b):

$$ a_{\text{n}} = \frac{{P - \sigma_{\text{n}} }}{{K_{\text{n}} }} $$
(7)

where a n is the fracture normal deformation (m), and K n is the fracture normal stiffness (MPa/m). According to the linear elastic theory, the total fracture aperture after the shear and tensile failures for the natural fractures is expressed as:

$$ a_{\text{f}} = a_{0} + a_{\text{n}} + a_{\text{s}} = a_{0} + \frac{{P - \sigma_{\text{n}} }}{{K_{\text{n}} }} + \frac{{\tau_{\text{n}} }}{{K_{\text{s}} }}\tan \left( {\varphi_{\text{dil}} } \right) $$
(8)

where a f and a 0 are the total natural fracture aperture and initial natural fracture aperture (m), respectively. The aperture of newly generated fracture that is perpendicular to the minimum principal stress direction is given by the following expression:

$$ a_{\text{f}} = \frac{{P - \sigma_{ \hbox{min} } }}{{K_{\text{n}} }} $$
(9)

The fracture permeability can be obtained by the cubic law, which is defined as:

$$ K_{\text{fl}} = \frac{{a_{\text{f}}^{3} }}{{12S_{\text{f}} }} $$
(10)

where S f is the fracture spacing (m), and K fl is the fracture permeability in the local coordinate system (µm2).

Some large-scale fractures are well developed in shale reservoirs and there always exists a certain angle between these fractures and the principal stress direction; the fracture permeability in Eq. 10 is calculated in a local coordinate system. Therefore, it is necessary to rotate the fracture permeability in the local coordinate system (see Fig. 2a) to the global coordinate system in the reservoir (see Fig. 2b). By rotating the local coordinate system x l−o−y l based on original point o to the global coordinate system x g−o−y g. The fracture permeability tensor in the global coordinate system is obtained and given by (Fanchi 2008):

$$ \underline{\underline{K}} = \left( {\begin{array}{*{20}c} {Kxx} & {Kxy} \\ {Kyx} & {Kyy} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {Kx\cos^{2} \alpha + Ky\sin^{2} \alpha } & {\left( {Kx - Ky} \right)\sin \alpha \;{ \cos }\;\alpha } \\ {\left( {Kx - Ky} \right)\sin \alpha \;{ \cos }\;\alpha } & {Kx\sin^{2} \alpha + Ky\cos^{2} \alpha } \\ \end{array} } \right) $$
(11)

where \( \underline{\underline{K}}\) is the fracture permeability tensor (µm2), K xx and K yy are the permeability in the x- and y-directions in the global coordinate system (µm2), K xy and K yx are the permeability in fracture direction in the global coordinate system (µm2), K x and K y are the permeability in the x- and y-directions in the local coordinate system (µm2), and α denotes the angle of clockwise rotation direction (°).

Fig. 2
figure 2

a Fracture permeability in the local coordinate system; b rotating the local coordinate system to the global coordinate system

Full size image

Fluid flow equation

It is known that the dual continuum model and discrete fracture model are commonly used for flow simulation in naturally fractured reservoir. Although the discrete fracture model can accurately describe the flow in the natural fracture, the computational efficiency is really low for the shale reservoir with large well-developed natural fractures. For simplification, the equivalent single porosity model can be adopted to represent double porosity model to simulate fluid flow in shale reservoirs (Nassir et al. 2012) when the density of natural fracture is sufficiently high. Hence, the mass conservation equation for single-phase compressible fluid is written as:

$$ \frac{\partial }{\partial x}\left( {\frac{{K_{\text{xx}} }}{\mu B}\left( {\frac{\partial P}{\partial x}} \right)} \right) + \frac{\partial }{\partial x}\left( {\frac{{K_{\text{xy}} }}{\mu B}\left( {\frac{\partial P}{\partial y}} \right)} \right) + \frac{\partial }{\partial y}\left( {\frac{{K_{\text{yx}} }}{\mu B}\left( {\frac{\partial P}{\partial x}} \right)} \right) + \frac{\partial }{\partial y}\left( {\frac{{K_{\text{yy}} }}{\mu B}\left( {\frac{\partial P}{\partial y}} \right)} \right) + q = \frac{\partial }{\partial t}\left( {\frac{\varphi }{B}} \right) $$
(12)

where φ is the reservoir porosity (dimensionless), q is the injection fluid volume per unit reservoir volume and time (s −1), μ is the fluid viscosity (mPa s), and B is the fracturing fluid volume coefficient (dimensionless).

For the compressible liquid, the expression of formation volume coefficient is defined as:

$$ B = \frac{{B_{{^{0} }} }}{{\left[ {1 + C_{\text{l}} \left( {P - P_{\text{i}} } \right)} \right]}} $$
(13)

where C l is the fluid compression coefficient (MPa−1), B 0 is the fluid volume coefficient under the reference pressure (dimensionless), and P i is the initial reservoir pressure (MPa).

The relationship between rock porosity and reservoir pressure is given by:

$$ \varphi = \varphi_{{^{0} }} \left[ {1 + C_{\text{r}} \left( {P - P_{\text{i}} } \right)} \right] $$
(14)

where C r is the rock compressibility (MPa−1), and φ 0 is the initial reservoir porosity (dimensionless).

Initial condition:

$$ P\left( {x,y,t} \right)\left| {_{t = 0} } \right. = P_{\text{i}} $$
(15)

Boundary condition:

$$ \frac{\partial P}{\partial x}\left| {_{x = 0} } \right. = 0,\quad \frac{\partial P}{\partial y}\left| {_{y = 0} } \right. = 0 $$
(16)
$$ \frac{\partial P}{\partial x}\left| {_{{x = X_{\text{e}} }} } \right. = 0,\quad \frac{\partial P}{\partial y}\left| {_{{y = Y_{\text{e}} }} } \right. = 0 $$
(17)

where X e and Y e are the length and width of the simulation element (m), respectively.

Numerical model and solution

Simulation of the SRV growth mainly needs to solve fluid continuity equation. In this paper, the finite difference method is used to discretize the continuity Eq. 12, and a nine diagonal finite difference equation is obtained and expressed in Eq. 18. Firstly, the pore pressure for all grid blocks are obtained by iterative solution of the discrete numerical model, and then shear failure and tensile failure criteria are used to judge whether any type of failure occurs. If the shear or tensile failure criterion is observed in any grid block, the fracture deformation and reservoir permeability are calculated according to Eqs. 6–11, and the permeability tensor in flow equation are updated. If the total simulation time is not finished, the time step is repeated. Finally, the failed rock volume is calculated to estimate the SRV.

$$ \begin{aligned} & {\text{SW}}_{ij} P_{i - 1j - 1}^{n + 1} + {\text{SS}}_{ij} P_{ij - 1}^{n + 1} + {\text{SE}}_{ij} P_{i + 1j - 1}^{n + 1} + {\text{WW}}_{ij} P_{i - 1j}^{n + 1} + {\text{CC}}_{ij} P_{ij}^{n + 1} \\ & \quad + {\text{EE}}_{ij} P_{i + 1j}^{n + 1} + {\text{NW}}_{ij} P_{i - 1j + 1}^{n + 1} + {\text{NN}}_{ij} P_{ij + 1}^{n + 1} + {\text{NE}}_{ij} P_{i + 1j + 1}^{n + 1} = Q_{ij} \\ \end{aligned} $$
(18)

In Eq. 18, SW, SS, SE, WW, CC, EE, NW, NN and NE are the transmissibility terms, which are defined from Eqs. 19 to 27. Q is the difference between the accumulation term and the sink or source term, which is defined in Eq. 28. Subscripts i and j indicate grid block number in the x- and y-directions, respectively.

Where

$$ {\text{SW}}_{ij} = \alpha_{xy} \left[ {\left( {\frac{{K_{yx} }}{\mu B}} \right)_{i,j - 1} + \left( {\frac{{K_{xy} }}{\mu B}} \right)_{i - 1,j} } \right] $$
(19)
$$ {\text{SS}}_{ij} = \alpha_{y1} \left( {\frac{{K_{yy} }}{\mu B}} \right)_{i,j - 1/2} $$
(20)
$$ {\text{SE}}_{ij} = - \alpha_{xy} \left[ {\left( {\frac{{K_{xy} }}{\mu B}} \right)_{i + 1,j} + \left( {\frac{{K_{yx} }}{\mu B}} \right)_{i,j - 1} } \right] $$
(21)
$$ {\text{WW}}_{ij} = \alpha_{x1} \left( {\frac{{K_{xx} }}{\mu B}} \right)_{i - 1/2,j} $$
(22)
$$ {\text{CC}}_{ij} = - \frac{{\phi C_{l} }}{{\Delta tB^{0} }} - \alpha_{x2} \left( {\frac{{K_{xx} }}{\mu B}} \right)_{i + 1/2,j} - \alpha_{x1} \left( {\frac{{K_{xx} }}{\mu B}} \right)_{i - 1/2,j} - \alpha_{y2} \left( {\frac{{K_{yy} }}{\mu B}} \right)_{i,j + 1/2} - \alpha_{y1} \left( {\frac{{K_{yy} }}{\mu B}} \right)_{i,j - 1/2} $$
(23)
$$ {\text{NW}}_{ij} = - \alpha_{xy} \left[ {\left( {\frac{{K_{xy} }}{\mu B}} \right)_{i - 1,j} + \left( {\frac{{K_{yx} }}{\mu B}} \right)_{i,j + 1} } \right] $$
(24)
$$ {\text{EE}}_{ij} = \alpha_{x2} \left( {\frac{{K_{xx} }}{\mu B}} \right)_{i + 1/2,j} $$
(25)
$$ {\text{NE}}_{ij} = \alpha_{xy} \left[ {\left( {\frac{{K_{xy} }}{\mu B}} \right)_{i + 1,j} + \left( {\frac{{K_{yx} }}{\mu B}} \right)_{i,j + 1} } \right] $$
(26)
$$ {\text{NN}}_{ij} = \alpha_{y2} \left( {\frac{{K_{yy} }}{\mu B}} \right)_{i,j + 1/2} $$
(27)
$$ Q_{ij} = - \left( {\frac{{\varphi C_{\text{l}} }}{{\Delta tB_{{^{0} }} }}} \right)P_{i,j}^{n} - q $$
(28)
$$ \alpha_{xy} = \frac{1}{{\left( {\Delta y_{j - 1/2} + \Delta y_{j + 1/2} } \right)\left( {\Delta x_{i - 1/2} + \Delta x_{i + 1/2} } \right)}} $$
(29)
$$ \alpha_{x1} = \frac{1}{{\Delta x_{i} \Delta x_{i - 1/2} }} $$
(30)
$$ \alpha_{x2} = \frac{1}{{\Delta x_{i} \Delta x_{i + 1/2} }} $$
(31)
$$ \alpha_{y1} = \frac{1}{{\Delta y_{j} \Delta y_{j - 1/2} }} $$
(32)
$$ \alpha_{y2} = \frac{1}{{\Delta y_{j} \Delta y_{j + 1/2} }} $$
(33)

where Δx and Δy are the grid sizes in the x- and y-directions (m), respectively; Δt is the time step (s). Superscript n + 1 and n denote the next time step and current time step, respectively.

Case studies

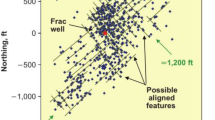
In order to apply this model to predict SRV, the micro-seismic monitoring data are adopted to calibrate the new model by adjusting the permeability in the x- and y-directions. As shown in Fig. 3, the shape and size of the predicted SRV are almost identical to the field micro-seismic cloud data. Therefore, this model can be used to simulate the SRV development in this area.

Fig. 3
figure 3

Simulation of SRV distribution and micro-seismic monitoring map

Full size image

Basic case

As shown in Fig. 1b, we select one stage of the horizontal multistage fracturing as an example. The length, width and height dimensions are 500 m × 200 m × 100 m for this representative segment, respectively. The block size for each grid is 10 m × 5 m × 100 m in this simulation, corresponding to length, width and height, respectively, and a local grid refinement of 5 × 1 × 1 is employed to describe the hydraulic fracture. The total number of grid blocks is 1450. Basic reservoir and treatment parameters are given in Table 1.

Table 1 Basic reservoir and treatment parameters used in this simulation
Full size table

The reservoir pore pressure distribution (see Fig. 4a) and the permeability enhancement distribution (see Fig. 4b–d) are displayed in Fig. 4. The figures show that the pore pressure in the SRV is far greater than the initial pore pressure and the minimum principal stress. It seems that the SRV grows much faster in the y-direction. The SRV shape is similar to an ellipse with a final approximate length of 360 m and width of 100 m after 100 min. Usually, the normal stress on the natural fracture surface is larger than the minimum principal stress. So the permeability of K y is much larger than that of K x and K xy because that the tensile fracture aperture controlled by minimum principal stress is far greater than that of the fracture aperture induced by natural fracture slippage or tensile failure. The variation trend of well block pressure with the injection time is presented in Fig. 5. It shows that the oscillation of well block pressure is sharp at early time and gradually becomes stable after 1 min. This is because that the tensile fracturing at injection point rapidly enhances well block permeability, resulting in sudden decrease in well block pressure. However, the well block pressure gradually builds up to force the near grid blocks to be fractured with the process of fluid injection.

Fig. 4
figure 4

Distribution of reservoir pore pressure and permeability enhancement

Full size image
Fig. 5
figure 5

Change of well block pressure for the base case with injection time

Full size image

The effect of initial reservoir pressure on SRV

Figure 6 presents the effect of reservoir pressure on SRV distribution. It can be seen that the SRV with initial reservoir pressure of 30 MPa is significantly larger than the SRV based on reservoir pressure of 20 MPa, and the SRV shape with initial reservoir pressure of 20 MPa is identical with the SRV shape with initial reservoir pressure of 30 MPa. This is because that the lower initial reservoir pressure needs more pressure increment to reach the fracture failure condition. Figure 7 shows the effect of initial reservoir pressure on the size of SRV. It is observed that the increase in SRV size is significant with the increasing initial reservoir pressure, resulting in almost 2 times of the SRV increment when increasing initial reservoir pressure from 16 to 32 MPa, and the higher the initial pore pressure is, the faster the growth rate of SRV will be. The effects of the initial reservoir pressure on the SRV length and width are illustrated in Fig. 8. It shows that both the SRV length and bandwidth increase with an increase in initial reservoir pressure, but the growth rate of SRV length is much faster than the growth rate of SRV width.

Fig. 6
figure 6

SRV distribution with initial reservoir pressure of a P i = 20 MPa and b P i = 30 MPa, respectively

Full size image
Fig. 7
figure 7

Effect of initial reservoir pressure on the SRV size

Full size image
Fig. 8
figure 8

Effect of initial reservoir pressure on the SRV length and SRV width

Full size image

The effect of injection fluid volume on SRV

Figure 9 shows the effect of injection fluid volume on the SRV size, while keeping the other parameters same as those in the base case. It shows that the SRV size increases with the injection fluid volume, which indicates that the injection fluid volume is an important factor affecting SRV size, the more the injection fluid volume is, the larger the SRV will be, and the SRV length and width also increase with the increasing injection fluid volume, as shown in Fig. 10. The SRV shape distribution with injection fluid volume of 500 and 1000 m3 is presented in Fig. 11, respectively, and it shows a similar SRV shape with injection fluid volume of 500 and 1000 m3, respectively.

Fig. 9
figure 9

Effect of injection fluid volume on the SRV size

Full size image
Fig. 10
figure 10

Effect of injection fluid volume on the SRV length and width

Full size image
Fig. 11
figure 11

SRV distribution with injection fluid volume of a V T = 500 m3 and b V T = 1000 m3, respectively

Full size image

The impact of natural fracture azimuth angle on SRV

Figure 12 shows the impact of natural fracture azimuth angle on the SRV size. It can be seen that the SRV size decreases slowly with the increasing fracture azimuth angle. However, the decrease of SRV size is rapid when the fracture azimuth angle is larger than 35°. The effect of natural fracture azimuth angle on the length and width of SRV is illustrated in Fig. 13. It shows that the SRV length increases with the increase in fracture azimuth angle, but the SRV width decreases with the increasing fracture azimuth angle. Figure 14 displays the distribution of SRV shape with the fracture azimuth angle of 30 and 50°, respectively. It can be observed that larger fracture azimuth angle makes it difficult to create a wider SRV, such as the case when the natural fracture azimuth angle is 50°. This is because that the natural fractures are more difficult to be activated and opened when the natural fracture azimuth is too large. Therefore, the natural fracture azimuth angle influences the shape of SRV significantly.

Fig. 12
figure 12

Impact of natural fracture azimuth angle on the SRV size

Full size image
Fig. 13
figure 13

Effect of natural fracture azimuth angle on the SRV length and width

Full size image
Fig. 14
figure 14

SRV distribution with natural fracture azimuth angle of a θ = 30° and b θ = 50°, respectively

Full size image

The impact of horizontal principal stress difference on SRV

Figure 15 presents the effect of horizontal principal stress difference on the SRV size, and the figure shows that the SRV size decreases linearly with the increasing horizontal principal stress difference. Figure 16 shows the impact of horizontal principal stress difference on the SRV length and width. The SRV length increases with an increase in horizontal principal stress difference. However, the SRV width decreases with the increasing principal stress difference. Figure 17 illustrates the effect of principal stress difference on SRV size when the natural fracture azimuth angle is 70°. The results indicate that high approaching angle but with low principal stress difference can still create a larger SRV. However, the SRV size decreases rapidly with the increase in horizontal principal stress difference, and there is no SRV when the principal stress difference increases to 6 MPa. Figure 18 shows the SRV distribution with principal stress difference of 1 MPa and of 3 MPa, respectively. The actual distribution of SRV proves that decreasing the principal stress difference will broaden the SRV width. Therefore, the principal stress difference is the key factor influencing the SRV.

Fig. 15
figure 15

Effect of horizontal principal stress difference on the SRV size (θ = 40°)

Full size image
Fig. 16
figure 16

Effect of horizontal principal stress difference on the SRV length and width

Full size image
Fig. 17
figure 17

Effect of horizontal principal stress difference on the SRV size (θ = 70°)

Full size image
Fig. 18
figure 18

SRV distribution with horizontal principal stress difference of a Δσ = 1 MPa and b Δσ = 3 MPa, respectively

Full size image

Conclusion

In this paper, a mathematical model for prediction of SRV in hydraulic fracturing shale reservoir is proposed based on the fluid diffusivity equation, the tensile and shear failure criteria. The model can simulate the SRV growth and permeability enhancement region with consideration of the natural fracture azimuth angle, fracture deformation and permeability variation. After calibration of the model with the field micro-seismic data, a sensitivity study is performed to analyze the initial pore pressure, the horizontal stress difference, the total injection fluid volume and natural fracture azimuth angle on the SRV length, SRV width, SRV shape and SRV size. The following conclusions can be made:

  1. 1.

    During the process of hydraulic fracturing in shale gas reservoirs, the reservoir pressure will rapidly elevate with high pumping rate, which may result in tensile failure and shear slippage of natural fractures, triggering the micro-seismic events. The SRV zone is developed into an enhanced permeability region or a failed reservoir zone.

  2. 2.

    Both the initial reservoir pressure and injection fluid volume have great impact on the SRV size. The SRV size, SRV length and width increases with the increase in injection fluid volume and initial reservoir pressure. They have similarity in SRV shape for different initial reservoir pressure and injection fluid volume.

  3. 3.

    The natural fracture azimuth angle has a great effect on the shape of SRV. The SRV size and width decrease with the increase in natural fracture azimuth angle, but the SRV length increases with the increasing fracture azimuth angle. Perhaps, the SRV cannot be created for the case of high fracture azimuth angle, but the case of high fracture azimuth angle with low principal stress difference can still create a larger SRV.

  4. 4.

    The SRV decreases with the increase in principal stress difference. The SRV width becomes narrower, but the SRV length becomes longer as the principal stress difference increases. The SRV shape is significantly influenced by the horizontal principal stress difference, and no SRV is created with the case of high principal stress difference.