Introduction

Recently, shale gas development in the United States has achieved great success by drilling a horizontal well and multistage hydraulic fracturing. The hydraulic fracture geometries in shale gas reservoirs are more likely to be complex fracture network rather than a single-plane fracture, as demonstrated by microseismic monitoring. Fluid injection may induce microseismic events due to natural fracture failure or new crack generation in naturally fractured reservoirs. Hence, the spatial distribution of microseismic clouds is used to estimate the stimulated reservoir volume (SRV). Figure 1 shows a microseismic monitoring map of Barnett shale with slickwater fracturing treatment in which the dots denote the occurrence of rock failure. The results showed that complex fracture network was developed in hydraulic fracturing of shale gas reservoirs. Moreover, an obvious positive relationship existed between the SRV and shale gas production performance (Mayerhofer et al. 2010). Therefore, the SRV is considered as an important optimization parameter for hydraulic fracturing in ultralow permeability reservoirs, such as shale and tight gas reservoirs. Prediction of SRV according to different treatment and reservoir parameters has become a critical step for optimizing the design of fracture treatment.

Fig. 1
figure 1

Microseismic monitoring map for Barnett shale (Cipolla 2009)

Full size image

At present, various mathematical models have been presented to simulate the complex fracture network growth (Zhang et al. 2014). Using a set of governing equations including fracture deformation, fluid flow, and proppant transport, the UFM model (Weng et al. 2011) could simulate complex fracture network propagation with discrete preexisting natural fractures. Xu et al. (2009, 2010) assumed that the natural fractures were two groups of parallel and orthogonal fractures and developed a wire-mesh model to approximate network fracture. Nagel et al. (2013) proposed the discrete element model to evaluate the effects of relative mechanical parameters on hydraulic fracturing of shale reservoirs. Roman Meyer and Bazan (2011) proposed a discrete fracture network model similar to the wire-mesh model to extend the orthogonal fracture network. Dahi-Taleghani and Olson (2011) used the extended finite element method to simulate the interaction between natural and hydraulic fractures. This achievement promoted the research on SRV, but it was a pity that they did not take the shear failure into account. Taleghani and Olson (Taleghani 2011) analyzed the induced stress at the tip of the extended hydraulic fracture using the XFEM method and revealed that tensile and shear stresses might lead to tensile or shear failure of cemented natural fractures, thus affecting the propagation path of hydraulic fractures. Tensile and shear failures have great influence on SRV and cannot be ignored.

Ge and Ghassemi (2012) calculated the shear stimulation volume using the Mohr–Coulomb criterion. Palmer et al. (2009) considered that the microseismic phenomenon was caused by shear failure of natural fractures and that the SRV contained the main fracture, tensile failure region, and shear failure region and presented an analytical model to evaluate the extent of shear failure region. The model established by Ge and Ghassemi (2012) and Palmer et al. (2009) were analytical models. Hence, many assumptions were introduced, causing deviation from the real situation.

In terms of numerical models, Palmer et al. (2013) developed a geomechanical model to predict the shear failure extent of a fractured well and obtained injection permeability and porosity of the stimulation zone by fitting the microseismic cloud data. This mathematical model ignored the tensile failure of the rocks. Shahid et al. (2015), Nassir et al. (2014), and Ghassemi et al. (2013) considered the influence of tensile failure in their studies based on the studies by Palmer et al. (2013). Shahid et al. (2015) put forward a coupled fluid flow and geomechanical model to simulate the reactivation of natural fractures and induced microseismic phenomena in hydraulic fracturing of shale gas reservoirs based on the continuum approach. Nassir et al. (2014) established a fully coupled fluid flow and geomechanical model to describe SRV development on the basis of tensile/shear failure principle and pseudo-continuum method. Ghassemi et al. (2013) built a three-dimensional (3D) poroelastic model to study the distribution of stress field and pore pressure around a stationary hydraulic fracture and predicted the shear and tensile failure zone. They analyzed the effects of horizontal stress, initial pore pressure, and rock cohesion on the permeability enhancement region. Coupled with the impacts of in situ stresses, poroelastic stress, and induced stress, Shahid (Shahid et al. 2015) and Ghassemi (Ghassemi et al. 2013) assumed that the main fracture did not propagate, which was quite different from the actual situation.

In addition, scholars have done a lot of meaningful work. Rutqvist et al. [v] conducted a numerical simulation analysis to evaluate the potential fault reactivation and induced microseismic phenomenon during hydraulic fracturing of shale gas reservoirs using the coupled thermo–hydro–mechanical simulator. Kim and Moridis (2015) performed a numerical analysis of the impacts of initial saturation, Young’s modulus, and injection rate on induced tensile fracture propagation for shale gas reservoirs. Ji et al. (2009) treated the hydraulic fracture as a highly permeable zone in the reservoir and proposed a fully coupled fluid–solid model to simulate the dynamic fracture extension by modifying the grid transmissibility and porosity. Adjusting the diffusivity coefficient and combining with the microseismic monitoring data, Yu and Aguilera (2012) used a 3D pressure diffusivity equation to simulate the SRV growth. Warpinski et al. (2001) put forward an analytical model to calculate the stress and pore pressure distribution around a hydraulic fracture and predicted the induced microseismic events during hydraulic fracturing operation on the basis of natural fracture slippage criterion.

This study was novel in presenting a new mathematical model to simulate the growth of SRV based on the shear slippage and tensile failure criterion of natural fractures, combination of main fracture propagation model, fluid flow equation, and reservoir permeability variation model. The model solved the governing equations of dynamic hydraulic fracture extension and reservoir fluid flow equation in a coupled manner to obtain reservoir pore pressure distribution. Then, the tensile and shear failure zones were determined according to the natural fracture failure criterion and pore pressure field. Finally, a sensitivity analysis was performed to study the impacts of injection fluid viscosity, natural fracture azimuth, and horizontal stress difference on different stimulation volumes. Therefore, the new model had important theoretical and practical engineering applications for predicting SRV and optimizing related treatment parameters.

SRV model

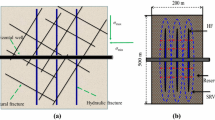
As for tight oil and gas reservoirs with well-developed natural fractures, such as shale and tight gas reservoirs, natural fractures may be activated when hydraulic fractures intersect natural fractures during the process of hydraulic fracturing in shale gas reservoirs. Then, fracturing fluid flows into the natural fracture system and the reservoir pore pressure is elevated. When the shear stress on the natural fracture surface exceeds the shear strength, shear slippage occurs on the natural fracture surface. With a further increase in the fluid pressure, the fluid pressure exceeds the normal stress on the natural fracture surface. Then, tensile failure is induced and natural fracture is completely opened. As shown in Fig. 2, three regions may co-exist for each of the natural fractures:

Fig. 2
figure 2

Different stimulation regions due to the intersection of hydraulic fracture and natural fractures

Full size image

Part 1: Natural fracture in this part is completely open in which two kinds of failure mechanisms, including shear and tensile failures of natural fractures, have been induced, and the pore pressure is larger than the normal stress. This part can be filled with a small quantity of proppants to produce higher-conductivity propped fracture.

Part 2: This is a pure shear slip part in which only shear failure has occurred and the fluid pressure is higher than the original pore pressure but less than the normal stress of the fracture surface.

Part 3: This is the swept part, where the natural fracture did not cause shear and tensile failure. However, the fluid pressure exceeds the original reservoir pore pressure.

Therefore, based on the aforementioned analysis, three different stimulation regions, including the swept region, shear failure zone, and tensile zone, can be distinguished for a hydraulically fractured well in the reservoir, similar to the conclusions drawn by Kresse and Weng (2013). The irreversible permeability enhancement region exists in the two parts of shear and tensile failure zones due to fracture shear slip. Therefore, the two parts are the effective stimulation zones after fracturing fluid flowback, while the swept region area may be invalid stimulation region outside the shear slippage zone. As shown in Fig. 3, the stimulated volume has the following formula for the three regions:

Fig. 3
figure 3

Sketch map of different stimulation regions for naturally fractured reservoirs

Full size image
$${V_{{\text{sb}}}} \geq {V_{{\text{ss}}}} \geq {V_{{\text{st}}}}$$
(1)

where Vsb, Vss, and Vst represent the total stimulation volume (104 m3), shear stimulation volume (104 m3), and tensile stimulation volume (104 m3), respectively. Lsb, Lss, and Lst denote the total SRV length (m), shear zone length of SRV (m), and tensile zone length of SRV, respectively. Wsb, Wss, and Wst represent the swept region bandwidth of SRV (m), the shear bandwidth of SRV (m), and the tensile region bandwidth of SRV (m), respectively.

Hydraulic fracture propagation model

When natural fractures are activated by the hydraulic fracture in a tight reservoir, part of the injection fluid is used to expand the hydraulic fracture volume. However, most of them leak into natural fractures, and the fluid continuity equation in the hydraulic fracture (Chong et al. 2014) is given by:

$$\frac{\partial }{{\partial s}}\left( {\frac{{{W_{\text{f}}}^{3}H}}{{12\mu }}\frac{{\partial {P_{\text{f}}}}}{{\partial s}}} \right)={q_{\text{L}}}+H\frac{{\partial {W_{\text{f}}}}}{{\partial t}}$$
(2)

The pumping rate is constant at the injection point of the wellbore, expressed as:

$$- \frac{{{W_{\text{f}}}^{3}}}{{12\mu }}\left( {\frac{{\partial {P_{\text{f}}}}}{{\partial n}}} \right)={Q_0}$$
(3)

At the tip of the hydraulic fracture, the following boundary condition is met:

$$- \frac{{{W_{\text{f}}}^{3}}}{{12\mu }}\left( {\frac{{\partial {P_{\text{f}}}}}{{\partial n}}} \right)=0$$
(4)

where qL is the fracturing fluid leak-off volume per unit length of the fracture, m2/s; Q0 is the pumping rate, m3/s; H is the fracture height, m; Wf is the fracture width, m; µ is the fracturing fluid viscosity, mPa s; and Pf is the fluid pressure in the hydraulic fracture, MPa.

If the natural fractures are activated, the fluid leaks into the natural fracture system because of the pressure difference between the hydraulic and natural fractures. Assuming that fluid permeates into the natural fracture system perpendicularly and linearly, the leak-off volume according to Darcy’s law can be expressed (Shahid et al. 2015) as:

$${q_{\text{L}}}=2Hv\left( {s,t} \right)=2H\frac{{{K_{\text{f}}}}}{\mu }\frac{{\partial {P_{\text{f}}}}}{{\partial n}}\left| {_{\Gamma }} \right.$$
(5)

where v (s,t) is the fluid flow rate, m/s; Kf is the natural fracture permeability, µm2; and Γ denotes the boundary of hydraulic fracture and natural fracture. The global volume balance equation is presented as follows:

$$\int\limits_{0}^{t} {{Q_{\text{T}}}(t)} {\text{d}}t=\sum\limits_{{i=1}}^{N} {\int\limits_{{ - \frac{{L(t)}}{2}}}^{{\frac{{L(t)}}{2}}} {H\overline {W} } } {\text{d}}s+\sum\limits_{{i=1}}^{N} {\int\limits_{{ - \frac{{L(t)}}{2}}}^{{\frac{{L(t)}}{2}}} {\int\limits_{0}^{t} {{q_{\text{L}}}} {\text{d}}t} } {\text{d}}s$$
(6)

where QT(t) is the total pumping rate, m3/s; L(t) represents the total length of hydraulic fracture at time t, m; and N is the number of perforation cluster, dimensionless.

Fluid flow equation

If the natural fractures are activated, fracturing fluid flows into the natural fractures and elevates the reservoir pore pressure. The continuum approach and equivalent single-porosity model were used to treat the tight reservoir with well-developed natural fracture so as to grasp the SRV distribution from a global perspective (Guo and Liu 2014). The mass conservation equation for single-phase compressible fluid in the naturally fractured reservoir is given as:

$$\nabla \left[ {\frac{{H{K_f}}}{{\mu B}}\nabla P} \right]+q=H\frac{\partial }{{\partial t}}\left( {\frac{\phi }{B}} \right)$$
(7)

Initial condition:

$$P\left( {x,y} \right)\left| {_{{t=0}}} \right.={P_{\text{s}}}$$
(8)

Boundary conditions:

$$\frac{{\partial P}}{{\partial x}}\left| {_{{x= \pm \frac{L}{2}}}} \right.=0$$
(9)
$$\frac{{\partial P}}{{\partial y}}\left| {_{{y= \pm \frac{W}{2}}}} \right.=0$$
(10)

where Cl and Cr are the liquid compression coefficient and rock compressibility, respectively, MPa−1; P is the reservoir pore pressure, MPa; φ is the reservoir porosity, dimensionless; B is the fracturing fluid volume coefficient, dimensionless; Ps is the original reservoir pressure, MPa; and L and W are the length and width of the unit model.

Mechanical conditions of shear slip and tensile failure of natural fractures

Natural fractures may be activated because of the intersection of the main fracture and natural fractures during the process of hydraulic fracturing in shale gas reservoirs. Therefore, the fluid pressure inside the natural fracture is increased to cause tensile failure or shear slippage owing to the fracturing fluid leak-off effect (Nassir et al. 2012), finally triggering microseismic events (Nassir et al. 2014). Based on the Mohr–Coulomb criterion, shear slippage occurs when the shear stress on the natural fracture surface exceeds the shear strength:

$${\tau _{\text{n}}} \geq {\tau _{\text{o}}}+({\sigma _{\text{n}}} - P)\tan \left( {{\varphi _{\text{f}}}} \right)$$
(11)

where τo is the cohesive force of natural fracture (MPa), τn is the shear stress on the natural fracture surface (MPa), σeff is the effective stress (MPa), and φf is the basic friction angle of natural fracture surface (°). Meanwhile, the fluid pressure inside the natural fracture should be lower than the normal stress applied on the natural fracture surface; otherwise, the fracture will open.

With a further increase in the pore fluid pressure, tensile failure occurs when the pore pressure is higher than the normal stress of the natural fracture surface:

$$P \geq {\sigma _{\text{n}}}+T$$
(12)

where σn is the normal stress on natural fracture surface (MPa) and P is the pore pressure in the reservoir (MPa).

Let the horizontal maximum principal stress and horizontal minimum principal stress be σH and σh, respectively, and the angle between the horizontal maximum principal stress and natural fractures be θ. According to the two-dimensional (2D) linear elastic theory, normal stress and shear stress of natural fracture or weak surface can be expressed as:

$${\sigma _{\text{n}}}=\frac{{{\sigma _{\text{H}}}+{\sigma _{\text{h}}}}}{2} - \frac{{{\sigma _{\text{H}}} - {\sigma _{\text{h}}}}}{2}\cos \left( {2\theta } \right)$$
(13)
$${\tau _{\text{n}}}=\frac{{{\sigma _{\text{H}}} - {\sigma _{\text{h}}}}}{2}\sin \left( {2\theta } \right)$$
(14)

The pore fluid pressure at the intersection point of the hydraulic fracture and natural fractures is expressed as:

$$P={\sigma _{\text{h}}}+{P_{{\text{net}}}}$$
(15)

where Pnet is the net pressure of hydraulic fracture, MPa. Substituting Eqs. (13), (14), and (15) into (11), the net pressure needed for the hydraulic fracture to activate natural fractures with shear failure can be obtained after the intersection of hydraulic and natural fractures.

$${P_{{\text{net}}}} \geq \frac{{{\tau _o}}}{{\tan ({\varphi _{{\text{basic}}}})}}+\frac{{{\sigma _{\text{H}}} - {\sigma _{\text{h}}}}}{2}\left[ {1 - \sin \left( {2\theta } \right)/\tan ({\varphi _{{\text{basic}}}}) - \cos \left( {2\theta } \right)} \right]$$
(16)

Similarly, substituting Eqs. (13) and (15) into Eq. (12), the net pressure condition for the tensile activation of natural fractures must be satisfied:

$${P_{{\text{net}}}} \geq \frac{{{\sigma _H} - {\sigma _h}}}{2}\left[ {1 - \cos \left( {2\theta } \right)} \right]{\text{+}}T$$
(17)

According to the aforementioned formulas and the basic parameters shown in Table 1, the net pressure for hydraulic fracture to activate the natural fractures and breakdown pressure of the natural fractures with different fracture azimuth angles were calculated. Figure 4 shows the minimum net pressure required to activate natural fractures with the variation in the azimuth angle and principal stress contrast. It shows that the minimum net pressure required for natural fractures to be activated with shear failure pattern first decreased and then increased with the azimuth angle. However, the net pressure required for the tensile activation of natural fractures always increased with the increase in the azimuth angle. The net pressure needed to open the natural fracture always increased with the increase in the principal stress difference. The net pressure for shear activation of natural fractures decreased with the increase in the principal stress difference when the azimuth angle was less than 60°, but increased with the principal stress difference when the azimuth angle was larger than 60°. The negative net pressure values indicate that natural fractures were activated when the hydraulic fracture intersected natural fractures with the natural fracture azimuth angle within the range of 10°–50° and the stress difference 6 and 9 MPa. Figure 5 shows the relationship between the failure pressure and the azimuth angle and the principal stress difference. It shows that the variation trend in failure pressure was similar to the net pressure, as illustrated in Fig. 4.

Table 1 Basic reservoir and treatment parameters used in this simulation
Full size table
Fig. 4
figure 4

Minimum net pressure required for natural fractures to be activated with the variation in the azimuth angle and principal stress

Full size image
Fig. 5
figure 5

Effects of natural fracture azimuth angle and stress deviator on shear and tensile failure pressure

Full size image

Reservoir permeability in the process of fluid injection

The shear and tensile failure of natural fractures result in a dramatic change in the reservoir permeability, mainly because of the change in the natural fracture aperture, including shear dilation aperture caused by shear slippage and the normal aperture change due to tensile failure (Hossain et al. 2002). As shown in Fig. 6, after the occurrence of a shear failure of natural fractures, the permanent fracture aperture increment due to shear slip greatly improved the fracture permeability. If a tensile failure occurs on the natural fracture surface and natural fractures are completely open, the natural fracture permeability can be further enhanced.

Fig. 6
figure 6

Schematic diagram of natural fracture shear failure [Palmer (Taleghani 2011)]

Full size image

According to the linear elastic theory, the shear displacement of natural fracture is directly proportional to the effective shear stress, and is expressed as:

$${U_{\text{s}}}=\frac{{\Delta \tau }}{{{K_{\text{s}}}}}$$
(18)

The effective shear stress, Δτ, is defined as:

$$\Delta \tau ={\tau _{\text{n}}} - {\sigma _{{\text{eff}}}}\tan \left( {{\varphi _{\text{f}}}+\varphi _{{\text{e}}}^{{{\text{eff}}}}} \right)$$
(19)

where \(\varphi _{{\text{e}}}^{{{\text{eff}}}}\) is the effective shear dilation angle, which characterizes the fracture surface roughness and is equal to the fracture roughness coefficient:

$$\varphi _{{\text{e}}}^{{{\text{eff}}}}=\frac{{{\varphi _{\text{e}}}}}{{1+9{\sigma _{{\text{eff}}}}/{\sigma _{{\text{nref}}}}}}$$
(20)

where σnref is the normal stress that causes a decrease in the fracture width by 90%. Φe is the dilation angle for laboratory measurement. When the pore fluid pressure in natural fractures is increased to be larger than the normal stress acting on the fracture surface, natural fractures will fully open because of fracture tensile failure. Then, the shear stress is totally used for shear slippage of the natural fracture surface. For the pure shear slippage region, the fracture aperture consists of the shear dilation aperture and the original fracture aperture, which can be written as (Nassir et al. 2012):

$${W_{\text{f}}}={W_{f0}}+\frac{{\Delta \tau }}{{{K_{\text{s}}}}}\tan \left( {\varphi _{{\text{e}}}^{{{\text{eff}}}}} \right)$$
(21)

The shear dilation of the natural fracture results in an increment in the fracture permeability, and the bulk permeability of the natural fracture is obtained using the cubic law:

$${K_f}=\frac{{{W_{\text{f}}}^{3}}}{{12{S_{\text{f}}}}}$$
(22)

where \({W_{{\text{f}}0}}\) is the initial natural fracture aperture, and Sf is the fracture spacing.

When the natural fractures intersect the hydraulic fracture, the natural fracture permeability at the intersection is greatly improved due to shear activation and shear dilation effect. Figure 7 presents the effects of natural fracture azimuth and horizontal stress difference on enhanced permeability caused by natural crack shear slip. It shows that natural fracture permeability first increased with the increase in the fracture azimuth angle and then decreased, and the maximum value was between 40° and 50°. It also shows that increasing the horizontal stress difference from 3 to 9 MPa resulted in a large permeability enhancement. This is because increasing the horizontal stress difference increased the possibility of natural fracture shear failure, and larger horizontal stress difference resulted in larger shear stress on natural fracture surface and a higher enhancement permeability due to shear slippage.

Fig. 7
figure 7

Effects of the horizontal principal stress difference and the natural fracture azimuth angle on shear dilation permeability

Full size image

Model solution

The numerical simulation method was used to solve the coupled governing equations of dynamic hydraulic fracture propagation and fluid flow in a reservoir because the integral mathematical model for simulation of the SRV growth process has a strong nonlinear characteristic. The filtration volume was used as the connection point for the solution of fracture propagation and reservoir fluid flow coupling. This method was used to the continuity equation of fracture propagation (Eq. 2) and the continuity equation of reservoir fluid flow (Eq. 7) containing solving variables of each other. In addition, the SRV mathematical model had strong nonlinear characteristics. Therefore, numerical simulation was used to solve the coupled fracture propagation and reservoir fluid flow equations, and an iterative method was adopted in every time step until the convergence condition was satisfied. The detailed iterative steps were as follows: (1) Obtain the initial fluid pressure \({P_{\text{f}}}\), fracture length \({L_{\text{f}}}\), and fracture width \({W_{\text{f}}}\) by solving the hydraulic fracture extension model. (2) Calculate the leak-off volume \({q_{\text{L}}}\). (3) Obtain the pore pressure \(P\) of each grid block by solving the reservoir fluid flow equation iteratively. (4) Determine whether the natural fracture satisfies the criterion of tension or shear fracture, and calculate and update the reservoir permeability \({K_{\text{f}}}\) if it satisfies. (5) Take the reservoir pore pressure obtained by iteration into the leak-off volume calculation Eq. (5), and re-solve the hydraulic fracture propagation model and update the \({P_{\text{f}}}\), \({W_{\text{f}}}\), and \({L_{\text{f}}}\). (6) Judge whether \({L_{\text{f}}}\) and \({W_{\text{f}}}\) satisfy the convergence condition. If the convergence condition is not satisfied, proceed to the next iteration until the condition is satisfied; if the convergence condition is satisfied, then enter the next time step or finish the calculation.

Based on the aforementioned solution method, MATLAB 2016 was used to program, and the specific solution process is shown in Fig. 8.

Fig. 8
figure 8

Solution process

Full size image

Example calculation

In this study, the formation of SRV was actually due to the intersection of hydraulic and natural fractures during the propagation process. Activation of natural fractures, resulting in a large fluid leak-off into fractured reservoirs and a rise in reservoir pore pressure, led to shear or/and tensile failure of natural fractures in reservoirs. The growth simulation of SRV can be approximately equivalent to the simulation of fracture propagation considering fluid leak-off. Therefore, the simulation results of PKN fracture propagation and Wan et al. (Cheng et al. 2015) under fluid leak-off were compared with the width of a wellbore of the main fracture calculated by the model in this study (Fig. 9).

Fig. 9
figure 9

Comparison of the present model with that of PKN and Wan et al. (Cheng et al. 2015) (G = 14 GPa; \(v\) = 0.25; CL = 0.0001 m ⋅ s1/2; Q0 = 6 m3/min; H = 30 m; \({\mu _{\text{e}}}\) = 2 mPa ⋅ s;\({\sigma _{\text{h}}}\) = 46.25 MPa; \({\sigma _{\text{H}}}\) = 52.5 MPa; \({\sigma _{\text{V}}}\) = 50 MPa)

Full size image

The calculation results (Fig. 9) showed that the fracture width calculated by the mathematical model established in this study was not much different from that calculated by the PKN and Wang et al. models (Cheng et al. 2015).

Basic case

Considering one stage of the multistage fractured horizontal well as an example (Fig. 10) and assuming that the physical model is 2D, the fractured reservoir is a dual porous reservoir, and the natural fracture is a continuous medium, two groups of conjugate natural fractures were present in the reservoir. The hydraulic fracture was perpendicular to the direction of the minimum principal stress and did not consider the propagation of height direction. Fracturing fluid flow in the reservoir was 2D plane flow, and the development of SRV height was not considered. The physical model according to the assumptions is shown in Fig. 10. The length, width, and height dimensions of a single stage are 500 × 200 × 90 m3. The basic reservoir and stimulation treatment parameters are listed in Table 1.

Fig. 10
figure 10

Schematic diagram of SRV simulation element

Full size image

The model reliability calibration was performed based on the shale fracturing microseismic data. The simulated SRV shape and size were similar to the actual microseismic cloud data after adjusting several parameters related to permeability characterization (Kim and Moridis 2015) (Fig. 11). Therefore, the model worked better and could be used for predicting SRV. The SRV shape distribution was obtained after combining the failure criterion of natural fractures on the basis of the reservoir pore pressure distribution after cessation of liquid injection, as illustrated in Fig. 12. The SRV was divided into three regions, including tensile failure region, shear failure region, and swept region, from the inside to the outside, as illustrated in Fig. 13. The shape of SRV was similar to an ellipsoid with an approximate length and width of 400 and 120 m, respectively. The length of shear zone and tensile failure zone were about 360 and 200 m, respectively. Figure 14 presents the pore fluid pressure at the intersection of hydraulic fracture and natural fractures. It shows that the pore fluid pressure varied in the range from 45 to 50 MPa. However, the shear failure pressure and tensile failure pressure of the natural fracture were 44 and 47 MPa, respectively. Therefore, it could be concluded that both tensile failure zone and shear failure region existed along the natural fracture. Figure 15 shows the enhanced permeability at the intersection of hydraulic fractures and natural fractures after the natural fractures were activated. It was observed that permeability enhancement of natural fractures decreased gradually from the injection point and along the fracture propagation direction, and the tensile failure zone permeability was higher than the pure shear zone. A sharp increase in reservoir permeability occurred compared with the original permeability of natural fractures.

Fig. 11
figure 11

Predicted SRV and field microseismic monitoring map

Full size image
Fig. 12
figure 12

Reservoir pore pressure distribution

Full size image
Fig. 13
figure 13

Distribution of SRV shape

Full size image
Fig. 14
figure 14

Pore pressure distribution at the intersection point between hydraulic and natural fractures

Full size image
Fig. 15
figure 15

Natural fracture permeability at the intersection between hydraulic and natural fractures

Full size image

Effect of fluid viscosity on SRV

Three different injection fluid viscosities were considered in this sensitivity study. The injection fluid viscosity was 1, 5, and 10 mPa s, respectively. The swept volume, shear stimulation volume, tensile stimulation volume, and the corresponding SRV length and bandwidth are provided in Table 2. Increasing the injection fluid viscosity from 1 to 10 mPa s was found to reduce the SRV length, swept volume, and shear stimulation volume. However, the tensile stimulation volume and SRV width increased with the fluid viscosity. Figure 16 depicts the pore pressure distribution in this naturally fractured reservoir after fluid injection, and Fig. 17 shows the distribution of corresponding different stimulation regions with the fluid viscosity of 5 and 10 mPa s, respectively. Combining this with the base case in Fig. 13, it was seen that the tensile failure region expanded with the increase in the fluid viscosity, while the pure shear slippage zone reduced. Therefore, the injection liquid viscosity had a great impact on the shape and size of SRV. This phenomenon mainly explained that increasing the fluid viscosity could elevate the hydraulic fracture net pressure so that the natural fractures were more prone to be activated by tensile failure, in turn increasing the fluid leak-off volume. Therefore, the length of SRV decreased and the SRV width increased with the injection fluid viscosity.

Table 2 SRV size, SRV length, and bandwidth with three different injection fluid viscosities
Full size table
Fig. 16
figure 16

Reservoir pore pressure distribution for different injection fluid viscosities (from left to right are 5 mPa s and 10 mPa s, respectively)

Full size image
Fig. 17
figure 17

SRV shape distribution for different injection fluid viscosities (from left to right are 5 mPa s and10 mPa s, respectively)

Full size image

The simulation results (Table 2; Fig. 17) showed that the low-viscosity liquid was stronger than the high-viscosity liquid in activating natural fractures, and the high-viscosity liquid was stronger than the low-viscosity liquid in making main fractures. In shale gas network fracturing, the fracturing fluid system of slickwater and linear glue was mostly used. Low viscosity, low flow resistance, and strong permeability made creation of complex fracture network by slickwater easier through activating natural fractures. However, the width of the shear fracture was narrow, making the displacement of proppant and development of high conductivity under high stress difficult. High viscosity, higher flow resistance, and poor permeability made it easier for the linear glue easier to create a wide double-wing fracture, cause proppant displacement, and maintain high conductivity under high stress, but it was difficult to create complex fracture network. “Low-viscosity slickwater + high-viscosity linear glue” fracturing fluid system reduced reservoir damage and enhanced the effect of fracture network, which was consistent with the theoretical calculation results in this study.

Effect of natural fracture azimuth angle on SRV

The effects of three different fracture azimuth angles on SRV size, SRV length, and bandwidth were studied, and the results are provided in Table 3. Increasing the natural fracture azimuth angle from 30° to 50° decreased the SRV size and length, but increased the SRV width. This was because the shear failure pressure and tensile failure pressure increased on increasing the natural fracture azimuth angle from 30° to 50° as shown in Fig. 5, reducing the SRV size. As illustrated in Fig. 7, the reservoir permeability increased as the azimuth angle increased due to shear activation. In addition, the larger fracture azimuth angle caused higher fracture permeability along the SRV width direction, increasing the leak-off rate and shortening the length of the main fracture because the natural fracture azimuth β represented the angle between natural fracture and the maximum principal stress. The pore pressure distribution and corresponding SRV distribution are displayed in Figs. 18 and 19. The natural fracture azimuth was shown to have an important impact on the SRV distribution.

Table 3 Impact of natural fracture azimuth angle on the SRV size, SRV length, and bandwidth
Full size table
Fig. 18
figure 18

Pore pressure distribution for different fracture azimuth angles (from left to right are 40° and 50°, respectively)

Full size image
Fig. 19
figure 19

SRV shape distribution for different fracture azimuth angles (from left to right are 40° and 50°, respectively)

Full size image

The calculation results indicated that slip cracks were easy to form when the azimuth angle was small. With the increase in the azimuth angle, tensional cracks formed gradually, consistent with the failure pressure at different azimuth angles shown in Fig. 5. The maximum horizontal principal stress was in the direction of x-axis in this example. The smaller the azimuth angle of natural fracture, the bigger the angle between the azimuth of natural fracture and the direction of maximum principal stress, and the greater the stress on the fracture surface, making activation of natural fractures more difficult. Conversely, the stress acting on the nature fracture surface was smaller, causing the development of tensile failure fracture and formation of double-wing fracture easier.

Effect of horizontal stress difference on SRV

The effects of various horizontal stress differences on the SRV size, SRV length, and bandwidth were investigated, and the results are given in Table 4. The swept volume, shear stimulation volume, and length of SRV increased with the increase in the principal stress difference from 3 to 9 MPa. However, the tensile stimulation volume and the SRV bandwidth decreased with the increase in the principal stress difference, especially the tensile failure volume. Figures 20 and 21 show the pore pressure distribution and corresponding SRV distribution with horizontal principal stress difference of 3 and 9 MPa, respectively. The actual distribution of the SRV shape demonstrated that higher principal stress difference resulted in a longer SRV length and smaller SRV width. The pure shear failure zone greatly increased and the tensile failure zone almost reduced to zero. This mainly explained that increasing the principal stress difference decreased the shear failure pressure and increased the difference between shear breakdown and tensile breakdown pressures when the natural fracture azimuth angle was 35°, which was more prone to cause shear failure, as illustrated in Fig. 5. However, smaller principal stress difference likely induced tensile failure, and the fluid leak-off volume rate through the hydraulic fracture wall into the reservoir due to the tensile activation was greater than that due to the shear activation, increasing the SRV width and decreasing the length.

Table 4 Impact of horizontal principal stress difference on the SRV size, SRV length, and bandwidth
Full size table
Fig. 20
figure 20

Pore pressure distribution for horizontal principal stress differences (from left to right are 3 and 9 MPa, respectively)

Full size image
Fig. 21
figure 21

Distribution of SRV shape for horizontal principal stress differences (from left to right are 3 and 9 MPa, respectively)

Full size image

When the horizontal principal stress difference was small, the formation of tensional fracture was easier, while when the horizontal principal stress difference was large, the formation of slip fracture was easier (Fig. 20). Therefore, with the low horizontal principal stress difference, the fracture may cause tensile failure, causing great variation in the width of the induced fracture. It is necessary to match different sizes of proppants to achieve the matching of different grades of fractures and proppants. The occurrence of shear failure and narrow fracture was easier under a high stress difference. Therefore, small-sized proppant should be selected to reduce the risk of sand plugging and establish a high-conductivity fracture network.

Conclusions

In this study, a new SRV evaluation model was presented to simulate the growth of SRV in hydraulic fracturing of tight and shale reservoirs based on the fluid diffusivity equation, the dynamic reservoir permeability, and the tensile and shear failure criterion of the natural fractures. The tensile and shear failure volumes in SRV were determined according to the reservoir pore pressure distribution after cessation of fluid injection and the natural fracture failure criterion. A sensitivity analysis was performed to study the effects of horizontal principal stress difference and natural fracture azimuth angle on the critical net pressure required to activate the natural fractures, fracture failure pressure, and shear dilation permeability. The impacts of injection fluid viscosity, horizontal principal stress difference, and natural fracture azimuth on the SRV and stimulation region shapes were also analyzed. The following conclusions were drawn:

  1. 1.

    The induced tensile failure and shear slip of the natural fractures because of the enhancement in reservoir pore pressure caused by fluid leak-off when hydraulic fractures intersected and activated natural fractures was the essential cause of SRV generation. The stimulation region may consist of three regions, including tensile failure region, shear failure region, and swept region.

  2. 2.

    When the natural fracture azimuth angle was less than 60°, increasing the principal stress difference lowered the shear failure pressure but increased the tensile failure pressure, thereby increasing the pure shear zone but decreasing the tensile failure zone. The shear failure pressure and tensile failure pressure increased with the increase in the principal stress difference when the fracture azimuth angle was larger than 60°.

  3. 3.

    The required net pressure for tensile activation of natural fractures increased with the increase in the principal stress difference and the azimuth angle. However, the required net pressure for the shear activation of natural fractures elevated with the increase in principal stress difference and azimuth angle when the azimuth angle was larger than 60°. The natural fractures were activated by shear stress under the conditions of high principal stress difference, and the natural fracture azimuth angle was less than 60°.

  4. 4.

    The natural fracture shear slip permeability first increased and then decreased with the increase in the natural fracture azimuth angle, and the maximum value was obtained when the azimuth angle was in the range of 40°–50°. The higher principal stress difference resulted in higher shear dilation permeability.

  5. 5.

    Increasing the fluid viscosity from 1 to 10 mPa s reduced the swept region and shear slippage zone, but expanded the tensile failure region. The SRV length decreased and the SRV width increased with an increase in the fluid viscosity.

  6. 6.

    Increasing the natural fracture azimuth angle from 30° to 50° decreased the SRV size and length, but increased the SRV width. The natural fracture azimuth had an important influence on the shape of SRV.

  7. 7.

    If natural fractures were within the range of azimuth angle that was most prone to induce shear failure, then increasing the principal stress difference increased the shear stimulation volume and SRV length but decreased the tensile stimulation volume and the SRV bandwidth. The horizontal stress difference had a great impact on the SRV shape, size of shear slippage region, and tensile failure zone.