Introduction

Hydraulic interactions between surface water flow channels and their adjoining aquifers play a critical role in defining the ecological characteristics of riparian areas. During high rainfall events, the stream stage may be at a higher elevation than the water table in the connected aquifer, resulting in a pressure wave that causes the water to move from the stream into the aquifer (Serrano et al. 2007). This phenomenon, wherein water is released from the stream into the adjoining aquifer is referred to as the bank storage (Squillace 1996). The water stored in stream banks is later released back into the stream during periods of low flow, when the stream stage falls below the water table. This release of water helps maintain flows in the stream during dry periods and sustains aquatic habitat (Postel and Richter 2003). In addition, the stream storage also provides water to riparian flora, particularly phreatophytes. Brush control and management of phreatophytes are being promoted as a water conservation strategy that can help sustain in-stream flows and also increase water availability for anthropogenic uses (Wilcox 2002). Understanding stream–aquifer hydraulics is vital for successfully implementing such management endeavors (Sophocleous 2002). In addition, the movement of water between the stream and the aquifer is also important to evaluate cross migration of contaminants from the stream into the aquifer and vice versa (Chen and Chen 2003).

Despite their importance, there is seldom sufficient field data to evaluate stream–aquifer hydraulics (Todd and Mays 2005). Therefore, mathematical models play a critical role in fostering an understanding of the stream–aquifer interactions. These models can be developed at a variety of scales with varying levels of complexity. For comprehensive site-specific evaluations, fully coupled three-dimensional, spatially distributed models may be warranted (Panday and Huyakorn 2004). However, in many regulatory and management applications—time, fiscal, and logistic constraints, as well as data availability limit the application of comprehensive models. In such instances, simpler mathematical representations are better suited to obtain preliminary insights and guide engineering and management decisions. Mathematical models amenable to analytical solutions can be very useful in this regard, as they are often easier to implement and quickly provide fundamental insights (Hantush 2005). In addition, these models also serve a valuable purpose of verifying the correctness of numerical codes. Furthermore, analytical solutions can be coupled with optimization and other operations research tools to develop decision support systems for engineering design and policy planning. In recent years, analytical solutions have been applied in field settings as well (Moench and Kisiel 1970; Barlow et al. 2000; Koussis et al. 2007).

Given their advantages, there has been a significant interest in developing analytical and semi-analytical solutions for stream–aquifer interactions. Starting with the seminal work of Cooper and Rorabaugh (1963), the one-dimensional Boussinesq equation, particularly in its linearized form, is commonly used to model stream–aquifer interactions under a variety of boundary conditions and external forcings. In more recent times, Govindaraju and Koelliker (1994) provided an analytical solution for a semi-infinite aquifer wherein the stream-stage exhibits a sudden change at the start of the simulation and stays there at subsequent times. Hogarth et al. (1997) improved the solution for both constant head and time-varying cases. Workman et al. (1997) used the principle of superposition and the concept of semi-groups to develop an analytical solution for time-varying stream-stage elevations in an aquifer whose landward boundary was assumed to be at a constant head. Barlow and Moench (1998), Moench and Barlow (2000) developed several transient analytical solutions for modeling aquifer response to stream-stage and recharge variations under step-response. These step-responses can be used in conjunction with the convolution integral to obtain the aquifer response under arbitrary forcing functions if the aquifer is assumed to be a linear time-invariant system. Singh (2004) provided analytical solutions for linear and sinusoidal stage variations and their effects on a semi-infinite aquifer under no recharge and also demonstrated the use of step and instantaneous stage variations in conjunction with the superposition principle. Serrano et al. (2007) developed analytical solutions for modeling sinusoidal stream fluctuations in a finite aquifer (i.e., a no-flow landward boundary) under both linear and non-linear aquifer behavior. The hydraulics of an aquifer bounded between two canals or streams has been studied by several researchers including Mustafa (1987), Rai and Singh (1992), Ram et al. (1994), Upadhyaya and Chauhan (2001) and Wang et al. (2011). Other relevant studies of stream–aquifer interaction modeling include Gill (1985), Srivastava et al. (2006), Akylas and Koussis (2007), Kim et al. (2007), Intaraprasong and Zhan (2009), Chen et al. (2010), and Moutsopoulos (2013).

Most analytical solutions for the Boussinesq equation assume the flood wave in the stream causes sinusoidal variations in the stream or require the use of superposition to model arbitrary time-variations of the river stage. However, if the basin is ungaged, a complete temporal profile of the stream stage will not be known. This limitation makes it difficult to ascertain the suitability of assuming a sinusoidal profile or modeling arbitrary variations using unit step responses. In such instances, the stream stage variations have to be specified based on professional judgment. Standard hydrologic analyses such as the rational method and the SCS-Curve number technique can be used to obtain a preliminary estimate of maximum discharge corresponding to a rainfall event, which in conjunction with a stage-discharge technique, can be used to obtain an estimate of the maximum stage (Bedient and Huber 2005). Furthermore, linear stream-stage rises have been employed in the literature to predict the arrival of a flood wave (Naba et al. 2002; Li et al. 2008). In the same vein, a triangular temporal stage variation profile can be constructed to model the rise and fall of the stream stage and to obtain preliminary insights with respect to stream–aquifer interactions in ungaged watersheds. Such a model is also helpful in assessing the impacts of future urbanization on stream–aquifer interactions, a situation where measured data are impossible to obtain.

Despite the above-mentioned importance, analytical solutions for the Bousinnesq equation under triangular stream variations are not readily available in the literature. A direct solution is more convenient than the application of the superposition principle as it avoids the need to perform cumbersome integrations. The primary goal of this study, therefore, is to develop an analytical solution for stream–aquifer interactions under triangular stream-stage variations. The developed model is then used to study the effects of urbanization on stream–aquifer interactions in a fast-growing watershed along the US–Mexico border region.

Mathematical model

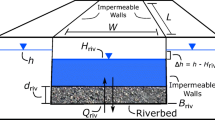
The conceptual model under consideration is depicted in Fig. 1. The major assumptions in the development of the analytical solution include the following: (1) the aquifer is homogeneous and isotropic; (2) the vertical variations of the hydraulic head are assumed to be negligible (Dupuit assumption); (3) the base of the aquifer is assumed to be horizontal and impermeable; (4) groundwater flow takes place in the horizontal plane that is normal to the stream; (5) the aquifer adjoining the stream is bounded (by a topographic high) at a finite distance from the stream; (6) the stream is either in perfect hydraulic connection with the aquifer or separated by a thin semi-permeable membrane whose thickness is negligible; and (7) there is also a net recharge (i.e., evapotranspiration—recharge) imposed on the aquifer, which is assumed to be uniform and time-invariant. These assumptions have been commonly invoked while developing analytical solutions (Barlow and Moench 1998). A detailed discussion of the modeling assumptions is presented as part of the model evaluation section.

Fig. 1
figure 1

Conceptual model of stream–aquifer interaction

Full size image

The governing equation that describes the hydraulic head in the aquifer can be obtained by substituting Darcy’s law into the conservation of mass equation as follows:

$$S_{y} \frac{\partial h}{\partial t} = \frac{\partial }{\partial x}\left( {Kh\frac{\partial h}{\partial x}} \right) + R,$$
(1)

where S y is the storage coefficient (dim), K is the horizontal hydraulic conductivity (m/days), and R is the net recharge rate (m/days). The recharge rate, R, will be negative when the evapotranspiration (ET) from the aquifer exceeds recharge due to precipitation or irrigation. Equation (1) is commonly referred to as the 1-D nonlinear Boussinesq equation. This equation is commonly linearized by assuming the product of the hydraulic head and hydraulic conductivity to be constant. The 1-D linear Boussinesq equation is written as (Govindaraju and Koelliker 1994)

$$S_{y} \frac{\partial h}{\partial t} = \frac{\partial }{\partial x}\left( {D\frac{\partial h}{\partial x}} \right) + R,$$
(2)

where D is the effective transmissivity (m2/days). The linearized version is strictly applicable for confined formations. However, it can be used to model hydraulic heads in an unconfined aquifer when the variations in the head are small relative to the thickness of the aquifer formation. For mathematical completeness, two boundary conditions and the initial hydraulic heads in the aquifer prior to the start of a simulation must be specified. The landward boundary condition and the initial conditions are specified as follows:

$$\frac{\partial h}{\partial x}(x = L,t) = 0$$
(3)
$$h(x,t = 0) = h_{o}$$
(4)

The specification of the stream-side boundary condition depends upon how the connection between the stream and the aquifer is conceptualized. If the stream and the aquifer are in perfect hydraulic connection, then the inlet boundary condition can be specified as a time-varying head boundary as follows:

$$h(x = 0,t) = H = F(t),$$
(5)

where H is the time-varying stream-stage (m) and is measured from the same datum as the water levels in the aquifer. If the stream and the aquifer are separated by a thin semi-permeable layer of thickness (Δz) and hydraulic conductivity, K s (see Fig. 1, inset), then, invoking Darcy’s law, and equating the flux on either side of the stream–aquifer boundary results in

$$- K_{s} \left( {\frac{h - H}{\Updelta z}} \right) = - K\frac{\partial h}{\partial x},$$
(6)

which is re-arranged to obtain the following expression:

$$\frac{\partial h}{\partial x} - Ch = - {\text{CH,}}$$
(7)

where the constant, C (termed conductance in this study), is the reciprocal of the streambank leakance (Barlow and Moench 1998), has the units of 1/m, and is given as

$${\text{C}} = \left( {\frac{{K_{s} }}{K\Updelta z}} \right)$$
(8)

The conductance is a measure of the hydraulic connection between the stream and the aquifer. If the conductance value is high, the stream and the adjoining aquifer are well connected. Note that when (h < H) the flux is positive (i.e., the flow is into the aquifer) and when (h > H) the flux is negative. The stream-stage, H, has the same meaning as in Eq. (5). Depending upon the conditions in the field, either Eq. (5) or (7) must be used in conjunction with Eqs. 2–4 to describe groundwater movement in the stream bank. Generally speaking, Eq. (7) is more appropriate when the stream carries significant amounts of silt and clay particles that could migrate into the stream bank and create the semi-permeable barrier. On the other hand, Eq. (5) may provide a reasonable approximation when the sediment load in the river is low and/or when the stream bank permeability is sufficiently high that the hydraulic connection between the stream and the aquifer is not hampered. The model described using Eqs. 2–5 is referred to as the “head controlled model”, while the model described using Eqs. 2–4 and 7 is referred to as the “flux controlled model.”

The stream stage, H, is assumed to increase linearly from some starting head H 1 to a maximum value H max which occurs at time t 1. Subsequently, the stream stage will decrease linearly back to H 1 at time t 2 and continue to stay at that level. Mathematically, the stream-stage variation can be written as

$$\begin{aligned} H & = \alpha t + H_{1} \quad \;\forall 0 \le t \le t_{1} \\ H & = \beta t + \gamma \quad \quad \forall t_{1} \le t \le t_{2} \\ H & = H_{1} \quad \quad \quad \;\forall t > t_{2} , \\ \end{aligned}$$
(9)

where

$$\alpha = \left( {\frac{{H_{\hbox{max} } - H_{1} }}{{t_{1} }}} \right)$$
(10)
$$\beta = \left( {\frac{{H_{1} - H_{\hbox{max} } }}{{t_{2} - t_{1} }}} \right)$$
(11)
$$\gamma = H_{\hbox{max} } - \beta t_{1}$$
(12)

Using the Heaviside step function, the above triangular variation can be described as

$$H = \left( {\alpha t + H_{1} } \right)\phi \left( t \right) - \left( {\alpha t + H_{1} } \right)\phi \left( {t - t_{1} } \right) + \left( {\beta t + \gamma } \right)\phi \left( {t - t_{1} } \right) - \left( {\beta t + \gamma } \right)\phi \left( {t - t_{2} } \right) + H_{1} \phi \left( {t - t_{2} } \right),$$
(13)

where, ϕ(t−t i) is the Heaviside step function, which assumes a value of 1 for t > t i and zero otherwise.

Solution scheme

The governing partial differential equation and the associated initial and boundary conditions can be solved using several different approaches (Powers 1972). The Laplace transform approach is selected here as it is well suited to handle piece-wise continuous functions and has been used in other similar problems (Barlow and Moench 1998). Taking the Laplace transform with respect to time and assuming that the derivatives with respect to the untransformed variable pass through the transform, the governing equation can be re-written as

$$S_{y} \left( {sU - h_{o} } \right) = D\frac{{{\text{d}}^{2} U}}{{{\text{d}}x^{2} }} + \frac{R}{s},$$
(14)

where U is the hydraulic head in the Laplace domain and s is the transform variable. Equation 14 can be re-written as

$$\varepsilon \frac{{{\text{d}}^{2} U}}{{{\text{d}}x^{2} }} - sU = - \left( {h_{o} + \frac{{R^{*} }}{s}} \right),$$
(15)

where

$$\varepsilon = \frac{D}{{S_{y} }}\quad {\text{and}}\quad R^{*} = \frac{R}{{S_{y} }}$$
(16)

The second-order ordinary differential equation can be easily solved using the method of undetermined coefficients to obtain the following general solution:

$$U = C_{1} \sinh \left( {\sqrt {\frac{s}{\varepsilon }} x} \right) + C_{2} \cosh \left( {\sqrt {\frac{s}{\varepsilon }} x} \right) + \left( {\frac{{h_{o} }}{s} + \frac{{R^{*} }}{{s^{2} }}} \right),$$
(17)

where C 1 and C 2 are the unknown constants that have to be determined from the boundary conditions. These constants are separately determined for the “head-controlled” and the “flux-controlled” cases as follows:

Head-controlled case

The boundary conditions in the case of the head-controlled case can be written as

$$U\left( {x = 0} \right) = F\left( s \right)$$
(18)
$$\frac{{{\text{d}}U}}{{{\text{d}}x}}\left( {x = L} \right) = 0$$
(19)

From Eq. (17), the derivative in Eq. (19) can be obtained as

$$\frac{{{\text{d}}U}}{{{\text{d}}x}} = C_{1} \sqrt {\frac{s}{\varepsilon }} \cosh \left( {\sqrt {\frac{s}{\varepsilon }} x} \right) + C_{2} \sqrt {\frac{s}{\varepsilon }} \sinh \left( {\sqrt {\frac{s}{\varepsilon }} x} \right)$$
(20)

Using the above equations, the unknown coefficients can be expressed as

$$C_{2} = \left\{ {F\left( s \right) - \left[ {\frac{{h_{o} }}{s} + \frac{{R^{*} }}{{s^{2} }}} \right]} \right\}$$
(21)
$$C_{1} = - C_{2} \tanh \left( {\sqrt {\frac{s}{\varepsilon }} L} \right) = - \left\{ {F\left( s \right) - \left[ {\frac{{h_{o} }}{s} + \frac{{R^{*} }}{{s^{2} }}} \right]} \right\}\tanh \left( {\sqrt {\frac{s}{\varepsilon }} L} \right)$$
(22)

Note that F(s) is the Laplace transform of the stream-stage function given in Eq. (13). Using the second shift theorem, and with some algebraic manipulations, the Laplace transform, F(s) can be obtained as

$$F\left( s \right) = \frac{\alpha }{{s^{2} }} + \frac{{H_{1} }}{s} + \left( {\beta - \alpha } \right)\frac{{e^{{ - t_{1} s}} }}{{s^{2} }} - \beta \frac{{e^{{ - t_{2} s}} }}{{s^{2} }}$$
(23)

Flux-controlled case

The boundary conditions for the flux-controlled case in the Laplace domain are given as

$$\left. {\frac{{{\text{d}}U}}{{{\text{d}}x}} - {\text{CU}}} \right|_{x = o} = - {\text{CF}}\left( s \right)$$
(24)
$$\frac{{{\text{d}}U}}{{{\text{d}}x}}\left( {x = L} \right) = 0$$
(25)

The unknown coefficients C 1 and C 2 are obtained using Eqs. 17, 20, and 23 in conjunction with the above boundary conditions.

$$C_{2} = \left[ {\frac{{{\text{CF}}\left( s \right) - \left( {\frac{{h_{o} }}{s} + \frac{{R^{*} }}{{s^{2} }}} \right)}}{{\left( {\sqrt {\frac{s}{\varepsilon }} \tanh \left( {\sqrt {\frac{s}{\varepsilon }} L} \right) + C} \right)}}} \right]$$
(26)
$$C_{1} = - C_{2} \tanh \left( {\sqrt {\frac{s}{\varepsilon }} L} \right)$$
(27)

These coefficients can be used in Eq. 17 to obtain values of hydraulic heads in the aquifer in the Laplace domain for the flux-controlled case.

The final step of the Laplace transform solution scheme is to invert the solution in the Laplace domain to that in the time domain. Given the algebraic complexity of the solutions, numerical inversion is used in many similar applications (Moench and Barlow 2000; Kim et al. 2007; Intaraprasong and Zhan 2009), and the same strategy is adopted here, as well. The Stehfest–Gaver algorithm (Stehfest 1970) and the de Hoog algorithm (de Hoog et al. 1982) are the two most commonly utilized numerical inversion methods in groundwater applications (Moench and Barlow 2000; Boupha et al. 2004; Kim et al. 2007). The Stehfest (1970) algorithm is known to perform poorly when the function is oscillatory or has increasing exponential characteristics (Hassanzadeh and Pooladi-Darvish 2007). As such, this algorithm was deemed unsuitable for this application, as the hydraulic heads are expected to exhibit an increasing trend at early times. Therefore, the de Hoog et al. (1982) algorithm was adopted. The model was implemented in the MATLAB programming environment using the inversion function developed by Hollenbeck (1998).

Model evaluation

Comparison with the analytical solution in Singh (2004)

In order to gain confidence in the developed solutions, it is imperative that the model results be compared with other similar schemes. Singh (2004) presented a closed-form solution, originally developed by Carslaw and Jaeger (1959) for the following problem:

$$\frac{{\partial^{2} h}}{{\partial x^{2} }} - \frac{1}{\beta }\frac{\partial h}{\partial t} = 0;\quad h\left( {0,t} \right) = ct;\quad h\left( {x,0} \right) = 0;\quad h\left( {\infty ,t} \right) = 0;\quad \beta = \frac{D}{{S_{y} }}$$
(28)

While the outer boundary in the above formulation does not match the “head-controlled” model developed here, a close agreement is to be expected at short distances from the stream and at early times. The head-controlled model was parameterized to the values provided in Singh (2004) and compared at distances of 1, 5, 10, and 100 m from the stream. The parameter values used are presented in Table 1 and the comparison in Fig. 2 indicates that the model matches the analytical solution reasonably well even at distances as high as 100 m from the stream. The analytical solution provided by Singh (2004) can also be used to approximately evaluate the flux-controlled solution when the streambed conductance is specified as a large value (i.e., the impervious bed is of negligible thickness to offer any resistance). The results shown in Fig. 3 again demonstrate a close agreement between the two analytical solutions and corroborate the correctness of the developed solutions.

Table 1 Model parameters for comparison with Singh (2004) solution
Full size table
Fig. 2
figure 2

Comparison of developed head-controlled model to Singh (2004) model—(analytical solutions)

Full size image
Fig. 3
figure 3

Comparison of developed flux-controlled model to Singh (2004) model—(analytical solutions)

Full size image

Comparison with numerical solutions

A more comprehensive evaluation of the analytical solutions developed here can be made by comparing the results with a numerical solution (Hogarth et al. 1997). This approach is more flexible as both the head and flux controlled boundary conditions can be evaluated against their numerical counterparts. Fully implicit finite difference models were developed for this purpose. Comparisons were made under the following assumptions—(1) no recharge; (2) positive net recharge, and (3) negative net recharge conditions for both analytical solutions using information provided in Table 2. Illustrative results for the “head-controlled case” and the “flux-controlled case” are presented in Figs. 4 and 5, respectively. As can be seen, the results from the developed analytical solutions match the numerical solutions. Similar results were noted at other locations as well but are not presented here in the interest of brevity. It can be concluded that the developed analytical solutions provide accurate results. The advantage of the analytical solutions, however, lies in the fact that computations can be directly made at select locations and times without having to make calculations at all previous times and over the entire domain as is needed for the implicit method.

Table 2 Model inputs used for comparing analytical and numerical solutions as well as the illustrative case-study
Full size table
Fig. 4
figure 4

Comparison of analytical and numerical results for various recharge assumptions (head–controlled case)

Full size image
Fig. 5
figure 5

Comparison of analytical and numerical results for various recharge assumptions (flux–controlled case)

Full size image

Illustrative case study

The developed analytical solutions were utilized to evaluate the stream–aquifer interactions in the Arroyo Colorado River Watershed located in south Texas. The river is the only source of freshwater to the ecologically sensitive Laguna Madre coastal embayment (Raines and Miranda 2002). The Arroyo Colorado River Watershed is approximately 1,813 km2 in area, of which 12 % is currently categorized as urban/developed area and nearly 60 % is agricultural land. This watershed houses several fast growing cities along the US–Mexico border region (Fig. 6). The focus of the study, therefore, was to evaluate how urbanization in the upstream areas would affect stream–aquifer interactions in the last 5,000 m downstream stretch of the river. The shallow aquifer in this region is formed by alluvial deposits from the Rio Grande River basin and is known to be roughly 300 m thick in the area of interest (Rose 1954; Chowdhury and Mace 2007). The hydrologic characteristics of the region and the hydraulic properties of the aquifer were obtained from a regional groundwater modeling study carried out by the Texas Water Development Board (Chowdhury and Mace 2007) and augmented with other available information and watershed modeling studies (Raines and Miranda 2002) and are summarized in Table 2 for this case study. The riparian region belongs to the south Texas plains natural region (TPWD 2009). Based on model calibration, Chowdhury and Mace (2007) report recharge and ET rates on the order of 2.13 × 10−6 and 1.24 × 10−6 m/d. As such, the net recharge was assumed to be negligible for the study area. Limited water quality monitoring in the study area indicated that the river water is relatively turbid with a significant amount of algae (Raines and Miranda 2002). Based on this information, a certain degree of impedance is to be expected between the stream bed and the adjoining aquifer. However, as site-specific values of streambank conductance were not available, model runs were carried out over a set of plausible values.

Fig. 6
figure 6

Land use land cover characteristics of the Arroyo Colorado River Watershed, Tx

Full size image

A triangular hydrograph corresponding to a rainfall intensity of 1 mm/h for a total duration of 4 h was constructed using a composite area weighted curve number for the four different scenarios listed in Table 3. The peak discharge, time to rise, and time to fall were computed using the following relationships:

$$T_{\text{r}} = t_{\text{p}} + \frac{{t_{\text{d}} }}{2} = \frac{{l^{0.8} \left( {S + 1} \right)^{0.7} }}{{1900\sqrt {S_{\text{w}} } }} + \frac{{t_{\text{d}} }}{2}$$
(29)
$$T_{\text{f}} = 2.67T_{\text{r}} ,$$
(30)

where T r is the time to rise since the beginning of the storm (hour); T f is the time to fall (hour), i.e., when the stream stage falls back to its pre-flood level; l is the length of the stream segment to the divide (m); t d is the total storm duration (hour); t p is the lag time (hour); S w is the average watershed slope (%); and S is the storage parameter computed from the curve number as

$$S = \frac{1000}{\text{CN}} - 10$$
(31)
Table 3 Urbanization scenarios and corresponding flooding parameters
Full size table

The peak flow was computed assuming a triangular hydrograph as follows:

$$Q_{p} = \frac{{2\left( {rA_{\text{w}} t_{\text{d}} } \right)}}{{T_{\text{f}} }},$$
(32)

where r is the rainfall excess intensity (m/days), A w is the watershed area (m2), and t d is the storm duration (days). The stage height corresponding to the peak discharge was computed from the Manning’s equation assuming a wide rectangular channel which is given as

$$Q_{p} = \frac{1}{n}BH^{{\left( {\tfrac{5}{3}} \right)}} \sqrt {S_{\text{c}} } ,$$
(33)

where n is the Manning’s coefficient, B is the width of the channel (m), H is the stage height rise (m), S c is the slope of the stream channel (m/m), and Q is the flow rate (m3s). The unknown stage was obtained by solving Eq. (33) using the secant method of root finding. The parameters required in the above equations were computed from high-resolution spatial datasets using ArcGIS (ESRI Inc., Redland, CA) and summarized in Table 4. All required calculations were made in the US customary units and converted to SI before being input into the stream–aquifer models.

Table 4 Parameters for estimating peak flow and stream-stage in the Arroyo Colorado River Watershed
Full size table

The volume of water discharged per unit area (referred to here as specific volume) of the river bank was computed by integrating the flux equation (LHS of Eq. 6). For the four different urbanization scenarios, the flux was positive (i.e., flow into the aquifer) for a period of approximately 13–15 days with the shorter period corresponding to increased urbanization scenario. The specific volumes depicted in Fig. 7 indicate that bank storage reduces significantly with increasing watershed urbanization. Urbanization of the watershed will lead to an increased peak flow which in turn increases the stage height that could lead to greater influx of water from the stream into the aquifer at least around the peak value. However, for a given rainfall excess, urbanization also reduces the time over which the effects of flooding are felt which in turn reduces the amount of influx into the aquifer. Model results indicate that this latter effect is more pronounced than the former for the conditions assumed in this study. Generally speaking, when the river channel is sufficiently wide, as to be expected in the downstream sections of the river, the stage height rises are likely to be smaller and the alteration of flood duration due to urbanization is the dominant factor that influences bank storage.

Fig. 7
figure 7

Specific volume for various urbanization and conductance scenarios

Full size image

Figure 7 also indicates that the presence of sufficient impedance between the stream and the adjoining river bank aquifer can effectively mask the effects of urbanization if the semi-pervious layer is well developed prior to the urbanization (see line AB on Fig. 7). By the same token, urbanization effects are more pronounced when the hydraulic connection between the aquifer and the stream is high (see line CD on Fig. 7).

Increasing urbanization in watersheds generally deteriorates the stream water quality, which in turn can lead to the formation of the semi-permeable barrier between the stream and the aquifer due to deposition of silts and other particulates as well as growth of microorganisms (Battin and Sengschmitt 1999; Schubert 2002; Wett et al. 2002). Therefore, the streambed conductance is likely to vary temporally and decrease with increasing urbanization. While a time-varying conductance has not been employed in this study, a preliminary understanding of this phenomenon can be ascertained from Fig. 7. By following along the transect CB, it can be seen that decreasing conductance with increasing urbanization will significantly reduce the amount of water stored in the river banks. This result provides an implicit assessment of how water quality alterations affected by urbanization affect streambank storage in riparian areas and highlights the need for understanding how water quality deteriorations affect the permeability of stream–aquifer interfaces.

Generally speaking, reduction in bank storage implies the flood wave will pass relatively un-attenuated and increase the risk of flooding downstream. It will also alter the inflow patterns in the receiving bodies (such as lakes and coastal bays) into which the streams and river discharge. The water available to riparian fauna as well as baseflows during the inter-storm period also decreases due to urbanization.

Summary and conclusions

The primary goal of this study was to develop a simple physically-based model to evaluate stream–aquifer interactions during a flooding event. As a first-cut approximation, the stream stage variation during the passage of the flood is conceptualized to vary in a triangular fashion. Semi-analytical solutions based on the numerical inversion of Laplace transforms were developed for two separate stream–aquifer boundary conditions, one where the hydraulic connection is perfect and another where the connection is impeded by a thin semi-pervious barrier. The results from the developed models were compared with other analytical and numerical solutions to evaluate their accuracy. Excellent agreement was noted during the comparisons which confirmed the correctness of the solutions.

The developed model was then applied to study the effects of urbanization on stream–aquifer interactions in the Arroyo Colorado River Watershed along the US–Mexico border region. The results indicate that increased urbanization reduces the amount of influx into the banks. The reduction in flood passage time was noted to have a greater impact than the associated rise in stage. The presence of a semi-permeable barrier was seen to mask the effects of urbanization. The model results also implicitly highlight the importance of how water quality variations due to urbanization can affect stream–aquifer interactions. The study fills an important gap with regard to available analytical and semi-analytical solutions for modeling stream–aquifer interactions, which can be used for evaluating numerical codes. The developed models can be very useful to obtain preliminary insights concerning urbanization, particularly when the underlying assumptions are borne in mind.