A coupled surface/subsurface flow model accounting for air entrapment and air pressure counterflow

Abstract

This work introduces the soil air system into integrated hydrology by simulating the flow processes and interactions of surface runoff, soil moisture and air in the shallow subsurface. The numerical model is formulated as a coupled system of partial differential equations for hydrostatic (diffusive wave) shallow flow and two-phase flow in a porous medium. The simultaneous mass transfer between the soil, overland, and atmosphere compartments is achieved by upgrading a fully established leakance concept for overland-soil liquid exchange to an air exchange flux between soil and atmosphere. In a new algorithm, leakances operate as a valve for gas pressure in a liquid-covered porous medium facilitating the simulation of air out-break events through the land surface. General criteria are stated to guarantee stability in a sequential iterative coupling algorithm and, in addition, for leakances to control the mass exchange between compartments. A benchmark test, which is based on a classic experimental data set on infiltration excess (Horton) overland flow, identified a feedback mechanism between surface runoff and soil air pressures. Our study suggests that air compression in soils amplifies surface runoff during high precipitation at specific sites, particularly in near-stream areas.

Introduction

Surface runoff models employ the Richards’ approach, when they simulate the water fluxes in the variably saturated soil compartment with partial differential equations, e.g. InHM (van der Kwaak and Loague 2001), HydroGeoSphere (Therrien et al. 2004), MODHMS (Panday and Huyakorn 2004), tRibs (Ivanov et al. 2008), ParFlow (Kollet and Maxwell 2006), PIHM (Qu and Duffy 2007), OpenGeoSys (OGS) (Delfs et al. 2009), CATHY (Camporese et al. 2010), and PAWS (Shen and Phanikumar 2010). These so-called integrated models combine a Richards’ equation with a hydrostatic shallow flow equation (dynamic, diffusive, or kinematic wave) by employing a variety of coupling algorithms (global implicit and sequential iterative coupling, asymetric linking) (see Furman 2008; Brunner et al. 2013, for reviews). Although the significance of integrated surface/subsurface flow models has been confirmed by a growing body of applications (e.g. Frei et al. 2009; Pérez et al. 2011), there is still a gap in research on numerical stability analysis of such codes.

Essentially, the integrated models cover an extended area compared to single-compartment models for surface and subsurface hydrology. To bridge between the model components, inter-compartment boundary conditions must be assigned at common interfaces (e.g. Discacciati and Quarteroni 2009; Mosthaf et al. 2011, regarding mass and momentum transfer). Two approaches have been established in water science for mass balance between hydrostatic shallow flow and subsurface flow (Ebel et al. 2009): enforcing pressure continuity (e.g. Smith and Woolhiser 1971; Kollet and Maxwell 2006) and the leakance concept (e.g. van der Kwaak and Loague 2001; Panday and Huyakorn 2004; Delfs et al. 2009; Shen and Phanikumar 2010). The leakance concept originates from theoretical studies by Hantush (1965) on stream water depletion during groundwater pumping (see also van Genuchten and Wierenga 1976; Gerke and van Genuchten 1993; Hunt 1999; Butler et al. 2001). It enables the modeler to control the inter-compartment fluid exchange for the cost of an additional leakance parameter (or an interface thickness). In general, leakances hinder fluid from migrating between compartments if their values fall below certain thresholds (Delfs et al. 2009; Ebel et al. 2009; Liggett et al. 2012). Threshold values for specific overland-soil water and river-aquifer systems have recently been stated in Liggett et al. (2012), Delfs et al. (2012a), respectively, but a generalization of the results is still missing.

The motivation to implement a coupled surface/two-phase flow model was mainly triggered through previous modelling studies of soil water and air interactions (e.g. Forsyth and Simpson 1991; Mosthaf et al. 2011) and experimental work (e.g. Wang et al. 1997, 1998; Culligan et al. 2000, Bogacz et al. 2006). In the experimental studies, soil air, which was compressed below water-ponded surfaces, impeded water from infiltrating into soil columns, a dike model, and field plots. Experimentators also observed fingering patterns of infiltrating water and series of air-outbreaks across water-covered surfaces if the compressed soil air cannot escape easily via alternative flowpaths (e.g. valves in Wang et al. 1998). Despite of this, precipitation runoff studies have not included feedbacks between surface water and soil air. In fact, the available integrated runoff models implicitly assume that the generation of surface runoff is controlled by the water phase in the subsurface and that the air phase is infinitely mobile at atmospheric pressure in the entire soil system.

This paper presents a novel approach for combining the flow processes of surface and subsurface flow compartments by coupling the partial differential equations for diffusive wave overland flow and two-phase flow in porous media. The primary goal of the presented study is to analyze the liquid and gas inter-compartment fluxes of a leakance concept (i.e. coupling via boundary conditions). First, the experimental data basis of this numerical study is introduced, namely the lab experiments by Smith and Woolhiser (1971) on Horton overland flow. Next are the governing flow equations (diffusive wave overland flow, isothermal incompressible two-phase flow in porous media), inter-compartment boundary conditions for water and air exchange, and the compartment coupling algorithm. After model verification with experimental water fluxes, the paper discusses modeling results concerning (1) a new algorithm to simulate air pressure counterflow from a liquid-covered prous medium, (2) the stability of the coupling algorithm, and (3) the soil discretization (leakance, soil columns). The findings of this research are concluded before the paper presents the spatial discretization methods (finite elements) of the coupled model in an “Appendix”.

Soil flume experiments by Smith and Woolhiser (1971) on Horton runoff

The laboratory experiments by Smith and Woolhiser (1971) provide a well-defined benchmark problem to test and inter-compare the ability of coupled and linked surface/subsurface flow models to reproduce Horton overland flow (Smith and Woolhiser 1971; Akan and Yen 1981; Govindaraju and Kavvas 1991; Singh and Bhallamudi 1998; Morita and Yen 2002; Therrien et al. 2004; Delfs et al. 2009). The liquid, which was used in the experiments, was a light oil to prevent algae growth in a soil flume (Fig. 1a). Surface runoff was collected at the outlet for 15-min precipitation duration (Fig. 1b). The moisture front in the soil was tracked at a vertical cross-section in the middle of the flum by γ -ray attenuation measurements in 30 s intervals. Smith and Woolhiser (1971) measured friction parameters for water depths higher than 4 mm, which exceeds the water depths during the Horton runoff measurements. Indeed, the surface friction parameters considerably affect the steep ascending early part of the hydrograph (Delfs et al. 2009). However, the hydrostatic pressure of the surface liquid enhances liquid infiltration only insignificantly in this system (e.g. Philip 1957).

Fig. 1

The laboratory experiments by Smith and Woolhiser (1971): a soil flume and sketch of 1D meshes to simulate overland flow and infiltration; b comparison of experimental runoff q _r at the outlet with results obtained by coupling diffusive wave overland flow and Richards’ flow in OGS (parametrization given in Delfs et al. 2009)

The experimental data basis for the following model exercise originates from an experimental run under initially drained conditions. The precipitation rate of 4.2 mm/min exceeded the saturated soil hydraulic conductivity by 2–3 times. As a first step in a Horton runoff generation mechanism, the liquid completely infiltrates until the soil at the surface becomes close to liquid saturation (Phase I in Fig. 1b). The hydrograph at the flume outlet rises sharply as liquid reaches the outlet from more and more parts of the flume surface (Phase II). Surface runoff continues to increase as the infiltration capacity of the soil declines with time (Phase III). The experimental hydrograph is well reproducible by Richards-based coupled models and reasonable friction and capillarity parameters (e.g. OGS in Fig. 1b with a homogeneous soil). However, a dip in the hydrograph during phase III was attributed to air pressure counterflow by the experimentators. Air bubbles were observed escaping from the liquid-coverd flume surface during experimental runs (compare with the previously mentioned infiltration studies, Forsyth and Simpson 1991; Wang et al. 1997, 1998; Culligan et al. 2000). Correspondingly, the Richards’-based coupled models were not able to reproducible the dip by using soil stratifications, which account for heterogeneities in the locally obtained sand.

Coupled modelling concept

Background

Water in the subsurface behaves differently from free water on the land surface. Thus, scientists split the water cycle into compartments (atmosphere, river, overland, soil, groundwater, etc.) and use specific experimental and theoretical approaches to meet specific challenges (risk assessment, water resources management, climate change research, etc.) in surface hydrology (e.g. Wöhling et al. 2013; Gayler et al. 2013) and subsurface hydrology (e.g. Klammler et al. 2013; Maier et al. 2013). For this reason, the OGS and OGS#SWMM codes contain an individual set of flow process descriptions for different catchment compartments (Table 1). Storage-flow relationships by Manning or Darcy–Weisbach describe surface friction phenomena, such as turbulence, in the overland and river compartments. The conductivity (permeability) in Darcy’s law is a friction parameter for laminar flow in porous media in the soil and aquifer compartments. Capillary forces can clearly dominate over friction forces in the variably saturated soil compartment, especially under dry conditions. Thus, the impact of soil water content on soil fluid fluxes is parameterized through soil–water characteristic curves as constitutive relationships (e.g. by van Genuchten 1980; Mualem 1976) in the numerical models.

Table 1 Flow compartments with governing equations and constitutive relationships in the OGS and OGS#SWMM models

Complex catchments are increasingly perceived by scientists as integrated systems that combine surface and subsurface flow and respond to the atmosphere with feedback loops (e.g. Fleckenstein et al. 2010; Partington et al. 2011; Altdorff et al. 2013; Elmer et al. 2013; Ghasemizadeh and Schirmer 2013; Grathwohl et al. 2013; Huggenberger et al. 2013; Krüger and Teutsch 2013; Kunkel et al. 2013; Marke et al. 2013; Lemke et al. 2013; Osenbrück et al. 2013; Richter et al. 2013; Strasser et al. 2013). In this context, OGS#SWMM is one of a few numerical models which couple the partial differential equations for river and groundwater flow (Delfs et al. 2012a). In a potential application to anthropogenically modified catchments, the groundwater flow paths are represented in great detail when simulating the water quantity and quality in river courses, e.g. to extend the work by Blumensaat et al. (2012), Walther et al. (2012), Schwientek et al. (2013), and Gräbe et al. (2013). To deconvolute surface runoff hydrographs into its components (e.g. groundwater contribution) with high precision, Delfs et al. (2012a) introduced Lagrangian particles and Partington et al. (2011) a mixing-cell algorithm into coupled surface/subsurface flow models. Overall, the integrated models are explicitly designed to facilitate the numerical analyis of interactions and feedbacks between compartments.

Water displaces air in soils quite easily if air in the soil compartment can escape into the atmosphere or into deeper subsurface regions. In this case, Richards’ models capture the water fluxes in the variably saturated soil compartment, provided that constitutive relationships (Table 1) are obtainable. However, water infiltration and soil air compression can create a feedback loop, if air displacement is hampered in the soil compartment by a water-covered surface (e.g. during Horton flow) and a near-surface water table. Enhanced soil air pressures may block the infiltration, resulting in a higher water content and hydrostatic pressure in the overland compartment. For this reason, overland flow and two-phase flow have been coupled within OGS. A model application to a classic flume experiment quanitifies the potential impact of soil air compression on the Horton runoff mechanism.

Shallow flow over the land surface

Precipitation and snow melt runs off mainly horizontally over topography and independently of the overlying air. Governing equations for shallow flow over a sufficiently flat region can be derived by depth-integrating the (Reynolds-averaged) Navier–Stokes equations (e.g. Gerbeau and Perthame 2001; Ferrari and Saleri 2004). The Saint-Venant and diffusive wave equations assume hydrostatic pressure in the depth-integrated flow field. Both shallow flow equations enable the modeler to reproduce flood waves in the river compartment and precipitation runoff in the overland compartment. The following 2D form of the diffusive wave equation is implemented in OGS (van der Kwaak and Loague 2001)

$$\phi_a\frac{\partial h}{\partial t} - \bar\nabla \cdot \left( \frac{C H_a^{\nu + 1}}{\left| \bar\nabla h \right|^{1-\mu}} \bar\nabla h \right) = q^p - q^H_{\rm c} , $$

(1)

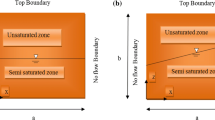
where $\bar\nabla = (\partial / \partial x, \partial / \partial y)^{\rm T}$ is the 2D Nabla operator. A surface porosity 0 ≤ ϕ _a (H) ≤ 1, where H is liquid depth, is unity for flow over a flat plane and varies between zero and unity for flow over an uneven surface (e.g. a surface roughness, depression storage or rills). The depth of mobile liquid is H _a  = max(h − b − a, 0) where h is liquid height, b height of the surface (∂b/∂t = 0) and a is a height of immobile liquid (Fig. 2). The parameter a is used later on to control overland flow initialization over permeable soils during precipitation q ^p in the presence of an overland-soil liquid exchange flux q ^H_c .

Fig. 2

Hydrological overland-soil compartment model with gas exchange between soil and atmosphere. Shown is precipitation run-off under normal flow (with flow rate $\tilde q$) on an permeable surface with slope S ₀. The liquid infiltrates from the overland compartment into the soil compartment via an interface with thickness a ^l and continues flowing vertically with a rate q ^l(z). Gas flows with a rate $q_{\rm c}^{\rm g}$ from the soil to the atmosphere via a second interface a ^g. A height of immobile liquid a in the overland compartment accounts for surface structures

To account for shear–stress phenomena in macroscopic and regional shallow flow, hydrostatic shallow flow equations are complemented by stage-flow equations as constitutive relationships. They read in the case of 1D flow

$$\tilde q = C S_0^{\mu} \tilde H_a^{\nu}, $$

(2)

where $\tilde q ([\tilde q]= \hbox{m}/\hbox{s})$ is the flow rate at normal flow depth $\tilde H_a,$ which depends on a surface roughness parameter C and bottom slope S ₀ =  − ∂b/∂x in x-direction. Uniform flow over a sufficiently long channel or (flood) plain adjusts to the normal flow stage, where momentum changes by gravity and shear–stresses counterbalance. The stage-flow relationship by Manning μ = 1/2, ν = 2/3 are supported by numerous field studies at natural rivers and artificial channels, where flow is turbulent (see e.g. Rügner et al. 2013). In contrast, the friction parameterization in the overland compartment is often unclear. The Darcy–Weisbach relationship for laminar flow is used in this work by setting μ = 1, ν = 2.

In contrast, a so-called critical flow stage can be found at strong variations in topography (free fall) and some flow regulators (e.g. weirs). The non-dimensional Froude-number becomes $Fr= \hat q/\sqrt{g\hat H_a^3}=1,$ where $\hat q$ is critical flow rate, g gravitational acceleration, and $\hat H_a$ critical flow depth. This can be written as

$$\hat q = \sqrt{g\hat H_a^3}. $$

(3)

Equation (3) is independent of friction and used in the verification example to simulate free-fall of a liquid at an outlet (Fig. 1a). Various types of flow regulators (e.g. weirs, sluices) can be incorporated in regional river and overland flow simulations with theoretically and empirically derived Cauchy boundary conditions.

Flow of a liquid in the overland compartment can be accurately simulated with the diffusive wave approach (1) under the following conditions:

• 1. Constant liquid density ρ ^l;

• 2. The horizontal scale l is much larger than the vertical one (liquid depth H), at least H/l < 0.1;

• 3. Absence of strong vertical accelerations (so-called short or deep-water waves);

• 4. Slow flow velocities to neglect inertia terms;

• 5. Negligible phase transfer (e.g. vaporization).

The hydrostatic pressure approach in the diffusive wave Eq. (1) requires conditions 1–3. The hydrostatic pressure at the surface

$$p^{H}=\rho^{\rm l} gH. $$

(4)

will be used later on in the liquid exchange fluxes between surface and subsurface flow. Condition 4 excludes supercritical flow (Froude-number Fr > 1), e.g. damm break waves, and is not required by the Saint-Venant equations. Condition 5 can be relaxed by (temperature-dependent) source/sink terms.

Simultaneous flow of water and air in porous media

Macroscopic flow of water and air in a porous medium (sand, silt, etc.) is conceptualized with continua. Porosity and physical properties (e.g. fluid density, pressure, chemical composition) are averaged values over a representative elementary volume (REV) and considered as piecewise continuous functions in space and time. Liquid, gas, and the solid skeleton are distinct parts, so-called phases, with homogeneous physical properties and separated by a meniscus. Mass conservation during a 3D transfer of the water component in the liquid phase (superscript l) and the air component in the gas phase (superscript g) can be written as (Helmig 1997)

$$ \begin{aligned} \phi \rho^{\rm l} \frac{\partial S^{\rm l}}{\partial p^{\rm c}} \dot p^{\rm c} + \nabla\cdot {\bf q}^{\rm l} &= q^{\rm l} ,\\ -\phi \rho^{\rm g} \frac{\partial S^{\rm l}}{\partial p^{\rm c}} \dot p^{\rm c} + \nabla\cdot {\bf q}^{\rm g} &= q^{\rm g}, \end{aligned} $$

(5)

where ϕ is soil porosity, S ^l is saturation of the liquid phase, ρ ^l, ρ ^g are liquid and gas density, respectively. Furthermore, ∇ = (∂/∂x, ∂/∂y, ∂/∂z)^T is the 3D Nabla operator, and q ^l, q ^g represent source/sink terms for the liquid and gas phase, respectively. Surface tension between a liquid (e.g. water, NAPL) and the gas phase causes a discontinuity, the capillary pressure p ^c = p ^g − p ^l across the phase boundary (meniscus), where p ^g is gas pressure and p ^l liquid pressure.

Water first enters small void spaces with higher capillary forces and the larger void spaces later on during imbibition. Vice-versa, if a soil is drained, a liquid retreats to small void spaces. As a consequence, a relationship between liquid saturation S ^l and capillary pressure p ^c is needed in the mass balance Eqs. (5), e.g. (van Genuchten 1980)

$$S^{\rm l}_{\rm e}(p^{\rm c}) = \left( 1 + \left|\frac{\alpha p^{\rm c}}{\rho^{\rm l} g}\right|^{\frac{1}{1-m}} \right)^{-m}, $$

(6)

where α is a pore size parameter, m is a grain size distribution parameter. The effective liquid saturation 0 < S ^l _e in porous media

$$S^{\rm l}_{\rm e} = \max\left( 0, \frac{S^{\rm l} - S^{\rm l}_{\rm r} - S^{\rm g}_{\rm r} }{ S^{\rm l}_{\rm m} - S^{\rm l}_{\rm r} }\right) $$

(7)

depends on the maximum liquid saturation $S^{\rm l}_{\rm m}$ ($S^{\rm l}_{\rm m} = 1$ in this work) and the liquid and gas residual saturations $S^{\rm l}_{\rm r}, S^{\rm g}_{\rm r}$ (gas saturation S ^g = 1 − S ^l). Equation (6) by van Genuchten (1980) relates liquid saturation S ^l with capillary pressure p ^c. Such relation is known as retention curve. It should be noted that capillary pressure p ^c in porous media depends not only on the current saturation state S ^l, but also on its past. Specifically, soils exhibit a higher capillary pressure p ^c during drainage than during imbibition for a given liquid saturation. This phenomenon known as capillary-hysteresis is neglected in this work.

A constitutive relation for the flow of water through a saturated soil (S ^l = 1) was originally derived from experimental observations by Darcy. Darcy’s law has meanwhile been theoretically derived from the Stokes’ equation by homogenization and extended to multicomponent flow (see e.g. Singh et al. 2013) through multiple phases (e.g. liquid, gas, NAPL) in porous media. Two flow rates, one for the liquid (superscript l) and one other for the gas (superscript g) phase describe advective flow in variably saturated porous media (Bear 1988)

$$ \begin{aligned} {\bf q}^{\rm l} &= -\rho^{\rm l}\frac{k_{\rm r}^{\rm l} {{\bf k}}}{\mu^{\rm l}} \nabla \left( p^{\rm g} - p^{\rm c} + \rho^{\rm l} gz \right), \\ {\bf q}^{\rm g} &= -\rho^{\rm g}\frac{k_{\rm r}^{\rm g} {{\bf k}}}{\mu^{\rm g}} \nabla \left( p^{\rm g} + \rho^{\rm g} gz \right), \end{aligned} $$

(8)

where k _r is relative permeability, μ ^l, μ ^g are liquid and gas dynamic viscosity, the vertical coordinate z is positive upwards, and the intrinsic soil permeability tensor k is independent of fluid properties.

During drainage, the liquid retreats to the smaller void spaces with larger shear–stresses (and capillary pressures) until the liquid forms disconnected clusters at residual saturation (S ^l = S ^l_r ). As a consequence, the ability of liquid and gas flow through porous media is governed by their relative permeabilities k _r, e.g. Mualem (1976)

$$ \begin{aligned} k^{\rm l}_{\rm r}(S^{\rm l}) &= \sqrt{S^{\rm l}_{\rm e}}\left[ 1- \left(1- \left(S^{\rm l}_{\rm e}\right)^{1/m}\right)^m \right]^2, \\ k^{\rm g}_{\rm r}(S^{\rm l}) &= \sqrt[3]{1-S^{\rm l}_{\rm e}}\left[ 1- \left(S^{\rm l}_{\rm e}\right)^{1/m} \right]^{2m}. \end{aligned} $$

(9)

The so-called soil–water characteristic-curves (6) and (9) by van Genuchten–Mualem are in widespread use to model macroscopic flow in the vadose zone (e.g. to optimise irrigation on agricultural soils). Soil–water characteristic-curves for three-phase flow (e.g. a NAPL in the vadose zone) can be found in the literature (e.g. Helmig 1997). Up-scaling to regional flow is subject to current research (see e.g. Grathwohl et al. 2013).

The following geometric restrictions are imposed on an interconnected void space at the microscopic scale: The spatial dimensions of the interconnected void space must be large compared to the mean free path length of fluid molecules (≈10⁻⁷ m) and, at the same time, small enough (≈7 mm) such that adhesive and cohesive forces at the phase boundaries control the fluids. Under these conditions, the porosity (continuum) concept and the soil–water characteristic-curves can be used.

In addition, the following assumptions are made for the soil compartment:

• 1. Negligible transfer of water and air between the liquid and gas phases (e.g. by vaporization);

• 2. Fluid properties ρ and μ are independent of chemical, thermal, mechanical or pressure gradients;

• 3. Non-swelling porous medium (rigid solid phase);

• 4. Slow flow velocities to apply Darcy’s law;

Assumptions 1–3 are made for the sake of simplicity in the verification example (see e.g. Watanabe et al. 2010; Singh et al. 2011; Wang et al. 2012) for non-isothermal flow with diffusion, mass transfer between phases, and mechanical deformation within OGS). The effect of gas compressibility $\beta_p^{\rm g} = \partial \rho^{\rm g}/\partial p |_T$ on infiltration was found as secondary in our simulations in agreement with the findings of Wang et al. (1998), Culligan et al. (2000) among others.

Finally, Richards’ approximation assumes a constant gas pressure p ^g throughout the soil compartment and reads in the pressure-formulation (Warrick 2003)

$$ \begin{aligned} & \Upphi \rho^{\rm l} \frac{\partial S^{\rm l}}{\partial p^{\rm l}} \dot p^{\rm l} + \nabla\cdot {\bf q}_{\rm r} = q^{\rm l}\\ & {\bf q}_{\rm r} = -\rho^{\rm l}\frac{k_{\rm r}^{\rm l} {\bf k}}{\mu^{\rm l}} \nabla \left( p^{\rm l} + \rho^{\rm l} gz \right). \end{aligned} $$

(10)

Leakance concept

Hydrostatic shallow flow interacts with subsurface flow through mass exchange (see e.g. Discacciati and Quarteroni 2009; Mosthaf et al. 2011, regarding mass and momentum transfer between non-hydrostatic free-flow and flow in porous media). As a tool to derive inter-compartment boundary conditions, the leakance concept (Hantush 1965) has been successfully established in water science through the coupled overland/Richards’ flow models HydroGeoSphere and InHM (van der Kwaak and Loague 2001). This section introduces the air exchange between the soil and atmosphere compartment into integrated hydrology.

The liquid phase (superscript l) in a porous medium (e.g. soil) is coupled with shallow flow (superscript H). The gas phase (superscript g) in the porous medium is connected with free-flow (e.g. the atmosphere). The mass exchange fluxes through the inter-compartment interfaces (Fig. 2) read:

$$ \begin{aligned} q_{\rm c}^{\rm l} &= -\rho^{\rm l}\lambda^{\rm l} \left( p^H + (p^{\rm c} - p^{\rm g}_{\rm e}) |_{\Upgamma_{\rm c}} \right), \\ q_{\rm c}^{\rm g} &=\rho^{\rm g} \lambda^{\rm g} p^{\rm g}_{\rm e}|_{\Upgamma_{\rm c}} ,\\ q_{\rm c}^H&= q_{\rm c}^{\rm l}, \end{aligned} $$

(11)

where $p^{\rm c}|_{\Upgamma_{\rm c}}, p^{\rm g}|_{\Upgamma_{\rm c}}$ are the capillary and gas pressures at a common compartment interface ${\Upgamma_{\rm c}} = \bar\Upomega.$ The fluxes ${q_{\rm c}^{l} = {\bf q}^{l}_\Upgamma {\bf n}_{\Upgamma_{\rm c}}}$ and ${q_{\rm c}^{g} = {\bf q}^{g}_\Upgamma {\bf n}_{\Upgamma_{\rm c}}}$ in normal direction ${\bf n}_{\Upgamma_{\rm c}}$ from the compartment boundary $\Upgamma_{\rm c}$ are Robin boundary conditions in the two-phase flow Eqs. (19) while $q_{\rm c}^H$ is a head-dependent source/sink term in the (diffusive wave) overland flow Eq. (22). The liquid pressure from surface flow p ^H is the hydrostatic pressure (4) at the compartment boundary, $p^{\rm g}_{\rm e}|_{\Upgamma_{\rm c}} = p^{\rm g}|_{\Upgamma_{\rm c}} - p^{\rm g}_{\rm atm}$ the atmospheric excess pressure and $p^{\rm g}_{\rm atm}$ the atmospheric pressure. The grade of compartment connection is specified by leakances

$$\lambda^{\rm l} = \frac{k_{\rm c}^{\rm l} k |_{\Upgamma_{\rm c}}}{\mu^{\rm l} a^{\rm l}}, \quad \lambda^{\rm g} = \frac{k_{\rm c}^{\rm g} k |_{\Upgamma_{\rm c}}}{\mu^{\rm g} a^{\rm g}}, $$

(12)

where a ^l, a ^g represent the thickness of interfaces in Fig. 2. $k |_{\Upgamma_{\rm c}}={{\bf n}_{\Upgamma_{\rm c}} \cdot{\bf k}{\bf n}_{\Upgamma_{\rm c}}}$ is the intrinsic permeability of a porous medium in normal direction from the compartment boundary $\Upgamma_{\rm c}.$ The leakances (12) are modified by relative interface permeabilities

$$ \begin{aligned} k_{c}^{\rm l} &= k_{c e}^{\rm l} (1- k_{c r}^{\rm g}),\\ k_{c}^{\rm g} &= k_{c e}^{\rm g} (1- k_{c r}^{\rm g}) + k_{c r}^{\rm g}, \end{aligned} $$

(13)

where $k_{c r}^{\rm g}$ is a residual gas interface permeability and

$$ \begin{aligned} k_{c e}^{\rm l} & = {\rm{min}}[S^{2(1-S)},1], \quad S=\frac{fH}{a^s}, \\ k_{c e}^{\rm g} & = (1- k_{c e}^{\rm l}) \end{aligned} $$

(14)

are effective relative interface permeabilities ($0 \leq k_{c e}^{\rm l}, k_{c e}^{\rm g} \leq 1$).

The effective relative liquid interface permeability $k_{c e}^{\rm l}$ is zero for dry surfaces (H = 0) and unity if the liquid depth H exceeds a thickness a ^s (let f = 1). This ensures that the liquid exchange flux $q_{\rm c}^{\rm l}$ does not exceed the available water H on the surface during infiltration into dry porous media, where the capillary pressure $p^{\rm c}|_{\Upgamma_{\rm c}}$ is high. The parameter a ^s in the saturation factor S equals the surface roughness parameter a ^s = a or is selected smaller to guarantee stability (Delfs et al. 2009). The relative gas interface permeability $0 \leq k_{c}^{\rm g} \leq 1$ equals the residual value $k_{c r}^{\rm g}$ for $k_{ce}^{\rm l} = 1.$As a consequence, the gas phase in the porous medium becomes disconnected from the free-flow region (e.g. atmosphere) during liquid ponding and runoff on the surface.

Under ponding conditions in infiltration experiments, soil air pressure often fluctuates between an upper threshold p _break, where air suddenly breaks out across the surface, and a lower threshold p _close, where the surface suddenly closes for air. For a numerical simulation of gas out-break events, leakances (12) follow a hysteresis curve. In the suggested algorithm (Fig. 3a), the flow control factor f in (14) is initially unity and is reduced to a minimum flow control factor 0 < f _break < 1 if the gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}}$ exceeds the gas-breaking gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}} \geq p_{\rm break}.$ At this moment, liquid leakance λ^l drops impeding liquid exchange while gas leakance λ ^g = 1 − λ^g rises. As a consequence, gas is released from a porous medium to a free-frow (e.g. the atmosphere) across a liquid-covered surface. Then, the gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}}$ drops (Fig. 3b). The surface closes again ($k_{c e}^{\rm l} =1, f=1$) when the gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}}$ falls below the gas-closing gas pressure p _close as a second threshold. Based on this algorithm, leakances act as a valve for gas pressure, which fluctuates between the thresholds p _break and p _close (Fig. 3b).

Fig. 3

Illustration of the flow control factor f in the effective relative interface permeabilities (14) to modify leakances (12) with soil gas pressure p ^g at the compartment interface $\Upgamma_{\rm c}:$ a hysteresis curve, b series of air-breaking and air-closing events

The leakance concept (Hantush 1965) introduces interface (transition) zones. The following assumptions are made, to couple two mass balance equations (e.g. the overland flow equations (1) with (5) for the soil) via mass exchange fluxes across interfaces:

• 1. Slow flow between compartments to approximate mass exchange fluxes $q_{\rm c}^{\rm l}, q_{\rm c}^{\rm g},$ and $q_{\rm c}^H$ with a differential pressure (compare with Darcy’s law);

• 2. A continuum to parameterize shear–stresses with leakances λ^l, λ^g;

• 3. Constant fluid properties ρ,  μ throughout the interface (transition) zone;

• 4. Negligible shearing forces which act tangential to the compartment boundary;

• 5. One-dimensional mass exchange fluxes in normal direction ${\bf n}_{\Upgamma_{\rm c}}$ from the compartment boundary $\Upgamma_{\rm c}.$

Regarding assumption 1, it is important to notice that worm holes and other distinctive structures (preferential flow paths) amplify the flow rate of water and air at the surface/subsurface transition zone in many practical cases (e.g. agricultural or forested field sites), which suggests an extension of the conceptual model (e.g. to dual-permeability).

Regarding assumption 2, leakances are continuous functions of surface liquid depth H by using the effective relative interface permeabilities $k_{r, e}^{\rm c}.$ In contrast, the flow control factor f depends on the capillary pressure $p^{\rm c}|_{\Upgamma_{\rm c}}$ as a step function at the thresholds $p^{\rm c}_{\rm break}$ and $p^{\rm c}_{\rm close}$ to simulate sudden air eruptions through a land surface (see e.g. Wang et al. 1998). Ebel et al. (2009) provided a list of chemical and physical clogging mechanisms, which can be potentially simulated by modifying leakance. Examples are unsaturated zones in riverbeds, biotic and non-biotic clogging (Sophocleus 2002; Hartwig et al. 2011).

Concerning assumptions 3-5, pressure gradients in the transition zone may decisively influence fluid properties, driving forces and, therefore, the fluid exchange between compartments. Pressure and momentum can be expected to vary strongly at compartment interfaces due to differences in shear–stresses (time scales). This is reflected in coupled models by the use of different concepts (e.g. potential theory vs. shallow wave theory, permeability vs. stage-flow relationships for shear stresses).

The first term in the liquid exchange flux $q_{\rm c}^{\rm l}$ represents the hydrostatic surface water pressure (4) while the following term accounts for the capillary pressure $p^{\rm c}|_{\Upgamma_{\rm c}}$ in the porous medium. The remaining term accounts for the pressure difference $p_{\rm e}^{\rm g}|_{\Upgamma_{\rm c}}$ between the gas in the soil and atmosphere. If water moves rapidly over the surface (see e.g. Stonedahl et al. 2010; Trauth et al. 2013), a dynamic pressure term is required and can be added into the liquid exchange fluxes. In the case of sequential iterative coupling, experience suggests to implement the capillary pressure term implicitly. In most practical cases, the hydrostatic surface water pressure term is of much lower importance than the capillary pressure term and can be neglected or explicitly implemented (see e.g. Delfs et al. 2009).

Compartment coupling

Flow of multiple phases or of differently mobile regions (dual permeability) in the soil compartment is simultaneously calculated in OGS by implicit coupling (e.g. Eq. (20) in the “Appendix”) to guarantee accurate and stable solutions in case that the flow processes interact strongly (e.g. Helmig 1997). For the sake of flexibility and ease, flow processes of different compartments are sequentially calculated and an iteration loop can be performed until convergence of the pressures (see e.g. Furman 2008; Kim et al. 2009). Fast convergence is achieved (usually less than 3 iterations) by solving the surface flow equation first. Thus, coupling the equations of overland flow (1) and two-phase flow (5) leads to the following algebraic equation system

$$A^H {\bf h} = {\bf b}^H , \quad \quad A^p \left(\begin{array}{c} {\bf p}^{c} \\ {\bf p}^{g} \end{array} \right) = \left(\begin{array}{c} {\bf b}^{l} \\ {\bf b}^{g} \end{array} \right), $$

(15)

where A are system matrices for surface flow (superscript H) and subsurface flow (superscript p) while b are right hand side vectors (see Eqs. 20, 22 in the “Appendix”).

OGS takes a multi-mesh approach by solving the partial differential equations of different flow compartments (overland, soil, etc.) on separate meshes. Thereby, mesh nodes of coupled processes are required to be topologically consistent at common compartment interfaces. Two options are implemented in OGS for coupled overland/soil systems (Fig. 4). First, each overland mesh node on the common compartment interface $\Upgamma_{\rm c} = \bar\Upomega$ (Fig. 4a) has a specific soil mesh node as a coupled node and vice versa. Assumption 5 in the mass exchange fluxes (11) is a geometric condition demanding that a mesh node and a coupled node match exactly (compare with a conforming mesh for fractured media, e.g. Pichot et al. 2010). Second, mesh nodes of an influence area ($\bar\Upomega$ in Fig. 4b) in the overland compartment have the uppermost node of a specific soil column as a coupled node. Correspondingly, the uppermost node of a soil column (on $\Upgamma_{\rm c}$ in Fig. 4b) has the overland nodes of a specific influence area as a set of coupled nodes. The second option is motivated by the fact that gravity causes water to flow mainly vertically in flat regions such that the soil compartment can be discretized with an array of vertical columns (see e.g. the verification example or Streck and Richter 1997; Beyer et al. 2009 concerning mass transport).

Fig. 4

Multi-mesh concept for a overland/soil compartment system: a side view of a 3D soil domain $\Upomega,$ where the boundary $\Upgamma_{\rm c}$ corresponds to the 2D domain of shallow water overland flow $\bar\Upomega.$ The brown dots represent (finite element) mesh nodes of both flow processes, which have to coincide; b the soil is represented by 1D soil columns. Shown is the specific case with one soil column, where the total overland flow domain $\bar\Upomega$ is an influence area to the soil column at the top boundary $\Upgamma_{\rm c}$

Results and discussion

Model verification: Richards’ vs. two-phase flow

No analytical solutions are available to verify the implementation of the coupling approach. In general, testing of integrated hydrological models strongly depends on experimental datasets (e.g. by Smith and Woolhiser 1971; Abdul and Gillham 1989) and code inter-comparison studies (e.g. Sulis et al. 2010; Delfs et al. 2012b).

Singh and Bhallamudi (1998) and our own numerical results indicated that spatial heterogeneity in the soil caused only insignificant lateral water fluxes in the Smith and Woolhiser (1971) experiment. Moreover, lateral air fluxes in the soil were not measured by the experimentators. For these reasons, both overland and two-phase flow are discretized by using 1D meshes (Fig. 4b). Liquid and gas exchange fluxes (11) are assigned at the top of a vertical soil column ($\Upgamma_{\rm c}$ in Fig. 4b) with a length of 30 cm. Gas escapes at the bottom of the soil column, where the gas pressure is enforced to equal the atmospheric pressure $p^{\rm g}_{\rm atm} = 101325$ Pa. It is clear that the numerical model does not behave realistically in this regard and the exit for air at 30 cm depth is somewhat arbitrary. However, since experimental data on soil air are lacking, the coupled model is run with the most simple representation of a two-phase soil system. In a following section (Fig. 10), 2D simulations evaluate lateral soil air fluxes towards preferential flow paths for air escape.

The soil is represented homogeneously and isotropically in the numerical model. Surface friction on top of the flume is described with the laminar Darcy–Weisbach relationship (μ = 1, ν = 2 in (2)). The liquid saturation is initially 0.2 throughout the soil, which provides a reasonable fit to observations at a vertical cross-section in the flume. Table 2 summarizes the parameters in the coupled overland and soil compartments. The parametrization represents a reference case in the following parameter sensitivity study. The interface thicknesses a ^l, a ^g and the parameter a ^s in the effective relative interface permeability (14) are selected as 1 mm. The parameter a ^s fulfils the condition a ^s ≤ a (Delfs et al. 2009) where a is the depth of immobile liquid in the overland flow Eq. (1). The effects of liquid and gas interface thicknesses a ^l, a ^g on the mass exchange fluxes (11) are studied in the following section (e.g. Fig. 6).

Table 2 Model parameters of the extended Smith and Woolhiser (1971) benchmark for coupled shallow/two-phase flow

For model verification, Fig. 5 compares results of the two-phase-based coupled model with experimental data and with the results of a Richards’-based coupled model. The simulation results of Richards’ and two-phase flow are obtained with the same parameters (Table 2) for the soil and liquid. This is achieved by enforcing the gas pressure in the two-phase model to equal the atmospheric pressure $p^{\rm g} = p^{\rm g}_{\rm atm}$ in the entire column. Figure 5a confirms that enhanced soil gas pressures amplify the Horton runoff $q_{\rm r} = \hat q/ L$ at the free-fall outlet (Fig. 1), where $\hat q$ is the critical flow rate (3) and l = 12.2 m the flume length. Air-counterflow through the flume surface increases the calculated runoff in the first half of the hydrograph (parameters in Table 2). Gas pressures in the two-phase flow model slow down the infiltration front only slightly (Fig. 5b). The maximum of the atmospheric excess gas pressure is located 2 cm below the interface $\Upgamma_{\rm c} (z=0).$ The value reaches roughly 200 Pa. To obtain a sense of the effect of soil gas pressures in these calculations, Fig. 1b showed previous results of the Richards’-based coupled model in OGS. The soil permeability k was selected 7% lower to match experimental and simulated hydrographs.

Fig. 5

Comparison of simulation results of OGS with experimental data: a surface runoff at the flume outlet. Flow in the soil compartment is calculated with Richards’ model (green), two-phase model with air pressure counterflow (red) and without air pressure counterflow (blue); b moisture fronts (red and green) and atmospheric excess gas pressure (violet) at a cross-section in the soil flume

Interface thicknesses

Interfaces with finite thicknesses a ^l, a ^g are introduced in a leakance concept (Hantush 1965) to provide discrete mass exchange fluxes (11). Thus, the coupling fluxes on the interface thicknesses are prone to sensitivity analysis to evaluate the importance of the processes for model predicitions. Interface thicknesses impeded the inter-compartment exchange of a liquid in previous studies, if their values exceeded certain thresholds (Ebel et al. 2009; Delfs et al. 2009, 2012a; Liggett et al. 2012). Thresholds and the problem of instability in sequential iterative coupling have recently been addressed in Delfs et al. (2012a) for a coupled river/aquifer system. The analysis of the mass exchange fluxes is extended to a coupled overland/two-phase flow system in the following. First, the parameters in Table 2 and a control factor of f = 1 (no gas out-breaks) are used as a reference case (Fig. 6). The following sections (Figs. 7, 8) address the effect of the parametrization (e.g. the porous medium properties and flow control factor f) on the fluid exchange between compartments.

Fig. 6

Influence of interface thicknesses a ^l, a ^g on coupling fluxes for the reference case with flow control factor f = 1 (no gas out-break): a liquid coupling flux q ^l_c ; b gas coupling flux q ^g_c

Fig. 7

Influence of interface thicknesses a ^l, a ^g on coupling fluxes for f = 1: a liquid coupling flux q ^l_c for a 100 times higher intrinsic soil permeability than in the reference case; b gas coupling flux q ^g_c for a 100 times higher soil permeability; c gas coupling flux q ^g_c for a 10 times longer soil column; d stability for a sequential iterative coupling algorithm (p ^g_atm  = 101325 Pa); e gas pressure at the compartment interface $\Upgamma_{\rm c}$ for a range of residual gas interface permeabilities k ^g_cr

Fig. 8

Liquid exchange flux $q_{\rm c}^{\rm l}=q_{\rm c}^H$ (black), overland liquid head h (green), soil liquid pressure head $p^{\rm l} |_{\Upgamma_{\rm c}} / \rho^{\rm l} g$ (blue) and gas pressure heads $p^{\rm g} |_{\Upgamma_{\rm c}} / \rho^{\rm l} g$ (red) during air pressure counterflow a f _break = 0.3 (reference case) and b f _break = 0.1

Thresholds for the reference case

Figure 6 shows mass exchange fluxes $q_{\rm c}^{\rm l}$ and $q_{\rm c}^{\rm g}$ for interface thicknesses a ^l and a ^g, respectively, ranging from 10⁻⁵ m to 1 m. Interface thicknesses impede the liquid and gas exchange if their values exceed thresholds

$$a^{\rm l}> a_{\rm c}^{\rm l},\quad \quad a^{\rm g}> a_{\rm c}^{\rm g}, $$

(16)

which are $a_{\rm c}^{\rm l} = 0.1$ mm for the liquid, $a_{\rm c}^{\rm g} = 1$ mm for the gas in the reference case, and independent of each other. Selection of smaller interfaces a ^l, a ^g does not enhance inter-compartment mass exchange. Instead, the results become insensitive to small variations in interface thicknesses or leakances (12). Our results generalize the sparse literature (e.g. Liggett et al. 2012; Delfs et al. 2012a): Low leakances λ_l, λ_g (high interface thicknesses) enable the modeler to control inter-compartment fluid exchange (11).

Thresholds for an alternating parametrization and geometry

The effect of the leakance is studied for alternative parametrizations and soil column lengths than the reference case. Figure 7a, b shows the coupling fluxes $q_{\rm c}^{\rm l}$ and $q_{\rm c}^{\rm g}$ for a 100 times higher intrinsic permeability k (isotropic soil) and precipitation rate q ^p, while the simulation time is reduced by a factor of 100. Both thresholds $a_{\rm c}^{\rm l}, a_{\rm c}^{\rm g}$ maintain their value resulting in leakances λ^l and λ^g which are 100 times higher at the threshold. The threshold $a_{\rm c}^{\rm g}$ for the gas interface thickness increases with the length of the soil column (Fig. 7c) while the threshold $a_{\rm c}^{\rm l}$ for the liquid interface thickness maintains its value. Leakances at the thresholds $a_{\rm c}^{\rm l}$ and $a_{\rm c}^{\rm g}$ are independent of the remaining porous medium properties (porosity ϕ, van Genuchten-Mualem parameter α, m). The hydrostatic surface water pressure (4) and, thus, the friction parameters C,  μ, ν in (2) affect only insignificantly the liquid coupling fluxes $q_{\rm c}^{\rm l}, q_{\rm c}^H$ for the water depths H≈ 3 mm in the verification example (e.g. Delfs et al. 2009). In general, leakances at the thresholds $a_{\rm c}^{\rm l}$ and $a_{\rm c}^{\rm g}$ for interface thicknesses depend solely on the intrinsic permeability k and the geometry (e.g. soil column length) of the subsurface porous medium system.

Stability of the coupling algorithm

Flow equations can be coupled global implicitly, in an iteration loop or asymetrically linked (e.g. Furman 2008). Present work assembles the system of partial differential Eqs. (1) for overland flow and (5) for two-phase flow as partially monolithic matrices (15). For compartment coupling, the flow fields in the surface and subsurface are sequentially calculated in an iteration loop. Iteration through flow compartments permits rapid coupling, but sometimes suffers from instability (numerical oscillations). Thus, a carefull examination of the stability range of the implemented coupling algorithm is needed for a reliable model application.

Liquid moves between the soil and overland compartments and gas between the soil and atmosphere via first-order fluxes (11). The fluxes are implicitly implemented in the coupling iteration (one part in the matrix and the other part in the right hand side of the algebraic equation system (15)). In the numerical results, the atmospheric excess gas pressure $p_{\rm e}^{\rm g}$ exhibits steps at the compartment interface $\Upgamma_{\rm c}$ (Fig. 7d) with a size of

$$\Updelta{p_{\rm e}^{\rm g}} |_{\Upgamma_{\rm c}}= 10^{-12} p^{\rm g}_{\rm atm} $$

(17)

(compare with Delfs et al. (2012a) for a coupled river-aquifer system). As a consequence, the inter-compartment gas flux in (11) has discontinuities with a step size of $\Updelta q_{\rm c}^{\rm g} = \lambda^{\rm g} \Updelta p_{\rm e}^{\rm g} = 10^{-12} \lambda^{\rm g} p^{\rm g}_{\rm atm}.$ In the reference case of the extended Smith and Woolhiser (1971) benchmark (Table 2), the step size (17) exceeds the water infiltration rate and considerably affects the hydrograph (not shown) for a ^g = 10⁻¹⁰ m ($\Updelta q^{\rm g} \approx 3\times 10^{-4}\;{\rm m/s})$. Concerning liquid flow in the reference case, the coupled model becomes unstable, if the liquid interface thickness is selected as a ^l = 10⁻⁶ m or thinner. In the use of inter-compartment coupling fluxes $q_{\rm c}^{\rm l}$ and $q_{\rm c}^{\rm g}$ with surface pressure terms $p^H, p_{\rm atm}^{\rm g}|_{\Upgamma_{\rm c}},$ it is important to ensure stability by selecting low leakances λ^l and λ^g without impeding fluid exchange. The criteria (16) and (17) guide the applier of the model to proper ranges for leakances λ^l and λ^g in practice.

The hydrostatic surface water pressure p ^H = ρ ^lgH is negligible in the liquid coupling flux (11) in many practical cases, e.g. the Smith and Woolhiser (1971) benchmark where H < 3 mm. Additionally, the atmospheric pressure can be set as zero ($p^{\rm g}_{\rm atm}= 0$). Then, the discontinuities in $\Updelta{p_{\rm e}^{\rm g}}|_{\Upgamma_{\rm c}}$ and $\Updelta{p^{\rm c}}|_{\Upgamma_{\rm c}}$ vanish and the numerical model remains stable for higher leakances despite of sequential iterative coupling. It is important to notice at this point that a following section (Fig. 9) addresses the effect of numerical grids on inter-compartment fluxes and model stability.

Fig. 9

Influence of soil grid (f = 1): a liquid and gas exchange fluxes $q_{\rm c}^{\rm l}, q_{\rm c}^{\rm g}$ for soil grids with a vertical resolutions of 1 mm (reference case), 3 cm, and 10 cm; b gas pressures $p^{\rm g}|_{\Upgamma_{\rm c}}$ at the compartment interface $\Upgamma_{\rm c}$ obtained with a vertical mesh resolution of 3 cm and a range of residual gas interface permeabilities $k_{c r}^{\rm g}$

Gas pressure counterflow

Infiltrating water induced air compression and air counterflow through water-ponded surfaces in many experimental studies (e.g. Smith and Woolhiser 1971; Wang et al. 1997, 1998; Culligan et al. 2000). For this reason, this work suggests an algorithm to simulate air-breaking and air-closing with a numerical model. The residual interface permeabilities (14) in the leakances (12) are modified with liquid and gas pressures to connect and disconnect the soil air and atmosphere.

Gas pressure at the compartment interface

The residual gas interface permeability $k_{\rm c}^{\rm g}$ is a continuous function with the liquid water depth H on the surface. The purpose is to disconnect the air in the soil from the atmosphere during overland flow initialization. Figure 7e shows a rapid rise in the gas pressure p ^g at the interface $\Upgamma_{\rm c}$ when the surface closes for gas exchange from the soil in the atmosphere in the simulations of the experiments by Smith and Woolhiser (1971). The residual gas interface permeability $k_{c r}^{\rm g}$ in (13) specifies the degree at which the interface is closed for gas flow during ponding on the surface (H > a ^s). Inspection of Fig. 7e reveals that the atmospheric excess gas pressure at the interface reaches a maximum of roughly $p_{\rm e}^{\rm g}= 200$ Pa for a residual gas interface permeability of $k_{c r}^{\rm g} = 10^{-9} (a^{\rm g} = 1$ mm reference case). Stability of the two-phase flow model requires a finite value for the residual gas interface permeability $k_{c r}^{\rm {g}} > 0.$

Gas-breaking and gas-closing

The compartment interface is partially closed for the liquid exchange flux $q_{\rm c}^{\rm l}=q_{\rm c}^H$ (and opened for the gas exchange flux $q_{\rm c}^{\rm g}$) during air pressure counterflow. The degree of disconnection can be specified with the minimum flow control factor f _break, which is introduced in this work. In the numerical results (Fig. 8), gas outbreaking causes a drop in the liquid exchange flux $q_{\rm c}^{\rm l},$ gas pressure p ^g and the liquid pressure p ^l at the interface $\Upgamma_{\rm c}.$ The gas pressure $p^{\rm {g}}|_{\Upgamma_{\rm {c}}}< p_{\rm {close}}$ continues to decline slowly as the liquid pressure $p^{\rm l}|_{\Upgamma_{\rm c}} = (p^{\rm g} - p^{\rm c}) |_{\Upgamma_{\rm c}}$ approaches $(H-a^{\rm l} / f_{\rm break}) \rho^{\rm l} g.$ The drop in the liquid exchange flux and liquid pressure is more pronounced if the minimum flow control factor f _break is selected low. When the gas pressure falls below the second threshold $p^{\rm {g}}|_{\Upgamma_{\rm {c}}}< p_{\rm {close}}$ and f becomes unity, gas pressure, liquid pressure $p^{\rm l}|_{\Upgamma_{\rm c}}$ and liquid coupling flux rise again. Result is a series of gas out-breaks at the surface while the flow control factor f follows a hysteresis curve (Fig. 3b). Regarding the general behavior of inter-compartment fluid exchange and soil fluid pressures, the numerical model agrees well with previous experimental findings (e.g. by Wang et al. 1997).

Based on soil column experiments, Wang et al. (1997) suggested to link the thresholds for gas-breaking and gas-closing with the van Genuchten parameter α. Specifically, the experimental results indicated for a gas breaking gas pressure of p _break = ρ ^lg/α and for a gas-closing gas pressure of p _close ≈ p _break/2. In disagreement to this findings, gas pressures calculated with the coupled overland/two-phase flow model did not come close to ρ ^lg/α ≈ 1200 Pa when the calculated Horton runoff was fitted to the experimental data by Smith and Woolhiser (1971). In fact, a gas-breaking gas pressure of p _break = 180 Pa (Table 2) was selected for model verification (Fig. 5), which is one order of magnitude smaller than suggested by Wang et al. (1997) (compare with Culligan et al. 2000). This disagreement might be caused by differences in the liquid depths on the soil surface in the Smith and Woolhiser (1971) benchmark (H < 3 mm) and in the infiltration experiments by Wang et al. (1997) (e.g. H = 2 cm). Obviously, a broader experimental data basis is needed for the determination of a general functional relationship between gas-breaking gas pressure, retention curve (6) and ponding depth.

Numerical discretization

Modelling flow processes in soils such as the infiltration fronts in the experiments by Smith and Woolhiser (1971) (Fig. 5a) or a capillary fringe (Abdul and Gillham 1989) requires a dense spatial discretization in Richards’ or two-phase flow to obtain accurate numerical simulations (Vogel and Ippisch 2008). As long as upscaling rules for complex-structured porous media (see e.g. Doro et al. 2013) are missing, the soil grid requirements (vertically less than 10 cm) impose a bottleneck in catchment modelling with partial differential equations. To simulate liquid infiltration and gas flow efficiently at a resolution of 1 mm in space, vertical soil columns (Fig. 4) were used (compare with Priesack et al. 2006; Ingwersen et al. 2010; Flipo et al. 2012) to produce the numerical results in Figs. 5, 6 7, 8. The resolution in overland flow is 12.2 cm and a constant time step size of 1 s chosen for both compartments. No sub-time steps are used for the fast flow processes overland flow and gas flow in the present study (see Bhallamudi et al. 2003; Kalbacher et al. 2011 for sub-time stepping and adaptive time stepping in OGS, respectively).

Figure 9 reveals the impact of the vertical grid resolution on the inter-compartment fluid exchange $q_{\rm c}^{\rm l}=q_{\rm c}^H, q_{\rm c}^{\rm g}$ and the gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}}.$ The fluxes in Fig. 9a show only small numerical oscillations for fine meshes (e.g. $\Updelta z = 3$ cm resolution). The instabilities are exacerbated by coarser meshes (e.g. $\Updelta z = 10$ cm) and independent of time step size. The maximum in the gas pressure $p^{\rm g}|_{\Upgamma_{\rm c}},$ vanishes by increasing the mesh element size (compare Fig. 9b with Fig. 7e). These results confirm the importance of high performance computing for in-situ applications of integrated models. Research of this type is currently in progress (Kollet et al. 2010; Kolditz et al. 2012 among others). It is worth noting at this point that different numerical models respond differently to rough discretization (see e.g. Delfs et al. 2012b) and may lead to contrasting results in their application.

2D simulations

Natural soils, especially in humid and forested sites, are heterogeneous containing holes from earthworms, degenerated roots, animal burrows, cracks, where soil air may escape into the atmosphere during water infiltration. Earthworms often create abundant vertical pipes depending on vegetation, climate, and soil management. Under many conditions, the potential infiltration rate can easily exceed 10⁻⁴ m/s at a square meter surface area (e.g. Weiler and Naef 2003) such that surface runoff hardly occurs. In general, low pipe densities are reported for polar and very wet regions in the world (e.g. Jones 1994).

This work addresses the influence of lateral gas flow towards preferential flow paths by using two-dimensional soil representations (y, z). The normal vector of the planes (y, z) are directed to x, i.e. the direction of the overland water fluxes. Figure 10a shows simulation results for plane widths up to B = 2 m in the direction of y (lateral extension). Gas can escape unimpeded at both sides y = 0 and y = B, where the gas pressure is set at atmospheric pressure $p^{\rm g} = p^{\rm g}_{\rm atm}.$ In contrast, no liquid passes this boundary (Fig. 10b). No-flow is assigned for both fluids at the bottom z = −30 cm and the flow control factor in the effective relative interface permeabilities (14) is f = 1 (no gas out-breaks).

Fig. 10

Influence of flume width B, when gas flows lateraly to a preferential flow path for gas escape (flow control factor f = 1): a surface runoff; b gas pressure distribution for a flume width of B = 2 m at a simulation time of t = 15 min

Figure 10a shows that Horton runoff is considerably increased by enhanced soil gas pressures for widths B = 2 m. As in the 1D simulations, the maximum gas pressure p ^g is located roughly 2 cm below the compartment interface $\Upgamma_{\rm c} (z=0).$ Below this maximum, the gas pressure p ^g quickly declines with height z to − 30 cm and reaches atmospheric pressure p _atm at the lateral boundaries (Fig. 10b). Thus, given the variability in soil pipe densities in nature (see e.g. Jones 1994) and the uncertainty in their effect on surface runoff, specific in-situ surface runoff experiments should be complemented by soil air measurements.

Conclusions and outlook

A coupled diffusive wave overland/two-phase flow model has been developed. Such detailed model concepts are needed to make well founded assumptions and obtain a better understanding about the range of applicability of state-of-the-art Richards’ models. In fact, overland/soil water exchange affects an array of processes in real-world catchments, e.g. evapotranspiration, groundwater recharge, stream response to storms (see e.g. Abdul and Gillham 1989; Ivanov et al. 2008; Engelhardt et al. 2013a, b; Schulz et al. 2013). Moreover, overland/soil water exchange sometimes interacts with soil air pressures, even with feedbacks (see also Forsyth and Simpson 1991; Wang et al. 1997, 1998; Culligan et al. 2000). Hence, it is desired having a flexible software platform on hand that allows for modelling the ongoing processes and interactions of separated compartments of the hydrologic cycle with clearly defined coupling conditions.

The implementation is available via the open source scientific software project OGS (http://www.opengeosys.net) for simulation of Thermo-Hydro-Mechanical/Chemical (THM/C) processes in porous-fractured media. OGS provides a flexible object-oriented software platform, where numerous process descriptions of different complexity can be simulated and inter-compared (e.g. regarding soils 1D/2D/3D two-phase and Richards’ flow, 1D Green-Ampt model). Coupled surface/subsurface flow can be coupled with heat transport, deformations (see e.g. Watanabe et al. 2010; Singh et al. 2011; Wang et al. 2012), and equilibrium and kinetically-controlled reactive processes (see e.g. Beyer et al. 2006; Centler et al. 2010). Besides skilled handling of flow, transport, and reaction processes, real-life application of a detailed surface/subsurface flow model involves tremendous technical challenges. For this reason, pre- and post-processing of heterogeneous data, 3D visualization, and high performance efficiency in object-oriented codes is subject to current and future work in the OGS-community (e.g. Wang et al. 2011; Rink et al. 2013).

Model verification

The coupled model was verified with a well-established benchmark provided by Smith and Woolhiser (1971) (Fig. 1), which serves for inter-comparing the ability of coupled hydrostatic surface/Richards’ flow models in simulating Horton runoff (Delfs et al. 2012b; Sebben et al. 2012). Smith and Woolhiser (1971) provided experimental data of Horton runoff and soil liquid saturation states (a light oil) for a soil flume. Present work addresses the impact of soil gas (air) pressures on the Horton runoff process by means of a unique overland/two-phase flow model.

The numerical study is conducted in large parts (Figs. 5, 6, 7, 8, 9) with 1D discretization of overland and soil. Liquid and air simultaneously flows through vertical soil columns (Fig. 1). Leakances (12) are modified by a flow control factor f, which is introduced in this work. With this approach, the calculated soil air pressure fluctuates between an upper threshold p _break, where air breaks out from the soil into the atmosphere, and a lower threshold p _close (Fig. 3), where the soil surface closes for air. Air also escapes from the soil at 30 cm depth by enforcing the air pressure to atmospheric pressure $p^{\rm g} = p_{\rm atm}^{\rm g}$ (Dirichet boundary condition). Since soil air will also flow lateraly towards preferential flow paths in nature, a 2D simulation was performed in addition to 1D simulation (Fig. 10). If data availability were high, the coupled model could also have been run in 3D mode for soil.

The extended Smith and Woolhiser (1971) benchmark led to the following results:

• Liquid infiltration results in a sharp rise in air pressure p ^g close to the compartment interface $\Upgamma_{\rm c}$ after overland flow initialization (Fig. 7e).

• The peak in atmospheric excess gas pressure $p_{\rm e}^{\rm g} \approx 200$ Pa is located a few centimeters below the compartment interface $\Upgamma_{\rm c}$ throughout the simulation time of 15 minutes (Figs. 5b, 10b).

• In the calculations, air compression caused an air out-break event through the flume surface during the early part of the hydrograph. Specifically, the new algorithm (13) increased the surface runoff in accordance to the experimental data regarding the amount (model parameters given in Table 2). However, by using a simplified 1D flow model component for soil, the coupled model did not capture the late rise in runoff, which was observed during the classic experiments (Fig. 5b).

• A relatively lower air-breaking pressure (p _break = 180 Pa in Table 2) was found compared to the experimental findings of Wang et al. (1997), who studied ponding on air-confined soil columns.

• 2D simulations demonstrated that soil air pressures act to enhance surface runoff considerably if the lateral distance to an atmospheric pressure boundary (e.g. a soil pipe where air escapes unimpeded) is of the order of 1 meter (Fig. 10).

So to conclude the investigation, soil air pressures amplify Horton runoff, if the water table is close to the surface and the soil air cannot escape unimpeded via abundant preferential flow paths. Truly, the predominant stream flow generation mechanism (Horton, Dunne, macropore, subsurface storm flow) during high precipitation is difficult to determine for a specific site (e.g. Ghasemizadeh and Schirmer 2013). If soil air compression is ignored in field and numerical studies, infiltration excess (Horton) overland flow in near-stream areas (e.g. the riparian zone) might often be misunderstood as saturation excess (Dunne) overland flow. Furthermore, soil air entrapment potentially reduces the infiltration capacity of floodplains and may affect the stability of flood embankments (e.g. Bogacz et al. 2006). The coupled overland/two-phase flow model also enables the applier to study the problem of instability (fingering) at infiltration fronts in presence of surface water ponding and surface runoff (see e.g. Wang et al. 1998; Bogacz et al. 2006). Essentially, our results call for the design of more laboratory and especially field experiments along with soil air measurements and a quantification of the worth of the measurement data (see e.g. Brunner et al. 2012; Wöhling et al. 2013) with the aim to produce reliable surface runoff models of adequate complexity (e.g. in terms of soil air fluxes, preferential flow) for smaller or medium sized catchments (e.g. as in van der Kwaak and Loague 2001; Pérez et al. 2011).

Compartment coupling

Water exchange between surface and subsurface compartments as well as air exchange between soil and atmosphere compartments were calculated in a leakance concept (Hantush 1965), where interface (transition) zones are introduced (Fig. 2). Leakances were modified with reference to state variables (pressures), e.g. to simulate air-pressure counterflow at soil surfaces with a numerical model. Concerning the coupling algorithm, overland and two-phase flow were sequentially calculated in an iteration loop. The study of the mass exchange fluxes (11) revealed:

• Liquid and gas exchange between flow compartments is impeded, if the compartment interface thicknesses exceed threshold values $a^{\rm l} > a^{\rm l}_{\rm c}$ and $a^{\rm g} > a^{\rm g}_{\rm c}$ (relation (16), compare also with Ebel et al. 2009; Liggett et al. 2012).

• Specifically, for the reference parameters in Table 2 holds $a^{\rm l}_{\rm c} = 0.1$ and $a^{\rm g}_{\rm c} = 1$ mm (Fig. 6).

• Leakances at the thresholds $a^{\rm l}_{\rm c}$ and $a^{\rm g}_{\rm c}$ depend linearly on the intrinsic soil permeability (Fig. 7a, b). In addition, the threshold $a^{\rm g}_{\rm c}$ for gas flow increases linearly with the length of the soil column (Fig. 7c). The remaining parameters (resistance in surface flow, soil porosity, soil–water characteristic-curves) are unable to affect leakances at the thresholds (compare with Delfs et al. 2012a).

• Sequential iterative coupling implies step functions in the mass exchange fluxes (Fig. 7d for gas exchange). The step sizes are exacerbated by smaller compartment interface thicknesses a ^l and a ^g (high leakances) according to relation (17). The coupled model becomes unstable for a ^l ≤ 10⁻⁶ m, a ^g ≤ 10⁻¹⁰ m in the reference case (Table 2).

• A lower atmospheric pressure $p^{\rm g}_{\rm atm}$ or hydrostatic surface water pressure p ^H = ρ ^l g H in the mass exchange fluxes (11) mitigates the step sizes in the mass exchange fluxes, which are caused by sequential coupling (Eq. 17).

• A coarse soil discretization (e.g. 10 cm) generates large numerical oscillations in the mass exchange fluxes $q_{\rm c}^{\rm l}=q_{\rm c}^H,$ $q_{\rm c}^{\rm g}$ (Fig. 9).

Clearly, sequential iterative coupling serves as an appropriate numerical tool to model the simultaneously ongoing flow processes and interactions of different hydrological compartments (overland, soil, etc.) and feedbacks (see also Furman 2008; Kim et al. 2009). The alternative is global implicit coupling, which has enormous computational costs and memory requirements. In addition, software development is complex. Thus, (iterative) sequential algorithms are often desired or even necessary, e.g. to select specialized numerical methods for different processes (see e.g. the “Appendix”) or to perform model-to-model coupling across compartment interfaces (e.g. the OGS#SWMM model in Table 1). Concerning feedbacks between groundwater and land surface processes, the primarily hydrogeological code OGS is currently coupled with the modular soil–plant simulation framework Expert-N for detailed evapotranspiration including crop growth and nutrient turnover (Priesack et al. 2006). Indeed, model robustness requires simultaneous solution if processes interact strongly, which is often the case in multi-phase flow (see e.g. Helmig 1997). For this reason, OGS performs implicit coupling in the multi-phase model component (Eq. 20). As a consequence, the governing equations of overland flow (1) and two-phase flow (5) are solved with a partially monolithic matrix assembly (15).

Appendix: Finite element methods

The software platform OGS is primarily an open source finite element simulator for coupled flow, associated transport, and mechanical deformations in porous and fractured media. Finite element methods are based on the variational formulation of a partial differential equation. A general 3D form of non-linear diffusion equations (e.g. flow Eqs. (1, 5) on an open domain $\Upomega \in \mathbb{R}^3$ with a sufficiently regular boundary $\Upgamma$ reads (Quarteroni and Valli 2008)

$$ \int\limits_\Upomega v a(u) \frac{\partial u}{\partial t} \, {\rm d}\Upomega + \int\limits_\Upomega \nabla v \cdot [ b(u) \nabla u ] \, {\rm d}\Upomega = \int\limits_\Upgamma v \underbrace{[ b(u) \nabla u]}_{\mathbf q_\Upgamma} \cdot {\mathbf n_\Upgamma} \, d\Upgamma + \int\limits_\Upomega v q \, {\rm d}\Upomega $$

(18)

where a(u), b(u) are given and depend on the primary variable $u \in H^1(\Upomega)$ or extensions from the Sobolev space $H^1(\Upomega)$ satisfying prescribed Dirichlet boundary conditions. Further, $v \in H^1(\Upomega)$ is a test function. Where the primary variable u is not specified by a Dirichlet boundary condition on $\Upgamma$, a flux ${\bf q}_{\Upgamma}$ arises as a Neumann boundary condition (${\bf n}_\Upgamma$ is the outward-pointing normal vector to the boundary $\Upgamma$).

Standard Galerkin method for flow in the subsurface

OGS discretizes subsurface flow processes (e.g. Richards’, two-phase, groundwater flow) in space with a centered (standard) Galerkin finite element approximation of first-order. The domain $\Upomega$ (Fig. 4) is partitioned into finite elements with $n_{\Upomega}$ mesh nodes at the element corners (see e.g. Helmig 1997). The unknown u and test function v are interpolated in a Galerkin method with piecewise linear shape functions N _j which are unity at certain mesh node $0 \leq j < n_{\Upomega}$, and zero for the remaining mesh nodes $i \neq j: u \approx \bar{u} =\sum_{j=1}^{n_{\Upomega}} u_j N_j, v \approx \bar{v} =\sum_{i=1}^{n_{\Upomega}} v_i N_i$, where $\bar{u}, \bar{v} \in \bar{H}^1 \subset H^1$. Equation (18) becomes an equation system

$$ \sum_{j=1}^{n_{\Upomega}} \bigg[ \frac{{\rm d}u_j}{{\rm d}t}\int\limits_\Upomega N_i a(u) N_j \, {\rm d}\Upomega + u_j \int\limits_\Upomega \nabla N_i \cdot[b(u) \cdot\nabla N_j ] \, {\rm d}\Upomega - \int\limits_\Upgamma N_i {\mathbf q_{\Upgamma}} \cdot {\mathbf n_\Upgamma} \, d\Upgamma - \int\limits_\Upomega N_i q {\rm d}\Upomega \bigg]=0 \quad i=1,\dots ,n_{\Upomega} . $$

(19)

The two-phase flow Eq. (5) can be written as (Park et al. 2011)

$$ \left(\begin{array}{cc} {C^{l}_{ij}} & 0 \\ -{C^{l}_{ij}} & 0 \end{array} \right) \left(\begin{array}{c} \dot{p}^c_{j} \\ \dot{p}^{\rm g}_{j} \end{array} \right) + \left(\begin{array}{cc} {K^{l}_{ij}} & -{K^{g}_{ij}} \\ 0 & {K^{g}_{ij}} \end{array} \right) \left(\begin{array}{c} p^c_{j} \\ p^{\rm g}_{j} \end{array} \right) = \left(\begin{array}{c} {g^{l}_{i}} + {q^{l}_{i}} \\ {g^{g}_{i}} + {q^{g}_{i}} \end{array} \right) $$

(20)

(sum over j), where capillary pressure p ^c and gas pressure p ^g are primary variables (pressure-pressure formulation mode in OGS). The entries of the capacitance matrix C ^l, conductance matrix K ^α, gravity vector g ^l, and the vector q ^l for source / sink term are given by (superscript α  ∈ { l, g})

$$ \begin{aligned} C_{ij}^{l} &= \int\limits_{\Upomega} N_i \phi \rho^{\rm l} \frac{\partial S^{\rm l}(p^c)}{\partial p^c} N_j \, {\rm d}\Upomega \approx \int\limits_{\Upomega} \phi \rho^{\rm l} \frac{\partial S^{\rm l}(p^c)}{\partial p^c} N_j \, {\rm d}\Upomega,\\ K_{ij}^{\alpha}&= \int\limits_{\Upomega} \nabla N_i \left[ \rho^\alpha \frac{k_{rel}^\alpha(S^{\rm l}(p^c)) k}{\mu^\alpha} \nabla N_j \right] \, {\rm d}\Upomega,\\ g_{i}^{\alpha}&= \int\limits_{\Upomega} \frac{\partial N_i}{\partial z} \rho^\alpha \frac{k_{rel}^\alpha(S^{\rm l}(p^c)) k}{\mu^\alpha} \rho^\alpha g\, {\rm d}\Upomega ,\\ q_{i}^{\alpha}&= \int\limits_{\Upgamma} N_i {{\bf q}_{\Upgamma}^{\alpha}} \cdot{{\bf n}_{\Upgamma}} \, d\Upgamma +\int\limits_{\Upomega}N_i q^\alpha \, {\rm d}\Upomega . \end{aligned} $$

(21)

The capacitance matrices are lumped ${\bf C}_{i}^\alpha \approx{\bf C}_{ij}^\alpha$ in (21) and a Gauss integration performed. Simultaneous solution of the equation system (20) with an implicit (backward) Euler method and Picard iteration ensures stable solutions even in the case of highly heterogeneous media. Classic test cases and comparative studies of centered and upwind finite element methods can be found in Helmig (1997), Park et al. (2011).

Upwind control-volume method for overland flow

The diffusive wave overland flow Eq. (1) is discretized in space with a control-volume finite-element method (Gottardi and Venutelli 1993; van der Kwaak and Loague 2001). With $\bar{\nabla}\sum_j u_j N_j = \bar{\nabla}\sum_{i\neq j} N_i (u_i - u_j)$ and mass-matrix lumping, Eq. (18) becomes for 2D overland flow (Gottardi and Venutelli 1993)

$$ \frac{{\rm d}h_j}{{\rm d}t} \int\limits_{\bar{\Upomega}} \phi_a \bar{N_j}\,d\bar{\Upomega} + \int\limits_{\bar{\Upomega}} \bar{\nabla} \bar N_i \times\left[ \sum_{i=1}^{n_{\bar{\Upomega}}} \underbrace{\frac{C H_a^{\nu +1}}{| \bar{\nabla} h|^{1-\mu}} }_{K_{ij}^{up}} \left(\bar{\nabla} \bar N_i \left(h_j - h_i\right) \right) \right]\, {\rm d}\bar{\Upomega} \\ -\int\limits_{\bar{\Upgamma}} \bar N_i {\mathbf q_{\bar{\Upgamma}}^H} \cdot {\mathbf n_{\bar{\Upgamma}}} \, {\rm d}\bar{\Upgamma}- \int\limits_{\bar{\Upomega}} \bar N_i (q^p + q_c^H) \, d\bar{\Upomega} = 0 \quad i=1,\dots ,n_{\Upomega} , $$

(22)

where $n_{\bar{\Upomega}}$ is the number of nodes in $\bar{\Upomega}\in \mathbb{R}^2$ (Fig. 4), $\bar{N_i}, \bar{N_j}$ are 2D shape functions, and the Neumann flux ${\bf q}_{\bar{\Upgamma}}^H$ can be a given flow rate at an inlet or outlet at $\bar{\Upgamma}$. Robin (third type) boundary conditions can be imposed, e.g. to describe uniform flow or free-fall by use of the normal depth (2) as $q_{\bar{\Upgamma}}^H = q^{nd}$, the critical depth (3) as $q_{\bar{\Upgamma}}^H = q^{nd}$, respectively. In order to guarantee fast and stable solutions, upstream weighting (van der Kwaak and Loague 2001)

$$ K_{ij}^{up}=\left \{ \begin{array}{ll} \frac{C H_{a\,j}^{\nu +1}}{|\bar{\nabla}h_j|^{1-\mu}} \quad \hbox{if}\;h_j > h_i\\ \frac{C H_{a\,i}^{\nu +1}}{| \bar{\nabla}h_i|^{1-\mu}} \quad \hbox{else} \end{array},\right.$$

(23)

implicit Euler time-stepping, and Newton linearization are used. The control-volume finite-element method combines in an efficient way the local mass conservation of the finite volume method with the spatial flexibility of finite elements (see van der Kwaak and Loague (2001) for an implicitly coupled surface-subsurface equation system). Qu and Duffy (2007) use an alternative finite volume method for the simulation of hydrostatic surface runoff over complex topographies.