1 Introduction

Fluid infiltration into unsaturated soil is of vital significance from many perspectives. Hydrogeologists, environmentalists, and water resource planners each view water and pollutant infiltration into unsaturated zone from their own viewpoints. A phreatic aquifer is replenished from above by water from various sources: precipitation, irrigation, artificial recharge, etc. In all cases, water moves downward, from ground surface to the water table, through the unsaturated zone. The understanding of and, consequently, the ability to calculate and predict the movement of water in the unsaturated zone is therefore essential when we wish to determine the replenishment of a phreatic aquifer (Bear and Chang 2010).

Transient fluid flow through unsaturated soil is usually described by Richards’ equation derived by combining Darcy’s law and conservation of mass. The equation is a nonlinear parabolic partial differential equation (PDE) for which many numerical and limited analytical solutions exist.

However, the choice of exponential model for water content and hydraulic conductivity linearizes the nonlinear Richards’ equation, making it possible to obtain an analytical solution via classical approaches.

In the last two decades, many numerical techniques have been proposed to investigate water flow infiltration through unsaturated soils. These techniques include finite difference method (FDM), finite element method (FEM), finite volume method (FVM), hp—FEM, and time splitting method (An et al. 2011, 2012; Diaw et al. 2001; Manzini and Ferraris 2004; Solin and Kuraz 2011; Paulus et al. 2013; Fahs et al. 2009; Montazeri Namin and Boroomand 2012; Johari and Hooshmand 2015; Akbari et al. 2012). Analytical solutions, on the other hand, are mainly offered for one-dimensional flow of water through the soil and for restrictive boundary and initial conditions. Exact analytical solutions are desirable because they give a better insight compared to a discrete numerical solution. As such, analytical solutions may be used as benchmark or reference results to test and verify numerical algorithms and codes. Though useful, analytical solutions to transient water infiltration into unsaturated soil samples for various boundary and initial conditions are still lacking.

Parlange et al. (1997) presented a general approximation for a solution to 1D Richards’ equation. Mollerup (2007) used Philip equation and showed that the power series solution may be applied for variable head ponded infiltration, when the ponding depth is described as a power series. Menziani et al. (2007) presented solutions to the linearized one-dimensional Richards’ equation for discrete arbitrary initial and boundary conditions. The result was soil water content at any required time and depth in a domain of semi-infinite unsaturated porous medium. Tracy (2006) developed clean two- and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers. Also, Tracy (2007) obtained three-dimensional analytical solutions for Richards’ equation when a box-shaped soil sample with piecewise-constant head boundary conditions on the top is utilized.

Chen et al. (2001) are developed multidimensional infiltration with arbitrary surface fluxes by a Fourier integral transform. They used exponential model to represent the hydraulic conductivity and pressure relation and the soil water release curve.

Wang et al. (2009) developed an algebraic solution for one-dimensional water infiltration and redistribution without evaporation. They established a relationship between Green–Ampt model and the algebraic solution to analyze physical features of the soil parameters. Ghotbi et al. (2011) applied homotopy analysis method (HAM) to solve the equation analytically and showed that the method is superior over traditional perturbation techniques in the sense that it was not dependent on the assumption of a small parameter as the initial step. Nasseri et al. (2012) presented three major cases for the governing PDE solved by traveling wave solution (TWS) method using general and modified forms of tanh functions. They used TWS as an initial value problem and considered the typical forms of diffusivity and conductivity functions proposed by Brooks and Corey (1964). Huang and Wu (2012) developed analytical solutions to 1D horizontal and vertical water infiltration in saturated–unsaturated soils. They considered variations of influx over time. Asgari et al. (2011) applied exp-function method to 1D Richards’ equation to evaluate its effectiveness and reliability and to reach a more generalized solution to the problem. They used Brooks and Corey (1964) model for soil properties. Basha (2011) developed approximate solutions to Richards’ equation for rational forms of the soil hydraulic conductivity and moisture retention functions by a perturbation expansion method.

A number of researchers investigated analytical solutions to the 1D Richards’ equation by variational iteration method (VIM) (He 1998; Moghimi and Hejazi 2007; Wazwaz 2007), and Adomian decomposition method (ADM) (Nasseri et al. 2008; Serrano and Adomian 1996; Serrano 1998, 2004; Pamuk 2005). They used ADM and VIM in an initial value problem for the equation; however, the series solution obtained by ADM and VIM often did not satisfy the PDE. A number of researchers studied analytical solutions for Richards’ equation in infinite and semi-infinite domains by TWS, Green function, and exponential time integration methods (Zlotnik et al. 2007; Basha 1999; Carr et al. 2011; Jaiswal et al. 2011). Also, Carr and Turner (2014) presented a new numerical approach for a Richards’ equation model of infiltration into unsaturated soils based on an unstructured vertex-centered finite volume method (FVM) and an exponential time integration method.

Unlike the literature, the current study presents new analytical solutions to linearized Richards’ equation for two-dimensional water infiltration and imbibition subject to nonsymmetrical boundary and nonuniform initial conditions. A total of 11 cases are considered, where high water content is imposed on the top, side, or bottom edges of the sample and water is infiltrated (from the top and/or side boundaries) and imbibed (from the bottom boundary) into the sample. Residual water content and/or no-flow boundary condition are assumed on other edges of the sample. Initial conditions include 7 cases of constant residual water content, 2 cases of sinusoidal and 2 cases of exponential water content functions over the sample. Presented analytical solutions are such that both steady and unsteady solutions may be obtained from a single closed-form solution. Two-dimensional and 3-D plots of water content are presented for the transient as well as steady-state conditions. To illustrate the use of the derived equations, water content values from a numerical solution are compared to that from an analytical solution for four cases.

2 Governing Equation

The movement of water flow in unsaturated soil is described by Richards’ equation. This equation is developed by the combination of continuity and Darcy’s law as a momentum equation. This equation is expressed in different forms. The 3-D θ-based form of the equation is (Richards 1931):

$$\frac{\partial \theta }{\partial t} = \frac{\partial }{\partial x} \left( {D_{x} \left( \theta \right)\frac{\partial \theta }{\partial x}} \right) + \frac{\partial }{\partial y} \left( {D_{y} \left( \theta \right)\frac{\partial \theta }{\partial y}} \right) + \frac{\partial }{\partial z} \left( {D_{z} \left( \theta \right)\frac{\partial \theta }{\partial z} + K_{z} \left( \theta \right)} \right)$$
(1)

where \(\theta \left( {\frac{{L^{3} }}{{L^{3} }}} \right)\) is the volumetric water content, \(D\left( \theta \right) = K\left( \theta \right)\frac{\partial h}{\partial \theta }\) is soil water diffusivity for an isotropic media, h(L) is the soil water pressure head (tension head in unsaturated zone), \(K \left( {\frac{L}{T}} \right)\) is the hydraulic conductivity, t(T) is the time, and Z(L) is the vertical space coordinate (upward positive). Water diffusivity, hydraulic conductivity, and water content are functions of soil water pressure head. Various empirical relationships have been used to relate K and θ to h (Brooks and Corey 1964; Van Genuchten 1980; Haverkamp et al. 1990; Fredlund and Xing 1994). Basha (1999) described K and θ in terms of h by the exponential expression:

$$\frac{{\theta - \theta_{r} }}{{\theta_{s} - \theta_{r} }} = S = \exp \left( {\alpha h} \right)$$
(2)
$$K\left( \theta \right) = K_{s} \frac{{\theta - \theta_{r} }}{{\theta_{s} - \theta_{r} }} = K_{s} S = K_{s} \exp \left( {\alpha h} \right)$$
(3)

where θ r is the residual water content, θ s is the saturated water content, \(K_{s} \left( {\frac{L}{T}} \right)\) is the saturated hydraulic conductivity, and \(\alpha \left( {\frac{1}{L}} \right)\) is the pore size distributions index. As stated by Basha (1999), in most cases, the expressions (2) and (3) do not fit experimental data very well over the entire range of h observed. However, they are applicable to situations where the water content variations are relatively small. Also, Tracy (2006, 2007) compared Van Genuchten model (1980) with exponential model (Eqs. 2, 3) for one type of soil and concluded that the exponential model for description of properties of unsaturated soils can pass a physically reasonable criteria.

Substituting (2) and (3) into D(θ) gives:

$$D\left( \theta \right) = K\left( \theta \right)\frac{\partial h}{\partial \theta } = \frac{{K_{s} }}{{\alpha \left( {\theta_{s} - \theta_{r} } \right)}}$$
(4)

Replacing Eqs. (2), (3), and (4) into Eq. (1) provides a linear form of Richards’ equation.

$$\frac{\partial \theta }{\partial t} = D \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + D \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + D \frac{{\partial^{2} \theta }}{{\partial z^{2} }} + f \frac{\partial \theta }{\partial z}$$
(5)

where D and f are:

$$D = \frac{{K_{s} }}{{\alpha \left( {\theta_{s } {-}\theta_{r} } \right)}} ,\quad f = \frac{{K_{s} }}{{\left( {\theta_{s } {-}\theta_{r} } \right)}}$$
(6)

In the present work, new two-dimensional analytical solutions are derived for Eq. (5) subject to nonsymmetrical boundary and nonuniform initial conditions.

3 Analytical Solutions for 2-D Water Infiltration

Richards’ equation in a vertical 2-D plane (x, z) may be expressed as (Eq. 5):

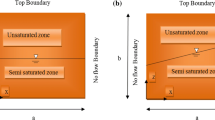
$$\frac{\partial \theta }{\partial t} = D \frac{{\partial^{2} \theta }}{{\partial z^{2} }} + f \frac{\partial \theta }{\partial z} + D \frac{{\partial^{2} \theta }}{{\partial x^{2} }}$$
(7)

where D and f are defined before. Clearly, the equation contains gravity effect in \(\frac{\partial \theta }{\partial z}\) term, a term that differentiates z- from x-axis. Two-dimensional vertical water infiltration has many applications in real world. To find analytical solutions for such applications, many simplifications shall be considered. As an example, vertical section of a homogeneous soil sample may be considered (Fig. 1) and subjected to various boundary and initial conditions. Unsteady analytical solutions to different boundary and initial conditions are sought in this section. Known high water contents of \(\theta_{0 } ( \gg \theta_{r } )\) and/or no-flow conditions are applied on the boundaries, and known water content distributions over the sample are used as the initial conditions.

Fig. 1
figure 1

Vertical section of a homogeneous soil sample in a 2-D (x, z) plane

Full size image

3.1 Case 1: Infiltration From Top and Side of the Sample

As a practical case, ponding an initially drained (to \(\theta_{r }\)) aquifer would cause the ground surface (as a boundary) to become saturated or close to it (\(\theta_{0 }\)). If an intermittent irrigation stream exists on the side and injects flow into the aquifer by maintaining a high water content there (\(\theta_{0 }\)), then vertical and horizontal infiltrations would occur from the ground surface and side of the aquifer. In this case, boundary and initial conditions may be mathematically expressed as:

$$\theta \left( {0,z,t} \right) = \theta_{r } , \quad \theta \left( {a,z,t} \right) = \theta_{0 }$$
(8a)
$$\theta \left( {x,0,t} \right) = \theta_{r } , \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(8b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(8c)

A schematic view of the problem statement is shown in Fig. 2.

Fig. 2
figure 2

Boundary and initial conditions for infiltration from top and side of the sample (case 1)

Full size image

A single closed-form analytical solution is sought that encompasses both steady and unsteady solutions. Thus, the general form of such a solution may be expressed as a combination of a steady (W) and an unsteady (V) term:

$$\theta \left( {x,z,t} \right) = V\left( {x,z,t} \right) + w\left( {x,z} \right)$$
(9)

Obviously, nonhomogenous boundary conditions are to satisfy w(x, z), the steady solution, and homogenous boundary conditions are for V(x, z, t), the unsteady solution. Substituting (9) into (7) and (8a)–(8c) yields:

$$D \frac{{\partial^{2} V}}{{\partial z^{2} }} + f\frac{\partial V}{\partial z} + D\frac{{\partial^{2} V}}{{\partial x^{2} }} - \frac{\partial V}{\partial t} = 0$$
(10a)
$$V\left( {x,0,t} \right) = 0\quad V\left( {x,b,t} \right) = 0$$
(10b)
$$V\left( {0,z,t} \right) = 0\quad V\left( {a,z,t} \right) = 0$$
(10c)
$$V\left( {x,z,0} \right) = \theta_{r } {-}w\left( {x,z} \right)$$
(10d)

Similarly, the PDE for w(x, z) may be written as:

$$D\frac{{\partial^{2} w}}{{\partial z^{2} }} + f\frac{\partial w}{\partial z} + D\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0$$
(11a)
$$w\left( {x,0} \right) = \theta_{r } \quad w\left( {x,b} \right) = \theta_{0 }$$
(11b)
$$w\left( {0,z} \right) = \theta_{r } \quad w\left( {a,z} \right) = \theta_{0 }$$
(11c)

If w(x, z) is assumed to have two components as:

$$w\left( {x,z} \right) = u\left( {x,z} \right) + q\left( x \right)$$
(12)

then the PDE for u(x, z) and q(x) may be written as:

$$Dq^{{\prime \prime }} \left( x \right) = 0$$
(13a)
$$q\left( a \right) = \theta_{0 } ,\quad q\left( 0 \right) = \theta_{r }$$
(13b)
$$D\frac{{\partial^{2} u}}{{\partial z^{2} }} + f\frac{\partial u}{\partial z} + D\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0$$
(14a)
$$u\left( {0,z} \right) = 0 \quad u\left( {a,z} \right) = 0$$
(14b)
$$u\left( {x,0} \right) = \theta_{r } - q\left( x \right) \quad u\left( {x,b} \right) = \theta_{0 } {-}q\left( x \right)$$
(14c)

Utilizing separation of variables for u(x, z), one would get w(x, z) as:

$$w\left( {x,z} \right) = e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \sin \left( { \beta x} \right) [A_{n}^{*} { \sinh }(\tau z) + B_{n}^{*} { \cosh }\left( {\tau z} \right)] + \frac{{\theta_{0 } - \theta_{r } }}{a}x + \theta_{r }$$
(15)

where \(\beta = \frac{n \pi }{a},\quad n = 1, 2, 3, \ldots , \infty\), and \(\tau = \frac{1}{2}\sqrt {\left( {\frac{f}{D}} \right)^{2} + 4\beta^{2} } .\) Also, \(A_{n}^{*}\) and B * n are defined as:

$$B_{n}^{*} = \frac{2}{a}\mathop \int \limits_{0}^{a} \frac{{\theta_{r } - \theta_{0 } }}{a}x\sin \left( {\beta x} \right){\text{d}}x = \frac{{2\left( {\theta_{r } - \theta_{0 } } \right)\left( { - 1} \right)^{n + 1} }}{n \pi }$$
(16a)
$$A_{n}^{*} = \frac{{ - \frac{{2\left( {\theta_{0 } {-}\theta_{r } } \right)}}{n \pi }\left( { \left( { - 1} \right)^{n} - 1} \right) + B_{n}^{*} \left( {1 - e^{{ - \frac{f}{2D}b}} \cosh \left( {\tau b} \right)} \right)}}{{e^{{ - \frac{f}{2D}b}} \sinh \left( {\tau b} \right)}}$$
(16b)

Now, utilizing separation of variables for V(x, z, t):

$$V\left( {x,z,t} \right) = Z\left( z \right) X\left( x \right) T\left( t \right)$$
(17)

And substituting (17) into (10a), one would get:

$$\frac{{X^{{\prime \prime }} }}{X} = - \frac{{Z^{{\prime \prime }} }}{Z} - \frac{f}{D}\frac{{Z^{{\prime }} }}{Z} + \frac{1}{D}\frac{{T^{{\prime }} }}{T} = \mu$$
(18)

where μ is an arbitrary constant. If \(\mu < 0\), say μ = −λ 2, λ > 0, then considering the boundary conditions of (10c), X(x) in (18) may be written as:

$$X_{n} = C_{n}^{*} \sin \left( {\lambda x } \right) ,\quad \lambda = \frac{n \pi }{a} ,\quad n = 1, 2, 3, \ldots , \infty$$
(19)

where C * n is a constant. Substituting −λ 2 into (18) for \(\frac{{X^{{\prime \prime }} }}{X}\) yields:

$$\frac{{Z^{{\prime \prime }} }}{Z} + \frac{f}{D}\frac{{Z^{{\prime }} }}{Z} = \lambda^{2} + \frac{1}{D}\frac{{T^{{\prime }} }}{T} = \rho$$
(20)

where ρ is an arbitrary constant. If ρ ≥ 0, then a trivial solution for Z(z) in (20) would be obtained. If ρ < 0, say \(\rho = - \gamma^{2} - \left( {\frac{f}{D}} \right)^{2} \frac{1}{4} ,\) γ > 0, then applying the boundary condition of (10b) in (20) would yield Z(z) as:

$$Z_{m} = D_{m}^{*} e^{{ - \frac{f}{2D}z}} \sin \left( {\gamma z} \right),\quad \gamma = \frac{m \pi }{b} ,\quad m = 1, 2, 3, \ldots , \infty$$
(21)

where D * m is a constant. Also, T(t) in (20) becomes:

$$T = E_{mn}^{*} e^{{ - \left( {\lambda^{2} + \gamma^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}}$$
(22)

where E * mn is a constant. Substituting (19), (21), (22) into (17) yields:

$$V\left( {x,z,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } C_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \gamma^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}}$$
(23)

where C mn is \(C_{n}^{*} D_{m}^{*} E_{mn}^{*} .\) Substituting the boundary condition of (10d) into (23) and using Fourier series properties for (23), C mn is written as:

$$\begin{aligned} C_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{r } e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) {\text{d}}z{\text{d}}x \\ & = \frac{4}{b}\left( { - \frac{1}{2}\left( {\frac{{A_{n}^{*} \gamma \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \gamma^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \gamma^{2} }}\left( {\gamma \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \gamma } \right)} \right)} \right. \\ \left. {\quad+\,\frac{{\left( {\theta_{r } {-}\theta_{0 } } \right)\left( { - 1} \right)^{n + 1} }}{n \pi } \frac{1}{{\left( {\frac{f}{2D}} \right)^{2} + \gamma^{2} }}\left( {e^{{ \frac{f}{2D}b}} \gamma \left( { - 1} \right)^{m + 1} + \gamma } \right)} \right) \\ \end{aligned}$$
(24)

Substituting (15) and (23) into (9), θ(x, z, t) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) & = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } C_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \gamma^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ &+\,e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \sin \left( { \beta x} \right) [A_{n}^{*} { \sinh }(\tau z) + B_{n}^{*} { \cosh }\left( {\tau z} \right)] + \frac{{\theta_{0 } {-}\theta_{r } }}{a}x + \theta_{r } \\ \end{aligned}$$
(25)

As seen, the equation consists of four terms: a function of (x, z, t), a function of (x, z), a function of x only, and a constant. All boundary and initial conditions of (8a)–(8c), as well as the PDE (Eq. 7), are satisfied by (25).

As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. In Eq. 25, summation convergence occurs very rapidly, partly because n and m (showing number of terms in the summation) lie in denominators of summations coefficients. Furthermore, due to the presence of a time-dependent exponential decay term in the first term of Eq. 25, many terms are needed for summation calculation at early times, while at longer times, often a handful of terms is sufficient to obtain a reasonable accuracy.

In order to confirm summations convergence in Eq. 25, water content at different positions is calculated using summations truncation with different values of n and m (Table 1). The table is generated for the following parameters:

$$t = 30\;{ \hbox{min} },\;a = 100 \;{\text{cm}},\; b = 100\;{\text{cm}},\; \theta_{0 } = 0.3,\; \theta_{r } = 0.0286,\; \theta_{s } = 0.3658, \;\alpha = 0.01\;{\text{cm}}^{ - 1} ,\;K_{s} = 10^{ - 3} {\text{cm}}\;{\text{s}}^{ - 1}$$
Table 1 Water content values for the analytical solution (with different summation truncations), FDM solution (with different mesh sizes), and the relative error for case 1 at t = 30 min
Full size table

To be consistent with the literature, \(\theta_{0 } , \;\theta_{r } ,\; \theta_{s } ,\; \alpha\) and K s values studied by Huang and Wu (2012) and Montazeri Namin and Boroomand (2012) are selected. As seen in Table 1, change in water content is negligible at n and m = 1 to 10 and higher. As a consequence, θ was calculated for n = m = 1 to 10 in Eq. 25.

To illustrate the use of the derived equations, water content values from an explicit scheme finite difference method (FDM) solution (to Eq. 7) are compared to the analytical solution (Eq. 25) for t = 30 min and various values of x and z (columns 7 and 8 in Table 1). Ninth column shows

$$Error_{\text{Relative}} = \frac{{\left| {\theta_{\text{Analytical}} - \theta_{\text{Numerical}} } \right|}}{{\left| {\theta_{\text{Analytical}} } \right|}} \times 100\; \%$$

based on columns 4 (incorporating > 100 summation terms) and column 8 (FDM for ∆t = 2 s, ∆z = 2.5 cm and ∆x = 2.5 cm). As shown, errors are all <2 % which may be deemed reasonable.

Based on Eq. (25), water content contours are drawn in Fig. 3a–d for t = 5, 15, 60 min and steady state, respectively.

Fig. 3
figure 3

Water content contours based on Eq. (25) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

Graphs clearly show the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm) and right (x = 100 cm) edges of the soil sample and at the residual value of \(\theta_{r } = 0.0286\) on the bottom (z = 0) and left (x = 0 cm) edges. A 3-D plot of water content–depth–distance for steady state (corresponding to Fig. 3d) is also visualized in Fig. 4.

Fig. 4
figure 4

3-D plot of water content–depth–distance based on the analytical solution for case 1 (Eq. 25) for the steady-state condition

Full size image

3.2 Case 2: Infiltration from Top and Imbibition from Bottom of the Sample

As a practical case, ponding an initially drained (to \(\theta_{r }\)) aquifer would cause the ground surface (as a boundary) to become saturated or close to that (\(\theta_{0 }\)). If a shallow water table exists at the bottom of the aquifer and maintains a high water content there (\(\theta_{0 }\)), then vertical infiltration from top and imbibition from bottom of the soil would occur. In this case, boundary and initial conditions may be mathematically expressed as:

$$\theta \left( {0,z,t} \right) = \theta_{r } \quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(26a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(26b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(26c)

Following similar mathematical procedure as before (case 1), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } C_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \gamma^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \sin \left( { \beta x} \right) [A_{n}^{*} { \sinh }(\tau z) + B_{n}^{*} { \cosh }\left( {\tau z} \right)] + \theta_{r } \\ \end{aligned}$$
(27)

where \(C_{mn} , A_{n}^{*} \;{\text{and}}\;B_{n}^{*}\) in the case are defined as:

$$\begin{aligned} C_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{r } e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) {\text{d}}z {\text{d}}x \\ = & \frac{4}{b}\left( { - \frac{1}{2}\left( {\frac{{A_{n}^{*} \gamma \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \gamma^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \gamma^{2} }}\left( {\gamma \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \gamma } \right)} \right)} \right) \\ \end{aligned}$$
(28a)
$$B_{n}^{*} = \frac{{2\left( {\theta_{0} - \theta_{r} } \right)(\left( { - 1} \right)^{n + 1} + 1) }}{n \pi }$$
(28b)
$$A_{n}^{*} = \frac{{B_{n}^{*} \left( {1 - e^{{ - \frac{f}{2D}b}} \cosh \left( {\tau b} \right)} \right)}}{{e^{{ - \frac{f}{2D}b}} \sinh \left( {\tau b} \right)}}$$
(28c)

Also, \(\gamma , \lambda , \beta\) and τ are identical to what was defined in case 1. As seen, Eq. (27) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. All boundary and initial conditions of (26a)–(26c), as well as the PDE (Eq. 7), are satisfied by (27). As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. Similar to case 1, θ is calculated for n = m = 1 to 10 in Eq. 27. Based on the equation, water content contours are drawn in Fig. 5a–d for t = 5, 15, 60 min and steady state, respectively. Soil parameters used for the problem are identical to those used in case 1.

Fig. 5
figure 5

Water content contours based on Eq. (27) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

Graphs clearly show the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm) and bottom (z = 0 cm) sides of the soil sample and at the residual value of \(\theta_{r } = 0.0286\) on the right (x = 100) and left (x = 0 cm) sides of the sample. Figures do not have symmetry about \(z = \frac{b}{2}{\text{line }}\) due to \(\frac{\partial \theta }{\partial z}\) term in Eq. (7) which represents the gravity term. Therefore, water content values on the upper half of the sample (where z > b/2) are somewhat greater than the values on the lower half. A 3-D plot of water content–depth–distance for steady-state condition (corresponding to Fig. 5d) is also visualized in Fig. 6.

Fig. 6
figure 6

3-D plot of water content–depth–distance based on the analytical solution for case 2 (Eq. 27) for the steady-state condition

Full size image

3.3 Case 3: Infiltration from Top and side, Imbibition from Bottom of the Sample

This case is a combination of two previous cases, whereby soil sample is initially drained to \(\theta_{r }\) and exposed to a high water content (\(\theta_{0 }\)) on top, bottom, and one side and to a low water content (\(\theta_{r }\)) on the other side. Boundary and initial conditions may be mathematically expressed as:

$$\theta \left( {0,z,t} \right) = \theta_{r } \quad \theta \left( {a,z,t} \right) = \theta_{0}$$
(29a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(29b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(29c)

Following similar mathematical procedure as before (case 1), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } C_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\gamma z} \right) \sin \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \gamma^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \sin \left( { \beta x} \right) [A_{n}^{*} { \sinh }(\tau z) + B_{n}^{*} { \cosh }\left( {\tau z} \right)] + \frac{{\theta_{0 } {-}\theta_{r } }}{a}x + \theta_{r } \\ \end{aligned}$$
(30)

where C mn, γ, λ, β, and τ are identical to what was defined in case 1. A * n is identical to case 2; however, B * n is defined as:

$$B_{n}^{*} = \frac{{2\left( {\theta_{0} - \theta_{r} } \right) }}{n \pi }$$
(31)

Obviously, boundary and initial conditions of (29a)–(29c), as well as the PDE (Eq. 7), are satisfied by (30). Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 30.

Based on the equation, water content contours are drawn in Fig. 7a–d for t = 5, 15, 60 min and steady state, respectively. Soil parameters used for the problem are identical to those used in case 1.

Fig. 7
figure 7

Water content contours based on Eq. (30) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

Graphs clearly show the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm), bottom (z = 0 cm), and right side of the soil sample, while the residual water content of \(\theta_{r } = 0.0286\) is maintained on the left (x = 0) side. Again, figures do not have symmetry about \(z = \frac{b}{2}{\text{line }}\) due to \(\frac{\partial \theta }{\partial z}\) term in Eq. (7) which represents the gravity term. Therefore, water content values on the upper half of the sample (where z > b/2) are slightly greater than the values on the lower half. A 3-D plot of water content–depth–distance for steady state (corresponding to Fig. 7d) is also visualized in Fig. 8.

Fig. 8
figure 8

3-D plot of water content–depth–distance based on the analytical solution for case 3 (Eq. 30) for the steady-state condition

Full size image

3.4 Case 4: Infiltration from Top with No Flow on One Side of the Sample

Again, a practical case is considered whereby ground surface ponding occurs on an initially drained (to \(\theta_{r }\)) aquifer, causing infiltration from the top boundary. If one side of the aquifer is impervious, then boundary and initial conditions may be mathematically expressed as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0\quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(32a)
$$\theta \left( {x,0,t} \right) = \theta_{r } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(32b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(32c)

A schematic view of the problem statement is shown in Fig. 9.

Fig. 9
figure 9

Boundary and initial conditions for infiltration from top and no flow on one side of the sample (case 4)

Full size image

A single closed-form analytical solution is sought that encompasses both steady and unsteady solutions. Thus, the general form of such a solution may be expressed as a combination of a steady (w) and an unsteady (V) term:

$$\theta \left( {x,z,t} \right) = V\left( {x,z,t} \right) + w\left( {x,z} \right)$$
(33)

Obviously, nonhomogenous boundary conditions are to satisfy w(x, z), the steady solution, and homogenous boundary conditions are for V(x, z, t), the unsteady solution. Substituting (33) into (7) and (32a)–(32c) yields:

$$D \frac{{\partial^{2} V}}{{\partial z^{2} }} + f\frac{\partial V}{\partial z} + D\frac{{\partial^{2} V}}{{\partial x^{2} }} - \frac{\partial V}{\partial t} = 0$$
(34a)
$$\frac{\partial V}{\partial x} \left( {0,z,t} \right) = 0\quad V\left( {a,z,t} \right) = 0$$
(34b)
$$V\left( {x,0,t} \right) = 0\quad V\left( {x,b,t} \right) = 0$$
(34c)
$$V\left( {x,z,0} \right) = \theta_{r } - w\left( {x,z} \right)$$
(34d)

Similarly, the PDE for w(x, z) may be written as:

$$D\frac{{\partial^{2} w}}{{\partial z^{2} }} + f\frac{\partial w}{\partial z} + D\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0$$
(35a)
$$w\left( {x,0} \right) = \theta_{r } \quad w\left( {x,b} \right) = \theta_{0 }$$
(35b)
$$\frac{\partial w}{\partial x} \left( {0,z} \right) = 0\quad w\left( {a,z} \right) = \theta_{r }$$
(35c)

If w(x, z) is assumed to have two components as:

$$w\left( {x,z} \right) = u\left( {x,z} \right) + q\left( x \right)$$
(36)

then the PDE for u(x, z) and q(x) may be written as:

$$Dq^{{\prime \prime }} \left( x \right) = 0$$
(37a)
$$q^{{\prime }} \left( 0 \right) = 0\quad q\left( a \right) = \theta_{r }$$
(37b)
$$D\frac{{\partial^{2} u}}{{\partial z^{2} }} + f\frac{\partial u}{\partial z} + D\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0$$
(38a)
$$\frac{\partial u}{\partial x} \left( {0,z} \right) = 0\quad u\left( {a,z} \right) = 0$$
(38b)
$$u\left( {x,0} \right) = \theta_{r } - q\left( x \right)\quad u\left( {x,b} \right) = \theta_{0 } {-}q\left( x \right)$$
(38c)

The solution to (37a) with boundary condition of (37b) is \(q\left( x \right) = \theta_{r } .\) Utilizing separation of variables for u(x, z) as:

$$u\left( {x,z} \right) = Z\left( z \right) X\left( x \right)$$
(39)

And substituting (39) into (38a), one would get:

$$\frac{{X^{{\prime \prime }} }}{X} = - \frac{{Z^{{\prime \prime }} }}{Z} - \frac{f}{D}\frac{{Z^{{\prime }} }}{Z} = \mu$$
(40)

where μ is an arbitrary constant. If μ ≥ 0, then a trivial solution for X(x) in (40) would be obtained. If μ < 0, say \(\mu = - \beta^{2}\), β > 0, then applying the boundary conditions of (38b) in (40) would yield X(x) as:

$$X_{n} = A_{n} \cos \left( {\beta x } \right),\quad \beta = \frac{{\left( {2n - 1} \right) \pi }}{2a},\quad n = 1, 2, 3, \ldots , \infty$$
(41)

Substituting −β 2 into (40) for \(\frac{{X^{{\prime \prime }} }}{X}\) and applying the boundary condition of \(u\left( {x,0} \right) = \theta_{r } - q\left( x \right)\) in (38c) yields:

$$Z = C_{1} e^{{ - \frac{f}{2D}z}} \sinh \left( {\tau z} \right),\quad \tau = \frac{1}{2}\sqrt {\left( {\frac{f}{D}} \right)^{2} + 4\beta^{2} }$$
(42)

Substituting (41) and (42) into (39) would give:

$$u\left( {x,z} \right) = e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } A_{n}^{*} \cos \left( { \beta x} \right) { \sinh }(\tau z)$$
(43)

where A * n is A n C 1. Now, using the boundary condition of \(u\left( {x,b} \right) = \theta_{0 } {-}q\left( x \right)\) in (38c) and Fourier series properties, A * n in (43) would be obtained as:

$$A_{n}^{*} = \frac{{4 \left( {\theta_{0} - \theta_{r} } \right) \left( { - 1} \right)^{n + 1} }}{{\pi \left( {2n - 1} \right) e^{{ - \frac{f}{2D}b}} \sinh \left( {\tau b} \right)}}$$
(44)

Utilizing separation of variables for V(x, z, t) as:

$$V\left( {x,z,t} \right) = Z\left( z \right) X\left( x \right) T\left( t \right)$$
(45)

And substituting (45) into (34a), one would get:

$$\frac{{X^{{\prime \prime }} }}{X} = - \frac{{Z^{{\prime \prime }} }}{Z} - \frac{f}{D}\frac{{Z^{{\prime }} }}{Z} + \frac{1}{D}\frac{{T^{{\prime }} }}{T} = \mu$$
(46)

where μ is an arbitrary constant. If \(\mu < 0\), say μ = −λ 2, λ > 0, then considering the boundary conditions of (34b), X(x) in (46) may be written as:

$$X_{n} = C_{n} \cos \left( {\lambda x } \right) ,\quad \lambda = \frac{{\left( {2n - 1} \right) \pi }}{2a},\quad n = 1, 2, 3, \ldots , \infty$$
(47)

where C n is a constant. Substituting -λ 2 into (46) for \(\frac{{X^{{\prime \prime }} }}{X}\) yields:

$$\frac{{Z^{{\prime \prime }} }}{Z} + \frac{f}{D}\frac{{Z^{{\prime }} }}{Z} = \lambda^{2} + \frac{1}{D}\frac{{T^{{\prime }} }}{T} = \rho$$
(48)

where ρ is an arbitrary constant. If ρ ≥ 0, then a trivial solution for Z(z) in (48) would be obtained. If ρ < 0, say \(\rho = - \nu^{2} - \left( {\frac{f}{D}} \right)^{2} \frac{1}{4} ,\) ν > 0, then applying the boundary condition of (34c) in (48) would yield Z(z) as:

$$Z_{m} = B_{m} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) ,\quad \nu = \frac{m \pi }{b},\quad m = 1, 2, 3, \ldots , \infty$$
(49)

where B m is a constant. Also, T(t) in (48) becomes:

$$T = C e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}}$$
(50)

where C is a constant. Substituting (47), (49) and (50) into (45) yields:

$$V\left( {x,z,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}}$$
(51)

where A mn is \(C_{n} B_{m} C\). Substituting the boundary condition of (34d) into (51) and using Fourier series properties for (51), A mn , is written as:

$$\begin{aligned} A_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{r } e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\nu z} \right) \sin \left( {\lambda x } \right) {\text{d}}z {\text{d}}x \\ = & - \frac{2}{b} \left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }}} \right) \\ \end{aligned}$$
(52)

Substituting (36), (43) and (51) into (33), θ(x, z, t) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } A_{n}^{*} \cos \left( { \beta x} \right) { \sinh }(\tau z) + \theta_{r} \\ \end{aligned}$$
(53)

Boundary and initial conditions of (32a)–(32c), as well as the PDE (Eq. 7), are all satisfied by (53). As seen, Eq. (53) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution.

In order to confirm summations convergence in Eq. 53, water content at different positions is calculated using summations truncation with different values of n and m (Table 2). The soil parameters used for the problem are identical to those used in case 1. As seen in Table 2, change in water content is negligible at n and m = 1 to 10 and higher. As a consequence, θ is calculated for n = m = 1 to 10 in Eq. 53. To illustrate the use of the derived equations, water content values from an explicit scheme finite difference method (FDM) solution (to Eq. 7) are compared to the analytical solution (Eq. 53) for t = 30 min and various values of x and z (columns 7 and 8 in Table 2). Ninth column shows ErrorRelative based on columns 4 (incorporating > 100 summation terms) and column 8 (FDM for ∆t = 2 s ∆z = 2.5 and ∆x = 2.5 cm). As shown, errors are all <2 % which may be deemed reasonable.

Table 2 Water content values for the analytical solution (with different summation truncations), FDM solution (with different mesh sizes), and the relative error for case 4 at t = 30 min
Full size table

Based on the equation, water content contours are drawn in Fig. 10a–d for t = 5, 15, 60 min and steady state, respectively.

Fig. 10
figure 10

Water content contours based on Eq. (53) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

Graphs clearly show the infiltrating water content front from the top side of the soil sample (z = 100 cm) that remains at θ 0 = 0.3 there, and the residual value of θ r = 0.0286 is retained on the right (x = 100) and bottom (z = 0 cm) sides. Evidently, water content contours are perpendicular to the left side of the sample, confirming a no-flow boundary condition there. A 3-D plot of water content–depth–distance for steady state (corresponding to Fig. 10d) is also visualized in Fig. 11.

Fig. 11
figure 11

3-D plot of water content–depth–distance based on the analytical solution for case 4 (Eq. 53) for the steady-state condition

Full size image

3.5 Case 5: Infiltration from Top and One Side with No Flow on the Other Side of the Sample

This case is similar to the previous case, except for the fact that the sample is infiltrated from both the top and one side. Boundary and initial conditions for this case may be mathematically expressed as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0\quad \theta \left( {a,z,t} \right) = \theta_{0}$$
(54a)
$$\theta \left( {x,0,t} \right) = \theta_{r } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(54b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(54c)

Following similar mathematical procedures as before (case 4), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \cos \left( { \beta x} \right)[ A_{n}^{*} { \sinh }(\tau z) + B_{n}^{*} {\text{cosh}}\left( {\tau z} \right)] + \theta_{0} \\ \end{aligned}$$
(55)

where \(A_{mn} , A_{n}^{*} and B_{n}^{*}\) in the case are defined as:

$$\begin{aligned} A_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{r } e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) {\text{d}}z{\text{d}}x \\ & = \frac{4}{b}\left( { - \frac{1}{2}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \nu^{2} }}\left( {\nu \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \nu } \right)} \right)} \right) \\ & +\,\frac{{2\left( {\theta_{r } {-}\theta_{0 } } \right)\left( { - 1} \right)^{n + 1} }}{{\left( {2n - 1} \right) \pi }} \frac{1}{{\left( {\frac{f}{2D}} \right)^{2} + \nu^{2} }}\left( {e^{{ \frac{f}{2D}b}} \nu \left( { - 1} \right)^{m + 1} + \nu } \right) \\ \end{aligned}$$
(56a)
$$B_{n}^{*} = \frac{{4\left( {\theta_{r } {-}\theta_{0 } } \right)\left( { - 1} \right)^{n + 1} }}{{\pi \left( {2n - 1} \right)}}$$
(56b)
$$A_{n}^{*} = - \frac{{B_{n}^{*} }}{{{ \tanh }\left( {\tau b} \right)}}$$
(56c)

Also, \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4. All boundary and initial conditions in (54a)–(54c), as well as the PDE (Eq. 7), are satisfied by (55). As seen, Eq. (55) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 55.

Based on the equation, water content contours are drawn in Fig. 12a–d for t = 5, 15, 60 min and steady state, respectively. Soil parameters used for the problem are identical to those used in case 1.

Fig. 12
figure 12

Water content contours based on Eq. (55) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

Graphs clearly show the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm) and the right (x = 100 cm) side of the sample, with the residual value of \(\theta_{r } = 0.0286\) on the bottom (z = 0 cm) side. Again, water content contours are perpendicular to the left side of the sample, confirming no-flow boundary condition there.

3.6 Case 6: Infiltration from Top and One Side, Imbibition from Bottom, with No Flow on the Other Side of the Sample

This case is similar to the previous one, except for the fact that the sample is allowed to imbibe water from the bottom side, too. Boundary and initial conditions for this case may be mathematically expressed as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0\quad \theta \left( {a,z,t} \right) = \theta_{0}$$
(57a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(57b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(57c)

Following similar mathematical procedures as before (case 4), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\theta \left( {x,z,t} \right) = \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} + \theta_{0}$$
(58)

where in this case \(A_{mn}\) is defined as:

$$A_{mn} = \frac{{8\left( {\theta_{r } {-}\theta_{0 } } \right)\left( { - 1} \right)^{n + 1} }}{{b \left( {2n - 1} \right) \pi }} \frac{1}{{\left( {\frac{f}{2D}} \right)^{2} + \nu^{2} }}\left( {e^{{ \frac{f}{2D}b}} \nu \left( { - 1} \right)^{m + 1} + \nu } \right)$$
(59)

Also, \(\nu , \lambda\) are identical to what was defined in case 4. All boundary and initial conditions of (57a)–(57c), as well as the PDE (Eq. 7), are satisfied by (58). As seen, Eq. (58) simply consists of two terms: a function of (x, z, t) and a constant.

As t → ∞, the first term vanishes, and θ 0 remains as the residual or the steady-state solution, meaning that, at the steady state the entire soil sample would have a uniform constant water content \((\theta_{0} )\).

Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 58.

Based on the equation, water content contours are drawn in Fig. 13a–d for t = 5, 15, 60 and 120 min, respectively. Soil parameters used for the problem are identical to those used in case 1. Graphs clearly show the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm) and right (x = 100 cm) sides and on the bottom of the sample. Evidently, water content contours are perpendicular to the left side of the sample verifying no-flow boundary condition there.

Fig. 13
figure 13

Water content contours based on Eq. (58) for: a t = 5 min, b t = 15 min, c t = 60 min, and d t = 120 min

Full size image

3.7 Case 7: Infiltration from Top, Imbibition from Bottom, and No Flow on One Side of the Sample

This case is similar to case 2 except for one side boundary which is changed to no-flow boundary. Boundary and initial conditions for this case may be mathematically written as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0 \quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(60a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(60b)
$$\theta \left( {x,z,0} \right) = \theta_{r }$$
(60c)

Following similar mathematical procedures as before (case 4), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \cos \left( { \beta x} \right)[ A_{n}^{*} \sinh (\tau z) + B_{n}^{*} \cosh \left( {\tau z} \right)] + \theta_{r} \\ \end{aligned}$$
(61)

where \(A_{mn} , A_{n}^{*} and B_{n}^{*}\) in the case are defined as:

$$\begin{aligned} A_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{r } e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right){\text{d}}z\,{\text{d}}x \\ = & - \frac{2}{b}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \nu^{2} }}\left( {\nu \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \nu } \right)} \right) \\ \end{aligned}$$
(62a)
$$B_{n}^{*} = \frac{{4\left( {\theta_{0 } {-}\theta_{r } } \right)\left( { - 1} \right)^{n + 1} }}{{\pi \left( {2n - 1} \right)}}$$
(62b)
$$A_{n}^{*} = \frac{{B_{n}^{*} \left( {e^{{ \frac{f}{2D}b}} - \cosh \left( {\tau b} \right)} \right)}}{{\sinh \left( {\tau b} \right)}}$$
(62c)

Also, \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4. All boundary and initial conditions of (60a) to (60c), as well as the PDE (Eq. 7), are satisfied by (61). As seen, Eq. (61) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution.

Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 61.

Based on the equation, water content contours are drawn in Fig. 14a–d for t = 5, 15, 60 min and steady state, respectively. Soil parameters used for the problem are identical to those used in case 1. Graphs depict the infiltrating water content front that remains at \(\theta_{0 } = 0.3\) on the top (z = 100 cm) and bottom (z = 0 cm) boundaries of the sample, with the residual value of \(\theta_{r } = 0.0286\) on the right (x = 100 cm) side. As shown, water content contours are perpendicular to the left side of the sample verifying no-flow boundary condition there. Again, figures do not have symmetry about \(z = \frac{b}{2}{\text{line }}\) due to \(\frac{\partial \theta }{\partial z}\) term in Eq. (7) which represents the gravity term. Therefore, water content values on the upper half of the sample (where z > b/2) are slightly greater than the values on the lower half.

Fig. 14
figure 14

Water content contours based on Eq. (61) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

3.8 Case 8: Infiltration from Top, Imbibitions from Bottom, No-Flow on One Side of the Sample, with A Sinusoidal Initial Condition

This case is similar to case 7 but with a sinusoidal initial condition for water content over the domain. Boundary and initial conditions for this case may be mathematically written as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0\quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(63a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(63b)
$$\theta \left( {x,z,0} \right) = \theta_{0 } \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi z}{b}} \right)$$
(63c)

The sinusoidal function for initial condition sets a maximum water content of θ 0 on the center of the sample, and a minimum of zero water content on all four edges. A 3-D plot of the initial condition (Eq. 63c) with θ 0 = 0.3, a = 100 and b = 100 cm is shown in Fig. 15.

Fig. 15
figure 15

3-D plot of the initial water content distribution (Eq. 63-c)

Full size image

Following similar mathematical procedures as before (case 7), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \cos \left( { \beta x} \right)[ A_{n}^{*} \sinh (\tau z) + B_{n}^{*} \cosh \left( {\tau z} \right)] + \theta_{r} \\ \end{aligned}$$
(64)

where \(A_{mn}\) in this case is defined as:

$$\begin{aligned} A_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left( {\theta_{0 } \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi z}{b}} \right)e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} } \right)\sin \left( {\nu z} \right) \cos \left( {\lambda x } \right){\text{d}}z\,{\text{d}}x \\ = & \frac{4}{ b}\left\{ {\left( {\theta_{0} \frac{4}{{\pi \left( {4n^{2} - 4n - 3} \right)}} \times \frac{{2Hb^{2} \pi^{2} m\left( {1 + e^{Hb} \left( { - 1} \right)^{m} } \right)}}{{H^{4} b^{4} + 2H^{2} b^{2} \pi^{2} + 2H^{2} b^{2} \pi^{2} m^{2} + \pi^{4} - 2\pi^{4} m^{2} + \pi^{4} m^{4} }}} \right.} \right. \\ & \left. { +\,\theta_{r} \frac{{2mb\left( {\left( { - 1} \right)^{n} - \left( { - 1} \right)^{n + m} be^{Hb} } \right)}}{{2nH^{2} b^{2} + 2nm^{2} \pi^{2} - H^{2} b^{2} - m^{2} \pi^{2} }}} \right) \\ & \left. { - \frac{1}{2}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \nu^{2} }}\left( {\nu \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \nu } \right)} \right)} \right\} \\ \end{aligned}$$
(65)

where \(A_{n}^{*} {\text{and }}B_{n}^{*}\) are identical to what was defined in case 7 and \(H = \frac{f}{2D}\). Also, \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4. All boundary and initial conditions of (63a)–(63c), as well as the PDE (Eq. 7), are satisfied by (64). As seen, Eq. (64) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 64.

Based on the equation, water content contours are drawn in Fig. 16a–d for t = 5, 15, 60 min and steady state, respectively. Soil parameters used for the problem are identical to those used in case 1.

Fig. 16
figure 16

Water content contours based on Eq. (64) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

At early times (Fig. 16a, b), water content contours reflect a combination of two distinct water content gradients: (1) from center of the domain outward due to the initial sinusoidal (bell shape) water content and (2) from top to bottom (the infiltrating front) due to the gradient in water contents on the top and bottom boundaries. As time elapses, the bell-shaped gradient attenuates, and eventually water content contours approach a steady-state profile associated with the last two terms in Eq. (64). Steady-state contours for this case (Fig. 16d) are exactly the same as contours for case 7 (Fig. 14d). A 3-D plot of water content–depth–distance for t = 5 min (corresponding to Fig. 16a) is also visualized in Fig. 17.

Fig. 17
figure 17

3-D plot of water content–depth–distance based on the analytical solution for case 8 (Eq. 64) for t = 5 min

Full size image

3.9 Case 9: Infiltration from Top, No Flow on One Side of the Sample, with a Sinusoidal Initial Condition

This case is similar to case 4 but with a sinusoidal initial condition for water content over the domain. Boundary and initial conditions for this case may be mathematically written as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0 \quad \left( {a,z,t} \right) = \theta_{r}$$
(66a)
$$\theta \left( {x,0,t} \right) = \theta_{r } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(66b)
$$\theta \left( {x,z,0} \right) = \theta_{0 } \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi z}{b}} \right)$$
(66c)

The sinusoidal initial function is identical to the one in the previous case, setting a maximum of theta0 on the center of the sample, and zero water content on all four edges. Following a similar mathematical procedure as before (case 4), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } A_{n}^{*} \cos \left( { \beta x} \right) \sinh (\tau z) + \theta_{r} \\ \end{aligned}$$
(67)

where A mn in this case is defined as:

$$\begin{aligned} A_{mn} = & \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{0 } \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi z}{b}} \right)e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right){\text{d}}z\,{\text{d}}x \\ = & \frac{4}{ b}\left\{ {\left( {\theta_{0} \frac{4}{{\pi \left( {4n^{2} - 4n - 3} \right)}} \times \frac{{2Hb^{2} \pi^{2} m\left( {1 + e^{Hb} \left( { - 1} \right)^{m} } \right)}}{{H^{4} b^{4} + 2H^{2} b^{2} \pi^{2} + 2H^{2} b^{2} \pi^{2} m^{2} + \pi^{4} - 2\pi^{4} m^{2} + \pi^{4} m^{4} }}} \right.} \right. \\ \left. {\left. { +\,\theta_{r} \frac{{2mb\left( {\left( { - 1} \right)^{n} - \left( { - 1} \right)^{n + m} be^{Hb} } \right)}}{{2nH^{2} b^{2} + 2nm^{2} \pi^{2} - H^{2} b^{2} - m^{2} \pi^{2} }}} \right) - \frac{1}{2}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }}} \right)} \right\} \\ \end{aligned}$$
(68)

where \(A_{n}^{*}\) is identical to what was defined in case 4 and \(H = \frac{f}{2D}\). Also, \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4. All boundary and initial conditions of (66a)–(66c), as well as the PDE (Eq. 7), are satisfied by (67). As seen, Eq. (67) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution.

In order to confirm summations convergence in Eq. 67, water content at different positions is calculated using summations truncation with different values of n and m (Table 3). The soil parameters used for the problem are identical to those used in case 1. As seen in Table 3, change in water content is negligible at n and m = 1 to 10 and higher. As a consequence, θ is calculated for n = m = 1 to 10 in Eq. 67. To illustrate the use of the derived equations, water content values from an explicit scheme finite difference method (FDM) solution (to Eq. 7) are compared to the analytical solution (Eq. 67) for t = 30 min and various values of x and z (columns 7 and 8 in Table 3). Ninth column shows ErrorRelative based on columns 4 (incorporating > 100 summation terms) and column 8 (FDM for ∆t = 2 s, ∆z = 2.5 cm and ∆x = 2.5 cm). As shown, errors are all <2 % which may be deemed reasonable.

Table 3 Water content values for the analytical solution (with different summation truncations), FDM solution (with different mesh sizes), and the relative error for case 9 at t = 30 min
Full size table

Based on the equation, water content contours are drawn in Fig. 18a–d for t = 5, 15, 60 min and steady state, respectively.

Fig. 18
figure 18

Water content contours based on Eq. (67) for: a t = 5 min, b t = 15 min, c t = 60 min, and d steady state

Full size image

At early times (Fig. 18a, b), water content contours reflect a combination of two distinct water content gradients: (1) from center of the domain outward due to the initial sinusoidal (bell shape) water content and (2) from top to bottom (the infiltrating front) due to the gradient in water contents on the top and bottom boundaries. As time elapses, the bell-shaped gradient attenuates, and eventually water content contours approach a steady-state profile associated with the last two terms in Eq. (67). Steady-state contours for this case (Fig. 18d) are exactly the same as contours for case 4 (Fig. 10d). A 3-D plot of water content–depth–distance for t = 5 min (corresponding to Fig. 18a) is also visualized in Fig. 19.

Fig. 19
figure 19

3-D plot of water content–depth–distance based on the analytical solution for case 9 (Eq. 67) for t = 5 min

Full size image

3.10 Case 10: Infiltration from Top, Imbibitions from Bottom, No Flow on One Side, with an Exponential Initial Condition

This case is similar to case 7 except for the constant initial water content which is changed to a diagonally exponential distribution over the domain. Boundary and initial conditions for this case may be mathematically written as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0 \quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(69a)
$$\theta \left( {x,0,t} \right) = \theta_{0 } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(69b)
$$\theta \left( {x,z,0} \right) = \theta_{0 } e^{{\left( { - \frac{x}{a} - \frac{z}{b}} \right)}}$$
(69c)

The exponential function sets a maximum water content of \(\theta_{0 }\) at the left bottom corner of the sample (at x = z=0) and a minimum water content at top right corner. A 2-D contour plot of the initial condition (Eq. 69c) with \(\theta_{0} = 0.3, \;a = 100 \;{\text{and}}\; b = 100\;{\text{cm}}\) is shown in Fig. 20.

Fig. 20
figure 20

2-D contour plot of the distribution of water content (69c)

Full size image

Following similar mathematical procedures as before (case 7), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } \cos \left( { \beta x} \right)[ A_{n}^{*} \sinh (\tau z) + B_{n}^{*} \cosh \left( {\tau z} \right)] + \theta_{r} \\ \end{aligned}$$
(70)

where \(A_{mn}\) in this case is defined as:

$$\begin{aligned} A_{mn} = & \frac{4}{ab}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left( {\theta_{0 } e^{{\left( { - \frac{x}{a} - \frac{z}{b}} \right)}} e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} } \right)\sin \left( {\nu z} \right)\cos \left( {\lambda x } \right) dz\,dx \\ & \frac{4}{ b}\left\{ {\left( {\theta_{0} \frac{{2\left( { - 2 + 2e^{ - 1} \pi \left( { - 1} \right)^{n} n - e^{ - 1} \pi \left( { - 1} \right)^{n} } \right)}}{{4 + 4\pi^{2} n^{2} - 4\pi^{2} n + \pi^{2} }} \times \frac{{bm\pi \left( { - 1 + e^{Hb - 1} \left( { - 1} \right)^{m} } \right)}}{{H^{2} b^{2} - 2Hb + 1 + m^{2} \pi^{2} }}} \right.} \right. \\ & \left. { + \theta_{r} \frac{{2mb\left( {\left( { - 1} \right)^{n} - \left( { - 1} \right)^{n + m} be^{Hb} } \right)}}{{2nH^{2} b^{2} + 2nm^{2} \pi^{2} - H^{2} b^{2} - m^{2} \pi^{2} }}} \right) \\ &\left. - \frac{1}{2}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }} + \frac{{B_{n}^{*} }}{{\tau^{2} + \nu^{2} }}\left( {\nu \cosh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} + \nu } \right)} \right)\right\}\\ \end{aligned}$$
(71)

where \(A_{n}^{*} \;{\text{and}}\;B_{n}^{*}\) are identical to what was defined in case 7 and \(H = \frac{f}{2D}.\) Also, \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4. Boundary and initial conditions of (69a)–(69c), as well as the PDE (Eq. 7), are all satisfied by (70). As seen, Eq. (70) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution. Similar to previous cases, θ is calculated for n = m = 1 to 10 in Eq. 70.

Based on the equation, water content contours are drawn in Fig. 21a, b for t = 5, 15 min, respectively. Soil parameters used for the problem are identical to those used in case 1. As time elapses, the initial gradient attenuates, and eventually water content contours approach a steady-state profile associated with the last two terms in Eq. (70).

Fig. 21
figure 21

Water content contours based on Eq. (70) for: a t = 5 min and b t = 15 min

Full size image

Steady-state contours for this case are exactly the same as contours for case 7 (Fig. 14d). A 3-D plot of water content–depth–distance for t = 5 min (corresponding to Fig. 21a) is also visualized in Fig. 22.

Fig. 22
figure 22

3-D plot of water content–depth–distance based on the analytical solution for case 10 (Eq. 70) for t = 5 min

Full size image

3.11 Case 11: Infiltration from Top, No Flow on One Side, with an Exponential Initial Condition

This case is similar to case 4 except for the initial condition which has changed to a diagonally exponential distribution over the domain. Boundary and initial conditions for this case may be mathematically written as:

$$\frac{\partial \theta }{\partial x} \left( {0,z,t} \right) = 0\quad \theta \left( {a,z,t} \right) = \theta_{r}$$
(72a)
$$\theta \left( {x,0,t} \right) = \theta_{r } \quad \theta \left( {x,b,t} \right) = \theta_{0 }$$
(72b)
$$\theta \left( {x,z,0} \right) = \theta_{0 } e^{{\left( { - \frac{x}{a} - \frac{z}{b}} \right)}}$$
(72c)

Following similar mathematical procedures as before (case 4), the answer for \(\theta \left( {x,z,t} \right)\) would be:

$$\begin{aligned} \theta \left( {x,z,t} \right) = & \mathop \sum \limits_{m = 1}^{\infty } \mathop \sum \limits_{n = 1}^{\infty } A_{mn} e^{{ - \frac{f}{2D}z}} \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) e^{{ - \left( {\lambda^{2} + \nu^{2} + \left( {\frac{f}{D}} \right)^{2} \frac{1}{4}} \right)D t}} \\ & + e^{{ - \frac{f}{2D}z}} \mathop \sum \limits_{n = 1}^{\infty } A_{n}^{*} \cos \left( { \beta x} \right) { \sinh }(\tau z) + \theta_{r} \\ \end{aligned}$$
(73)

where \(A_{mn}\) in this case is defined as:

$$\begin{aligned} A_{mn} = \frac{4}{a b}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} ( \theta_{0 } e^{{\left( { - \frac{x}{a} - \frac{z}{b}} \right)}} e^{{ \frac{f}{2D}z}} - w\left( {x,z} \right)e^{{ \frac{f}{2D}z}} ) \sin \left( {\nu z} \right) \cos \left( {\lambda x } \right) dz dx \hfill \\ = \frac{4}{ b}\left\{ \left(\theta_{0} \frac{{2\left( { - 2 + 2e^{ - 1} \pi \left( { - 1} \right)^{n} n - e^{ - 1} \pi \left( { - 1} \right)^{n} } \right)}}{{4 + 4\pi^{2} n^{2} - 4\pi^{2} n + \pi^{2} }} \times \frac{{\pi \left( { - 1 + e^{Hb - 1} \left( { - 1} \right)^{m} } \right)}}{{H^{2} b^{2} - 2Hb + 1 + m^{2} \pi^{2} }}\right.\right. \hfill \\ \left.\left.+ \theta_{r} \frac{{2mb\left( {\left( { - 1} \right)^{n} - \left( { - 1} \right)^{n + m} be^{Hb} } \right)}}{{2nH^{2} b^{2} + 2nm^{2} \pi^{2} - H^{2} b^{2} - m^{2} \pi^{2} }}\right) - \frac{1}{2}\left( {\frac{{A_{n}^{*} \nu \sinh \left( {\tau b} \right)\left( { - 1} \right)^{m + 1} }}{{\tau^{2} + \nu^{2} }}} \right)\right\} \hfill \\ \end{aligned}$$
(74)

Also A * n , \(\nu , \lambda , \beta\) and τ are identical to what was defined in case 4 and \(H = \frac{f}{2D}.\) All boundary and initial conditions of (72a)–(72c), as well as the PDE (Eq. 7), are satisfied by (73). As seen, Eq. (73) consists of three terms: a function of (x, z, t), a function of (x, z), and a constant. As t → ∞, the first term vanishes, and the rest remain as residuals or the steady-state solution.

In order to confirm summations convergence in Eq. 73, water content at different positions is calculated using summations truncation with different values of n and m (Table 4). The soil parameters used for the problem are identical to those used in case 1. As seen in Table 4, change in water content is negligible at n and m = 1 to 10 and higher. As a consequence, θ is calculated for n = m = 1 to 10 in Eq. 73. To illustrate the use of the derived equations, water content values from an explicit scheme finite difference method (FDM) solution (to Eq. 7) are compared to the analytical solution (Eq. 73) for t = 30 min and various values of x and z (columns 7 and 8 in Table 4). Ninth column shows ErrorRelative based on columns 4 (incorporating > 100 summation terms) and column 8 (FDM for \(\Delta t = 2 s, \;\Delta z = 2.5\; {\text{cm}}\) and \(\Delta x = 2.5 \;{\text{cm}}\)). As shown, errors are all < 2 % which may be deemed reasonable.

Table 4 Water content values for the analytical solution (with different summation truncations), FDM solution (with different mesh sizes), and the relative error for case 11 at t = 30 min
Full size table

Based on the equation, water content contours are drawn in Fig. 23a–b for t = 5, 15 min, respectively.

Fig. 23
figure 23

Water content contours based on Eq. (73) for: a t = 5 min and b t = 15 min

Full size image

As time elapses, the initial gradient attenuates, and eventually water content contours approach to a steady-state profile associated with the last two terms in Eq. (73).

Steady-state contours for this case are exactly the same as contours for case 4 (Fig. 10d). A 3-D plot of water content–depth–distance for t = 5 min (corresponding to Fig. 23a) is also visualized in Fig. 24.

Fig. 24
figure 24

3-D plot of water content–depth–distance based on the analytical solution for case 11 (Eq. 73) for t = 5 min

Full size image

4 Conclusions

New analytical solutions to 2-D vertical and horizontal infiltration and imbibition into unsaturated soils were presented for linearized Richards’ equation under nonsymmetrical boundary and nonuniform initial conditions. Separation of variables and Fourier series expansion techniques were used to derive the solutions. Solutions have the general form of infinite series with exponential terms whereby both steady and unsteady solutions may be obtained from a single closed-form solution. Solutions were derived for constant water content and no-flow boundary conditions along with constant, sinusoidal, or exponential water contents as initial conditions. Two-dimensional and 3-D plots of water content were presented for the transient as well as steady-state conditions. A total of 11 different cases were studied, and analytical solutions were compared to numerical FDM results for four cases in order to check validity and accuracy of the numerical solution, where a maximum error of <2 % was observed. The presented analytical solutions may be used as a benchmark for verification and accuracy assessment of numerical approaches where nonsymmetrical boundary and/or nonuniform initial conditions exist.