Introduction

Copper exploitation is a major water quality problem due to acid mine drainage (AMD) generation in Sarcheshmeh mine, Kerman Province, southeast Iran. The oxidation of sulphide minerals, in particular pyrite exposed to atmospheric oxygen during or after mining activities generates acidic waters with high concentrations of dissolved iron (Fe), sulphate (SO4) and heavy metals (Williams 1975; Moncur et al. 2005). The low pH of AMD may cause further dissolution and the leaching of additional metals (Mn, Zn, Cu, Cd, and Pb) into aqueous system (Zhao et al. 2007). AMD containing heavy metals have detrimental impact on aquatic life and the surrounding environment. Shur River in the Sarcheshmeh copper mine polluted by AMD with pH values ranging between 2 and 4.5 and high concentrations of heavy metals. The prediction of heavy metals in Shur River is useful in developing proper remediation and monitoring methods.

The Sarcheshmeh copper deposit recognised to be the fourth largest mine in the world contains 1 billion tonnes averaging 0.9% copper and 0.03% molybdenum (Banisi and Finch 2001). This ore body is located at southeast of Iran, Kerman Province. Mining operation has placed many low-grade waste dumps and has posed many environmental problems. Environmental problems of sulphide minerals oxidation and AMD generation in the Sarcheshmeh copper mine and its impact on the Shur River have been investigated in the past (Marandi et al. 2007; Shahabpour and Doorandish 2008; Doulati Ardejani et al. 2008; Bani Assadi et al. 2008).

Many investigations have been carried out on the behaviour of the heavy metals in AMD and their impact on the receiving water bodies (Govil et al. 1999; Merrington and Alloway 1993; Hammack et al. 1998; Herbert 1994; Moncur et al. 2005; Smuda et al. 2007; Wilson et al. 2005; Lee and Chon 2006; Dinelli et al. 2001; Canovas et al. 2007). The conventional method of measuring the heavy metals is involved in the sampling and a time-consuming and expensive laboratory analysis. Less study has been carried out for the prediction of heavy metals in AMD. Therefore, investigation of a method that can predict the concentrations of heavy metals in water affected by AMD is necessary to develop an appropriate remediation and monitoring method for comprehensive assessment of the potential environmental impacts of AMD.

Artificial neural networks (ANN) have gained an increasing popularity in different fields of engineering in the past few decades, because of their capability of extracting complex and nonlinear relationships. Kemper and Sommer (2002) estimated the heavy metal concentration in soils from reflectance spectroscopy using back propagation network and multiple linear regression. Almasri and Kaluarachchi (2005) applied the modular neural networks to predict the nitrate distribution in ground water using the on-ground nitrogen loading and recharge data. Khandelwal and Singh (2005) predicted the mine water quality by the physical parameters using back propagation neural network (BPNN) and multiple linear regression. Singh et al. (2009) modelled the backpropagation neural network to predict water quality in the Gomti River (India). Erzin and Yukselen (2009) used the back propagation neural network for the prediction of zeta potential of kaolinite.

The literature review has shown that despite many research works having been conducted related to the application of the ANN method in mining and relevant environmental problems, the ANN method has not been directly used to predict heavy metals in AMD. In this paper, attention has been focused on the prediction of the heavy metals in the Shur River impacted by AMD. The results obtained from the predictions using ANN and MLR are compared with the measured concentrations of major heavy metals sampled and analysed in Shur River of Sarcheshmeh copper mine, southeast Iran.

Site description

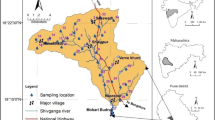
Sarcheshmeh copper mine is located 160 km to southwest of Kerman and 50 km to southwest of Rafsanjan in Kerman province, Iran. The main access road to the study area is Kerman–Rafsanjan–Shahr Babak road. This mine belongs to Band Mamazar-Pariz Mountains. The average elevation of the mine is 1,600 m. The mean annual precipitation of the site varies from 300 to 550 mm. The temperature varies from +35°C in summer to −20°C in winter. The area is covered with snow for about 3–4 months per year. The wind speed sometimes exceeds 100 km/h. A rough topography is predominant at the mining area; Fig. 1 shows the geographical position of the Sarcheshmeh copper mine.

Fig. 1
figure 1

Location of the Sarcheshmeh mine and Shur River (modified after Shahabpour and Doorandish 2008; Derakhshandeh and Alipour 2010)

Full size image

The orebody in Sarcheshmeh is oval shaped with a long dimension of about 2,300 m and a width of about 1,200 m. This deposit is associated with the late Tertiary Sarcheshmeh granodiorite porphyry stock (Waterman and Hamilton 1975). The porphyry is a member of a complex series of magmatically related intrusives emplaced in the Tertiary volcanics at a short distance from the edge of an older near-batholith-sized granodiorite mass. Open pit mining method is used to extract copper deposit in Sarcheshmeh. A total of 40,000 tons of ore (average grades 0.9% Cu and 0.03% molybdenum) is approximately extracted per day in Sarcheshmeh mine (Banisi and Finch 2001).

Sampling and field methods

Sampling of waters in the Shur River downstream from the Sarcheshmeh mine was carried out in February 2006. Water samples consist of water from Shur River (Fig. 1) originating from Sarcheshmeh mine, acidic leachates of heap structure, run-off of leaching solution into the River and samples affected by tailings along the Shur River. The water samples were immediately acidified by adding HNO3 (10 cc acid/1,000 cc sample) and stored under cool conditions. The equipments used in this study were sample container, GPS, oven, autoclave, pH meter, atomic adsorption and ICP analysers. The pH of the water was measured using a portable pH meter in the field. Other physical parameters were total dissolved solids (TDS), electric conductivity (EC) and temperature. Analyses for dissolved metals were performed using atomic adsorption spectrometer (AA220) in water lab of the National Iranian Copper Industries Company (NICIC). Although not given here, ICP (model 6000) was also used to analyse the concentrations of those heavy metals that are detected in the range of ppb. Table 1 gives the minimum, maximum and the mean values of some physical and chemical parameters.

Table 1 Maximum, minimum and mean physical and chemical constituents including heavy metals of the Shur River
Full size table

Method

Back propagation neural network design

Artificial neural networks (ANN) are generally defined as information processing representation of the biological neural networks. ANN has gained an increasing popularity in different fields of engineering in the past few decades, because of their ability of deriving complex and nonlinear relationships. The mechanism of the ANN is based on the following four major assumptions (Hagan et al. 1996):

  • Information processing occurs in many simple elements that are called neurons (processing elements).

  • Signals are passed between neurons over connection links.

  • Each connection link has an associated weight, which, in a typical neural network, multiplies the signal being transmitted.

  • Each neuron applies an activation function (usually nonlinear) to its net input in order to determine its output signal.

Figure 2 shows a typical neuron. Inputs (P) coming from another neuron are multiplied by their corresponding weights (W 1,R), and summed up (n). An activation function (f) is then applied to the summation, and the output (a) of that neuron is now calculated and ready to be transferred to another neuron. Many types of neural network architectures and algorithms are available. In this study, a generalised regression neural network (GRNN) is used.

Fig. 2
figure 2

A typical neuron (Demuth and Beale 2002)

Full size image

In this network, each element of the input vector p is connected to each neuron input through the weight matrix W. The ith neuron has a summer that gathers its weighted inputs and bias to form its own scalar output n (i). The various n (i) taken together form an S-element net input vector n. Finally, the neuron layer outputs form a column vector a (Eqs. 1, 2).

$$ n_{j} = \sum\limits_{i = 1}^{R} {\left( {p_{i} w_{ij} + b_{j} } \right)} \,\, ,\;j = 1,\,2, \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} S $$
(1)

where

$$ b = \left[ \begin{gathered} b_{1} \hfill \\ b_{2} s \hfill \\ b_{S} \hfill \\ \end{gathered} \right],P = \left[ \begin{gathered} P_{1} \hfill \\ P_{2} \hfill \\ \hfill \\ P_{R} \hfill \\ \end{gathered} \right],\;W = \left[ \begin{gathered} w_{1,1} w_{1,2} \ldots w_{1,R} \hfill \\ w_{2,1} w_{2,2} \ldots w_{2,R} \hfill \\ \hfill \\ \hfill \\ w_{S,1} w_{S,2} \ldots w_{S,R} \hfill \\ \end{gathered} \right] $$

Then, final output of network is calculated by:

$$ a_{S} = f(n_{S} ) $$
(2)

Here, f is an activation function, typically a step function or a sigmoid function, which takes the argument n and produces the output a. Figure 3 shows examples of various activation functions.

Fig. 3
figure 3

Three examples of transfer functions (Demuth and Beale 2002)

Full size image

Backpropagation neural networks (BPNN) are recognised for their prediction capabilities and ability to generalise well on a wide variety of problems. These models are supervised type of networks; in other words, trained with both inputs and target outputs. During training the network tries to match the outputs with the desired target values. Learning starts with the assignment of random weights. The output is then calculated and the error is estimated. This error is used to update the weights until the stopping criterion is reached. It should be noted that the stopping criteria is usually the average error or epoch.

Network training: the over fitting problem

One of the most common problems in the training process is the over fitting phenomenon. This happens when the error on the training set is driven to a very small value, but when new data is presented to the network the error is large. This problem occurs mostly in case of large networks with only few available data. Demuth and Beale (2002) have shown that there are a number of ways to avoid over fitting problem. Early stopping and automated Bayesian regularization methods are most common. However, with immediate fixing of the error and the number of epochs to an adequate level (not too low/not too high) and dividing the data into two sets, training and testing, one can avoid such problem by making several realizations and selecting the best of them. In this paper, the necessary coding was added through MATLAB multi-purpose commercial software to implement the automated Bayesian regularization for training BPNN. In this technique, the available data is divided into two subsets. The first subset is the training set, which is used for computing the gradient and updating the network weights and biases. The second subset is the test set. This method works by modifying the performance function, which is normally chosen to be the sum of squares of the network errors on the training set. The typical performance function that is used for training feed forward neural networks is the mean sum of squares of the network errors according to the following equation:

$$ {\text{mse}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {(e_{i} )^{2} } = \frac{1}{N}\sum\limits_{i = 1}^{N} {(t_{i} - a_{i} )^{2} } $$
(3)

where, N represents the number of samples, a is the predicted value, t denotes the measured value and e is the error.

It is possible to improve generalisation if we modify the performance function by adding a term that consists of the mean of the sum of squares of the network weights and biases which is given by:

$$ {\text{msereg}} = \gamma {\kern 1pt} {\text{mse}} + (1 - \gamma ){\kern 1pt} {\kern 1pt} {\text{msw}} $$
(4)

Where, msereg is the modified error, γ is the performance ratio, and msw can be written as:

$$ {\text{msw}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {w_{i} } $$
(5)

Performance function will cause the network to have smaller weights and biases, and this will force the network response to be smoother and less likely to over fit (Demuth and Beale 2002).

Heavy metals prediction using BPNN

According to the correlation matrix (Table 2), pH, SO4 and Mg that have most dependent on heavy metals (Cu, Mn and Zn) concentrations were selected as inputs of the network. The outputs of network were heavy metals concentrations including Cu, Fe, Mn and Zn. In view of the requirements of the neural computation algorithm, the data of both the independent and dependent variables were normalised to an interval by transformation process. In this study, normalisation of data (inputs and outputs) was done for the range of (−1, 1) using Eq. 6 and the number of training data (44) and test data (12) were then selected randomly.

$$ p_{n} = 2{\frac{{p - p_{\min } }}{{p_{\max } - p_{\min } }}} - 1 $$
(6)

where, P n is the normalised parameter, p denotes the actual parameter, p min represents a minimum of the actual parameters and p max stands for a maximum of the actual parameters.

Table 2 Correlation matrix between heavy metals concentrations and independent variables
Full size table

In this research, several architectures (varied numbers of neurons in hidden layer) with Automated Bayesian Regularization algorithm for ANN model with the default parameter values for algorithm (Demuth and Beale 2002) are used to predict heavy metals concentrations using BPNN. Two criteria were used to evaluate the effectiveness of each network and its ability to make accurate predictions. The root mean square error (RMS) can be calculated as follows:

$$ {\text{RMS}} = \sqrt {{\frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{n}}} $$
(7)

where, y i is the measured value, \( \hat{y}_{i} \) denotes the predicted value, and n stands for the number of samples. RMS indicates the discrepancy between the measured and predicted values. The lower the RMS, the more accurate the prediction is. Furthermore, the efficiency criterion, R 2, is given by:

$$ R^{2} = 1 - {\frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {y_{i}^{2} - {\frac{{\sum\nolimits_{i = 1}^{n} {\hat{y}_{i}^{2} } }}{n}}} }}} $$
(8)

where R 2 efficiency criterion represents the percentage of the initial uncertainty explained by the model. The best fitting between measured and predicted values, which is unlikely to occur, would have RMS = 0 and R 2 = 1. Table 3 gives the correlation coefficient (R) and RMS between predicted and measured concentrations in training and test from any architect.

Table 3 R and RMS between predicted and measured heavy metals concentrations in training and test data
Full size table

The indices 1 and 2 for R and RMS in Table 3 are related to the training and test data, respectively and n is the number of neurons in the hidden layer.

The optimal network for this study is a feed forward multilayer perceptron (Cybenko 1989; Hornik et al. 1989; Haykin 1994; Noori et al. 2009, 2010), having one input layer with three inputs (pH, SO4, Mg), one hidden layer with six neurons that each neuron has a bias and is fully connected to all inputs and utilises sigmoid hyperbolic tangent (tansig) activation function (Fig. 4). The output layer has four neurons (Cu, Fe, Mn and Zn) with a linear activation function (purelin) without bias. Linear activation function can provide any range of data in output without any limitation for output values.

Fig. 4
figure 4

a Backpropagation neural network architecture, b general schematic diagram of network and its layers, c structure of hidden layer (Layer 1)

Full size image

Bayesian regularization algorithm (trainbr) was used as training function to prevent overtraining of the ANN models. Figure 4a shows the backpropagation neural network architecture. In Fig. 4b, Layer 1 is hidden layer and Layer 2 is output layer. Figure 4c shows the structure of the hidden layer.

Figure 5 shows the training process of the network. In this figure, SSE is the sum square error for training data. One feature of this algorithm is that it provides a measure of how many network parameters (weights and biases) are being effectively used by the network. The final trained network employs approximately 44 parameters out of the 52 total weights and biases in the 3-6-4 network. The training may stop with the message “Maximum MU reached”. This is typical, and is a good indication that the algorithm has truly converged. In the present case, the algorithm was stopped in 171 epochs. In this network learning rate was 0.5.

Fig. 5
figure 5

Sum squared error, sum squared weighs and effective number of parameters versus the epoch in training step

Full size image

The selected BPNN (3 neurons in input layer, 6 neurons in hidden layer and 4 neurons in output layer) provided a good-fit model for two data sets of Cu, Mn and Zn concentrations and poor fit for Fe concentration. The correlation coefficient (R) values for the training and test data and the respective values of RMS for the two data sets are highlighted in Table 3. Figure 6a–h compares the network predictions versus measured concentrations for training and test data.

Fig. 6
figure 6figure 6

Comparison of the network predictions and measured concentrations for training and test data using BPNN model. a Correlation between BPNN Cu versus measured Cu (training data). b Correlation between BPNN Cu versus measured Cu (test data). c Correlation between BPNN Fe versus measured Fe (training data). d Correlation between BPNN Fe versus measured Fe (test data). e Correlation between BPNN Mn versus measured Mn (training data). f Correlation between BPNN Mn versus measured Mn (test data). g Correlation between BPNN Zn versus measured Zn (training data). h Correlation between BPNN Zn versus measured Zn (test data)

Full size image

GRNN model

General regression neural network has been proposed by Specht (1991). GRNN is a type of supervised network and also trains quickly on sparse data sets but, rather than categorising it. GRNN applications are able to produce continuous valued outputs. GRNN is a three-layer network where there must be one hidden neuron for each training pattern.

GRNN is a memory-based network that provides estimates of continuous variables and converges to the underlying regression surface. GRNNs are based on the estimation of probability density functions, having a feature of fast training times and can model nonlinear functions. GRNN is an one-pass learning algorithm with a highly parallel structure. GRNN algorithm provides smooth transitions from one observed value to another even with sparse data in a multidimensional measurement space. The algorithmic form can be used for any regression problem in which an assumption of linearity is not justified. GRNN can be thought as a normalised radial basis functions (RBF) network in which there is a hidden unit centred at every training case. These RBF units are usually probability density functions such as the Gaussian. The only weights that need to be learned are the widths of the RBF units. These widths are called “smoothing parameters”. The main drawback of GRNN is that it suffers badly from the curse of dimensionality. GRNN cannot ignore irrelevant inputs without major modifications to the basic algorithm. So GRNN is not likely to be the top choice if there are more than 5 or 6 non-redundant inputs. The regression of a dependent variable, Y, on an independent variable, X, is the computation of the most probable value of Y for each value of X based on a finite number of possibly noisy measurements of X and the associated values of Y. The variables X and Y are usually vectors. To implement system identification, it is usually necessary to assume some functional form. In the case of linear regression, for example, the output Y is assumed to be a linear function of the input, and the unknown parameters, a i , are linear coefficients.

The method does not need to assume a specific functional form. A Euclidean distance (D 2 i ) is estimated between an input vector and the weights, which are then rescaled by the spreading factor. The radial basis output is then the exponential of the negatively weighted distance. The GRNN equation can be written as:

$$ D_{i}^{2} = (X - X^{i} )^{T} (X - X^{i} ) $$
(9)
$$ Y(X) = {\frac{{\sum\nolimits_{i = 1}^{n} {Y_{i} \exp \left( { - {\frac{{D_{i}^{2} }}{{2\sigma^{2} }}}} \right)} }}{{\sum\nolimits_{i = 1}^{n} {\exp \left( { - {\frac{{D_{i}^{2} }}{{2\sigma^{2} }}}} \right)} }}} $$
(10)

where σ is the smoothing factor (SF).

The estimate Y(X) can be visualised as a weighted average of all of the observed values, Y i , where each observed value is weighted exponentially according to its Euclidian distance from X. Y(X) is simply the sum of Gaussian distributions centred at each training sample. However, the sum is not limited to being Gaussian. In this theory, the optimum smoothing factor is determined after several runs according to the mean squared error of the estimate, which must be kept at minimum. This process is referred to as the training of the network. If a number of iterations pass with no improvement in the mean squared error, that smoothing factor is determined as the optimum one for that data set. While applying the network to a new set of data, increasing the smoothing factor would result in decreasing the range of output values (Specht 1991). In this network, there are no training parameters such as the learning rate, momentum, optimum number of neurons in hidden layer and learning algorithms as in backpropagation network but there is a smoothing factor that its optimum is gained as trial and error. The smoothing factor must be greater than 0 and can usually range from 0.1 to 1 with good results. The number of neurons in the input layer is the number of inputs in the proposed problem, and the number of neurons in the output layer corresponds to the number of outputs. Because GRNN networks evaluate each output independently of the other outputs, GRNN networks may be more accurate than backpropagation networks when there are multiple outputs. GRNN works by measuring how far the given sample pattern is from the patterns in the training set. The output that is predicted by the network is a proportional amount of all the output in the training set. The proportion is based upon how far the new pattern is from the given patterns in the training set.

Heavy metals prediction using GRNN

In this method, the training and test data in BPNN were used. To obtain the best network, the GRNN was trained by different smooth factors to gain the optimum smooth factor according to correlation coefficient and RMS error between measured and predicted values in training and test data. The results are given in Table 4.

Table 4 R and RMS with different smooth factors in training and test data
Full size table

In Table 4, the indices 1 and 2 for R and RMS are related to training and test data, respectively and SF stands for smooth factor. The optimum smooth factor (SF) was selected 0.10 according to evaluated criteria in training and test data in Table 2. Taking this SF into consideration, Fig. 7 shows the schematic diagram of GRNN network. The general diagram of network, the associated layers and the structure of hidden layer are shown in Fig. 8a and b, respectively. This network (Fig. 7) has three layers; input layer with 3 neurons (pH, SO4 and Mg), hidden layer incorporating 44 neurons (number of training samples) with radbas activation function in all neurons and output layer with 4 neurons (Cu, Fe, Mn and Zn) with linear activation function. In Fig. 8a, Layer 1 is hidden layer and Layer 2 is output layer and as mentioned above, Fig. 8b is the structure of hidden layer.

Fig. 7
figure 7

Schematic diagram of GRNN network

Full size image
Fig. 8
figure 8

a General diagram of network and its layers, b structure of hidden layer (Layer 1)

Full size image

Figure 9 compares the measured and predicted concentrations of heavy metals in training and test data. The selected GRNN (3 nodes in input layer, 44 nodes in hidden layer, and 4 nodes in output layer) provided a good-fit model for the two data sets of Cu, Mn and Zn concentrations and poor fit for Fe concentration. The correlation coefficients (R) for the training and test data and the respective values of RMS for two data sets are shown in Table 4. A closely followed pattern of variation by the measured and predicted heavy metals, R and RMS values suggest a good-fit of the heavy metals (Cu, Mn and Zn) model to the data set. The poor-fit model for Fe ion is a result of low correlation between Fe and independent variables in Table 2.

Fig. 9
figure 9figure 9

Comparison of the network predictions and measured concentrations for training and test data using GRNN model. a Correlation between GRNN Cu versus measured Cu (training data). b Correlation between GRNN Cu versus measured Cu (test data). c Correlation between GRNN Fe versus measured Fe (training data). d Correlation between GRNN Fe versus measured Fe (test data). e Correlation between GRNN Mn versus measured Mn (training data). f Correlation between GRNN Mn versus measured Mn (test data). g Correlation between GRNN Zn versus measured Zn (training data). h Correlation between GRNN Zn versus measured Zn (test data)

Full size image

Multiple linear regression

Multiple linear regression (MLR) is an extension of the regression analysis that incorporates additional independent variables in the predictive equation. Here, the model to be fitted is:

$$ y = B_{1} + B_{2} x_{2} + \cdots + B_{n} x_{n} + e $$
(11)

where y is the dependent variable, x i s are the independent random variables and e is a random error (or residual) which is the amount of variation in y not accounted for by the linear relationship. The parameters B i s, stand for the regression coefficients, are unknown and are to be estimated. However, there is usually substantial variation of the observed points around the fitted regression line. The deviation of a particular point from the regression line (its predicted value) is called the residual value. The smaller the variability of the residual values around the regression line, the better is model prediction.

In this study, regression analysis was performed using the training and test data employed in neural network data. Heavy metal concentrations were considered as the dependent variables and pH, SO4 and Mg were considered as the independent variables. A computer-based package called SPSS (Statistical Package for the Social Sciences) was used to carry out the regression analysis. The estimated regression relationships for heavy metals are given as below:

$$ {\text{Cu}} = 2 9. 6 3 9- 10. 4 2 3\times {\text{pH}} + 0.0 1 3 5 4\times {\text{SO}}_{ 4} + 0. 6 4 9\times {\text{Mg}} $$
(12)
$$ {\text{Fe}} = 7. 7 9 6- 0. 4 5 2\times {\text{pH}} + 0.00 1 60 9\times {\text{SO}}_{ 4} - 0.0 3 1 1 8\times {\text{Mg}} $$
(13)
$$ {\text{Mn}} = 3 4. 4 5 1- 5. 70 8\times {\text{pH}} + 0.00 4 6 3 9\times {\text{SO}}_{ 4} + 0. 1 4 5\times {\text{Mg}} $$
(14)
$$ {\text{Zn}} = 1 5. 9 2 7- 2. 7 8\times {\text{pH}} + 0.00 2 3 7 6\times {\text{SO}}_{ 4} + 0.0 6 10 9\times {\text{Mg}} $$
(15)

The statistical results of the model are given in Table 5. Heavy metal concentrations were estimated according to the Eqs. 12–15. Figure 10 shows the correlation between measured heavy metal concentrations and those predicted using MLR with three inputs.

Table 5 Statistical characteristics of the multiple regression models
Full size table
Fig. 10
figure 10figure 10

Comparison of the predicted concentrations using MLR and measured concentrations for training and test data. a Correlation between MLR Cu versus measured Cu (training data). b Correlation between MLR Cu versus measured Cu (test data). c Correlation between MLR Fe versus measured Fe (training data). d Correlation between MLR Fe versus measured Fe (test data). e Correlation between MLR Mn versus measured Mn (training data). f Correlation between MLR Mn versus measured Mn(test data). g Correlation between MLR Cu versus measured Cu (training data). h Correlation between MLR Zn versus measured Zn (test data)

Full size image

As can be seen in Fig. 10, the inappropriate predictions of the heavy metals shown by negative values is the most important disadvantage of the MLR method compared to ANN method.

Table 6 compares the correlation coefficient R and root mean square error (RMS) associated with three methods for both training and test data. It is well illustrated in Table 6 that the BPNN and GRNN methods predicted some what similar results. Furthermore, a close agreement can be seen between the predicted concentrations and measured data when the ANN method (BPNN and GRNN) is used. Low correlation values between the model predictions and measured data using MLR method describes its low capability in prediction heavy metals.

Table 6 The comparison of the results (R, RMS) of three methods in training and test data
Full size table

In Table 6, the indices 1 and 2 for R and RMS are related to training a test data, respectively.

Conclusions

A new method to predict major heavy metals in Shur River impacted by AMD has been presented using ANN method. The predictions for heavy metals (Cu, Fe, Mn and Zn) using ANN method incorporating BPNN and GRNN approaches together with MLR method are presented and compared with the measured data. The input data for the ANN and MLR models have been selected based on the high values of the correlation coefficients between heavy metals and pH, SO4 and Mg2+ concentrations. In this paper, the BPNN model has three layers including input layer (pH, SO4 and Mg2+), hidden layer (6 neurons) with tansig activation function and output layer (Cu, Fe, Mn and Zn) with linear activation function. Whereas, the GRNN consists of three layers, i.e. input layer (pH, SO4 and Mg2+), hidden layer (44 neurons) with radbas activation function and output layer (Cu, Fe, Mn and Zn) with linear activation function. An optimal smoothing factor of 0.10 was obtained for GRNN model by a trial and error process. It was found that the BPNN and GRNN methods predicted some what similar results. Furthermore, a close agreement was achieved between the predicted and measured concentrations for heavy metals (Cu, Mn and Zn) when the ANN method (BPNN and GRNN) was used. However, the correlation factor was low between predicted Fe concentration and its associated measured data. Low correlation values between the model predictions and measured data using MLR method describes its low capability in prediction heavy metals.