1 Introduction

To keep pace with the ever increasing demand for electrical energy, it has become inevitable for the utilities to increase the generation by adding new generating sources to the existing grid but on the flip-side addition of new generators to the grid involves high capital cost and environmental concerns. Efficient utilization of the existing transmission infrastructure by reducing line losses is an attractive alternative to relieve the grid from the burden of increasing energy demand. Line losses can be reduced by placing FACTS devices (Hingorani Gyugyi 2000) at appropriate locations in the system. Fortunately, the advent of FACTS coincided with deregulation of the electric power sector and many new opportunities unfolded for enhancing the capacity of the existing electrical network (Galiana FD et al. 1996; Mani and Seksena 2017; Nartu et al. 2019). Because of the capital cost involved with the fitting of FACTS devices, it is paramount to trace the optimal location at which the maximum benefits of the installed device can be yielded without violating the system constraints.

UPFC is a versatile member of the FACTS devices family. Its major advantage lies in its potential to simultaneously control active and reactive power. To realize the full capacity of UPFC, it is unequivocally vital to position it at an optimal location. Copious optimization techniques have been proposed for finding the appropriate location to install UPFC for achieving different objectives. The concept of system loading sensitivity is suggested in (Singh and Erlich 2005) to optimally place UPFC in the system. In (Venkatesh and Gooi 2006) the optimal location of UPFC is traced by fuzzy evolutionary programming. In (Shaheen et al. 2008) genetic algorithm (GA) and Particle swarm optimization (PSO) techniques were proposed to screen the optimal position for installation of UPFC. In (Taher and Amooshahi 2012) an approach utilizing a hybrid immune algorithm (HIA) for optimal UPFC placement is developed to achieve optimal power flow. To determine the optimal position of UPFC a gravitational search algorithm (GSA) technique is introduced in (Sarker et al. 2013). The superiority of the hybrid chemical reaction algorithm (HCRO) over its peers PSO and GA in tracing the best position of UPFC is established in (Dutta et al. 2015). A power loss sensitivity index (PLSI) is used in (Shrawane Kapse et al. 2018) to find the optimal location of UPFC. Moth flame optimization (MFO) in its natural form as well as in hybrid form called JAYA blended MFO (JMFO) is applied for finding the optimal location of FACTS devices in (Dash et al. 2019). Although the algorithms used are most recent ones, only single objective is considered in this study. To enhance the dynamic stability of the power system in a recent study reported in (Vijay and Ramaiah 2019) UPFC is optimally located by using modified slap swarm algorithm.

The existing studies on power loss minimization by optimally locating FACTS device are inclined mostly towards single objective optimization. Multiobjective optimization catering to the simultaneous reduction of active and reactive power loss reduction is seldom explored in the available literature. In this paper, a novel attempt is made by the authors by choosing active and reactive power loss reduction as a multiobjective optimization problem. Multiobjective cuckoo search algorithm (MOCS) presented in (Yang and Deb 2011) as an upgrade to the standard CS algorithm (Yang and Deb 2010, 2011) is incorporated for this purpose. The results obtained are compared with that of MOPSO, to the best knowledge of the authors of this article; no such comparison has been reported in the literature so far. The results indicate the superiority of the MOCS algorithm over MOPSO in solving multiobjective optimization problems. In addition to MOPSO, multiobjective firefly algorithm (MOFA) is also implemented to solve the multiobjective optimization problem and compared with MOCS.

The rest portion of this paper is sectioned as follows. Section 2 is about UPFC and its modeling equations. The multiobjective optimization algorithms employed are discussed in Sect. 3. The multiobjective function and the limiting constraints are discussed in Sect. 4. Section 5 deals with the Pareto-optimal method and fuzzy logic method. The numerical results generated are illustrated in Sect. 6. Section 7 outlines the conclusion of the article.

2 Unified power flow controller

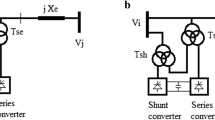
UPFC is a multifaceted device under FACTS family which exhibits the capabilities of series compensation, voltage regulation and phase shifting (Gyugyi et al. 1995; Mathur and Varma 2002). The basic model of UPFC is depicted in Fig. 1. It comprises of two voltage source converters (VSC), one interfaced in series with the line and the other connected in shunt with the line through two different interface transformers. A common capacitor bank provides the necessary dc voltage for the converters. The series-connected VSC injects an ac voltage of desired magnitude and phase angle. As a consequence, the series-connected converter trades both active and reactive power with the line. The shunted connected VSC affords the real power demand of the series-connected VSC.

Fig. 1
figure 1

Basic model of UPFC

Full size image

2.1 Steady-state modeling of UPFC

UPFC, as mentioned above, has two converters. The UPFC model used in this study is described below. This model is considered to study the influence of UPFC on the power system under steady-state condition.

2.2 Series connected VSC model

The series VSC can be modeled as a controllable series voltage source \({V}_{se}\) connected in-between bus-\(i\) and bus-\(j\) in series with a line of reactance \( X_{s}\) (Noroozian et al. 1997; Mithu 2013). Figure 2 shows the series-connected voltage source converter model and the effect of \(V_{se}\) on the system response is

$$ V^{\prime}_{i} = V_{{{\text{se}}}} + V_{i} $$
(1)
Fig. 2
figure 2

Series connected VSC model

Full size image

Here, \(V_{se} \) is controllable in both magnitude and phase

$$ V_{se} = rV_{i} e^{j\gamma } $$
(2)

where

$$ 0 \le r \le r_{{\max}} \,{\text{and}}\,0 \le \gamma \le 360^\circ $$
(3)

The injection model as shown in Fig. 3 can be obtained by replacing the voltage source \(V_{se}\) with a current source \(I_{s} = - jb_{s} V_{se}\) in parallel with the line (Noroozian and Andersson 1993)

$$ {\text{where}}\,b_{s} = \frac{1}{{X_{s} }} $$
(4)
Fig. 3
figure 3

Injection model of series-connected VSC

Full size image

The injecting powers \(S_{is}\) and \(S_{js}\).corresponding to \(I_{s}\) are given by

$$ S_{is} = V_{i} \left( { - I_{s} } \right)^{*} $$
(5)
$$ S_{js} = V_{j} \left( {I_{s} } \right)^{*} $$
(6)

Substituting \(I_{s}\) in Eq. (5) and (6),

$$ \begin{array}{*{20}c} {S_{is} = V_{i} \left( {jb_{s} \left( {rV_{i} e^{j\gamma } } \right)} \right)^{*} = P_{is} + jQ_{is} } \\ { = - b_{s} rV_{i}^{2} \sin \gamma - jb_{s} rV_{i}^{2} \cos \gamma } \\ \end{array} $$
(7)
$$ \begin{gathered} S_{js} = V_{j} \left( { - jb_{s} \left( {rV_{i} e^{j\gamma } } \right)} \right)^{*} = P_{js} + jQ_{js} \hfill \\ = b_{s} rV_{i} V_{j} \sin \left( {\delta_{ij} + \gamma } \right) + jb_{s} rV_{i} V_{j} \cos \left( {\delta_{ij} + \gamma } \right) \hfill \\ \end{gathered} $$
(8)

where \(\delta_{ij}\) represents the phase shift between bus-\(i\) and bus-\(j\) respectively.

2.3 Shunt-connected VSC model

The shunt converter in UPFC maintains constant voltage profile within tolerable limits. It also supplies active power which is fed into the system through a voltage source connected in series. If we neglect the losses then

$$ P_{{{\text{conv}}1}} = P_{{{\text{conv}}2}} $$
(9)

The apparent power supplied by the series voltage source converter is

$$ \begin{gathered} S_{{{\text{conv}}2}} = V_{s} I_{ij}^{*} = P_{{{\text{conv}}2}} + jQ_{{{\text{conv}}2}} \hfill \\ = rV_{i} e^{j\gamma } \left( {\frac{{V_{i}^{^{\prime}} - V_{j} }}{{jX_{s} }}} \right)^{*} \hfill \\ \end{gathered} $$
(10)

After simplification,

$$ P_{{{\text{conv}}2}} = b_{s} rV_{i} V_{j} \sin \left( {\delta_{ij} + \gamma } \right) - b_{s} rV_{i}^{2} \sin \gamma $$
(11)
$$ Q_{{{\text{conv}}2}} = - b_{s} rV_{i} V_{j} \cos \left( {\delta_{ij} + \gamma } \right) + b_{s} rV_{i}^{2} \cos \gamma + b_{s} r^{2} V_{i}^{2} $$
(12)

At last, the overall model of UPFC can be obtained by combining both shunt and series voltage source converter models as shown below. The overall UPFC model is depicted in Fig. 4.

$$ P_{i}^{{{\text{UPFC}}}} = b_{s} rV_{i}^{2} \sin \gamma - b_{s} rV_{i} V_{j} \sin \left( {\delta_{ij} + \gamma } \right) $$
$$ P_{j}^{{{\text{UPFC}}}} = b_{s} rV_{i} V_{j} \sin \left( {\delta_{ij} + \gamma } \right) $$
(13)
$$ Q_{i}^{{{\text{UPFC}}}} = - b_{s} rV_{i}^{2} \cos \gamma $$
$$ Q_{j}^{{{\text{UPFC}}}} = b_{s} rV_{i} V_{j} \cos \left( {\delta_{ij} + \gamma } \right) $$
(14)
Fig. 4
figure 4

Overall model of UPFC

Full size image

3 Optimization methods

3.1 Multiobjective cuckoo search algorithm

Cuckoo search (CS) algorithm was initially presented by Xin-She Yang and Suash Deb, inspired by the interesting breeding strategy of some cuckoo species (Yang and Deb 2009). Guria and Ani species of cuckoo family exhibit a peculiar behaviour concerning procreation. They identify a nest of any ill-fated host bird to dump their eggs. Such a breeding strategy alleviates the cuckoos from egg hatching, nurturing chicks, and protecting them from potential predators.

The CS algorithm makes use of levy flights for its global search. Steps of a Levy flight are defined by step-lengths having probability distribution (Yang and Deb 2009). Levy flight is credited to be the optimal strategy for pursuing a target in an unknown environment as the probability of visiting the previously visited site is low. Levy flights application to optimization problems resulted in positive outcomes (Yang and Deb 2011).

The standard version of the CS algorithm consists of the following rules.

  • Each cuckoo dumps one egg in any arbitrarily chosen nest

  • The nests having best quality eggs will be made available for the next generations

  • The number of available host nests being fixed, any fortunate host bird may identify the cuckoo eggs with a probability pa ϵ (0, 1). In such a situation, the host bird either abandons the nest or discards the eggs.

    The modified first and last rules for the MOCS algorithm with n objectives are:

  • Every cuckoo dumps n eggs in an arbitrarily chosen nest

  • Fortunate host bird abandons each nest with probability pa and a fresh nest will be created with n eggs based on the similarities/differences of the eggs. Random mixing can be employed to create diversity.

For every cuckoo \(i\), a fresh solution \(x^{{\left( {k + 1} \right)}}\) can be produced from the old one \(x^{{\left( {k + 1} \right)}}\) by levy flight

$$ x_{i}^{{\left( {k + 1} \right)}} = x^{\left( k \right)} + \alpha \oplus L\dot{e}vy\left( \lambda \right) $$
(15)

where \(\alpha\) is the step size which is related to the scales of the specific problem, \(\oplus\) is the Hadamard product operator. To provide room for the diversity in the quality of solution,\( \alpha\) is produced as per the following equation.

$$ \alpha = \alpha_{0} \left( {x_{j}^{\left( k \right)} - x_{i}^{\left( k \right)} } \right) $$
(16)

where αo is a constant and \(\left( {x_{j}^{\left( k \right)} - x_{i}^{\left( k \right)} } \right)\) is the difference of two arbitrary solutions which is adopted to represent the fact that similar eggs are less probable to detection by the host bird. Hence new solutions are produced by the proportionality of their difference. The step size, s, is defined as

$$ S = \alpha_{0} \left( {x_{j}^{\left( k \right)} - x_{i}^{\left( k \right)} } \right){ } \oplus L\dot{e}vy\left( \lambda \right)\sim 0.01\frac{U}{{\left| V \right|^{1/\lambda } }}\left( {x_{j}^{\left( k \right)} - x_{i}^{\left( k \right)} } \right) $$
(17)

where U and V are obtained from normal distributions. That is

$$ U\sim N\left( {0,\sigma_{U}^{2} } \right),V\sim N\left( {0,\sigma_{V}^{2} } \right) $$
(18)

with

$$ \sigma _{U} = \left\{ {\frac{{\Gamma \left( {1 + \lambda } \right)\sin \left( {\pi \lambda /2} \right)}}{{\lambda \Gamma \left[ {\left( {1 + \lambda } \right)/2} \right]2^{{\left( {\lambda - 1} \right)/2}} }}} \right\}^{{1/\lambda }} ,{\mkern 1mu} \sigma _{V} = 1,$$
(19)

where \({\Gamma }\) is the standard Gamma function.

3.2 Multiobjective PSO:

Particle swarm optimization algorithm is introduced first by Kennedy and Eberhart (1995). PSO algorithm draws its inspiration from food foraging patterns of fish and bird swarms. The merits of PSO over its peers include reduced parameter requirements and shorter computation time. PSO algorithm consists of particles that are represented by their position and velocity. The location of a particle in search space is governed based on its own experience and from experience gained by its neighbor particles. Position and velocity are updated according to the following equations.

$$ V_{i} \left( {k + 1} \right) = w \times V_{i} \left( k \right) + c1 \times r1 \times \left( {p{\text{best}}_{i} \left( k \right) - X_{i} \left( k \right)} \right) + c2 \times r2 \times \left( {g{\text{best}}\left( k \right) - X_{i} } \right) $$
(20)
$$ X_{i} \left( {k + 1} \right) = X_{i} \left( k \right) + V_{i} \left( {k + 1} \right) $$
(21)

where Xi is the position of the ith particle and velocity of the ith particle is Vi. k represents the current iteration, k + 1 represents the next iteration values of the algorithm. \(p{\text{best}}_{i}\) is the best particle value of ith particle and \( g{\text{best}}\) is the global best value among all particles. The overall flowchart for the optimization algorithms used is shown in Fig. 5.

Fig. 5
figure 5

Flowchart of MOCS and MOPSO algorithm

Full size image

4 Fitness function for minimization of losses

In general, an optimization problem with multi objectives comprises of multiple functions as a set of control variables that are to be minimized or maximized without violating the constraint limits.

$$ {\text{Minize }}f_{j} \left( {X,\sigma } \right) = 0,\,j = 1,2, \ldots \ldots ..k_{{{\text{obj}}}} $$
(22)

Such that, \(g\left( {X,\sigma } \right) = 0\) and \(h\left( {X,\sigma } \right) = 0\).


where \(f_{j}\) is the \(j^{th}\) fitness function, \(k_{{{\text{obj}}}}\) is the number of fitness functions, \(g\left( {X,\sigma } \right)\) is the equality constraints of the function and \(h\left( {X,\sigma } \right)\) is inequality constraints of the function.

4.1 Formulation of objective functions

This study considers the following minimization functions for the estimation of power loss.

$$ {\text{Min}}(P_{{{\text{Loss}}}} ) = \mathop \sum \limits_{m = 1}^{NL} P_{m} $$
(23)
$$ {\text{Min}}\left( {Q_{{{\text{Loss}}}} } \right) = \mathop \sum \limits_{m = 1}^{NL} Q_{m} $$
(24)

where \(NL\) is the number of lines, \(P_{m}\) is the active power loss in the line m, \(Q_{m}\) is the reactive power loss in the same line m

$$ P_{m} = \left( {V_{i}^{2} + V_{j}^{2} - 2V_{i} V_{j} \cos \delta_{ij} } \right)\left( {G_{ij} } \right) $$
(25)
$$ Q_{m} = \left( {V_{i}^{2} + V_{j}^{2} - 2V_{i} V_{j} \cos \delta_{ij} } \right)\left( {B_{ij} } \right) $$
(26)

Where,

\(V_{i}\) is the voltage magnitude at bus-\(i\).

\(V_{j}\) is the voltage magnitude at bus-\(j\).

\(G_{ij}\) is the conductance of the line admittance between bus-\(i\) and bus-j.

\(B_{ij}\) is the susceptance of the line admittance between bus-j and bus-j.

\(\delta_{ij}\) is the phase shift between bus-\(i\) and bus-j respectively.

The variable constraints are given as follows:

  1. (a)

    a. Equality constraints

$$ P_{gi} - P_{di} = V_{i} \mathop \sum \limits_{j = 1}^{Nb} V_{j} \left( {G_{ij} \cos \delta_{ij} + B_{ij} \sin \delta_{ij} } \right) $$
(27)
$$ Q_{gi} - Q_{di} = V_{i} \mathop \sum \limits_{j = 1}^{Nb} V_{j} \left( {G_{ij} {\text{sn}}\delta_{ij} - B_{ij} \cos \delta_{ij} } \right) $$
(28)

where \(Nb\) is the number of buses, \(P_{gi}\) and \(Q_{gi}\) are the real and reactive power generation at bus-\(i\), \(P_{di}\) and \(Q_{di}\) are the real and reactive power demand at bus-\(i\).

  1. (b)

    Inequality constraints

$$ V_{Li}^{{\min}} \le V_{Li} \le V_{Li}^{{\max}} $$
(29)
$$ V_{Gi}^{{\min}} \le V_{Gi} \le V_{Gi}^{{\max}} $$
(30)
$$ Q_{Gi}^{{\min}} \le Q_{Gi} \le Q_{Gi}^{{\max}} $$
(31)
$$ Q_{c}^{{\min}} \le Q_{c} \le Q_{c}^{{\max}} $$
(32)
$$ T_{s}^{{\min}} \le T_{s} \le T_{s}^{{\max}} $$
(33)
$$ V_{um}^{{\min}} \le V_{um} \le V_{um}^{{\max}} $$
(34)
$$ \gamma_{um}^{{\min}} \le \gamma_{um} \le \gamma_{um}^{{\max}} $$
(35)

Where:

\(V_{Li}\) is the value of voltage at \(i^{th}\) load bus.

\(V_{Gi}\) is the value of voltage at \( i^{th}\) generator bus.

\(Q_{Gi}\) is the reactive power generation at \(i^{th}\) generator bus.

\(Q_{c}\) is the shunt capacitor reactive power generation at \(i^{th}\) bus.

\(T_{s}\) is the transformer tap setting ratio.

\(V_{um}\) is the voltage magnitude of UPFC at line-\(m\), \(\gamma_{um}\) is the angle of UPFC at line-\(m\).

5 Solution of the multiobjective problem

5.1 Pareto-optimal method

To solve the multiobjective optimization problem the Pareto-optimal method is exploited here in this work to produce a set of solutions. This method has the concept of dominance as its underlying principle. Vector V1 keeps dominating vector V2 given the below conditions are satisfied.

$$ \forall k = \left\{ {1,2, \ldots \ldots p\} ,f_{k} \left( {V1} \right) \le f_{k} \left( {V2} \right)} \right. $$
(36)
$$ \exists l \in \left\{ {1,2, \ldots .p\} f_{l} \left( {V1} \right) < f_{l} \left( {V2} \right)} \right. $$
(37)

where \(p\) denotes the number of control variables.

5.2 Best-compromise solution

The best-compromise solution from the given set of Pareto-optimal solution is decided by the fuzzy logic method (Solmaz et al.2015). For this sake, a fuzzy membership function is devised for every objective function which is given as follows.

$$ \mu_{k} (x) = \left\{ {\begin{array}{*{20}c} {f_{k}^{\max } - f_{k} (x)} & {if} & {f_{k}^{\min } < f_{k} < f_{k}^{\max } } \\ {1,} & {if} & {f_{k} < f_{k}^{\min } } \\ {0,} & {if} & {f_{k} < f_{k}^{\max } } \\ \end{array} } \right. $$
(38)

where \( f_{k}^{min}\) and \(f_{k}^{max}\) corresponds to a totally permissible value and clearly impermissible value respectively, for the kth objective function. The membership function is given as follows.

$$ \mu^{r} = \frac{{\mathop \sum \nolimits_{k = 1}^{NO} \mu_{k}^{r} }}{{\mathop \sum \nolimits_{k = 1}^{ND} \mathop \sum \nolimits_{k = 1}^{NO} \mu_{k}^{r} }} $$
(39)

where, for the rth non-dominated solution, NO and ND and are the number of objective functions and the number of Pareto-optimal solutions respectively. The solution that yields maximum membership is the best compromise solution.

6 Simulation results

To test the efficacy of the proposed MOCS algorithm for solving the multiobjective optimization problem under consideration, simulation is carried out in MATLAB on a standard IEEE 30 bus whose structure is shown in Fig. 6. The power losses are first calculated by MOCS algorithm without installing UPFC. Later, MOCS applied is applied to estimate power losses by installing UPFC a strategic position to show the effectiveness of UPFC in the reduction of power loss.

Fig. 6
figure 6

Standard IEEE 30 bus system

Full size image

6.1 Power losses reduction without UPFC

Initially, a regular system without installing UPFC is considered and losses are computed. The share of active power loss is found to be 5.5933 MW, and the share of reactive power loss is 21.0658 MVar. Now to the test system is subjected to MOCS, MOPSO and MOFA techniques to compute the power loss. Table 1 presents the Pareto-optimal solution obtained after the application of MOCS, MOPSO and MOFA. The fuzzy logic method is employed to select the best-compromise solution from the pool of Pareto-optimal solution. The best-compromise solution generated by MOPSO for active power loss is 5.3046 MW and for reactive power loss is 20.4657 MVar while it is 5.2831 MW and 20.4437 MVar by MOCS for active power loss and reactive power loss respectively. The best-compromise solution obtained by MOFA for active power loss is 5.292 MW and for reactive power loss is 20.4561 MVar. It is evident from the results that the three algorithms are quite effective in the reduction of system power loss. The best-compromise solution obtained from MOFA is better that of MOPSO. It can also be noted that MOCS outperforms both MOPSO and MOFA as the obtained best-compromise solution for power loss reduction from MOCS is better than that of MOPSO and MOFA. Figure 7 comparatively depicts the results obtained from MOCS, MOPSO and MOFA algorithms.

Table 1 Comparison of Pareto-optimal solution without UPFC
Full size table
Fig. 7
figure 7

Comparison of the best-compromise solution without UPFC

Full size image

The individual CPU time taken to run all the algorithms is shown in Table 2. It is observed that MOPSO is taking relatively less time when compared to MOCS and MOFA. Although MOCS gave a better result, its run time is relatively high.

Table 2 CPU time without UPFC
Full size table

6.2 Power losses reduction with UPFC:

In this study, the line losses are calculated after installing UPFC. For tracing the optimal position of UPFC installation, the total system losses are estimated by fitting UPFC at all the lines of the test system considering one line at a time. Table 3 shows the total losses with UPFC placement. It is evident from Table 3 that the lowest magnitude of the system losses is 5.2754 MW and 20.0162 MVar which is found at position 27–30. Hence the optimal position to install UPFC is the line connecting buses 27 and 30. The optimized parameters of UPFC are for the Eq. (13) and Eq. (14) are \(r = 0.006\) and \( \gamma = 90^{0}\). The parameters are tuned by considering the range mentioned in (Noroozian et al. 1997).

Table 3 Total losses with UPFC placement
Full size table

Now the test system is subjected to MOCS, MOPSO and MOFA techniques to compute the power loss by fixing UPFC at the optimal position, i.e., at 27–30. Table 4 shows the Pareto-optimal solution obtained after the application of MOCS, MOPSO and MOFA. The fuzzy logic method is employed to extract the best-compromise solution from the pool of Pareto-optimal solution. The best-compromise solution generated by MOPSO for active power loss is 5.0631 MW and for reactive power loss is 19.8832 MVar while it is 5.0375 MW and 19.8762 MVar by MOCS for active power loss and reactive power loss respectively. The best-compromise solution generated by MOFA for active power loss is 5.0406 MW and for reactive power loss is 19.8783 MVar It is evident from the results that UPFC placement resulted in a reduction of system power loss. It can also be noted that MOCS outperforms both MOFA and MOPSO as the obtained best-compromise solution for power loss reduction from MOCS is better than that of MOFA and MOPSO. Figure 8 comparatively depicts the results obtained from MOCS, MOPSO and MOFA algorithms.

Table 4 Comparison of Pareto-optimal solution with UPFC
Full size table
Fig. 8
figure 8

Comparison of best-compromise solution with UPFC

Full size image

The individual CPU time taken to run all the algorithms after installation of UPFC at the optimal location is shown in Table 5. It is observed that MOPSO is taking relatively less time when compared to MOCS and MOFA. Although MOCS gave a better result, its run time is relatively high. It is also evident that the run time of all the algorithms increased after installing the UPFC.

Table 5 CPU time with UPFC
Full size table

A summary of all the results is shown in Table 6. It can be noted that before the installation of UPFC the power loss can be brought down by optimization. After the installation of UPFC, the power losses are further reduced. In both cases, MOCS has shown its superiority over MOPSO.

Table 6 Summary of results with and without UPFC
Full size table

7 Conclusion and future scope

In this study, a multiobjective problem is presented to simultaneously reduce active and reactive power loss by fitting UPFC at a strategic position. MOCS a very popular and effective multiobjective algorithm is incorporated for this purpose. To ascertain the merit of UPFC installation in power loss reduction, the multiobjective function is optimized with and without installation of UPFC. Simulation results show that the optimal placement of UPFC can minimize the power losses. Reduction of power losses will enhance the system capacity without augmenting the generation capacity. Furthermore, the multiobjective problem considered is solved using MOPSO. Obtained results indicate that the MOCS algorithm is relatively more effective in optimizing the considered multiobjective problem. In this study, the methodology is verified on a standard IEEE 30 bus test system but the authors are of the opinion that the methodology may also be tested on various other standard test systems as an extension of this study. Furthermore, the robustness of the MOCS algorithm against various standard indices may also be checked. Also, various other FACTS devices like SVC, TCSC may be incorporated to reduce the power losses and comparison can be made among these devices to identify the better one.