1 Introduction

Nowadays, multi-attribute decision-making (MADM) problem is a potential research tool in modern decision science. The main aim of this method is to select the best alternative among the finite set of alternatives as claimed by decision makers under the preference values of the alternatives. It has been extensively applied with quantitative or qualitative attribute values and has a board application in operation research (Pourhassan and Raissi 2017), management science (Levy et al. 2016; Teixeira et al. 2018), economic (Ronaynea and Brown-Gordon 2017), market prediction and engineering technology (Abbasian et al. 2018; Viriyasitavat 2016), etc. As our modern society move forward with the decision-making process, so it always faces imprecise, vague and uncertain facts to take a decision in solving decision-making problems. In order to solve imprecise and uncertain data, (Atanassov 2012) initiated the idea of intuitionistic fuzzy set (IFS) characterize by membership function and non-membership function, a powerful extension of fuzzy set (Zadeh 1965) whose part has only membership function.

The aggregated results for the execution of the criteria for alternatives, weighted and order weighted aggregation operators (Yager 1998; Yager and Kacprzyk 1997) takes a significant role during the combination of the information process. At that point, Xu (2007) built up a novel work on averaging operators like IFWA operator, IFOWA operator, and IFHA operator. Xu and Yager (2006) also built up some geometric aggregation operators, such as IFWG operator, IFOWG operator and IFHG operator and provided an example of the real application of IFHG operator to MADM issues. For more information on other operators and terminology, the readers are referred to Beliakov et al. (2007), Beliakov et al. (2011), Chen and Tan (1994), Chen and Chiou (2015), Garg (2016), He et al. (2015), Kumar and Garg (2018), Li (2011), Li and Ren (2015), Liu et al. (2016), Lourenzuttia and Krohling (2013), Wan and DF (2014), Wan and DF (2015), Wei (2008), Wei (2009), Wei (2010), Wei and Zhang (2018) and Zhang et al. (2018).

Although, intuitionistic fuzzy sets (IFS) and interval-valued intuitionistic fuzzy sets (IVIFS) successfully applied (He et al. 2015a; Ye 2009; Zhang et al. 2018a) to solve the uncertainty of the real world problems, but it has seen generally for the information analysis of an object that corresponding to each property there exists a counter property. In that view, Zhang (1994, 1998) originated another extension of fuzzy sets called bipolar fuzzy set (BFS) whose membership degree extended to \([-1,1]\). The bipolar fuzzy sets was characterized by two-component pair, one is positive membership degree belongs to the interval [0, 1] and other is negative membership degree belongs to the interval \([-1,0]\). Then BFS treated as a new tool to depict uncertainty in decision science. Bipolar fuzzy sets have not only applied in bipolar logical reasoning and bipolar set theory (Han et al. 2015; Zhang and Zhang 2004) but also applied in other application areas such as computational psychiatry (Zhang et al. 2011), medicine science (Lu and Busemeyer 2014; Zhang et al. 2009), bipolar quantum logic-based computing (Zhang 2013; Zhang and Peace 2014), quantum cellular combinatorics (Zhang 2013), decision analysis and organizational modeling (Fink and Yolles 2015; Li 2016), physics and philosophy (Zhang 2016) and bipolar fuzzy graph and its applications (Samanta and Pal 2012, 2012a, 2014; Singh and Kumar 2014; Yang et al. 2013). Lately, Gul (2015) introduced the concept of bipolar fuzzy aggregation operators, defined bipolar fuzzy weighted averaging operator (BFWAA) and bipolar fuzzy weighted geometric operator (BFWGA) and then utilized these operators to develop a multiple-attribute group decision-making problems. Thereafter, some decision-making problems have been developed using in the environment of bipolar fuzzy numbers as for example, Wang et al. (2018) introduced the notion of Frank Choquet Bonferroni mean operators on the bipolar neutrosophic environment and then utilized it to multi-criteria decision-making problems. Wei et al. (2018b) studied recently an MADM problem based on bipolar fuzzy Hamacher aggregation operator. They have proposed bipolar fuzzy Hamacher weighted averaging (BFHWA) operator, bipolar fuzzy Hamacher ordered weighted averaging (BFHOWA) operator, bipolar fuzzy Hamacher hybrid weighted averaging (BFHHWA) operator, bipolar fuzzy Hamacher weighted geometric (BFHWGA) operator, bipolar fuzzy Hamacher ordered weighted geometric (BFHOWGA) operator and bipolar fuzzy Hamacher hybrid weighted geometric (BFHHWGA) operator and explained related properties of these operators. Also, Gao et al. (2018) combined the concept of Hamacher operations and prioritized aggregation operators, and then defined dual hesitant bipolar fuzzy hamacher prioritized weighted average (DHBFHPWA) operator and dual hesitant bipolar fuzzy hamacher prioritized weighted geometric (DHBFHPWG) operator and studied a MADM problem using these operators for the relevance and effectiveness of the proposed methodology. Wei et al. (2017) proposed hesitant bipolar fuzzy weighted averaging (HBFWA) operator, hesitant bipolar fuzzy ordered weighted averaging (HBFOWA) operator, hesitant bipolar fuzzy hybrid weighted averaging (HBFHWA) operator, hesitant bipolar fuzzy weighted geometric (HBFWGA) operator, hesitant bipolar fuzzy ordered weighted geometric (HBFOWGA) operator and hesitant bipolar fuzzy hybrid weighted geometric (HBFHWGA) operator, and then developed a MADM problem for the evaluation of quality constructional engineering software selection. Xu and Wei (2017) provided dual hesitant bipolar fuzzy arithmetic aggregation operators and dual hesitant bipolar fuzzy geometric aggregation operators and then solved an MADM problem by using these proposed operators. Xu (1990) used the concept of linguistic variables to rank alternatives among the set of criteria, with emphasis placed on modeling the decision-making process. In (Garg and Nancy 2018), utilized linguistic prioritized aggregation operators to develop a multiple-attribute decision-making method under single-valued neutrosophic environment. Chen et al. (2018) represented a method combining social relation analysis with linguistic VIKOR to simultaneously evaluate and select a new project involving ambient intelligence products in accordance with the overall performance of a new product and the degree of influence of this product on the existing ambient intelligence products. Lu et al. (2017) introduced the notion of bipolar 2-tuple linguistic set, and using this concept defined bipolar 2-tuple linguistic hybrid average (B2TLHA) operator and bipolar 2-tuple linguistic hybrid geometric (B2TLHG) operator. Therefore, they utilized these operators to develop MADM problem for studying a real-world decision-making method. Wei et al. (2018a) studied risk evaluation of enterprise human capital investment problem in the environment of interval-valued bipolar 2-tuple linguistic numbers (IVB2TLNs). They investigated arithmetic and geometric aggregation operators with IVB2TLN information and analyze differently properties of these operators. In (Deschrijver et al. 2004; Deschrijver and Kerre 2002; Xia et al. 2012; Xu and Xia 2011), proposed some aggregation operators based on algebraic working laws for intuitionistic fuzzy numbers (IFNs), which is a special case of t-norm and t-conorm. Different generalizations of t-norms and t-conorms are available in literature, such as Archimedean t-norms and t-conorms, Hamacher t-norms and t-conorms, Algebraic t-norms and t-conorms, Einstein t-norms and t-conorms, Frank t-norms and t-conorms and Dombi t-norms and t-conorms. Liu (2014) utilized Hamacher aggregation operators in interval-valued intuitionistic fuzzy numbers (IVIFNs) and developed MAGDM methods. Zhang (2017) proposed Frank aggregation operators for IVIFNs and their applications to multiple attribute group decision-making. Zhao and Wei (2013) proposed Einstein hybrid aggregation operators for IFNs and apply it to multiple attribute decision-making method. Yu (2013) introduced Choquet aggregation operator based on Einstein operational laws for IFNs. Dombi (1982) introduced a new operations known as Dombi t-norm and Dombi t-conorm, which has a good precedence of change with the operation of parameters. For this advantage, Liu et al. (2018) utilized Dombi operations on intuitionistic fuzzy sets and developed multiple attribute group decision making problem using Dombi Bonferroni mean operator in the environment of intuitionistic fuzzy information. Chen and Ye (2017) developed multiple attribute decision-making problem using Dombi operations in single-valued neutrosophic environment. He (2018) used Dombi operations in hesitant fuzzy environment and based on this theory typhoon disaster assessment investigated. Keeping in mind from the fact that the bipolar fuzzy set has an effective capacity to prove the questionable and uncertain data which emerges in real-world issues. Therefore, decision-making problems in different uncertain fuzzy aggregation environment under Dombi operations makes us enough motivation to develop our present paper. There is a significant interest to research aggregation operators based on Dombi operation and their application to MADM problems. Therefore, based on Dombi operation, how to aggregate these bipolar fuzzy numbers is a tremendous topic. To solve this issue, in this paper, we shall define some bipolar fuzzy Dombi aggregation operators on the basis of traditional arithmetic (Xu 2007; Yager 1998), geometric operations (Xu and Yager 2006; Xu and Da 2003) and Dombi operations (Chen and Ye 2017; Dombi 1982; He 2018; Liu et al. 2018; Wei and Wei 2018).

The remainder of this paper is organized as follows: In the next Section, we briefly introduced some essential definition of the BFEs and some operational principles for BFEs. In Sect. 3, we defined Dombi operations for the bipolar fuzzy set. In Sect. 4, we developed bipolar fuzzy Dombi weighted averaging (BFDWAA) operator, bipolar fuzzy Dombi order weighted averaging (BFDOWAA) operator, bipolar fuzzy Dombi hybrid weighted averaging (BFDHWAA) operator. In Sect. 5, we proposed bipolar fuzzy Dombi weighted geometric (BFDWGA) operator, bipolar fuzzy Dombi order weighted geometric (BFDOWGA) operator, bipolar fuzzy Dombi hybrid weighted geometric (BFDHWGA) operator. In the next Section, we utilized those operators to create bipolar fuzzy multi-attribute decision-making problems. An interpretative case is specified for selection emerging technology enterprise systems in Sect. 7. In Sect. 8, we analyzed the effect of a parameter on decision-making results. Finally, in Sect. 9, the conclusion and scope of future research are outlined and discussed.

2 Preliminaries

In this section, we recall some basic concepts related to bipolar fuzzy sets (BFSs) over the universe of discourse X.

2.1 Bipolar fuzzy sets

Definition 1

Wei et al. (2018b) A bipolar fuzzy sets (BFS) is defined over the universe of discourse X as

$$\begin{aligned} \widetilde{S}=\{\langle x,{\hat{\mu }}^{+}_S(x),{\hat{\nu }}^{-}_S(x)\rangle |x\in X\}, \end{aligned}$$
(1)

where \({\hat{\mu }}^{+}_S(x): X\rightarrow [0,1]\) represent positive degree of membership to satisfy corresponding property of an element x to a BFS and \({\hat{\nu }}^{-}_S(x): X\rightarrow [-1,0]\) represent negative degree of membership to satisfy counter-property of an element x to a BFS, for every \(x\in X\). The set \(\langle (\mu ^{+}_S,\nu ^{-}_S)\rangle\) denotes bipolar fuzzy numbers (BFNs), i.e, bipolar fuzzy elements (BFEs).

Wei et al. (2018b) provided some basic operations on BFEs given as follows:

Definition 2

Wei et al. (2018b) Let \({\tilde{S}}=(\langle {\hat{\mu }}^{+}_S(x), {\hat{\nu }}^{-}_S(x)\rangle )\) and \({\tilde{T}}=(\langle {\hat{\mu }}^{+}_T(x), {\hat{\nu }}^{-}_T(x)\rangle )\) be two BFEs over the universe X. The following operations between two BFEs are defined as:

  1. (i)

    \({\tilde{S}}\subseteq {\tilde{T}}\), if \({\hat{\mu }}^{+}_S(x)\le {\hat{\mu }}^{+}_T(x)\), \({\hat{\nu }}^{-}_S(x)\ge {\hat{\nu }}^{-}_T(x)\) for all \(x\in X\)

  2. (ii)

    \({\tilde{S}}\cup {\tilde{T}}=\{\langle x, \max \{{\hat{\mu }}^{+}_S(x),{\hat{\mu }}^{+}_T(x)\}, \min \{{\hat{\nu }}^{-}_S(x),{\hat{\nu }}^{-}_T\}\rangle |x\in X\}\)

  3. (iii)

    \({\tilde{S}}\cap {\tilde{T}}=\{\langle x, \min \{{\hat{\mu }}^{+}_S(x),{\hat{\mu }}^{+}_T(x)\}, \max \{{\hat{\nu }}^{-}_S(x),{\hat{\nu }}^{-}_T\}\rangle |x\in X\}\)

  4. (iv)

    \(\overline{S}=\{\langle x, 1-{\hat{\mu }}^{+}_S(x), |{\hat{\nu }}^{-}_S(x)|-1 \rangle |x\in X\}\) for all \(x\in X\).

Definition 3

Wei et al. (2018b) Let \({\tilde{S}}=({\hat{\mu }}_S,{\hat{\nu }}_S)\) be a bipolar fuzzy element (BFE), then score function \({\hat{E}}\) and accuracy function \({\hat{L}}\) for BFEs is calculated as follows:

$$\begin{aligned} {\hat{E}}({\tilde{S}})=\frac{1+{\hat{\mu }}^{+}_S+{\hat{\nu }}^{-}_S}{2}, \quad {\hat{E}}({\tilde{S}})\in [0,1] \end{aligned}$$
(2)

and accuracy function is evaluated as:

$$\begin{aligned} {\hat{L}}({\tilde{S}})=\frac{{\hat{\mu }}^{+}_S-{\hat{\nu }}^{-}_S}{2}, \quad {\hat{L}}({\tilde{S}})\in [0,1] \end{aligned}$$
(3)

Based on score function \({\hat{E}}({\tilde{S}})\) and accuracy function \({\hat{L}}({\tilde{S}})\), defined order relation on two bipolar fuzzy elements \({\tilde{S}}=(\langle {\hat{\mu }}^{+}_S(x), {\hat{\nu }}^{-}_S(x)\rangle )\) and \({\tilde{T}}=(\langle {\hat{\mu }}^{+}_T(x), {\hat{\nu }}^{-}_T(x)\rangle )\) as follows:

Definition 4

Wei et al. (2018b) Let \({\tilde{S}}\) and \({\tilde{T}}\) be any two BFEs.

  1. (i)

    If \({\hat{E}}({\tilde{S}}) <{\hat{E}}({\tilde{T}})\), then \({\tilde{S}}\prec {\tilde{T}}\)

  2. (ii)

    If \({\hat{E}}({\tilde{S}})> {\hat{E}}({\tilde{T}})\), then \({\tilde{S}} \succ {\tilde{T}}\)

  3. (iii)

    If \({\hat{E}}({\tilde{S}})= {\hat{E}}({\tilde{T}})\), then

    1. (1)

      If \({\hat{L}}({\tilde{S}}) < {\hat{L}}({\tilde{T}})\), then \({\tilde{S}}\prec {\tilde{T}}\).

    2. (2)

      If \({\hat{L}}({\tilde{S}})> {\hat{L}}({\tilde{T}})\), then \({\tilde{S}}\succ {\tilde{T}}\).

    3. (3)

      If \({\hat{L}}({\tilde{S}})={\hat{L}}({\tilde{T}})\), then \({\tilde{S}}\sim {\tilde{T}}\).

Wei et al. (2018b) provided some operations on bipolar fuzzy numbers that are as follows:

Definition 5

Wei et al. (2018b) Let \({\tilde{S}}=(\langle {\hat{\mu }}^{+}_S(x),{\hat{\nu }}^{-}_S(x)\rangle )\) and \({\tilde{T}}=(\langle {\hat{\mu }}^{+}_T(x),{\hat{\nu }}^{-}_T(x)\rangle )\) be two BFEs over the universe X, then following operations are defined as follows:

  1. (i)

    \({\tilde{S}}\wedge {\tilde{T}}=\{\langle x, \min \{{\hat{\mu }}^{+}_S(x),{\hat{\mu }}^{+}_T(x)\}, \max \{{\hat{\nu }}^{-}_S(x),{\hat{\nu }}^{-}_T\}\rangle |x\in X\}\)

  2. (ii)

    \({\tilde{S}}\vee {\tilde{T}}=\{\langle x, \max \{{\hat{\mu }}^{+}_S(x),{\hat{\mu }}^{+}_T(x)\}, \min \{{\hat{\nu }}^{-}_S(x),{\hat{\nu }}^{-}_T\}\rangle |x\in X\}\)

  3. (iii)

    \({\tilde{S}}\oplus {\tilde{T}}=\big (\big \langle {\hat{\mu }}^{+}_S(x)+{\hat{\mu }}^{+}_T(x)-{\hat{\mu }}^{+}_S(x){\hat{\mu }}^{+}_T(x), -|{\hat{\nu }}^{-}_S(x)| |{\hat{\nu }}^{-}_T(x)|\big \rangle \big )\)

  4. (iv)

    \({\tilde{S}}\otimes {\tilde{T}}=\big (\big \langle {\hat{\mu }}^{+}_S(x){\hat{\mu }}^{+}_T(x), {\hat{\nu }}^{-}_S(x)+{\hat{\nu }}^{-}_T(x)-{\hat{\nu }}^{-}_S(x){\hat{\nu }}^{-}_T(x)\big \rangle \big )\)

  5. (v)

    \(\lambda {\tilde{S}}=\big (1-(1-{\hat{\mu }}^{+}_S(x))^{\lambda }, -|{\hat{\nu }}_S(x)|^{\lambda }\big )\)

  6. (vi)

    \({\tilde{S}}^{\lambda }=\big ({\hat{\mu }}_S^{\lambda }(x), -1+|1+{\hat{\nu }}^{-}_S(x))|^{\lambda }\big )\).

Based on the Definition 5, Wei et al. (2018b) derived the following operations:

Definition 6

Wei et al. (2018b) Let \({\tilde{S}}=(\langle {\hat{\mu }}^{+}_S, {\hat{\nu }}^{-}_S\rangle )\) and \({\tilde{T}}=(\langle {\hat{\mu }}^{+}_T, {\hat{\nu }}^{-}_T\rangle )\) be two BFEs over the universe X and \(\lambda ,\lambda _1,\lambda _2>0\), then

  1. (i)

    \({\tilde{S}}\oplus {\tilde{T}}= {\tilde{T}}\oplus {\tilde{S}}\)

  2. (ii)

    \({\tilde{S}}\otimes {\tilde{T}}= {\tilde{T}}\otimes {\tilde{S}}\)

  3. (iii)

    \(\lambda ({\tilde{S}}\oplus {\tilde{T}})=\lambda {\tilde{S}}\oplus \lambda {\tilde{T}}\)

  4. (iv)

    \(({\tilde{S}}\otimes {\tilde{T}})^{\lambda }={\tilde{S}}^{\lambda }\otimes {\tilde{T}}^{\lambda }\)

  5. (v)

    \(\lambda _1{\tilde{S}}\oplus \lambda _2 {\tilde{S}}=(\lambda _1+\lambda _2){\tilde{S}}\)

  6. (vi)

    \({\tilde{S}}^{\lambda _1}\otimes {\tilde{S}}^{\lambda _2}={\tilde{S}}^{(\lambda _1+\lambda _2)}\)

  7. (vii)

    \(({\tilde{S}}^{\lambda _1})^{\lambda _2}={\tilde{S}}^{\lambda _1\lambda _2}\).

3 Dombi operations on bipolar fuzzy numbers

3.1 Dombi operations

Dombi proposed operations Dombi product and Dombi sum which are special causes of t-norms and t-conorms given in the following definitions.

Definition 7

Dombi (1982) Let x and y be any two real numbers. Then, Dombi t-norms and Dombi t-conorms are defined in the following expression

$$Dom(x,y)= \frac{1}{1+ \left\{ \left(\frac{1-x}{x} \right)^{k}+\left(\frac{1-y}{y} \right)^{k} \right\}^{1/k}}$$
(4)
$$Dom^{*}(x,y)= 1-\frac{1}{1+ \left\{ \left(\frac{x}{1-x} \right)^{k}+ \left(\frac{y}{1-y} \right)^{k} \right\}^{1/k}}$$
(5)

where \(k\ge 1\) and \((x,y)\in [0,1]\times [0,1]\).

Based on the Dombi t-norm and Dombi t-conorm, we defined Dombi operations on BFEs.

3.2 Dombi operations on bipolar fuzzy elements

In this section, we shall introduce the notion of Dombi operations on bipolar fuzzy sets and find some properties of these operations. Let \({\tilde{B}}_1\) and \({\tilde{B}}_2\) be two bipolar fuzzy sets and \(\lambda>0\), then Dombi product and Dombi sum of the two BFEs \({\tilde{B}}_1\) and \({\tilde{B}}_2\) are respectively denoted as \(({\tilde{B}}_1\otimes {\tilde{B}}_2)\)and for right side

and \(({\tilde{B}}_1\oplus {\tilde{B}}_2)\) and defined by

$$\begin{aligned} \mathrm{(i)}\, {\tilde{B}}_1\oplus {\tilde{B}}_2& = \left\langle 1-\frac{1}{1+\left\{ \left( \frac{{\hat{\mu }}^{+}_1}{1-{\hat{\mu }}^{+}_1} \right) ^{k}+ \left( \frac{{\hat{\mu }}^{+}_2}{1-{\hat{\mu }}^{+}_2} \right) ^{k} \right\} ^{1/k}},\right. \\&\left. \frac{-1}{1+ \left\{ \left( \frac{1+{\hat{\nu }}^{-}_1}{|{\hat{\nu }}^{-}_1|} \right) ^{k}+ \left( \frac{1+{\hat{\nu }}^{-}_2}{|{\hat{\nu }}^{-}_2|} \right) ^{k} \right\} ^{1/k}} \right\rangle \\ \mathrm{(ii)}\, {\tilde{B}}_1\otimes {\tilde{B}}_2 &= \left\langle \frac{1}{1+ \left\{ \left( \frac{1-{\hat{\mu }}^{+}_1}{{\hat{\mu }}^{+}_1} \right) ^{k}+ \left( \frac{1-{\hat{\mu }}^{+}_2}{{\hat{\mu }}^{+}_2} \right) ^{k} \right\} ^{1/k}}, \right. \\&\left. -\,1+\frac{1}{1+ \left\{ \left( \frac{|{\hat{\nu }}^{-}_1|}{1+{\hat{\nu }}^{-}_1} \right) ^{k}+ \left( \frac{|{\hat{\nu }}^{-}_2|}{1+{\hat{\nu }}^{-}_2} \right) ^{k} \right\} ^{1/k}} \right\rangle \\ \mathrm{(iii)}\, \lambda .\;{\tilde{B}}_1&= \left\langle 1-\frac{1}{1+ \left\{ \lambda \left( \frac{{\hat{\mu }}^{+}_1}{1-{\hat{\mu }}^{+}_1} \right) ^{k} \right\} ^{1/k}},\right. \\&\left. \frac{-1}{1+ \left\{ \lambda \left( \frac{1+{\hat{\nu }}^{-}_1}{|{\hat{\nu }}^{-}_1|} \right) ^{k} \right\} ^{1/k}} \right\rangle \\ \mathrm{(iv)}\, ({\tilde{B}}_1)^{\lambda }_1 &= \left\langle \frac{1}{1+ \left\{ \lambda \left( \frac{1-{\hat{\mu }}^{+}_1}{{\hat{\mu }}^{+}_1} \right) ^{k} \right\} ^{1/k}},\right. \\&\left. -\,1+\frac{1}{1+ \left\{ \lambda \left( \frac{|{\hat{\nu }}^{-}_1|}{1+{\hat{\nu }}^{-}_1} \right) ^{k} \right\} ^{1/k}} \right\rangle . \end{aligned}$$

4 Bipolar fuzzy Dombi arithmetic aggregation operators

In this section, we propose Dombi arithmetic aggregation operators with bipolar fuzzy numbers such as bipolar fuzzy Dombi weighted averaging operator (BFDWA), bipolar fuzzy Dombi ordered weighted averaging operator (BFDOWA) and bipolar fuzzy Dombi hybrid weighted averaging operator (BFDHWA).

Definition 8

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\) (\(t=1,2,\ldots ,n)\) be a collection of BFEs. Then bipolar fuzzy Dombi weighted averaging BFDWA operator is a function \({\tilde{B}}^{n}\rightarrow {\tilde{B}}\) such that

$$\begin{aligned} BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigoplus \limits _{t=1}^{n}(\mho _t{\tilde{B}}_t) \end{aligned}$$
(6)

where \(\mho =(\mho _1,\mho _2,\ldots ,\mho _n)^{T}\) be the weight vector of \(B_t\)\((t=1,2,\ldots ,n)\) with \(\mho _j> 0\) and \(\sum \nolimits _{t=1}^{n}\mho _j=1\).

We get the following theorem that follows the Dombi operations on BFEs.

Theorem 1

\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\) (\(t=1,2,\ldots ,n)\)be a collection of bipolar fuzzy elements, then aggregated value ofthem using the BFDWA operation is also a BFEs, and

$$\begin{aligned}&BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n) =\bigoplus \limits _{t=1}^{n}(\mho _t{\tilde{B}}_t)\nonumber \\&\quad =\left\langle 1-\frac{1}{1+\left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle \end{aligned}$$
(7)

where\(\mho =(\mho _1,\mho _2,\ldots ,\mho _n)\)be the weight vector of\({\tilde{B}}_t\)\((t=1,2,\ldots ,n)\)such that\(\mho _t> 0\), and\(\sum \nolimits _{t=1}^{n}\mho _t=1\).

Thus Theorem 1 can be prove by the method of mathematical induction as follows:

Proof

(i) When \(n=2\), based on Dombi operations on BFEs we obtain the following results

$$\begin{aligned} BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2)={\tilde{B}}_1\bigoplus {\tilde{B}}_2= ({\hat{\mu }}^{+}_1,{\hat{\nu }}^{-}_1)\bigoplus ({\hat{\mu }}^{+}_2,{\hat{\nu }}^{-}_2) \end{aligned}$$
(8)

and for right side of (8), we have

$$\begin{aligned}& \left\langle 1-\frac{1}{1+ \left\{\mho _1\left(\frac{{\hat{\mu }}^{+}_1}{1-{\hat{\mu }}^{+}_1} \right)^{k}+\mho _2 \left(\frac{{\hat{\mu }}^{+}_2}{1-{\hat{\mu }}^{+}_2} \right)^{k} \right\}^{1/k}}, \frac{-1}{1+ \left\{\mho _1 \left(\frac{1+{\hat{\nu }}^{-}_1}{|{\hat{\nu }}^{-}_1|} \right)^{k}+ \mho _2 \left(\frac{1+{\hat{\nu }}^{-}_2}{|{\hat{\nu }}^{-}_2|} \right)^{k} \right\}^{1/k}} \right\rangle \nonumber \\ &\quad = \left\langle 1-\frac{1}{1+ \left\{\sum \limits _{t=1}^{2}\mho _t \left(\frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right)^{k}\right\}^{1/k}}, \frac{-1}{1+ \left\{\sum \limits _{t=1}^{2}\mho _t \left(\frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right)^{k} \right\}^{1/k}} \right\rangle. \end{aligned}$$
(9)

Thus, (7) holds is true for \(n=2\). (ii) Assume that (7) holds for \(n=p\), where \(p\in N (set of natural numbers)\),

then based on Eq. (9), we have

$$\begin{aligned}&BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{b}}_p)=\bigoplus \limits _{t=1}^{p}(\mho _t{\tilde{B}}_t)\nonumber \\&\quad = \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{p}\mho _t \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{p}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle . \end{aligned}$$
(10)

Now for \(n=p+1\), then \(BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_p,{\tilde{B}}_{p+1})\)

\(=\bigoplus \limits _{t=1}^{p}(\mho _tB_t)\bigoplus (\mho _{p+1}B_{p+1})\)

$$\begin{aligned}&= \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{p}\mho _t \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{p}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle \nonumber \\&\qquad \bigoplus \left\langle 1-\frac{1}{1+ \left\{ \mho _{p+1} \left( \frac{{\hat{\mu }}^{+}_{p+1}}{1-{\hat{\mu }}^{+}_{p+1}} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \mho _{p+1} \left( \frac{1+{\hat{\nu }}^{-}_{p+1}}{|{\hat{\nu }}^{-}_{p+1}|} \right) ^{k} \right\} ^{1/k}} \right\rangle \nonumber \\&= \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{p+1}\mho _j \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{p+1}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle . \end{aligned}$$
(11)

Thus, (7) is true for \(n=p+1\).

Hence, we conclude that (7) is true for any \(n\in N\). \(\square\)

Example 1

Suppose there are four BFEs \(B_1=(0.6,-0.3)\), \(B_2=(0.5,-0.4)\), \(B_3=(0.7,-0.2)\) and \(B_4=(0.2,-0.3)\), \(\mho =(0.2,0.1,0.3,0.4)\) is the weight vector for these BFEs \(B_t\)\((t=1,2,3,4)\). Then \(BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{b}}_4)\)\(=\bigoplus \nolimits _{t=1}^{4}(\mho _t{\tilde{B}}_t)\)

$$\begin{aligned}&= \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{4}\mho _t \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}},\, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{4}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle \\&=\left\langle 1-\frac{1}{1+ \left( 0.2\times (\frac{0.6}{1-0.6})^{2}+0.1\times (\frac{0.5}{1-0.5})^{2}+0.3\times (\frac{0.7}{1-0.7})^{2}+ 0.4\times (\frac{0.2}{1-0.2})^{2} \right) ^{2}} \right. \\&\left. \quad ,\frac{-1}{1+ \left( 0.2\times (\frac{1-0.3}{|-0.3|})^{2}+0.1\times (\frac{1-0.4}{|-0.4|})^{2}+ 0.3\times (\frac{1-0.2}{|-0.2|})^{2}+0.4\times (\frac{1-0.3}{|-0.3|})^{2} \right) ^{2}} \right\rangle \\&= \left\langle 0.5978,-0.2578 \right\rangle \end{aligned}$$

We prove easily the following properties by using the operator BFDWA.

Theorem 2

(Idempotency Property) If\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs and are all equal, i.e.,\({\tilde{B}}_t={\tilde{B}}\)for allt, then

$$\begin{aligned} BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)={\tilde{B}}. \end{aligned}$$
(12)

Proof

Since \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)={\tilde{B}}\)\((t=1,2,\ldots , n)\). Then, we have by Eq. (10),

$$\begin{aligned}&BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\\&\quad =\bigoplus \limits _{t=1}^{n}(\mho _t{\tilde{B}}_t)= \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, \right. \\&\left. \qquad \frac{-1}{1+\left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1+{\hat{\nu }}^{-}_t}{|{\hat{\nu }}^{-}_t|} \right) ^{k} \right\} ^{1/k}} \right\rangle \\&\quad = \left\langle 1-\frac{1}{1+ \left\{ \left( \frac{{\hat{\mu ^{+}}}}{1-{\hat{\mu }}^{+}} \right) ^{k} \right\} ^{1/k}}, \frac{-1}{1+ \left\{ \left( \frac{1+{\hat{\nu }}^{-}}{|{\hat{\nu }}^{-}|} \right) ^{k} \right\} ^{1/k}} \right\rangle \\&\quad = \left\langle 1-\frac{1}{1+\frac{{\hat{\mu }}^{+}}{1-{\hat{\mu }}^{+}}}, \frac{-1}{1+\frac{1+{\hat{\nu }}^{-}}{|{\hat{\nu }}^{-}|}} \right\rangle =({\hat{\mu }}^{+},{\hat{\nu }}^{-})={\tilde{B}}. \end{aligned}$$

Thus, \(BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)={\tilde{B}}\) holds. \(\square\)

Theorem 3

(Boundedness Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t, {\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. Let\({\tilde{B}}^{-}=\min ({\tilde{B}}_1,{\tilde{B}}_2,\ldots , {\tilde{B}}_n)=({\hat{\mu '}}^{-},{\hat{\nu '}}^{-})\)and\({\tilde{B}}^{+}=\max ({\tilde{B}}_1,{\tilde{B}}_2,\ldots , {\tilde{B}}_n)=({\hat{\mu '}}^{+},{\hat{\nu '}}^{+})\).

Then, \({\tilde{B}}^{-}\le BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {\tilde{B}}^{+}.\)

Proof

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t, {\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\) be a collection of BFEs. Let \({\tilde{B}}^{-}=\min ({\tilde{B}}_1,{\tilde{B}}_2,\ldots , {\tilde{B}}_n)=({\hat{\mu '}}^{-},{\hat{\nu '}}^{-})\) and \({\tilde{B}}^{+}=\max ({\tilde{B}}_1,{\tilde{B}}_2,\ldots , {\tilde{B}}_n)=({\hat{\mu '}}^{+},{\hat{\nu '}}^{+})\). We have \({\hat{\mu '}}^{-}=\min \limits _{t}\{{\hat{\mu }}^{+}_t\}\), \({\hat{\nu '}}^{-}=\max \limits _{t}\{{\hat{\nu }}^{-}_t\}\), \({\hat{\mu '}}^{+}=\max \limits _{t}\{{\hat{\mu }}^{+}_t\}\), and \({\hat{\nu '}}^{+}=\min \limits _{t}\{{\hat{\nu }}^{-}_t\}\). Then,

$$\begin{aligned} 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{{\hat{\mu '}}^{-}}{1-{\hat{\mu '}}^{-}} \right) ^{k} \right\} ^{1/k}}\le & {} 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{{\hat{\mu }}^{+}}{1-{\hat{\mu }}^{+}} \right) ^{k} \right\} ^{1/k}}\le 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{{\hat{\mu '}}^{+}}{1-{\hat{\mu '}}^{+}} \right) ^{k} \right\} ^{1/k}}\\ \frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1+{\hat{\nu '}}^{-}}{|{\hat{\nu '}}^{-}|} \right) ^{k} \right\} ^{1/k}}\le & {} \frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1+{\hat{\nu }}^{-}}{|{\hat{\nu }}^{-}|} \right) ^{k} \right\} ^{1/k}}\le \frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1+{\hat{\nu '}}^{+}}{|{\hat{\nu '}}^{+}|} \right) ^{k} \right\} ^{1/k}}. \end{aligned}$$

This result conclude between

$$\begin{aligned} {\tilde{B}}^{-}\le BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {\tilde{B}}^{+}. \end{aligned}$$
(13)

\(\square\)

Theorem 4

(Monotonicity Property) Let\({\tilde{B}}_t\)\((t=1,2,\ldots ,n)\)and\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots ,n)\)be two sets of BFEs, if\({\tilde{B}}_t\le {\tilde{B}}^{'}_t\)for allt, then\(BFDWA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le BFDWA_{\mho }({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n).\)

Proof

Proof follows from definition. \(\square\)

Now, we introduce bipolar fuzzy Dombi ordered weighted averaging operator BFDOWA.

Definition 9

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\) be a collection of BFEs. A bipolar fuzzy Dombi ordered weighted average (BFDOWA) operator of dimension n is a function \(BFDOWA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\) with associated vector \(w=(w_1, w_2,\ldots , w_n)^{T}\) such that \(w_t>0\), and \(\sum \nolimits _{t=1}^{n}w_t=1\).

Therefore,

$$\begin{aligned} BFDOWA_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigoplus \limits _{t=1}^{n}(\mho _t{\tilde{B}}_{t(\sigma )}) \end{aligned}$$
(14)

where \((\sigma (1),\sigma (2),\ldots ,\sigma (n))\) are the permutation of \(\sigma (t)\)\((t=1,2,\ldots ,n)\), for which \({\tilde{B}}_{\sigma (t-1)}\ge {\tilde{B}}_{\sigma (t)}\) for all \(t=1,2,\ldots ,n.\)

The following theorem is develop based on Dombi product operation on BFEs.

Theorem 5

Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. A bipolar fuzzy Dombi ordered weighted average (BFDOWA) operator of dimensionnis a function\(BFDOWA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\)with associated vector\(w=(w_1,w_2,\ldots ,w_n)^{T}\)such that\(w_t>0\), and\(\sum \nolimits _{t=1}^{n}w_t=1\). Then,

$$\begin{aligned}&{BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)= \bigoplus \limits _{t=1}^{n}(w_t{\tilde{B}}_{t(\sigma )})\nonumber \\&\quad =\Bigg \langle 1-\frac{1}{1+\Big \{\sum \limits _{t=1}^{n}w_t\Big (\frac{{\hat{\mu }}^{+}_{\sigma (t)}}{1-{\hat{\mu }}^{+}_{\sigma (t)}}\Big )^{k}\Big \}^{1/k}}, \frac{-1}{1+\Big \{\sum \limits _{t=1}^{n}w_t\Big (\frac{1+{\hat{\nu }}^{-}_{\sigma (t)}}{|{\hat{\nu }}^{-}_{\sigma (t)}|}\Big )^{k}\Big \}^{1/k}}\Bigg \rangle \end{aligned}$$
(15)

where\((\sigma (1),\sigma (2),\ldots ,\sigma (n))\)are the permutationof\(\sigma (t)\)\((t=1,2,\ldots ,n)\), for which\(B_{\sigma (t-1)}\ge B_{\sigma (t)}\)for all\(t=1,2,\ldots ,n.\)

Example 2

Let \({\tilde{B}}_1=(0.6,-0.4)\), \({\tilde{B}}_2=(0.3,-0.5)\), \({\tilde{B}}_3=(0.5,-0.4)\) and \({\tilde{B}}_4=(0.3,-0.6)\) be four BFEs and \(w=(0.2,0.1,0.3,0.4)^{T}\) is the weight vector of these BFEs. Then aggregated values of BFEs for \((k=3)\) and by Definition 9, scores of \({\tilde{B}}_t\)\((t=1,2,3,4)\) can be evaluated as follows:

\({\hat{E}}({\tilde{B}}_1)=\frac{1+0.6-0.4}{2}=0.6\), \({\hat{E}}({\tilde{B}}_2)=\frac{1+0.3-0.5}{2}=0.4\), \({\hat{E}}({\tilde{B}}_3)=\frac{1+0.5-0.4}{2}=0.55\), \({\hat{E}}({\tilde{B}}_4)=\frac{1+0.3-0.6}{2}=0.35\). Since,

$$\begin{aligned} {\hat{E}}({\tilde{B}}_1)> {\hat{E}}({\tilde{B}}_3)> {\hat{E}}({\tilde{B}}_2)> {\hat{E}}({\tilde{B}}_4), \end{aligned}$$

then \({\tilde{B}}_{\sigma (1)}={\tilde{B}}_1=(0.6,-0.4)\), \({\tilde{B}}_{\sigma (2)}={\tilde{B}}_3=(0.5,-0.4)\), \({\tilde{B}}_{\sigma (3)}={\tilde{B}}_2=(0.3,-0.5)\) and \({\tilde{B}}_{\sigma (4)}={\tilde{B}}_4=(0.3,-0.6)\). Then, by definition of BFDOWA operator:

$$\begin{aligned}&{BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_4)= \bigoplus \limits _{t=1}^{4}(w_t{\tilde{B}}_{\sigma (t)})\\&\quad = \left\langle 1-\frac{1}{1+ \left\{ \sum \limits _{t=1}^{4} w_t \left( \frac{{\hat{\mu }}^{+}_{\sigma (t)}}{1-{\hat{\mu }}^{+}_{\sigma (t)}} \right) ^{3} \right\} ^{1/3}}, \frac{-1}{1+ \left\{ \sum \limits _{t=1}^{4}w_t \left( \frac{1+{\hat{\nu }}^{-}_{\sigma (t)}}{|{\hat{\nu }}^{-}_{\sigma (t)}|} \right) ^{3} \right\} ^{1/3}} \right\rangle \\&\quad = \left\langle 1-\frac{1}{1+ \left\{ 0.2\times \left( \frac{0.6}{1-0.6} \right) ^{3}+0.1\times \left( \frac{0.5}{1-0.5} \right) ^{3}+0.3\times \left( \frac{0.3}{1-0.3} \right) ^{3}+ 0.4\times \left( \frac{0.3}{1-0.3} \right) ^{3} \right\} ^{1/3}}, \right. \\&\left. \qquad \frac{-1}{1+ \left\{ 0.2\times \left( \frac{1-0.4}{|-0.4|} \right) ^{3}+0.1\times \left( \frac{1-0.4}{|-0.4|} \right) ^{3}+0.3\times \left( \frac{1-0.5}{|-0.5|} \right) ^{3}+0.4\times \left( \frac{1-0.6}{|-0.6|} \right) ^{3} \right\} ^{1/3}} \right\rangle \\&\quad = \left\langle (0.4845,-0.3381) \right\rangle . \end{aligned}$$

The following properties easily proved by BFDOWA operator.

Theorem 6

(Idempotency Property) If\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)are all equal,

i.e. \({\tilde{B}}_t={\tilde{B}}\) for all t , then \({BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)={\tilde{B}}.\)

Theorem 7

(Boundedness Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. Let\(B^{-}=\min \nolimits _{t}{\tilde{B}}_t\), and\({\tilde{B}}^{+}=\max \nolimits _{t}{\tilde{B}}_t\). Then,

$$\begin{aligned} {\tilde{B}}^{-}\le {BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {\tilde{B}}^{+}. \end{aligned}$$
(16)

Theorem 8

(Monotonicity Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\) and \({\tilde{B}}^{'}_t\)\((t=1,2,\ldots ,n)\)be two sets of BFEs, if\({\tilde{B}}_t\le {\tilde{B}}^{'}_t\)for allt, then

$$\begin{aligned} {BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {BFDOWA}_{w}({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n). \end{aligned}$$
(17)

Theorem 9

(Commutativity Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)and\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots ,n)\)be two sets of BFEs, then \({BFDOWA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)= {BFDOWA}_{w}({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n)\)where\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots , n)\)is any permutation of\({\tilde{B}}_t\)\((t=1,2,\ldots , n)\).

Above Definitions 8 and 9, we see that BFDWA operator weights only the bipolar fuzzy values, on the other hand the BFDOWA operator weights only the ordered positions of the bipolar fuzzy values instead of weights of the bipolar fuzzy values themselves. Therefore, the weights used in the operators BFDWA and BFDOWA have in different aspects. But, they are considered only one of them. To avoid this disadvantage, we introduce bipolar fuzzy Dombi hybrid averaging (BFDHA) operator.

Definition 10

A bipolar fuzzy Dombi hybrid average (BFDHA) operator of dimension n is a function \(BFDHA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\), with associated weight vector \(w=(w_1, w_2,\ldots , w_n)\) such that \(w_t> 0\), and \(\sum \nolimits _{t=1}^{n}w_t=1\). Therefore, BFDHWA operator can be evaluated as

$$\begin{aligned}&{BFDHWA}_{w,\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)= \langle w_1\dot{{\tilde{B}}}_{\sigma (1)}\rangle +\langle w_2\dot{{\tilde{B}}}_{\sigma (2)}\rangle +\ldots +\langle w_n\dot{{\tilde{B}}}_{\sigma (n)} \rangle \nonumber \\&\quad =\Bigg \langle 1-\frac{1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{\dot{{\hat{\mu }}^{+}}_{\sigma (t)}}{1-\dot{{\hat{\mu }}^{+}}_{\sigma (t)}}\Big )^{k}\Big \}^{1/k}}, \frac{-1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{1+\dot{{\hat{\nu }}^{-}}_{\sigma (t)}}{|\dot{{\hat{\nu }}}^{-}_{\sigma (t)}|}\Big )^{k}\Big \}^{1/k}}\Bigg \rangle \end{aligned}$$
(18)

where \(\dot{{\tilde{B}}}_{\sigma (t)}\) is the tth largest weighted bipolar fuzzy values \(\dot{{\tilde{B}}}_{t}\)\((\dot{{\tilde{B}}_t}=n\mho _t{B}_t, t=1,2,\ldots , n)\) , and \(\mho =(\mho _1,\mho _2,\ldots , \mho _n)^{T}\) be the weight vector of \(\dot{{\tilde{B}}}_t\) with \(\mho _t> 0\) and \(\sum \nolimits _{t=1}^{n}\mho _t=1\), where n is the balancing coefficient. When \(w=(1/n,1/n,\ldots , 1/n)\), then BFDWA operator is a special case of BFDHA operator. Let \(\mho =(1/n,1/n,\ldots ,1/n)\), then BFDOWA is a special case of the operator BFDHA. Thus, BFDHA operator is a generalization of both the operators BFDWA and BFDOWA, which reflects the degrees of the given arguments and their ordered positions.

Example 3

There are four BFEs \({\tilde{B}}_1=(0.5,-0.3)\), \({\tilde{B}}_2=(0.6,-0.3)\), \({\tilde{B}}_3=(0.7,-0.3)\) and \({\tilde{B}}_4=(0.2,-0.4)\), and \(\mho =(0.20,0.30,30,0.20)^{T}\) weight vector of these four BFEs and \(W=(0.2,0.1,0.3,0.4)^{T}\) is the associated weight vector. Then, by Definition 10 aggregated of BFEs for \((k=3)\), by the way

$$\begin{aligned} \dot{{\tilde{B}}}_{1} & = \left\langle \left( 1-\frac{1}{1+ \left\{ 4\times 0.20 \times \left(\frac{0.5}{1-0.5} \right)^{3} \right\}^{1/3}}, \frac{-1}{1+ \left\{4\times 0.20\times \left(\frac{1-0.3}{|-0.3|} \right)^{3} \right\}^{1/3}} \right) \right\rangle \\ &= \left\langle 0.4814, -0.3158 \right\rangle \\ \dot{{\tilde{B}}}_{2} & = \left\langle \left( 1-\frac{1}{1+ \left\{4\times 0.30 \times \left(\frac{0.6}{1-0.6} \right)^{3}\right\}^{1/3}}, \frac{-1}{1+ \left\{4\times 0.30\times \left(\frac{1-0.3}{|-0.3|} \right)^{3} \right\}^{1/3}} \right) \right\rangle \\ & = \left\langle 0.6145, -0.2874 \right\rangle \\ \dot{{\tilde{B}}}_{3} & = \left\langle \left( 1-\frac{1}{1+ \left\{4\times 0.30 \times \left(\frac{0.7}{1-0.7} \right)^{3} \right\}^{1/3}}, \frac{-1}{1+ \left\{4\times 0.30\times \left(\frac{1-0.3}{|-0.3|} \right)^{3} \right\}^{1/3}} \right) \right\rangle \\ & = \left\langle 0.7126, -0.2874 \right\rangle \\ \dot{{\tilde{B}}}_{4} & = \left\langle \left( 1-\frac{1}{1+ \left\{4\times 0.20 \times \left(\frac{0.2}{1-0.2} \right)^{3} \right\}^{1/3}}, \frac{-1}{1+ \left\{4\times 0.20\times (\frac{1-0.4}{|-0.4|})^{3} \right\}^{1/3}} \right) \right\rangle \\ & = \left\langle 0.1884, -0.4180 \right\rangle. \end{aligned}$$

Scores of \({\tilde{B}}_t\) (t=1,2,3,4) calculated as follows:

\({\hat{E}}(\dot{{\tilde{B}}}_{1})=\frac{1+0.4814-0.3158}{2}=0.5828\),

\({\hat{E}}(\dot{{\tilde{B}}}_{2})=\frac{1+0.6145-0.2874}{2}=0.6636\),

\({\hat{E}}(\dot{{\tilde{B}}}_{3})=\frac{1+0.7126-0.2874}{2}=0.7126\) ,

\({\hat{E}}(\dot{{\tilde{B}}}_{4})=\frac{1+0.1884-0.4180}{2}=0.3852\).

Since,

$$\begin{aligned} {\hat{E}}(\dot{{\tilde{B}}}_{3})> {\hat{E}}(\dot{{\tilde{B}}}_{2})> {\hat{E}}(\dot{{\tilde{B}}}_{1})> {\hat{E}}(\dot{{\tilde{B}}}_{4}). \end{aligned}$$

Then, \(\dot{{\tilde{B}}}_{\sigma (1)}=\dot{{\tilde{B}}}_{3}=(0.7126, -0.2874)\),

\(\dot{{\tilde{B}}}_{\sigma (2)}=\dot{{\tilde{B}}}_{2}=(0.6145, -0.2874)\),

\(\dot{{\tilde{B}}}_{\sigma (3)}=\dot{{\tilde{B}}}_{1}=(0.4814, -0.3158 )\) and

\(\dot{{\tilde{B}}}_{\sigma (4)}=\dot{{\tilde{B}}}_{4}=(0.1884, -0.4180)\). Therefore, aggregated values of BFEs \((k=3)\) by the definition of BFDHWA operator:

$$\begin{aligned}&{BFDHWA}_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_4)\\ &\quad=\bigoplus \limits _{t=1}^{4}(\mho _t\dot{{\tilde{B}}}_{\sigma (t)}) = \left\langle 1-\frac{1}{1+ \left\{\sum \limits _{t=1}^{4}\mho _t \left(\frac{\dot{{\hat{\mu }}^{+}}_{\sigma (t)}}{1-\dot{{\hat{\mu }}^{+}}_{\sigma (t)}} \right)^{3} \right\}^{1/3}}, \frac{-1}{1+ \left\{\sum \limits _{t=1}^{4}\mho _t \left(\frac{1+\dot{{\hat{\nu }}^{-}}_{\sigma (t)}}{|\dot{{{\hat{\nu }}^{-}}}_{\sigma (t)}|}\right)^{3} \right\}^{1/3}} \right\rangle \\&\quad = \left\langle 1-\frac{1}{1+ \left\{0.2 \times \left(\frac{0.7126}{1-0.7126}\right)^{3}+ 0.1\times \left(\frac{0.6145}{1-0.6145}\right)^{3}+0.3\times \left(\frac{0.4814}{1-0.4814} \right)^{3}+ 0.4\times \left(\frac{0.1884}{1-0.1884} \right)^{3} \right\}^{1/3}} \right.\\& \left.\qquad , \frac{-1}{1+ \left\{0.2\times \left(\frac{1-0.2874}{|-0.2874|}\right)^{3}+0.1\times \left(\frac{1-0.2874}{|-0.2874|}\right)^{3}+0.3\times \left(\frac{1-0.3158}{|-0.3158|} \right)^{3}+0.4\times \left(\frac{1-0.4180 }{|-0.4180|} \right)^{3} \right\}^{1/3}} \right\rangle \\&\quad = \left\langle (0.6073,-0.3271)\right\rangle . \end{aligned}$$

5 Bipolar fuzzy Dombi geometric aggregation operators

To this part, we shall propose Dombi geometric aggregation operators with bipolar fuzzy numbers such as bipolar fuzzy Dombi weighted geometric operator (BFDWGA), bipolar fuzzy Dombi ordered weighted geometric operator (BFDOWGA) and bipolar fuzzy Dombi hybrid weighted geometric operator (BFDHWGA).

Definition 11

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\) (\(t=1,2,\ldots ,n)\) be a collection of BFEs. Then, BFDWGA operator is a function \({\tilde{B}}^{n}\rightarrow {\tilde{B}}\) such that

$$\begin{aligned} {BFDWGA}_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigotimes \limits _{t=1}^{n}({\tilde{B}}_t)^{\mho _t} \end{aligned}$$
(19)

where \(\mho =(\mho _1,\mho _2,\ldots ,\mho _n)^{T}\) be the weight vector of \({\tilde{B}}_t\)\((t=1,2,\ldots , n)\) such that \(\mho _t> 0\) and \(\sum \nolimits _{t=1}^{n}\mho _t=1\).

Bipolar fuzzy BFDWGA operator is evaluated as in the following theorem and can be prove by mathematical induction.

Theorem 10

\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\) (\(t=1,2,\ldots ,n)\)be a collection of bipolar fuzzy elements, then aggregated value of them using the BFDWGA operator is also a BFE, and

$$\begin{aligned}&{BFDWGA}_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n) =\bigotimes \limits _{t=1}^{n}({\tilde{B}}_t)^{\mho _t}\nonumber \\&\quad = \left\langle \frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{1-{\hat{\mu }}^{+}_t}{{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, -1+\frac{1}{1+ \left\{ \sum \limits _{t=1}^{n}\mho _t \left( \frac{|{\hat{\nu }}^{-}_t|}{1+{\hat{\nu }}^{-}_t}\right) ^{k} \right\} ^{1/k}} \right\rangle \end{aligned}$$
(20)

where \(\mho =(\mho _1,\mho _2,\ldots ,\mho _n)\) be the weight vector of \({\tilde{B}}_t\)\((t=1,2,\ldots ,n)\) such that \(\mho _t> 0\), and \(\sum \nolimits _{t=1}^{n}\mho _t=1\), \(\gamma>0\).

Proof

Proof of the theorem follows from Theorem 1. \(\square\)

Example 4

Suppose there are four BFEs \(B_1=(0.6,-\,0.3)\), \(B_2=(0.5,-\,0.4)\), \(B_3=(0.7,-\,0.2)\) and \(B_4=(0.2,-\,0.3)\), and \(\mho =(0.2,0.1,0.3,0.4)\) is the weight vector for these BFEs \(B_t\)\((t=1,2,3,4)\). Then \(BFDWGA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_4)\)\(=\bigoplus \nolimits _{t=1}^{4}(\mho _t{\tilde{B}}_t)\)

$$\begin{aligned} & = \left( \frac{1}{1+ \left\{ \sum \limits _{t=1}^{4}\mho _t \left( \frac{1-{\hat{\mu }}^{+}_t}{{\hat{\mu }}^{+}_t} \right) ^{k} \right\} ^{1/k}}, -1+\frac{1}{1+ \left\{ \sum \limits _{t=1}^{4}\mho _t \left( \frac{|{\hat{\nu }}^{-}_t|}{1+{\hat{\nu }}^{-}_t} \right) ^{k} \right\} ^{1/k}} \right) .\\ & = \left\langle \frac{1}{1+ \left( 0.2\times \left( \frac{1-0.6}{0.6} \right) ^{3}+0.1\times \left( \frac{1-0.5}{0.5} \right) ^{3}+0.3\times \left( \frac{1-0.7}{0.7} \right) ^{3}+ 0.4\times \left( \frac{1-0.2}{0.2} \right) ^{3} \right) ^{1/3}},\right. \\&\left. \quad -\,1+\frac{1}{1+ \left( 0.2\times \left( \frac{|-0.3|}{1-0.3} \right) ^{3}+0.1\times \left( \frac{|-0.4|}{1-0.4} \right) ^{3}+ 0.3\times \left( \frac{|-0.2|}{1-0.2} \right) ^{3}+0.4\times \left( \frac{|-0.3|}{1-0.3} \right) ^{3} \right) ^{1/3}} \right\rangle \\ & = \left\langle \left( 0.2529,-0.3025 \right) \right\rangle . \end{aligned}$$

Following properties for BFDWGA operator can be prove easily.

Theorem 11

(Idempotency Property) If\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)collection of BFEs and all are equal,i.e.,\({\tilde{B}}_t={\tilde{B}}\)for allt, then\(BFDWGA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)={\tilde{B}}\).

Theorem 12

(Boundedness Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. Let\({\tilde{B}}^{-}=\min \nolimits _{t}{\tilde{B}}_t,\;\;\ {\tilde{B}}^{+}=\max \nolimits _{t}{\tilde{B}}_t\). Then

$$\begin{aligned} {\tilde{B}}^{-}\le BFDWGA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {\tilde{B}}^{+}. \end{aligned}$$
(21)

Theorem 13

(Monotonicity Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)and\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots ,n)\)be twosets of BFEs, if\({\tilde{B}}_t\le {\tilde{B}}^{'}_t\)for allt, then\(BFDWGA_{\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le BFDWGA_{\mho }({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n).\)

Now, we introduce bipolar fuzzy Dombi ordered weighted geometric BFDOWGA operator.

Definition 12

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\) be a collection of BFEs. A bipolar fuzzy Dombi ordered weighted geometric (BFDOWGA) operator of dimension n is a function \(BFDOWGA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\) with associated vector

\(w=(w_1, w_2,\ldots , w_n)^{T}\) such that \(w_t>0\), and \(\sum \nolimits _{t=1}^{n} w_t=1\). Therefore,

$$\begin{aligned} BFDOWGA_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigotimes \limits _{t=1}^{n}({\tilde{B}}_{t(\sigma )})^{w_t} \end{aligned}$$
(22)

where \((\sigma (1),\sigma (2),\ldots ,\sigma (n))\) are the permutation of \((t=1,2,\ldots ,n)\), for which \({\tilde{B}}_{\sigma (t-1)}\ge {\tilde{B}}_{\sigma (t)}\) for all \(t=1,2,\ldots ,n.\)

The following theorem is develop based on Dombi product operation on BFEs using BFDOWGA operator.

Theorem 14

Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. A BFDOWGA operator ofdimensionnis a function\(BFDOWGA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\). Furthermore,

$$\begin{aligned}&BFDOWGA_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigotimes \limits _{t=1}^{n}({\tilde{B}}_t)^{w_t}\nonumber \\&\quad =\Bigg \langle \frac{1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{1-{\hat{\mu }}^{+}_t}{{\hat{\mu }}^{+}_t}\Big )^{k}\Big \}^{1/k}}, -1+\frac{1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{|{\hat{\nu }}^{-}_t|}{1+{\hat{\nu }}_t}\Big )^{k}\Big \}^{1/k}}\Bigg \rangle \end{aligned}$$
(23)

where \((\sigma (1),\sigma (2),\ldots ,\sigma (n))\) is the permutation of \(\sigma (t)\)\((t=1,2,\ldots ,n)\), for which \({\tilde{B}}_{\sigma (t-1)}\ge {\tilde{B}}_{\sigma (t)}\) for all \((t=1,2,\ldots ,n)\), with associated weight vector \(w=(w_1, w_2,\ldots , w_n)^{T}\) such that \(w_t>0\), and \(\sum \nolimits _{t=1}^{n} w_t=1\).

Example 5

Let \({\tilde{B}}_1=(0.6,-0.4)\), \({\tilde{B}}_2=(0.3,-0.5)\), \({\tilde{B}}_3=(0.5,-0.4)\) and \({\tilde{B}}_4=(0.3,-0.6)\) be four BFEs with \(w=(0.2,0.1,0.3,0.4)^{T}\) is the weight vector of these BFEs. Then aggregated BFEs is for \((k=3)\) and by Definition 9, scores of \({\tilde{B}}_t\)\((t=1,2,3,4)\) can be evaluated as follows:

\({\hat{E}}({\tilde{B}}_1)=\frac{1+0.6-0.4}{2}=0.6,\)\({\hat{E}}({\tilde{B}}_2)=\frac{1+0.3-0.5}{2}=0.4\), \({\hat{E}}({\tilde{B}}_3)=\frac{1+0.5-0.4}{2}=0.55\), \({\hat{E}}({\tilde{B}}_4)=\frac{1+0.3-0.6}{2}=0.35\).

Since,

$$\begin{aligned} {\hat{E}}({\tilde{B}}_1)> {\hat{E}}({\tilde{B}}_3)> {\hat{E}}({\tilde{B}}_2)> {\hat{E}}({\tilde{B}}_4), \end{aligned}$$

then \({\tilde{B}}_{\sigma (1)}={\tilde{B}}_1=(0.6,-0.4)\), \({\tilde{B}}_{\sigma (2)}={\tilde{B}}_3=(0.5,-0.4)\), \({\tilde{B}}_{\sigma (3)}={\tilde{B}}_2=(0.3,-0.5)\) and \({\tilde{B}}_{\sigma (4)}={\tilde{B}}_4=(0.3,-0.6)\). Then, by definition of BFDOWGA operator:

$$\begin{aligned}&{BFDOWGA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_4)= \bigoplus \limits _{t=1}^{4}(w_t{\tilde{B}}_{\sigma (t)})\\&\quad =\Bigg \langle \frac{1}{1+\Big \{\sum \limits _{t=1}^{4}w_t\Big (\frac{1-{\hat{\mu }}^{+}_{\sigma (t)}}{{\hat{\mu }}^{+}_{\sigma (t)}}\Big )^{3}\Big \}^{1/3}}, -1+\frac{1}{1+\Big \{\sum \limits _{t=1}^{4}w_t\Big (\frac{|{\hat{\nu }}^{-}_{\sigma (t)}|}{1-{\hat{\nu }}^{-}_{\sigma (t)}}\Big )^{3}\Big \}^{1/3}}\Bigg \rangle \\&\quad =\Big \langle \frac{1}{1+\Big \{0.2\times \Big (\frac{1-0.6}{0.6}\Big )^{3}+0.1\times \Big (\frac{1-0.5}{0.5}\Big )^{3}+0.3\times \Big (\frac{1-0.3}{0.3}\Big )^{3}+ 0.4\times \Big (\frac{1-0.3}{0.3}\Big )^{3}\Big \}^{1/3}},\\&\qquad -1+\frac{1}{1+\Big \{0.2\times \Big (\frac{|-0.4|}{1-0.4}\Big )^{3}+0.1\times \Big (\frac{|-0.4|}{1-0.4}\Big )^{3}+0.3\times \Big (\frac{|-0.5|}{1-0.5}\Big )^{3}+0.4\times \Big (\frac{|-0.6|}{1-0.6}\Big )^{3}\Big \}^{1/3}}\Big \rangle \\&\quad =\Big \langle \Big (0.3242,-0.5460\Big )\Big \rangle . \end{aligned}$$

The following properties can be proved easily by BFDOWGA operator.

Theorem 15

(Idempotency Property) If\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)are equal BFEs,

i.e.,\({\tilde{B}}_t={\tilde{B}}\)for allt, then\(BFDOWGA_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)={\tilde{B}}.\)

Theorem 16

(Boundedness Property) Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)be a collection of BFEs. Let\({\tilde{B}}^{-}=\min \nolimits _{t}{\tilde{B}}_t\), and\({\tilde{B}}^{+}=\max \nolimits _{t}{\tilde{B}}_t\). Then,\({\tilde{B}}^{-}\le {BFDOWGA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {\tilde{B}}^{+}.\)

Theorem 17

(Monotonicity Property)

Let \({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\) \((t=1,2,\ldots ,n)\) and

\({\tilde{B}}^{'}_t\) \((t=1,2,\ldots ,n)\) be two sets of BFEs, if \({\tilde{B}}_t\le {\tilde{B}}^{'}_t\) for all t , then

\({BFDOWGA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)\le {BFDOWGA}_{w}({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n).\)

Theorem 18

(Commutativity Property)Let\({\tilde{B}}_t=({\hat{\mu }}^{+}_t,{\hat{\nu }}^{-}_t)\)\((t=1,2,\ldots ,n)\)and\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots ,n)\)be twosets of BFEs, then\({BFDOWGA}_{w}({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)= {BFDOWGA}_{w}({\tilde{B}}^{'}_1,{\tilde{B}}^{'}_2,\ldots ,{\tilde{B}}^{'}_n)\)where\({\tilde{B}}^{'}_t\)\((t=1,2,\ldots , n)\)is any permutation of\({\tilde{B}}_t\)\((t=1,2,\ldots , n)\).

Follows from Definition 11 and Definition 12, we see that BFDWGA operator weights only the bipolar fuzzy values, on the other hand, the BFDOWGA operator weights only the ordered position of the bipolar fuzzy values instead of weights of the bipolar fuzzy values themselves. Therefore, weights represent in both the operators BFDWGA and BFDOWGA are in different aspects. But, they are considered only one of them. To avoid this disadvantage, we introduce bipolar fuzzy Dombi hybrid geometric (BFDHWGA) operator.

Definition 13

A bipolar fuzzy Dombi hybrid geometric (BFDHGA) operator of dimension n is a function \(BFDHWGA: {\tilde{B}}^{n}\rightarrow {\tilde{B}}\), with associated weight vector \(w=(w_1, w_2,\ldots , w_n)\) such that \(w_t> 0\), and \(\sum \nolimits _{t=1}^{n} w_t=1\). Therefore, BFDHWGA operator can be evaluated as

$$\begin{aligned}&BFDHWGA_{w,\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_n)=\bigotimes \limits _{t=1}^{n}(\dot{{\tilde{B}}}_{\sigma (t)})^{w_t}\nonumber \\&\quad =\Bigg \langle \frac{1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{1-\dot{{\hat{\mu }}^{+}}_{\sigma (t)}}{\dot{{\hat{\mu }}^{+}}_{\sigma (t)}}\Big )^{k}\Big \}^{1/k}}, -1+\frac{1}{1+\Big \{\sum \limits _{t=1}^{n} w_t\Big (\frac{\dot{|{\hat{\nu }}^{-}}_{\sigma (t)}|}{1+\dot{{\hat{\nu }}}_{\sigma (t)}}\Big )^{k}\Big \}^{1/k}} \Bigg \rangle \end{aligned}$$
(24)

where \(\dot{{\tilde{B}}}_{\sigma (t)}\) is the tth largest weighted bipolar fuzzy values \(\dot{{\tilde{B}}}_{t}\)\((\dot{{\tilde{B}}_t}=n\mho _t{B}_t, t=1,2,\ldots , n)\) , and \(\mho =(\mho _1,\mho _2,\ldots , \mho _n)^{T}\) be the weight vector of \(\dot{{\tilde{B}}}_t\) with \(\mho _t> 0\) and \(\sum \nolimits _{t=1}^{n}\mho _t=1\), where n is the balancing coefficient. When \(w=(1/n,1/n,\ldots , 1/n)\), then BFDWGA operator is a special case of BFDHGA operator. Let \(\mho =(1/n,1/n,\ldots ,1/n)\), then BFDOWGA is a special case of the operator BFDHGA. Thus, BFDHGA operator is a generalization of both the operators BFDWGA and BFDOWGA, which reflects the degrees of the given arguments and their ordered positions.

Example 6

Let \(B_1=(0.5,-0.3)\),

\(B_2=(0.6,-0.3)\), \(B_3=(0.7,-0.3)\) and \(B_4=(0.2,-0.4)\) be four BFEs and \(\mho =(0.20,0.30,0.30,0.20)^{T}\) is the weight vector of these four BFEs and \(W=(0.2,0.1,0.3,0.4)^{T}\) is the associated weight vector. Then, by Definition 13 for aggregated of BFEs for \((k=3)\), by the way

$$\begin{aligned}&\dot{{\tilde{B}}}_{1}=\Big \langle \Big ( \frac{1}{1+\Big \{4\times 0.20 \times (\frac{1-0.5}{0.5})^{3}\Big \}^{1/3}}, -1+\frac{1}{1+\Big \{4\times 0.20\times (\frac{|-0.3|}{1-0.3})^{3}\Big \}^{1/3}}\Big )\Big \rangle \\&\quad =\Big \langle \Big ( 0.5186, -0.2846 \Big )\Big \rangle \\&\dot{{\tilde{B}}}_{2}=\Big \langle \Big (\frac{1}{1+\Big \{4\times 0.30 \times (\frac{1-0.6}{0.6})^{3}\Big \}^{1/3}}, -1+\frac{1}{1+\Big \{4\times 0.30\times (\frac{|-0.3|}{1-0.3})^{3}\Big \}^{1/3}}\Big )\Big \rangle \\&\quad =\Big \langle \Big ( 0.5853, -0.3129\Big ) \Big \rangle \\&\dot{{\tilde{B}}}_{3}=\Big \langle \Big ( \frac{1}{1+\Big \{4\times 0.30 \times (\frac{1-0.7}{0.7})^{3}\Big \}^{1/3}}, -1+\frac{1}{1+\Big \{4\times 0.30\times (\frac{|-0.3|}{1-0.3})^{3}\Big \}^{1/3}}\Big )\Big \rangle \\&\quad =\Big \langle \Big ( 0.6871, -0.3129\Big )\Big \rangle \\&\dot{{\tilde{B}}}_{4}=\Big \langle \Big (\frac{1}{1+\Big \{4\times 0.20 \times (\frac{1-0.2}{0.2})^{3}\Big \}^{1/3}}, -1+\frac{1}{1+\Big \{4\times 0.20\times (\frac{|-0.4|}{1-0.4})^{3}\Big \}^{1/3}}\Big )\Big \rangle \\&\quad =\Big \langle \Big (0.2122, -0.3823 \Big )\Big \rangle . \end{aligned}$$

Scores of \(B_t\) (t = 1,2,3,4) calculated as follows:

\({\hat{E}}(\dot{{\tilde{B}}}_{1})=\frac{1+0.5186-0.2846 }{2}=0.617\),

\({\hat{E}}(\dot{{\tilde{B}}}_{2})=\frac{1+0.5853-0.3129}{2}=0.6362\),

\({\hat{E}}(\dot{{\tilde{B}}}_{3})=\frac{1+0.6871-0.3129}{2}=0.6871\) ,

\({\hat{E}}(\dot{{\tilde{B}}}_{4})=\frac{1+0.2122-0.3823}{2}=0.4150\).

Since,

$$\begin{aligned} {\hat{E}}(\dot{{\tilde{B}}}_{3})> {\hat{E}}(\dot{{\tilde{B}}}_{2})> {\hat{E}}(\dot{{\tilde{B}}}_{1})> {\hat{E}}(\dot{{\tilde{B}}}_{4}). \end{aligned}$$

Then, \(\dot{{\tilde{B}}}_{\sigma (1)}=\dot{{\tilde{B}}}_{3}=(0.6871,-0.3129)\),

\(\dot{{\tilde{B}}}_{\sigma (2)}=\dot{{\tilde{B}}}_{2}=(0.5853, -0.3129)\),

\(\dot{{\tilde{B}}}_{\sigma (3)}=\dot{{\tilde{B}}}_{1}=(0.5186, -0.2846)\) and

\(\dot{{\tilde{B}}}_{\sigma (4)}=\dot{{\tilde{B}}}_{4}=(0.2122, -0.3823)\). Therefore, aggregated values of BFEs \((k=3)\) by the definition of BFDHWGA operator:

$$\begin{aligned}&{BFDHWGA}_{w,\mho }({\tilde{B}}_1,{\tilde{B}}_2,\ldots ,{\tilde{B}}_4)=\bigotimes \limits _{t=1}^{4}(\dot{{\tilde{B}}}_{\sigma (t)})^{w_t}\\&\quad =\Bigg \langle \frac{1}{1+\Big \{\sum \limits _{t=1}^{4} w_t\Big (\frac{1-\dot{{\mu }}_{\sigma (t)}}{\dot{{\mu }}_{\sigma (t)}}\Big )^{3}\Big \}^{1/3}}, -1=\frac{1}{1+\Big \{\sum \limits _{t=1}^{4}w_t\Big (\frac{|\dot{{\nu }}_{\sigma (t)}|}{1+\dot{{\nu }}_{\sigma (t)}}\Big )^{3}\Big \}^{1/3}}\Bigg \rangle \\&\quad =\Big \langle \frac{1}{1+\Big \{0.2\times (\frac{1-0.6871}{0.6871})^{3}+0.1\times (\frac{1-0.5853}{ 0.5853})^{3}+0.3\times (\frac{1-0.5186}{0.5186})^{3}+ 0.4\times (\frac{1-0.2122}{0.2122})^{3}\Big \}^{1/3}}, \\&\qquad -1+\frac{1}{1+\Big \{0.2\times (\frac{|-0.3129|}{1-0.3129})^{3}+0.1\times (\frac{|-0.3129|}{1-0.3129})^{3}+0.3\times (\frac{|-0.2846|}{1-0.2846})^{3}+0.4\times (\frac{|-0.3823|}{1-0.3823})^{3}\Big \}^{1/3}}\Big \rangle \\&\quad =\Big \langle (0.3582,-0.3429)\Big \rangle . \end{aligned}$$

6 Model for MADM using bipolar fuzzy information

In this section, we develop multiple attribute decision making (MADM) method using bipolar fuzzy aggregation operators in which attribute weights are real numbers and attribute values are bipolar fuzzy element. Here multiple-attribute decision-making problem used to develop usefulness of evaluation emerging technology commercialization with bipolar fuzzy Dombi information. Let \({\tilde{Q}}=\{{\tilde{Q}}_1, {\tilde{Q}}_2,\ldots , {\tilde{Q}}_m\}\) be the discrete set of alternatives and \({\tilde{G}}=\{{\tilde{G}}_1, {\tilde{G}}_2, \ldots , {\tilde{G}}_n\}\) be the set of attributes. Let \(\mho =(\mho _1,\mho _2,\ldots ,\mho _n)\) be the weight vector of the attribute \({\tilde{G}}_t\)\((t=1,2,\ldots ,n)\) are completely known such that \(\mho _t>0\) and \(\sum \nolimits _{t=1}^{n}\mho _t=1\). Suppose \({\tilde{M}}=({\hat{\mu }}_{ht},{\hat{\nu }}_{ht})_{m\times n}\) is a bipolar fuzzy decision matrix, where \({\hat{\mu }}_{ht}\) is the degree of the positive membership for which alternative \({\tilde{Q}}_t\) satisfies the attribute \({\tilde{G}}_t\) given by the decision makers, and \({\hat{\nu }}_{ht}\) provided the degree that the alternative \({\tilde{Q}}_h\) does not satisfy the attribute \({\tilde{G}}_t\) given by the decision maker, where \({\hat{\mu }}_{ht}\subset [0,1]\) and \({\hat{\nu }}_{ht}\subset [-1,0]\) such that \(-1\le {\hat{\mu }}_{ht}+{\hat{\nu }}_{ht}\le 1\), \((h=1,2,\ldots ,m)\) and \((t=1,2,\ldots ,n)\).

We propose the following algorithm to solve MADM problem with bipolar fuzzy information using BFDWA and BFDWGA operators.

Algorithm

Input: To select best alternatives.

Output: Best alternative.

Step 1. We employ the decision information given in matrix M, and the operator BFDWAA

$$\begin{aligned} \tilde{\beta }_h & = BFDWAA(\tilde{\beta }_{h1},\tilde{\beta }_{h2},\ldots ,\tilde{\beta }_{hn})= \bigoplus \limits _{t=1}^{n}(\mho _t\tilde{\beta }_{ht})\nonumber \\ & = \Bigg \langle 1-\frac{1}{1+\Big \{\sum \limits _{t=1}^{n}\mho _t\Big (\frac{{\hat{\mu }}^{+}_t}{1-{\hat{\mu }}^{+}_t}\Big )^{k}\Big \}^{1/k}}, \frac{-1}{1+\Big \{\sum \limits _{t=1}^{n}\mho _t\Big (\frac{1+{\hat{\nu }}^{+}_t}{|{\hat{\nu }}^{-}_t|}\Big )^{k}\Big \}^{1/k}}\Bigg \rangle \end{aligned}$$
(25)

or \(\tilde{\beta }_h=BFDWGA({\tilde{\beta }}_{h1},\tilde{\beta }_{h2},\ldots ,{\tilde{\beta }}_{hn})=\bigoplus \limits _{t=1}^{n}(\beta _{ht})^{\mho _t}\)

$$\begin{aligned} =\Bigg \langle \frac{1}{1+\Big \{\sum \limits _{t=1}^{n}\mho _t\Big (\frac{1-{\hat{\mu }}^{+}_t}{{\hat{\mu }}^{+}_t}\Big )^{k}\Big \}^{1/k}}, -1+\frac{1}{1+\Big \{\sum \limits _{t=1}^{n}\mho _t\Big (\frac{|{\hat{\nu }}^{-}_t|}{1+{\hat{\nu }}^{-}_t}\Big )^{k}\Big \}^{1/k}}\Bigg \rangle \end{aligned}$$
(26)

to obtained the overall preference values \({\tilde{\beta }}_h\)\((h=1,2,\ldots ,m)\) of the alternative \({\tilde{Q}}_h\).

Step 2. Calculate the score function \({\hat{E}}({\tilde{\beta }}_h)\)\((h=1,2,\ldots , m)\) based on overall bipolar fuzzy information \({\tilde{\beta }}_h\)\((h=1,2,\ldots ,m)\) in ordered to rank all the alternative \({\tilde{Q}}_h\)\((h=1,2,\ldots ,m)\) to select best choice \({\tilde{Q}}_h\). If there is no difference between the score functions \({\hat{E}}({\tilde{\beta }}_h)\) and \({\hat{E}}({\tilde{\beta }}_t)\), then we proceed to calculate accuracy degrees of \({\hat{L}}({\tilde{\beta }}_h)\) and \({\hat{L}}({\tilde{\beta }}_t)\) based on overall bipolar fuzzy information of \({\tilde{\beta }}_h\) and \({\tilde{\beta }}_t\), and rank the alternative \({\tilde{Q}}_h\) depending on the accuracy degrees of \({\hat{L}}({\tilde{\beta }}_h)\) and \({\hat{L}}(\tilde{\beta }_t)\).

Step 3. Rank all the alternatives \({\tilde{Q}}_h\)\((h=1,2,\ldots ,m)\) in order to choose the best one(s) in accordance with \({\hat{E}}({\tilde{\beta }}_h)\)\((h=1,2,\ldots ,m)\).

Step 4. End.

7 Numerical Example

With the rapid development and wide application of information technology, the selection of emerging technology enterprise becomes more and more important. The aim of this paper is to evaluate the best emerging technology enterprise from the different companies of the emerging technology enterprise performances, that provide alternatives of enterprise. Therefore, to this section, we shall present a numerical result to establish the potential assessment of technology commercialization depicted in Wei (2016) with bipolar fuzzy information in order to investigate our proposed method in this paper. There is a committee which selects five possible emerging technology enterprises \({\tilde{Q}}_h\)\((h=1,2,\ldots , 5)\). They choose four attributes to assess five possible emerging technology enterprises as follows:

\(G_1\) :

: Technical Advancement

\(G_2\) :

: Potential market and market risk

\(G_3\) :

: Industrialization infrastructure, human resources and financial conditions

\(G_4\) :

: The employment creation and the development of science and technology.

In order to avoid dominance against other, decision makers are required to exempt the four possible emerging technology enterprises \({\tilde{Q}}_h\)\((h=1,2,\ldots , n)\) under the above attributes whose weight vector \(\mho =(0.2,0.1,0.3,0.4)^{T}\) presented by decision makers, where decision matrix \(\widetilde{M}=(\beta _{ht})_{5\times 4}\) which is given in the following table, where \(\beta _{ht}\) are in the form of BFEs (Table 1).

Table 1 Bipolar fuzzy elements
Full size table

In order to select the most desirable emerging technology enterprises \({\tilde{Q}}_h\)\((h=1,2,\ldots , n)\), we utilize the BFDWA and BFDWGA operator to develop multi-attribute decision-making a theory with bipolar fuzzy information, which can be evaluated as follows:

  • Step 1. For \(k=1\), using the BFDWA operator to calculate the overall preferences values \(\tilde{\beta }_h\) of emerging technology enterprises \({\tilde{A}}_h\)\((h=1,2,\ldots ,5)\)

    \(\widetilde{\beta }_1= (0.5862, -0.1980),\) \(\widetilde{\beta }_2= (0.5792, -0.2564,)\) \(\widetilde{\beta }_3= (0.3860, -0.2182,)\)

    \(\widetilde{\beta }_4= (0.5922, -0.1796),\) \(\widetilde{\beta }_5= (0.4940, -0.2927)\)

  • Step 2. Calculate the values of the score functions \(scor({\tilde{\beta }}_h)\)\((h=1,2,\ldots ,5)\) of the overall bipolar fuzzy elements \(\tilde{\beta }_h\)\((i=1,2,\ldots ,5)\) as follows:

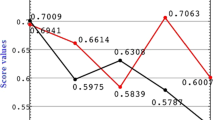
    \({\hat{E}}(\widetilde{\beta }_1)=0.6941\), \({\hat{E}}(\widetilde{\beta }_2)=0.6614\), \({\hat{E}}(\widetilde{\beta }_3)=0.5839\), \({\hat{E}}(\widetilde{\beta }_4)= 0.7063\), \({\hat{E}}(\widetilde{\beta }_5)=0.6007\)

  • Step 3. Rank all the emerging technology enterprise systems \({\tilde{Q}}_h\)\((h=1,2,\ldots ,5)\) in accordance with the value of the score functions \({\hat{E}}(\widetilde{\beta }_h)\)\((h=1,2,\ldots ,5)\) of the overall bipolar fuzzy elements as \(Q_4\succ Q_1\succ Q_2\succ Q_5\succ Q_3\).

  • Step 4.\(Q_4\) is selected as the most desirable emerging technology enterprise.

If BFDWGA operator is implemented instead, then the problem can be solved similarly as above.

  • Step 1. For \(k=1\), using the BFDWGA operator to calculate the overall preferences values \({\tilde{\beta }}_h\) of emerging technology enterprises \({\tilde{Q}}_h\)\((h=1,2,\ldots ,5)\)

    \(\widetilde{\beta }_1= (0.5035, -0.3548)\), \(\widetilde{\beta }_2= (0.4867, -0.3121)\), \(\widetilde{\beta }_3= (0.2830, 0.4400)\),

    \(\widetilde{\beta }_4= (0.4970, -0.3434)\), \(\widetilde{\beta }_5= (0.4444, -0.3801)\)

  • Step 2. Calculate the values of the score functions \(scor({\tilde{\beta }}_h)\)\((h=1,2,\ldots ,5)\) of the overall bipolar fuzzy elements \(\tilde{\beta }_h\)\((h=1,2,\ldots ,5)\) as follows:

    \({\hat{E}}(\widetilde{\beta }_1)=0.5744\), \({\hat{E}}(\widetilde{\beta }_2)=0.5873\), \({\hat{E}}(\widetilde{\beta }_3)=0.4215\), \(scor(\widetilde{\beta }_4)= 0.5768\), \({\hat{E}}(\widetilde{\beta }_5)=0.5322\)

  • Step 3. Rank all the emerging technology enterprise systems \({\tilde{Q}}_h\)\((h=1,2,\ldots ,5)\) in accordance with the value of the score functions \({\hat{E}}(\widetilde{\beta }_h)\)\((h=1,2,\ldots ,5)\) of the overall bipolar fuzzy elements as \(Q_2\succ Q_4\succ Q_1\succ Q_5\succ Q_3\).

  • Step 4. Return \(Q_2\) is selected as the most desirable emerging technology enterprise system.

From the inspection, it is evident up to expectation though overall ranking values on the alternatives are distinctive through the use of two operators, but the ranking order concerning the alternatives are similar, the most desirable alternative is \(Q_4\) for BFDWAA and \(Q_2\) for BFDWGA operator.

In order to diagnose the effect of parameter \(k\in [1,10]\) on the ranking of the alternatives in the BFDWA and BFDWGA operators, which are shown in Tables 2 and 3.

Table 2 Ranking order for various working parameters of the BFDWA operator
Full size table
Table 3 Ranking order for various working parameters of the BFDWGA operator
Full size table

8 Analysis on the effect of parameter k on decision making results

To describe the effect of the operational parameters k on multi-attribute decision-making results, we shall use different values of k to rank the alternatives. The results of the score function and ranking order of the alternatives \(Q_t\)\((t=1,2\ldots ,5)\) in the range of \(1\le k\le 10\) based on BFDWA and BFDWGA operators are presented in Tables 2 and 3 correspondingly.

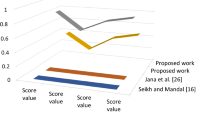
From Table 2, it is evident that when the value of k is changed for BFDWA operator, the rankings are separate, and the corresponding best alternatives are additionally non-identical. When, \(1\le k\le 2\), then we get \(Q_4\succ Q_1\succ Q_2\succ Q_5\succ Q_3\) and \(Q_4\succ Q_1\succ Q_2\succ Q_3\succ Q_5\), thus best choice is \(Q_4\). When \(3\le k\le 10\), then corresponding ranking is \(Q_4\succ Q_1\succ Q_2\succ Q_3\succ Q_5\), then the best one is also \(Q_4\). From Table 3, it is seen that when the value of k is changed for BFDWGA operator, the rankings are separate, and the corresponding best alternatives are additionally non-identical. When, \(1\le k\le 3\), then ranking orders are \(Q_2\succ Q_4\succ Q_1\succ Q_5\succ Q_3\), \(Q_2\succ Q_1\succ Q_4\succ Q_5\succ Q_3\), and \(Q_2\succ Q_1\succ Q_5\succ Q_4\succ Q_3\) and best choice are \(Q_2\). When \(4\le k\le 10\), then corresponding ranking is \(Q_1\succ Q_2\succ Q_5\succ Q_4\succ Q_3\), the best one is \(Q_1\).

To these MADM problems based on BFDWA and BFDWGA operators, we see that the different values of working parameters, k can be changed corresponding ranking orders of the alternatives for BFDWGA operator, which is more responsive to k in this MADM process; while for various values of working parameters k could be changed raking forms corresponding to BFDWA operator, which is less responsive to k in this MADM process.

Analyze our introduced method with existing related methods (Chen and Ye 2017; He 2018; Liu et al. 2018), the MADM problem in this paper dealt with bipolar fuzzy environment, while existing methods (Chen and Ye 2017; He 2018; Liu et al. 2018) dealt with the single-valued neutrosophic environment, hesitant fuzzy environment or intuitionistic fuzzy environment but not in bipolar fuzzy sets.

Therefore, our proposed MADM method for BFDWA and BFDWGA operators investigate the improvement of its flexibility in real utilization. Thus, the advanced aggregation operators implement a new flexible measure for decision makers to control bipolar fuzzy MADM problems.

9 Conclusions

In this article, we have studied multi-attribute decision-making problem using bipolar fuzzy information. We have introduced arithmetic and geometric operations to develop some bipolar fuzzy Dombi aggregation operators from the motivation of Dombi operations as bipolar fuzzy Dombi weighted average (BFDWA) operator, bipolar fuzzy Dombi order weighted average (BFDOWA) operator, bipolar fuzzy Dombi hybrid weighted average (BFDHWA) operator, bipolar fuzzy Dombi weighted geometric (BFDWGA) operator, bipolar fuzzy Dombi order weighted geometric (BFDOWGA) operator and bipolar fuzzy Dombi hybrid weighted geometric (BFDHWGA) operator. The different feature of those recommend operators is deliberated. Then, we have used those operators to expand a few strategies to remedy multi-attribute decision-making issues. Ultimately, a realistic instance for emerging technology enterprise system selection is provided to develop a strategy and in accordance with the relevance and the effectiveness of the proposed methodology. In future, the application of our proposed model can be applied in decision-making theory, risk evaluation and other domains under ambiguous environments.