1 Introduction

One of the principle aspects of automatic generation control (AGC) in power systems is the maintenance of frequency and power change over the tie lines at their scheduled values. Therefore, it is a simultaneous load frequency control [1]. In the load frequency control (LFC) problem, each area has its own generator(s), and it is responsible for its own load and scheduled interchanges with neighboring areas. The tie lines are utilities for contracted energy exchange between areas and they provide interarea support in abnormal conditions. Area load changes and abnormal conditions lead to mismatch in frequency and scheduled power interchanges between areas. These mismatches have to be corrected by LFC, which is defined as the regulation of the power output of generators within a prescribed area [2–4]. Therefore, the LFC task is very important in interconnected and restructure power systems. Since parameters of the power systems are a function of the operating point, and the load is never constant, thus nonlinearity and uncertainty always exist in the power systems.

To maintain these large-scale power systems, the control algorithm must be able to deal with mechanical and electrical nonlinear dynamics and must be operated under imprecise and uncertain conditions which are mainly caused by random load demands. It is obvious that the fixed gain controllers which have been designed at nominal operating conditions fail to provide best control performance over a wide range of operating conditions, which means that controller must be updated to keep system performance near its optimum. But it is essential to consider that system performance gets worse when noise and uncertainty exist in the power systems while operating conditions are changed simultaneously; so, it motivated the authors to investigate this problem.

Thus, nonfixed gain controllers have received considerable attentions [5–17]. In [5–8], some classical adaptive controllers have been presented for LFC. Despite the promising results, the control algorithms are complicated and require some online model identifications. Artificial Neural Networks (ANNs), Fuzzy Logic Systems (FLSs), and Fuzzy Neural Networks (FNNs) have been widely used as a direct adaptive controller [9–13]. These controllers are tuned online and they consume much time for learning due to the large inputs and nonlinear properties of these systems. Fuzzy gain scheduling techniques have been presented in some literatures [14–16] where FLSs have been used to tune the proportional-integral (PI) or proportional-integral-derivative (PID) controller gains according to fuzzy rules. Clearly, it is difficult to pinpoint the exact definition of FLS rules and also, the fuzzy variables are not optimum when the operating points change. In [17], an adaptive neuro-fuzzy inference system (ANFIS) has been trained by genetic algorithm to provide a general mapping between the operating conditions and the optimal control gains. In mentioned work, the trained ANFIS is able to obtain integral gains in the online application even at the off-nominal operating points.

In the aforesaid literatures, all of the fuzzy logic systems are called Type-1 Fuzzy Logic Systems (T1FLS) which have two-dimensional membership functions. The extension of the T1FLS is the Type-2 Fuzzy Logic System (T2FLS) with three-dimensional membership functions. This extra dimension provides a new degree of freedom that lets the uncertainties to be handled in totally new ways [18–20]. A Type-2 fuzzy set can be visualized as a three-dimensional, primary, and secondary membership function. The primary membership is any subset in [0, 1], and there is a secondary membership value corresponding to each primary membership value that defines the possibility for primary membership.

T2FLSs have been applied in many practical applications such as mobile robot control [21], airplane flight control [22], and Hot Strip Mill (HSM) process [23]. In 2012, Sepulveda and coworkers have shown that the hardware implementation of T2FLS controller is easier when high speed processing is needed [24, 25]. But the important issue in the application of T2FLS is how to set the parameters of the consequent parts as well as the antecedent parts, such as standard deviations and means. Therefore, chemical optimization paradigm, particle swarm optimization, evolutionary method, simulated annealing, and genetic algorithm (GA) have been employed to search optimal values of these system parameters [26–33]. In [34], authors have designed a decentralized controller based on T2FLS for the LFC. In this work, the T2FLS is the main controller with the fixed structure and its rules have been tuned based on a trial-and-error method. In the industrial system such as LFC, the PID controller is the main controller not only due to its simplicities but also due to its success in large number of industrial applications. Furthermore, updating PID gains according to the variation of operating points is an important issue that needs to be considered.

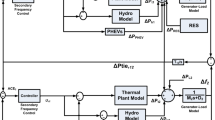
Thus, the main contribution of this work is to introduce an applicable Multi-Input Multi-Output (MIMO) T2FLS which can tune PID gains online. This integrated system (T2FLS and PID) leads to the robust controller which handles power system in nominal and off-nominal points in the presence of measurement noise and uncertainty. Algorithm of proposed method is illustrated in Fig. 1.

Fig. 1
figure 1

The algorithm of proposed method

Full size image

Above strategy can be called Type-2 Fuzzy Gain scheduling (T2FG) technique. The power system parameters (i.e., power system time constant, T pi , the synchronizing power coefficient, T ij , and the frequency bias setting, B i ) that may change are considered the inputs of the T2FLS , and the PID controller gains are the outputs. The T2FLS is trained off-line according to precomputed table which consists of some nominal operating points and their related PID gains. Meanwhile, this table has been designed by particle swarm optimization (PSO) algorithm. In the online applications, the trained T2FLS is able to infer PID gains according to the monitored parameters even at the off-nominal points and noisy conditions. A two-area restructure power system is assumed for demonstrating efficiency of proposed method. The proposed T2FG controller has been compared with the Type-1 Fuzzy Gain Scheduling (T1FG) and the PID controllers through some simulations.

The remaining parts of the paper are organized as follows: the dynamic model of a two-area restructure power system is presented in Sect. 2. The design procedure of the PID controller by PSO is expressed in Sects. 3 and 4. Also, online adaptive T2FG technique is derived in the next section. In Sect. 5, simulation results for a two-area power system are stated. Finally, the conclusion is addressed in Sect. 6.

2 Model Description

In a traditional power system structure, generation, transmission, and distribution are owned by a single entity called a vertically integrated utility (VIU), which supplies power to the customers at regulated rates. All such control areas are interconnected by tie lines. Following a load disturbance within an area, the frequency of that area experiences a transient change, and the feedback mechanism comes into play and generates an appropriate rise/lower signal to the turbine to make the generation follow the load. In steady state, the generation is matched with the load, and the tie line power and frequency are enforced to zero.

In the restructured power systems, the VIU no longer exists, however, the common objectives, i.e., restoring the frequency and the net interchanges to their desired values for each control area remain. In the vertically integrated power system structure, it is assumed that each bulk generator unit is equipped with secondary control and frequency regulation requirements, but in an open energy market, Gencos may or may not participate in the AGC problem. In that environment, Gencos sell power to various Discos at competitive price. Thus, Discos have the liberty to choose the Gencos for contract. The concept of a “generation participation matrix (GPM)’’ is used to make the visualization of contracts easier. The GPM shows the participation factors of each Genco in the considered control area and each control area is determined by a Disco. The rows of a GPM correspond to Genco and the columns correspond to control areas that contract power. For example, for a large-scale power system with m control area (Discos) and n Gencos, the GPM will have the following structure:

$${\text{GPM}} = \left[ {\begin{array}{*{20}c} {gpf_{11} } & {gpf_{12} } & { \ldots \,} & {gpf_{1(m - 1)} } & {gpf_{1m} } \\ {gpf_{21} } & {gpf_{22} } & { \ldots \,} & {gpf_{2(m - 1)} } & {gpf_{2m} } \\ \vdots & { \vdots \,} & \vdots & { \vdots \,} & { \vdots \,} \\ {gpf_{(n - 1)1} } & {gpf_{(n - 1)2} } & \ldots & {gpf_{(n - 1)(m - 1)} } & {gpf_{(n - 1)(m)} } \\ {gpf_{n1} } & {gpf_{n2} } & \ldots & {gpf_{n(m - 1)} } & {gpf_{nm} } \\ \end{array} } \right]$$
(1)

where gpf ij refers to “generation participation factor” and shows the participation factor of Genco i in load flowing of area j (based on a specified bilateral contract). The sum of all the entries in a column in this matrix is unity, i.e.,

$$\sum\limits_{i = 1}^{n} {gpf_{ij} } = 1.$$
(2)

To illustrate effectiveness of the proposed control design and modeling strategy, a two-control area power system is considered as a test system. It is assumed that each control area includes two Gencos and two Discos. A block diagram of the generalized LFC scheme for control area i will be obtained in a deregulated environment as shown in Fig. 2 [35].

Fig. 2
figure 2

The configuration of i-th control area

Full size image

The dashed line shows the demand signals based on the possible contracts between Gencos and Discos, which carry information as to which Genco has to follow a load demand by which Disco.

These new information signals were absent in the traditional LFC scheme. As there are many Gencos in each area, the area control error (ACE) signals have to be distributed among them due to their ACE participation factor in the LFC task and \(\sum\nolimits_{j = 1}^{n} {\alpha_{ij} } = 1\). In Fig. 2, we have the following:

∆fi

Frequency deviation

T ti

Turbine time constant

∆P gi

Governor valve position

T ij

Tie line synchronizing coefficient between areas i and j

∆P ci

Governor load set point

B i

Frequency bias

∆P ti

Turbine power

R i

Drooping characteristic

∆P tie _ i

Net tie line power flow

α ij

ACE participation factor

∆P di

Area load disturbance

N

Number of control areas

K ′ pi

Proportional gain constant

∆PLj

Contracted demand of area j

T pi

Power system time constant

∆PLoc_i

Contracted/uncontracted local demand in area i

T gi

Governor time constant

  
$$w_{{ 1 {\text{i}}}} \, = \, \Delta {\text{P}}_{{{\text{Loc\_i}}}} \, + \, \Delta {\text{P}}_{\text{di}} { ,}$$
(3)
$$w_{2i} = \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{N} {T_{ij} } \Delta f_{j} ,$$
(4)

where \(w_{{ 1 {\text{i}}}} \,\) is the total of contracted and uncontracted local demand in area I and \(w_{{ 2 {\text{i}}}} \,\) is other area frequency deviations effect on area i.

The scheduled ∆P tie_i is obtained for an N control area power system as follows [35]:

$$w_{3i} = \sum {({\text{Total export power - Total import power}})} = \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{N} {\left( {\sum\limits_{k = 1}^{n} {gpf_{kj} } } \right)} \Delta P_{Lj} - \sum\limits_{k = 1}^{n} {\left( {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray} }^{N} {gpf_{jk} } } \right)} \Delta P_{Li} ,$$
(5)

where \(w_{{ 3 {\text{i}}}} \,\) is the scheduled ∆P tie_i (net tie line power flow).

According to Fig. 2, it can be written

$$\, \Delta {\text{P}}_{\text{tie - i,error}} \, = \, \Delta {\text{P}}_{\text{tie - i,actual}} \, - {\text{w}}_{{ 3 {\text{i}}}} .$$
(6)

And the elements of vector w 4i can be expressed as

$$\begin{aligned} w_{4i - 1} = \sum\limits_{j = 1}^{N} {gpf_{1j} \Delta P_{Lj} } \hfill \\ \vdots \hfill \\ w_{4i - n} = \sum\limits_{j = 1}^{N} {gpf_{nj} \Delta P_{Lj} } , \hfill \\ \end{aligned}$$
(7)

where \(w_{{ 4 {\text{i}}}} \,\) is the generation of each Genco in area i.

The generation of each Genco must track the contracted demands of Discos in steady state. The desired total power generation of a Genco i in terms of GPM entries can be calculated as follows:

$$\Delta P_{mi} = \sum\limits_{j = 1}^{N} {gpf_{ij} \Delta P_{Lj} } ,$$
(8)

where \(\Delta P_{mi}\) is the desired total power generation of a Genco i. The input signal for controller, K(s), is ACE that can be defined from Fig. 2, and it can be expressed as follows:

$$\Delta ACE_{i} = \Delta {\text{P}}_{\text{tie - i,error}} + B_{i} \Delta f_{i} ,$$
(9)

where \(\Delta ACE_{i}\) is the i-th area control error.

3 PID Controller Design for LFC by PSO Algorithm

It is well known that the PID controller is the most popular approach for industrial process control, such as the LFC problem. Therefore, several techniques have been developed to tune this controller. In the LFC problem and for i-th area, (by taking the ACE i as the system output), the control signal for the PID controller (Fig. 2) in the continuous form can be given as follows:

$$u_{i} (t) = \Delta P_{ci} (t) = K_{P} ACE_{i} (t) + K_{D} A\dot{C}E_{i} (t) + K_{I} \int_{0}^{t} {ACE_{i} (\tau ){\text{d}}\tau } ,$$
(10)

where K P , K D , and K I are the proportional, derivative, and integral gains and they should be designed so that the system is functioning properly. Also \(u_{i} (t)\) or \(\Delta P_{ci} (t)\) is governor load set point which can be called as “control effort.” In classical methods, there are some approaches to tune the PID controller such as Ziegler–Nichols and Cohen–Coon methods [36]. Since mentioned methods consume much time and they do not have sufficient accuracy, the applications of these methods have been restricted for large-scale and complicated systems. Also, the population-based techniques such as GA and PSO have been used to design the PID controller parameters [17, 37, 38]. In these approaches, the PID gains are searched in the feasible region of response until a determined cost function is minimized. It should be noted that to improve the transient and steady-state response of controlled system, different cost functions have been considered. The following cost function for i-th area controller design is utilized for PSO:

$$\cos t = \sum\limits_{i = 1}^{n} {ITAE_{i} } \,,\,\quad ITAE_{i} = \int_{0}^{{t_{f} }} t \left| {ACE_{i} } \right|{\text{d}}t.$$
(11)

The PSO must minimize above cost function by finding appropriate PID gains for each area. Since the same parameters are considered for each area of power system (for simplicity), the same PID gains are also obtained for each area. It should be noted that when the operating points of the power system change, it leads to change in the T pi , T ij , and B i , and eventually, the PID gains must be adjusted. The calculated PID gains for i-th area of the power system corresponding to the 48 patterns of operating points are listed in Table 1.

Table 1 PID controller gains at different operating conditions
Full size table

4 Online Type-2 Fuzzy Gain Scheduling Technique

In this section, the online T2FG technique is proposed for LFC. According to the Table 1, the operating points and the related PID gains are considered as the inputs and outputs of the T2FLS, respectively. The first step to achieve the online T2FG is training process; then, the trained T2FLS should be tested to guaranty the performance of online T2FG approach.

4.1 Type-2 Fuzzy Logic Systems

There are two different approaches to FLSs design: Type-1 FLSs (T1FLSs) and type-2 FLSs (T2FLSs). In designing of T1FLSs, expertise and knowledge are needed to make the Membership Functions (MFs) and fuzzy rules. The linguistic terms that are used in antecedents and consequents have different meanings for different experts. Specialists often provide different conclusions for the same rule base. The T1FLSs are unable to directly handle rule uncertainties. To deal with this problem, the concept of type-2 fuzzy sets was introduced by Zadeh as an extension of T1FLSs with the intention of being able to model the uncertainties that invariably exist in the rule base of the system [18]. Compared with T1FLSs, T2FLSs can better handle the vagueness inherent in linguistic words. The uncertainties are modeled by membership functions. Therefore, T2FLSs are more suitable under circumstances where it is difficult to determine the exact MF for a fuzzy set [39, 40]. In type-1, fuzzy sets membership functions are totally certain, whereas in type-2 fuzzy sets membership functions are themselves fuzzy. As the result, at the type-2 fuzzy sets, the antecedents and the consequents of the rules are uncertain. While a type-1 membership grade is a crisp number in [0, 1], a type-2 membership grade can be any subset in [0, 1] which is called the primary membership. Additionally, there is a secondary membership value corresponding to each primary membership value that defines the possibility for primary memberships [18]. Whereas the secondary membership functions can take values in the interval of [0, 1] in generalized T2FLSs, they are uniform functions that only take value of 1 in interval T2FLSs. As we know, the computational burden of the general T2FLSs is very high. Due to the fact that the computations are more easily manageable, the use of interval T2FLSs is more commonly seen in literatures. An interval type-2 fuzzy set, \(\tilde{A}\), may be represented as follows [18]:

$$\tilde{A} = \int\limits_{x \in X} {\int\limits_{{u \in J_{x} }} {\frac{{\mu_{{\tilde{A}}} (x,u)}}{(x,u)}} } \,\quad J_{x} \in [0,1],$$
(12)

where \(\iint {}\) denotes union over all admissible x and u. Also, \(J_{x}\) is called the primary membership function of x and \(\mu_{{\tilde{A}}} (x,u)\) is the secondary membership function value corresponding to each primary membership value that in the interval type- 2 fuzzy sets all \(\mu_{{\tilde{A}}} (x,u)\) are equal 1. It is well known that in the type-1 fuzzy sets, the membership function does not contain any uncertainty (Fig. 3a). In other words, there exists a clear membership value for every input data point. Therefore, for considering of uncertainty in the type-2 fuzzy sets at the antecedent and consequent membership functions, if the points on the Gaussian function in Fig. 3a are shifted either to the left or to the right, Fig. 3b can be obtained. In this figure, the membership function does not have a single value for a specific value of x.

Fig. 3
figure 3

The Fuzzy type-1 membership function (a) and the Fuzzy type-2 membership function (b)

Full size image

Figure 3b shows a type-2 Gaussian MF with an adjustable uncertain mean in [\(m_{1} , \, m_{2}\)] and standard deviation \(\sigma\). It can be described by

$$\mu_{{\tilde{A}}} (x) = \exp \left[ { - \frac{1}{2}\left( {\frac{x - m}{\sigma }} \right)^{2} } \right], \, m \in [m_{1} ,m_{2} ].$$
(13)

It can be seen from Fig. 3b, the type-2 fuzzy set has a region called footprint of uncertainty (FOU) and bounded by an upper MF and a lower MF, which are denoted as \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{{\tilde{A}}} (x)\) and \(\bar{\mu }_{{\tilde{A}}} (x)\), respectively. Also, the T2FLS rules and inference engine section will remain the same as in T1FLSs, but the antecedents and/or the consequents are different.

Mamdani and Tagaki–Sugeno–Kang (TSK) systems are the two most popular FLSs used today. Both are characterized by IF–THEN rules and have the same antecedent structures. They only differ in the structure of the consequent part. The consequent of Mamdani is a fuzzy set, whereas the consequent of TSK is a function.

4.2 TSK Type-2 Fuzzy Logic System for LFC

A TSK type-2 fuzzy logic system (TSK T2FLS) can be classified into three groups [18].

  1. (i)

    A2-C1 model: The antecedents are type-2 fuzzy sets, and consequents are type-1 fuzzy sets;

  2. (ii)

    A2-C0 model: The antecedents are type-2 fuzzy sets, and consequents are crisp numbers;

  3. (iii)

    A1-C1 model: The antecedents are type-1 fuzzy sets, and consequents are type-1 fuzzy sets.

In this work, A2-C0 model described by fuzzy IF–THEN rules is used. For instance, in a zero-order type-2 TSK model (A2-C0) and in MIMO form, the rule base is as follows:

$$R^{j} : \, if \, \,x_{1} \,is\,\tilde{A}_{j1} \,{\text{ and }}\,x_{2} \,is\,\tilde{A}_{j2} \, \,{\text{and }} \ldots {\text{ and }}\, \, x_{n} \,is\,\tilde{A}_{jn} \,\quad THEN\,\,y_{j}^{k} = C_{0j}^{k}$$
(14)

where x 1 , x 2 , …, x n are the input variables, y k j are the k th output variables, and \(\tilde{A}_{ji}\) are the type-2 MFs for j th rule and i th input. The parameters of consequent part of the rules are C k 0j .

The kth output of the fuzzy system in closed form is obtained by [41]:

$$Y_{{{\text {TSK}}/A_{2} - C_{0} }}^{k} = \,\frac{{\sum\nolimits_{{j = 1}}^{M} {{\underline{f}} _{j} C_{{0j}}^{k} } }}{{\sum\nolimits_{{j = 1}}^{M} {{\underline{f}} _{j} + \sum\nolimits_{{j = 1}}^{M} {\bar{f}_{j} } } }} + \frac{{\sum\nolimits_{{j = 1}}^{M} {\bar{f}_{j} C_{{0j}}^{k} } }}{{\sum\nolimits_{{j = 1}}^{M} {{\underline{f}} _{j} + \sum\nolimits_{{j = 1}}^{M} {\bar{f}_{j} } } }},$$
(15)

where M is number of the rules. Also, \(\bar{f}_{j}\) and \({\underline{f}}_{j}\) are given by:

$$\begin{aligned} &\bar{f}_{j} (x) = \bar{\mu }_{Aj1} (x_{1} ) *\ldots* \bar{\mu }_{Ajn} (x_{n} ) \hfill \\ &\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{f}_{j} (x) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{Aj1} (x_{1} ) * \ldots* \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{Ajn} (x_{n} ), \hfill \\ \end{aligned}$$
(16)

where * shows the t-norm operation (which is considered the product operator in this study). \(\bar{\mu }_{Ajn} (x_{i} )\) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{Ajn} (x_{i} )\) are the upper and lower amount of MFs, respectively. The structure of proposed MIMO TSK T2FLS is depicted in Fig. 4.

Fig. 4
figure 4

The structure of MIMO TSK T2FLS

Full size image

4.3 Training of TSK T2FLS using PSO

To achieve the gain scheduling technique, the operating points and related PID gains of Table 1 are used for training of the TSK T2FLS (Fig. 4). Over the years, a lot of optimization methods have been employed to adjust the parameters of type-1 and type-2 fuzzy models. These optimization methods can basically be put in two categories: derivative-based and derivative-free optimization methods. GA [33] and PSO [32] can be addressed as some main examples of derivative-free algorithms. On the other hand, examples of derivative-based optimization methods are gradient descent [42], simplex method [43], least square [44], and Extended Kalman Filter (EKF) [45]. Derivative-free methods are less likely to get entrapped in local minima. They are also easier to implement because they do not need derivatives which may be hard to calculate while they generally converge faster. In this paper, due to simple relations and high convergence speed of PSO [46], this optimization algorithm has been used to train the MIMO TSK T2FLS in (15). The only parameters that must be tuned are the consequent parameters C k 0j . Since the input ranges (x 1  = T pi , x 2  = T ij , and x 3  = B i ) are known, thus the antecedent parameters such as m 1 , m 2 , and \(\sigma\) are considered fixed, and their values are stated in Table 2. In addition, the related MFs for each input are depicted in Fig. 5.

Table 2 The antecedent and consequent parameters value of T2FLS and T1FLS
Full size table
Fig. 5
figure 5

The membership functions for inputs: x1 = T pi , x2 = T ij , and x3 = B i

Full size image

By taking three inputs and three MFs for each input, we have 27 rules. Also, by defining Y 1, Y 2, and Y 3 as the outputs of T2FLS, the number of adjustable parameters is 27 × 3=81. The first 38 patterns of PSO-optimized PID gains in Table 1 have been used for training the MIMO TSK T2FLS to find a general mapping between the operating points and the related PID gains. Furthermore, the remaining 10 patterns are used for testing process. As we know, in industrial system such as LFC problem, we only have access to noisy measurements. So, when noise and uncertainty are considered, the test data are assumed to be corrupted by uniformly distributed nonstationary additive noise. The results of training and testing process for proposed T2FLS and T1FLS for each output are shown in Figs. 6, 7, and 8. The structure of used T1FLS is similar to the T2FLS except that the MFs of antecedent part are type-1. Additionally, the calculated consequent parameters obtained by PSO (C 1 0j , C 2 0j , and C 3 0j ) are presented in Table 2.

Fig. 6
figure 6

Training and testing process of T2FLS and T1FLS for proportional gain (K P )

Full size image
Fig. 7
figure 7

Training and testing process of T2FLS and T1FLS for integral gain (KI)

Full size image
Fig. 8
figure 8

Training and testing process of T2FLS and T1FLS for derivative gain (K D )

Full size image

By considering these figures, since the noise and uncertainties in the training process are nearly small, both T2FLS and T1FLS have similar behavior and they can successfully approximate the target data. Moreover, they have the same number of adjustable parameters. On the other hand, it is obvious from the testing process that the T2FLS has a better performance in dealing with noise and uncertainties.

5 Simulation Results

To demonstrate the efficiency of the proposed controller, some simulations are performed. For this purpose, a two-control area power system, shown in Fig. 9, is considered as a test system. It is assumed that each control area includes two Gencos, which use the same ACEi participation factor. The nominal parameters of the two-area interconnected power system which are used in the simulation are given in Tables 3 and 4. As illustrated in Fig. 10, the linear model of the nonreheating turbine given in Fig. 2 is replaced by the nonlinear model that introduces a saturation element with d = 0.02. This replacement has been done in order to take the generation rate constraint (GRC) limit on the response speed of a Turbine [13].

Fig. 9
figure 9

Two-control area power system

Full size image
Table 3 Applied data for Gencos
Full size table
Table 4 Applied control area parameters
Full size table
Fig. 10
figure 10

Nonlinear turbine model with GRC

Full size image

The considered system is controlled by using three strategies:

  1. (i)

    The proposed T2FG technique shown in Fig. 11,

    Fig. 11
    figure 11

    The proposed strategy for area i

    Full size image
  2. (ii)

    The T1FG which is similar to the proposed methods except that the MFs of antecedent part are type 1,

  3. (iii)

    And the PID controller. In this method to get the PID gains, the characteristics of closest nominal operating points are used.

Furthermore, for both cases, the Discos contract with the available Gencos is assumed according to the following GPM:

Case 1

Case 2

\({\text{GPM}} = \left[ {\begin{array}{*{20}c} {0.25} & {0.25} & {0.25} & {0.25} \\ {0.25} & {0.25} & {0.25} & {0.0} \\ {0.0} & {0.25} & {0.5} & {0.5} \\ {0.5} & {0.25} & {0.0} & {0.25} \\ \end{array} } \right]\)

\({\text{GPM}} = \left[ {\begin{array}{*{20}c} {0.25} & {0.0} & {0.25} & {0.25} \\ {0.25} & {0.25} & {0.25} & {0.0} \\ {0.0} & {0.5} & {0.5} & {0.5} \\ {0.5} & {0.25} & {0.0} & {0.25} \\ \end{array} } \right]\)

5.1 Case 1

In this case, the closed loop performance is tested in the face of both step contracted load demand and changing in power system operating points. It is assumed that a large step load is demanded by Discos of areas 1 and 2 as follows: ∆P L1 = 0.2 pu, ∆P L2 = 0.2 pu, ∆P L3 = 0.1 pu, ∆P L4 = 0.1 pu

The nominal values for the parameters of power system are according to Tables 3 and 4. For considering noisy inputs for trained T2FLSs which cause off-nominal operating point, we assume the variable parameters are T p1,2 = 20, T 12 = 0.2, B 1,2 = 0.2. In online application, these parameters are measured and used as inputs to the trained T2FLS (or T1FLS). Eventually, both T2FLS and T1FLS are supposed to adjust the PID gains properly; the inferred PID gains are given in Table 5.

Table 5 Inferred PID gains by three strategies
Full size table

The responses of ∆f 1 and ∆f 2 are shown in Fig. 12. The simulation results indicate that the proposed T2FG controller is superior to the other ones. In other words, the trained T2FLS has better performance than type 1 counterpart in obtaining PID gains when the inputs are corrupted by noise. This leads to the facts that when the system is equipped with the proposed controller (Fig. 11), the frequency deviations are remarkably damped to zero.

Fig. 12
figure 12

The frequency deviations for the first (a) and second (b) areas for case 1

Full size image

5.2 Case 2

In this case, Discos may violate a contract by demanding more power than that specified in the contract. This excess power is reflected as a local load of the area (uncontracted demand). It is assumed that in addition to specified contracted load demands, the Disco 1 and Disco 2 demand 0.1 and 0.2 pu MW (∆P d1 = 0.1 and ∆P d2 = 0.2) as a large uncontracted load, respectively. The amount of these violated demands are distributed among the Gencos according to values of the ACE participation factors αij. It is obvious that based on these values each Genco must be increased its generation. For example, we set the amount of α (for all Gencos in each area) in the same value, αij = 0.5. The uncontracted load of Discos is taken up by Gencos of their areas according to ACE participation factors in the steady state. For operating points, the off-nominal operation condition parameters (T p1,2 = 13, T 12 = 0.3, B 1,2 = 0.3) are used for two areas. It is assumed that a large step load is demanded by Discos of areas 1 and 2 as follows (contracted demands): ∆P L1 = 0.1 pu, ∆P L2 = 0.1 pu, ∆P L3 = 0.1pu, ∆P L4 = 0.1 pu.

The responses of ∆f 1 and ∆f 2 are shown in Fig. 13. Due to the fact that the proposed T2FG has adjusted the PID gains properly, both overshoot and settling time has the least amount compared to others. The deduced PID gains for this case are shown in Table 5.

Fig. 13
figure 13

The frequency deviations for the first (a) and second (b) areas for case 2

Full size image

6 Conclusion

In this paper, an adaptive controller has been proposed based on T2FLS technique for LFC in the restructure power system. First of all, PSO algorithm has employed to obtain the PID gains at some nominal operating points (48 patterns). Afterward, these results have been used to train and test MIMO T2FLS in order to obtain a general mapping between the operating condition and the PID controller gains. Also, the same PSO is used for training the T2FLS. In online applications, the trained T2FLS is able to adjust the PID controller gains properly even at the off-nominal operating points and in the presence of measurement noise. In addition, a two-area power system has been used as a test system to demonstrate the effectiveness of the proposed methods under various operating conditions and area load disturbances. The simulation results show that the proposed T2FG controller has better performance compared to the T1FG and the PID controllers even in the presence of GRC.