1 Introduction

Ball bearing which is one of the most vulnerable components of machines is most widely used in modern life (Crocker 1979), especially in rotational machines. The service life of ball bearing is cognized into nonlinear distribution because of its poor ability to withstand shocks. Many faults of rotational machine (El Hachemi Benbouzid 2000; Nandi and Toliyat 1999) are related with the ball bearing when some impact is overload than the designed standards. The quality of ball bearing influence machine status seriously: some minor faults make machines loss certain functions and heavy ones cause serious injury even catastrophic accidents. Technology of ball bearing diagnosis (Nandi et al. 2005; Jung et al. 2006), therefore, becomes particularly important in recent years.

According to different mechanisms, the faults diagnosis are classified into five categories: oscillation diagnostics (Singh and Ahmed Saleh Al Kazzaz 2003; Peng and Chu 2004; Mirafzal et al. 2006), oil analysis diagnostic (Miller and Kitaljevich 2000), acoustic diagnostics (James Li and Li 1995; Tan et al. 2007), optical diagnostics (Zhao and Ladommatos 1998), thermal diagnostics (Chen and Hsu 2003) and so on. Depending on their own characteristics, they are applied in different fields of ball bearing diagnosis.

In real active monitoring systems, the oscillation diagnostics is the primary diagnosis method using wave signal, frequency spectrum or time–frequency distribution for classification. The contact sensor used to monitor the oscillatory signals directly, however, must be fixed in the bearing housing in signal acquisition process. Because the sampled signals contain oscillatory signals coursed by the chassis and sensor self, the oscillation diagnostics is relatively weak for early prediction. The oil analysis diagnostic techniques using various methods to reduce the phenomenon of misdiagnosis have less actually applications due to sensor setting limitation and data transmission. The optical diagnostic techniques use optical fiber which has high sensitivity of ministers and directly reflect the work of rolling surface ware, lubrication and clearance, etc. This method, however, is only enforceable for the cases the fiber sensors are able to be installed in the rolling environments. For thermal diagnostic techniques, the changing of temperature is not necessarily caused by the changing of rolling movements. At the same time, it could not be sensitive enough for early detection because the faults have arisen to a serious level before the rolling temperature changes significantly.

The acoustic emission (AE) fault diagnostics technology (Tandon and Nakra 1990) uses instantaneous energy released by internal material particles in movement to recognize and understand the material or structure of the internal structure. The normal ball bearing signal, however, also includes AS signals caused by contact of inside and outside bearing rings and rolling elements during the operation. The AE signals caused by the failure, therefore, are very weak comparing with the AE signals of original system and environment noise, especially for the early failure. It is difficult to diagnose the small fault and identify the classification in time, and when the failure becomes seriously that leads to huge economic losses.

In this paper, we propose a new approach using AE signals to diagnose early fault. The fault signals are transformed from time domain to frequency spectrum with a fast Fourier transform (FFT) function. Based on the hypothesis that the frequencies of original system and fault component are orthotropic, some researchers proposed to separate the frequency components with conventional principal component analysis (PCA) and independent component analysis. These methods were difficult to diagnose the faults of the balls bearing and small abrasions because the frequency spectrums of ball bearing were too weak and certain related with the frequency of original system. However, we use a normal signal as a comparing basic signal and combined it with an AE signal to obtain a signal array. The main and residual frequency components were separated from this array using PCA and ICA. Then, we introduced the cross-correlation between sample signals and detection signals to obtain the eigenvalue for machine learning which we designed a binary classification support vector machine (SVM). The absolute correlation coefficient has different degrees of disturbance because the frequency components and energies of background noise are changing over time. Therefore, we proposed a normalization function to increase the coefficient distance and reduce the interference of environment noise. Experiment results indicated that our approach was able to distinguish small faults from normal signals with different rotating speed.

This paper is organized as follows. We firstly describe the related conventional algorithms for frequency separation with PCA/ICA and the original SVM in Sect. 2. Then the new approach which we proposed is described in Sect. 3. The experiment results and discussion are indicated in Sect. 4. Finally, we summarize our conclusions and remarks.

2 Related algorithms

Denote the frequency spectrums of rolling bearing in normal situation are F r , the basic frequency spectrums of machine base are F b , and the spectrums of environment noise and human active are F n . Thus, the frequency spectrums of received signals F s are

$$ F_s = F_r + F_b + F_n $$
(1)

The faults of inner/outer rolling or the balls produce certain failure spectrums F d and weak the default F r to \(F_r^{\prime}.\) Thus, the spectrum of detected signals could be written as

$$ F_s^{\prime} = F_r^{\prime} + F_b +F_d + F_n $$
(2)

The purpose is to separate the the spectrum components \(F_r - F_r^{\prime}\) and F d to identify the faults. Most of components extraction techniques have based on linear technique such as PCA (Jolliffe 2002), linear discriminant analysis (LDA) (Altman et al. 1994), and independent component analysis (ICA) (Hyvärinen et al. 2001). Using the eigenvalue estimated form PCA or ICA, it’s easy to classify the faults using certain classifier techniques such as SVM (Cortes 1995), Gaussian mixture model (GMM) (Lee and Lewicki 2000) and artificial neural network (ANN) (Byvatov et al. 2003). We introduce the PCA and ICA for frequency separation and SVM for classification in this paper.

2.1 Principal component analysis

Principal component analysis is a statistical technique that linearly transforms an original set of variables into a substantially smaller set of uncorrelated variables that represents most of the information in the original set of variables. It can be viewed as a classical method of multivariate statistical analysis for achieving a dimensionality reduction.

Denote we have a set of input vectors \(x_{t}(t = 1,\ldots, l\, \& \, \sum_{t = 1}^{l} x_t = 0),\) each of which is m dimension \(x_t = (x_{t}(l), x_t(2), \ldots, x_{t}(m))^T\) (usually m < l), the vector x t is transformed into a new s t by PCA as follows:

$$ s_t = U^{T}x_{t} $$
(3)

where U is the m × m orthogonal matrix. PCA solves the eigenvalue estimation

$$ \lambda_{i}u_{i} =C\,u_i,\quad i = 1,\ldots, m $$
(4)

where u i is the corresponding eigenvector in matrix U and λ i is one of the eigenvalues of C

$$ C = \frac{1}{l}\sum\limits_{i=1}^{l}x_tx_t^T $$
(5)

Thus, the components of s t are then calculated as the orthogonal transformations of x t

$$ s_t(i)=u_{i}^T x_{t},\quad i = 1,\ldots, m $$
(6)

The new components are called principal components. By using only the first several eigenvectors sorted in descending order of the eigenvalues, the number of principal components in s t can be reduced.

2.2 Independent component analysis

Independent component analysis is a statistical technique for revealing hidden factors that underlie measurement sets of independent signals sources, precess noise or disturbance. In following ICA algorithm, its is assumed that the data mixed matrix \(X = [x(1), x(2),\ldots, x(n)] \in R^{l \times n}\) can be expressed as the linear combination of m non-Gaussian independent components S. The relationship is given by:

$$ X = A\cdot S + E $$
(7)

where \(A=[a_1,a_2,\ldots, a_m]\in R^{l\times m}\) is unknown mixing matrix, \(S = [s(1), s(2),\ldots, s(n)]\in R^{m\times n}\) is the independent component matrix, \(E\in R^{l\times n}\) is residual matrix, and n is the number of sample. The basic problem of ICA is to estimate both the mixing matrix A and the independent components S from only the observed data X. Therefore, it is necessary to find a de-mixing matrix W which is given as:

$$ \hat{S} = W\cdot X = W\cdot A\cdot S \approx S $$
(8)

The reconstructed vector \(\hat{S}\) becomes as independent as possible. For convenience, we assume d = m and E(SS T) = I. Consider a d-dimensional vector x(k) at sample k, the whitening transformation is expressed as:

$$ z(k) = Qx(k) = QAs(k) = Bs(k) $$
(9)

where whitening matrix \(Q = \Uplambda^{-1/2}U^T; \) B is an orthogonal matrix as verified by the following relation:

$$ E[z(k)z^T(k)] = BE[s(k)s^T(k)]B^T = BB^T = I $$
(10)

The relation between W and B can be expressed as

$$ W = B^TQ $$
(11)

Hence, Eq. 8 can be rewritten as:

$$ \begin{aligned} \hat{s}(k)&=Wx(k) = B^Tz(k)\\ &=B^TQx(k) = B^T\Uplambda^{-1/2}U^Tx(k) \end{aligned} $$
(12)

According to Eq. 12, the ICA problem can be reduced to find an orthogonal matrix B. To calculate B, \(Hyv\ddot{a}rinen\) introduced a fast fixed-point algorithm for ICA (Fast ICA) based on approximate form from the negentropy (Hyvärinen 1999). This algorithm calculated the column vector \(b_i(i = 1, 2, \ldots, m)\) of B through iterative steps. The detailed procedure can refer to the Hyvärinen and Oja (2000). In this paper, the Fast ICA algorithm was used and increased the number of selecting initial value to avoid problem of convergence cause by selecting initial value randomly.

The fault detection methods using ICA are similar to those of fault detection using PCA. The ICA model is built based on historical data \(X\in R ^{l\times n}\) collected during normal operation.

2.3 Support vector machine

Support vector machine is a new computational learning method based on the statistical learning theory presented by Vapnik (2000). Denote the input vector \(x_{i}(i = 1, 2,\ldots, N)\) correspond with labels \(y_i\in\{-1,+1\}, \) n is the number of samples, To construct optimal separating hyperplane, using a non-linear vector function \(\varphi(X) = (\phi_1(x),\ldots, \phi_l(x))\) to map the input data x i into l-dimensional feature space. All of the train sample must satisfy

$$ \sum\limits_{j = 1}^Nw_j\varphi_j(x)+ b \geq 0 $$
(13)

where w is weight vector and b is a scalar. Considering that some data could not be classified correctly, introducing a slack variable ξ i  ≥ 0 to ensure classification correctness. The optimal classifier, ||w|| should be minimized under the following constraints

$$ y_{i}\left[\sum\limits_{j = 1}^N w_{j}\phi_{j}(x) + b\right]\geq 1- \xi_{i} $$
(14)

According to the structure of risk minimization principal, the optimal problem is formulated as an objective function L

$$ \begin{aligned} &\min L = \min \left\{ \frac{1}{2}\parallel w \parallel^2 + c\sum\limits_{i = 1}^N s_{i} \xi_i \right\} \\ &s.t\quad y_i\left[\sum\limits_{j = 1}^N w_j \phi_j(x) + b\right] - 1 + \xi_i \geq 0 \\ &\xi_i \geq 0 \end{aligned} $$
(15)

where c is the margin parameter and s i is weighted coefficient. According to Lagrange function

$$ \begin{aligned} L &= \frac{1}{2}\| w \| ^2 + c\sum\limits_{i = 1}^Ns_i\xi_i \\ &\quad -\sum\limits_{i=1}^N\beta_i\xi_i-\sum\limits_{i=1}^N\alpha_i\{y_i[w^T\phi(x_i)+b]-1+\xi_i\} \end{aligned} $$
(16)

where, α i , β i are Lagrange multipliers. Solving the partial derivatives of w, b, ξ and setting their derivative value is ∂L/∂w = 0, ∂L/∂b = 0, ∂L/∂ξ = 0. Then obtain w = ∑ N i=1 α i y i ϕ(x i ) and ∑ N i=1 α i y i  = 0, c = α i  + β i . Using them in Eq. 15, we can change the minimization problem of L into the maximization problem of α:

$$ \begin{aligned} \max L_D &= \sum\limits_{i=1}^N\left(\alpha_{i}-\frac{1}{2}\alpha_{i}\alpha_{j} y_{i} y_{j} \phi(x_i)\phi(x)j\right) \\ & = \sum\limits_{i = 1}^N\left(\alpha_{i}- \frac{1}{2}\alpha_{i}\alpha_{i} y_{i} y_{j} K(x_{i},x_{j})\right)\\ s.t. &\quad \sum\limits_{i = 1}^N\alpha_iy_i = 0\quad 0\leq\alpha_{i}\leq cs_{i} \end{aligned} $$
(17)

Here, \(K(x_{i},x_{j}) = \phi(x_{i})\cdot\phi(x_{j})\) is called kernel function. SVM tries to map input vector \(x_{i}\in R^d\) into a higher feature space, and can solve the linearly non-separable case. The mapping process is based on the chosen kernel function. Some popular kernel functions are including to linear kernel, polynomial kernel, radial basis and sigmoid kernel functions. The radial basis function is used in this study in the mapping process.

2.4 General correlation coefficient

The coefficient of general cross-correlation (GCC) which is obtained by dividing the covariance of the two variables by the product of their standard deviations is also introduced in our approach. The population correlation coefficient ρ X,Y between two random variables X and Y with expected values μ X and μ Y and standard deviations σ X and σ Y is defined as:

$$ \begin{aligned} \rho_{X,Y}&= corr(X,Y)\\ & = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}\\ & = \frac{E[(X-\mu_{X})(Y-\mu_{Y})]}{\sigma_{X}\sigma_{Y}} \end{aligned} $$
(18)

where E is the expected value operator, cov means covariance, and corr a widely used alternative notation for the correlation.

If we have a series of n measurements of X and Y written as x i and y i , where \(i = 1, 2,\ldots, n , \) then the sample correlation coefficient can be used to estimate the population correlation r between X and Y. The sample correlation coefficient is written

$$ \begin{aligned} r_{xy}&= \frac{\sum\nolimits_{i=1}^n(x_{i}-\overline{x})(y_{i}-\overline{y})}{(n-1)s_{x}s_{y}}\\ & = \frac{\sum\nolimits_{i = 1}^n(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum\nolimits_{i = 1}^n(x_{i}-\overline{x})^2\sum\nolimits_{i = 1}^n(y_{i}-\overline{y})^2}} \end{aligned} $$
(19)

where \(\overline{x}\) and \(\overline{y}\) are the sample means of X and Y, and s x and s y are the sample standard deviations of X and Y.

3 Proposed approach

In our work, vibration and current signature for detection and diagnose of faults in nuclear power motor are considered as a kind of pattern recognition paradigm. We have a sound database D which contains some known normal and faults sound records d

$$ D = \{d_1,d_2,\ldots, d_n\} $$
(20)

The purpose is to classify a new monitored signal d Test to the most similar d i

$$ i = M\{d_{i}, d_{Test}\} $$
(21)

M is the maximum likelihood. Eigenvalue estimation and machine learning is widely used in conventional diagnosis approach. These approaches, however, are difficult to distinguish early faults such as ball bearing error and normal signal because the fault AE is very weak for eigenvalue extraction. We propose a new method using the combination of PCA and GCC to increase the coefficient distance. A multi-class classification method based on binary-tree SVM is proposed in the machine learning part.

3.1 Coefficient estimation

We define the average value of random interceptions of the normal sound source as the comparison base d normal . The first interception of sound record in the database is used to be a comparison base records {d Base }. The sound source is pretreated with a low pass filter and used to estimate the frequency spectrum using fast Fourier transform.

We use \(\bigoplus\) to combine F normal and F Base to vectors {F normal , F Base }. Frequency separation approach, such as PCA or ICA, is used to separate the vectors to F main and F residual . The new frequency component which is more similar with F normal is defined as F main , and the other one is F residual . The main operation is indicated in Fig. 1.

Fig. 1
figure 1

Frequency separation processing using the normal comparison base

Full size image

Replace the d Base with the sample sound source to obtain the new frequency components \(\overrightarrow{F}_{Sample}\) and generate to a new vector {F Sample }. Correlation coefficient \(\overrightarrow{C}_{Sample}\) is estimated from \(\overrightarrow{F}_{Base}\) and \(\overrightarrow{F}_{Sample}\) for the training of machine learning (Fig. 2). \(\overrightarrow{C}_{Sample}\) also contains C Sample main and C Sample residual which are the cross-correlation coefficients of main frequency components and residual frequency components

$$ {C_{main}^{Sample} = corr(F_{main}^{Sample},F_{main}^{Base})} $$
(22)
$$ C_{residual}^{Sample} = corr(F_{residual}^{Sample},F_{residual}^{Base}) $$
(23)
Fig. 2
figure 2

The main processing of proposed approach

Full size image

For the monitoring data d Test , we use the same approach in Fig. 1 to obtain \(\overrightarrow{F}_{Test}\) and generate to \(\{\overrightarrow{F}_{Test}\}.\) We use the same process to obtain \(\overrightarrow{C}_{Test}\) with \(\overrightarrow{F}_{Test}\) for classification (Fig. 2).

3.2 Multi-class classification

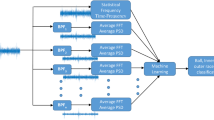
To improves the speed of training and diagnosis for multi-classification with unequal sample data, we select binary-tree SVM which is based on the cascaded multi-class classification (Viola and Jones 2001) for the machine learning. Figure 3 shows the details step:

  • Select the faults having highest frequency as the first class in k number of faults while the k−1 number of faults as the other class to build a binary classification SVM model.

  • Do the same things until the last two classed are used to set up binary classification SVM model and all the history faults are classified.

This method used the least number of classifier and repeated training sample.

Fig. 3
figure 3

Fault diagnosis methods using binary-tree SVMs

Full size image

The environment sounds, such as human active, would influence the results in the sampling processing. Conventional PCA–SVM approach is unable to overwhelm these problems because the eigenvalue of principal component would be disturbed easily for few frequency spectrums with large energy. The related distance, however, between \(\overrightarrow{F}_{Test}\) and \(\{\overrightarrow{F}_{Base}\}\) have very small changing. A distance normalization function, therefore, is proposed to reduce the interference of environment sounds

$$ \begin{aligned} \hat{C}_{main} &= C_{main}/E\\ \hat{C}_{residual} & = C_{residual}/E \end{aligned} $$
(24)

where \(E = \sqrt{C_{main}^2 + C_{residual}^2}.\)

4 Experiments and results

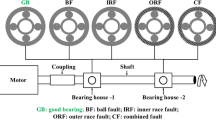
The experiment is conducted using test ring that consists of motors and microphone shown in Fig. 4. This machine can be operated under several condition of simulated defects, such as inner and outer race defect (large, middle, small) or ball defects by changing bearing elements, in addition to normal conditions’s operation. An example of defects is shown in the right side in Fig. 4. The measurement was made using hand type microphone with digital sampling of 44.1 kHz and record 10 s length. The data were measured under different rotating speed with 500, 1,000, 1,500, 2,000, 3,000 rpm (Table 1). We selected the 3,000 rpm group for detail discussion in the experiments. The bandpass of low-pass filter was set 2,000 Hz using Chebyshev type 1 filter. The window length of system is 2,048 points which means using 0.464 s wave data for generation. The first 5 s data was used for training and second 5 s data for testing. The sequential minimal optimization for binary SVM with L 1-soft margin was used for machine learning. Here IS, Im, IL, OS, OM, OL, Br, Nm are the shorten of inner-small/middle/large, outer-small/middle/large, ball bearing and normal.

Fig. 4
figure 4

Mockup facility of rolling bearing and simulated failures

Full size image
Table 1 Fault types in our experiments
Full size table

4.1 Results of conventional PCA–SVM

The conventional approaches of AE diagnosis used separation algorithm such as PCA and ICA to obtain the eigenvalue, and classifier like SVM, Gaussian mixture models (GMM), artificial neural networks (ANN) to recognize the faults of AE signals. Here we selected the simple PCA–SVM combination to compare with our method.

Figure 5 illustrated the classification results using PCA and one-to-one SVM for 3,000 rpm sound sources. The eigenvalues of inner faults obtained from PCA directly were separated significantly even with different damnify degree, and the distance between inner and outer was very clear. However, the division around the OutSmall, Ball and Normal are so ambiguous to classify clearly. Especially for the OutSmall and Normal signals, the recognition ratio was only 91.7% (Table 2). It is difficult for conventional PCA–SVM approach to distinguish a small fault in outer and ball bearing.

Fig. 5
figure 5

Classification results using conventional PCA and one-to-one SVM for 3,000 rpm data

Full size image
Table 2 Classification ratio of traditional PCA and one-to-one SVM using 3,000 rpm data
Full size table

4.2 Results of PCA–GCC–SVM

The approach we proposed using PCA–GCC–SVM overwhelmed the difficulty of small faults diagnosis. Figure 6 illustrated the frequency spectrum separation of ball bearing fault using PCA for 3,000 rpm data. The above ones were the original frequency spectrums of normal base signal and ball bearing. The spectrum of 500 Hz, 1,500 Hz in the ball bearing with faults were significantly large than the normal ones. The left bottom one showed the F main and the right bottom one indicated the F residual after the PCA separation for the mixing vector using above two. The main frequency components were almost the same as frequency spectrum of normal one, and the residual frequency components could be considered as the frequency characteristic of ball bearing faults.

Fig. 6
figure 6

The frequency spectrum separation of ball faults at 3,000 rpm using PCA separation

Full size image

Different with traditional PCA–SVM approach which using the original eigenvalue obtained from PCA, we used the coefficient of GCC of main and residual frequency spectrums between the comparison base and sample/test signals as the input of SVM (Fig. 2). Figure 6 plotted the classification results using binary SVM, in which the horizontal axis was the coefficients of main frequency and vertical axis was the coefficients of related residual frequency. It seems that not only the main frequency component but also the residual frequency were much similar with the same fault type. The results in Table 3 listed the fault classification using PCA and SVM to different kernel without normalization processing at 3,000 rpm states. The fault diagnosis of rolling ball were not so ideal comparing with others because of the frequency spectrums were too similar with the small faults and normal signals. The fault classification results were increased after we introduced the normalization to increase the distance (Figs. 7, 8; Table 3 below one).

Table 3 Fault classification using PCA and SVM to kernel without and with normalization processing at 3,000 rpm states
Full size table
Fig. 7
figure 7

PCA and SVM results of ball faults at 3,000 r/m without normalization using poly kernel function

Full size image
Fig. 8
figure 8

PCA and SVM results of ball faults at 3,000 r/m with normalization using poly kernel function

Full size image

To compare the most popular blind source separation algorithm, such as ICA, we tested the experiment results with ICA and SVM both without and with normalization (Fig. 9; Table 4). The diagnosis results of outer large fault were not so better comparing with the results of PCA because of the non-Gaussian characteristic interference for ICA. The performance of fault classification using ICA and SVM with normalization, however, was significantly better than the results without normalization.

Fig. 9
figure 9

ICA and SVM results of ball faults at 3,000 r/m without and with normalization using poly kernel function

Full size image
Table 4 Fault classification using ICA and SVM to kernel without and with normalization processing at 3,000 rpm states
Full size table

Table 5 indicated the diagnosis results of all type faults using PCA–GCC–SVM approach. We reduced the pass band for the sound sources with different speed. The classification ratio were all wonderful with our approach.

Table 5 Classification ratio results of all type faults with out approach
Full size table

5 Conclusion

An integrated method based on PCA–GCC–SVM is proposed in this paper, and this can be used to detect AE diagnosis with many disturbance for complex industry distillation process. The fault feature extraction is one important step in fault monitoring process because it can remove the redundancy and avoid the curse the dimensionality phenomenon.

The residual frequency components was separated more significantly using a mixing matrix with comparison base and detection signal.

We set the GCC coefficients of main frequency and residual frequency as the parameter of machine learning. This method increased the distance between the same classes and different class even if it confused the distribution of other classes. The binary-tree machine learning based on the cascaded multi-class classification adopted for this coefficient estimation approach. It is shown that the experiment results of PCA–GCC–SVM can archive higher diagnosis accuracy than original PCA–SVM models for weak faults detection. Based on the comparison of ICA–GCC–SVM results, this method can be extend to other source separation and machine learning algorithm.