Relativistic anisotropic models of ultra-dense stellar objects under embedding class I

Abstract

In this paper, we present a new class of exact solutions satisfying Einstein’s field and modified TOV-equations. The thermodynamic quantities of stellar matter like anisotropic pressures, baryon density, red-shift and velocity of sound have been investigated using the embedding class I methodology with the Karmarkar condition. The solutions satisfy the static stability criterion, energy conditions, stability factor, adiabatic index and causality condition. In addition to it, we perform complete graphical analysis of neutron stars in Vela $X-1$ and Her $X-1$ in the setting of the Karmarkar space-time.

1 Introduction

Studies on relativistic stellar objects commenced in 1916, with a productive insight of the Schwarzschild vacuum solution of Einstein’s field equations (EFEs) with the forecasting of the existence of a black hole. In the same year, Schwarzschild [1] also gave a second solution of Einstein’s field equations which describes a uniform density compact star. Initially, compact stars were believed to be composed of isotropic perfect fluids only. Jeans [2] foretold that under extreme intricacy prevailing inside stellar objects, the difference of radial and tangential pressures, i.e., the measure of anisotropy is accented for a better realizing of the matter distribution.

The anisotropy is considered as one of the key features of stellar configurations and plays a pivotal role in realistic modeling of relativistic stellar systems. The concept of anisotropy was proposed by Ruderman [3] and Canuto [4]. Bowers and Liang [5] were the first who reported the presence of anisotropic spheres in the framework of general relativity. Dev and Gleiser [6, 7] observed that the component of pressure anisotropy can cause drastic changes in many fundamental properties of highly compact spheres. Recent observations on anisotropic pressures confirm the necessity of nonzero anisotropy in realistic modeling of highly compact spheres. The presences of 3A super-fluid [8], phase transitions [9], magnetic or strong electromagnetic field [10, 11], slow rotational motion [12], fluids of different types [13], pion condensation [14], etc., are some of the few reasons for the anisotropy in relativistic stellar systems. A systematic review regarding the origins and effects of local anisotropy in astrophysical objects can be found in [15, 16].

It is well known that EFEs describe gravity as geometry of space-time due to the presence of the matter distribution. Based on embedding problems, space-time can be categorized into various classes. Any spherically symmetric space-time can be embedded in a 6-D pseudo-Euclidean space, i.e., class II. Similarly, plane symmetric space-times are believed to be of class III. Some famous solutions like FLRW, Schwarzschild exterior, Schwarzschild interior and the Kerr space-time are considered to be of classes I, II, I and V, respectively. A number of classes are equivalent to the extra dimension(s) to embed the space-time into pseudo-Euclidean space.

In recent works, the technique of finding exact solutions of Einstein’s field equations in embedding class I has attracted a great interest among the researchers. In this class, the two metric functions $g_{rr}$ and $g_{tt}$ are linked via the Karmarkar condition [17]. In fact, by assuming one of the metric functions arbitrarily, the other one can be evaluated easily. Several authors [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42, 47] have studied various physically realistic models under the Karmarkar condition by choosing various general forms of metric potentials which include polynomials, trigonometric and hyperbolic functions having important physical applications to construct plausible astrophysical models. Recently, some researchers developed core-envelope models to the compact stars where the core region equipped with linear equation of state whereas the envelope region endowed with quadratic equation of state [43,44,45].

In this work, we consider a new class of hyperbolic metric potential and explore new interior anisotropic models for astrophysical compact stars. Here, we have studied two compact stars [46], i.e., the neutron star in Vela $X-1$ (mass $M=1.77 M_{\odot }$, radius $R=9.57$ km) and intermediate-mass X-ray binary star Hercules $X-1$ (Her $X-1$ ($M=0.85 M_{\odot }$, $R=8.1$ km).

The article is machinated as follows: We begin with Sect. 2 that consists of spherically symmetric interior space-time and the Einstein field equations for anisotropic matter distribution. Section 3 provides background of the Karmarkar condition mentioning the non-vanishing components for Riemannian tensor along with embedding class I condition for spherically symmetric metric. In Sect. 4, we obtain a new family of well-behaved solutions of the Einstein field equations for anisotropic compact stars. The matching of interior and exterior space-time over the boundary is given in Sect. 5. Physical viable conditions for anisotropic models are mentioned in Sect. 6. Discussion on viable trends of physical features for our models is reported in Sect. 7. In Sect. 8, stability analysis through Harrison–Zeldovich–Novikov criterion, modified Tolman–Oppenhimer–Volkoff equation equilibrium condition and Herrera cracking concept are given. Results and Discussion are provided in Sect. 9. The conclusion of our findings is described in the last section.

2 Spherically symmetric line element and Einstein’s field equations

The interior of an anisotropic fluid sphere in Schwarzschild’s canonical coordinates is described by the spherically symmetric line element as

$$\begin{aligned} \hbox {d}s^2 = \hbox {e}^{\nu (r)}\hbox {d}t^2 - \hbox {e}^{\lambda (r)}\hbox {d}r^2 - r^2(\hbox {d}\theta ^2 + \sin ^2{\theta }\hbox {d}\phi ^2). \end{aligned}$$

(1)

The energy-momentum tensor for anisotropic compact star can be given as

$$\begin{aligned} T_{jk} = [(p_t+\rho )v_{j}v_{k}-p_t g_{jk}+(p_r-p_t)\chi _j\chi _k], \end{aligned}$$

(2)

where symbols have their usual meaning. The energy density ($\rho$) is measured by a comoving observer with the fluid, the radial pressure ($p_r$) is measured in the direction of the spacelike vector, while the transverse pressures ($p_t$) are considered in the orthogonal direction to $p_r$.

The system of Einstein field equations (assuming $G = c = 1)$ for the line element (1) and energy momentum tensor are given by

$$\begin{aligned} \rho= & {} \frac{\left( 1 - \hbox {e}^{-\lambda }\left( 1-r\lambda '\right) \right) }{8\pi r^2}, \end{aligned}$$

(3)

$$\begin{aligned} p_r= & {} \frac{\left( \hbox {e}^{-\lambda }(1+r \nu ') - 1 \right) }{8\pi r^2} , \end{aligned}$$

(4)

$$\begin{aligned} p_t= & {} \frac{\hbox {e}^{-\lambda } \left( 2\nu '' r+ {\nu '}^2 r - \nu '\lambda ' r + 2(\nu '-\lambda ')\right) }{32\pi r} \end{aligned}$$

(5)

where $(')$ and $('')$ represent $\hbox {d}/\hbox {d}r$ and $\hbox {d}^2/\hbox {d}r^2$, respectively.

Using (4) and (5), the measure of anisotropy can be obtained as [47]

$$\begin{aligned} \Delta = p_t-p_r = \frac{\hbox {e}^{-\lambda }\left( 2r^2\nu ''-r(\lambda ' + \nu ')(r\nu '+2)+4 (\hbox {d}^\lambda -1)\right) }{32 \pi r^2}. \end{aligned}$$

(6)

3 Karmarkar’s condition under embedding class I

The space $M^{\mu +1}$ represents embedding class I (i.e., $M^{\mu +1}$ can be embedded as a hypersurface of a pseudo-Euclidean space $E^{\mu +2}$) if there exists a symmetric tensor $b_{\mu \nu }$ which satisfies the following Gauss–Codazzi equations [48, 49]

$$\begin{aligned}&R_{\mu \nu \delta \eta } = 2\epsilon b_{\mu [\delta }b_{\eta ]\nu },\\&b_{\mu [\nu ;\delta ]}-\Gamma ^{\eta }_{[\nu \delta ]} b_{\mu \eta }+\Gamma ^{\eta }_{\mu [\nu b_{\delta }]\eta } = 0. \end{aligned}$$

Here, $\epsilon$ takes the values $+1$ or $-1$, whenever the normal to the manifold is space-like or time-like, $R_{\mu \nu \delta \eta }$ represents curvature tensor, square brackets denote antisymmetrization, the symbol (; ) represents covariant derivatives and $b_{\mu \nu }$ are the coefficients of second differential form.

Eiesland [50] combined Gauss–Codazzi equations and found a necessary and sufficient condition for the space-time represented by the metric (1) in a more concise form

$$\begin{aligned} R_{1414}R_{2323}= R_{1212}R_{3434}+R_{1224}R_{1334}. \end{aligned}$$

(7)

The condition (7) is called the Karmarkar condition in which the labels (1, 2, 3, 4) represent coordinates $(r, \theta , \phi, t )$.

For the line element (1), the nonzero Riemann curvature tensor components are

$$\begin{aligned} R_{1414}= & {} -\hbox {e}^{\nu }\left( \frac{\nu ^{''}}{2}+\frac{\nu {'}^2}{4}-\frac{\lambda '\nu '}{4}\right) , \end{aligned}$$

(8)

$$\begin{aligned} R_{2323}= & {} -\hbox {e}^{-\lambda }r^2\sin ^2{\theta }(\hbox {e}^{\lambda }-1),\end{aligned}$$

(9)

$$\begin{aligned} R_{1212}= & {} \frac{1}{2}r{\lambda }',\end{aligned}$$

(10)

$$\begin{aligned} R_{3434}= & {} -\frac{1}{2}r\sin ^2{\theta }\nu '\hbox {e}^{\nu -\lambda }. \end{aligned}$$

(11)

Using the above Riemann tensor components in (7) yields the following differential equation (in the static case):

$$\begin{aligned} \frac{2\nu ^{''}}{\nu '}+\nu '=\frac{\lambda '\hbox {e}^{\lambda }}{\hbox {e}^{\lambda }-1}. \end{aligned}$$

(12)

Such class of solutions of the Einstein field equations are also termed as embedding class I solutions provided it satisfies Pandey and Sharma condition [51], i.e., $R_{2323}\ne 0$.

Integrating (12), we get the following relation between $\nu$ and $\lambda$:

$$\begin{aligned} \hbox {e}^{\nu }={\Big (S+T\int _{0}^{r}\sqrt{\hbox {e}^{\lambda }-1}\hbox {d}r\Big )}^2, \end{aligned}$$

(13)

where S and T are integration constants.

In view of (6), measure of anisotropy $\Delta$ can be expressed as [47]

$$\begin{aligned} \Delta =\frac{\nu {'}}{4\hbox {e}^{\lambda }}\Big [\frac{2}{r}-\frac{\lambda '}{\hbox {e}^{\lambda }-1}\Big ]\Big [\frac{\nu '\hbox {e}^{\nu }}{2rB^2}-1\Big ]. \end{aligned}$$

(14)

In the case of isotropic static fluid sphere, i.e., putting $\Delta =0$ in the above equation, we get either an interior Schwarzschild’s uniform density model or a Kohler–Chao solution with boundary at infinity. Both the solutions are not physically relevant from astrophysical points of view as one leads to constant density model while the later provides infinite boundary model.

4 Generating a new family of embedding class I solutions for anisotropic stellar model

In this paper, we consider a new family of hyperbolic trigonometric metric potential given as

$$\begin{aligned} \hbox {e}^{\lambda (r)}=1+a r^2 h_n(r), \end{aligned}$$

(15)

where

$$\begin{aligned} h_n(r) = {{\,\mathrm{csch}\,}}^n(b r^2+c), \end{aligned}$$

where $a~{(\hbox {km})}^{-1}$, $b~{(\hbox {km})}^{-1}$ and c are positive constants and n is any even integer. We select the metric potential $\hbox {e}^{\lambda (r)}$ in such away that it should be nonnegative, regular, monotonically increasing function throughout interior of the star and takes the value one at center which emphasizes that at the center, the tangent 3 space is flat and EFEs can be integrated, resulting a realistic solution for star modeling.

Substituting the value of $\hbox {e}^{\lambda (r)}$ from (15) in (13), we get $\hbox {e}^{\nu (r)}$ as

$$\begin{aligned} \hbox {e}^{\nu (r)}= & {} {\left( S-\frac{\alpha _1(r) \alpha _2(r) T \sqrt{a h_n(r)}}{4 b}\right) }^2, \end{aligned}$$

(16)

where S and T are integrating constants.

Using (15) and (16), the expressions of $\rho$, $p_r$, $\Delta$ and $p_t$ can be written as

$$\begin{aligned} \rho= & {} \frac{a h_n(r) \left( r^2 \left( a h_n(r)-2 b n \coth \left( b r^2+c\right) \right) +3\right) }{\left( a r^2 h_n(r)+1\right) {}^2} , \end{aligned}$$

(17)

$$\begin{aligned} p_r= & {} \frac{2 \alpha _3(r) \sqrt{a h_n(r)} \sqrt{-\sinh ^2\left( b r^2+c\right) }}{\alpha _4(r) \left( a r^2 h_n(r)+1\right) }, \end{aligned}$$

(18)

$$\begin{aligned} \Delta= & {} \frac{\left( \alpha _5-\alpha _6\right) r^2 \left( a h_n+b n \coth \left( b r^2+c\right) \right) }{\left( \alpha _7-\alpha _8\right) \left( a r^2 h_n+1\right) {}^2},\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} p_t= & {} p_r+\Delta , \end{aligned}$$

(20)

where

$$\begin{aligned} \alpha _1(r)= & {} \, _2F_1\left( \frac{1}{2},\frac{n+2}{4};\frac{3}{2};\cosh ^2\left( b r^2+c\right) \right) ,\\ \alpha _2(r)= & {} \sinh \left( 2 \left( b r^2+c\right) \right) \left( -\sinh ^2\left( b r^2+c\right) \right) ^{\frac{n-2}{4}},\\ \alpha _3(r)= & {} a \alpha _1 T h_{n+1} \cosh \left( b r^2+c\right) \left( -\sinh ^2\left( b r^2+c\right) \right) ^{\frac{n+2}{4}}\\&+2 b S \sqrt{a h_n}-4 b T,\\ \alpha _4(r)= & {} \alpha _1 T \sqrt{a h_n} \sinh \left( 2 \left( b r^2+c\right) \right) \left( -\sinh ^2\left( b r^2+c\right) \right) ^{n/4}\\&-4 b S \sqrt{-\sinh ^2\left( b r^2+c\right) },\\ \alpha _5(r)= & {} 4 b \sinh \left( b r^2+c\right) \left( T \sqrt{a h_n}-a S h_n\right) ,\\ \alpha _6(r)= & {} \alpha _1 T \left( a h_n\right) {}^{3/2} \sinh \left( 2 \left( b r^2+c\right) \right) \left( -\sinh ^2\left( b r^2+c\right) \right) ^{n/4}, \\ \alpha _7(r)= & {} 4 b S \sqrt{-\sinh ^2\left( b r^2+c\right) },\\ \alpha _8(r)= & {} \alpha _1 T \sqrt{a h_n} \sinh \left( 2 \left( b r^2+c\right) \right) \left( -\sinh ^2\left( b r^2+c\right) \right) ^{n/4}. \end{aligned}$$

The mass function m(r), gravitational red-shift z(r) and compactification factor u(r) at the surface and within the interior of the stellar system are given by

$$\begin{aligned} m(r)= & {} \frac{a r^3 \text {csch}^n\left( b r^2+c\right) }{2 \left( a r^2 \text {csch}^n\left( b r^2+c\right) +1\right) }, \end{aligned}$$

(21)

$$\begin{aligned} z(r)= & {} \frac{4 b}{4 b S-\alpha _1(r) \alpha _2(r) T \sqrt{a h_n(r)}}-1, \end{aligned}$$

(22)

$$\begin{aligned} u(r)= & {} \frac{a r^3 \text {csch}^n\left( b r^2+c\right) }{2 \left( a r^2 \text {csch}^n\left( b r^2+c\right) +1\right) } . \end{aligned}$$

(23)

5 Matching of interior and exterior space-time over the boundary

To find constants a,  b,  c,  S and T in the above class of solutions, the interior metric should be matched over the boundary

$$\begin{aligned} \hbox {d}s^2= & {} \Big (1-{2M\over r}\Big ) \hbox {d}t^2-\Big (1-{2M\over r}\Big )^{-1}\hbox {d}r^2-r^2(\hbox {d}\theta ^2+\sin ^2 \theta d\phi ^2). \end{aligned}$$

(24)

(24) is known as the Schwarzschild exterior metric. By comparing (1) with (24) at the boundary $r=R$ (Darmois–Israel conditions), we obtain

$$\begin{aligned} \hbox {e}^{\nu _b}= & {} 1-{2M \over R}\left( S-\frac{\alpha _1(R) \alpha _2(R) T \sqrt{a h_n(R)}}{4 b}\right) {}^2 , \end{aligned}$$

(25)

$$\begin{aligned} \hbox {e}^{-\lambda (r)_b}= & {} 1-{2M \over R} = \frac{1}{1+a R^2 h_n(R)}, \end{aligned}$$

(26)

$$\begin{aligned} p_r(R)= & {} 0 . \end{aligned}$$

(27)

The above boundary conditions (25–27) yield

$$\begin{aligned} a= & {} -\frac{2 M \text {csch}^{-n}\left( b R^2+c\right) }{R^2 (2 M-R)}, \end{aligned}$$

(28)

$$\begin{aligned} S= & {} -\frac{\sqrt{1-\frac{2 M}{R}} \left( a \alpha _1(R) \cosh \left( b R^2+c\right) \left( -\sinh ^2\left( b R^2+c\right) \right) ^{\frac{n+2}{4}} \text {csch}^{n+1}\left( b R^2+c\right) -4 b\right) }{4 b}, \end{aligned}$$

(29)

$$\begin{aligned} T= & {} \frac{1}{2} \sqrt{1-\frac{2 M}{R}} \sqrt{a \text {csch}^n\left( b R^2+c\right) }. \end{aligned}$$

(30)

Here, M and R are mass and radius of a particular compact stars, while b and c are free parameters.

6 Physical viable conditions for anisotropic models

The following conditions should be satisfied by the solutions of anisotropic models in order to achieve physical feasible configuration:

• 1. The metric potentials $\hbox {e}^{\lambda }$ and $\hbox {e}^\nu$ should be positive and non-singular inside the stellar interior and at the center $\hbox {e}^\nu =$ constant and $\hbox {e}^{-\lambda }=1$.

• 2. The density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ should be nonnegative inside the stellar objects and monotonically decreasing outward.

• 3. In a stable fluid sphere, the equation of state parameters $\omega _r=p_r/\rho ,~\omega _t=p_t/\rho$ should be positive and satisfy Zeldovich’s condition [52] at the center, i.e., $0 <\omega _r, ~\omega _t \le 1$.

• 4. For a physically stable static model, the energy conditions, i.e., $\rho >0$, $\rho +p_r \ge 0, \rho + p_t \ge 0$ and $\rho + p_r +2 p_t \ge 0$, should be satisfied throughout the interior of the stellar object.

• 5. The model should satisfy Harrison–Zeldovich–Novikov stability condition, i.e., $\frac{{\hbox {d}}M (\rho _0)}{{\hbox {d}}\rho _{0}} > 0$ [52, 53].

• 6. For stable model, the adiabatic index $\Gamma = \frac{\rho + p_r}{p_r} \frac{{\hbox {d}}p_r}{{\hbox {d}}\rho } \ge \frac{4}{3}$ (Bondi condition) [54].

• 7. The sound speeds should be less than that of light throughout the stellar object, i.e., $0< v_r^2=\frac{dp_r}{d\rho }\le 1, 0 < v_t^2=\frac{{\hbox {d}}p_t}{{\hbox {d}}\rho }\le 1$ (causality condition).

• 8. The solutions of anisotropic stellar objects should satisfy Hererra cracking stability condition, i.e., $-1 \le v_t^2-v_t^2 \le 0$ [56, 57].

• 9. The gravitational, hydrostatic and anisotropic forces in the interior of stellar objects should satisfy the modified Tolman–Oppenheimer–Volkoff condition [58].

7 Discussion on viable trends of physical features for our model

7.1 Trends of Geometrical and Physical parameters

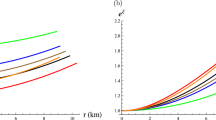
• (1) The metric potentials (geometrical parameters) for neutron stars in Vela $X-1$ and Her $X-1$ at the center $(r=0)$ give the values $\hbox {e}^\nu |_{r=0}=$ positive constant and $\hbox {e}^{-\lambda (r)}|_{r=0}=1$ for the range of n mentioned in Table 1. This shows that the metric potentials are regular and free from geometric singularities inside the stars. Also, both metric potentials $\hbox {e}^\nu (r)$ and $\hbox {e}^{-\lambda (r)}$ are monotonically increasing and decreasing, respectively, with r (Fig. 1).

• (2) The matter density $\rho$, radial pressure $p_r$ and transverse pressure $p_t$ for the stars Vela $X-1$ and Her $X-1$ are nonnegative inside the stars and monotonically decreasing from center to surface of the stars for the n values given in Table 1 (see, Figs. 2, 3). The profiles of pressure-to-density ratios (equation of state parameter $p_r/\rho , ~p_t/\rho$) with r are shown in Fig. 4 for both the stars for the same values of n mentioned in Table 1.

• (3) The mass function m(r) and gravitational red-shift z(r) function of two stars are increasing and decreasing, respectively, with r. The variation of m(r) and z(r) is shown in Figs. 5 and 6 for both the stars Vela $X-1$ and Her $X-1$ for the same range of n mentioned in Table 1. Also, compactification factor u(r) for both the stars is increasing functions with r, shown in Fig. 7, and lies within the Buchdahl limit [59].

• (4) In Fig. 8, the radial pressures ($p_r$) coincide with tangential pressures ($p_t$) at the center of neutron stars Vela $X-1$ and Her $X-1$ for the range n mentioned in Table 1, i.e., pressure anisotropies vanish at the center, $\Delta (0) = 0$ and are increasing outward.

Fig. 1

Variation of $\hbox {e}^{-\lambda (r)}$, $\hbox {e}^{\nu (r)}$ with r for (1) Vela $X-1$ with mass $M=1.77 M_{\odot }$ and radius $R=9.57$ km for parameters values of $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ with mass $M=0.85 M_{\odot }$ and radius $R=8.1$ km for parameters values of $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 2

Variation of $\rho$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 3

Variation of $p_r$, $p_t$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 4

Variation of $p_r/\rho$ and $p_t/\rho$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 5

Variation of mass (m(r)) with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2, c=3.5$

Fig. 6

Variation of red-shift with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 7

Variation of the compactification factor u(r) with r (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 8

Variation of anistropy $\Delta (r)$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

8 Stability analysis

8.1 Zeldovich’s condition for equation of state parameters

The values of $p_r$, $p_t$ and $\rho$ at the center of the stars are given by

$$\begin{aligned} 8\pi p_{rc}= & {} 8\pi p_{tc}\nonumber \\= & {} \frac{2 \sqrt{a \text {csch}^n(c)} \left( -2 \sqrt{a} S b+a \alpha _1 T (-1)^{\frac{n-2}{4}} \cosh (c)+4 b T \sqrt{\sinh ^n(c)}\right) }{2 S b \sqrt{\text {csch}^n(c)}-\sqrt{a} \alpha _1 T (-1)^{\frac{n-2}{4}} \cosh (c)}>0, \end{aligned}$$

(31)

and

$$\begin{aligned} 8\pi \rho _c = 3 a {{\,\mathrm{csch}\,}}^n(c)>0 ~~\textit{if}~~a > 0 . \end{aligned}$$

(32)

Using Zeldovich’s condition [52], i.e., $\omega _{r_c}={p_{rc}}/ {\rho _c} \le 1$, we get

$$\begin{aligned} \frac{-2 \sqrt{a} S b+a \beta _1 T (-1)^{\frac{n-2}{4}} \cosh (c)+4 b T \sqrt{\sinh ^n(c)}}{6 \sqrt{a} S b-3 a \beta _1 T (-1)^{\frac{n-2}{4}} \cosh (c)}\le 1. \end{aligned}$$

For $n=4k+2$ form (k being any integer), the last equation becomes

$$\begin{aligned} \frac{-2 \sqrt{a} S b+a \beta _1 T \cosh (c)+4 b T \sqrt{\sinh ^n(c)}}{6 \sqrt{a} S b-3 a \beta _1 T \cosh (c)}\le 1. \end{aligned}$$

(33)

In view of (31, 32) and (33), we get the following inequality

$$\begin{aligned} \frac{2b\sqrt{a}}{4b\sqrt{(\sinh (c))^n}+a \cosh (c)\beta _1}\le \frac{T}{S} \le \frac{2b\sqrt{a}}{b\sqrt{(\sinh (c)1)^n}+a \cosh (c)\beta _1}, \end{aligned}$$

(34)

where

$$\begin{aligned} \beta _1= & {} \, _2F_1\left( \frac{1}{2},\frac{n+2}{4};\frac{3}{2};\cos ^2(c)\right) . \end{aligned}$$

8.1.1 Hererra cracking stability and causality condition of anisotropic fluid sphere

The Hererra cracking method [56] is used to analyze the stability of anisotropic stars under radial perturbations. Using the concept of cracking, Abreu et al. [57] gave the idea that the region of an anisotropic fluid sphere is potentially stable when it satisfies the condition $-1< v^2_t-v^2_r \le 0.$ For a physically feasible model of anisotropic fluid sphere, the radial and transverse velocities of sound should be less than 1, which are known as causality conditions. The profiles of $v^2_r$ and $v^2_t$ of neutron stars in Vela $X-1$ and Her $X-1$ for the same even integer range of n given in Table 1 (see, Fig. 9) show that $0< v^2_r \le 1$ and $0< v^2_t \le 1$ everywhere within the stellar configuration. Therefore, both the speeds satisfy the causality conditions and monotonically decreasing nature. Here, we use the Herrera cracking method for analyzing the stability of anisotropic stars under the radial perturbations. Figure 10 clearly depicts that our model is potentially stable inside the both neutron stars in Vela $X-1$ and Her $X-1$ for the same range of n mentioned in Table 1.

Fig. 9

Variation of $v_r^2$, $v_t^2$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

Fig. 10

Variation of ${v_t}^2-{v_r}^2$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

8.1.2 Bondi stability condition for adiabatic index

For a relativistic anisotropic sphere, the stability counts on the adiabatic index $\Gamma _r$, the ratio of two specific heats, defined in [60],

$\Gamma _r = \frac{\rho + p_r}{p_r} \frac{\partial p_r}{\partial \rho }$.

Bondi [54] suggested that for a stable Newtonian sphere, $\Gamma$ value should be greater than $\frac{4}{3}$. For an anisotropic relativistic sphere, the stability condition is

$\Gamma > \frac{4}{3}+ \big [\frac{4 (p_{t0}-p_{r0})}{3 |p^{'}_{r0}|r}+\frac{\rho _{0}p_{r0}}{2 |p^{'}_{r0}|}r\big ]$,

where $p_{r0}, p_{t0}$ and $\rho _0$ represent the initial radial pressure, tangential pressure and energy density, respectively, in static equilibrium [55]. The first and last terms inside the square brackets represent the anisotropic and relativistic corrections, respectively. Moreover, both the quantities are positive and increase the unstable range of $\Gamma$.

The present class of solutions satisfies Bondi condition for the neutron stars in Vela $X-1$ and Her $X-1$ in the same range of n mentioned in Table 1.

Fig. 11

Variation of $\Gamma (r)$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

8.1.3 Energy conditions

For a physically stable static configuration of a stellar object, it is essential to verify the following energy conditions [61]:

• (i) Null energy condition (NEC): $\rho + p_r \ge 0$

• (ii) Strong energy condition (SEC): $\rho +p_r+2p_t \ge 0$

• (iii) Weak energy condition (WEC$_r$): $\rho + p_r \ge 0$, $\rho \ge 0$ and weak energy condition (WEC$_t$): $\rho + p_t \ge 0$, $\rho \ge 0$.

The profiles of energy conditions, i.e., NEC, WEC$_r$, WEC$_t$ and SEC, are displayed in Fig. 12. Our models satisfy all the energy conditions for both the neutron stars in Vela $X-1$ and Her $X-1$ for the same range of n mentioned in Table 1.

Fig. 12

Variation of energy conditions (WEC, SEC, DEC) with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

8.2 Modified Tolman–Oppenheimer–Volkoff condition for equilibrium under three forces

The modified Tolman–Oppenheimer–Volkoff (TOV) equation [58] for anisotropic fluid matter distribution is given as

$$\begin{aligned} -{M_g(r)(\rho +p_r) \over r^2}~\hbox {e}^{(\lambda (r)-\nu (r))/2}-{{\hbox {d}}p_r \over {\hbox {d}}r}+{2\Delta (r) \over r}=0, \end{aligned}$$

(37)

where $F_g$, $F_h$, $F_a$ are gravitational, hydrostatic and anisotropic forces, respectively, and $M_g(r)$ is the gravitational mass can be calculated by the Tolman–Whittaker formula

$$\begin{aligned} M_g(r)= & {} {1\over 2}~r^2 \nu '(r) \hbox {e}^{(\nu (r)-\lambda (r))/2}. \end{aligned}$$

(38)

The modified TOV Eq. (37) can be expressed in the following balanced force equation

$$\begin{aligned} F_g+F_h+F_a=0 . \end{aligned}$$

(39)

In an equilibrium state, all the three forces $F_g$, $F_h$ and $F_a$ satisfy the modified TOV equation. The profiles of the three forces of neutron stars Vela $X-1$ and Her $X-1$ for the same range of n mentioned in Table 1 are displayed in Fig. 13. In Fig. 13, $F_g$ overshadows the other two forces $F_h$ and $F_a$ in such a way that the system remains in static equilibrium.

Fig. 13

Variation of balancing forces $F_a, ~F_g,~ F_a,~ F_a+F_g+F_h$ with r for (1) Vela $X-1$ of the models $n=-32, -24, ~ -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

8.3 Harrison–Zeldovich–Novikov static stability criterion

The Harrison–Zeldovich–Novikov static stability criteria for non-rotating spherically symmetric equilibrium stellar models suggest that the mass of compact stars must be an increasing function of its central density under small radial pulsation, i.e.,

$$\begin{aligned} \frac{\partial M}{\partial \rho _c}>0. \end{aligned}$$

(40)

The above criterion ensures that the model is static and stable. It was proposed by Harrison et al. [53] and Zeldovich–Novikov [52] independently for stable stellar models. With the help of Eq. (32) and total mass,

$$\begin{aligned} M=m(R)=\frac{1}{2} R \left( 1-\frac{1}{a R^2 \text {csch}^n\left( b R^2+c\right) +1}\right) , \end{aligned}$$

(41)

the expression of the mass in terms of the central density is given by

$$\begin{aligned} M(\rho _c)= \frac{1}{2} R \left( 1-\frac{3 \text {csch}^n(c)}{\rho R^2 \text {csch}^n\left( b R^2+c\right) +3 \text {csch}^n(c)}\right) . \end{aligned}$$

Also,

$$\begin{aligned} \frac{3 R^3 \text {csch}^n(c) \text {csch}^n\left( b R^2+c\right) }{2 \left( \rho R^2 \text {csch}^n\left( b R^2+c\right) +3 \text {csch}^n(c)\right) ^2}>0, \end{aligned}$$

satisfies (Fig. 14) the static stability criterion (40).

The present class of solutions holds Harrison–Seldovich–Novikov condition for neutron stars in Vela $X-1$ and Her $X-1$ for the same range of n mentioned in Table 1.

Fig. 14

Variation of $p_r/\rho$ and $p_t/\rho$ with r for (1) Vela $X-1$ of the models $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ of the models $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$

9 Results and discussion

A new parametric class of non-singular solutions of the Einstein field equations for compact stars under embedding class I spacetime is presented. Graphical analysis of respective neutron stars in Vela $X-1$ and Her $X-1$ is performed for the parameter values $n=-32, -24, -16$, $b = 0.0001/{\text {km}}^2$, $c=3.5$ and $n=-\,34,-\,26,-\,18$, $b = 0.00006/{\text {km}}^2$, $c=3.5$. Geometrical parameters $\hbox {e}^{-\lambda (r)}$ and $\hbox {e}^{\nu (r)}$ are decreasing and increasing, respectively, throughout the interior of both the stars and both the respective curves meet at their boundaries (Fig. 1). The physical parameters, like density, radial and tangential pressures, pressures-to-density ratios, red-shift and velocities in the above-defined range of n, are nonnegative at the center and monotonically decreasing from the center to the surface of both the stars (Figs. 2, 3, 4, 6, 9). However, the physical parameters mass, compactification factor, anisotropy and adiabatic index are increasing outward (Figs. 5, 7, 8, 11).

The present models for the above range of n satisfy all the stability conditions for both the neutron stars, i.e., Herrera cracking condition ($-1<v_t^2-v_r^2<0$, $0<v_r^2,~ v_t^2<1$), Bondi condition ($\Gamma >4/3$), Zeldovich’s condition ($0<\frac{p_r}{\rho },~\frac{p_r}{\rho }<1$) and Harrison–Zeldovich–Novikov criterion ($\frac{\partial M}{\partial \rho _c}>0$) (see Figs. 10, 11, 14) besides satisfying all the energy conditions ($\rho >0$, $\rho +p_r>0$, $\rho +p_t>0$, $\rho +p_r+2p_t>0$) (Fig. 12). Moreover, our models represent a static anisotropic stellar fluid in equilibrium configuration as the forces $F_g$, $F_h$ and $F_a$ counterbalance each other through the modified TOV equation in the interior of stellar objects (Fig. 13).

The physical parameters values of $\Gamma$, $\rho$, $p_{r}$, z(r) at the center and compactification factor ($u(r)=\frac{GM}{cR^2}$), z(r) at the surface are given in Table 1. From Table 1, we conclude that for higher even values of n, the profiles of $\Gamma _c$ and $p_{r_c}$ show decreasing nature, whereas the profiles of $\rho _c$ and $z_c(r)$ show increasing nature. Other physical parameters, i.e., u(r) and z(r) at the boundary, remain the same for any even n values in that range.

10 Conclusions

In this paper, we have explored a new parametric class of solutions for anisotropic matter distribution to model the neutron star in vela $X-1$ and Her $X-1$ in the setting of the Karmarkar space-time by assuming one of metric potential $\hbox {e}^{\lambda (r)}=1+ar^2 {{{\,\mathrm{csch}\,}}(br^2+c)}^n$. The thermodynamic quantities of stellar matter like anisotropic pressures, baryon density, red-shift and velocity of sound have been investigated extensively using the embedding class I methodology with the Karmarkar condition. The solution profiles satisfy static stability criterion, energy conditions, stability factor, adiabatic index and causality condition for the following values of the parameters; neutron star in Vela $X-1$ with mass $M=1.77 M_{\odot }$ and radius $R=9.57$ km for $n=-32, -24, -16$, $b = 0.0001/{\text {km}}^2$ and $c=3.5$; Her $X-1$ with mass $M=0.85 M_{\odot }$ and radius $R=8.1$ km for $n=-\,34,-\,26,-\,18$ $b = 0.00006/{\text {km}}^2$ and $c=3.5$. The solutions are well-behaved for both the stars corresponding to the above-defined range of even negative values of n.

Table 1 Variation in physical parameters, i.e., central adiabatic index, central density, central red-shift, surface red-shift and compactness factor for different models of (1) Vela $X-1$ with mass $M=1.77 M_{\odot }$ and radius $R=9.57$ km for parameters $n=-32, -24, -16$ for the values of $b = 0.0001/{\text {km}}^2$, $c=3.5$; (2) Her $X-1$ with mass $M=0.85 M_{\odot }$ and radius $R=8.1$ km for parameters $n=-\,34,-\,26,-\,18$ for the values of $b = 0.00006/{\text {km}}^2$, $c=3.5$, $G=6.67 \times 10^{-11}~{\text {m}}^3~{\text {kg}}^{-1}~{\text {s}}^{-2}$, $M_{\odot }= 2\times 10^{30}$ kg and $C=3\times 10^8~{\text {m s}}^{-1}$