1 Introduction

There are several mathematical challenges to deal with a complex chemical reaction mechanism in chemical kinetics, like the stoichiometry of reaction mechanism, different reaction completion routes, net-reaction from the catalytic mechanism, analysis of dependent and independent species, the behavior of involved chemical species and time analysis. The problems connected with complex chemical reactions with their analysis are present in the applications of the chemical engineering process. The complex biochemical reaction network catalyzed by an enzyme achieves both the growth of cells and transformation of raw materials to products. To deal with complex chemical reactions, we require the reaction mechanism that consists of several elementary steps, the stoichiometry of reaction mechanisms and key and non-key components of the reaction mechanism [1], the general structures of a mechanism for catalytic and non-catalytic reactions that consist of many elementary steps and reaction routes [2]. There are wide applications in the chemical process like polymer production, food processing and dehydrogenation process. Several researchers [3,4,5,6,7] planned the characteristics of homogeneous and inhomogeneous reactions in different fluids flow with the addition of activation energy (AE) and thermal radiation.

Mathematical sciences are rapidly changing by modern computational techniques and the latest technologies, offering the prospect to examine complex issues with great generality and accuracy. Order reduction is also an important part to deal with the large models efficiently in simulation, control or optimization. Within this context, we derive the kinetic equations (KE) and then obtain their steady state solutions. Constales et al. [2] also explained the overall reaction in catalytic reaction mechanisms, key and non-key components and solution behavior of different reacting species in the single-route reaction mechanism.

To examine the physical behavior of kinetic equations, several methods have been introduced so far, i.e., quasi-steady states (QSS), quasi-equilibrium states (QES) and limiting steps and subsystems [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. These methods are quite efficient to study the steady state behavior of reduced species with respect to time and comparison of the invariant manifold. Sultan et al. [23] discussed different available reaction routes mathematically and found their invariants.

The careful view of the existing literature demonstrates that mostly the researchers were restricted to the steady state behavior of reduced species in the reaction mechanism. In the current article, the steady state behavior of all participating species is investigated and the transition time for the common species of both routes in the reaction mechanism is compared.

2 Calculation procedure

A reversible chemical reaction can be represented as:

$$\sum\limits_{i = 1}^{n} {a_{i} A_{i} \Leftrightarrow \sum\limits_{i = 1}^{n} {b_{i} B_{i} } } .$$
(1)

where \(A_{i}\) and \(B_{i}\) are reactants and products and \(a_{i}\) and \(\,b_{i}\) are the stoichiometric coefficients of reactants and products. The reaction rate of each elementary step \(R\) can be measured by calculating its forward (\(R_{\text{f}}\)) and backward (\(R_{\text{b}}\)) reaction rates, i.e.,

$$R = R_{\text{f}}^{ + } - R_{\text{b}}^{ - }$$
(2)

By applying mass action law, forward and backward reaction rates can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {R_{\text{f}}^{ + } = k^{ + } \prod {c_{{A_{i} }}^{{\alpha_{i} }} } = k^{ + } c_{{A_{1} }}^{{\alpha_{1} }} c_{{A_{2} }}^{{\alpha_{2} }} \ldots } \hfill \\ {R_{\text{b}}^{ - } = k^{ - } \prod {c_{{B_{i} }}^{{\beta_{i} }} } = k^{ - } c_{{B_{1} }}^{{\beta_{1} }} c_{{B_{2} }}^{{\beta_{2} }} \ldots } \hfill \\ \end{array} } \right.$$
(3)

Moreover, the system (2) attains its equilibrium state when \(R_{\text{f}} = R_{\text{b}}\). Here, \(C_{{A_{i} }}\) and \(C_{{B_{i} }}\) are the concentrations of reactant and product species and \(\alpha_{i}\) and \(\beta_{i}\) are the stoichiometric coefficients and \(k^{ \pm }\) are the reaction rate coefficients for the forward and backward reactions, respectively. However, the difference between stoichiometric coefficients (gain–loss) is the stoichiometric vector, i.e.,

$$\gamma :\gamma = \beta - \alpha$$

Finally, the sum of the product of rate equation and stoichiometric vectors gives kinetic equations, i.e.,

$$\dot{c}{ = }\sum\limits_{s = 1}^{r} {\gamma R_{s} (c)}$$
(4)

Mathematically, the number of independent reaction routes \(N_{\text{rr}}\) can be measured by implementing Horiuti’s rule [23].

$$N_{\text{rr}} = N_{\text{st}} - N_{\text{int}} + N_{\text{as}}$$
(5)

From Eq. (5), we can find different available reaction routes in completes mechanism. Here, \(N_{\text{int}}\), \(N_{\text{st}}\) and \(N_{\text{as}}\) are the number of intermediates, number of reaction steps and the active sites, respectively.

2.1 Kinetic patterns

To study the different reaction routes, we need to consider a two-route non-homogeneous reversible reaction mechanism with a common step and having seven chemical components \({\text{C}}_{4} {\text{H}}_{6} ,\,{\text{C}}_{4} {\text{H}}_{8} {\text{Z}},\,{\text{Z}},\,{\text{H}}_{2} ,\,{\text{C}}_{4} {\text{H}}_{6} {\text{Z}},\,{\text{C}}_{4} {\text{H}}_{8} ,\,{\text{C}}_{4} {\text{H}}_{6} {\text{Z}}\) and \({\text{C}}_{4} {\text{H}}_{10}\). Here, (C, H and Z) are three independent elements.

The four-step mechanism is dehydrogenation of butane represented by a set of equations and graph of Fig. 1. The weights of the edges are: \(w_{1}^{ + } = k_{1}^{ + } c_{{{\text{C}}_{4} {\text{H}}_{10} }}\), \(w_{1}^{ - } = k_{1}^{ - } c_{{{\text{H}}_{2} }}\), \(w_{2}^{ + } = k_{2}^{ + }\), \(w_{2}^{ - } = k_{2}^{ - } c_{{{\text{C}}_{4} {\text{H}}_{8} }}\), \(w_{3}^{ + } = k_{3}^{ + }\), \(w_{3}^{ - } = k_{3}^{ - } c_{{{\text{H}}_{2} }}\), \(w_{4}^{ + } = k_{4}^{ + }\) and \(w_{4}^{ - } = k_{4}^{ - } c_{{{\text{C}}_{4} {\text{H}}_{6} }}\).

Fig. 1
figure 1

Representation of the two-route reaction mechanism (dehydrogenation of butane)

Full size image

The spanning trees for the node points \({\text{Z}},\,{\text{C}}_{4} {\text{H}}_{8} {\text{Z}}\) and \({\text{C}}_{4} {\text{H}}_{6} {\text{Z}}\) along with their weights are shown in Fig. 2.

Fig. 2
figure 2

Spanning trees for the node points \({\text{Z,}}\,{\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\) and \({\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z}}\)

Full size image

In addition, the total weight \(W\) of all three spanning trees is:

$$\begin{aligned} W & = \left( {k_{3}^{ + } + k_{4}^{ + } } \right)k_{1}^{ + } c_{{{\text{C}}_{4} {\text{H}}_{10} }} + \left( {k_{3}^{ - } + k_{3}^{ + } } \right)k_{1}^{ - } c_{{{\text{H}}_{2} }} + \left( {k_{1}^{ - } + k_{3}^{ - } } \right)k_{4}^{ - } c_{{{\text{H}}_{2} }} c_{{{\text{C}}_{4} {\text{H}}_{6} }} \\ & \quad + k_{2}^{ - } k_{4}^{ + } c_{{{\text{C}}_{4} {\text{H}}_{8} }} + k_{2}^{ + } k_{2}^{ - } k_{3}^{ + } k_{4}^{ - } c_{{{\text{C}}_{4} {\text{H}}_{6} }} c_{{{\text{C}}_{4} {\text{H}}_{8} }} + k_{2}^{ + } k_{3}^{ + } k_{4}^{ + } \\ \end{aligned}$$
(6)

It is clear from Eq. (5) and Fig. 1 that there are only two reaction routes in the mechanism, i.e.,

$$N_{\text{rr}} = 4 - 3 + 1 = 2.$$

2.2 First reaction route R − 1

A first reaction route completes its cycle in the two steps 1st and 2nd, and the total number of participating chemical species in the first route formed by three elements (Ne = 3) is Nc = 5.

 

\(\alpha_{1}\)

\({\text{C}}_{4} {\text{H}}_{10} + {\text{Z}}\overset {k_{1}^{ + } = 1} \rightleftharpoons {\text{C}}_{4} {\text{H}}_{8} {\text{Z}} + {\text{H}}_{2}\)

1

\({\text{C}}_{4} {\text{H}}_{8} {\text{Z}}\overset {k_{2}^{ + } = 1} \rightleftharpoons {\text{C}}_{4} {\text{H}}_{8} + {\text{Z}}\)

1

In two-step reversible reaction mechanism, \({\text{C}}_{4} {\text{H}}_{10}\) and \({\text{H}}_{2}\) reacting to each other in the presence of catalyst Z give the product \({\text{C}}_{4} {\text{H}}_{8}\).

Now, to get the overall reaction mechanism by eliminating the intermediates \({\text{Z}}\,{\text{and}}\,{\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\). Multiplying reaction equation in 1st and 2nd steps with the Horiuti matrix \(\left[ {1\,\,\,1} \right]^{\text{T}}\), respectively we get

$$\begin{aligned} {\text{C}}_{ 4} {\text{H}}_{ 1 0} + {\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}} + {\text{Z}} & \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{8} + {\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}} + {\text{H}}_{2} + {\text{Z}} \\ \Rightarrow {\text{C}}_{ 4} {\text{H}}_{10} & \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{8} + {\text{H}}_{2} \\ \end{aligned}$$

The overall reaction mechanism involves three terminal species \({\text{C}}_{ 4} {\text{H}}_{ 1 0} ,\;{\text{H}}_{ 2}\) and \({\text{C}}_{ 4} {\text{H}}_{8}\), while, \({\text{Z,}}\;{\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\) and \({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\) are the surface intermediates.

2.3 Second reaction route R − 2

The second reaction route completes its cycle in first, third and fourth steps of the whole mechanism.

 

\(\alpha_{2}\)

\({\text{C}}_{ 4} {\text{H}}_{10} + {\text{Z}}\overset {k_{1}^{ + } = 1} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}} + {\text{H}}_{2}\)

1

\({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\overset {k_{2}^{ + } = 1} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z}} + {\text{H}}_{2}\)

1

\({\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z}}\overset {k_{2}^{ + } = 1} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{6} + {\text{Z}}\)

1

Here, the total number of chemical species (\(N_{\text{c}} = 6\)) is six that are formed by three chemical elements (\(N_{\text{e}} = 3\)) participating to complete its cycle.

3 Results and discussion

The goal of finding the steady state is usually not to calculate the concentrations of the participating species but to calculate the elapsed time of species in both reaction routes. This period allows us comparing the efficiency of both reaction routes with respect to time.

Initially, the first reaction route mechanism is considered with the initial parameters taken as:

$$c_{1} = 0.5000,\quad c_{2} = 0.2000,\quad c_{3} = 0.1000,\quad c_{4} = 0.4000,\quad c_{5} = 0.2000.$$

The stoichiometric vectors and reaction rates are given by Eq. (2):

$$\begin{aligned} r_{1} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 1} & { - 1} \\ \end{array} } & 1 & 1 & 0 \\ \end{array} } \right],\quad R_{1} = R_{{{\text{f}}1}}^{ + } - R_{{{\text{b}}1}}^{ - } = k_{1}^{ + } c_{1} c_{2} - k_{1}^{ - } c_{3} c_{4} , \\ r_{2} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } & { - 1} & 0 & 1 \\ \end{array} } \right],\quad R_{2} = R_{{{\text{f}}2}}^{ + } - R_{{{\text{b}}2}}^{ - } = - k_{2}^{ - } c_{4} c_{5} - k_{2}^{ + } c_{3} . \\ \end{aligned}$$
(7)

By applying (3), we get the balancing equations

$$M.c = {\text{const}} .\Rightarrow \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \begin{aligned} 4 \hfill \\ 10 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} \hfill \\ \hfill \\ \hfill \\ \end{aligned} & \begin{aligned} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{aligned} \\ \end{array} } & \begin{aligned} \hfill \\ \hfill \\ \hfill \\ \end{aligned} & \begin{aligned} 4 \hfill \\ 8 \hfill \\ 1 \hfill \\ \end{aligned} & \begin{aligned} \begin{array}{*{20}c} {} & 0 & {} & 4 \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & 2 \\ \end{array} } & {} & 8 \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & 0 \\ \end{array} } & {} & 0 \\ \end{array} \hfill \\ \end{aligned} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ {c_{4} } \\ {c_{5} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{const}}_{ 1} } \\ {{\text{const}}_{ 2} } \\ {{\text{const}}_{ 3} } \\ \end{array} } \right],$$
(8)

whereas the system of kinetic equations is given by (4) as follows:

$$\begin{aligned} c_{1}^{ \cdot } & = k_{1}^{ - } c_{3} c_{4} - k_{1}^{ + } c_{1} c_{2} \\ c_{2}^{ \cdot } & = k_{1}^{ - } c_{3} c_{4} - k_{1}^{ + } c_{1} c_{2} - k_{2}^{ - } c_{2} c_{5} + k_{2}^{ + } c_{3} \\ c_{3}^{ \cdot } & = k_{2}^{ - } c_{2} c_{5} + k_{1}^{ + } c_{1} c_{2} - k_{2}^{ + } c_{3} - k_{1}^{ - } c_{3} c_{4} \\ c_{4}^{ \cdot } & = k_{1}^{ + } c_{1} c_{2} - k_{1}^{ - } c_{3} c_{5} \\ c_{5}^{ \cdot } & = k_{2}^{ + } c_{3} - k_{2}^{ - } c_{5} c_{2} \\ \end{aligned}$$
(9)

Similarly, the initial parameters for the second route of the reaction mechanism are: \(c_{1} = 0.5000,\,\,c_{2} = 0.2000,\,\,c_{3} = 0.1000,\,\,c_{4} = 0.4000,\,\,c_{5} = 0.2000,\,c_{6} = 0.1000\). Their stoichiometric vectors are

$$\begin{aligned} r_{1} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 1} & { - 1} \\ \end{array} } & {\,\,1} & {\,1} & {\,\,0\,\,\,\,\,\,0} \\ \end{array} } \right],\quad R_{1} = R_{{{\text{f}}1}}^{ + } - R_{{{\text{b}}1}}^{ - } = k_{1}^{ + } c_{1} c_{2} - k_{1}^{ - } c_{3} c_{4} , \\ r_{2} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\,\,0} & {\,\,\,0} \\ \end{array} } & { - 1} & 1 & {\,\,\,1\,\,\,\,\,\,0} \\ \end{array} } \right],\quad R_{2} = R_{{{\text{f}}2}}^{ + } - R_{{{\text{b}}2}}^{ - } = k_{2}^{ + } c_{3} - k_{2}^{ - } c_{4} c_{5} . \\ r_{3} & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\,\,0} & {\,\,\,1} \\ \end{array} } & {\,\,\,0} & 0 & { - 1\,\,\,\,\,\,1} \\ \end{array} } \right],\quad R_{3} = R_{{{\text{f}}3}}^{ + } - R_{{{\text{b}}3}}^{ - } = k_{3}^{ + } c_{5} - k_{3}^{ - } c_{2} c_{6} . \\ \end{aligned}$$
(10)

Applying (3), we get:

$$M.c = {\text{const}} .\Rightarrow \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \begin{aligned} 4 \hfill \\ 10 \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} \hfill \\ \hfill \\ \hfill \\ \end{aligned} & \begin{aligned} 0 \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{aligned} \\ \end{array} } & \begin{aligned} \hfill \\ \hfill \\ \hfill \\ \end{aligned} & \begin{aligned} 4 \hfill \\ 8 \hfill \\ 1 \hfill \\ \end{aligned} & \begin{aligned} \begin{array}{*{20}c} {} & 0 & {} & {4\,\,\,\,\,\,\,4} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & 2 \\ \end{array} } & {} & {6\,\,\,\,\,\,\,6} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & 0 \\ \end{array} } & {} & {1\,\,\,\,\,\,\,\,0} \\ \end{array} \hfill \\ \end{aligned} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ {c_{4} } \\ \begin{aligned} c_{5} \hfill \\ c_{6} \hfill \\ \end{aligned} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{const}}_{ 1} } \\ {{\text{const}}_{ 2} } \\ {{\text{const}}_{ 3} } \\ \end{array} } \right],$$
(11)

while Eq. (4) implies:

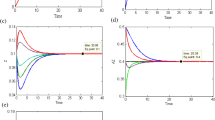
$$\begin{aligned} c_{1}^{ \cdot } & = k_{1}^{ - } c_{3} c_{4} - k_{1}^{ + } c_{1} c_{2} \\ c_{2}^{ \cdot } & = k_{3}^{ + } c_{5} - k_{1}^{ + } c_{1} c_{2} - k_{1}^{ - } c_{2} c_{6} + k_{1}^{ - } c_{3} c_{4} \\ c_{3}^{ \cdot } & = k_{1}^{ + } c_{1} c_{2} - k_{2}^{ + } c_{3} - k_{1}^{ - } c_{3} c_{4} + k_{2}^{ - } c_{4} c_{5} \\ c_{4}^{ \cdot } & = k_{2}^{ + } c_{3} + k_{1}^{ + } c_{1} c_{2} - k_{2}^{ - } c_{4} c_{5} - k_{1}^{ - } c_{3} c_{4} \\ c_{5}^{ \cdot } & = k_{2}^{ + } c_{3} - k_{2}^{ - } c_{4} c_{5} + k_{3}^{ - } c_{2} c_{6} - k_{3}^{ + } c_{5} \\ c_{6}^{ \cdot } & = k_{3}^{ + } c_{5} - k_{3}^{ - } c_{2} c_{6} \\ \end{aligned}$$
(12)

Consequently, we implement a mathematical approach to find the transition period of each chemical species involved in both reaction routes. Fig. 3a–e shows the transition time taken by each chemical species \({\text{C}}_{ 4} {\text{H}}_{ 1 0}\), \({\text{C}}_{ 4} {\text{H}}_{8} ,{\text{ Z}}\), \({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z }}\;{\text{and}}\;{\text{ H}}_{ 2}\) of the first route, that starts from different initials all the trajectories approaching toward their equilibrium point after completing their transition period.

Fig. 3
figure 3

Three possible kinds of trajectories that are started from different initials 0, 0.3 and 0.6 approach its equilibrium state after completing the transition period. A transition period of species for the consecutive mechanism \({\text{C}}_{ 4} {\text{H}}_{10} + {\text{Z}}\overset {} \rightleftharpoons {\text{C}}_{4} {\text{H}}_{ 8} {\text{Z}} + {\text{H}}_{2} ,\;{\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\overset {} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{8} + {\text{Z}};\,\,k_{1}^{ + } = k_{2}^{ + } = 1\)

Full size image

The transition time of species participating in the second route \({\text{C}}_{ 4} {\text{H}}_{10}\), \({\text{C}}_{ 4} {\text{H}}_{ 8} , {\text{ Z}}\), \({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z, }}\;{\text{H}}_{ 2}\),\({\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z and}}\,{\text{C}}_{ 4} {\text{H}}_{ 6}\) with rate constants \(\,k_{1}^{ + } = k_{2}^{ + } = 1,\,k_{3}^{ + } = 0.1\) is presented in Fig. 4a–f, respectively, the transition period for the second route of the reaction mechanism of each species that participates in reaction, i.e.

Fig. 4
figure 4

After completing their transition period, species are approaching their equilibrium state. The transition time of the species for the second route of the reaction mechanisms \({\text{C}}_{ 4} {\text{H}}_{10} + {\text{Z}}\overset {} \rightleftharpoons {\text{H}}_{2} + {\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\),\({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\overset {} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z}} + {\text{H}}_{2}\) and \({\text{C}}_{ 4} {\text{H}}_{ 6} {\text{Z}}\overset {} \rightleftharpoons {\text{C}}_{ 4} {\text{H}}_{6} + {\text{Z}}\) with rate constants \(\,k_{1}^{ + } = k_{2}^{ + } = 1,\,k_{3}^{ + } = 0.1\)

Full size image

3.1 Reaction route comparison

A comparison of the elapsed time between common species of both reaction routes is depicted in Fig. 5a–d. The common species in both routes are \({\text{C}}_{ 4} {\text{H}}_{ 1 0} ,\;{\text{Z}}\), \({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z, H}}_{ 2}\).

Fig. 5
figure 5

Comparison between the common species of both reaction routes is given. The square indicates the point after that species attain their equilibrium in the first and second routes, respectively

Full size image

Here, transition time of four species \({\text{C}}_{ 4} {\text{H}}_{ 1 0} ,\,{\text{Z,}}\,{\text{C}}_{ 4} {\text{H}}_{ 8}\) and \({\text{C}}_{ 4} {\text{H}}_{ 8} {\text{Z}}\) presented for both route and time difference is presented graphically in Fig. 6.

Fig. 6
figure 6

Graphical representation of species \({\text{C}}_{ 4} {\text{H}}_{10} ,\,{\text{Z}},\,{\text{C}}_{4} {\text{H}}_{8} {\text{Z}}\,{\text{and}}\,{\text{H}}_{2}\) involved in both reaction routes

Full size image

Table 1 ensures the reaction completion time of both reaction routes. Moreover,\({\text{C}}_{ 4} {\text{H}}_{ 1 0}\) in the first route takes 18.43 s to attain its steady state, but in the second route, the same species takes 29.34 s to complete its transition time. Similarly, the remaining common species of both routes are presented with respect to time in the following table.

Table 1 The transition period of the common species and difference in time of both reaction routes
Full size table

4 Conclusion

In this article, a two-route complex reaction mechanism is considered in detail. To measure the behavior of the involved species, we have distinctly measured the transition period and partial equilibrium of each species in both cases of the reaction route.

  • Although the involved species in both routes approach their equilibrium after passing through a different transition period, they have a different time period. This shows that some reactions are faster than others.

  • Similarly, it indicates that the activation energy required for the system is different in both the reaction routes.

  • The results have been observed for both the reaction routes graphically, while the difference in the tabulated form.