1 Introduction

Nonlinear partial differential equations are widely used to describe many important phenomena and dynamic processes in physics, chemistry, biology, fluid dynamics, plasma, optical fibers and other areas of engineering. As mathematical models of phenomena, the investigation of exact solutions of these equations will help us to understand these phenomena better. In recent decades, various effective approaches have been developed to construct the exact traveling wave solutions of these equations. Symbolic computations such as Mathematica or Maple are used for seeking the exact solutions of the nonlinear PDEs. Many powerful methods for solving the nonlinear PDEs are appeared in open literature, such as the modified simple equation method [1–6], the exp-function method [6–15], the \((G^{\prime }/G)\)-expansion method [16–21], the multiple exp-function method [22, 23], the first integral method [24–26], the generalized Kudryashov method [27, 28], the symmetry method [29, 30], the soliton ansatz method [31–53], the Riccati equation expansion method [34, 35] and so on.

The objective of this paper is to apply the modified simple equation method, the exp-function method, the soliton ansatz method, the Riccati equation expansion method, and the \(\left( G^{\prime }/G\right)\)-expansion method for finding the exact solutions, the solitary wave solutions and the trigonometric function solutions of the following nonlinear foam drainage equation [54]:

$$\begin{aligned} u_{t}=\frac{1}{2}uu_{xx}+2u^{2}u_{x}+\left( u_{x}\right) ^{2}, \end{aligned}$$
(1)

where \(u=u\left( x,t\right)\). Eq. (1) is an important nonlinear evolution equation appearing in the study of the drainage of liquid foams. These methods are of the most direct and effective algebraic methods for finding the exact solutions, the solitary wave solutions and the trigonometric function solutions of nonlinear PDEs in mathematical physics.

2 Description of the modified simple equation method

Suppose that a nonlinear PDE has the following form:

$$\begin{aligned} F(u,u_{t},u_{x},u_{tt},u_{xt},u_{xx}, \ldots )=0, \end{aligned}$$
(2)

where \(u=u(x,t)\) is an unknown function, F is a polynomial in \(u=u(x,t)\) and its partial derivatives, in which the highest order derivatives and nonlinear terms are involved.

The main steps of the modified simple equation method [1–6] are described as follows:

Step 1 First of all, we use the wave transformation:

$$\begin{aligned} u(x,t)=U(\zeta ),\quad \zeta =kx+wt, \end{aligned}$$
(3)

where k and w are nonzero constants, to reduce the PDE (2) into the following nonlinear ordinary differential equation (ODE):

$$\begin{aligned} P(U,U^{\prime },U^{\prime \prime },U^{\prime \prime \prime }, \ldots )=0, \end{aligned}$$
(4)

where P is a polynomial in \(U(\zeta )\) and its total derivatives \(U^{\prime },U^{\prime \prime },U^{\prime \prime \prime }, \ldots\) such that \(U^{\prime }=\frac{dU}{d\zeta }\), \(U^{\prime \prime }=\frac{d^{2}U}{d\zeta ^{2}}\) and so on.

Step 2 We suppose that Eq. (4) has the formal solution:

$$\begin{aligned} U(\zeta )=\sum _{i=0}^{N}A_{i}\left[ \frac{\psi ^{\prime }(\zeta )}{\psi (\zeta )}\right] ^{i}, \end{aligned}$$
(5)

where \(A_{i}\) are constants to be determined, such that \(A_{N}\ne 0\). The function \(\psi (\zeta )\) is an unknown function to be determined later, such that \(\psi ^{\prime }(\zeta )\ne 0\).

Step 3 We determine the positive integer N in Eq. (5) by balancing the highest order derivatives and the highest nonlinear terms in Eq. (4).

Step 4 We substitute Eq. (5) into Eq. (4), then we calculate all the necessary derivatives \(U^{\prime },U^{\prime \prime }, \ldots\) of the unknown function \(U(\zeta ).\) As a result of substitutions, we get a polynomial of \(\psi ^{-j}\) \((j=0,1,2, \ldots )\). In this polynomial, we gather all the terms of the same power of \(\psi ^{-j}\) \((j=0,1,2, \ldots )\), and equate them to zero. This operation yields a system of algebraic equations which can be solved to find \(A_{i}\) and \(\psi (\zeta )\). Thus, we can get the exact traveling wave solutions of Eq. (2).

3 Description of the exp-function method

In this section, we give the main steps of the exp-function method [6–15] as follows:

Step 1 We consider the Eqs. (2)–(4) of Sect. 2.

Step 2 According to the exp-function method, which is developed by He and Wu [7], we assume that the wave solution of Eq. (4) can be expressed in the following form:

$$\begin{aligned} U(\zeta )=\frac{\sum _{n=-d}^{c}a_{n}\exp (n\zeta )}{\sum _{m=-q}^{p}b_{m}\exp (m\zeta )}, \end{aligned}$$
(6)

where p, q, c, d are positive integers to be determined and \(a_{n},b_{m}\) are constants to be determined too. We can write (6) in the following equivalent form:

$$\begin{aligned} U(\zeta )=\frac{a_{c}\exp (c\zeta )+ \cdots +a_{-d}\exp (-d\zeta )}{b_{p}\exp (p\zeta )+ \cdots +b_{-q}\exp (-q\zeta )}. \end{aligned}$$
(7)

Step 3 We determine the values of c and p by balancing the linear term of the highest order of Eq. (4) with the highest order nonlinear term. Similarly, we determine the values of d and q by balancing the linear term of the lowest order of Eq. (4) with the lowest order nonlinear term.

Step 4 We substitute Eq. (7) into Eq. (4) and calculate all the coefficients of \(\exp (j\zeta )\ (j=0,\) \(\pm 1, \ldots )\). Setting all the coefficients to zero, we get a set of algebraic equations which can be solved by using the Maple. Consequently, we can get the exact traveling wave solutions of Eq. (2).

4 Exact solutions to the nonlinear foam drainage equation

In order to find the exact solutions of Eq. (1), we use the wave transformation:

$$\begin{aligned} u(x,t)=U(\zeta ),\quad \zeta =Kx+Lt, \end{aligned}$$
(8)

to reduce Eq. (1) into the following nonlinear ODE:

$$\begin{aligned} -LU^{\prime }+\frac{1}{2}K^{2}UU^{\prime \prime }+2KU^{2}U^{\prime }+K^{2}U^{\prime 2}=0, \end{aligned}$$
(9)

where K and L are nonzero constants.

4.1 On solving Eq. (9) using the modified simple equation method

To this aim, balancing \(UU^{\prime \prime }\) with \(U^{2}U^{\prime }\) in Eq. (9), we have \(N=1.\) Thus we get the formal solution

$$\begin{aligned} U(\zeta )=A_{0}+A_{1}\left[ \frac{\psi ^{\prime }(\zeta )}{\psi (\zeta )}\right] , \end{aligned}$$
(10)

where \(A_{0},A_{1}\) are constants to be determined, such that \(A_{1}\ne 0\). It is easy to see that:

$$\begin{aligned} U^{\prime }(\zeta )= A_{1}\left[ \frac{\psi ^{\prime \prime }}{\psi }-\frac{\psi ^{\prime 2}}{\psi ^{2}}\right] , \end{aligned}$$
(11)
$$\begin{aligned} U^{\prime \prime }(\zeta )= A_{1}\left[ \frac{\psi ^{\prime \prime \prime }}{\psi }-\frac{3\psi ^{\prime }\psi ^{\prime \prime }}{\psi ^{2}}+\frac{2\psi ^{\prime 3}}{\psi ^{3}}\right] . \end{aligned}$$
(12)

Substituting Eqs. (10)–(12) into Eq. (9) and equating all the coefficients of \(\psi ^{-j}\) \((j=1,2,3,4)\) to zero, we respectively obtain the following algebraic equations:

$$\begin{aligned}&\psi ^{-1}: \left( 2KA_{0}^{2}-L\right) \psi ^{\prime \prime }+\frac{1}{2}K^{2}A_{0}\psi ^{\prime \prime \prime }=0, \end{aligned}$$
(13)
$$\begin{aligned}&\psi ^{-2}: \left( L-2KA_{0}^{2}\right) \psi ^{\prime 2}+\left( 4KA_{0}A_{1}-\frac{3}{2}K^{2}A_{0}\right) \psi ^{\prime }\psi ^{\prime \prime }+\frac{1}{2}A_{1}K^{2}\psi ^{\prime }\psi ^{\prime \prime \prime }+A_{1}K^{2}\psi ^{\prime \prime 2}=0, \end{aligned}$$
(14)
$$\begin{aligned}&\psi ^{-3}: \left( A_{0}K^{2}-4A_{0}A_{1}K\right) \psi ^{\prime 3}+\left( 2KA_{1}^{2}-\frac{7}{2}K^{2}A_{1}\right) \psi ^{\prime 2}\psi ^{\prime \prime }=0, \end{aligned}$$
(15)
$$\begin{aligned}&\psi ^{-4}: 2KA_{1}^{2}\left( K-A_{1}\right) \psi ^{\prime 4}=0. \end{aligned}$$
(16)

Since \(A_{1}\ne 0\) and \(\psi ^{\prime }\ne 0,\) we deduce from Eq. (16) that \(A_{1}=K\). Let us now discuss the following cases:

Case 1 If \(A_{0}=0\), we deduce from Eqs. (13)–(15) that \(\psi ^{\prime }=0\). This is an impossible case, which is rejected.

Case 2 If \(A_{0}\ne 0\), we deduce from Eqs. (13)–(15) that

$$\begin{aligned}&2\left( 2KA_{0}^{2}-L\right) \psi ^{\prime \prime }+K^{2}A_{0}\psi ^{\prime \prime \prime }=0, \end{aligned}$$
(17)
$$\begin{aligned}&2\left( L-2KA_{0}^{2}\right) \psi ^{\prime 2}+5K^{2}A_{0}\psi ^{\prime }\psi ^{\prime \prime }+K^{3}\psi ^{\prime }\psi ^{\prime \prime \prime }+2K^{3}\psi ^{\prime \prime 2}=0, \end{aligned}$$
(18)
$$\begin{aligned}&3K^{2}\left( 2A_{0}\psi ^{\prime }+K\psi ^{\prime \prime }\right) \psi ^{\prime 2}=0. \end{aligned}$$
(19)

Since \(\psi ^{\prime }\ne 0,\) we deduce from Eqs. (17) and (19) that

$$\begin{aligned} \frac{\psi ^{\prime \prime \prime }}{\psi ^{\prime \prime }}= -\frac{2\left( 2KA_{0}^{2}-L\right) }{K^{2}A_{0}}, \end{aligned}$$
(20)
$$\begin{aligned} \psi ^{\prime }= -\frac{K}{2A_{0}}\psi ^{\prime \prime }. \end{aligned}$$
(21)

Consequently, we deduce that

$$\begin{aligned} \psi ^{\prime \prime }= c_{1}\exp \left( -\frac{2\left( 2KA_{0}^{2}-L\right) }{K^{2}A_{0}}\zeta \right) , \end{aligned}$$
(22)
$$\begin{aligned} \psi ^{\prime }= & {} -\frac{K}{2A_{0}}\psi ^{\prime \prime }=-\frac{c_{1}K}{2A_{0}}\exp \left( -\frac{2\left( 2KA_{0}^{2}-L\right) }{K^{2}A_{0}}\zeta \right) , \end{aligned}$$
(23)

and then

$$\begin{aligned} \psi =c_{2}+\frac{c_{1}K^{3}}{4\left( 2KA_{0}^{2}-L\right) }\exp \left( -\frac{2\left( 2KA_{0}^{2}-L\right) }{K^{2}A_{0}}\zeta \right) , \end{aligned}$$
(24)

where \(c_{1}\) and \(c_{2}\) are arbitrary constants of integration. Substituting Eqs. (22) and (23) into Eqs. (18) we deduce that \(A_{0}=\pm \sqrt{\frac{L}{K}},\) where \(LK>0.\)

Now, the exact solution \(U(\zeta )\) takes the form:

$$\begin{aligned} U(\zeta )=A_{0}-\left[ \frac{\frac{c_{1}K^{2}}{2A_{0}}\exp \left( -\frac{2A_{0}}{K}\zeta \right) }{c_{2}+\frac{c_{1}K^{2}}{4A_{0}^{2}}\exp \left( -\frac{2A_{0}}{K}\zeta \right) }\right] . \end{aligned}$$
(25)

Consequently, we have the exact traveling wave solution of Eq. (1) in the form:

$$\begin{aligned} u\left( x,t\right) =A_{0}-\left\{ \frac{\frac{c_{1}K^{2}}{2A_{0}}\exp \left[ -\frac{2A_{0}}{K}\left( Kx+Lt\right) \right] }{c_{2}+\frac{c_{1}K^{2}}{4A_{0}^{2}}\exp \left[ -\frac{2A_{0}}{K}\left( Kx+Lt\right) \right] }\right\} . \end{aligned}$$
(26)

If we set \(c_{1}=\frac{4A_{0}^{2}}{K^{2}},c_{2}=1,\) then we have the solitary wave solution of Eq. (1)

$$\begin{aligned} u\left( x,t\right) =\sqrt{\frac{L}{K}}\tanh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(27)

while, if we set \(c_{1}=\frac{4A_{0}^{2}}{l},c_{2}=-1,\) then we have the singular solitary wave solution of Eq. (1)

$$\begin{aligned} u\left( x,t\right) =\sqrt{\frac{L}{K}}\coth \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] . \end{aligned}$$
(28)

4.2 On solving Eq. (9) using the exp-function method

Let us now determine the positive integers p, q, c, d of Eq. (6). To this aim, we balance the highest order of \(UU^{\prime \prime }\) and \(U^{2}U^{\prime }\) in Eq. (9) to get

$$\begin{aligned} U\left( \zeta \right) U^{\prime \prime }\left( \zeta \right) =\frac{c_{1}\exp \left[ (2c+3p)\zeta \right] + \cdots }{c_{2}\exp \left( 5p\zeta \right) + \cdots }, \end{aligned}$$
(29)

and

$$\begin{aligned} U^{2}\left( \zeta \right) U^{\prime }\left( \zeta \right) =\frac{c_{3}\exp \left[ (2p+3c)\zeta \right] + \cdots }{c_{4}\exp \left( 5p\zeta \right) + \cdots }, \end{aligned}$$
(30)

where \(c_{i}\) \((i=1-4)\) are constants. From (29) and (30) we have

$$\begin{aligned} 2c+3p=2p+3c, \end{aligned}$$
(31)

which leads to the result

$$\begin{aligned} p=c. \end{aligned}$$
(32)

In the same way, to determine the values of d, q we balance the linear term of the lowest order in Eq. (9) to get

$$\begin{aligned} U\left( \zeta \right) U^{\prime \prime }\left( \zeta \right) =\frac{ \cdots +d_{1}\exp \left[ -(2d+3q)\zeta \right] }{ \cdots +d_{2}\exp \left( -5q\zeta \right) }, \end{aligned}$$
(33)

and

$$\begin{aligned} U^{2}\left( \zeta \right) U^{\prime }\left( \zeta \right) =\frac{ \cdots +d_{3}\exp \left[ -(2q+3d)\zeta \right] }{ \cdots +d_{4}\exp \left( -5q\zeta \right) }, \end{aligned}$$
(34)

where \(d_{i}\) \((i=1-4)\) are constants. From Eqs. (33) and (34) we obtain

$$\begin{aligned} -\left( 2d+3q\right) =-\left( 2q+3d\right) , \end{aligned}$$
(35)

which leads to the result

$$\begin{aligned} q=d. \end{aligned}$$
(36)

For simplicity, we set \(p=c=1\) and \(q=d=1.\) Thus Eq. (9) has the formal solution

$$\begin{aligned} U\left( \zeta \right) =\frac{a_{1}\exp (\zeta )+a_{0}+a_{-1}\exp (-\zeta )}{b_{1}\exp (\zeta )+b_{0}+b_{-1}\exp (-\zeta )}, \end{aligned}$$
(37)

where \(a_{i},b_{i}\) \((i=0,\pm 1)\) are constants to be determined later.

Substituting Eq. (37) into Eq. (9) and collecting all the coefficients of \(\exp (j\zeta )\) \((j=0,\pm 1,\pm 2,\pm 3)\) and equating them to zero, we have the following set of of algebraic equations:

$$\begin{aligned}&\begin{array}{ll} e^{3\zeta }:&2La_{0}b_{1}^{3}+4Ka_{1}^{3}b_{0}+K^{2}a_{1}a_{0}b_{1}^{2}-2La_{1}b_{0}b_{1}^{2}-K^{2}a_{1}^{2}b_{1}b_{0}-4Ka_{1}^{2}a_{0}b_{1}=0, \end{array}\nonumber \\&\begin{array}{ll} e^{2\zeta }: &{}\begin{array}{l} 4La_{-1}b_{1}^{3}+8Ka_{1}^{3}b_{-1}+3K^{2}a_{1}^{2}b_{0}^{2}+3K^{2}a_{0}^{2}b_{1}^{2}-6K^{2}a_{1}a_{0}b_{1}b_{0}-4La_{1}b_{-1}b_{1}^{2}-4K^{2}a_{1}^{2}b_{1}b_{-1}\\ +4K^{2}a_{1}a_{-1}b_{1}^{2}-8Ka_{1}^{2}a_{-1}b_{1}-4La_{1}b_{0}^{2}b_{1}+4La_{0}b_{1}^{2}b_{0}-8Ka_{1}a_{0}^{2}b_{1}+8Ka_{1}^{2}a_{0}b_{0}=0,\end{array} \end{array}\nonumber \\&\begin{array}{ll} e^{\zeta }: &{} \begin{array}{l} -6K^{2}a_{1}b_{0}a_{-1}b_{1}-18K^{2}a_{1}b_{-1}a_{0}b_{1}+2La_{0}b_{1}b_{0}^{2}+K^{2}a_{0}a_{1}b_{0}^{2}-K^{2}a_{0}^{2}b_{1}b_{0}+4Ka_{0}^{2}a_{1}b_{0}\\ +11K^{2}a_{1}^{2}b_{0}b_{-1}+13K^{2}a_{-1}b_{1}^{2}a_{0}-2La_{1}b_{0}^{3}-4Ka_{0}^{3}b_{1}-24Ka_{1}a_{0}a_{-1}b_{1}-12La_{1}b_{0}b_{1}b_{-1}\\ +10La_{-1}b_{1}^{2}b_{0}+2La_{0}b_{1}^{2}b_{-1}+4Ka_{1}^{2}a_{-1}b_{0}+20Ka_{1}^{2}a_{0}b_{-1}=0,\end{array}\end{array}\nonumber \\&\begin{array}{ll} e^{0}: &{} \begin{array}{l} 6K^{2}a_{1}a_{0}b_{-1}b_{0}-8La_{1}b_{-1}^{2}b_{1}-10K^{2}a_{0}^{2}b_{1}b_{-1}-16Ka_{1}a_{-1}^{2}b_{1}-8La_{1}b_{0}^{2}b_{-1}-16Ka_{0}^{2}a_{-1}b_{1}\\ +12K^{2}a_{1}^{2}b_{-1}^{2}-2K^{2}a_{1}a_{-1}b_{0}^{2}+12K^{2}a_{-1}^{2}b_{1}^{2}+6K^{2}a_{0}a_{-1}b_{1}b_{0}+8La_{-1}b_{1}^{2}b_{-1}+16Ka_{1}a_{0}^{2}b_{-1}\\ +8La_{-1}b_{1}b_{0}^{2}+16Ka_{1}^{2}a_{-1}b_{-1}-24K^{2}a_{1}b_{-1}a_{-1}b_{1}=0,\end{array}\end{array}\nonumber \\&\begin{array}{ll} e^{-\zeta }: &{} \begin{array}{l} -6K^{2}a_{1}b_{0}a_{-1}b_{-1}-18K^{2}a_{-1}b_{1}a_{0}b_{-1}-2La_{0}b_{-1}b_{0}^{2}+K^{2}a_{0}a_{-1}b_{0}^{2}-K^{2}a_{0}^{2}b_{-1}b_{0}-4Ka_{0}^{2}a_{-1}b_{0}\\ +11K^{2}a_{-1}^{2}b_{0}b_{1}+13K^{2}a_{1}b_{-1}^{2}a_{0}+2La_{-1}b_{0}^{3}+4Ka_{0}^{3}b_{-1}+24Ka_{-1}a_{0}a_{1}b_{-1}+12La_{-1}b_{0}b_{1}b_{-1}\\ -10La_{1}b_{-1}^{2}b_{0}-2La_{0}b_{-1}^{2}b_{1}-4Ka_{-1}^{2}a_{1}b_{0}-20Ka_{-1}^{2}a_{0}b_{1}=0,\end{array}\end{array}\nonumber \\&\begin{array}{ll} e^{-2\zeta }: &{} \begin{array}{l} -4La_{1}b_{-1}^{3}-8Ka_{-1}^{3}b_{1}+3K^{2}a_{-1}^{2}b_{0}^{2}+3K^{2}a_{0}^{2}b_{-1}^{2}-6K^{2}a_{-1}a_{0}b_{-1}b_{0}+4La_{-1}b_{1}b_{-1}^{2}\\ -4K^{2}a_{-1}^{2}b_{1}b_{-1}+4K^{2}a_{1}a_{-1}b_{-1}^{2}+8Ka_{-1}^{2}a_{1}b_{-1}+4La_{-1}b_{0}^{2}b_{-1}-4La_{0}b_{-1}^{2}b_{0}\\ +8Ka_{-1}a_{0}^{2}b_{-1}-8Ka_{-1}^{2}a_{0}b_{0}=0,\end{array}\end{array}\nonumber \\&\begin{array}{ll} e^{-3\zeta }:&\begin{array}{l} -2La_{0}b_{-1}^{3}-4Ka_{-1}^{3}b_{0}+K^{2}a_{-1}a_{0}b_{-1}^{2}+2La_{-1}b_{0}b_{-1}^{2}-K^{2}a_{-1}^{2}b_{-1}b_{0}+4Ka_{-1}^{2}a_{0}b_{-1}=0.\end{array}\end{array} \end{aligned}$$
(38)

Solving the above algebraic equations Eq. (38) using the Maple, we have the following cases:

Case 1

$$\begin{aligned} L=K^{3}, \quad a_{-1}=-Kb_{-1}, \quad a_{0}=0, \quad a_{1}=Kb_{1}, \quad b_{1}=b_{1} \quad ,b_{0}=0, \quad b_{-1}=b_{-1}. \end{aligned}$$
(39)

Substituting Eq. (39) into Eq. (37) along with Eq. (8), we obtain the following exact solution of Eq. (1):

$$\begin{aligned} u(x,t)=K\left[ \frac{b_{1}\exp (\zeta )-b_{-1}\exp (-\zeta )}{b_{1}\exp (\zeta )+b_{-1}\exp (-\zeta )}\right] . \end{aligned}$$
(40)

If \(b_{-1}=b_{1},\) then Eq. (1) has the solitary wave solution

$$\begin{aligned} u(x,t)=K\tanh \left[ K\left( x+K^{2}t\right) \right] , \end{aligned}$$
(41)

which is equivalent to the solution (27) if \(L=K^{3}.\)

If \(b_{-1}=-b_{1},\) then Eq. (1) has the singular solitary wave solution

$$\begin{aligned} u(x,t)=K\coth \left[ K\left( x+K^{2}t\right) \right] , \end{aligned}$$
(42)

which is equivalent to the singular solution (28) if \(L=K^{3}.\)

Case 2

$$\begin{aligned} L=\frac{1}{4}K^{3}, \quad a_{-1}=-\frac{Kb_{0}^{2}}{8b_{1}}, \quad a_{0}=0, a_{1}=\frac{1}{2}Kb_{1}, \quad b_{-1}=\frac{b_{0}^{2}}{4b_{1}}, \quad b_{1}=b_{1}, \quad b_{0}=b_{0}. \end{aligned}$$
(43)

Substituting Eq. (43) into Eq. (37) along with Eq. (8), we obtain the following exact solution of Eq. (1):

$$\begin{aligned} u(x,t)=\frac{1}{2}K\left[ \frac{4b_{1}^{2}\exp (\zeta )-b_{0}^{2}\exp (-\zeta )}{4b_{1}^{2}\exp (\zeta )+4b_{0}b_{1}+b_{0}^{2}\exp (-\zeta )}\right] . \end{aligned}$$
(44)

If \(b_{0}=2b_{1},\) then Eq. (1) has the solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\tanh \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(45)

which is equivalent to the solution (27) if \(L=\frac{1}{4}K^{3}.\)

If \(b_{0}=-2b_{1},\) then Eq. (1) has the singular solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\coth \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(46)

which is equivalent to the singular solution (28) if \(L=\frac{1}{4}K^{3}.\)

Case 3

$$\begin{aligned} L=\frac{1}{4}K^{3}, \quad a_{-1}=-\frac{K^{2}b_{0}^{2}-4a_{0}^{2}}{8Kb_{1}}, \quad a_{0}=a_{0}, \quad a_{1}=\frac{1}{2}Kb_{1}, \quad b_{-1}=\frac{K^{2}b_{0}^{2} -4a_{0}^{2}}{4K^{2}b_{1}}, \quad b_{1}=b_{1}, \quad b_{0}=b_{0}. \end{aligned}$$
(47)

Substituting Eq. (47) into Eq. (37) along with Eq. (8), we obtain the following exact solution of Eq. (1):

$$\begin{aligned} u(x,t)=\frac{1}{2}K\left[ \frac{4K^{2}b_{1}^{2}\exp (\zeta )+8Ka_{0}b_{1}-\left( K^{2}b_{0}^{2}-4a_{0}^{2}\right) \exp (-\zeta )}{4K^{2}b_{1}^{2}\exp (\zeta )+4K^{2}b_{0}b_{1}+\left( K^{2}b_{0}^{2}-4a_{0}^{2}\right) \exp (-\zeta )}\right] . \end{aligned}$$
(48)

If \(a_{0}=0,b_{0}=2b_{1},\) then Eq. (1) has the solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\tanh \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(49)

which is equivalent to the solution (45).

If \(a_{0}=0,b_{0}=-2b_{1},\) then Eq. (1) has the singular solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\coth \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(50)

which is equivalent to the singular solution (46).

Case 4

$$\begin{aligned} L=\frac{1}{4}K^{3}, \quad a_{-1}=0, \quad a_{0}=-\frac{1}{2}Kb_{0}, \quad a_{1}=\frac{1}{2}Kb_{1}, \quad b_{-1}=0, \quad b_{1}=b_{1}, \quad b_{0}=b_{0}. \end{aligned}$$
(51)

Substituting Eq. (51) into Eq. (37) along with Eq. (8), we obtain the following exact solution of Eq. (1):

$$\begin{aligned} u(x,t)=\frac{1}{2}K\left[ \frac{b_{1}\exp (\zeta )-b_{0}}{b_{1}\exp (\zeta )+b_{0}}\right] . \end{aligned}$$
(52)

If \(b_{0}=b_{1},\) then Eq. (1) has the solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\tanh \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(53)

which is equivalent to the solution (45).

If \(b_{0}=-b_{1},\) then Eq. (1) has the singular solitary wave solution

$$\begin{aligned} u(x,t)=\frac{1}{2}K\coth \left[ \frac{1}{2}K\left( x+\frac{1}{4}K^{2}t\right) \right] , \end{aligned}$$
(54)

which is equivalent to the singular solution (46).

Case 5

$$\begin{aligned} L=\frac{1}{4}K^{3}, \quad a_{1}=0, \quad a_{0}=\frac{1}{2}Kb_{0}, \quad a_{-1}=-\frac{1}{2}Kb_{-1}, \quad b_{1}=0, \quad b_{-1}=b_{-1}, \quad b_{0}=b_{0}. \end{aligned}$$
(55)

The result of case 5 follows from the result of case 4 with the interchanges \(a_{1}\leftrightarrow a_{-1},b_{1}\leftrightarrow b_{-1}\) and \(\zeta \leftrightarrow -\zeta\).

5 The soliton ansatz method for solving Eq. (1)

In this section, we determine the 1-soliton solution of Eq. (1) as follows:

5.1 The 1-soliton solutions of Eq. (1)

The 1-soliton solution of Eq. (1) is the ansatz:

$$\begin{aligned} u(x,t)=A\tanh ^{P}\tau , \end{aligned}$$
(56)

with

$$\begin{aligned} \tau =B\left( Kx+Lt\right) , \end{aligned}$$
(57)

where A is the amplitude, B is the inverse width of the soliton, K is the frequency of the soliton and L is the soliton velocity, while the exponent P is the order of the soliton which is unknown at this stage. It is easy to see that

$$\begin{aligned} u_{t}= & {} ABPL\left[ \tanh ^{P-1}\tau -\tanh ^{P+1}\tau \right] , \end{aligned}$$
(58)
$$\begin{aligned} u_{x}= & {} ABPK\left[ \tanh ^{P-1}\tau -\tanh ^{P+1}\tau \right] , \end{aligned}$$
(59)
$$\begin{aligned} u_{xx}= & {} AB^{2}K^{2}P\left[ \left( P-1\right) \tanh ^{P-2}\tau -2P\tanh ^{P}\tau +\left( P+1\right) \tanh ^{P+2}\tau \right] . \end{aligned}$$
(60)

Substituting Eqs. (56)–(60) into Eq. (1) we have

$$\begin{aligned}&-ABPL\left[ \tanh ^{P-1}\tau -\tanh ^{P+1}\tau \right] +\frac{1}{2}A^{2}B^{2}K^{2}P\left[ \left( 3P-1\right) \tanh ^{2P-2}\tau +\left( 3P+1\right) \tanh ^{2P+2}\tau \right] \nonumber \\&\quad -3A^{2}B^{2}K^{2}P^{2}\tanh ^{2P}\tau +2A^{3}BPK\left[ \tanh ^{3P-1}\tau -\tanh ^{3P+1}\tau \right] =0. \end{aligned}$$
(61)

From (61) equating the highest exponents \(3P+1\) and \(2P+2\) give \(P=1.\) Consequently, we get

$$\begin{aligned} 2A^{2}BK\left( BK-A\right) \tanh ^{4}\tau +AB\left( 2A^{2}K-3ABK^{2}+L\right) \tanh ^{2}\tau +AB\left( ABK^{2}-L\right) =0. \end{aligned}$$
(62)

Equating all the coefficients of \(\tanh ^{i}\tau\) \((i=0,2,4)\) to zero, we get

$$\begin{aligned} ABK^{2}-L&= 0, \nonumber \\ 2A^{2}K-3ABK^{2}+L&= 0, \nonumber \\ BK-A&= 0. \end{aligned}$$
(63)

Solving Eq. (63) we have

$$\begin{aligned} A=\pm \sqrt{\frac{L}{K}}, \quad B=\pm \frac{1}{K}\sqrt{\frac{L}{K}}, \end{aligned}$$
(64)

provided that \(LK>0.\)

Now the 1-soliton solution of Eq. (1) is given by:

$$\begin{aligned} u\left( x,t\right) =\sqrt{\frac{L}{K}}\tanh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(65)

which is equivalent to the soliton solution (27).

5.2 Singular 1-soliton solutions of Eq. (1)

We assume that the singular 1-soliton solution has the form:

$$\begin{aligned} u\left( x,t\right) =A\coth ^{P}\tau , \end{aligned}$$
(66)

where P is the order of the singular soliton which is unknown at this stage and \(\tau\) is given by (57). It is easy to see that

$$\begin{aligned} u_{t}= ABPL\left[ \coth ^{P-1}\tau -\coth ^{P+1}\tau \right] , \end{aligned}$$
(67)
$$\begin{aligned} u_{x}= ABPK\left[ \coth ^{P-1}\tau -\coth ^{P+1}\tau \right] , \end{aligned}$$
(68)
$$\begin{aligned} u_{xx}= AB^{2}K^{2}P\left[ \left( P-1\right) \coth ^{P-2}\tau -2P\coth ^{P}\tau +\left( P+1\right) \coth ^{P+2}\tau \right] . \end{aligned}$$
(69)

Substituting Eqs. (66)–(69) into Eq. (1) we have

$$\begin{aligned}&-ABPL\left[ \coth ^{P-1}\tau -\coth ^{P+1}\tau \right] +\frac{1}{2}A^{2}B^{2}K^{2}P\left[ \left( 3P-1\right) \coth ^{2P-2}\tau +\left( 3P+1\right) \coth ^{2P+2}\tau \right] \nonumber \nonumber \\&\quad -3A^{2}B^{2}K^{2}P^{2}\coth ^{2P}\tau +2A^{3}BPK\left[ \coth ^{3P-1}\tau -\coth ^{3P+1}\tau \right] =0. \end{aligned}$$
(70)

From Eq. (70) equating the highest exponents 3\(P+1\) and \(2P+2\) give \(P=1.\) Consequently, we get

$$\begin{aligned} 2A^{2}BK\left( BK-A\right) \coth ^{4}\tau +AB\left( 2A^{2}K-3ABK^{2}+L\right) \coth ^{2}\tau +AB\left( ABK^{2}-L\right) =0. \end{aligned}$$
(71)

From (71) we have

$$\begin{aligned} A=\pm \sqrt{\frac{L}{K}}, \quad B=\pm \frac{1}{K}\sqrt{\frac{L}{K}}, \end{aligned}$$
(72)

provided that \(LK>0.\)

Now the singular 1-soliton solution of Eq. (1) is given by:

$$\begin{aligned} u\left( x,t\right) =\sqrt{\frac{L}{K}}\coth \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(73)

which is equivalent to the singular soliton solution (28).

6 Riccati equation expansion method and \(\left( {\bf G}^{\prime }/{\bf G}\right)\)-expansion method for solving Eq. (1)

In this section, we use the above two methods for finding the solitary wave solutions as well as the trigonometric function solutions of Eq. (1). To this aim, we assume that Eq. (1) has the formal solution

$$\begin{aligned} u\left( x,t\right) =A\phi \left[ \tau (x,t)\right] , \end{aligned}$$
(74)

where \(\phi \left[ \tau (x,t)\right]\) is the amplitude component of the soliton and \(\tau \left( x,t\right) =B\left( Kx+Lt\right)\). A, B, K and L are respectively the amplitude, the width, the frequency and the velocity of the soliton.

Substituting Eq. (74) into Eq. (1), one obtains the following nonlinear ODE:

$$\begin{aligned} -L\phi ^{\prime }+\frac{1}{2}ABK^{2}\phi \phi ^{\prime \prime }+2A^{2}K\phi ^{2}\phi ^{\prime }+ABK^{2}\phi ^{\prime 2}=0, \end{aligned}$$
(75)

where \(^{\prime }=\frac{d}{d\tau }.\)

Eq. (75) can be solved to obtain the soliton amplitude \(\phi \left( \tau \right)\) using the Riccati equation expansion method and \(\left( G^{\prime }/G\right)\)-expansion method, that are shown in details in the following subsections:

6.1 Riccati equation expansion method for solving Eq. (75)

In this subsection, we perform the Riccati equation expansion method to Eq. (75). Suppose that \(\phi \left( \tau \right)\) satisfies the Riccati equation in the form

$$\begin{aligned} \phi ^{\prime }\left( \tau \right) =l_{0}+l_{2}\phi ^{2}\left( \tau \right) , \end{aligned}$$
(76)

where \(l_{0}\) and \(l_{2}\) are real constants. Exact solutions to Eq. (76) are listed in [55] as follows:

figure a

where \(\tau _{0}\) is a constant.

Substituting Eq. (76) into Eq. (75) leads to:

$$\begin{aligned} 2AKl_{2}\left( A+BKl_{2}\right) \phi ^{4}\left( \tau \right) +\left( 2A^{2}Kl_{0}+3ABK^{2}l_{0}l_{2}-l_{2}L\right) \phi ^{2}\left( \tau \right) +l_{2}\left( ABK^{2}l_{0}-L\right) =0. \end{aligned}$$
(81)

According to the homogeneous balance principle, setting the coefficients of each power of \(\phi \left( \tau \right)\) in Eq. (81) to zero gives

$$\begin{aligned} A=\mp l_{2}\sqrt{-\frac{L}{l_{0}l_{2}K}}, \quad B=\pm \frac{1}{K}\sqrt{-\frac{L}{l_{0}l_{2}K}}, \end{aligned}$$
(82)

provided that \(l_{0}l_{2}KL<0.\)

If \(l_{0}l_{2}<0,\) then from (77) we have the soliton solution of Eq. (1) in the form:

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\tanh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) -\frac{\epsilon \ln \tau _{0}}{2}\right] , \quad \text {\ if }\tau _{0}>0, \end{aligned}$$
(83)

which is equivalent to the soliton solutions (Eqs. (27) and (65)).

Also, from Eq. (78) we have the singular soliton solution of Eq. (1) in the form:

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\coth \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) -\frac{\epsilon \ln \left( -\tau _{0}\right) }{2}\right] , \quad \text {\ if }\tau _{0}<0, \end{aligned}$$
(84)

which is equivalent to the singular soliton solutions (28) and (73).

If \(l_{0}l_{2}>0,\) then from Eqs. (79) and (80) the trigonometric periodic solutions of Eq. (1) are given by:

$$\begin{aligned} u(x,t)=-\sqrt{-\frac{L}{K}}\tan \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) +\tau _{0}\right] , \end{aligned}$$
(85)

or

$$\begin{aligned} u(x,t)=\sqrt{-\frac{L}{K}}\cot \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) +\tau _{0}\right] . \end{aligned}$$
(86)

6.2 \(\left( G^{\prime }/G\right)\)-expansion method for solving Eq. (75)

In this subsection, we perform the \(\left( G^{\prime }/G\right)\)-expansion method to Eq. (75). Suppose that \(\phi \left( \tau \right)\) has the formal solution

$$\begin{aligned} \phi \left( \tau \right) =\frac{G^{\prime }\left( \tau \right) }{G\left( \tau \right) }, \end{aligned}$$
(87)

where \(G=G\left( \tau \right)\) satisfies the second order linear differential equation in the form

$$\begin{aligned} G^{\prime \prime }\left( \tau \right) +\lambda G^{\prime }\left( \tau \right) +\mu G\left( \tau \right) =0, \end{aligned}$$
(88)

where \(\lambda\) and \(\mu\) are constants. It is easy to see that

$$\begin{aligned} \phi ^{\prime }\left( \tau \right) =-\left[ \mu +\lambda \phi \left( \tau \right) +\phi ^{2}\left( \tau \right) \right] , \end{aligned}$$
(89)

and

$$\begin{aligned} \phi ^{\prime \prime }\left( \tau \right) =\lambda \mu +\left( \lambda ^{2}+2\mu \right) \phi \left( \tau \right) +3\lambda \phi ^{2}\left( \tau \right) +2\phi ^{3}\left( \tau \right) . \end{aligned}$$
(90)

It is well known that the ratio \((G^{\prime }/G)\) has the following forms:

figure b

where \(c_{1}\) and \(c_{2}\) are arbitrary constants.

Substituting Eqs. (89) and (90) into Eq. (75) leads to:

$$\begin{aligned}&2AK\left( BK-A\right) \phi ^{4}\left( \tau \right) +AK\lambda \left( \frac{7}{2}BK-2A\right) \phi ^{3}\left( \tau \right) +\left[ \frac{3}{2}ABK^{2}(\lambda ^{2}+2\mu )-2A^{2}\mu K+L\right] \phi ^{2}\left( \tau \right) \nonumber \\&\quad +\lambda \left( L+\frac{5}{2}A\mu BK^{2}\right) \phi \left( \tau \right) +\mu \left( L+A\mu BK^{2}\right) =0. \end{aligned}$$
(94)

According to the homogeneous balance principle, setting the coefficients of each power of \(\phi \left( \tau \right)\) in Eq. (94) to zero gives

$$\begin{aligned} A=\pm \sqrt{-\frac{L}{\mu K}}, \quad B=\pm \frac{1}{K}\sqrt{-\frac{L}{\mu K}},\quad \lambda =0, \end{aligned}$$
(95)

provided that \(\mu KL<0.\)

Now, we consider the following cases:

Case1 If \(\lambda ^{2}-4\mu >0,\) that is to say \(\mu <0,\) then from (91), (74) and using (95), we have the hyperbolic solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\left\{ \frac{c_{1}\sinh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] +c_{2}\cosh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] }{c_{1}\cosh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] +c_{2}\sinh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] }\right\} \end{aligned}$$
(96)

Substituting Eqs. (8), (10) and (12) obtained by Peng [21] into Eq. (96), we have the following exact solitary wave solutions of Eq. (1):

If \(\ \left| c_{1}\right| >\left| c_{2}\right| \ne 0,\) then we obtain the soliton solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\tanh \left\{ \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] +sgn(c_{1}c_{2})\psi _{1}\right\} , \end{aligned}$$
(97)

if \(\ \left| c_{2}\right| >\left| c_{1}\right| \ne 0,\) then we obtain the singular soliton solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\coth \left\{ \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] +sgn(c_{1}c_{2})\psi _{1}\right\} , \end{aligned}$$
(98)

where \(\psi _{1}=\tanh ^{-1}(\left| c_{2}\right| /\left| c_{1}\right| ),\) \(\psi _{2}=\coth ^{-1}(\left| c_{2}\right| /\left| c_{1}\right| )\) and \(sgn(c_{1}c_{2})\) is the well-known sign function.

If \(\left| c_{1}\right| >\left| c_{2}\right| =0,\) then we have the soliton solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\tanh \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(99)

which is equivalent to the soliton solutions Eqs. (27), (65) and (83).

If \(\left| c_{2}\right| >\left| c_{1}\right| =0,\) then we have the singular soliton solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{\frac{L}{K}}\coth \left[ \sqrt{\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(100)

which is equivalent the singular soliton solutions (Eqs. (28), (73) and Eq. (84)).

If \(\left| c_{1}\right| =\left| c_{2}\right| ,\) then we have the trivial solution which is rejected.

Case 2 If \(\lambda ^{2}-4\mu <0,\) that is to say \(\mu >0,\) then from Eqs. (92), (74) and using Eq. (95), we have the trigonometric periodic solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{-\frac{L}{K}}\left\{ \frac{c_{1}\cos \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] -c_{2}\sin \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] }{c_{1}\sin \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] +c_{2}\cos \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] }\right\} . \end{aligned}$$
(101)

If we set \(c_{1}=0,\) then we have the trigonometric periodic solution of Eq. (1):

$$\begin{aligned} u(x,t)=-\sqrt{-\frac{L}{K}}\tan \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] , \end{aligned}$$
(102)

while, if we set \(c_{2}=0,\) then we have the trigonometric periodic solution of Eq. (1):

$$\begin{aligned} u(x,t)=\sqrt{-\frac{L}{K}}\cot \left[ \sqrt{-\frac{L}{K}}\left( x+\frac{L}{K}t\right) \right] . \end{aligned}$$
(103)

The solutions (Eqs. (102) and (103)) are equivalent to the trigonometric periodic solutions (Eqs. (85) and (86)).

7 Physical explanations for some solutions

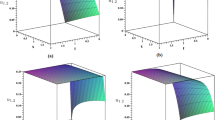
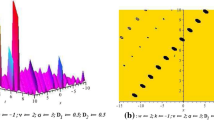
In this section, we illustrate the applications of the results established above. Solitary wave solutions describe different nonlinear waves. These solutions have a remarkable property that keeps its identity upon interacting with other. Using the software Maple, the plots of some obtained solutions have been shown in Figs 1, 2, 3 and 4. For more convenience, the graphical representations of u(x, t) for Eqs. (27), (28), (85) and (86) of Eq. (1) are shown in Figs. 1, 2, 3 and 4 when \(K=1\) and \(-10\le\) \(x,t\le 10\).

Fig. 1
figure 1

Plot the soliton solution (27) when \(L=1\)

Full size image
Fig. 2
figure 2

Plot the singular soliton solution (28) when \(L=1\)

Full size image
Fig. 3
figure 3

Plot the trigonometric periodic solution (85) when \(L=-1,\tau _{0}=0\)

Full size image
Fig. 4
figure 4

Plot the trigonometric periodic solution (86) when \(L=-1,\tau _{0}=0\)

Full size image

8 Conclusions

In this paper, we have applied the modified simple equation method, the exp-function method, the soliton ansatz method, the Riccati equation expansion method and the \(\left( G^{\prime }/G\right)\)-expansion method to calculate the exact solutions, the solitary wave solutions and the trigonometric function solutions for the nonlinear foam drainage equation (Eq. (1)). On comparing our results with the well-known results obtained in [54], we conclude that our results for Eq. (1) are new and not published elsewhere. Further, the different methods used in this paper are powerful and effective techniques in finding the exact traveling wave solutions and the solitary wave solutions for a wide range of nonlinear problems. In Sect. 7, we have given some figures expressing the behavior of the obtained solutions of Eq. (1) which give some perspective readers how the behavior solutions are produced. Finally, our results have been checked with the aid of the Maple by putting them back into the original Eq. (1).