Some analytic models of relativistic compact stars

Abstract

We present charged anisotropic Durgapal IV interior solutions of the general relativistic field equations in curvature coordinates. These exact solutions can be used to model stable and well-behaved compact stars. Using these solutions we have presented models of well-known neutron and quark stars such as PSR J1903+0327, RX-J1856.5-3754, PSR B1913+16, PSR J0737-3039A and Cyg X-2. The equation of state (EoS) corresponding to the modeled objects are studied using their compression moduli. According to our solutions it is found that the EoS for Cyg X-2 (neutron star) is stiffer than any other object presented and therefore more massive. Furthermore, the EoS for RX J1856.5-3754 (Quark star) is the softest one, rendering it least massive. These solutions satisfy all the energy conditions. Finally, all our presented stellar models satisfy the equilibrium condition of Cooperstock and de la Cruz i.e. M ² > Q ².

1 Introduction

In 1916, Schwarzschild constructed the first exterior exact solution of the Einstein field equations (EFEs) for a static and spherically symmetric matter distribution that predicted the existence of a singularity or Black Hole (BH). Later, Schwarzschild himself also constructed the first exact interior solution with constant density. Although this interior solution with constant density seems to be physically insignificant, it is historically important as it is the first interior solution for a bounded configuration. At later stages new parameters or degrees of freedom like the cosmological constant, anisotropic pressure, charge, rotation etc. are introduced into the EFEs. Entirely new classes of interior Schwarzschild-like charged anisotropic solutions have been obtained by Singh and Pant [1]. This particular class of solution are distinct for $p_{r} > p_{ \bot }$, possessing the following salient features: (1) constant stability factor, (2) p _⊥ becomes repulsive near the surface, (3) the causality condition is satisfied everywhere inside the stellar configuration and (4) the solutions feature a non-singular central density which decreases towards the stellar surface. These new interior solutions with charge are matched to the exterior Reissner–Nordström solution.

Efinger [2] has been interested in the behavior of charged particles in general relativity and thus model a static charged sphere. Historically charged solutions of the EFEs do not draw much interest amongst researchers as one expected that the contribution of the electromagnetic field to the behavior of the stellar fluid is negligible. Since the electric field is only along the radial direction, it affects the radial pressure ($p_{r}$) making it different from the transverse pressure (p _⊥). Today it is well known that inclusion of electric charge makes the fluid anisotropic. Interest in the study of anisotropic bounded configurations has received widespread attention (Gron [3], de Leon [4] and Roy et al. [5]).

Buchdahl [6], has derived an upper bound for the compactness parameter M/R beyond which there is a formation of singularity. By making a few physically reasonable assumptions on the matter such as non-increasing density w.r.t. the radial coordinate, a perfect fluid and the exterior solution being the Schwarzschild vacuum solution, he finds the upper bound of the compactness parameter to be 4/9. This is because of the quantity 1 − 2 M/R must be strictly positive. However, this ratio can acquire a minimum value of 1/9. This minimum limit arises from the condition that $g_{00}$ must be non-negative everywhere.

This upper bound is generalized for a charged anisotropic object by Andréasson [7] where he imposes an additional condition $p_{r} + 2p_{ \bot } \le \rho$ and found a sharp bound given as $M/R \le \left[ {1 + \sqrt {1 + 3Q^{2} /R^{2} } } \right]^{2} /9$ called the Buchdahl–Andréasson bound. The radius of all configurations satisfying Buchdahl–Andréasson condition is above the gravitational radius given by $r_{ + } = M + \sqrt {M^{2} - Q^{2} }$. For the case of a neutral configuration Q = 0, we immediately get $r_{ + } = 2M$ which is the Schwarzschild limit. For the case of $Q = R, M/R$ is essentially ≤1. Hence the upper bound gives R = M and the configuration is within a gravitational radius $r_{ + } = M$. The extreme conditions $r_{ + } = R = Q = M$ configuration is of Quasi-Black Holes. From the equation of gravitational radius $r_{ + } = M + \sqrt {M^{2} - Q^{2} }$, it is easily seen that due to the inclusion of electric charge (for Q ≠ 0) makes $r_{ + }$ smaller without the formation of a singularity. Hence we can conclude that inclusion of electric charge inhibits the formation of black hole and thus avoids the mathematical singularity. This very idea is also presented by Ivanov [8] and Bonnor [9]. Mehra [10] has constructed an interior solution that inhibits singularity. Florides [11] has also considered charged perfect fluid solutions that described the interior of bounded configurations.

Cooperstock and de La Cruz [12] have discussed a charged fluid distribution in equilibrium. Their studies show that a necessary condition is to maintain equilibrium of charged configuration: $m(r)^{2} > q(r)^{2}$. This condition can be easily appreciated from the concept of Buchdahl–Andréasson bound and its corresponding gravitational radius. If $m(r)^{2} < q(r)^{2}$ is satisfied, then the gravitational radius $r_{ + }$ becomes non-physical as the term $\sqrt {m(r)^{2} - q(r)^{2} }$ is imaginary.

During the contracting stages of collapsing stars, there would never be any free fall because of the virial theorem, which says that a self-gravitating system would become hotter and emit radiation, Mitra [13]. Consequently, pressure gradient forces would always be present even if a star loses hydrostatic equilibrium. Usually the pressure is of kinetic origin, however for a hot star, there is always some radiation pressure. Even by Newtonian physics, there could be sufficiently hot and massive configurations where hydrostatic equilibrium is maintained almost entirely by radiation pressure rather than kinetic gas pressure. This idea was proposed long back by Hoyle and Fowler, when they postulated that the so-called “Black Holes (BH)” at the center of quasars could be Newtonian super-massive stars supported entirely by radiation pressure (Hoyle and Fowler [14]; Fowler [15]). A virial theorem in general relativity is obtained by Mitra [16] showing that physical gravitational collapse must always be accompanied by emission of radiation and no pressure free or even adiabatic gravitational collapse. Using these concepts Singh and Pant [17] modeled the central engine of a quasar, which turns out to be a huge radiation-supported star (Eddington’s Star) rather than a true BH. Pant and Tewari [18] and Pant and Tewari [19] have also presented similar models of radiating stars. The inclusion of radiation not only makes the model more physically viable but also plays a significant role in avoiding the formation of a singularity or BH.

There have been numerous studies incorporating pressure anisotropy in stellar models, e.g. a solid core composed of type-IIIA superfluid, Kippenhahn and Weigert [20]. Sokolov [21] has suggested that phase transitions from normal states of pions to superconducting states can generate pressure anisotropy. Sawyer [22] has also suggested that a phase transition from normal state of meson to condensate state leads to anisotropy. At such high densities ≈10¹⁵ g cm³, nuclear matter may be anisotropic when its interactions are relativistic [23]. During the post main-sequence of a star, due to flux conservation, its magnetic field is confined in a smaller region and the surface magnetic field reaches up to 10¹¹–10¹³ G when it forms a NS. Weber [24] has suggested that this immense magnetic field may generate pressure anisotropy. Furthermore a strong magnetic field may affect the transport coefficients and may render transport properties anisotropic. This can lead to anisotropy in pressure as well, Yakovlev [25, 26]. If the magnetic field exceeds 10¹⁸–10¹⁹ G, the virial theorem is violated leading to dynamical instability during hydrostatic equilibrium [27]. In other words, the magnetic energy must not exceed the gravitational binding energy i.e. B ² R ³/6 ≤ 3GM ²/5R.

The possible existence of stable quark stars is discussed by Baym and Chin [28], Keister and Kisslinger [29]. Witten [30] has pointed out that $Fe^{56}$ is not the true ground state of the hadrons where nuclear fusion stops at the stages of post-main sequences. Witten [30] has argued that there is in fact no NS at all. Strange matter consisting roughly of equal numbers of u, d and s quarks with small amount of electrons to guarantee charge neutrality, is absolutely stable at densities comparable to atomic nuclei. They can exist in lumps of size ranging from a few fm to strange stars of radius ~10 km.

Recently, many articles have been presented not only for charged configuration but also include pressure anisotropy. Dev and Gleiser [31, 32], Marcelo and Dev [33] have shown that the presence of anisotropic pressures in charged matter enhances the stability of the configuration under radial adiabatic perturbations as compared to isotropic matter. Herrera and Santos [34] have also discussed an anisotropic model that can be a stable configuration if $- 1 \le v_{ \bot }^{2} - v_{r}^{2} \le 0$. There have been several recent investigations of bounded fluid configuration incorporating charge and pressure anisotropy: Pradhan and Pant [35], Singh et al. [36, 37], Pant et al. [38] and Maharaj and Govender [39, 40]. The study of charged stellar configurations in the presence of pressure anisotropy and an equation of state are studied by several authors utilizing curvature coordinates (Takisa et al. [41], Takisa and Maharaj [42], Maharaj et al. [43], Sunzu et al. [44, 45]). Charged compact stars obeying a linear equation of state and pressure anisotropy is discussed by Ngubelanga et al. [46]. Utilising isotropic coordinates and a transformation due to Kustaanheimo and Qvist [47], they are able to derive exact solutions of the EFE’s for charged, static spheres which have accounted for the observed masses of strange star candidates. These results are later generalized to include a quadratic equation of state (Ngubelanga and Maharaj [48]).

2 Conditions for well-behaved solutions

In order to generate physically viable solutions describing anisotropic fluid spheres the following conditions should be satisfied:

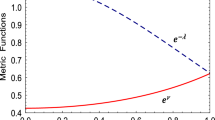
• 1. The solution should be free from physical and geometric singularities; i.e. it should yield finite and positive values of the central pressure, central density and nonzero positive value of $e^{\nu } \left. \right|_{r = 0}$ and $e^{\lambda } \left. \right|_{r = 0} = 1$.

• 2. Following Bondi [49] and Esculpi et al. [50], the solution should have positive value for ratio of trace of energy stress tensor to energy density (p _r  + 2p _⊥)/c ² ρ, and less than 1 (weak energy condition) and less than 1/3 (strong energy condition) throughout the interior of star, decreasing monotonically outward.

• 3. The casualty condition should be obeyed i.e. velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing towards the surface i.e. $\frac{d}{dr}\frac{{dp_{r} }}{d\rho } < 0$ or $\frac{{d^{2} p_{r} }}{{d\rho^{2} }} > 0$ and $\frac{d}{dr}\frac{{dp_{ \bot } }}{d\rho } < 0$ or $\frac{{d^{2} p_{ \bot } }}{{d\rho^{2} }} > 0$ for 0 ≤ r ≤ r _b i.e. the velocity of sound is increasing with the increase of density and it should be decreasing outwards.

• 4. $\frac{{dp_{r} }}{d\rho } \ge \frac{{p_{r} }}{\rho }$ should be satisfied everywhere within the ball. The adiabatic index, $\gamma = \frac{{p_{r} + \rho }}{{p_{r} }} \frac{{dp_{r} }}{d\rho }$ for realistic matter should be γ > 1.

• 5. The red shift z should be positive, finite and monotonically decreasing in nature with the increase in r.

• 6. Electric field intensity E, such that $E_{r = 0} = 0$, is taken to be monotonically increasing. The proper charges density $\sigma (r)$ also has to be well behaved in the interior.

• 7. The anisotropy factor $\varDelta$ should be zero at the center and increasing towards the surface.

• 8. For a stable anisotropic compact star, $- 1 \le v_{ \bot }^{2} - v_{r}^{2} \le 0$ must be satisfied, Herrera and Santos [34].

• 9. For realistic stars, the compression modulus $k_{e} = \gamma p_{r}$ must be decreasing outwards.

3 Einstein–Maxwell field equations of anisotropic charged fluid distributions

The interior metric of a static spherically symmetric matter distribution in curvature coordinates is given by,

$$ ds^{2} = c^{2} e^{\nu \left( r \right)} dt^{2} - e^{\lambda \left( r \right)} dr^{2} - r^{2} \left( {d\theta^{2} + \sin^{2} \theta d\phi^{2} } \right) $$

(1)

The Einstein–Maxwell field equations for a charged and anisotropic fluid distribution are given as

$$ R_{\xi }^{\mu } - \frac{1}{2} R g_{\xi }^{\mu } = - \frac{8\pi G}{{c^{4} }} T_{\xi }^{\mu } $$

(2)

The quantity $T_{\xi }^{\mu }$ is the energy–momentum tensor

$$ T_{\xi }^{\mu } = \left[ {\left( {p_{ \bot } + \rho c^{2} } \right) v^{\mu } v_{\xi } - p_{ \bot } \delta_{\xi }^{\mu } + \left( {p_{r} - p_{ \bot } } \right) \chi_{\xi } \chi^{\mu } + \frac{1}{4\pi } \left( { - F^{\mu \alpha } F_{\xi \alpha } + \frac{1}{4}\delta_{\xi }^{\mu } F_{\alpha \beta } F^{\alpha \beta } } \right)} \right] $$

(3)

where $R_{\xi }^{\mu }$ is Ricci tensor, T ^μ _ξ is energy–momentum tensor, R the scalar curvature, $F^{\alpha \beta }$ is the electromagnetic field tensor, p _r and $p_{ \bot }$ denotes radial and transverse pressure, ρ the density distribution, $v_{i}$ the four velocity and $\chi_{j}$ is the unit space-like vector in radial direction. The energy–momentum tensor can be represented by a matrix as given below:

$$ T_{\xi }^{\alpha } = \left[ {\begin{array}{*{20}l} {\rho c^{2} + E^{2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - p_{r} + E^{2} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - p_{ \bot } - E^{2} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - p_{ \bot } - E^{2} } \hfill \\ \end{array} } \right] $$

(4)

Here $E = q(r)/r^{2}$ represents the electric field intensity due to the presence of electric charge. The quantity $F_{\xi }^{\alpha }$ is the electromagnetic field tensor defined by

$$ F_{\xi }^{\alpha } = \frac{{\partial A^{\alpha } }}{{\partial x^{\xi } }} - \frac{{\partial A^{\xi } }}{{\partial x^{\alpha } }} $$

(5)

satisfying the Maxwell’s equations given as

$$ \frac{1}{{\sqrt { - g} }} \frac{\partial }{{\partial x^{\alpha } }} \left( {\sqrt { - g} F_{\xi }^{\alpha } } \right) = - 4\pi j_{\xi } \quad {\text{and}}\quad F_{;\xi }^{\alpha \beta } + F_{;\alpha }^{\beta \xi } + F_{;\beta }^{\xi \alpha } = 0 $$

(6)

Here the quantity g is the determinant of $g_{\xi }^{\alpha } , A^{\mu } = \left( {\varphi \left( r \right),0,0,0} \right)$ with $\varphi (r)$ is the magnetic scalar potential. Also the $j_{\xi }$ is the 4-current density and defined by

$$ j_{ }^{\xi } = \frac{\sigma }{{\sqrt {g_{00} } }} \frac{{dx^{\xi } }}{{dx^{0} }} $$

(7)

where $\sigma$ is the proper charge density. For a static fluid configuration, the non-zero components of the four-current density is $j^{0}$ and function of r only because of spherical symmetry. From Eq. (6) we get

$$ F^{01} = - e^{{\left( {\nu + \lambda } \right)/2}} \frac{q(r)}{{r^{2} }}\quad {\text{with}}\quad q(r) = 4\pi \mathop \int \limits_{0}^{r} e^{\lambda /2} \sigma \psi^{2} d\psi $$

(8)

For the metric Eq. (1), the Einstein–Maxwell field equations reduce to the following system:

$$ \kappa p_{r} = \frac{{\nu^{{\prime }} }}{r} e^{ - \lambda } - \frac{{1 - e^{ - \lambda } }}{{r^{2} }} + \frac{{q^{2} }}{{r^{4} }} $$

(9)

$$ \kappa p_{ \bot } = e^{ - \lambda } \left( {\frac{{\nu^{{\prime \prime }} }}{2} {-}\frac{{\lambda^{{\prime }} \nu^{{\prime }} }}{4} + \frac{{\nu^{'2} }}{4} + \frac{{\nu^{{\prime }} - \lambda^{{\prime }} }}{2r}} \right) - \frac{{q^{2} }}{{r^{4} }} $$

(10)

$$ \kappa \rho = \frac{{\lambda^{{\prime }} }}{r} e^{ - \lambda } + \frac{{1 - e^{ - \lambda } }}{{r^{2} }} - \frac{{q^{2} }}{{r^{4} }} $$

(11)

$$ \sigma (r) = \frac{{e^{ - \lambda /2} }}{{4\pi r^{2} }} \left( {r^{2} E} \right)^{'} $$

(12)

where a prime (′) denotes differentiation w.r.t. the radial coordinate, κ = 8πG/c ⁴ and q is the charge enclosed within a sphere of radius r. By assuming $e^{ - \lambda } = Y, e^{\nu } = B\left( {1 + x} \right)^{4}$ (Durgapal [51]) with $x = c_{1} r^{2}$, Eqs. (9) and (10) reduce to

$$ \frac{dY}{dx} + \frac{{7x^{2} - 2x - 1}}{{x\left( {1 + 5x} \right) \left( {1 + x} \right)}} Y + \frac{ x + 1}{{ \left( {1 + 5x} \right)}} \left( {\frac{1}{x } - \frac{\varDelta }{{c_{1} }} - \frac{{2E^{2} }}{{c_{1} }}} \right) = 0\quad {\text{where}}\quad \varDelta = \kappa \left( {p_{ \bot } - p_{r} } \right). $$

(13)

4 A new class of solutions

To solve Eq. (13) we assume that

$$ \frac{\varDelta }{{c_{1} }} = \frac{{\delta x\left( {1 + 5x} \right)^{ - 2s} }}{{\left( {1 + x} \right)^{3} }} \;\frac{{E^{2} }}{{c_{1} }} = \frac{{c_{1} q^{2} }}{{x^{2} }} = \frac{{Kx \left( {1 + 5x} \right)^{ - 2n} }}{{\left( {1 + x} \right)^{3} }} $$

(14)

Here $\delta , K \ge 0$ are the measure of the anisotropy and charge respectively. We have assumed the anisotropy and electric field intensity in such a way that Eq. (13) is integrable and the solutions are well-behaved. Also anisotropy and electric field intensity must be increasing from the center to the surface in order to obtain physically acceptable solutions. Choosing such forms of anisotropy and electric field in Eq. (14) makes the solutions comparatively simpler. Moreover, the choices in Eq. (14) ensure that the resulting solutions of Eq. (13) are physically viable. With these choices the solutions of Eq. (13) are

$$ Y(x) = \frac{1}{{\left( {x + 1} \right)^{2} }} \left[ {\frac{{7 - 10x - x^{2} }}{7} + \frac{{\delta x \left( {1 + 5x} \right)^{ - 2s} }}{2 - 10s} + \frac{{Kx \left( {1 + 5x} \right)^{ - 2n} }}{2 - 10n}} \right] + \frac{{A x\left( {1 + 5x} \right)^{ - 2/5} }}{{\left( {x + 1} \right)^{2} }} $$

(15)

Now the pressures, density and proper charge density reduce to

$$ \begin{aligned} \frac{\kappa}{{c_{1} }} p_{r} = & - \frac{{16\left( {x^{2} + 7x - 2} \right)}}{{7\left( {1 + x} \right)^{3} }} + \frac{{A\left( {7x - 1} \right)}}{{\left( {1 + x} \right)^{3} \left( {1 + 5x} \right)^{{\frac{2}{5}}} }} - \frac{{\delta \left( {1 + 9x} \right)\left( {1 + 5x} \right)^{ - 2s} }}{{\left( {10s - 2} \right)\left( {1 + x} \right)^{3} }} \\ \quad & + \;\frac{{K\left( {5nx - 10x - 1} \right) \left( {1 + 5x} \right)^{ - 2n} }}{{\left( {10n - 2} \right)\left( {1 + x} \right)^{3} }} \\ \end{aligned} $$

(16)

$$ \frac{\kappa}{{c_{1} }} p_{ \bot } = \frac{\kappa}{{c_{1} }} p_{r} + \frac{{\delta x\left( {1 + 5x} \right)^{ - 2s} }}{{\left( {1 + x} \right)^{3} }} $$

(17)

$$ \begin{aligned} \frac{\kappa}{{c_{1} }} \rho c^{2} & = \frac{{8\left( {x^{2} + 2x + 9} \right)}}{{7\left( {1 + x} \right)^{3} }} + \frac{{A\left( {19x^{2} + 2x - 1} \right)}}{{\left( {1 + x} \right)^{3} \left( {1 + 5x} \right)^{7/5} }} - \frac{{\delta \left( {20sx^{2} + 5x^{2} + 20sx - 14x - 3} \right)}}{{\left( {10s - 2} \right)\left( {1 + x} \right)^{3} \left( {1 + 5x} \right)^{2s + 1} }} \\ & \quad + \;\frac{{K\left( {45nx^{2} + 25nx - 15x - 3} \right)}}{{\left( {10n - 2} \right)\left( {1 + x} \right)^{3} \left( {1 + 5x} \right)^{2n + 1} }} \\ \end{aligned} $$

(18)

$$ \sigma (x) = \frac{{c_{1} \sqrt K }}{4\pi } Y(x) \left( {\frac{{3 - 5\left( {2n - 3} \right)x - 10nx^{2} }}{{\left( {1 + x} \right)^{5/2} \left( {1 + 5x} \right)^{n + 1} }}} \right) $$

(19)

By differentiating Eqs. (16)–(18) with respect to x we get

$$ \frac{\kappa}{{c_{1} }}\frac{{dp_{r} }}{dx} = \frac{{16\left( {x^{2} + 12x - 13} \right)}}{{7\left( {1 + x} \right)^{4} }} - \frac{{12A\left( {7x^{2} - 2x - 1} \right)}}{{\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{{\frac{7}{5}}} }} - K f_{1} \left( x \right) + \delta f_{2} (x) $$

(20)

$$ \frac{\kappa}{{c_{1} }}\frac{{dp_{ \bot } }}{dx} = \frac{\kappa}{{c_{1} }}\frac{{dp_{r} }}{dx} - \delta \left[ {\frac{{10\left( {1 + s} \right)x^{2} + \left( {10s - 3} \right)x - 1}}{{\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{2s + 1} }}} \right] $$

(21)

$$ \frac{{\kappa c^{2} }}{{c_{1} }}\frac{d\rho }{dx} = K f_{3} \left( x \right) + \delta f_{4} \left( x \right) - f_{5} \left( x \right) - \frac{{4A\left( {51x^{3} - x^{2} - 13x - 3} \right)}}{{\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{{\frac{12}{5}}} }} $$

(22)

where

$$ f_{1} (x) = \frac{{7 + 15x - 100x^{2} + 50n^{2} x\left( {1 + x} \right) - 5n\left( {10x^{2} + 25x + 3} \right)}}{{\left( {10n - 2} \right)\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{2s + 1} }} $$

(23)

$$ f_{2} (x) = \frac{{5s\left( {9x^{2} + 10x + 1} \right) + 45x^{2} - 6x - 3}}{{\left( {5s - 1} \right)\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{2s + 1} }} $$

(24)

$$ f_{3} (x) = \frac{{5n\left( {90x^{3} + 9x^{2} - 44x - 11} \right) + 50n^{2} x\left( {9x^{2} + 14x + 5} \right) - 9\left( {1 + 5x} \right)^{2} }}{{\left( {10n - 2} \right)\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{2n + 1} }} $$

(25)

$$ f_{4} (x) = \frac{{5s\left( {25x^{3} + 3x^{2} - x - 3} \right) + 100s^{2} x^{2} \left( {1 + x} \right) + 25x^{3} + 35x^{2} - 29x - 15}}{{\left( {5s - 1} \right)\left( {1 + x} \right)^{4} \left( {1 + 5x} \right)^{{2\left( {s + 1} \right)}} }} $$

(26)

$$ f_{5} (x) = \frac{{8\left( {10x^{4} + 40x^{3} + 61x^{2} + 46x + 33} \right)}}{{7\left( {1 + x} \right)^{4} }} $$

(27)

5 Properties of the new solutions

The central pressures and density are non-singular finite positive numbers, which are necessary for a physical system and are given as

$$ \left[ {\frac{\kappa}{{c_{1} }} p_{r} } \right]_{r = 0} = \left[ {\frac{\kappa}{{c_{1} }} p_{ \bot } } \right]_{r = 0} = \frac{32}{7} = \frac{K}{10n - 2} - \frac{\delta }{10s - 2} - A > 0 $$

(28)

This gives an upper limit on A as

$$ A < \frac{32}{7} - \frac{K}{10n - 2} - \frac{\delta }{10s - 2} $$

(29)

The central density can be shown to be a finite value

$$ \left[ {\frac{\kappa}{{c_{1} }} \rho c^{2} } \right]_{r = 0} = \frac{72}{7} - \frac{3K}{10n - 2} + \frac{3\delta }{10s - 2} - A > 0 $$

(30)

The proper charge density possesses a finite value at the center of the star and thus well behaved i.e.

$$ \sigma (r = 0) = \frac{{3c_{1} \sqrt K }}{4\pi } > 0 $$

(31)

It can also be shown that the pressures and density decrease from the centre to the surface i.e.

$$ \left[ {\frac{\kappa}{{c_{1} }}\frac{{d^{2} p_{r} }}{{dx^{2} }}} \right]_{r = 0} < 0 ;\quad \left[ {\frac{\kappa}{{c_{1} }}\frac{{d^{2} p_{ \bot } }}{{dx^{2} }}} \right]_{r = 0} < 0 ;\quad \left[ {\frac{{\kappa c^{2} }}{{c_{1} }}\frac{{d^{2} \rho }}{{dx^{2} }}} \right]_{r = 0} < 0 $$

(32)

Further the square of speed of sound may be found as

$$ v_{r}^{2} = \frac{{dp_{r} }}{d\rho } ;\quad v_{ \bot }^{2} = \frac{{dp_{ \bot } }}{d\rho } $$

(33)

In order to ensure that the causality condition is obeyed we must have $v_{r}^{2} /c^{2} < 1$ and v ²_⊥ /c ² < 1. For a stable configuration under radial perturbation, the stability factor must satisfy $- 1 \le v_{ \bot }^{2} - v_{r}^{2} \le 0$ [33]. The expression for gravitational red-shift and adiabatic index can be written as

$$ z = e^{ - \nu /2} - 1 = \frac{{\left( {1 + x} \right)^{ - 2} }}{\sqrt B } - 1 ;\quad \gamma = \frac{{\left( {p_{r} + \rho } \right)}}{{p_{r} }} \frac{{dp_{r} }}{d\rho } $$

(34)

Since the central value of gravitational red-shift should be non-zero positive finite, we have a constraint on B as $0 < \sqrt B < 1$. In order to compare the stiffness or softness of the corresponding EoSs obtained from our solutions; the best way is to compare the compression moduli, $\kappa_{e}$ defined as (Haensel et al. [52])

$$ k_{e} = \gamma p_{r} $$

(35)

Since we expect the core of the star to be more compact, the value of compression modulus must be highest at the center and decreases outwards.

6 Boundary conditions

The interior solution of a charged stellar model is expected to match smoothly and continuously with the exterior Reissner–Nordström solution given by

$$ ds^{2} = \left( {1 - \frac{2GM}{{c^{2} r}} + \frac{{e^{2} }}{{r^{2} }}} \right)c^{2} dt^{2} - \left( {1 - \frac{2GM}{{c^{2} r}} + \frac{{e^{2} }}{{r^{2} }}} \right)^{ - 1} dr^{2} - r^{2} \left( {d\theta^{2} + \sin^{2} \theta d\varphi^{2} } \right) $$

(36)

where M and e are the mass and total electric charge respectively of the stellar object as seen by an external observer.

At the boundary of the star, M is the mass of the fluid ball as determined by the external observer and $r \ge r_{b}$ is the radial coordinate of the exterior region. Since Eq. (36) is considered as the exterior solution, we shall arrive at the following conclusions by matching with Eq. (1):

$$ e^{{\nu_{b} }} = \left( {1 - \frac{2GM}{{c^{2} r_{b} }} + \frac{{e^{2} }}{{r_{b}^{2} }}} \right) = B(1 + X)^{4} $$

(37)

$$ e^{{ - \lambda_{b} }} = \left( {1 - \frac{2GM}{{c^{2} r_{b} }} + \frac{{e^{2} }}{{r_{b}^{2} }}} \right) = Y(X) $$

(38)

Here $X = c_{1} r_{b}^{2}$ and $q(r = r_{b} ) = e$. For a vacuum exterior the internal radial pressure must vanishing at the surface i.e.

$$ p_{r} (r = r_{b} ) = 0 $$

(39)

Using Eq. (39), we can determine the constant of integration A

$$ A = \frac{{\left( {1 + 5X} \right)^{2/5} }}{7X - 1} \left[ {\frac{{16\left( {X^{2} + 7X - 2} \right)}}{7} - \frac{{K \left( {5nX - 10X - 1} \right)}}{{\left( {10n - 2} \right)\left( {1 + 5X} \right)^{2n} }} + \frac{{\delta \left( {1 + 9X} \right)}}{{\left( {10s - 2} \right)\left( {1 + 5X} \right)^{2s} }}} \right] $$

(40)

Using Eqs. (37) and (38), we can determine the second constant of integration B

$$ B = \frac{1 }{{\left( {X + 1} \right)^{6} }} \left[ {\frac{{7 - 10X - X^{2} }}{7} + \frac{{KX\left( {1 + 5X} \right)^{ - 2n} }}{2 - 10n} + \frac{{\delta X\left( {1 + 5X} \right)^{ - 2s} }}{2 - 10s}} \right] + \frac{{AX\left( {1 + 5X} \right)^{ - 2/5} }}{{\left( {1 + X} \right)^{6} }} $$

(41)

Using Eq. (37) the mass of the stellar system can be found as

$$ M = \frac{{c^{2} r_{b} }}{2G} \left[ {1 - B\left( {1 + X} \right)^{4} + \frac{{KX^{2} \left( {1 + 5X} \right)^{ - 2n} }}{{2\left( {1 + X} \right)^{3} }}} \right] $$

(42)

Over and above the discussions for physically acceptable solutions, one should also check whether the energy conditions are satisfied or not. Our presented solutions need to satisfy all the energy conditions, such as Null Energy Condition (NEC), Weak Energy Condition (WEC), Strong Energy Condition (SEC) and Dominant Energy Condition (DEC) throughout the interior region:

$$ \begin{aligned} & \rho + p_{r} \ge 0;\quad \rho + p_{ \bot } \ge 0; \rho \ge 0; \quad \rho + p_{r} + 2p_{ \bot } \ge 0; \quad \\ & \rho \ge \left| {p_{ \bot } } \right|\& \left| {p_{r} } \right|;\quad \rho + E^{2} \ge 0;\quad \rho + p_{ \bot } + E^{2} \ge 0;\quad \rho + 2p_{ \bot } + p_{r} + E^{2} \ge 0 \\ \end{aligned} $$

(43)

7 Results and discussions

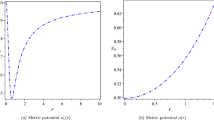
It has been observed that the physical parameters ($p_{r} , p_{ \bot } , \rho , p_{r} /\rho c^{2} , p_{ \bot } /\rho c^{2} , v_{r}^{2} , v_{ \bot }^{2} , z$, energy conditions, $k_{e}$ and $(p_{r} + 2p_{ \bot } )/\rho c^{2} )$ are positive at the center and within the limits of a realistic equation of state and monotonically decreasing (Figs. 1, 3–7). Furthermore, the anisotropic parameter, electric field and adiabatic index possess minimum at the center and increase outward (Figs. 2 and 6). Thus the solutions are well behaved for all values of $X, k$ and δ. By changing these parameters, we can model many different types of ultra-cold compact stars. We also note from Fig. 8, the stability parameter satisfies the stability condition $- 1 \le v_{ \bot }^{2} - v_{r}^{2} \le 0$, which means that our presented solution for Cyg X-2 and all other models of compact stars are stable. The proper charge density is finite at the center and decreasing outward indicating the well-behaved nature (Fig. 9).

Fig. 1

Variation of pressures with radius for Cyg X-2

Fig. 2

Variation of anisotropy and electric field intensity with radius for Cyg X-2

Fig. 3

Variation of pressure to energy density ratio with radius for Cyg X-2

Fig. 4

Variation of $v^{2} /c^{2}$ with radius for Cyg X-2

Fig. 5

Variation of compression modulus, red-shift and ratio of trace of energy stress tensor to energy density with radius for Cyg X-2

Fig. 6

Variation of NEC, WEC, SEC, DEC, density and adiabatic index with radius for Cyg X-2

Fig. 7

Variation and comparison of compression moduli for the presented models of few compact objects

Fig. 8

Variation of stability factor with radius for Cyg X-2

Fig. 9

Variation of proper charge density with radius for Cyg X-2

The M–R diagram in Fig. 10 signifies that for increasing radius, the mass of the compact star increases linearly till up to a certain configuration. However, beyond this radius, the mass seems to saturate and increases in very small increments. Referring to the Fig. 4, one interesting fact of the presented solution for Cyg X-2 is that the square of velocity of sound v ² _r and $v_{ \bot }^{2}$ are constant up to some fraction of radius from center to about 0.2 (~1.66 km) and decrease very rapidly beyond this point. The constant velocity of sound may be interpreted as the nature of quark core exhibiting similarity with the MIT Bag model of non-interacting quark matter. Moreover the constant behavior of the velocity of sound implies that the quark core is highly compact and almost of uniform density (i.e. $\rho_{0} = 1.48 \times 10^{15} \;{\text{g }}\;{\text{cm}}^{ - 3}$ and $\rho \left( {r = 1.66 \;{\text{km}}} \right) = 1.44 \times 10^{15} \;{\text{g }}\;{\text{cm}}^{ - 3} ).$

Fig. 10

Variation of mass with radius

Moreover, from Fig. 4, it is clear that $v_{r}^{2} \approx v_{ \bot }^{2}$ from a fraction of radius around 0.8 (≡6.65 km) up to the surface. This can be easily explained if we refer to Fig. 2 where the anisotropy factor Δ is almost constant from a fraction of radius around 0.8 till up to the surface. Therefore $d\varDelta /dx$ is very small or almost zero, leading to $v_{r}^{2} \approx v_{ \bot }^{2}$. Our finding points to Cyg X-2 having a quark core allowing us to propose that Cyg X-2 to be a “Hybrid Star”.

In Table 1 we have presented some physical quantities of NS and QS models based on our solutions. Here we have given masses, radii, central densities, minimum time period of rotation and central pressures for the corresponding compact stars. In Fig. 7, Cyg X-2 has the highest $\kappa_{e}$ and decreases rapidly, which may be because Cyg X-2 has a quark core. For all the presented stars, the mass to charge ratio M/Q is more than one (Table 1) showing that $M^{2} > Q^{2}$, which is required for equilibrium configuration as given by Cooperstock and de la Cruz [12].

Table 1 Calculated masses, radii, central densities and pressures, mass to charge ratios and minimum period of rotation of few well known compact star candidates

Our presented models of super dense quark stars and neutron stars are based on the assumptions that the surface density for quark star is $\rho_{b} = 4.6888 \times 10^{14} \;{\text{g }}\;{\text{cm}}^{ - 3}$ and for neutron star is $\rho_{b} = 2.7 \times 10^{14} \;{\text{g }}\;{\text{cm}}^{ - 3}$. The parameters for PSR J1903+0327 are $n = 0.1,$ $s = 0.284, K = 0.1, \delta = 0.4$ and $X = 0.23$. The observed mass is in agreement with the experimentally observed value of $1.667 \pm 0.021\;{\text{M}}_{ \odot }$ as mentioned by Freire et al. [53].

For RX J1856.5-3754, the related parameters are $n = 0.304, s = 0.29, K = 0.961,$ δ = 0.118 and $X = 0.17$. The observed mass is between 0.5 and 1 ${\text{M}}_{ \odot }$ and radius within the range of 3.8–8.2 km, Kohri et al. [54], which is in agreement with our presented models. PSR B1913 + 16 can be modeled using the parameters as $n = 0.304, s = 0.29, K = 0.857,$ δ = 0.118 and $X = 0.17$. Its observed mass is $1.4398 \pm 0.0002 \;{\text{M}}_{ \odot }$ as given by Weisberg et al. [55] and is also in agreement with our model.

The parameters with values $n = 0.304.\,s = 0.29, K = 0.921, \delta = 0.1$ and X = 0.17 may be used to model PSR J0737-3039A. The observed mass according to Burgay et al. [56] is ≤1.35 ${\text{M}}_{ \odot }$ and therefore seems to be quite reasonable with our predictions. Finally the parameters $n = 0.38, s = 0.5, K = 0.4, \delta = 0.3$ and X = 0.245 would be appropriate to model Cyg X-2. Its observed mass is $1.71 \pm 0.21\;{\text{M}}_{ \odot }$ as determined by Casares et al. [57] and found to be well fitted with our exact solution.

8 Conclusions

We have presented a class of solutions of the Einstein–Maxwell field equations which describe bounded charged configurations with anisotropic pressures. We have shown that our solutions can model both NS and QS, and predict observed physical quantities such as masses and radii within acceptable statistical errors. And all the solutions satisfy the Buchdahl–Andréasson condition as well as Cooperstock and de la Cruz condition.