1 Introduction

General Relativity (GR) refers to infinite space curvature (singularity) in black holes and at early stages of our Universe. Quantum mechanics correctly describing physics at small distances would be able to resolve such singularity problem, where one quantity becomes infinite (undefined) while another one approaches a certain value. As no real good theory for quantum gravity is available so-far, the entitlement of (non)singular begin of our University (Big Bang) without gravity quantization would be seen as an unwarranted claim. The current paper is devoted to clarify this and warns from illusive conclusions based on approaches stemming from consequences of minimal length. These are not the other way around.

Black holes are well-known singular solutions of GR, where considerable matter is concentrated in a tiny space. They are much well characterized than singular Big Bang. Black holes are characterized by mass (M), electric charge (Q), angular momentum (\(\vec{J}\)) [1–3]. For instance, the principle property that specifies Reissner–Nordström black hole from de-Sitter–Schwarzschild-type is the electric charge (Q). Corresponding to quantum geometry, \(S_{BH}=A/4 \ell _{p}^{2}\) [4–7] and the energy density \(\rho =3/2A\), where A is the cross-sectional area of the black hole horizon and \(\ell _{p}=(\hbar G/c^{3})^{1/2}\) is the Planck length.

Various quantum gravity approaches tackle concrete quantum description of some problems in presence of gravitational fields. They estimate a minimal length which is likely related to the Planck scale and modifies the Heisenberg uncertainty principle, i.e. generalized (gravitational) uncertainty principle (GUP) [8, 9]. So-far, GUP has found many implications [10–16]. Nevertheless, GUP can not replace a real good theory for quantum gravity.

Based on various astrophysical observations, energy–momentum relation in \(\gamma \)–TeV-rays and threshold anomalies of ultra-high energy cosmic ray, the Lorentz invariance violation [17–20], where the velocity of light (c) should differ from the maximum attainable velocity of a material [9] could be confirmed. This inters the literature as modified dispersion relations (MDR) [21–30].

With emergent cosmic space, a special type of the Universe evolution is meant that having the following properties:

  • almost static at the very beginning, i.e. \(t\rightarrow -\infty \) but becomes isotropic and homogeneous at large scales, and

  • ever existing, i.e. no timelike singularity took place.

The resulting Universe was/is large enough to apply even classical description of spacetime and may be described by some exotic matter equation-of-states. The latter likely violates the energy conservation. Last but not least, the acceleration of the Universe expansion agrees well with the recent measurements on high redshift type Ia supernovae. The scale factor that satisfies this type of the Universe evolution is given as

$$ a(t) = a_0 \left[ \lambda +\exp \left( \mu \, T_1\right) \right] ^n. $$
(1)

\(\lambda >0\) to avoid timelike singularity. \(a_0>0\) to assure positive scale factor, i.e. an expanding Universe. The same role is played by \(n>0\). \(T_1=t-\tau \) is introduced by the fractional action cosmology (FAC). In light of this, it is not surprising to have non-singular begin, i.e. Big Bang, and infinite end from the assumption of an emergent cosmic space [31].

For the sake of completeness, we recall that the scale factor expressed as power law, such as

$$ a(t) = T_1^{n},$$
(2)

which leads to a slower expansion than that of an emergent (and the other FAC’s logamediate and intermediate) scenario.

In the present work, we systemically analyse the dependence of the modified Landau–Raychaudhuri equations in a large class of spacetimes and in dependence on various equations-of-states, etc. We implement different approaches for GUP and MDR. For detailed calculations of thermodynamics of three black hole metrics and their connections to Friedmann equation, the readers are advised to consult Ref. [32, 33]. We have estimated the corresponding Friedmann equations and then applied these to Landau–Raychaudhuri equations in emergence of cosmic space framework from fixed point method [31]. We aim to highlight the very strong model-dependence of singularity-treatments based on GUP and MDR approaches. The connections between current paper and references [32, 33] are that the latter presents background for the earlier, i.e. that of modified Landau–Raychaudhuri-equations and (non)singularity Big Bang. The current paper deals with the possible modifications on Landau–Raychaudhuri equations and their (non)singularities due to many matrices, different GUP/MDR approaches and various equations-of-state.

A very short reminder about GUP and MDR approaches is given in Sect. 2. In Sect. 3.1, we compute the modified thermodynamic quantities and the corresponding Friedmann equation in four dimensional de Sitter–Schwarzschild black hole. Section 3.2 is devoted to four dimensional Reissner–Nördstrom black hole. The calculations for Garfinkle–Horowitz–Strominger black hole are elaborated in Sect. 3.3. Detailed calculations are available in Refs. [32, 33]. The present work introduces modifications of Landau–Raychaudhuri equations in Sect. 4. Assuming that the cosmic background geometry is filled with various types of relativistic equations-of-states, we study the time derivative of Hubble parameter, dH/dt versus H for quadratic and linear GUP and MDR approaches in Sect. 5. The final conclusion are detailed in Sect. 6. The nonsingular solutions are strongly depending on metric types, equations of state, and quantum gravity approaches.

2 Short reminder about minimal length and maximal momentum approaches

There are various approaches for the measurable minimal length and the maximal momentum [9, 32, 33]. They have some indirect analogies with quantum gravity approaches, for instance, the phase space can be discretized. For a recent extensive review on GUP and MDP approaches and their implications, see Refs. [8, 9].

  • Quadratic GUP: quadratic order of momentum implemented a minimal length \(\delta x_0 \approx \hbar \alpha \) is presented as [9],

    $$ \delta x\, \delta p\ge \frac{\hbar }{2}\left[ 1+ \alpha ^{2} \, (\delta p)^{2}\right] , $$
    (3)

    where \(\alpha =\alpha _0 \sqrt{1/(M_p\, c^2) }= \alpha _0 l_p /\hbar \) is a constant coefficient referring to the gravitational effects in Heisenberg uncertainty principle. The Hilbert representation on momentum space can be satisfied by space noncommutativity,

    $$\begin{aligned} \hat{x}\, \cdot \psi (p) &= i\, \hbar \, \left( 1+ \alpha ^{2} p^{2}\right) \partial _{p} \, \psi (p), \nonumber \\ \hat{p}\, \cdot \psi (p) &= p_0\, \psi (p). \end{aligned}$$
    (4)

  • Linear GUP: minimal length uncertainty \(\delta x_{0} \approx \hbar \alpha \) and maximum measurable momentum \(p_{max} \approx 1/4\alpha \) are implemented,

    $$ \delta x\, \delta p\ge \frac{\hbar }{2} \left( 1-2\, \alpha \, \delta p +4\, \alpha ^{2} \delta p^{2} \right). $$
    (5)

    The Hilbert representation on momentum space in space noncommutativity,

    $$\begin{aligned} \hat{x}\, \cdot \psi (p)&= i\, \hbar (1 -\alpha {\vec{p}}_{0} +2\, \alpha ^{2}\, p_{0}^{2}) \partial _p\, \psi (p), \nonumber \\ \hat{p}\, \cdot \psi (p)&= p_0\, \psi (p). \end{aligned}$$
    (6)

    The GUP parameter is defined as \(\alpha =\alpha _0/(M_{p} c)=\alpha _0 \ell _p/\hbar \), where \(c,\; \hbar \) and \(M_p\) are speed of light and Planck constant and mass, respectively. The Planck length \(\ell _p\, \approx \, 10^{-35}\) m and the Planck energy \(M_p\, c^2 \,\approx \, 10^{19}\) GeV. \(\alpha _0\) is the proportionality constant. The bounds on \(\alpha _0\), which are summarized in Refs. [32, 34–37], should be a subject of precise astronomical observations, for instance gamma ray bursts [15].

  • MDR approaches [21–30]:

    $$\begin{aligned} \overrightarrow{p}\cdot \overrightarrow{p}=(\overrightarrow{p})^2=f(E,m;\ell _{p})\simeq E^2-\mu ^2+\alpha _1 \ell _{p}^{2} E^4+\alpha _2 \ell _{p}^4 E^6+{\mathcal{O}}\left( \ell _{p}^6 E^8\right) . \end{aligned}$$
    (7)

    The corresponding generalized uncertainty in \({\mathcal {O}}(E^{4})\) can be estimated as follows.

    $$\begin{aligned} E\; \delta x \ge 1- \frac{3 \alpha _{1}}{2} \frac{\ell _{p}^{2}}{(\delta x)^{2}}- \left( \frac{5 \alpha _{2}}{2}-\frac{23 \alpha _{1}^{2}}{8}\right) \frac{\ell _{p}^{4}}{(\delta x)^{4}}. \end{aligned}$$
    (8)

    In natural units, \(\ell _{p}\) can be omitted.

At apparent horizon of Friedmann–Lemaitre–Robertson–Walker (FLRW) Universe, the modified Landau–Raychaudhuri equations due to the correction on the entropy-area relation can be obtained for different types of black holes [38–40].

$$ \left( \dot{H} - \frac{K}{a^{2}} \right) S^{'}(A) = -4 \pi (\rho +p), $$
(9)

where \( S^{'}(A) \equiv dS(A)/dA.\)

3 Modified Friedmann equation

The corrections due to the various GUP and MDR approaches have impacts on Friedmann equation. Detailed calculations are given in Refs. [32, 33]. It is worthwhile to recall that almost the same modifications are found in Landau–Raychaudhuri equations, Sect. 4. To fit with the scope of this paper, we just give the metric element and then jump to modified Friedmann equations.

3.1 De Sitter–Schwarzschild black hole

In GR, the unique spherically symmetric vacuum solution is the Schwarzschild metric [41]

$$\begin{aligned} d s^{2}=-\left( 1-\frac{2M}{r}\right) dt^{2}+\left( 1-\frac{2M}{r}\right) ^{-1} dr^{2}+r^{2}d\Omega ^{2}. \end{aligned}$$
(10)

  • Quadratic GUP: from the corrected entropy-area relation, the modified Friedmann equations can be determined. For apparent horizon of FLRW Universe, the second Friedmann equation can be obtained [38–40]

    $$\begin{aligned}&\left( \dot{H}-\frac{\kappa }{a^{2}}\right) \left[ 1+\frac{\alpha ^{2} \pi }{4} \frac{1}{s} + \left( \frac{\alpha ^{2} \pi }{4} \right) ^2 \frac{1}{2s^2}+\cdots \right] \nonumber \\&\quad = -16\pi \left[ p+\rho + \frac{\alpha ^{2}\pi }{3}\rho ^{2} +2 \frac{(\alpha ^{2}\pi )^2}{27}\rho ^{3}+ \cdots \right] . \end{aligned}$$
    (11)

  • Linear GUP: for apparent horizon of FLRW Universe, we modify Friedmann equation by using corrected entropy-area relation and unmodified entropy \(s=A/4\)

    $$\begin{aligned} \left( \dot{H}+\frac{\kappa }{a^{2}}\right) \left[ 1- \frac{\alpha \sqrt{\pi }}{\sqrt{s}}+ \frac{\left( \alpha \sqrt{\pi } \right) ^2 }{s}+\cdots \right] =-16\pi \left[ p+ \rho -\frac{4 \sqrt{2}}{3 \sqrt{3}} \alpha \sqrt{\pi } \rho ^{3/2} +\frac{1}{3}(\alpha \sqrt{\pi })^{2} \rho ^{2} +\cdots \right] . \end{aligned}$$
    (12)

  • MDR approaches: the second Friedmann equation reads

    $$\begin{aligned}&\left( \dot{H}-\frac{k}{a^{2}} \right) \left[ 1-\frac{3 \alpha _{1}\pi }{8s}-\frac{5 \pi ^{2}}{32s} \left( \alpha _{1}^{2} - 4 \alpha _{2} \right) +\cdots \right] \nonumber \\&\quad =-16 \pi \left[ p+\rho -\frac{\alpha _{1} \pi }{2} \rho ^{2}-\frac{5 \pi ^{2}}{12}\left( \alpha _{1}^{2}-4\alpha _{2}\right) \rho ^{3}+\cdots \right] . \end{aligned}$$
    (13)

3.2 Reissner–Nördstrom black hole

The line element in Reissner–Nordström geometry which has static electrical charged [42, 43] reads

$$\begin{aligned} ds^2= f(r) dt^2 -\frac{dr^2}{f(r)}- r^2 d \Omega ^{2}, \quad f(r)=1-\frac{2M}{r}+\frac{Q^2}{r^2}. \end{aligned}$$
(14)

Two possible outer and inner horizons can be defined [42, 43],

$$\begin{aligned} r=M \pm \sqrt{M^2-Q^2}, \quad r=r_s -\frac{Q^2}{r_s}-\frac{Q^4}{{r_s}^3}. \end{aligned}$$
(15)

Therefore, when the black hole becomes electrically charged, the event horizon shrinks, and another event horizon appears near the singularity. The more charged the black hole is, the closer the two horizons become [38]. As more and more electric charge is thrown into the black hole, the inner event horizon starts to get larger, while the outer horizon starts to shrink [38].

  • Quadratic GUP: according to position uncertainty \(\delta x =r\), Eq. (15), the horizon area \(A =4\pi r_{+}^{2} \) and the condition \(Q\ll r\) should be fulfilled. The modified second Friedmann equation for charged black hole corresponding to the interchange of the quantum entropy, Eq. (9), is given as

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1 +(\alpha \pi )^{2} \left( \frac{1}{4s} + \frac{Q^{2}}{s^{2}}+4\frac{Q^{4}}{s^{3}}\right) +(\alpha \pi )^{4} \left( \frac{1}{8 s^{2}}+ \frac{Q^{2}}{s^{3}}+\frac{Q^{4}}{s^{4}}\right) + \cdots \right] =\,-16 \pi \nonumber \\&\quad\left[ p +\rho + \frac{64}{27} (\alpha \pi )^2 Q^2 \left( \rho ^{3} + 8 Q^2 \rho ^{4} \right) + \frac{512}{27}(\alpha \pi )^4 \left( \frac{\rho ^{3}}{8} + 2 Q^2 \rho ^{4}+ \frac{2 Q^4}{3} \rho ^5 \right) + \cdots \right] . \end{aligned}$$
    (16)

  • Linear GUP: for FLRW Universe, the modified Friedmann equation becomes

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1-2\frac{\alpha \pi }{\sqrt{s}}+\frac{\alpha ^{2}\pi }{s-\pi Q^{2}} - 2 \alpha \pi \frac{\sqrt{\alpha ^{2}\pi +4\pi Q^{2}}\, \sqrt{\alpha ^{2}+2Q^{2}} }{ 4 \pi Q^{2} \sqrt{s}} + \cdots \right] =-16 \pi \nonumber \\&\quad\left[ p+ \rho -\frac{4\sqrt{2}}{3\sqrt{3}} \alpha \, \pi \, \rho ^{3/2}- \frac{\alpha ^{2}}{\pi Q^{2}}\rho \,+ \frac{3 \alpha ^{2}}{8 \pi ^{3}Q^{4}} \ln {\left( \frac{3}{2 \,\rho }\right) }+ \cdots \right] . \end{aligned}$$
    (17)

  • MDR approaches: the second Friedmann equation is given as

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1+\frac{3 \alpha _{1} \pi }{2} \left[ \frac{1+8 \pi Q}{4 s} -\, \frac{3 \pi Q^{2}}{s^{2}}\right] -\, \frac{5 \pi ^{2}}{128} \left( \alpha _{1}^{2}-4 \alpha _{2}\right) \left[ \frac{1}{ s^{2}}+\frac{2 \pi Q}{s^{3}}-\frac{3 \pi ^{2} Q^{2}}{s^{4}}\right] + \cdots \right] \nonumber \\&\quad = -16 \pi \left[ p+\rho +\frac{\alpha _{1} \pi }{2} \left[ (1+24 \pi Q)\rho ^{2}-\, \pi Q^{2} \rho ^{3}\right] +\frac{32}{27}\pi ^{2} (\alpha _{1}^{2} -\,4 \alpha _{2})\left[ \frac{5}{2}\rho ^{3}+\,\frac{5 \pi Q}{16} \rho ^{4} -\,\pi Q^{2} \rho ^{5} \right] +\cdots \right] . \end{aligned}$$
    (18)

3.3 Garfinkle–Horowitz–Strominger black hole

Metric of Garfinkle–Horowitz–Strominger dilatonic black hole is expressed as

$$ ds^{2}=\left( 1-2\frac{M}{r}\right) \, dt^{2}+\, \left( 1-2\frac{M}{r}\right) ^{-1} dr^{2}\,+r(r-2a)\, d\Omega ^{2},$$
(19)

where \(a=Q^{2}e^{-2 \phi } _{0}/2M\).

  • Quadratic GUP:

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1+ \frac{\alpha ^2 \pi }{2} \left( \frac{1}{2s}-\frac{\sqrt{\pi } a}{s^{3/2}} -\frac{\pi a^2}{ s^2}\right) +\left( \frac{\alpha ^2 \pi }{2}\right) ^2 \left( \frac{1}{4 s^2}-\frac{\pi a^2}{ s^3}\right) +\cdots \right] \nonumber \\&\quad =-16 \pi \left[ p+ \rho + \alpha ^{2}\pi \left( \frac{\rho ^2}{3} - \frac{16\sqrt{6 \pi \, a}}{45} \rho ^{5/2} \right)\quad - \frac{64}{27} (\alpha ^{2}\pi )^2 \left( \frac{(\alpha ^2 - 4 a^2)}{4} \rho ^{3} - a^2 \pi \rho ^4 \right) + \cdots \right] . \end{aligned}$$
    (20)

  • Linear GUP:

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1-\frac{\alpha \sqrt{\pi } }{\sqrt{s}} +(a+\alpha )\frac{\alpha \pi }{s}+\cdots \right] \nonumber \\&\quad =-16\pi \, \left[ p+ \rho - \frac{4\sqrt{2}}{3\sqrt{3}} \alpha \sqrt{\pi } \rho ^{3/2}+\frac{4}{3}\alpha \pi (a+\alpha )\rho ^{2}+\cdots \right] . \end{aligned}$$
    (21)

  • MDR approaches:

    $$\begin{aligned}&\left( \dot{H} - \frac{\kappa }{a^{2}} \right) \left[ 1 -\frac{3 \pi \alpha _{1}}{8 s}+\frac{3 \pi ^{3/2} a \alpha _{1}}{4 s^{3/2}}-\frac{5 \pi ^2 \left( \alpha _{1} ^2-4 \alpha _{2}\right) }{128 s^2} - \frac{5 \pi ^{5/2} a \left( \alpha _{1}^{2} -\, 4 \alpha _{2}\right) }{32 s^{5/2}}+\cdots \right] = \nonumber \\ &\quad -16 \pi \left[ p+ \rho -\frac{\alpha _{1} \pi }{2} \rho ^{2} +\frac{5\sqrt{2}}{8\sqrt{3}} +\,{\alpha _{1} \pi ^{3/2} a} \rho ^{5/2} -\,\frac{5 \pi ^{2}}{3} \left( \alpha _{1}^{2} -\, 4 \alpha _{2}\right) \left( \frac{\rho ^{3}}{18}-\frac{8}{21} \sqrt{\frac{2}{3}} a \pi ^{1/2} \rho ^{7/2}\right) +\cdots \right] . \end{aligned}$$
    (22)

4 Modified Landau–Raychaudhuri equations

Modifications in Landau–Raychaudhuri equations for the various types of black holes and from the different approaches for the quantum gravity are discussed. From corrections in the entropy-area relation and in various thermodynamic quantities, we can estimate the time derivative of the Hubble parameter d H/d t. More details can be found in Ref. [32]. The resulting modified Landau–Raychaudhuri equations for different metric types, various equations-of-state and the MDR and GUP approaches are elaborated in next sections.

4.1 de Sitter–Schwarzschild black hole

From Eqs. (11)–(13), the modified Landau–Raychaudhuri equations in de Sitter–Schwarzschild black holes due to the minimal length, the higher-order GUP and the MRD approaches, respectively, can be determined as a result of modified entropy-area relation and the energy density [32, 33]. Starting from entropy-area and energy density relations, \(S=A/4\), and \(\rho =3/2A\), respectively, with \(\rho =3 H^2 /8 \pi \) in flat Universe, i.e. vanishing curvature constant \(\kappa \), the derivatives of Hubble parameter with respect to the comoving time, dH/dt, can be given in dependence on H, from linear and quadratic GUP and MDR approaches, receptively,

$$ \dot{H} \, \left[ 1 + \frac{\alpha ^2 }{4} H^2 +\cdots \right] = -3 H^2 \left[ 2 (1+\omega )+ \frac{1}{4}\alpha ^2 H^2 + \cdots \right] , $$
(23)
$$ \dot{H} \, \left[ 1 + \alpha ^2 H^2 - \alpha H +\cdots \right]= -3 H^2 \left[ 6 (1+\omega )+ \frac{3 \alpha ^2 }{8} H^2 - 4 \alpha H +\cdots \right] ,$$
(24)
$$ \dot{H} \left[ 1-\frac{3}{8} \alpha _1 H^2- \frac{15}{32}\left( \alpha _1^2-4\alpha _2\right) H^4 \right]= -3 H^2 \left[ 96 \left( 1+\omega \right) + 18 \alpha _1 H^2 + \frac{45}{8} \left( \alpha _1^2- 4 \alpha _2\right) H^4\right] . $$
(25)

4.2 Reissner–Nördstrom black hole

In the same way, the modified Landau–Raychaudhuri equations for Reissner–Nördstrom black hole can be deduced from Eqs. (16)–(18) from the linear and quadratic GUP and the MDR approaches, receptively,

$$ \dot{H} \, \left[ 1 + \frac{\alpha ^2}{4} Q H^4 + \alpha ^2 \frac{4 Q^4}{ 3 \pi } H^6 + \cdots \right] = -3 H^2 \left[ \frac{2}{3} (1+\omega )+ \frac{2 \alpha ^2}{3} (Q H^2 + Q^2 H^4) H^4 +\cdots \right] ,$$
(26)
$$ \dot{H} \, \left[ 1 - \alpha \, H + \alpha ^2 (1 + Q) H^2 +\cdots \right] = -3 H^2 \left[ 2 (1+\omega )-\frac{4}{3} \alpha \, H +\frac{\alpha ^2}{4} H^2 + \cdots \right],$$
(27)
$$ \begin{aligned}\dot{H} \left[ 1 -\alpha _1 \left( 1+ 8 Q\right) H^2 - \frac{5}{128} \left( \alpha _1^2- 4 \alpha _2\right) H^4 \right] &= -3 H^2 \left[ 2 (1+ \omega ) + \frac{3 \alpha _1}{8} (1+3 Q) H^2 \right. \nonumber \\&\qquad + \left. \frac{5}{6} (\alpha _1^2- 4 \alpha _2) H^4 + \cdots \right]. \end{aligned}$$
(28)

4.3 Garfinkle–Horowitz–Strominger black hole

The modified Landau–Raychaudhuri equations can also be determined in Garfinkle–Horowitz–Strominger black hole from Eqs. (20)–(22) and the linear and quadratic GUP and the MDR approaches, receptively,

$$\begin{aligned} \dot{H} \left[ 1+ \frac{\alpha ^2}{4} H^2 + \frac{a\, \alpha ^2 }{2} H^3 + \frac{a\, \alpha ^2 }{2} H^4 + \cdots \right]&= - 3 H^2 \left[ 30 (1+ \omega ) + 60 \alpha ^2 \left( 1 - \frac{8}{9} a^2 \right) H^2 \right. \nonumber \\&\quad -\,\left. 48 \alpha ^2 a H^3 - 5 (8 a^2+1) \alpha ^4 H^4 +\cdots \right] , \end{aligned}$$
(29)
$$ \dot{H} \left[ 1- \alpha H + \alpha (a+ \alpha ) H^2 +\cdots \right] = -3 H^2 \left[ 2 (1 +\omega ) -\frac{4}{3} \alpha H + \alpha (a+ \alpha ) H^2 +\cdots \right] , $$
(30)
$$\begin{aligned} \dot{H} \left[ 1 - \alpha _1 (1+3a) H^2+ \frac{5}{32} \left( \alpha _1^2-4 \alpha _2\right) H^4 \right] &= -3 H^2 \left[ 2 (1+ \omega ) - \frac{3 \alpha _1}{8} \left( 1+ \sqrt{\frac{3}{8}}a\right) H^2 \right. \nonumber \\&\quad -\,\left. \frac{5}{128} \left( \alpha _1^2-4 \alpha _2\right) H^4 \right] \end{aligned}$$
(31)

5 Results and discussion

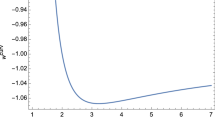
Figure 1 gives the dependence of dH/dt on H for various types of singularities (black holes) and equations-of-state and from different quantum gravity approaches, i.e. different modified Landau–Raychaudhuri equations. The curves in first two top panels are calculated assuming that the equation of state is characterized by \(\omega =-1\) and \(-2/3\), respectively. These \(\omega \)-values cover the range that has been claimed in Ref. [31], where nonsingular Big Bang has been proposed according to infinite cosmic time resulted from the integration of Hubble parameter at arbitrary finite values of H [44]. Despite the normalization in Fig. 1, what matters is the existence of two fixed points. It is obvious that nonsingularity solution is only characterizing the de Sitter-Schawarzschild-type metric from linear GUP approach at \(\omega =-2/3\) (b) and the Reissner–Nördstrom-type metric at \(\omega =-2/3\) (f). At \(\omega =-1\) [top panels (a), (e), and (i)], and for the whole class of spacetimes, there is no nonsingularity from two fixed points method. The nonsingular solutions are associated with infinitely-aged Universe [31].

Fig. 1
figure 1

(Color online) The top panel [(a), (e) and (i)] gives the time derivative of the Hubble parameter, d H/d t, as function of H for de Sitter–Schwarzschild (left-hand side), Reissner–Nördstrom (middle) and Garfinkle–Horowitz–Strominger (right-hand panel) black holes at \(\omega =-1\). The minimal length GUP (solid curve), higher order GUP (dotted curve) and modified dispersion relation (dashed curve) show different results and accordingly different (non)singular solutions. The second [(b), (f) and (j)], third [(c), (g) and (k)] and fourth [(d), (h) and (l)] panels from top to bottom top are the same but at \(\omega =-2/3\), 0, 1/3, respectively

Full size image

For matter- and radiation-dominated background geometry, \(\omega =0\) [third panel from top (c), (g), and (k)] and \(\omega = 1/3\) [bottom panels (d), (h), and (l)], respectively, the nonsingular solutions appear only for Garfinkle–Horowitz–Strominger-type metric from the quadratic GUP approach, at \(\omega =0\) (panel k). The other panels (c), (g), (d), (h), and (l) refer to singular Big Bang. The entire set of parameters is summarized in Table 1 as [32, 33]. It is apparent that \(\alpha _1\) and \(\alpha _2\) are nothing but \(\alpha _1 \ell _p^2\) and \(\alpha _2 \ell _p^2\), respectively. However, in natural units, \(\ell _p\) can be omitted. This means that the parameters \(\alpha \), \(\alpha _1\) and \(\alpha _2\) are compatible with each other and should have the same effect.

Table 1 Summarizing the parameters of GUP approaches [32, 33]
Full size table

It is worthwhile to notice that our results show that the implementation of MDR approaches results in no nonsingular solutions for all metric-types and all equations of state. We find that the MDR approaches are confirmed by various observations [17–21], especially for the violation of Lorentz invariance principle, for instance an experimental test can be performed by setting upper bounds to \(\alpha \). The modification to the dispersion relation is equivalent to assigning to the velocity of light (c) a value differs from the maximum attainable velocity of a material body. This small adjustment of c leads to a modification in the energy–momentum relation and results in \(\delta \textit{v}\) of gamma ray burst, which is found nonvanishing [17–21]. The latter means that the vacuum dispersion relation becomes sensitive to the type of quantum gravity effect. For details on other astronomical observations, the readers can consult Ref. [15]. In addition to that, another argumentation in favor for MDR is the possibility that the relation connecting energy and momentum in Special Relativity (SR) may be modified at Planck scale because of the threshold anomalies of ultra-high energy cosmic ray (UHECR). This enters the literature as the modified dispersion relations (MDR) [21–30] and can provide new sensitive tests for SR. Successful searches would reveal a surprising connection between particle physics and cosmology [17–20]. A short list of astronomical observations supporting MDR is given in [15]. This includes early-type galaxies, whether distant neutrinos feel z-shift? and the time delay in ultra high-energy cosmic rays, etc. Both linear and quadratic GUP approaches are more controversial than MDR. That the latter are orthogonal to the misleading conclusion of Ref. [31] should not hold under.

We have calculated the deceleration parameter \(q=d H^{-1}/dt-1\) and found that the values of q-parameter vary with \(\omega \); the types of the equations of state. At \(\omega =0\) and 1 / 3, q becomes positive and at \(w=-2/3\), q switches to negative values. q is undefined (infinite), at \(\omega =-1\), Table 2. The comparison with corresponding results based on the modified Friedmann equation proposed in Ref. [31] shows clear irregularities.

Table 2 Values of deceleration parameter q in various metrics, equations of state and GUP and MDR approaches compared with Ref. [31]
Full size table

Eq. (60) in [31] can be solved. It results in an inverse function. With a first-order approximation, it turns to be a naive exercise to prove that the slope becomes infinite, especially when t vanishes, i.e. very regular singular solution, Figs. 2 and 3.

Fig. 2
figure 2

The dependence of t on H is determined from linear GUP approach for various equations of states and two spacetimes; Reissner–Nördstrom (a) and Garfinkle–Horowitz–Strominger (b)

Full size image
Fig. 3
figure 3

The same as in Fig. 2 but from quadratic GUP (top panel (a), (b) and (c)] and MDR [bottom panel (d), (e) and (f)] approaches and the whole class of spacetimes

Full size image

The two fixed point method as done in Ref. [31] is questionable. Accordingly, the conclusion is apparently a misinterpretation. To illustrate this, we solve H in dependence on t, where H has the dimension of \(t^{-1}\). In Figs. 2 and 3, imaginary solutions are classified as nonphysical and they are not shown here. According to the two fixed point method, Fig. 1 should have two cases of non-singularity. These are

  • at \(\omega =-2/3\) from linear GUP in de Sitter Schwarzschild and Reissner–Nördstrom spacetimes, and

  • at \(\omega =0\) from quadratic GUP in Garfinkle–Horowitz–Strominger spacetime.

These singularities are simply missing in Figs. 2 and 3. At \(\omega =-2/3\), the solutions from linear GUP in de Sitter Schwarzschild (reported in [31]) and Reissner–Nördstrom spacetimes are apparently nonphysical. At \(\omega =0\) from quadratic GUP in Garfinkle–Horowitz–Strominger spacetime, the dependence of t on H is given in top right-hand panel of Fig. 3, which is obviously singular; H diverges at vanishing t.

6 Conclusions

In light of the present results, conclusions as the ones drawn in Ref. [31] is badly simply model-dependent. In the present paper, we emphasize that the (non)singular solutions are strongly (just three of out of twelve cases) dependent on the metric types, the equations of state, and the quantum gravity approaches.

Defining Landau–Raychaudhuri singularity solutions based in Ref. [44] should have been proposed after additional investigations for the time dependence of Hubble parameter, Figs. 2 and 3, and scale factor, etc. Further systematic studies should be first conducted before formulating an edge-cutting conclusion about (non)singular solutions. One should not lose sight of the various theoretical studies and astrophysical observations potentially approving the singular solutions, when applying quantum corrections to Freidmann and/or Landau–Raychaudhuri equations.

Last but not least, the absence of a good theory for quantum gravity should not lead real scientists to make any conclusions about (non)singular Big Bang. Horava–Lifshitz gravity is conjectured as a good candidate for quantum gravity. In an ongoing work [45], we have estimated the impacts of various equations-of-state on the (non)singular Big Bang solutions based on Horava–Lifshitz gravity (detailed and non-detailed balance). The present work aims to emphasize the very strong model-dependence of studies based on GUP and MDR approaches.