1 Introduction

The fusion reactions at energies in the close vicinity of Coulomb barrier represent an ideal opportunity to study the quantum mechanical tunneling of colliding nuclei and the sub-barrier fusion reactions that can be used as a spectroscopic tool to explore the nature of nuclear interactions and nuclear structure of participating nuclei [1–3]. It has been well recognized that the energy dependence of the sub-barrier fusion cross sections is strongly influenced by the internal structure degrees of freedom of reacting nuclei such as nuclear shape deformation, multi-phonon vibrational states of colliding nuclei, rotations of nuclei during collision, neck formation and nucleon transfer reactions. The couplings to such relevant intrinsic channels strongly modify the behavior of tunneling probability in such a way that it produces substantially large fusion enhancement at below-barrier energies over the predictions of one-dimensional barrier penetration model [4–7]. The role of static deformation and the inelastic surface vibrational states of colliding pairs on the energy dependence of sub-barrier fusion cross sections have been properly addressed by various theoretical models [1–7]. However, the various dynamical aspects related to the multi-neutron transfer channels are not fully understood because the mechanism of multi-nucleon transfer channels involves a complex rearrangement of nucleons between the fusing nuclei and generally occurs at much larger inter-nuclear separations between fusing nuclei [1–9].

Theoretically, the effective nucleus–nucleus potential is one of the most important ingredients that displays very strong impression on the behavior of sub-barrier fusion excitation functions. In this connection, many attempts have been made to deduce the relevant information regarding the optimum form of nuclear potential by analyzing the large set of experimental data [10–17]. Generally, the static Woods–Saxon potential is most frequently used to address the heavy-ion reactions. Significantly larger values of diffuseness of Woods–Saxon potential ranging from a = 0.75 fm to a = 1.5 fm have been used for the explanation of sub-barrier fusion data, while a much smaller value of diffuseness parameter (a = 0.65 fm) is required for description of elastic scattering process. This diffuseness anomaly, which reflects the inconsistency of static Woods–Saxon potential for simultaneously exploring of elastic scattering and fusion process, may be associated with various kinds of static and dynamical physical effects [1–7, 18–20]. To understand the cause of diffuseness anomaly and the puzzling behavior of sub-barrier fusion data, in the present work we have analyzed the fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems within the context of the coupled channel approach and the energy-dependent Woods–Saxon potential model (EDWSP model) [21–33]. The role of internal structure degrees of freedom of colliding nuclei is entertained within the framework of coupled channel calculations performed by using the code CCFULL [34]. In EDWSP model, the energy dependence of Woods–Saxon potential induces similar kinds of static and dynamical physical effects as deduced from the channel coupling effects and hence brings the larger fusion enhancement at below-barrier energies with respect to the energy-independent one-dimensional barrier penetration model as evident from the earlier works [21–33].

In the presence of strong multi-phonon vibrational states of collision partners, it is very difficult to single out the contribution of multi-neutron transfer channels, and thus, the rich interplay of multi-phonon vibrational states and multi-nucleon transfer channel still attracts the analysis of fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems [35, 36]. The simultaneous existence of the strong octupole vibrations in \( {}_{40}^{96} {\text{Zr}} \) nucleus and the neutron transfer channels puzzles relative importance of inelastic surface vibrational couplings and neutron transfer couplings in the enhancement of sub-barrier fusion excitation function data. Various coupled channel models have predicted that the fusion of \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) and \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems have the dominance of inelastic surface excitations of colliding nuclei, while the fusion of \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system has the dominance of inelastic surface excitations as well as the neutron transfer channels. The coupled channel calculations and the EDWSP model calculations reasonably explain the observed fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) reactions. This unambiguously has suggested that the energy dependence in Woods–Saxon potential introduces barrier modification effects (barrier height, barrier position, barrier curvature) in closely similar way as reflected from the coupled channel approach and hence simulates the influences of nuclear structure degrees of freedom of colliding pairs. The brief description of the method of calculation is given in Sect. 2. The results are discussed in detail in Sect. 3, while the conclusions are drawn in Sect. 4.

2 Theoretical formalism

2.1 One-dimensional Wong formula

The partial wave fusion cross section is given by the following expression [4, 5]

$$ \sigma_{F} = \frac{\pi}{k^{2}}\sum\limits_{\ell = 0}^{\infty} (2\ell + 1 )T_{\ell}^{F} $$
(1)

Hill and Wheeler [37] have proposed an expression for tunneling probability (\( T_{\ell }^{F} \)) which is based upon the parabolic approximation, wherein the effective interaction between collision partners is replaced by an inverted parabola

$$ T_{\ell }^{\text{HW}} = \frac{1}{{1 + \exp \left[ {\frac{2\pi }{{\hbar \omega_{\ell } }}\left( {V_{\ell } - E} \right)} \right]}} $$
(2)

This expression has been further simplified by Wong using the following assumptions for barrier position, barrier curvature and barrier height [38].

$$ R_{\ell } = R_{\ell = 0} = R_{B} $$
$$ \omega_{\ell } = \omega_{\ell = 0} = \omega $$
$$ V_{\ell } = V_{B} + \frac{{\hbar^{2} }}{{2\mu R_{B}^{2} }}\left[ {\ell + \frac{1}{2}} \right]^{2} $$

Using above assumptions and Eq. (2) into Eq. (1), one can write the fusion cross section as

$$ \sigma_{F} = \frac{\pi }{{k^{2} }}\sum\limits_{\ell = 0}^{\infty } {\frac{(2\ell + 1)}{{\left[ {1 + \exp \frac{2\pi }{\hbar \omega }\left( {V_{\ell } - E} \right)} \right]}}} $$
(3)

Since the infinite number of partial wave contributes to the fusion process, one can change the summation over ℓ into integral with respect to ℓ in Eq. (3). Therefore, by solving the integral one can obtain final expression for Wong formula which can be used for evaluating the fusion cross section in all range of energies [38].

$$ \sigma_{F} = \frac{{\hbar \omega \,R_{B}^{2} }}{2E}\ell n\left[ {1 + \exp \left( {\frac{2\pi }{\hbar \omega }\left( {E - V_{B} } \right)} \right)} \right] $$
(4)

2.2 Energy-dependent Woods–Saxon Potential model (EDWSP model)

In the previous work, the energy-dependent Woods–Saxon potential model (EDWSP model) has been successfully used to address the role of inelastic surface vibrations of colliding pairs and the multi-neutron transfer channels [21–33]. The form of static Woods–Saxon potential is defined as

$$ V_{N} (r) = \frac{{ - V_{0} }}{{\left[ {1 + \exp \left( {\frac{{r - R_{0} }}{a}} \right)} \right]}} $$
(5)

with \( R_{0} = r_{0} (A_{P}^{\frac{1}{3}} + A_{T}^{\frac{1}{3}} ) \). The quantity ‘V 0’ is depth and ‘a’ is diffuseness parameter of the nuclear potential. In EDWSP model, the depth of real part of Woods–Saxon potential is given by the following expression

$$ V_{0} = \left[ {A_{P}^{\frac{2}{3}} + A_{T}^{\frac{2}{3}} - \left( {A_{P} + A_{T} } \right)^{\frac{2}{3}} } \right]\left[ {2.38 + 6.8\left( {1 + I_{P} + I_{T} } \right)\frac{{A_{P}^{\frac{1}{3}} A_{T}^{\frac{1}{3}} }}{{\left( {A_{P}^{\frac{1}{3}} + A_{T}^{\frac{1}{3}} } \right)}}} \right]\,{\text{MeV}} $$
(6)

here \( I_{P} = \left( {\frac{{N_{P} - Z_{P} }}{{A_{P} }}} \right) \) and \( I_{T} = \left( {\frac{{N_{T} - Z_{T} }}{{A_{T} }}} \right) \) are the isospin asymmetry of projectile and target nuclei, respectively. The present parameterization of potential depth is based upon the reproduction the fusion excitation function data of wide range of projectile–target combinations ranging from Z P Z T  = 84 to Z P Z T  = 1640 [21–33]. In fusion process, the various kinds of static and dynamical physical effects such as variations of densities of colliding nuclei, dissipation of kinetic energy of relative motion into internal structure degrees of freedom, different kinds of channel couplings effects (influences of inelastic surface vibrational states, rotational states of deformed nuclei, multi-nucleon transfer channels) or other static and dynamical physical effects occur in the surface region of nuclear potential or in the tail region of Coulomb barrier. Such kinds of different physical effects are responsible for the modification of parameters of static Woods–Saxon potential. Furthermore, the surface diffuseness as well as the surface energy of colliding pairs, which strongly depends on the collective motion of all nucleons inside the nucleus, gets fluctuated and also bring a requirement of modifications in the value of potential parameters. The first term in the square bracket of Eq. (6), which is directly proportional to surface energy of the colliding nuclei, accommodates such static and dynamical physical effects. All these physical effects bring the necessity of larger diffuseness parameter ranging from a = 0.75 fm to a = 1.5 fm for accounting the sub-barrier fusion data [21–33]. In addition, the isotopic effects are generally evident if a common projectile is bombarded on a series of target isotope or vice versa, and these isotopic effects are incorporated in the present model via isospin of colliding nuclei.

In fusion dynamics, different kinds of static and dynamical physical effect such as variation of surface energy, N/Z ratio, variation of densities in neck region, dissipation of kinetic energy of relative motion to internal structure of collision partners, which causes the modification in the value of diffuseness of static Woods–Saxon potential, are accurately accommodated in the present model. In EDWSP model calculations, these static and dynamical physical effects are included through energy-dependent diffuseness parameter which is defined by the following expression

$$ a(E) = 0.85\left[ {1 + \frac{{r_{0} }}{{13.75\left( {A_{P}^{{ - \frac{1}{3}}} + A_{T}^{{ - \frac{1}{3}}} } \right)\left( {1 + \exp \left( {\frac{{\frac{E}{{V_{B0} }} - 0.96}}{0.03}} \right)} \right)}}} \right]\,{\text{fm}} $$
(7)

In EDWSP model calculations, depending upon the value of range parameter (r 0) and bombarding energy of colliding pairs, the above expression provides a wide range of diffuseness parameter. The range parameter r 0 is treated as free parameter in order to vary the value of diffuseness parameter required to address the fusion excitation function data of system under consideration. It is shown later that the theoretical calculations based upon static Woods–Saxon potential must include the effects of couplings to internal nuclear structure degrees of freedom such as inelastic surface excitations of colliding pairs, rotational states of deformed nuclei and multi-nucleon transfer channels or other static and dynamical physical effects to reproduce the sub-barrier fusion data. However, the energy dependence in the Woods–Saxon potential induces barrier modification effects and hence adequately addresses the sub-barrier fusion dynamics of various heavy-ion fusion reactions. Strictly speaking, in the EDWSP model, the variation of diffuseness parameter is effectively equivalent to increase of capture radii of reacting nuclei, and thus, this increase of capture radii of fusing system suggests that the sub-barrier fusion process starts at much larger inter-nuclear separation between colliding nuclei [21–33].

2.3 Coupled channel model

This section briefly reviews the details of coupled channel approach used to analyze the fusion dynamics of various heavy-ion fusion reactions. From theoretical point of view, the different kinds of channel coupling effects can be addressed by using the coupled channel formulation. In coupled channel calculations, it is very difficult to include all intrinsic channels simultaneously, but one can consider the effects of relevant channels [34, 39–41]. Therefore, the set of coupled channel equation can be written as

$$ \left[ {\frac{{ - \hbar^{2} }}{2\mu }\frac{{{\text{d}}^{2} }}{{{\text{d}}r^{2} }} + \frac{{J\left( {J + 1} \right)\hbar^{2} }}{{2\mu r^{2} }} + V_{N} (r) + \frac{{Z_{P} Z_{T} e^{2} }}{r} + \varepsilon_{n} - E_{\text{cm}} } \right]\psi_{n} (r) + \sum\limits_{m} {V_{\text{nm}} (r)} \psi_{m} (r) = 0 $$
(8)

where \( \vec{r} \) is the radial coordinate representing the relative motion between fusing nuclei. μ is the reduced mass of the projectile–target system. The quantities E cm and ɛ n represent the bombarding energy in the center of mass frame and the excitation energy of the nth channel, respectively. The V nm is the matrix elements of the coupling Hamiltonian, which in the collective model consists of Coulomb and nuclear components. In code CCFULL [34], the coupled channel equations are solved numerically by entertaining the two basic approximations. The first approximation is no-Coriolis or rotating frame approximation which has been used to reduce the number of the coupled channel equations [34, 39–41]. If there is no transfer of the angular momentum from the relative motion of colliding nuclei to their intrinsic motion, the total orbital angular momentum quantum number L can be replaced by the total angular momentum quantum number J. Under this approximation, which is also known as the isocentrifugal approximation, the number of coupled channel equation is reduced to a great extent. The second approximation is ingoing wave boundary conditions which are well applicable for heavy-ion reactions. According to IWBC, there are only incoming waves at r = r min, which is taken as the minimum position of the Coulomb pocket inside the barrier, and there are only outgoing waves at infinity for all channels except the entrance channel (n = 0). The code CCFULL [34] employs static Woods–Saxon potential to entertain the effects of nuclear structure degrees of freedom such as inelastic surface excitations of colliding pairs, rotational states of deformed nuclei, multi-nucleon transfer channel or other static and dynamical physical effects. By including the effects of all relevant internal degrees of freedom, the fusion cross section becomes

$$ \sigma_{F} (E) = \sum\limits_{J} {\sigma_{J} } (E) = \frac{\pi }{{k_{0}^{2} }}\sum\limits_{J} {\left( {2J + 1} \right)} P_{J} (E) $$
(9)

where P J (E) is the total transmission coefficient corresponding to the angular momentum J. For coupled channel calculations, the vibrational couplings in the harmonic limit are taken into account. The operator in the nuclear coupling Hamiltonian for vibrational couplings is given by

$$ \hat{O}_{V} = \frac{{\beta_{\lambda } }}{{\sqrt {4\pi } }}R_{T} \left( {a_{\lambda 0}^{\dag } + a_{\lambda 0} } \right) $$
(10)

with R T is parameterized as \( r_{\text{coup}} A^{\frac{1}{3}} \), β λ is the deformation parameter and \( a_{\lambda 0}^{{{\dag }}} \)(\( a_{\lambda 0} \)) is the creation (annihilation) operator of the phonon of vibrational mode of multipolarity λ. In general, the nuclear coupling matrix elements are evaluated as

$$ V_{\text{nm}}^{(N)} = \left\langle n \right|V_{N} (r,\hat{O})\left| m \right\rangle - V_{N}^{(0)} \delta_{n,m} $$

The matrix elements of \( \hat{O}_{V} \) between the n phonon state \( \left| n \right\rangle \) and the m phonon state \( \left| m \right\rangle \), which are needed for the vibrational coupling, is defined as

$$ \hat{O}_{V(n\,m)} = \frac{{\beta_{\lambda } }}{{\sqrt {4\pi } }}R_{T} \left( {\delta_{n,m - 1} \sqrt m + \delta_{n,m + 1} \sqrt n } \right) $$
(11)

The Coulomb coupling matrix elements for vibrational couplings are computed by the linear coupling approximation and is defined as

$$ V_{{V({\text{nm}})}}^{(C)} = \frac{{\beta_{\lambda } }}{{\sqrt {4\pi } }}\frac{3}{2\lambda + 1}Z_{P} Z_{T} e^{2} \frac{{R_{T}^{\lambda } }}{{r^{\lambda + 1} }} \times (\sqrt m \delta_{n,\,m - 1} + \sqrt n \delta_{n,\,m + 1} ) $$
(12)

The total coupling matrix elements are obtained by taking the sum of \( V_{\text{nm}}^{(N)} \) and \( V_{\text{nm}}^{(C)} \).

3 Results and discussion

This paper highlights the barrier modification effects introduced due to the EDWSP model and the coupled channel model in sub-barrier fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) reactions. In addition, the relative importance of strong octupole vibrational state of \( {}_{40}^{96} {\text{Zr}} \) nucleus, strong quadrupole vibrational state of \( {}_{16}^{32} {\text{S}} \) nucleus and multi-neutron transfer channels, which puzzles the behavior of sub-barrier fusion enhancement of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) reactions, is still unclear. Therefore, from the present work, the unambiguous conclusion with regard to the relative importance of multi-phonon vibrational couplings and neutron transfer couplings is directly evident. The values of the deformation parameters and their corresponding energies of low-lying 2+ and 3− vibrational states of all these nuclei are listed in Table 1. The barrier height, barrier position and barrier curvature of the fusing nuclei used in the EDWSP model calculations are listed in Table 2. The values of range, depth and diffuseness of EDWSP model for various combinations of projectile and target nuclei are listed in Table 3. In Table 4, the ground state Q-values for neutron pickup channels for the fusion of \( {}_{16}^{32} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems are listed, while all the ground state Q-values for neutron pickup channel are negative for the fusion of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems, and hence, these are not listed in Table 4.

Table 1 Deformation parameter (\( \beta_{\lambda } \)) and the energy (\( E_{\lambda } \)) of the quadrupole and octupole vibrational states of colliding nuclei [35, 36]
Full size table
Table 2 Values of V B0, R B and \( \hbar \omega \) used in the EDWSP model calculations for various heavy-ion fusion reactions
Full size table
Table 3 Range, depth, diffuseness parameters of Woods–Saxon potential used in the present calculations for various heavy-ion fusion reactions [21–33]
Full size table
Table 4 Q-values (MeV) for ground state to ground state neutron pick-up transfer channels for various S + Zr systems [35]
Full size table

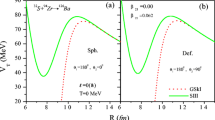
The fusion of spherical nuclei, wherein only inelastic surface vibrational states are dominating, is expected to be more simple as compared to the fusion of neutron-rich nuclei. In neutron-rich nuclei, in addition to multi-phonon vibrational states, the possibility of neutron transfer channel with positive ground state Q-value exists that must be incorporating to account the sub-barrier fusion enhancement. The fusion dynamics of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) and \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) systems has the dominance of low-lying 2+ and 3− vibrational states, while in the fusion of the \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system, there is rich interplay of inelastic surface vibrations and neutron transfer channels. In both projectiles, the 3− vibrational states lie at high excitation energies and have comparable strengths, while the 2+ vibrational state of lighter projectile \( {}_{16}^{32} {\text{S}} \) is significantly larger and lies at low excitation energy as compared to the corresponding values of \( {}_{16}^{36} {\text{S}} \) nucleus. The lighter target (\( {}_{40}^{90} {\text{Zr}} \)) nucleus is doubly magic, and in the heavier target (\( {}_{40}^{96} {\text{Zr}} \)) nucleus due to low excitation energy and large coupling strengths, it exhibits strong octupole vibrations. Therefore, the effects of 2+ vibrational state of lighter projectile (\( {}_{16}^{32} {\text{S}} \)) and 3− vibrational states of heavier target (\( {}_{40}^{96} {\text{Zr}} \)) are expected to produce more pronounced impact on the fusion enhancement at sub-barrier fusion energies. Before going into the details of coupled channel calculations of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) reactions, the barrier modification effects introduced due to the energy-dependent Woods–Saxon potential model (EDWSP model) in the fusion dynamics of these reactions is discussed. In EDWSP model-based calculations, the energy-dependent diffuseness parameter generates energy-dependent fusion barriers of varying heights as shown in Fig. 1(a)–1(h). This kind of physical effect is a direct manifestation of the enhancement of the fusion cross section at energies below the energy of the Coulomb barrier. The barriers whose heights are lowers than that of the Coulomb barrier produce substantially large sub-barrier fusion cross section over the expectations of energy-independent one-dimensional barrier penetration model. At below-barrier energies, a = 0.98 fm is the largest value of the diffuseness parameter (a = 0.98 fm for \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) and a = 0.97 fm for \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) reaction) that produce lowest fusion barrier which in turn leads to the maximum flux lost from the elastic channel to fusion channel. With increase of incident energy, the value of diffuseness parameter goes on decreasing and the height of the corresponding fusion barrier gradually increases as depicted in Fig. 1(a)-1(h). At above-barrier energies, the diffuseness parameter attains its minimum value (a = 0.85 fm), wherein the predictions of static Woods–Saxon potential, the EDWSP model and coupled channel model coincide with each other. At such energies, the present model leads the highest fusion barrier, and for all cases (\( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems), this highest fusion barrier produced in the EDWSP model calculations is still smaller than that of corresponding values of the Coulomb barrier as listed in Table 2. Therefore, as a consequence of lowering of fusion barrier between colliding nuclei, the present model adequately addresses the observed fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems. The comparisons of the EDWSP model calculations and the coupled channel calculations for the fusion of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems reflect that the energy dependence in Woods–Saxon potential introduces barrier modification effects (barrier height, barrier position, barrier curvature) in somewhat similar way to that of coupled channel formulation.

Fig. 1
figure 1

Fusion barrier (FB) for \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems obtained by using the EDWSP model [21–33]

Full size image

In the fusion of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) system as shown in Fig. 2, if colliding nuclei are considered as inert, the experimental data are substantially larger than theoretical predictions. The coupling to one phonon 2+ vibrational state in projectile as well as one phonon 2+ and 3− vibrational states of target along with their mutual couplings strongly enhance the fusion cross section as compared to no coupling calculations but unable to account the experimental data in whole range of energy. The addition of higher phonon states of target like two phonon 3− vibrational states improves the coupled channel predictions, but still there remain large discrepancies between theoretical calculations and experimental data. The coupling of one phonon 2+ vibrational state in projectile, one phonon 2+ vibrational state and three phonon 3− vibrational states of target along with the mutual excitations such as (3−)3, \( (2^{ + } \otimes (3^{ - } )^{2} ) \) vibrational states bring the close agreement between coupled channel calculations and fusion data. Similar results are found for \( {}_{16}^{36} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system as shown in Fig. 3, wherein the target possesses strong octupole vibrations and strongly modify the energy dependence of fusion cross section at below-barrier energies. In addition of coupling to single phonon 2+ and 3− vibrational states along with their mutual couplings in projectile, the inclusion of three phonon 3− vibrational states in target reasonably account the observed fusion enhancement of \( {}_{16}^{36} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system. For \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems, the ground state Q-values are negative for all neutron transfer channels which suggests that the effects of neutron transfer channel seem to be undesirable. Therefore, the relative fusion enhancement of sub-barrier fusion cross section with respect to one-dimensional barrier penetration model can be attributed to the presence multi-phonon vibrational states of fusing nuclei. It is quite interesting to see the predictions of EDWSP model adequately reproduce the fusion excitation function data of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems in an economical way.

Fig. 2
figure 2

Fusion excitation function of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) system obtained by using the EDWSP model [21–33] and using coupled channel code CCFULL [34]. The results are also compared with the available experimental data [36]

Full size image
Fig. 3
figure 3

Fusion excitation function of \( {}_{16}^{36} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system obtained by using the EDWSP model [21–33] and using coupled channel code CCFULL [34]. The results are also compared with the available experimental data [36]

Full size image

If one is able to reproduce the fusion excitation function data by including the coupling to the inelastic surface excitations for \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems, the same should be true for \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) system because the neutron transfer channel are also suppressed in this case. For this system, coupling to low-lying surface vibrations are playing decisive role in the fusion enhancement at sub-barrier energies. The inclusion of two and three phonon 3− vibrational states alone in the target produces larger sub-barrier fusion enhancement as compared to no coupling calculations. However, such coupling fails to provide close agreement between theoretical calculations and the experimental data. This suggests the significance of addition of higher multi-phonon vibrational states of fusing nuclei. The couplings to one phonon 2+ vibrational state of both colliding nuclei and two phonon 3− vibrational states in the target along with their mutual couplings reasonably account the experimental data in whole range of energy as shown in Fig. 4.

Fig. 4
figure 4

Same as Fig. 2 but for \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) systems. The results are compared with available experimental data [35]

Full size image

The fusion of \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system helps in disentangling the relative dominance of neutron transfer channels and the inelastic surface excitations in the sub-barrier fusion dynamics. In target nucleus, six neutrons outside of neutron shell closure, which occurs at N = 50, offer the large probabilities of transferring of four neutrons with positive ground state Q-values (see Table 4) from target to projectile. The coupling to one phonon 2+ and 3− vibrational states in projectile as well as in target along with their mutual couplings significantly produces larger fusion cross section as compared to uncoupled case, but still there are large discrepancies between theoretical calculations and fusion data. The further addition to higher multi-phonon vibrational states such as two phonon and three phonon states in target improves the results quantitatively but fails miserably to account the experimental data. The existence of a strong octupole vibration in \( {}_{40}^{96} {\text{Zr}} \) nucleus and strong quadrupole vibration in \( {}_{16}^{32} {\text{S}} \) nucleus [35, 36] suggests that couplings to such multi-phonon vibrational states have strong impact on the energy dependence of fusion cross section in below-barrier energy regions. Besides, coupling to these dominant channels, there is large deviation between theoretical calculations and experimental data in sub-barrier energy regions as shown in Fig. 5. However, if scenario of experimental data of \( {}_{16}^{32} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems is treated under the formwork of the EDWSP model, it produces the required orders of magnitude of sub-barrier fusion cross section data. This clearly suggests that the energy dependence in Woods–Saxon potential governs the similar kinds of barrier modification effects as reflected from the channel coupling effects. It is worth noting hear that the larger barrier curvature required in the EDWSP model calculations for addressing the sub-barrier fusion data of \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) reaction is the consequence of dominance of neutron transfer channels, and hence, similar conclusions are also evident from the previous work [21–33].

Fig. 5
figure 5

Same as Fig. 2 but for \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) systems. The results are compared with available experimental data [35]

Full size image

The fusion dynamics of \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) and \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems is quite insensitive to the neutron transfer channels because of negative ground state Q-values for all neutron transfer channels and larger sub-barrier fusion enhancement of these systems with respect to one-dimensional barrier penetration model can be understood in terms of inelastic surface vibrational states of reacting nuclei. The substantially larger fusion enhancement of \( {}_{16}^{32} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system in comparison with other S + Zr combinations can only be accounted if one includes the influences of inelastic surface excitations and neutron (multi-neutron) transfer channels with positive ground state Q-values. To track the isotopic effects, the comparison of fusion excitation function data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90,96} {\text{Zr}} \) and \( {}_{20}^{40} {\text{Ca}} + {}_{40}^{94} {\text{Zr}} \) reactions are shown in Figs. 6 and 7. The striking difference in the fusion cross section data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90} {\text{Zr}} \) as shown in Fig. 6 and \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) systems as shown in see Fig. 7 is a consequence of different structures of projectiles. With the increase of coupling strengths of inelastic surface excitations such as 2+ and 3− vibrational states of projectiles, the corresponding sub-barrier fusion enhancement increases as evident from Fig. 6. The larger fusion cross-sectional data of \( {}_{16}^{32} {\text{S}},{}_{20}^{40} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) systems in comparison with that of \( {}_{16}^{36} {\text{S}},{}_{20}^{48} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) systems can be correlated with the existence of neutron pickup channels, which is evident from Fig. 7. The similar conclusions with regard to the relative importance of inelastic surface vibrations of colliding nuclei and multi-neutron transfer channels are pointed out in the previous work [21–33] and also from the pioneering work of several authors [1–7].

Fig. 6
figure 6

Fusion excitation functions data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90} {\text{Zr}} \) systems [35, 36, 42, 43] are compared

Full size image
Fig. 7
figure 7

Fusion excitation functions data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) systems [35, 36, 42, 43] are compared

Full size image

In Fig. 8, a comparison of experimental data of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems indicates that the substantially larger fusion enhancement of \( {}_{16}^{36} {\text{S}} + {}_{40}^{96} {\text{Zr}} \) system over \( {}_{16}^{36} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) system can be attributed to the existence of strong octupole vibration in \( {}_{40}^{96} {\text{Zr}} \) nucleus. The larger fusion data for \( {}_{16}^{32} {\text{S}} + {}_{40}^{90} {\text{Zr}} \) system in comparison with \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems can be correlated with coupling to strong quadrupole vibrational state of \( {}_{16}^{32} {\text{S}} \) nucleus. The comparison of the fusion excitation function data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90,96} {\text{Zr}} \) and \( {}_{20}^{40} {\text{Ca}} + {}_{40}^{94} {\text{Zr}} \) systems is shown in Fig. 9, wherein relative sub-barrier fusion enhancement mirrors the dominance of either inelastic surface vibrational states or neutron transfer channels. The magnitude of sub-barrier fusion excitation function data of \( {}_{16}^{32} {\text{S}},{}_{20}^{40} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) and \( {}_{20}^{40} {\text{Ca}} + {}_{40}^{94} {\text{Zr}} \) systems are strongly enhanced with reference to other reactions due to the combined effects of inelastic surface vibrational states and multi-neutron transfer channels, while the fusion enhancement of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90} {\text{Zr}} \) and \( {}_{20}^{48} {\text{Ca}} + {}_{40}^{96} {\text{Zr}} \) systems is a consequence of dominance of inelastic surface excitations of collision partners.

Fig. 8
figure 8

Fusion excitation functions data of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems are compared [35, 36]

Full size image
Fig. 9
figure 9

Fusion excitation functions data of \( {}_{16}^{32,36} {\text{S}},{}_{20}^{40,48} {\text{Ca}} + {}_{40}^{90,96} {\text{Zr}} \) systems [35, 36, 42, 43] and \( {}_{20}^{40} {\text{Ca}} + {}_{40}^{94} {\text{Zr}} \) system [44] are compared

Full size image

It is well known that different types of channel coupling effects are dominating only at sub-barrier energies, while such static and dynamical physical effects are unimportant in above-barrier energy regions. Therefore, the above-barrier fusion data should be accurately reproduced by one-dimensional barrier penetration model [18–20]. According to one-dimensional barrier penetration model, the abnormally larger values of diffuseness of static Woods–Saxon potential are required to account the experimental fusion data [1–7, 18–20]. In this regard, the predictions of the EDWSP model calculations in above-barrier energy regions are shown in Fig. 10. In the previous work, the experimental data of \( {}_{6}^{12} {\text{C}} + {}_{40}^{92} {\text{Zr}} \), \( {}_{8}^{16} {\text{O}} + {}_{40}^{92} {\text{Zr}} \), \( {}_{14}^{28} {\text{Si}} + {}_{40}^{92} {\text{Zr}} \),\( {}_{17}^{35} {\text{Cl}} + {}_{40}^{92} {\text{Zr}} \) and \( {\text{Ca}} + {\text{Ca}} \) systems are analyzed which has the precision of about 1 % at energies above the Coulomb barrier [30]. For these projectile–target combinations, the EDWSP model is able to reproduce the above-barrier portion of the fusion excitation function data within 5 % with probability larger than 90 % as evident from the previous work [30]. The above portion of experimental data of \( {}_{16}^{36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems has the precision of 15 % while that of \( {}_{16}^{32} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems has the precision of 0.8 %. For these fusing systems, it is possible to achieve an agreement with the experimental cross section within 10 %. Within EDWSP model, only at 4 fusion data points out of 90 fusion data points deviation exceeds 5 %, whereas 86 fusion data points lies within 5 %. Therefore, the present model is able to reproduce the above-barrier fusion data within 5 % within with a probability greater than 90 %.

Fig. 10
figure 10

Ratio of \( \xi = \frac{{\sigma_{\text{th}} }}{{\sigma_{ \exp } }} \) as the function of \( \frac{{V_{B0} }}{Ec.m.} \) for 4 reactions listed in Table 2

Full size image

In coupled channel calculations, larger value of diffuseness parameter a ≈ 0.90 fm is required to reproduce the sub-barrier fusion enhancement. In same analogy, the EDWSP model-based calculation requires significantly larger value of diffuseness parameter ranging from a = 0.85 fm to a = 0.98 fm for addressing the sub-barrier fusion data, and therefore, the energy dependence in the Woods–Saxon potential reflects similar characteristics of sub-barrier fusion mechanism as inferred from the static Woods–Saxon potential with abnormally large diffuseness parameter. Ghodsi and Zanganeh [45] have shown that the M3Y+repulsion and static Woods–Saxon potential with large diffuseness parameter accurately reproduce the fusion dynamics of \( {}_{6}^{12} {\text{C}} + {}_{40}^{92} {\text{Zr}} \), \( {}_{8}^{16} {\text{O}} + {}_{40}^{92} {\text{Zr}} \), \( {}_{14}^{28} {\text{Si}} + {}_{40}^{92} {\text{Zr}} \) and \( {}_{17}^{35} {\text{Cl}} + {}_{40}^{92} {\text{Zr}} \) systems. This unambiguity reveals that M3Y+repulsion and static Woods–Saxon potential with large diffuseness parameter explore similar behavior of sub-barrier fusion dynamics, and hence, the effects of M3Y+repulsion potential can be correctly reproduced by static Woods–Saxon potential with abnormally large diffuseness parameter ranging from a = 0.75 fm to a = 1.5 fm. The similarity between M3Y+repulsion potential and static Woods–Saxon potential with large diffuseness parameter is also evident from the work of Esbensen et al. [46, 47] and Stefanini et al. [48, 49]. The successful exploration of fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems within the framework of the EDWSP model indicates that the energy dependence in Woods–Saxon potential reflects similar characteristics of heavy-ion fusion reactions as deduced from static Woods–Saxon potential with large diffuseness parameter and consequently form M3Y+repulsion potential.

In heavy-ion fusion reactions, it is well populated that the effect of couplings to internal degree of freedom such as static deformation, surface inelastic channels and neutron transfer channels is to split the Coulomb barrier into spectrum of barriers having different heights which is known as barrier distribution [1–7, 35, 36, 42–44, 46–49]. In this spectrum, the barriers whose heights are lower than that of the Coulomb barrier can be ascribed for the substantially larger sub-barrier fusion enhancement over the expectations of the one-dimensional barrier penetration model [1–7]. In similar fashion, the energy-dependent Woods–Saxon potential produces a distribution of barriers of varying heights as depicted in Fig. 1. The lowering of fusion barrier between colliding nuclei is the main ingredient of the EDWSP model, and hence, as a consequence of lowering of fusion barrier, the EDWSP model is capable of addressing the sub-barrier fusion excitation functions of various heavy-ion fusion reactions. This raises number of questions on the role of internal structure degrees of freedom of colliding pairs in the sub-barrier fusion enhancement. Therefore, the different kinds of channel coupling effects such as vibrational degrees of freedom, rotational degrees of freedom and nucleon (multi-nucleon) transfer channel whether represent a true picture of the relevant channels in the enhancement of sub-barrier fusion excitation function data or simply mimics the inconsistency of static Woods–Saxon potential parameters is still not clear. Whether the energy dependence of the diffuseness parameter (that is the energy dependence of the Woods–Saxon potential) is true representation of the nuclear potential or simulates other static and dynamical physical effects is still not clear.

4 Conclusions

The present work explores the role of barrier modification effects introduced due to energy-dependent nucleus–nucleus potential and the coupled channel model in sub-barrier fusion dynamics. For this, the present paper has systematically analyzed the fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) systems wherein the inelastic surface vibrational couplings and neutron transfer couplings puzzle behavior of the sub-barrier fusion enhancement over the expectations of one-dimensional barrier penetration model. The theoretical calculations based upon static Woods–Saxon potential performed by using code CCFULL require the inclusion of internal nuclear structure degrees of freedom of colliding nuclei such as inelastic surface vibrational states and multi-neutron transfer channels for reproducing the sub-barrier fusion excitation function data. In contrast to this, the EDWSP model along with one-dimensional Wong formula adequately addresses the observed fusion dynamics of \( {}_{16}^{32,36} {\text{S}} + {}_{40}^{90,96} {\text{Zr}} \) reactions. This clearly suggests that the energy dependence in Woods–Saxon potential introduces barrier modification effects (barrier height, barrier position, barrier curvature) in somewhat similar way as reflected from the coupled channel formulation and hence simulates the effects of dominant channel coupling effects. The EDWSP model-based calculation requires significantly larger values of diffuseness parameter ranging from a = 0.85 fm to a = 0.98 fm, which is much larger than a value (a = 0.65 fm) extracted from the elastic scattering data, for accounting the sub-barrier fusion data. Furthermore, within the context of EDWSP model, it is possible to achieve an agreement with the fusion cross-sectional data within 10 %, and hence, the EDWSP model is able to reproduce the above-barrier portion of the fusion cross-section data within 5 % with a probability greater than 90 %.