1 Introduction

The coupled nonlinear evolution equations (NLEEs) arise in various areas of applied mathematics and theoretical physics. Some of the commonly seen applications of these coupled NLEEs are in nonlinear optics, fluid dynamics, plasma physics and various other areas. The issue of integrability is one of the major focuses of these coupled NLEEs. Several techniques of integrability, developed particularly in the last decade, address the integrability aspects of NLEEs as well as coupled NLEEs. Some of these techniques of integrability are variational iteration method, Adomian decomposition method, exp-function method \(G^{\prime}/G\)-expansion method, simplest equation method, variational principle and so on [1–25].

In this paper one such coupled NLEE has been studied. It is the Bona-Chen (BC) equation, first studied by Bona and Chen in 1998 and subsequently re-visited by several other authors [1, 4, 12]. This equation appears in the study of surface water waves. The solitary wave ansatz method is applied to retrieve the 1-soliton solution to this equation. Subsequently, the multiplier method is applied to find the conservation laws of this equation. The Jacobi elliptic function method has been also used to obtain the cnoidal wave solutions and in the limiting case the solitary wave solutions fall out.

Compared to other methods for finding exact solutions for nonlinear equations such as inverse scattering transform, dressing method, Hirota method and others, the ansatz method has the advantage that it can also handle nonlinear nonintegrable equations [25]. By using the ansatz method the equations are reduced from partial differential equation to algebraic equations. For the case of the BC system the ansatz system depends on only two parameters that are then manipulated by an algebraic relationship. The conservation law that will be derived in this paper will utilize the multiplier method from Lie symmetry. It is otherwise going to be extremely cumbersome to derive the only conservation law for the BC equation.

The Jacobi’s elliptic function method directly extracts the cnoidal and snoidal wave solutions from the BC equation. This is a less involved approach than the approach adopted in 2007, where a series solution in terms of the elliptic cn function is initially assumed [4]. The limiting cases of the solutions also lead to the solitary wave solutions as will be seen later in this paper. The explode decay mode solutions and the singular solitary wave solutions will also be derived in this paper. In the final section of this paper, a few numerical simulations will be given to complete the analysis of this equation. The advantages of these methods of integration are that these methods are direct approaches to integrate the equation. This keeps the methods simple enough.

2 Mathematical analysis

The dimensionless form of the BC equation is given by [1–5, 12]

$$ q_t + a_1r_x + a_2qq_x + a_3r_{xxx} + a_4q_{xxt} = 0 $$
(1)
$$ r_t + b_1q_x + b_2(qr)_x + b_3q_{xxx} + b_4r_{xxt} = 0 $$
(2)

For this coupled system of equations q(x, t) and r(x, t) are the dependent variables while x and t are the independent variables. The real valued constants are a i and b i for i = 1, 2, 3, 4.

BC equations, modeled by Eqs. (1) and (2), approximate the small amplitude long waves on the surface of an ideal fluid due to gravitational force. Thus, physically Eqs. (1) and (2) approximately represent the two-dimensional propagation of surface waves in an uniform horizontal channel with irrotational, incompressible and inviscid fluid with an undisturbed state. Thus, the dimensionless variables q(x, t) represent the deviation of the water surface from its undisturbed position while r(x, t) is the horizontal velocity at a certain water level [4, 5, 20].

The BC equation given by Eqs. (1) and (2) have been solved in this section by the aid of ansatz method. The search is for a 1-soliton solution. To start off, the hypotheses

$$ q(x,t) = A_1 \hbox{sech}^{p_1} \tau $$
(3)

and

$$ r(x,t) = A_2 \hbox{sech}^{p_{2}} \tau $$
(4)

are selected where,

$$ \tau = B(x-vt) $$
(5)

Here in Eqs. (3) and (4), A 1 and A 2 are the amplitudes of the solitary waves, while in Eq. (5) B represents the inverse width of the solitary wave and v is the soliton velocity. Substitution of these assumptions into Eqs. (1) and (2), reduces them to

$$ \begin{aligned} &p_1vA_1B \hbox{sech}^{p_{1}} \tau - a_1 p_2 A_2 B \hbox{sech}^{p_{2}} \tau - a_2 p_1 A_1^{2} B \hbox{sech}^{2p_{1}} \tau \\ \qquad \quad &- a_3 p_2^2 A_2 B^3 \hbox{sech}^{p_{2}} \tau + a_3 p_2(p_2+1)(p_2+2)A_2 B^3 \hbox{sech}^{p_{2}+2} \tau \\ &+ a_4 p_1^3A_1B^3v \hbox{sech}^{p_{1}} \tau - a_4 p_1(p_1+1)(p_1+2)A_2B^3 v \hbox{sech}^{p_1+2} \tau = 0 \\ \end{aligned} $$
(6)

and

$$ \begin{aligned} & p_2vA_2B \hbox{sech}^{p_2} \tau - b_1p_1A_1B \hbox{sech}^{p_1} \tau - b_2(p_1+p_2)A_1A_2B \hbox{sech}^{p_1+p_2} \tau \\ \qquad \quad &- b_3p_1^3A_1B^3 \hbox{sech}^{p_1} \tau + b_3 p_1(p_1+1)(p_1+2)A_1B^3 \hbox{sech}^{p_1+2} \tau \\ &+ b_4 p_2^3A_2B^3v \hbox{sech}^{p_2} \tau - b_4 p_2(p_2+1)(p_2+2)A_2B^3v \hbox{sech}^{p_2+2} \tau = 0\\ \end{aligned} $$
(7)

respectively. From Eq. (6), equating the exponents 2p 1 and p 2 + 2 gives

$$ 2p_1 = p_2+2 $$
(8)

Again from Eq. (7), equating the exponents p 1 + p 2 and p 1 + 2 gives

$$ p_1 + p_2 = p_2 + 2 $$
(9)

From Eqs. (8) and (9),

$$ p_1 = p_2 = 2 $$
(10)

Now from Eqs. (6) and (7), the linearly independent functions are \(\hbox{sech}^{p_{i}+j}\) for i = 1, 2 respectively, where j = 1, 2. Thus, setting their respective coefficients to zero yields, from Eq. (6)

$$ v = \frac{A_2 \left(a_1 + 4a_3B^2 \right)}{A_1\left(1+4a_4B^2 \right)} $$
(11)
$$ v = \frac{12a_3A_2B^2 - a_2A_1^2}{12a_4A_2B^2} $$
(12)

while from Eq. (7),

$$ v = \frac{A_1 \left(b_1 + 4b_3B^2 \right)}{A_2\left(1+4b_4B^2 \right)} $$
(13)
$$ v = \frac{A_1 \left( 6b_3B^2 - b_2A_2 \right)}{6b_4A_2B^2} $$
(14)

Equating the two values of v from Eqs. (11) and (13) gives the width of the soliton as

$$ B = \left(\frac{M}{N} \right)^{\frac{1}{4}} $$
(15)

where

$$ M = a_4b_1A_1^2 + b_3A_1^2 - a_1a_4A_2^2 - a_3A_2^2 + \left\{ \left(a_4b_1A_1^2 + b_3A_1^2 - a_1a_4A_2^2 - a_3A_2^2\right)^2 + 4\left(b_1A_1^2 - a_1A_2^2 \right) \left(a_3b_4A_2^2 - a_4b_3A_1^2\right) \right\}^{\frac{1}{2}} $$
(16)
$$ N = 8 \left( a_3b_4A_2^2 - a_4b_3A_1^2 \right) $$
(17)

Similarly, from Eqs. (12) and (14)

$$ B = \left[ \frac{A_1\left(2a_4b_2A_2 - a_2A_1\right)}{12 \left(a_4b_3A_1 - a_3A_2 \right)} \right]^{\frac{1}{2}} $$
(18)

Finally, equating the two values of the width B from Eqs. (15) and (18) yields the relation between the amplitudes of the solitary waves as

$$ \frac{M}{N} = \frac{A_1\left(2a_4b_2A_2 - a_2A_1\right)}{12 \left(a_4b_3A_1 - a_3A_2 \right)}, $$
(19)

where M and N are respectively given by Eqs. (16) and (17). Thus, finally, the 1-soliton solution to BC equation is given by

$$ q(x,t) = A_1 \hbox{sech}^2 [B(x-vt)] $$
(20)

and

$$ r(x,t) = A_2 \hbox{sech}^2 [B(x-vt)] , $$
(21)

where the amplitudes A 1 and A 2 are connected by the relation (19), while the inverse width is given by Eq. (15) or Eq. (18). Finally, the velocity of the soliton is given by Eq. (11) or Eq. (12) or Eq. (13) or Eq. (14).

2.1 Conservation law

In Eq. (1), if a 1 is replaced by f′(t), then the system of Eqs. (1) and (2) has a nontrivial conserved flow by the multiplier (1, f(t)) which leads to the conserved density

$$ T^t= q+\frac{1}{3} \left(a_4 q_{ xx}+f(t) \left(3 r+b_4 r_{ xx}\right)\right). $$

Thus, the given system of Eqs. (1) and (2) has a conserved flow with f′ = a 1 and f = a 1 t, viz.,

$$ \Upphi^{t}=\frac{1}{3} \left\{3 q+3(a_1t+k)r+a_4 q_{ xx}+a_1 b_4tr_{xx}\right\}. $$

Hence the conserved quantity is given by

$$ \begin{aligned} I &= \int \limits_{-\infty}^{\infty} \Upphi^{t} dx = \frac{1}{3} \int \limits_{-\infty}^{\infty}\left\{ 3q + 3(a_1 t +k )r + a_4q_{xx}+a_1 b_4 t r_{xx} \right\} dx\\ &= \frac{2}{B} \left\{ A_1 + (a_1t + k) A_2 \right\}\\ \end{aligned} $$
(22)

Since I is a conserved quantity it is necessary to have dI/dt = 0. This gives the condition a 1 = 0 for \(\Upphi^{t}\) to be a conserved density.

3 Jacobi elliptic function solutions

In this section we have derived solitary wave solutions (SWSs) and explode decay mode solutions as infinite period counterparts of Jacobi elliptic function (JEF) solutions [8, 10].

We consider the traveling wave solution given in Eq. (5) for Eqs. (1) and (2) so that they reduce to the ordinary differential equations (ODEs)

$$ - B v q_{\tau} + a_1 B r_{\tau} + a_2 B q q_{\tau} + a_3 B^3 r_{\tau\tau\tau} - a_4 B^3 v q_{\tau\tau\tau}= 0 $$
(23)

and

$$ - B v r_{\tau} + b_1 B q_{\tau} + b_2 B (qr)_{\tau} + b_3 B^3 q_{\tau\tau\tau} - b_4 B^3 v r_{\tau\tau\tau}= 0. $$
(24)

Integrating Eqs. (23) and (24) with respect to τ, we get

$$ - v q + a_1 r + \frac{1}{2} a_2 q^2 + a_3 B^2 r_{\tau\tau} - a_4 B^2 v q_{\tau\tau} = K_1 $$
(25)

and

$$ - v r + b_1 q + b_2 q r + b_3 B^2 q_{\tau\tau} - b_4 B^2 v r_{\tau\tau} = K_2, $$
(26)

where, K 1 and K 2 are integration constants.

3.1 Solitary wave solutions

We assume solutions for Eqs. (25) and (26) in the form

$$ q = A_1\,\hbox{cn}^{{\rm s}_1}(\tau),\quad r = A_2\, \hbox{cn}^{{\rm s}_2}(\tau), $$
(27)

where A 1 and A 2 are constants.

Equating the nonlinear terms and the highest derivative terms in Eqs. (25) and (26) we can easily see that s 1 = 2 and s 2 = 2.

Thus our solutions of Eqs. (25) and (26) are in the form

$$ q = A_1\, \hbox{cn}^{2}(\tau),\quad r = A_2\, \hbox{cn}^{2}(\tau). $$
(28)

Substituting Eq. (28) in Eqs. (25) and (26), and equating the coefficients of powers of cn(τ), we arrive at the equations

$$ \frac{1}{2} a_2 A_1^2 - 6 m^2 a_3 B^2 A_2 + 6 m^2 a_4 B^2 v A_1 = 0, $$
(29)
$$ - v A_1 + a_1 A_2 + 4 (2 m^2 - 1) a_3 B^2 A_2 -4 (2 m^2 - 1) a_4 B^2 v A_1 = 0, $$
(30)
$$ 2 (1 - m^2) a_3 B^2 A_2 - 2 (1 - m^2) a_4 B^2 v A_1 = K_1, $$
(31)
$$ b_2 A_1 A_2 - 6 m^2 b_3 B^2 A_1 + 6 m^2 b_4 B^2 v A_2 = 0, $$
(32)
$$ - v A_2 + b_1 A_1 + 4 (2 m^2 - 1) b_3 B^2 A_1 -4 (2 m^2 - 1) b_4 B^2 v A_2 = 0, $$
(33)
$$ 2 (1 - m^2) b_3 B^2 A_1 - 2 (1 - m^2) b_4 B^2 v A_2 = K_2, $$
(34)

where m is the modulus of the JEFs. When \(m\rightarrow 1,\, \hbox{cn} \tau\rightarrow \hbox{sech}\tau.\) From Eqs. (31) and (34), we get a relation between A 1 and A 2 given by

$$ A_2 = \frac{K_1 b_3 + K_2 a_4 v}{K_2 a_3 + K_1 b_4 v} A_1. $$
(35)

Substituting for A 2 from Eq. (35) in Eq. (29), we obtain explicit expressions for A 1 and A 2 given by

$$ A_1 = \frac{12 m^2 B^2 K_1}{a_2} \left(\frac{a_3 b_3 - a_4 b_4 v^2}{K_2 a_3 + K_1 b_4 v}\right), $$
(36)
$$ A_2 = \frac{12 m^2 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_3 b_3 - a_4 b_4 v^2)}{a_2 (K_2 a_3 + K_1 b_4 v)^2}. $$
(37)

From Eq. (32), we can derive an equivalent expression for A 1 which is

$$ A_1 = \frac{6 m^2 B^2 K_2}{b_2} \left(\frac{a_3 b_3 - a_4 b_4 v^2}{K_1 b_3 + K_2 a_4 v}\right). $$
(38)

Equating Eqs. (36) and (38), we get an explicit expression for v as a function of the coefficients a’s and b’s and the integration constants K 1 and K 2 in the form

$$ v = \frac{2 b_2 b_3 K_1^2 - a_2 a_3 K_2^2} {K_1 K_2 (a_2 b_4 - 2 a_4 b_2)}. $$
(39)

Now, using the remaining two Eqs. (30) and (34) we arrive at two constraint relations

$$ K_1a_1b_3+4(2m^2-1)K_1a_3b_3B^2+K_2(a_1a_4-a_3)v -\left[4(2m^2-1)B^2a_4b_4+b_4\right]K_1v^2=0, $$
(40)
$$ K_2a_3b_1+4(2m^2-1)K_2a_3b_3B^2+K_1(b_1b_4-b_3)v -\left[4(2m^2-1)B^2a_4b_4+a_4\right]K_2v^2=0. $$
(41)

In fact, we can also derive expressions for the inverse width B of the wave as functions of the coefficients a’s and b’s and the integration constants K 1 and K 2 from the two constraint relations.

Thus the periodic wave solutions of Eqs. (1) and (2) are,

$$ q = \frac{12 m^2 B^2 K_1}{a_2} \left(\frac{a_3 b_3 - a_4 b_4 v^2}{K_2 a_3 + K_1 b_4 v}\right)\,\hbox{cn}^{2}(B (x - v t)), $$
(42)
$$ r = \frac{12 m^2 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_3 b_3 - a_4 b_4 v^2)}{a_2 (K_2 a_3 + K_1 b_4 v)^2}\,\hbox{cn}^{2}(B (x - v t)). $$
(43)

In the infinite period limit, when \(m \rightarrow 1,\) the periodic wave solutions will give rise to the SWSs

$$ q = \frac{12 B^2 K_1}{a_2} \left(\frac{a_3 b_3 - a_4 b_4 v^2}{K_2 a_3 + K_1 b_4 v}\right) \hbox{sech}^{2}(B (x - v t)), $$
(44)
$$ r = \frac{12 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_3 b_3 - a_4 b_4 v^2)}{a_2 (K_2 a_3 + K_1 b_4 v)^2} \,\hbox{sech}^{2}(B (x - v t)). $$
(45)

3.2 Explode decay mode solutions

Now we look for explode decay mode solutions. For this purpose, we assume solutions for Eqs. (25) and (26) in the form

$$ q = A_1\,\hbox{sn}^{{\rm s}_1}(\tau),\quad r = A_2\, \hbox{sn}^{{\rm s}_2}(\tau), $$
(46)

where A 1 and A 2 are constants.

Equating the nonlinear terms and the highest derivative terms in Eqs. (25) and (26) we can again see that s 1 = 2 and s 2 = 2.

Thus in this case our solutions to Eqs. (25) and (26) are in the form

$$ q = A_1\, \hbox{sn}^{2}(\tau),\quad r = A_2\, \hbox{sn}^{2}(\tau). $$
(47)

Substituting Eq. (47) in Eqs. (25) and (26), and equating the coefficients of powers of ns(τ), we arrive at the equations

$$ \frac{1}{2} a_2 A_1^2 + 6 a_3 B^2 A_2 - 6 a_4 B^2 v A_1 = 0, $$
(48)
$$ - v A_1 + a_1 A_2 - 4 (1 + m^2) a_3 B^2 A_2+ 4 (1 + m^2) a_4 B^2 v A_1 = 0, $$
(49)
$$ 2 m^2 a_3 B^2 A_2 - 2 m^2 a_4 B^2 v A_1 = K_1, $$
(50)
$$ b_2 A_1 A_2 + 6 b_3 B^2 A_1 - 6 b_4 B^2 v A_2 = 0, $$
(51)
$$ - v A_2 + b_1 A_1 - 4 (1 + m^2) b_3 B^2 A_1 + 4 (1 + m^2) b_4 B^2 v A_2 = 0, $$
(52)
$$ 2 m^2 b_3 B^2 A_1 - 2 m^2 b_4 B^2 v A_2 = K_2. $$
(53)

From Eqs. (50) and (53), we get a relation between A 1 and A 2 given by

$$ A_2 = \frac{K_1 b_3 + K_2 a_4 v}{K_2 a_3 + K_1 b_4 v} A_1. $$
(54)

Substituting for A 2 from Eq. (54) in Eq. (48), we obtain explicit expressions for A 1 and A 2 given by

$$ A_1 = \frac{12 B^2 K_1}{a_2} \left(\frac{a_4 b_4 v^2 - a_3 b_3}{K_2 a_3 + K_1 b_4 v}\right), $$
(55)
$$ A_2 = \frac{12 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_4 b_4 v^2 - a_3 b_3)}{a_2 (K_2 a_3 + K_1 b_4 v)^2}. $$
(56)

From Eq. (51), we can derive an equivalent expression for A 1 which is

$$ A_1 = \frac{6 m^2 B^2 K_2}{b_2} \left(\frac{a_3 b_3 - a_4 b_4 v^2}{K_1 b_3 + K_2 a_4 v}\right). $$
(57)

Equating Eqs. (55) and (57), we get an explicit expression for v as a function of the coefficients a’s and b’s and the integration constants K 1 and K 2 in the form

$$ v = \frac{2 b_2 b_3 K_1^2 - a_2 a_3 K_2^2} {K_1 K_2 (a_2 b_4 - 2 a_4 b_2)}, $$
(58)

which is the same as Eq. (39).

Now, as in the previous case, using the remaining two Eqs. (49) and (52) we arrive at two constraint relations

$$ K_1a_1b_3-4(1+m^2)K_1a_3b_3B^2+K_2(a_1a_4-a_3)v +\left[4(1+m^2)B^2a_4b_4-b_4\right]K_1v^2=0, $$
(59)
$$ K_2a_3b_1-4(1+m^2)K_2a_3b_3B^2+K_1(b_1b_4-b_3)v +\left[4(1+m^2)B^2a_4b_4-a_4\right]K_2v^2= 0. $$
(60)

As in the previous subsection, we can derive expressions for the inverse width B of the wave as functions of the coefficients a’s and b’s and the integration constants K 1 and K 2 from the two constraint relations.

Thus another set of possible periodic wave solutions to Eqs. (1) and (2) are,

$$ q = \frac{12 B^2 K_1}{a_2} \left(\frac{a_4 b_4 v^2 - a_3 b_3}{K_2 a_3 + K_1 b_4 v}\right)\,\hbox{sn}^{2}(B (x - v t)), $$
(61)
$$ r = \frac{12 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_4 b_4 v^2 - a_3 b_3)}{a_2 (K_2 a_3 + K_1 b_4 v)^2}\,\hbox{sn}^{2}(B (x - v t)). $$
(62)

In the infinite period limit, when \( m \rightarrow 1,\) the periodic wave solutions will give rise to the explode decay mode solutions

$$ q = \frac{12 B^2 K_1}{a_2} \left(\frac{a_4 b_4 v^2 - a_3 b_3}{K_2 a_3 + K_1 b_4 v}\right)\,\hbox{csch}^{2}(B (x - v t)), $$
(63)
$$ r = \frac{12 B^2 K_1 (K_1 b_3 + K_2 a_4 v) (a_4 b_4 v^2 - a_3 b_3)}{a_2 (K_2 a_3 + K_1 b_4 v)^2}\, \hbox{csch}^{2}(B (x - v t)). $$
(64)

4 Numerical analysis

4.1 Solitary wave solution

In this section we present the numerical simulation of the obtained results. For the solution obtained in Sect. 2 we let a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1 and a 4 = b 4 =  −1. Because of relationship given by Eq. (19) one of the amplitude A 1 and A 2 can be chosen to be a parameter. In this case we pick arbitrarily A 2 and solve for A 1. If we solve for A 1 we get four possible solutions a solution that will lead to a real value of A 1. In this we have that

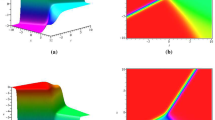
$$ A_1 = \frac{1}{2} \left(-3-2A_2+\sqrt{4 A_2^2+9}\right) $$
(65)

The solution of q(x, t) and r(x, t) are plotted in Fig. 1(a) and (b) respectively.

Fig. 1
figure 1

(a) Soliton solution, q(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1 and a 4 = b 4 =  −1. (b) Soliton solution, of r(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1 and a 4 = b 4 =  −1

Full size image

4.2 Periodic solution

We now examine the periodic solutions obtained in terms of the Jacobi elliptic functions are shown in Fig. 2(a) and (b). In case we again choose the values for a’s and b’s as in the preceding section. This time, however, we have that the values of A 1 and A 2 will depend on K 1 and K 2. We choose the values of K 1 = 1 and K 2 = 4. This values were chosen arbitrary but in such a way that A 1 and A 2 be defined and different from 0. We show the periodic solutions for different values m = 0.5, 0.75, 0.9, 0.99 and see how the solution is converging towards sech2[B(x − vt)].

Fig. 2
figure 2

(a) Periodic solution of q(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1, a 4 = b 4 =  −1, K 1 = 1 and K 2 = 4. (b) Periodic solution of r(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1 and a 4 = b 4 =  −1

Full size image

4.3 Explode decay mode solution

In this final subsection we show the decay mode solutions. The values for a’s and b’s are the usual. Similar to the previous section we can choose values appropriate K. Thus it is natural to use again K 1 = 1 and K 2 = 4. For the explode decay values we let m = 0.5, 0.75, 0.9, 0.99 and see how the solution is converging towards csch2[B(x − vt)] (Fig. 3).

Fig. 3
figure 3

(a) Solution of q(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1, a 4 = b 4 =  −1., K 1 = 1 and K 2 = 4. (b) Solution of r(x, t) at t = 10 with parameters a 1 = a 2 = a 3 = b 1 = b 2 = b 3 = 1, a 4 = b 4 =  −1., K 1 = 1 and K 2 = 4

Full size image

5 Conclusions

In this paper the BC equation that arises in the study of shallow water waves, was studied. The ansatz method obtained the solitary wave solution. Subsequently, the Jacobi’s elliptic function method obtained the cnoidal wave solution. In the limiting case the SWSs were obtained and thus the results matched with that of the ansatz method. This second method also obtained an additional piece of information, namely the singular solitary wave solutions were also obtained. The conserved density and hence the conserved quantity was also calculated using the multiplier approach. Finally, the numerical simulations were also given to supplement the analytical results.

It needs to be noted that all the results of this paper matches with the results that are published earlier. The difference is that the integration architecture that is adopted in this paper is different from the previously published results. The SWSs that are obtained by the ansatz method matches with the results that were derived in 1998 [5] and 2011 [12]. Additionally, the cnoidal wave solutions that are derived in this paper also match with those results that were published in 2007 [4]. Additionally, the numerical results that are obtained in this paper are in conjunction with the analytical development here.

There are certain disadvantages though with the integration tools that are adopted in this paper, in order to extract these variety of solutions. One disadvantage of the ansatz method is that this method cannot extract the soliton radiation that is unavoidable in the dynamics of solitary waves. Additionally, the ansatz method cannot obtain N-soliton solution to the equation of study. The same is the problem with the Jacobi’s elliptic function approach. The soliton radiation or the multi-soliton solution cannot be covered using this approach.