1 Introduction

Reliability, availability and maintainability (RAM) of the equipment play an important role in controlling both the quantity, and quality of the products. They aim at estimating and predicting the probability of the failure, and optimizing the operational management related to the provision of the failures, i.e., maintenance policies. Factors that affect RAM of an industrial system include machinery operating conditions, maintenance conditions, infrastructural facilities, and so forth [1–3]. As the industrial systems are growing complexity and hence it is difficult for the system analyst for enhancing/maintaining the production or productivity of the entire system in such as way that each component/system of the entire production plant will run failure free. However, failure is an inevitable phenomenon in a system. Therefore, the system or components undergo several failure–repair cycles that include logistic delays while performing repair leads to the degradation of systems’ overall performance. Thus to improve the reliability and availability of the system, a proper maintenance strategy plays an important role. On the other hand, the availability of the system can be improved by improving its reliability and maintainability under the consume resources such as cost, weight, volume etc. Thus, keeping all these views, behavior of such systems can be studied in terms of RAM. For this, a composite measure of all these indices which influences the system performance directly has been introduced, named as RAM-index, for measuring the performance of the system.

Often, reliability of the component is not specific. This is due to that the reliability of a component/system depends on operational and environmental conditions. Moreover, in the early design phase reliability of a system may be taken into account and hence it is difficult to determine the reliability specifically. Further, the causes may be age, adverse operating conditions and the vagaries of manufacturing processes which affect each part/unit of the system differently. Finally for measuring the performance of the system, the data require are taken in the form of failure rate and repair time from the historical or available records which are usually out of date or representing the past behavior of the system but unable to predict the future behavior of the system and thus subject to the issue of uncertainty. Thus, the probabilistic approach to the conventional reliability analysis is inadequate to account for such built-in uncertainties in the data. For this reason and to handling these issues, the concept of fuzzy set theory or fuzzy reliability has been introduced because if the data are used as such in the calculations, the results will be highly uncertain.

Thus for computing the RAM parameters and consequently their behavior, an approach gave by Knezevic and Odoom [4] and Garg [5] may be used for computing their parameters in terms of fuzzy membership functions. But it has been analyzed from the study that their approach is limited to a small size structure and hence not suitable for the complex structured system due to various fuzzy arithmetic operations used in the analysis. Therefore spread of the reliability index must be optimized up to a desired degree of accuracy so that plant personnel may use these for improving the performance of the system. In that direction, researchers [6–8] have attempted an approach for computing the membership function of the reliability indices by formulating a nonlinear optimization problem and hence solve with the evolutionary algorithm like GA, PSO etc. In the present study, particle swarm optimization based lambda–tau (PSOBLT) technique is used [6, 7]. With this technique, expression of the system parameters is obtained by using a lambda–tau methodology while their corresponding membership functions are generated by formulating a nonlinear programming problem and then solve with PSO. The major advantage of this technique is that it gives the compressed search space for each computed reliability index by utilizing available information and uncertain data than other existing techniques. These suggest that decision maker/ system analyst has smaller and more sensitive region to make more sound and effective decision to improve the system performance in lesser time.

In the framework of RAM analysis, some researcher pay attention on that issue in which they analyze the performance of the system by considering reliability, availability or maintainability as an objective function. In their analysis they adopt a suitable methodology for analyzing their behavior and help the plant personnel to plan and adapt suitable maintenance strategies for increasing the performance and productivity of the system. For instance, Sharma and Kumar [9] analyzed the performance of urea fertilizer plant in terms of RAM parameters by applying Markovian approach. Rajpal et al. [10] developed an artificial neural network (ANN) model for assessing the effect of input parameters on RAM analysis of a repairable system. In their analysis, historical data are used to train the ANN. But there exists some obstacle during their analysis. The major one is due to their static in nature as they used the values of RAM parameter at specified times because in real-life situation, the behavior of the industrial system varies with time and hence it does not give the exact idea about the behavior of the system. Also they used historical data without quantifying their uncertainties in the analysis. On the other hand, these limitations have been overcome by the researchers [2, 8] by quantifying the uncertainties in the form of triangular fuzzy numbers and then analyzed their consequent RAM parameters in the form of fuzzy membership function by using soft computing based hybridized techniques. As most of the above researcher has analyzed the performance of the system by considering the constant failure and repair rates i.e., follow the exponential distribution. Also it was assumed by the researchers that all the components follow the same types of fuzzy numbers. But in real-life situation, however, it is common to have a system of components having different failure probability density functions. As we know, the most popular reliability distributions are Weibull and normal distributions. Therefore, it seems that there is a need for a more generalized methodology that can be applied for variable rates.

Thus the objective of the paper is to quantify the uncertainty in the data during the evaluation of the RAM parameters for a complex repairable industrial system. For this composite measure of the RAM named as the RAM-index has been analyzed for measuring the performance of the system. The time varying failure rate model which follows Weibull and normal distribution has been taken instead of following the exponential distribution for accessing the effect of failure and repair pattern on to a system performs. The technique has been demonstrated through a case study of the crankcase manufacturing plant. The results may be helpful for plant personnel for analyzing the system behavior and may improve the system performance by adopting suitable maintenance strategies.

2 Notations

The following are the notations that have been used in the entire paper.

β, γ :

Shape parameters of failure and repair rate of the Weibull distribution respectively.

θ, η :

Scale parameters of failure and repair rate of the Weibull distribution respectively.

μ, ν :

Mean of the failure and repair rate parameters of normal distribution respectively.

σ 1, σ 2 :

Standard deviation of the failure and repair rate of normal distribution respectively.

t :

Operating time.

\(\Upphi(\cdot)\) :

Distribution function of the standard normal distribution.

λ :

Failure rate of the system.

λ r :

Repair rate of the system.

τ :

Repair time of the system.

T :

Continuous random variable.

A :

Crisp set.

\(\widetilde{A}\) :

Fuzzy set.

\(\mu_{\widetilde{A}}\) :

Membership function of the fuzzy set.

3 Basic Concepts of Fuzzy Set Theory

3.1 Classical Versus Fuzzy Set

A classical (crisp) set is normally defined as a collection of elements or objects x  ∈ X which can be finite, countable or overcountable. Each single element can either belong to or not belong to a set A. Such set is represented by using the characteristic function, in which 1 indicated membership and 0 nonmembership. Most of our traditional tools for formal modeling, reasoning, and computing are crisp, deterministic and precise in character. Although the probability approach has been applied successfully to many real world engineering reliability problems [11–13] but still there are some complications arises during the modeling of the system. The two major complications in modeling arise are [14]

  1. (i)

    Real situations are very often not crisp and deterministic and they cannot be prescribed precisely.

  2. (ii)

    The complete description of a real system often would require by far more detailed data than a human being could ever recognize simultaneously, process it and understand.

To overcome these difficulties, mathematical modeling of fuzzy concepts (a generalization of crisp or classical set approach) was presented by Zadeh [15] by allowing images of elements to be in the interval [0,1] rather than being restricted to the two-element set {0,1}. In other words, the theory of fuzzy sets deals with a subset \(\widetilde{A}\) of the universe of discourse X, where the transition between full membership and no membership is gradual rather than abrupt. The fuzzy subset has no well-defined boundaries whereas the universe of discourse X covers a definite range of the objects. Fuzzy set theory is a generalization of classical set theory in which ambiguity and vagueness types of inexactness concepts are handled. Let X be a classic set of objects, whose generic elements is denoted by x. A fuzzy set \(\widetilde{A}\) defined on X is a mapping from X to the unit interval [0, 1], is denoted by

$$ \widetilde{A}=\{x,\mu_{\widetilde{A}}(x) \mid x \in X \} $$
(1)

where \(\mu_{\widetilde{A}}(x)\) indicates the degree of membership of x in \(\widetilde{A}\) and its value lies between zero and one.

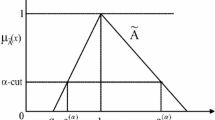
3.2 α-Cuts

α-Cuts is one of the most significant and extensively used concept in fuzzy set theory [16]. It is defined as all those element x ∈ X such that its membership value be greater than some threshold α  ∈ [0, 1]. The ordinary set of elements is the α-cut A (α) of fuzzy set \(\widetilde{A}\) and is represented mathematically as

$$ A^{(\alpha)} = \{x\in X \mid \mu_{\widetilde{A}}(x) \geq \alpha\} $$
(2)

For a fuzzy set \(\widetilde{A}\),

$$ A^{(\alpha)} = \{x\in X \mid \mu_{\widetilde{A}}(x) > \alpha\};\quad \alpha \in[0, 1) $$
(3)
$$ A^{(\alpha)} = \{x\in X \mid \mu_{\widetilde{A}}(x) \geq \alpha\};\quad \alpha \in(0, 1] $$
(4)

are called the strong α-cut and weak α-cut respectively. It the membership function is continuous, the distinction between strong and weak is not necessary due to the logical development inherent in the cut. If the support set (i.e., the whole set X) is a real number set and the membership function is continuous, the weak cut of convex fuzzy set is a closed interval.

3.3 Fuzzy Number and Arithmetic Operations

By a fuzzy number, we mean a number that is characterized by a possibility distribution or is a fuzzy subset of real numbers. In general, a fuzzy number is either a convex or concave fuzzy subset of the real line. A special case of a fuzzy number is an interval. Let \(\widetilde{A}\) be a fuzzy set then it is a fuzzy number if and only if there exists a close interval [a, b] ≠ ϕ such that

$$ \begin{aligned} \mu_{\widetilde{A}}(x)= \left\{ \begin{aligned} l(x); \quad & \hbox {for} \; x \in (-\infty,a) \\ 1; \quad & \hbox {for}\; x \in [a, b] \\ r(x); \quad & \hbox {for} \; x \in (b,\infty) \\ \end{aligned}\right. \end{aligned} $$
(5)

where l is a function from (−∞, a) to [0,1] that is monotonic increasing, continuous from the right, and r is a function from (b, ∞) to [0,1] that is monotonic decreasing, continuous from the left.

There is an infinite set of fuzzy numbers, but triangular fuzzy numbers (TFNs) are more often used when fuzziness exist on both sides of a single value/parameter. A TFN is defined by the ordered triplet \(\widetilde{A}=(a,b,c)\) representing, respectively, the lower value, the modal value, and the upper value of a triangular fuzzy membership function. Its membership function \(\mu_{\tilde{A}}: \mathbb{R} \longrightarrow [0,1]\), is defined as:

$$ \begin{aligned} \mu_{\widetilde{A}}(x)= \left\{ \begin{aligned} \frac{x-a}{b-a}; \quad & a \leq x \leq b \\ 1; \quad & x = b \\ \frac{c-x}{c-b}; \quad & b \leq x \leq c \\ 0; \quad & \hbox{otherwise} \end{aligned}\right. \end{aligned} $$
(6)

Alternately, TFN can be characterized by the interval of confidence at α-cut level like.

$$ A_{\alpha} = [a^{(\alpha)}, c^{(\alpha)}] = [(b-a)\alpha+a, -(c-b)\alpha+c] \quad \forall\;\alpha \in [0,1] $$
(7)

The normal membership function with mean b and standard deviation σ is defined as

$$ \mu_{\tilde{A}}(x)= \begin{aligned} \left\{\begin{array}{ll} e^{-(\frac{x-b}{\sigma})^2} & \hbox{if}\; x \leq b \\ 1 & \hbox {if $x=b$}\cr e^{-(\frac{b-x}{\sigma})^2} & \hbox{if}\; b\leq x \end{array}\right. \end{aligned} $$
(8)

Viewed in this perspective, fuzzy arithmetic may be viewed as a generalization of interval arithmetic. Thus the four main arithmetic operations on two fuzzy sets \(\widetilde{A}\) and \(\widetilde{B}\) described by the α-cuts are given below for the following intervals: A (α) = [A (α)1 , A (α)3 ] and B (α) = [B (α)1 , B (α)3 ],   α  ∈ [0, 1]

  1. (i)

    Addition: \(\tilde{A}+\tilde{B}=[A_{1}^{(\alpha)}+B_{1}^{(\alpha)}, A_{3}^{(\alpha)}+B_{3}^{(\alpha)}]\)

  2. (ii)

    Subtraction: \(\tilde{A}-\tilde{B}=[A_{1}^{(\alpha)}-B_{3}^{(\alpha)}, A_{3}^{(\alpha)}-B_{1}^{(\alpha)}]\)

  3. (iii)

    Multiplication: \(\tilde{A}\cdot\tilde{B}=[H^{(\alpha)}, G^{(\alpha)}]\) where H (α) = min(A (α)1 · B (α)1 , A (α)1 · B (α)3 , A (α)3 · B (α)1 , A (α)3 · B (α)3 ) and G (α) = max(A (α)1 · B (α)1 , A (α)1 · B (α)3 , A (α)3 · B (α)1 , A (α)3 · B (α)3 )

  4. (iv)

    Division : \(\tilde{A}\div \tilde{B}= \tilde{A} \cdot \frac{1}{\tilde{B}}\), if \(0 \notin \tilde{B}\)

It is clear that the multiplication and division of two TFNs is not again a TFN with linear sides but it is a new fuzzy number with parabolic sides.

4 Reliability Aspects

This section introduce RAM concepts that are used for deriving the composite measures of these parameters named as RAM-index.

4.1 Reliability

Reliability is a characteristic of an item(component or system), expressed by the probability that the item (component/system) will perform its required function under given conditions for a stated time interval [17]. From a qualitative point of view, reliability can be defined as the ability of the item to remain functional. Quantitatively, reliability specifies the probability hat no operational interruptions will occur during a stated time interval. Mathematically, define continuous random variable T to be the time to failure of the component/system; T ≥ 0, then the basic reliability function R(t) is defined for time to failure of the system (or subsystem) as

$$ R(t)=Pr(T> t) = 1-\int\limits_{0}^{t} f(u)\;du $$
(9)

where \(R(t) \geq 0,\; R(0) = 1\), and \(\lim\limits_{t \rightarrow \infty} R(t) = 0\) and f(t) failure probability density function. For Weibull and normal distribution, reliability of the system is defined as

$$ R(t) = Pr(T> t) = \exp\bigg[-\bigg(\frac{t}{\theta}\bigg)^{\beta}\bigg] $$
(10)

and

$$ R(t) = Pr(T>t) = 1-\Upphi \bigg( \frac{t - \mu}{\sigma_1} \bigg) $$
(11)

for respective distributions.

The failure rate (λ) function of the system is given by

$$ \lambda(t) = \frac{f(t)}{R(t)} $$

4.2 Maintainability

Maintainability refers to the measures taken during the development, design, and installation of a manufactured product that reduce required maintenance, manhours, tools, logistic cost, skill levels, and facilities, and ensure that the product meets the requirements for its intended use [1]. Thus, maintainability deals with duration of maintenance outages or how long it takes to complete the (ease and speed) maintenance actions. The key maintainability figures of merit are the MTTR and a limit for the maximum repair time. To quantify the repair time, let T be the continuous random variable representing the time to repair a failed unit, having a probability density function of h(t), then the cumulative distribution function M(t) is defined below [1]

(12)

This equation is the probability that a repair will be accomplished within time t. The MTTR is defined as:

$$ \hbox{MTTR}=\int\limits_{0}^{\infty}t\,h(t)dt=\int\limits_{0}^{\infty}(1-M(t))dt $$
(13)

For Weibull and normal distribution, maintainability of the system is defined as

$$ M(t) = Pr(T< t) = 1-\exp\bigg[-\bigg(\frac{t}{\eta}\bigg)^{\gamma}\bigg] $$
(14)
$$ M(t) = Pr(T< t) = \Upphi \bigg( \frac{\nu - t}{\sigma_2} \bigg) $$
(15)

for respective distributions.

The repair rate (λ r ) function of the system is given by

$$ \lambda_r(t) = \frac{h(t)}{M(t)} $$

4.3 Availability

Availability is the probability that a system or component is performing its required function at a given point in time or over a stated period of time when operated and maintained in a prescribed manner [1]. Consider a system (device) which can be in one of two states, namely ‘up’ and ‘down’ i.e., in other words the system is still functioning and is not functioning state; in the latter case it is being repaired or replaced, depending on whether the system is repairable or not. Let the state of the system be given by a binary variable:

$$ \begin{aligned} X(t)= \left\{\begin{aligned} 1, \quad & \hbox {if the system is up at time}\,{t} \\ 0, \quad & \hbox {otherwise} \end{aligned}\right. \end{aligned} $$
(16)

An important characteristic of a repairable system is availability. Barlow and Proschan [18] define four measures of availability performance: the availability function, limiting availability, the average availability function and limiting average availability. All of these measures are based on the function X(t), which denotes the status of a repairable system at time t. The instant availability at time t (or point availability) is defined by:

$$ A(t) = P(X (t)=1) $$
(17)

This is the probability that the system is operational at time t. Mathematically, it is represented through the differential equation of first order as given below

$$ \frac{d}{dt}A(t)+[\lambda(t)+\lambda_r(t)] A(t) = \lambda_r(t); \quad A(0)= e^{\int(\lambda(t)+\lambda_r(t))\,dt}\mid_{t=0} $$
(18)

and its corresponding solution is

$$ A(t)= e^{-\int(\lambda(t)+\lambda_r(t))\,dt } \bigg[ \int \lambda_r(t) \; e^{\int(\lambda(t)+\lambda_r(t))\,dt}\,dt + c \bigg] $$
(19)

Because it is very difficult to obtain an explicit expression for A(t), other measures of availability have been taken. One of these measures is the steady system availability (or steady state availability, or limiting availability) of a system, which is defined by

$$ A = \lim\limits_{t \rightarrow \infty} A(t) $$
(20)

This quantity is the probability that the system will be available after it has been run for a long time, and is a very significant measure of performance of a repairable system.

4.4 RAM-Index

System reliability, maintainability and availability have assumed great significance in recent years due to a competitive environment and overall operating and production costs. Performance of equipment depends on the reliability and availability of the equipment used, operating environment, maintenance efficiency, operation process and technical expertise of operators, etc. When the reliability and availability of systems are low, efforts are needed to improve them by reducing the failure rate or increasing the repair rate for each component or subsystem. Thus, RAM are the important key features for keeping the production and productivity of the system high. For maintaining this, a composite measure of RAM parameters named as the RAM-index has been analyzed by the researchers [8–10] for increasing the performance of the system. But the disadvantages of Sharma and Kumar [9] approach are that they applied Markovian approach by utilizing historical crisp data without quantification of involved uncertainties. On the other hand, Rajpal et al. [10] developed an artificial neural network (ANN) model for assessing the effect of input parameters on system performance at specified times i.e., its values does not change with time. But in real life situations, industrial system behavior changes with time. Thus it does not provide the actual trend of the system behavior. Also it is unable to access and analyze the sensitive component of the system. Komal et al. [8] extend this idea by quantifying the uncertainty in the analysis. But their approach is limited to a system whose components follow the constant failure rate model i.e., following the exponential distribution. Thus there is a need of a generalized index for a time varying component parameter for measuring the performance of the system such that system analyst may find the component on which more attention should be given to save money, manpower and time. Therefore, the proposed RAM-index is valid for a time varying failure and repair rate (Weibull and normal distribution) instead of constant failure rate model (exponential distribution) and is given as below

$$ RAM(t) = w_1 \times R(t) + w_2 \times A(t) + w_3 \times M(t) $$
(21)

where w i  ∈ (0,1) be the weights such that \(\sum\nolimits_{i=1}^{3} w_i = 1\) and R(t), A(t) and M(t) are the systems RAM expression for a given mission time t. The same value of weight set w = [0.36, 0.30, 0.34], as used by the researchers [2, 8, 10], are used here for the analysis. The benefit of this index is that it simultaneously considers all the three key indices which influence the system performance directly. Also measure advantage of this index is that by varying individual component’s failure rate and repair time parameters, the impact onto the system’s performance by the change in its behavior can be analyzed effectively to make the future course of action.

5 Methodology for Analyzing the Behavior

5.1 Lambda–Tau Methodology

Traditionally in order to analyze the behavior of the repairable systems, fault tree analysis has been used for modeling the system while their system failure rates (λ s ) and repair times (τ s ) associated with logical AND- and OR-gates are obtained by using the basic expression of the lambda–tau methodology which are summarized in Table 1 [19]. But the disadvantage of this methodology is that they do not consider the uncertainties which are present in the data. Because most of the databases collected from the various resources or records are represent the past behavior of the data and hence unable to predict the future behavior of the system. Moreover, if as such data are used in the analysis then they have a high range of uncertainties and hence do not give the accurate idea about the behavior of the system. Knezevic and Odoom [4] highlighted this idea and presented an approach named as fuzzy lambda–tau (FLT) methodology for repairable industrial systems. In their approach, the uncertainty in the data is handled with the help of the defining their fuzzy membership functions and system is modeled with the help of Petri nets instead of fault tree. Triangular fuzzy numbers (TFNs) are used for handling the uncertainties in the analysis. After obtaining the input of all components in the form of TFNs, the resultant fuzzy numbers for failure rate and repair time for the top place of PN model, can be obtained using the extension principle, coupled with α-cut and interval arithmetic operations on conventional AND/OR-expression, as listed in Table 1. The interval expression for the triangular fuzzy number, for the failure rate \(\tilde{\lambda}\) and repair time \(\tilde{\tau}\), for AND/OR-transitions are as follows:

Table 1 Basic expressions of lambda–tau methodology
Full size table

Expressions for AND-Transitions

$$ \begin{aligned} \lambda^{(\alpha)} &= \Bigg[\prod\limits_{i=1}^{n}\{(\lambda_{i2}-\lambda_{i1})\alpha+\lambda_{i1}\}\cdot \sum_{j=1}^{n}\bigg[\prod\limits_{i=1\atop i\neq j}^{n}\{(\tau_{i2}-\tau_{i1})\alpha+\tau_{i1}\}\bigg],\\ &\prod\limits_{i=1}^{n}\{-(\lambda_{i3}-\lambda_{i2})\alpha+\lambda_{i3}\}\cdot \sum_{j=1}^{n}\bigg[\prod\limits_{i=1\atop i\neq j}^{n}\{(\tau_{i3}-\tau_{i2})\alpha+\tau_{i3}\}\bigg]\Bigg] \end{aligned} $$
(22)
$$ \begin{aligned} \tau^{(\alpha)}&= \Bigg[\frac{\prod\nolimits_{i=1}^{n}\{(\tau_{i2}-\tau_{i1})\alpha+\tau_{i1}\}}{\sum\nolimits_{j=1}^{n}[\prod\nolimits_{i=1\atop i\neq j}^{n}\{-(\tau_{i3}-\tau_{i2})\alpha+\tau_{i3}\}]},\\ &\frac{\prod\nolimits_{i=1}^{n}\{(\tau_{i3}-\tau_{i2})\alpha+\tau_{i3}\}}{\sum\nolimits_{j=1}^{n}[\prod\nolimits_{i=1\atop i\neq j}^{n}\{(\tau_{i2}-\tau_{i1})\alpha+\tau_{i1}\}]}\Bigg] \end{aligned} $$
(23)

Expressions for OR-Transitions

$$ \begin{aligned} \lambda^{(\alpha)}&= \Bigg[\sum_{i=1}^{n}\{(\lambda_{i2}-\lambda_{i1})\alpha+\lambda_{i1}\},\\ &\sum_{i=1}^{n}\{-(\lambda_{i3}-\lambda_{i2})\alpha+\lambda_{i3}\} \Bigg] \end{aligned} $$
(24)
$$ \begin{aligned} \tau^{(\alpha)} =& \Bigg[\frac{\sum\nolimits_{i=1}^{n}[\{(\lambda_{i2}-\lambda_{i1})\alpha+\lambda_{i1}\}\cdot \{(\tau_{i2}-\tau_{i1})\alpha+\tau_{i1}\}]}{\sum\nolimits_{i=1}^{n}\{-(\lambda_{i3}-\lambda_{i2})\alpha+\lambda_{i3}\}},\\ & \frac{\sum\nolimits_{i=1}^{n}[\{-(\lambda_{i3}-\lambda_{i2})\alpha+\lambda_{i3}\}\cdot \{-(\tau_{i3}-\tau_{i2})\alpha+\tau_{i3}\}]}{\sum\nolimits_{i=1}^{n}\{(\lambda_{i2}-\lambda_{i1})\alpha+\lambda_{i1}\}}\Bigg]\\ \end{aligned} $$
(25)

5.2 Shortcoming of the Existing Methodologies

The following shortcoming are observed during the analysis of the repairable industrial system when FLT methodology has been applied for computing the reliability parameters.

  1. (a)

    They computed only defuzzified values of failure rates and repair times and then used these values for obtaining the defuzzified values of other reliability parameters.

  2. (b)

    The fuzzy arithmetic operations have been used by them for computing the systems’ parameters and hence the method will not produce the actual trend of values of these reliability parameters as per the variations in uncertainties levels.

  3. (c)

    Their approach is limited for small size structure i.e., for a large structured system or when system configuration is in complex then the computed parameters have a wide range of uncertainties in the form of spread due to various fuzzy arithmetic operations involved in the analysis.

5.3 PSOBLT Methodology

PSOBLT technique is a novel technique [6, 7] for analyzing the behavior of an industrial system by utilizing uncertain data up to a desired degree of accuracy. In this technique, particle swarm optimization (PSO) and lambda–tau methodology has been hybridized to each other. The uncertainties in the data are handled with the help of defining their corresponding fuzzy numbers. After obtaining the basic events of the systems in the form of the fuzzy numbers, the system reliability expression is obtained by formulating the non-linear optimization problem instead of fuzzy arithmetic operations at each cut level α. PSO has been used for solving the optimization problem for constructing their fuzzy membership functions. The following tools are adopted in the methodology for removing the critical shortcoming of the existing methodologies, which may give good results (close to real conditions):

  1. (i)

    As Weibull and normal distribution are the most important in the field of reliability so hence the instead of considering the constant failure rate model, a time varying data which follow the normal and Weibull distribution has been taken in the analysis.

  2. (ii)

    Triangular and normal fuzzy numbers are used for handling the uncertainties in the data corresponding to the Weibull and normal distribution respectively instead of considering only triangular fuzzy numbers.

  3. (iii)

    Sensitivity analysis on the system performance i.e., on RAM-index has been analyzed for showing the effect of individual components on its performance.

The detail of the strategies followed for the RAM analysis of an industrial system is explained as below:

The methodology starts with the information extraction phase in which data related to failure and repair rates of the constituent components are extracted from the historical records, databases etc. and are integrated with the plant personnel. Most of the data are collected or estimated from the historical record which involves a large amount of uncertainties because most of the databases on which reliability analyzes depend are either out of date or collected under different operating and environmental conditions. So to handle the vagueness and uncertainties in the analysis, fuzzy set theory is used in PSOBLT technique. Triangular and normal fuzzy numbers are used for this purpose with some known spread (support) suggested by decision makers (DM), design maintenance expert, system reliability analyst.

After quantifying the uncertainties in the data in the form of fuzzy numbers, the expression of the system’s parameters are obtained by using the results of lambda–tau methodology i.e., by using Table 1 results. For a complex or large structure system, the expression of these reliability indices is highly nonlinear in nature and hence when fuzzy arithmetic operations are used for computing their membership functions then the high level of uncertainties exit in them. To overcome this problem, a nonlinear optimization problem for each of the computed reliability indices has been constructed by utilizing the quantified fuzzy data at cut level α in the form of bounded interval as decision variable. Once, the quantified input data at cut level α in the form of bounded interval is substituted in the expression of each obtained reliability index, the finally computed reliability index at cut level α has a wide range of solutions and it becomes smaller and smaller as the analysis progresses further i.e., cut level α increases from 0 to 1. Thus, the lower and upper boundary values of reliability indices are computed at cut level α by solving the optimization problem (26)

$$ \begin{aligned} \,&\hbox{Minimize}/\hbox{Maximize}:\\ \,&\qquad \tilde{F}(\lambda_{1},\lambda_{2},\dots,\lambda_{n},\tau_1,\tau_2,\dots,\tau_m)\\ \,&\begin{array}{lll} \hbox{Subject to}:& \mu_{\lambda_i}(x)\geq\alpha,\\ &\mu_{\tau_j}(x)\geq\alpha,\\ &0\leq\alpha\leq1,\\ &i=1,2,\dots,n;&j=1,2,\dots,m.\\ \end{array} \end{aligned} $$
(26)

where \(\tilde{F}(\lambda_1,\lambda_2,\ldots,\lambda_n,\tau_1,\tau_2,\ldots,\tau_m)\) are time dependent fuzzy RAM indices parameter. The obtained minimum and maximum value of F are denoted by F min and F max respectively. The membership function values of F at F min and F max are both α that is,

$$ \mu_{\tilde{F}}(F_{\min})=\mu_{\tilde{F}}(F_{\max})=\alpha $$

Since the problem is nonlinear in nature so it requires an efficient technique to solve this problem. Out of existence of a variety of traditional and non-traditional methods for solving such types of problems, evolutionary algorithms are found to be very promising global optimizers. PSO is one of the most popular evolutionary algorithms [20, 21] and has been applied effectively to many different problems like system reliability/availability/redundancy allocation [6, 22–25]. Recently, Garg and Sharma [26] used PSO to solve the reliability-redundancy allocation problem under fuzzy environment by taking linear and nonlinear membership functions for defining their fuzzy goals. Thus in the light of applicability, this paper use PSO as a tool to solve the optimization problem (26) in the process of determining the fuzzy membership function of RAM parameters. The objective function for maximization problem and the reciprocal of the objective function for minimization problem is taken as the fitness function. To stop the optimization process maximum number of generations or order of relative error equal to 10−6, whichever is achieved first.

Finally, as soon as the reliability parameters are obtained in the form of membership functions then the system analyst or decision makers make a decision based on their results. In order to obtain a crisp result from fuzzy output, defuzzification is carried out. In the literature various techniques for defuzzification such as centroid, bisector, middle of the max, weighted average exists. The criterion’s for their selection are disambiguated (result in unique value), plausibility (lie approximately in the middle of the area) and computational simplicity [27]. In the present study, the centroid method is used for defuzzification as it gives mean value of the parameters. Mathematically centroid or center of gravity (COG) method is represented as Eq. (27)

$$ \bar{x}=\frac{\int\nolimits_x x\cdot\mu_{\tilde{B}}(x)dx}{\int\nolimits_x \mu_{\tilde{B}}(x)dx} $$
(27)

where \(\widetilde{B}\) is the output fuzzy set, and \(\mu_{\tilde{B}}\) is the membership function.

5.4 PSO Algorithm Overview

Particle swarm optimization (PSO), first introduced by Kennedy and Eberhart [20, 28], is an evolutionary computation technique, developed for optimization of continuous non linear, constrained and unconstrained, non differentiable multimodal functions. It uses common evolutionary computation techniques: (a) It is initialized with a population of random solutions. (b) It searches for the optimum by updating generations, and (c) population evolution is based on the previous generations. PSO algorithm works by initializing a flock of birds randomly over the searching space, where every bird is called as a “particle” are flown through the problem space by following the current optimal particles. The update of the particles is accomplished by adjusting its velocity vector and the influence of its best position (pbest) as well as the best position of its neighbors (gbest). Suppose the dimension for a searching space is D, the total number of particles is n, the position of the ith particle can be expressed as vector \(x_i=[x_{i1},x_{i2},\ldots,x_{iD}]\) the best position of the ith particle is denoted as \(pbest_i=[pbest_{i1}, pbest_{i2},\ldots,pbest_{iD}]\), and the best position of the total particle swarm is denoted as vector \(gbest=[gbest_{1}, gbest_{2},\ldots,gbest_{D}]\), the velocity of the ith particle is represented as vector \(v_i=[v_{i1},v_{i2},\ldots,v_{iD}]\). Then the position and velocity of the particle are updated by the following relations [21, 29]

$$ \begin{aligned} v_i(t+1)&= w\ast v_i(t)+c_1\ast r_1\ast(pbest_i(t)-x_i(t))\\ &\quad+ c_2 \ast r_2 \ast (gbest(t)-x_i(t)) \end{aligned} $$
(28)
$$ x_i(t+1) = x_i(t)+ v_i(t+1) $$
(29)

where c 1 and c 2 are constants, r 1 and r 2 are random variable with uniform distribution between 0 and 1, w is inertia weight, which shows that the effect of previous velocity vector on the new vector and provided improved performance in a number of applications. The pseudo code of the algorithm is described in Algorithm 1.

figure a

6 Illustrative Example

The above mentioned technique for RAM analysis of the system is demonstrated through a case study of the crankcase manufacturing plant of a repairable industrial system [3]. The brief description of the system is given as below.

6.1 System Description

The crank-case manufacturing plant consists of nine single unit subsystems named as modulo machine-1, module SPM widma-1, modulo machine-2, module SPM widma-2, module machine-3, fine bores, horizontal milling machine, tapping machine-1 and tapping machine-2. All these sub-systems are single units subjected to revealed as well as unrevealed failure. The first machine in the crank-case line is the module machine-1, is used to drill on the sides of the crank-case. Module SPM widma-1 machine is used to drill on the face of the raw crank-case. The module machine-2 is used for side tapping. The module SPM widma-2 is used for tapping. Module machine-3 is used for further tapping. Fine bores are drilled with the help of micro fine boring machine. Milling is done with the help of horizontal milling machine. Then tapping is done on tapping machine-1 and finally on tapping machine-2. Undergoing all these processes serially, we get a finished crank-case. The systematic diagram of the system is shown in Fig. 1 [3].

Fig. 1
figure 1

Systematic flow diagram of the crank-case manufacturing system

Full size image

7 Results and Discussions

7.1 Parametric Setting

In all algorithms, the values of the common parameters such as population size and total evaluation number are chosen to be the same. Population size and the maximum evaluation number are taken as 20 × D, where D is the dimension of the problem and 1500 respectively for the function. The method has been implemented in Matlab (MathWorks) and in order to eliminate stochastic discrepancy, 30 independent runs has been made that involves 30 different initial trial solutions. The termination criterion has been set either limited to a maximum number of generations or to the order of relative error equal to 10−6, whichever is achieved first. The other randomly specified parameters of algorithms are given below:

GA Settings In our experiment, real coded genetic algorithm, is utilized to find optimal values. The roulette wheel selection criterion is employed to choose better fitted chromosomes. One-point crossover with the rate of 0.9 and random point mutation with the rate of 0.01 are used in the present analysis for the reproduction of new solutions.

PSO Settings Except common parameters (population number and maximum evaluation number), cognitive (c 1) and social (c 2) components are constants that can be used to change the weighting between personal and population experience, respectively. In our experiments cognitive and the social components were both set to 1.49. Inertia weight (w), which determines how the previous velocity of the particle influences the velocity in the next iteration, was defined as the linearly decreases from initial weight w 1 = 0.9 to final weight w 2 = 0.4 with the relation w = w 2 + (iter max − iter)(w 1 − w 2)/iter max where iter max is the maximum number of iterations and iter is used an iteration number [21].

7.2 Computation of RAM Parameters

The analysis for computing the RAM parameters for the above system is explained as below.

  1. (i)

    Under the information extraction phase, the data related to failure and repair rates of the main components of the system are collected from the records/textbooks etc. and are integrated with the plant personnel given in Table 2 [3].

  2. (ii)

    As the data given in Table 2 is collected from the various historical records/textbooks/databases etc. and hence it contains some sort of uncertainty. This is because of the human error or various other practical constraints that affect during the analysis of data. Moreover, historical records represent the past behavior but unable to predict the future behavior of the system. Thus uncertainties in the collected data are handled with the help of fuzzy set theory. For this, crisp data are converted into triangular fuzzy numbers corresponding to Weibull related parameters and normal fuzzy number corresponding to normal distribution parameters with ±15 % spreads on both sides of the data.

  3. (iii)

    After converting the input data into the fuzzy number, an optimization problem (26) has been formulated for the considered system for evaluating the RAM-parameters at the mission time t = 10(h). The obtained problem has been solved with the evolutionary techniques corresponding to their parametric setting, given in Sect. 7.1, for obtaining their membership function at each α-cut level. The computed fuzzy RAM of the system have been plotted and shown in Fig. 2 along with crisp, FLT and genetic algorithm based lambda–tau (GABLT) results. The complete analysis of these plots is described as follows.

    1. (a)

      The results computed by the crisp or traditional methodology are independent of the uncertainty level α i.e., it remains constant at all values of α. It shows that while obtaining the results by these methods, attention has not been paid to the uncertainties in the data. Thus this methodology is not practically sound and hence their results will be suitable only for a system with precise data.

    2. (b)

      The results computed by the FLT approach contains a wide range of uncertainties as compared to other approaches. This is due to the reason that the membership functions of the reliability parameter are computed with the help of fuzzy arithmetic operations and hence it contains a wide spread or support during the analysis. Thus these results are not so much practical as it does not give the exact idea about the behavior of the system.

    3. (c)

      The results computed by evolutionary algorithms (EAs) contains less range of uncertainties as compared to FLT approach because EAs provide a solution near to optimal solution. It can be seen from the plots that the proposed methodology have compressed range of uncertainties as compared to other existing methodologies. Thus results computed by PSOBLT technique have smaller spread at each cut level α which leads to more sound and effective decision for future course of actions in lesser time.

      In order to compute the decrease of uncertainties or spread during the analysis by the proposed approach over the existing approaches, an analysis has been done in which spread during the analysis has been computed and given in Table 3. From the table it has been clearly seen that availability and reliability are the parameters corresponding to which the largest and the smallest decrease in spreads occur from FLT results while these decreases correspond to maintainability and reliability respectively from GABLT results when PSOBLT technique has been applied, which means a prediction range of reliability indices decreased. This analysis suggests that the maintenance engineer or plant personnel may preserve the particular parameter for increasing the performance of the system and to achieve the goals of maximum profit.

  4. (iv)

    In order to make a decision in real-life situations, the obtained fuzzified output should be converted into crisp or single valued output. For this, the center of gravity method has been taken and the crisp, defuzzified values at different spreads (±15, ±25 and ±50 %) has been calculated and compared with FLT and GABLT results through Table 4. It shows that the crisp value does not change with the change of spread while the defuzzified value changes with the change of spread. From Table 4, it is evident that defuzzified values obtained by PSOBLT technique are in between crisp and the other technique results i.e., PSOBLT technique acts as a bridge between Markov process (crisp values) and other techniques. Also, the variations in the defuzzified values are quite less as compared to other methodologies values and trends (increase or decrease) achieved by FLT and GABLT techniques are also preserved by proposed technique. Thus, the discussed technique is conservative in nature which may be more beneficial for a system expert/analyst for future course of action.

Table 2 Data related to failure and repair rates of the system [3]
Full size table
Fig. 2
figure 2

Fuzzy RAM parameters plots

Full size image
Table 3 Decrease in the uncertainties level during analysis in RAM parameters
Full size table
Table 4 Defuzzified values of the reliability parameters at different spread
Full size table

In order to improve the performance of the system, current condition of the system should be changed according to effective maintenance program. Thus plant personnel should have to plan a suitable maintenance program for enhancing the production and productivity of the system. But it is difficult for them to find the particular component or the most sensitive components on which more attention should be given to save money, manpower and time. For overcoming this problem, RAM analysis has been carried out by using the proposed RAM-index.

7.3 RAM-Index Analysis

The RAM-index, given in Eq. (21), is a composite measure of RAM of the system and are used for measuring the performance of the system. The major advantage of using this index is that system performance is analyzed by varying their consequent component’s parameters individually or simultaneously. For analyzing their effects on performance, first of all behavior of the RAM-index for a mission time t = 10 h are analyzed, shown in Fig. 3a, in the form of fuzzy membership function by the proposed approach along with their FLT and GABLT techniques result. It is evident from this figure that the proposed technique performs consistently well as compared to other in terms of reducing their uncertainty level during the analysis. The effect of uncertainties ranging from 0 to 100 (in %) on RAM-index has been investigated and a plot between spread and RAM-index at time t = 10 h is plotted and shown in Fig. 3b. This analyst suggests that for achieving higher performance of the systems, involved uncertainties should be minimized. For further analysis, 15 % uncertainties are taken into account suggested by maintenance personnel and performance of the RAM-index for a different time period ranging from 0 to 35 h are depicted graphically in Fig. 3c. It shows that the behavior of the index firstly increases from 0 to 18 h and attains its maximum in the range 0.8753603–0.9056689 at time t = 18 h and then decreases after that. This suggests for the system analyst or plant personnel that necessary actions should be given after time t = 18 h for increasing the performance of the system.

Fig. 3
figure 3

Behavior of the RAM-index

Full size image

Now in order to find the most critical components or equipments on which more attention should be given for saving money, power and time, sensitivity analysis has been done on the performance of the system i.e., on RAM-index by varying their corresponding components failure and repair rates parameters and fixing the other component parameters at the same time. The effects of individual components on system performance have been notified and are shown graphically in Fig. 4 while the variation of their maximum and minimum values of the RAM-index during analysis is tabulated in Table 5. It has been computed from the results that for increasing the performance of the system, failure and repair rate parameters of its constituent components should be decreased. For instance, Fig. 4a indicates for machine module machine-1 that when the time between failures and time to repair changes from 485.724 to 657.156 h and from 3.197 to 4.326 h respectively then the system index is decreased by 14.207 %. Similarly for other component changes have been seen from their respective figure. Moreover, it is evident from the Fig. 4 and Table 5 that the largest and smallest decrease (in %) in their index values occurs corresponding to the fine boring machine and tapping machine-1 component respectively. This suggests the fine boring machine is the most critical component as compared to others and hence suitable maintenance actions should be given to it for increasing the productivity of the system. Hence, on the basis of results tabulated, it is analyzed that to improve the performance of the system, more attention should be given to the components in order fine boring machine, modulo SPM widma-1, modulo SPM widma-2, module machine-2, module machine-1, tapping machine-2, Module machine-3, horizontal milling machine and tapping machine-1. These results of the system will help the concern managers to plan and adapt suitable maintenance practices/strategies for improving system performance and thereby reduce operational and maintenance costs.

Fig. 4
figure 4

Variation of RAM-index with the variation of systems MTBF and MTTR of the components

Full size image
Table 5 Variation in system availability when the failure and repair rate parameters of each component vary simultaneously
Full size table

8 Conclusion

This paper reports a RAM analysis of process industrial system by utilizing uncertain, vague and limited data. A crank-case manufacturing plant has been taken to demonstrate the approach. The uncertainties in the data are handled with the help of fuzzy approach in order to increase the efficiency of the system and their membership functions are computed by using PSOBLT technique. A time varying failure and repair rate model has been used during the analysis instead of constant failure rate model. The results obtained are compared with the existing crisp, FLT and GABLT techniques results and concluded that proposed results have lesser range of uncertainties and hence predictions. Apart from that a conceptual model has been suggested through which it is illustrated, how a suitable performance analysis-based maintenance can be identified. Components of all the subsystems/units of the manufacturing plant which have excessive failure rates, long repair time or high degree of uncertainty associated with these values, are identified and reported in preferential order. Using these analyses and results tabulated in tables, it has been concluded that more attention should be given in preferential order to the components; fine boring machine, modulo SPM widma-1, modulo SPM widma-2, module machine-2, module machine-1, tapping machine-2, Module machine-3, horizontal milling machine and tapping machine-1 for improving the performance of the system.