Introduction

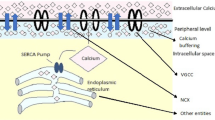
Computational neuroscience has emerged as a new research area for mathematicians and theoretical scientists due to its complex physiology. One of the notable examples is modelling calcium signalling in glial cell like astrocytes. Astrocytes are found to be the most diverse population of glial cells in nervous system. Twenty years ago, the traditional view of astrocytes was merely as supportive cells providing only structural and metabolic support to neurons [1,2,3]. Recent studies of astrocytes have suggested that these cells not only supports the neurons but actively participates in the dynamic regulation of cerebral microcirculation, synaptic transmission and neuronal activation [2, 4,5,6]. Astrocytes are now widely accepted as nerve cells that propagate Ca2+ over long distances in response to stimulation and similar to neurons release transmitters (called gliotransmitters) in a Ca2+-dependent manner [4, 7]. Spontaneous astrocytic Ca2+ oscillations have been observed and implicated in important functions of the brain. However, the mechanism of spontaneous Ca2+ oscillations is still unclear. Therefore, it is critical to understand how the Ca2+ oscillations are generated and modulated [7, 8].

There are so many processes involved in calcium signalling that effects the calcium concentration in cytosol. The notable examples are calcium buffering, entrance of calcium ion Ca2+ through voltage gated channels, etc. Mathematical problems have been formulated in the form of reaction–diffusion equation, advection diffusion equation for one- and two-dimensional cases. Tripathi et al. have studied the effect of several parameters like sodium calcium exchanger, buffer concentration, diffusion coefficients etc. on calcium concentration [Ca2+] in neuron [9,10,11]. Tewari et al. have developed the mathematical model to study the effect of sodium calcium exchanger, calcium buffering, VGCC etc. on calcium concentration in neuron for one- and two-dimensional cases [12, 13]. To find the solution, different numerical and analytical techniques have been used like Laplace transform, finite difference method (FDM), FEM, finite volume method (FVM), etc. FEM has gained general acceptance for handling the diversity of problems along with diverse geometrical configurations and boundary conditions which can be examined by a single computer programme. Jha et al. have developed two-dimensional reaction diffusion equation to study the effect of buffer concentration on cytosol in astrocytes [14]. Later on, the model is extended to study the comparative effect of buffer concentration and VGCC on cytosolic calcium concentration in astrocytes [15]. Naik et al. have studied the effect of RyR calcium channel, ER and SERCA pump on calcium distribution in Oocytes cell [16]. Before this, authors have studied the effect of various parameters in oocytes and T-lymphocyte using finite element method. In this paper we have extended the already present models [17,18,19] in three-dimensional mathematical model. The physiological results obtained are interpreted with neurological disorders like Alzheimer’s and Parkinson’s diseases using one and two dimensional mathematical models [20, 21]. In previous paper, study has been made for only point source. In this paper line source is incorporated to modulate more realistic situation. FEM is used to solve the problem. A computer program is developed for the entire problem to simulate the results.

Mathematical Formulation

Mathematical model is developed in the form of diffusion equation for steady state case. Calcium buffering and VGCC are included in the model. The formulation of calcium buffering and VGCC is given in subsequent subsections.

Calcium Buffering

Calcium buffers were examined for their ability to reduce evoked transmitter release when injected into the presynaptic terminal of the squid giant synapse. Ethylene glycol tetraacetic acid (EGTA) is virtually ineffective at reducing transmitter release, even at estimated intracellular concentrations. Conversely, the buffer 1,2-bis(o-aminophenoxy)ethane-N,N,N,N-tetraacetic acid (BAPTA) has an equilibrium affinity for calcium similar to that of EGTA, which produced a substantial reduction in transmitter release when injected in presynapse [22, 23]. Experimentally Wang et al. [23] first reported and illustrated directly that cytoplasmic calcium buffering constitutes an important and powerful mechanism for modulating astrocytic Ca2+ waves.

Calcium kinetics in astrocytes is governed by a set of reaction–diffusion equations which can be framed assuming the following bimolecular reaction between Ca2+ and buffer species [24, 25]

$$ \left[ {Ca^{2 + } } \right] + \left[ {B_{j} } \right]\mathop \Leftrightarrow \limits_{{k_{j}^{ - } }}^{{k_{j}^{ + } }} \left[ {CaB_{j} } \right] $$
(1)

where [Bj] and [CaBj] are free and bound buffer respectively, and ‘j’ is an index over buffer species. The resulting partial differential equations in three dimensions for Eq. (1) using Fickian diffusion can be stated as [24, 26]

$$ \frac{{\partial \left[ {Ca^{2 + } } \right]}}{\partial t} = D_{Ca} \left( {\frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial x^{2} }} + \frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial y^{2} }} + \frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial z^{2} }}} \right) + \sum\limits_{j} {R_{j} } + J_{VGCC} - P_{out} \left[ {Ca^{2 + } } \right] $$
(2)
$$ \frac{{\partial \left[ {B_{j} } \right]}}{\partial t} = D_{{B_{j} }} \left( {\frac{{\partial^{2} \left[ {B_{j} } \right]}}{{\partial x^{2} }} + \frac{{\partial^{2} \left[ {B_{j} } \right]}}{{\partial y^{2} }} + \frac{{\partial^{2} \left[ {B_{j} } \right]}}{{\partial z^{2} }}} \right) + R_{j} $$
(3)
$$ \frac{{\partial \left[ {CaB_{j} } \right]}}{\partial t} = D_{{CaB_{j} }} \left( {\frac{{\partial^{2} \left[ {CaB_{j} } \right]}}{{\partial x^{2} }} + \frac{{\partial^{2} \left[ {CaB_{j} } \right]}}{{\partial y^{2} }} + \frac{{\partial^{2} \left[ {CaB_{j} } \right]}}{{\partial z^{2} }}} \right) - R_{j} $$
(4)

where

$$ R_{j} = - k_{j}^{ + } [B_{j} ][Ca^{2 + } ] + k_{j}^{ - } [CaB_{j} ] $$
(5)

\( D_{Ca\,} ,\,D_{{B_{j} }} ,\,D_{{CaB_{j} }} \) are diffusion coefficients of free calcium, free buffer and Ca2+ bound buffer respectively. \( k_{j}^{ + } \) and \( k_{j}^{ - } \) are association and dissociation rate constants for buffer ‘j’ respectively.

Voltage Gated (Operated) Calcium Channel

Astrocytes were shown to express voltage-gated [Ca2+] channels similar to those found in neurons [1, 27]. Later, it was found that Ca2+ influx through voltage-gated ion-channels significantly increases cytosolic calcium concentration [Ca2+]i in astrocytes. Voltage-gated Ca2+ channels form an important path way for [Ca2+] entry in excitable cells; the later have been found to express a variety of [Ca2+] channels, differing in their voltage dependence, kinetics, and pharmacological properties [28, 29]. Calcium channels are integral membrane proteins composed of five subunits, each playing a distinct role in channel function. MacVicar first demonstrated Ca2+ action potentials in cAMP-treated cultured cortical astrocytes when the K+ conductance was blocked and 10 mM Ba2+ was added [30]. The Ca2+ current has been modelled using the Goldman–Hodgkin–Katz (GHK) current equation as given below [26, 30].

$$ I_{Ca} = P_{Ca} z_{Ca}^{2} \frac{{F^{2} V_{m} }}{RT}\frac{{\left[ {Ca} \right]_{i} - \left[ {Ca} \right]_{0} \exp \left( { - z_{Ca} \frac{{FV_{m} }}{RT}} \right)}}{{1 - \exp \left( { - z_{Ca} \frac{{FV_{m} }}{RT}} \right)}} $$
(6)

where \( \left[ {Ca^{2 + } } \right]_{i} \) and \( \left[ {Ca^{2 + } } \right]_{0} \), are the intracellular and extracellular calcium concentrations respectively. \( P_{Ca} \) is the permeability of calcium ion, \( z_{Ca} \) is the valency of calcium ion. F is Faraday’s constant. \( V_{m} \) is membrane potential. R is Real gas constant and T is Absolute temperature. Equation (6) is converted into molar/second by using the following equation

$$ \sigma_{Ca} = \frac{{ - I_{Ca} }}{{z_{Ca} FV_{Ast} }} $$
(7)

The negative sign in Eq. (7) is taken because, by convention the inward current is taken to be negative. GHK current equation gives the current density as a function of voltage. The GHK equation is derived from the constant field which assumes that the electric field in the membrane is constant and thus ions move in the membrane as in free solution.

For stationary immobile buffers of fixed buffers \( D_{{B_{j} }} = D_{{CaB_{j} }} = 0 \). Further Eqs. (2–7) can be written for steady state as

$$ \begin{aligned} & D_{Ca} \left( {\frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial x^{2} }} + \frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial y^{2} }} + \frac{{\partial^{2} \left[ {Ca^{2 + } } \right]}}{{\partial z^{2} }}} \right) - k_{j}^{ + } \left[ B \right]_{\infty } \left( {\left[ {Ca^{2 + } } \right] - \left[ {Ca^{2 + } } \right]_{\infty } } \right) \\ & \quad + \frac{{P_{Ca} z_{Ca} FV_{m} }}{{RTV_{Ast} }}\frac{{\left[ {Ca} \right]_{i} - \left[ {Ca} \right]_{0} \exp \left( { - z_{Ca} \frac{{FV_{m} }}{RT}} \right)}}{{1 - \exp \left( { - z_{Ca} \frac{{FV_{m} }}{RT}} \right)}} - P_{out} \left[ {Ca^{2 + } } \right] + \sigma_{Ca} = 0 \\ \end{aligned} $$
(8)

Considering the point source of calcium at. Thus the VGCC at boundary condition can be given as

$$ \left. {\begin{array}{*{20}c} { - D_{Ca} \frac{{d\left[ {Ca^{2 + } } \right]}}{dx} = \sigma_{Ca} ,\,\,\,x = 0\,\,,\,0 \le y \le 5,\,\,0 \le z \le 5.} \\ { - D_{Ca} \frac{{d\left[ {Ca^{2 + } } \right]}}{dy} = \sigma_{Ca} ,\,\,\,y = 0\,\,,\,0 \le x \le 5,\,\,0 \le z \le 5.} \\ { - D_{Ca} \frac{{d\left[ {Ca^{2 + } } \right]}}{dz} = \sigma_{Ca} ,\,\,\,z = 0\,\,,\,0 \le x \le 5,\,\,0 \le y \le 5.} \\ \end{array} } \right\}\quad x = y = z = 0 $$
(9)

Also, the background concentration of [Ca2+] is 0.1 µM. As moving far away from the source. The calcium concentration

$$ \left[ {Ca^{2 + } } \right] = 0.1\,\upmu M\,\,\,\,at\,\,\,x = y = z = 5 $$
(10)

For the convenience the Eq. (8) can be written as

$$ \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }} - au + b = 0 $$
(11)

The discretized variational form of Eq. (11) can be written as:

$$ I^{(e)} = \frac{1}{2}\iiint\limits_{\varOmega } {\left\{ {\left( {\frac{{\partial u^{(e)} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial z}} \right)^{2} + au^{{(e)^{2} }} - 2bu^{(e)} } \right\}dxdydz}\, - \mu^{(e)} \int\limits_{{x_{i} }}^{{x_{j} }} {\left( {\frac{\sigma }{{D_{Ca} }}\left. {u^{(e)} } \right|_{x = 5} } \right)} dy $$
(12)

Here, we have used ‘u’ in lieu of [Ca2+] for our convenience, e = 1 2…125. In the term outside the integral, µ(e) = 1 for e = 1 and µ(e) = 0 for rest of the elements. The shape function of concentration variation within each element is defined by [31] and shown in Fig. 1.

$$ u^{\left( e \right)} = c_{1}^{\left( e \right)} + c_{2}^{\left( e \right)} x + c_{3}^{\left( e \right)} y + c_{4}^{(e)} z + c_{5}^{\left( e \right)} xy + c_{6}^{\left( e \right)} yz + c_{7}^{\left( e \right)} zx + c_{8}^{(e)} xyz $$
(13)
$$ u^{(e)} = P^{T} c^{(e)} $$
(14)

where, \( P^{T} = \left[ {\begin{array}{*{20}c} 1 & x & y \\ \end{array} \,\,\,\,\,z\,\,\,\,xy\,\,\,\,yz\,\,\,\,zx\,\,\,\,xyz} \right] \) and

$$ c^{{\left( e \right)^{T} }} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {c_{1}^{(e)} } & {c_{2}^{(e)} } & {c_{3}^{(e)} } & {c_{4}^{(e)} } \\ \end{array} } & {\begin{array}{*{20}c} {c_{5}^{(e)} } & {c_{6}^{(e)} } & {c_{7}^{(e)} } & {c_{8}^{(e)} } \\ \end{array} } \\ \end{array} } \right] $$
(15)
Fig. 1
figure 1

Descretization of the domain in three dimensions

Full size image

From Eq. (14) and (15) we get

$$ {\bar{{u}}}^{(e)} \, = \,P^{(e)} c^{(e)} $$
(16)

where \( {\bar{u}}^{(e)} \, = \,\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{i} } \\ {u_{j} } \\ {u_{k} } \\ {u_{l} } \\ \end{array} } \\ {\begin{array}{*{20}c} {u_{{i^{'} }} } \\ {u_{{j^{'} }} } \\ {u_{{k^{'} }} } \\ {u_{{l^{'} }} } \\ \end{array} } \\ \end{array} } \right] \) and \( P^{(e)} = \,\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {x_{i} } & {y_{i} } & {z_{i} } \\ 1 & {x_{j} } & {y_{j} } & {z_{j} } \\ 1 & {x_{k} } & {y_{k} } & {z_{k} } \\ 1 & {x_{l} } & {y_{l} } & {z_{l} } \\ \end{array} } & {\begin{array}{*{20}c} {x_{i} y_{i} } & {y_{i} z_{i} } & {z_{i} x_{i} } & {x_{i} y_{i} z_{i} } \\ {x_{j} y_{j} } & {y_{j} z_{j} } & {z_{j} x_{j} } & {x_{j} y_{j} z_{j} } \\ {x_{k} y_{k} } & {y_{k} z_{k} } & {z_{k} x_{k} } & {x_{k} y_{k} z_{k} } \\ {x_{l} y_{l} } & {y_{l} z_{l} } & {z_{l} x_{l} } & {x_{l} y_{l} z_{l} } \\ \end{array} } \\ {\begin{array}{*{20}c} 1 & {x_{i}^{'} } & {y_{i}^{'} } & {z_{i}^{'} } \\ 1 & {x_{j}^{'} } & {y_{j}^{'} } & {z_{j}^{'} } \\ 1 & {x_{k}^{'} } & {y_{k}^{'} } & {z_{k}^{'} } \\ 1 & {x_{l}^{'} } & {y_{l}^{'} } & {z_{l}^{'} } \\ \end{array} } & {\begin{array}{*{20}c} {x_{i}^{'} y_{i}^{'} } & {y_{i}^{'} z_{i}^{'} } & {z_{i}^{'} x_{i}^{'} } & {x_{i}^{'} y_{i}^{'} z_{i}^{'} } \\ {x_{j}^{'} y_{j}^{'} } & {y_{j}^{'} z_{j}^{'} } & {z_{j}^{'} x_{j}^{'} } & {x_{j}^{'} y_{j}^{'} z_{j}^{'} } \\ {x_{k}^{'} y_{k}^{'} } & {y_{k}^{'} z_{k}^{'} } & {z_{k}^{'} x_{k}^{'} } & {x_{k}^{'} y_{k}^{'} z_{k}^{'} } \\ {x_{l}^{'} y_{l}^{'} } & {y_{l}^{'} z_{l}^{'} } & {z_{l}^{'} x_{l}^{'} } & {x_{l}^{'} y_{l}^{'} z_{l}^{'} } \\ \end{array} } \\ \end{array} } \right] \)

From the Eq. (14) we have

$$ c^{(e)} \, = \,R^{(e)} {\bar{u}}^{(e)} $$
(17)

where

$$ R^{(e)} = P^{{(e)^{ - 1} }} $$
(18)

Substituting c(e) from Eqs. (14), (16) and (17) we get

$$ u^{(e)} \, = \,P^{T} R^{(e)} {\bar{u}}^{(e)} $$
(19)

Now the integral I(e) can be written in the form

$$ I^{\left( e \right)} \, = \,I_{k}^{\left( e \right)} + I_{m}^{\left( e \right)} - I_{s}^{\left( e \right)} - I_{z}^{\left( e \right)} $$
(20)

where

$$ I_{k}^{(e)} = \frac{1}{2}\iiint\limits_{\varOmega } {\left\{ {\left( {\frac{{\partial u^{(e)} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial u^{(e)} }}{\partial z}} \right)^{2} } \right\}}dxdydz $$
(21)
$$ I_{m}^{(e)} = \frac{1}{2}\iiint\limits_{\varOmega } {\frac{{u^{{(e)^{2} }} }}{{\lambda^{2} }}}\,dxdydz $$
(22)
$$ I_{s}^{(e)} = \frac{1}{2}\iiint\limits_{\varOmega } {\left\{ {\frac{{2u^{(e)} u_{\infty } }}{{\lambda^{2} }}} \right\}}\,dxdydz $$
(23)
$$ I_{z}^{(e)} = \frac{1}{2}\mu^{(e)} \int\limits_{{x_{i} }}^{{x_{j} }} {\left( {\frac{\sigma }{{D_{Ca} }}\left. {u^{(e)} } \right|_{x = 5} } \right)} dy $$
(24)

Now we extremize I w.r.t. each nodal calcium concentration ui as given below

$$ \frac{dI}{{d\bar{u} }} = \sum\limits_{e = 1}^{N} {{\bar{M}}^{(e)}} \frac{{dI^{(e)} }}{{d{\bar{u}}^{(e)} }} {\bar{M}}^{(e)T} = 0$$
(25)

where, \( {\bar{M}}^{(e)} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ . & . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ . & . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 0 \\ \end{array} } \\ 1 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \\ 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \) and \( I = \sum\limits_{e = 1}^{125} {I^{(e)} } \,\,\,\,\,\,\,\,\,{\bar{u}} = \,\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ : \\ : \\ \end{array} } \\ {\begin{array}{*{20}c} : \\ : \\ : \\ {u_{216} } \\ \end{array} } \\ \end{array} } \right] \)

$$ \frac{{dI^{(e)} }}{{d{\bar{u}}^{(e)} }} = \frac{{dI_{k}^{(e)} }}{{d{\bar{u}}^{(e)} }} + \frac{{dI_{m}^{(e)} }}{{d{\bar{u}}^{(e)} }} - \frac{{dI_{s}^{(e)} }}{{d{\bar{u}}^{(e)} }} - \frac{{dI_{p}^{(e)} }}{{d{\bar{u}}^{(e)} }} $$
(26)

This leads to a following system of linear algebraic equations.

$$ \left[ K \right]_{216\, \times \,216} \left[ {\bar{u} } \right]_{216\, \times \,1} = \left[ F \right]_{216\, \times \,1} $$
(27)

Here \( {\bar{u}} = \,u_{1} ,\,u_{2} ,\, \ldots \,u_{216} \), K is the system matrices, and F is system vector. The Gaussian elimination method is employed to solve the system (27).

Results and Discussion

The numerical results for calcium profile against different biophysical parameters have been obtained using numerical values of parameter given in Table 1 unless stated along with the figures.

Table 1 Values of physiological parameters of astrocytes [15, 17, 24]
Full size table

Figure 2 shows the variation of [Ca2+] along the distance in x-axis. Cytosolic [Ca2+] profile moves from high concentration to low concentration so it is highest at the source and it decrease rapidly up to 2 µm and after that it attains its background concentration of 0.1 μM as it goes far away from the source. The combined effect of buffer and VGCC has been shown in Fig. 2. The obtained result is in agreement with the previous results obtained in literature [14,15,16]. For the comparative study, the graph is plotted below to show the effect of low and high amount of buffer concentration and VGCC along x, y, and z directions.

Fig. 2
figure 2

Calcium distribution along x direction with buffer and VGCC

Full size image

In Fig. 3, the spatial variation in calcium profile is shown in two-dimensional way considering (a) x and y (b) x and z and (c) y and z directions. Calcium concentration is higher at the mouth of the channel and it decrease rapidly up to 2 µm far from the source and then attains the background concentration. Since space is taken cubical and the flow of ion is considered smooth, the movement of calcium profile is found same in all x, y, and z directions. The behaviour of calcium profile is same as that of shown in Fig. 2. Since buffers exist near the plasma membrane of the cell, most of the free calcium ions are bonded by the buffers and makes calcium bound buffer near the source. Due to calcium buffering nerve cells control the flow of transmitters from one cell to another cell or synapse. Also this mechanism saves the nerve cell from the toxicity rendered due to high amount of calcium.

Fig. 3
figure 3

Spatial variation of calcium concentration in a x and b y and x and z and c y and z direction in presence of buffers and VGCC

Full size image

Figure 4a, b shows the variation in calcium profile along x and y directions. Calcium concentration decrease rapidly up to x = 2 µm (Fig. 4a) and x = 1 µm (Fig. 4b) then maintain the background concentration of 0.1 µM as move far away from the source. This difference is due to the presence and low of VGCC. Due to presence of voltage gated calcium channel more free calcium ion remains present in cytosol, so that concentration remains high near the source. Due to high free calcium concentration level, neurotransmitter (in glial cell like astrocytes) moves from one cell to another or in synapse in vesicular way. Both the buffers and the voltage gated calcium channels play important role in signalling process of nervous system. Thus from Fig. 4a, b it is observed that the voltage gated calcium channel affect the calcium concentration level significantly in astrocytes.

Fig. 4
figure 4

a, b Calcium Concentration at different distance from point source along x and y direction for B = 30 µM k+=1.5 µM/s, DCa = 250 µM2/s in presence and low of VGCC

Full size image

Figure 5 shows the calcium profile along two direction namely x and y axis in (a) presence and (b) low of VGCC. The line source is considered at the boundary. It is assumed that more channels are nearer to each other and makes line source. Calcium concentration decrease rapidly near the source and maintain the background concentration as it moves far away from the source. In low of VGCC (Fig. 5b) calcium profile decrease more sharply than the presence of VGCC (Fig. 5a). Thus, both the buffers and voltage gated calcium channel plays their important role in calcium distribution in nerve cells like astrocytes.

Fig. 5
figure 5

a, b Calcium concentration at different distance from line source along x and y direction for B = 30 µM k+=1.5 µM/s, DCa = 250 µM2/s in presence and low of VGCC

Full size image

Figure 6a shows the variation of [Ca2+] along the x-axis for different amount of buffer at different position (x = 1, 2, 3, 4 µm) in cytosol in presence of different amount of buffer concentration B = 0–100 μ M and in presence of VGCC. As with the increase in the buffer concentration it is observed that with increase in buffer concentration, the calcium concentration decreases at x = 1 μm, 2 μm. Figure 6b shows the variation of [Ca2+] along the x-axis for different amount of buffer at different positions (x = 1, 2, 3, 4 µm) in cytosol due to different values of buffer concentration B = 0–100 μ M in low of VGCC. We observe significant difference in concentration profiles in astrocytes from Fig. 6a in the presence of VGCC. It happens due to presence and low of VGCC.

Fig. 6
figure 6

a, b Calcium concentration at different distance from source, B = 5–200 µM, k+=1.5 µM/s, DCa = 250 µM2/s in presence and low of VGCC

Full size image

Conclusion

The three-dimensional finite element model has been developed for a steady state case to study effect of buffer EGTA and VGCC, and influx on calcium concentration distribution in astrocytes. The dimension of the model is extended from two dimensions to three dimensions. The finite element method is quite flexible and versatile in the present situation as it has been possible to incorporate the parameters like EGTA, VGCC, influx and diffusion coefficient in the model. The results indicate that EGTA and VGCC has significant effect on calcium profile in the astrocytes. Also, the influx has significant effect on calcium distribution in astrocytes. Further, it can be concluded that VGCC plays more important role in calcium regulation in the low amount of buffers. The buffers are completely saturated and do not have the capacity to bind or in case of failure of buffers to bind calcium due to any abnormality or damage caused to buffers, etc. As any alteration in calcium distribution in nerve cells are directly related neurological disorders like Alzheimer’s and Parkinson’s diseases. Such models can be developed further to study the relationship among various parameters under normal and abnormal conditions to generate information which can be of great use to biomedical scientists for clinical applications in neuronal diseases.