Depletion and Conservation of Forestry Resources: A Mathematical Model

Abstract

A mathematical model to study the depletion and conservation of forestry biomass in presence of industrialization is proposed and analyzed. In the modeling process, it is assumed that due to forestry biomass industries migrate in the region under consideration and their growth increases due to the availability of forestry biomass. It is also assumed that both the intrinsic growth rate and carrying capacity of forestry biomass depend on industrialization and technological efforts. The model analysis shows that the increase in carrying capacity of forestry biomass due to technological efforts has destabilizing effect. It is found that, by taking growth rate coefficient of carrying capacity of forestry biomass due to technological efforts as a bifurcation parameter, periodic solutions may arise through Hopf-bifurcation. Further, using center manifold theory, the direction and stability of periodic solutions have also been discussed. Numerical simulation is performed to support analytic results.

Introduction

Forests are important natural resource which maintains the ecological balance in ecosphere. Forests reduce carbon dioxide from environment through photosynthesis and thus global warming. During photosynthesis process trees absorb carbon dioxide and produce oxygen, which is vital for the survival of various species including human on earth. Apart from this important phenomenon, forest also restricts soil erosion and maintains ground water level, biodiversity, etc. [13]. The population of various countries is significantly increasing and thus industrialization [8]. This rapidly growing industrialization affects the forests negatively, as the trees are cut down to provide raw material for products and land being cleared to develop new factories. The pollutants emitted from industries also affect the growth rate of forest biomass. Due to continuous increase in industrialization, forests are depleting and now the depletion of forests has become a major problem. A typical example for deforestation due to industrialization is Doon Valley in Uttarakhand, India [20, 21]. There are some industries (e.g. pulp-paper, timber, furniture, etc.), those are wholly dependent on forestry biomass. Industrialization affects the growth rate of forestry biomass in two ways, namely; (i) reducing its intrinsic growth rate, and (ii) reducing the forest area and thus the carrying capacity. The emission of pollutants from industries decreases both the intrinsic growth rate and carrying capacity but in the case of development of new industries, the required land is obtained by clearing the forests, which decrease only the carrying capacity of forestry biomass in the region under consideration. Thus for the conservation of forestry biomass it is necessary to increase the carrying capacity of forestry biomass along with its intrinsic growth rate by using appropriate technological efforts. These technological efforts may be considered as genetically engineered plants, which increase the intrinsic growth rate and the carrying capacity of forestry biomass in the region under consideration.

In the last few decades, some mathematical models have been proposed and analyzed to study the depletion of forestry biomass due to population [3, 12, 19, 22, 24], pollution [4, 18, 23] and industrialization ([17, 20, 21] and the references therein). In particular, Shukla and Dubey [22] presented a mathematical model for the depletion of forest biomass due to population and pollution. In this study, it is shown that the density of forestry biomass decreases as the population or pollution increases and it may extinct if the population and pollution increase without control. They have also proposed a model for the conservation of density of forest biomass and it is shown that it can be maintained at a desired level if appropriate efforts are applied to conserve forest biomass and control the population and pollution. Damage of ecosystem can be minimized by using taxation, license fees, lease of property rights, seasonal harvesting, etc. [16]. Naresh et. al. [18] have studied the effects of toxicant on plant biomass by using a non-linear mathematical model. In this study, it is shown that as the emission rate of pollutants increases, the density of biomass decreases. Toxicants are affecting the growth of plants and the proper dose of fertilizers is the best way to ensure the optimal growth of plants [1]. Dubey et. al [5, 8, 9] have proposed and analyzed mathematical models to study the depletion of forestry resources due to population, pollution and population pressure augmented industrialization. Further the survival of biological species, which depends on the resource biomass, has been studied by using mathematical models [6, 10].

The conservation of forestry biomass is very important for maintaining the ecological balance in ecosphere but a little attention has been paid on this aspect. Keeping this in mind, in this paper, we propose and analyze a nonlinear mathematical model to study the depletion of forestry biomass due to industrialization and its conservation by using some technological efforts.

The organization of the paper is as follows. In the next section we develop our model. In “Equilibrium Analysis” section, we derive criteria for the existence of equilibria. Local stability behavior and the existence of Hopf-Bifurcation are discussed in “Stability Analysis” section and “Existence of Hopf-Bifurcation” sections respectively. In “Direction and Stability of Hopf-Bifurcation” section, we have shown the direction and stability of periodic solutions arising through Hopf-bifurcation. A numerical example to illustrate our results is discussed in “Numerical Simulation” section. A brief discussion takes place in the final section.

Mathematical Model

We consider a forest habitat where forests are depleted due to rapid increase in industrialization. It is assumed that the density of forestry biomass is governed by generalized logistic model. It is further assumed that the intrinsic growth rate as well as carrying capacity of the forestry biomass are depleted due to industrialization and some technological efforts are used to increase them. Again it is considered that some forest based industries migrate in the region and their growth rate increases in accordance with the density of forestry biomass. Thus, the system dynamics is governed by following non-linear ordinary differential equations:

$$\begin{aligned} \frac{dB}{dt}&= sB\left( 1-\frac{B}{L}\right) -\beta BI-\beta _1 B^2I+\phi _1BT + \phi _2B^2T,\nonumber \\ \frac{dI}{dt}&= \nu B +\theta \beta BI+\theta _1\beta _1 B^2I - \theta _m I^2,\\ \frac{dT}{dt}&= \phi \left( L - B\right) - \phi _0T,\nonumber \end{aligned}$$

(1)

where $B(0)\ge 0,\, I(0)\ge 0,\, T(0)\ge 0$.

In the model system (1), $B$ is the density of forestry biomass, $I$ is the density of industrialization and $T$ is the intensity of technological efforts applied for the conservation of forestry biomass. The constants $s$ and $L$ are intrinsic growth rate and carrying capacity of forestry biomass respectively in absence of industrialization. The constants $\beta$ and $\beta _1$ represent the depletion rate coefficients in intrinsic growth rate and carrying capacity of forestry biomass respectively, due to industrialization. The constants $\phi _1$ and $\phi _2$ are the growth rate coefficients of intrinsic growth rate and carrying capacity of forestry biomass respectively due to technological efforts. The constants $\beta _1$ and $\phi _2$ affect only the carrying capacity of forestry biomass (it has been discussed further in detail). In model system (1), $\nu$ is the growth-rate coefficient of industrialization caused by migration of industries to the forest region under consideration, which is assumed to be proportional to the density of forestry biomass. The coefficients $\theta$ and $\theta _1$ are the proportionality constants which represent growth of industrialization due to forestry biomass. The constant $\theta _m > 0$ corresponds to the intraspecific interference coefficient between industries. The constants $\phi$ and $\phi _0$ are growth rate and natural depletion rate coefficients of technological efforts applied for the conservation of forestry biomass respectively.

For the explanation of the terms $\beta BI$ and $\phi _1BT$ in the first equation of model system (1), reader is referred to Dubey et al. [9, 11] and Dubey [4]. In the following, we provide an explanation for the terms $\beta _1 B^2I$ and $\phi _2B^2T$. As we know that the logistic equation for the growth rate of forestry biomass with intrinsic growth rate $s$ and carrying capacity $L$ is

$$\begin{aligned} \frac{dB}{dt}=sB\left( 1-\frac{B}{L}\right) \!. \end{aligned}$$

(2)

By incorporating the terms $\beta _1 B^2I$ and $\phi _2B^2T$, the above equation modifies as

$$\begin{aligned} \frac{dB}{dt}&= sB\left( 1-\frac{B}{L}\right) -\beta _1 B^2I + \phi _2B^2T\nonumber \\&= sB-\left( \frac{s}{L}+\beta _1I - \phi _2T\right) B^2\nonumber \\&= sB\left( 1-\frac{B}{L_m}\right) \!, \end{aligned}$$

(3)

where $L_m$ is the modified carrying capacity of forestry biomass and is given by the relation

$$\begin{aligned} \frac{1}{L_m}=\left( \frac{1}{L}+\frac{\beta _1I - \phi _2T}{s}\right) \!. \end{aligned}$$

From this relation it is evident that $L_m$ decreases as industrialization increases and it increases as technological efforts increases. Thus from the right hand side of Eq. (3) we can say that the terms $\beta _1 B^2I$ and $\phi _2B^2T$ affect only the carrying capacity of forestry biomass without affecting its intrinsic growth rate.

Equilibrium Analysis

The above model system (1) has following two non-negative equilibria.

$$\begin{aligned} \mathrm{(i)}\; E_0\left( 0,0,\frac{\phi L}{\phi _0}\right) \quad \mathrm{and}\quad \mathrm{(ii)}\; E_1(B^*,\, I^*,\, T^*). \end{aligned}$$

The existence of equilibrium $E_0$ is obvious, hence omitted. In the following, we prove the existence of equilibrium $E_1$.

Existence of $E_1(B^*, I^*, T^*)$

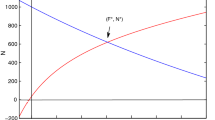
In the equilibrium $E_1$, the values of $B^*,\, I^*$ and $T^*$ are the positive solutions of the following algebraic equations:

$$\begin{aligned}&s\left( 1-\frac{B}{L}\right) -(\beta +\beta _1B)I+(\phi _1 + \phi _2B)T = 0, \end{aligned}$$

(4)

$$\begin{aligned}&\theta _mI^2 - (\theta \beta B + \theta _1 \beta _1 B^2)I-\nu B=0,\end{aligned}$$

(5)

$$\begin{aligned}&\phi (L - B) - \phi _0 T=0. \end{aligned}$$

(6)

From Eq. (5), we get

$$\begin{aligned} I&= \frac{1}{2\theta _m}\left[ (\theta \beta B + \theta _1\beta _1B^2) + \sqrt{(\theta \beta B + \theta _1 \beta _1 B^2)^2 + 4\theta _m\nu B } \right] \nonumber \\&= f(B)\ (\hbox {say}). \end{aligned}$$

(7)

Again from Eq. (6), we have

$$\begin{aligned} T=\frac{\phi (L - B)}{\phi _0}. \end{aligned}$$

(8)

By using above values of $I$ and $T$ in Eq. (4), we get the following equation in $B$:

$$\begin{aligned} F(B)=s\left( 1-\frac{B}{L}\right) -(\beta +\beta _1B)f(B)+ (\phi _1+\phi _2B)\frac{\phi (L - B)}{\phi _0}=0. \end{aligned}$$

(9)

From Eq. (8), we may note that $T<0$ for $B>L$. Thus for positive value of $T^*$, we are interested in a root of Eq. (9), which lies in the open interval $(0, \, L)$.

Now from Eq. (9), we may easily note the following facts:

• (i) $F(0)=s + {\phi \phi _1L}\ /{\phi _0}$, which is positive,

• (ii) $F(L)=-(\beta +\beta _1L)f(L)$, which is negative.

The above points (i) and (ii) together imply that there exists a positive root $(B=B^*)$ of Eq. (9) in the interval $(0,\ L)$. Further this root will be unique provided ${F}^{\prime }(B)$ is negative in $(0,\ L)$.

After knowing the value of $B=B^*$, we get the positive values of $I=I^*$ and $T=T^*$ from Eqs. (7) and (8) respectively.

Stability Analysis

The local stability behavior of equilibria $E_0$ and $E_1$ may be determined by finding the sign of eigenvalues of the corresponding Jacobian matrix. For this purpose, the Jacobian matrix $J$ for the model system (1) is given as follows:

$$\begin{aligned} J=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -a_{11} &{} -(\beta +\beta _1 B)B&{} (\phi _1+\phi _2B)B \\ b_{11}&{}-b_{12}&{}0 \\ -\phi &{}0&{}-\phi _0\\ \end{array}\right) \!, \end{aligned}$$

where

$$\begin{aligned} a_{11}&= s\left( 1-\frac{2B}{L}\right) - \beta I - 2\beta _1 B I+\phi _1T+2\phi _2BT,\\ b_{11}&= (\nu +\theta \beta I +2\theta _1\beta _1 BI), \quad b_{12}=(-\theta \beta B -\theta _1\beta _1 B^2+2\theta _m I). \end{aligned}$$

Let $J_i$ be the matrix $J$, evaluated at the equilibrium $E_i(i=0,1)$. Now from matrix $J_0$, we may note that one eigenvalue of this matrix is always positive, so it is unstable in $B$-direction.

The stability behavior of interior equilibrium $E_1$ follows from the following theorem:

Theorem 1

The interior equilibrium $E_1$ is locally asymptotically stable iff the following conditions hold:

$$\begin{aligned} A_{1}> 0,\, A_{3}> 0 \quad and \quad A_{1}A_{2}-A_{3}> 0. \end{aligned}$$

(10)

Proof

The characteristic equation for $J_1$ is given as follows:

$$\begin{aligned} \lambda ^3 + A_1\lambda ^2+ A_2\lambda +A_3 = 0, \end{aligned}$$

(11)

where

$$\begin{aligned}&A_{1} = a_{1} + \phi _0 +b_2, \\&A_2= a_1\phi _0+a_1b_2+b_2\phi _0+a_2b_1+a_3\phi ,\\&A_3=a_1b_2\phi _0+a_2b_1\phi _0+a_3b_2\phi , \end{aligned}$$

In the above expressions of $A_1,\, A_2$ and $A_3$, the values of $a_1,\, a_2,\, a_3,\, b_1$ and $b_2$ are given as follows:

$$\begin{aligned}&a_1 = \left( \frac{s}{L}+\beta _1I^*-\phi _2T^*\right) B^*, \quad a_2=(\beta + \beta _1B^*)B^*,\quad a_3 =(\phi _1+\phi _2B^*)B^*,\\&b_1= (\nu +\theta \beta I^*+2\theta _1\beta _1B^*I^*), \quad b_2=\left( \frac{\nu B^*}{I^*}+\theta _mI^*\right) . \end{aligned}$$

Here it may be noted that if the condition

$$\begin{aligned} \frac{s}{L}+\beta _1I^*-\phi _2T^*>0 \end{aligned}$$

(12)

is satisfied then all the conditions stated in (10) are satisfied. Now using Routh–Hurwitz criterion, we can say that the interior equilibria $E_1$ is locally asymptotically stable.

From the above condition (12), we may easily note that for large values of $\phi _2$ this condition may not be satisfied and thus the conditions stated in (10) may also be violated. This implies that system (1) may lose its stability and Hopf-bifurcation may occur for large values of $\phi _2$. Keeping this in mind, we study the behavior of dynamical system (1) in detail with respect to this parameter. $\square$

Existence of Hopf-Bifurcation

Now we investigate the possibility of Hopf-bifurcation from the interior equilibrium $E_1$ by choosing $\phi _2$ as a bifurcation parameter and leaving the remaining parameters fixed.

Theorem 2

The necessary and sufficient conditions for the occurrence of Hopf-bifurcation from the interior equilibrium $E_1$ are that there exists a $\phi _2 = {\phi _2}_c$ such that

$$\begin{aligned}&\mathrm{(i)}\quad A_1({\phi _2}_c) > 0 \hbox { and } A_3({\phi _2}_c) > 0,\\&\mathrm{(ii)}\quad G({\phi _2}_c)=A_1({\phi _2}_c) A_2({\phi _2}_c)- A_3({\phi _2}_c)=0,\\&\mathrm{(iii)}\quad \mathrm{Re}\left[ \frac{d({\lambda }_j)}{d \phi _2}\right] _{\phi _2={\phi _2}_c}\ne 0 \hbox { for } j= 1,2. \end{aligned}$$

Proof

For $\phi _2 = {\phi _2}_c$, we have $A_3=A_1A_2$. Using this fact, the characteristic equation (11) reduces to the following form:

$$\begin{aligned} (\lambda +A_1)(\lambda ^2+A_2) =0, \end{aligned}$$

(13)

which has three roots $\lambda _{1,2}=\pm i w$ and $\lambda _3= \mu$, where $\mu = -A_1= -(a_1+b_2+\phi _0)$ and $w=\sqrt{A_2}=\sqrt{ a_1\phi _0+a_1b_2+b_2\phi _0+a_2b_1+a_3\phi }$. Since $A_2 > 0$ at $\phi _2 = {\phi _2}_c$ so for some $\epsilon > 0$ there exists an $\epsilon$-neighborhood of ${\phi _2}_c$ say $({\phi _2}_c-\epsilon , {\phi _2}_c + \epsilon )$ for which ${\phi _2}_c - \epsilon > 0$ such that $A_2 > 0$ for $\phi _2 \in ({\phi _2}_c-\epsilon , {\phi _2}_c + \epsilon )$. Thus for $\phi _2 \in ({\phi _2}_c-\epsilon , {\phi _2}_c + \epsilon )$, the characteristic equation (13) cannot have real positive root.

• $\lambda _1(\phi _2)=u(\phi _2)+iv(\phi _2),$

• $\lambda _2(\phi _2)=u(\phi _2)-iv(\phi _2),$

• $\lambda _3=-A_1(\phi _2).$

To show the transversality condition, we substitute $\lambda = u(\phi _2)+i v(\phi _2)$ in Eq. (11) and separating the real and imaginary parts we have

$$\begin{aligned}&u^3(\phi _2)-3u(\phi _2)v^2(\phi _2)+A_1(\phi _2)(u^2(\phi _2) -v^2(\phi _2))\nonumber \\&\quad +A_2(\phi _2)u(\phi _2)+A_3(\phi _2)=0 \end{aligned}$$

(14)

$$\begin{aligned}&3u^2(\phi _2)v(\phi _2)-v^3(\phi _2)+2A_1(\phi _2)u(\phi _2) v(\phi _2)+A_2(\phi _2)v(\phi _2)=0. \end{aligned}$$

(15)

Now differentiating (14) and (15) with respect to $\phi _2$, we get

$$\begin{aligned} F_1(\phi _2)u^{\prime }(\phi _2)-F_2(\phi _2)v^{\prime }(\phi _2)+F_3(\phi _2)&= 0,\nonumber \\ F_2(\phi _2)u^{\prime }(\phi _2)+F_1(\phi _2)v^{\prime }(\phi _2)+F_4(\phi _2)&= 0, \end{aligned}$$

(16)

where

$$\begin{aligned} F_1(\phi _2)&= 3(u^2(\phi _2)-v^2(\phi _2))+2A_1(\phi _2)u(\phi _2)+A_2(\phi _2), \\ F_2(\phi _2)&= 6u(\phi _2)v(\phi _2)+2A_1(\phi _2)v(\phi _2), \\ F_3(\phi _2)&= {A_3}^{\prime }(\phi _2)+(u^2(\phi _2)-v^2(\phi _2)){A_1}^{\prime } (\phi _2)+u(\phi _2){A_2}^{\prime }(\phi _2), \\ F_4(\phi _2)&= 2u(\phi _2)v(\phi _2){A_1}^{\prime }(\phi _2)+v(\phi _2){A_2}^{\prime }(\phi _2). \end{aligned}$$

Since $F_1(\phi _2)F_3(\phi _2)+F_2(\phi _2)F_4(\phi _2) \ne 0$, we have

$$\begin{aligned} \hbox {Re}\left[ \frac{d\lambda _j}{d\phi _2}\right] _{\phi _2={\phi _2}_c} =-\frac{F_1F_3+F_2F_4}{{F_1}^2+{F_2}^2} \ne 0 \end{aligned}$$

and

$$\begin{aligned} \lambda _3({\phi _2}_c) = -A_1({\phi _2}_c) \ne 0. \end{aligned}$$

Therefore the transversality condition holds. This implies that Hopf-bifurcation occurs at $\phi _2 = {\phi _2}_c$ (see [7, 15]). $\square$

Direction and Stability of Hopf-Bifurcation

To analyze the direction and stability of Hopf-bifurcation, we will follow the method given in [14]. To describe the center manifold and analyze the flow therein, we first translate the origin of the coordinate system to the equilibrium $(B^*, I^*, T^*)$ by writing

$$\begin{aligned} \overline{B}=B-B^*,\qquad \overline{I}=I-I^*,\qquad \overline{T} = T-T^*. \end{aligned}$$

(17)

Then the model system (1) can be written in the form

$$\begin{aligned} \displaystyle \frac{d}{dt}\left( \begin{array}{cc} \overline{B} \\ \overline{I}\\ \overline{T}\\ \end{array} \right) = J_1 \left( \begin{array}{cc} \overline{B} \\ \overline{I}\\ \overline{T}\\ \end{array} \right) +\left( \begin{array}{cc} h_1 \\ h_2\\ h_3\\ \end{array}\right) \!. \end{aligned}$$

(18)

Here the nonlinear terms are

$$\begin{aligned} h_1&= -\frac{s\overline{B}^2}{L}-\beta \overline{B} \, \overline{I}-\beta _1\overline{B}^2 \overline{I}-\beta _1\overline{B}^2 I^*-2\beta _1B^*\overline{B} \, \overline{I}\nonumber \\&\quad \,\,+\phi _1\overline{B} \, \overline{T}+\phi _2\overline{B}^2 \overline{T}+\phi _2\overline{B}^2 T^*+2\phi _2 B^*\overline{B} \, \overline{T},\nonumber \\ h_2&= \theta \beta \overline{B} \, \overline{I}+\theta _1\beta _1\overline{B}^2\overline{I}+ \theta _1\beta _1\overline{B}^2 I^*+2\theta _1\beta _1B^*\overline{B} \, \overline{I} - \theta _m\overline{I}^2,\nonumber \\ h_3&=0. \end{aligned}$$

If the eigenvectors of $J_1$ corresponding to $\lambda _{1,2}$ are $W_1 \pm i W_2$ and the eigenvector associated with $\lambda _3$ is $W_3\, (W_1,\, W_2$ and $W_3$ are real), then it can be shown that the matrix $M = (W_1, W_2, W_3)$ is non-singular and

$$\begin{aligned}\ M^{-1}J_1M=\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} w&{} 0 \\ -w&{}0&{}0 \\ 0&{}0&{} \mu \\ \end{array}\right) \!. \end{aligned}$$

For model system (1), we have calculated the matrix $M$ and it is given as follows:

$$\begin{aligned} M&= \left( \begin{array}{c@{\quad }c@{\quad }c} a_3b_2 &{} a_3 w &{} a_3(b_2+\mu ) \\ a_3b_1&{}0&{}a_3b_1 \\ a_1b_2+a_2b_1-w^2&{}w(a_1+b_2)&{}(a_1+\mu )(b_2+\mu )+a_2b_1\\ \end{array} \right) \!. \end{aligned}$$

(19)

Now

$$\begin{aligned} M^{-1}&= \displaystyle \frac{1}{D}\left( \begin{array}{c@{\quad }c@{\quad }c} q_{11} &{} q_{12}&{} q_{13}\\ q_{21}&{}q_{22}&{}q_{23}\\ q_{31} &{}q_{32}&{}q_{33}\\ \end{array} \right) =Q \quad \mathrm{(say)}, \end{aligned}$$

(20)

where

$$\begin{aligned} q_{11}&= -a_3b_1w(a_1+b_2),\\ q_{12}&= -a_3w(\mu ^2+a_2b_1-{b_2}^2),\\ q_{13}&= b_1w{a_3}^2,\\ q_{21}&= -a_3b_1(\mu ^2+\mu a_1+\mu b_2 +w^2),\\ q_{22}&= a_3(\mu {b_2}^2+\mu ^2b_2-\mu a_2b_1 +\mu w^2+b_2w^2),\\ q_{23}&= \mu {a_3}^2b_1,\\ q_{31}&= a_3b_1w(a_1+b_2),\\ q_{32}&= -a_3w({b_2}^2+w^2-a_2b_1),\\ q_{33}&= -{a_3}^2b_1w,\\ \mathrm{and} \quad D&= -(\mu ^2+w^2){a_3}^2b_1w. \end{aligned}$$

Now we use the linear transformation

$$\begin{aligned} \left( \begin{array}{cc} \overline{B} \\ \overline{I}\\ \overline{T}\\ \end{array} \right) = M \left( \begin{array}{cc} k_1 \\ k_2\\ k_3\\ \end{array}\right) \!, \end{aligned}$$

(21)

which can be written as

$$\begin{aligned} \overline{S} = M K, \end{aligned}$$

(22)

where $\overline{S} = (\overline{B} \, \overline{I} \, \overline{T})^{\prime }$ and $M$ is given by (19).

Now using (22) in Eq. (18), we get

$$\begin{aligned} \frac{d}{dt}(MK) = J_1MK+F(MK), \end{aligned}$$

(23)

where $F(\overline{S})=(h_1, h_2, h_3)^{\prime }$. From above equation, we have

$$\begin{aligned} \frac{dK}{dt}=(M^{-1}J_1M)K +M^{-1}F(MK), \end{aligned}$$

(24)

where $K=(k_1, k_2, k_3)^{\prime }$.

Further we can write (24) in the following form:

$$\begin{aligned} \dot{x}&= H_1x + G_1(x, y),\nonumber \\ \dot{y}&= H_2y+G_2(x,y), \end{aligned}$$

(25)

where

$$\begin{aligned} x=\left( \begin{array}{cc} k_1 \\ k_2\\ \end{array} \right) ,\quad y=(k_3),\, H_1=\left( \begin{array}{c@{\quad }c} 0 &{} w \\ -w &{} 0\\ \end{array} \right) ,\quad H_2 = (\mu ),\, G_1=\left( \begin{array}{cc} g^1 \\ g^2\\ \end{array} \right) \quad \mathrm{and}\quad G_2 = (g^3). \end{aligned}$$

Here both $G_1$ and $G_2$ are $C^2$ functions.

Now system (24) can be written as follows:

$$\begin{aligned} \frac{d}{dt}\left( \begin{array}{cc} k_1 \\ k_2\\ k_3\\ \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c} 0&{}w&{}0\\ -w&{}0&{}0\\ 0&{}0&{}\mu \\ \end{array}\right) \left( \begin{array}{cc} k_1 \\ k_2\\ k_3\\ \end{array} \right) +Q\left( \begin{array}{cc} h_1 \\ h_2\\ h_3\\ \end{array}\right) \!. \end{aligned}$$

(26)

Now we use the following theorems.

Theorem 3

System (26) has a local center manifold $y= \eta (x), |x| < \delta$ where $\eta$ is $C^2$.

The function $\eta (x)$ can be approximated to any degree of accuracy as proved in the following theorem:

Theorem 4

Let $\psi$ be a $C^1$ mapping of a neighborhood of the origin in $R^2$ into $R$ with $\psi (0)=0, \psi ^{\prime }(0)=0$ and $(N\psi )(x)=O({|x|}^p)$ as $x \rightarrow 0$, where $N\psi (x)=\psi ^{\prime }(x)[H_1x+G_1(x,\psi (x))]-H_2\psi (x)-G_2(x, \psi (x))$ and $p > 1$. Then $|\eta (x)-\psi (x)|= O({|x|}^p)$ as $x \rightarrow 0$.

For the proofs of Theorems 3 and 4 see Carr [2].

Following the result of Theorem 4, we approximate the center manifold upto a quadratic approximation as

$$\begin{aligned} k_3 = \eta (k_1, k_2)=\frac{1}{2}\left( k_{11}k_1^2+2k_{12}k_1k_2+k_{22}k_2^2\right) +\hbox {h.o.t.} \end{aligned}$$

(27)

where h.o.t. stands for higher order terms.

From (27), it follows that

$$\begin{aligned} \frac{dk_3}{dt}&= \left( \frac{\partial \eta }{\partial k_1}.\frac{d k_1}{d t}+\frac{\partial \eta }{\partial k_2}\frac{d k_2}{d t}\right) \nonumber \\&= w(-k_{11}+k_{22})k_1 k_2+ w k_{12}k_1^2- w k_{12}k_2^2, \end{aligned}$$

(28)

Also from (25), we have

$$\begin{aligned} \frac{dk_3}{dt}&= \mu k_3 + g^3,\nonumber \\&= \frac{\mu }{2}\left( k_{11}k_1^2+2k_{12}k_1k_2+k_{22}k_2^2\right) + \left[ Q_1k_1^2+ Q_2k_1k_2+Q_3k_2^2\right] , \end{aligned}$$

(29)

where

$$\begin{aligned} Q_1&=\frac{1}{D}\left[ q_{31}\left( -\frac{s}{L}p_{11}^2-\beta p_{11}p_{21}-\beta _1I^*p_{11}^2-2\beta _1B^*p_{11}p_{21}+\phi _1p_{11}p_{31}\right. \right. \\&\left. \left. \quad \,\,+\phi _2T^*p_{11}^2+2\phi _2B^*p_{11}p_{31}\right) +q_{32}(\theta \beta p_{11}p_{21}+\theta _1 \beta _1{I^*}^2p_{11}^2\right. \\&\left. \quad \,\,+2\theta _1 \beta _1 B^*p_{11}p_{21} -\theta _mp_{21}^2)\right] ,\\ Q_2&=\frac{1}{D}\left[ q_{31}\left( -\frac{2s}{L}p_{11}p_{12}-\beta p_{12}p_{21}-2\beta _1I^*p_{11}p_{12}-2\beta _1B^*p_{12}p_{21}\right. \right. \\&\left. \left. \quad \,\,+\phi _1(p_{11}p_{32} +p_{12}p_{31})+2\phi _2T^*p_{11}p_{12} +2\phi _2B^*(p_{11}p_{32}+p_{12}p_{31})\right) \right. \\&\left. \quad \,\,+q_{32}(\theta \beta p_{12}p_{21}+2\theta _1\beta _1I^*p_{11}p_{12}+2\theta _1 \beta _1B^*p_{12}p_{21})\right] ,\\ Q_3&=\frac{1}{D}\left[ q_{31}\left( -\frac{s}{L}p_{12}^2-\beta _1I^*p_{12}^2+ \phi _1p_{12}p_{32}+ \phi _2T^*p_{12}^2+2\phi _2B^*p_{12}p_{32}\right) \right. \\&\left. \quad \,\,+q_{32}\theta _1\beta _1I^*p_{12}^2\right] \!. \end{aligned}$$

Equating (28) and (29) and comparing the coefficients $k_1^2,\,k_{1}k_{2}$ and $k_2^2$, we obtain a system of linear equations for $k_{11}, k_{12}$ and $k_{22}$. On solving these equations, we get

$$\begin{aligned} k_{11}&= -\left[ \frac{w^2(Q_1+Q_3)+\frac{\mu }{2}(wQ_2+\mu Q_1)}{\frac{\mu ^3}{4}+w^2\mu }\right] \!,\nonumber \\ k_{12}&= -\left[ \frac{\frac{\mu ^2 Q_2}{4}+\frac{w\mu }{2}(Q_3-Q_1)}{\frac{\mu ^3}{4}+w^2\mu }\right] \!,\\ k_{22}&= -\left[ \frac{\frac{\mu ^2 Q_3}{2}-\frac{w\mu Q_2}{2}+w^2(Q_1+Q_3)}{\frac{\mu ^3}{4}+w^2\mu }\right] \!.\nonumber \end{aligned}$$

(30)

The flow on the central manifold is governed by the following two-dimensional system:

$$\begin{aligned} \dot{x} = H_1 x + G_1(x, \eta (x)). \end{aligned}$$

(31)

Now, we state a theorem which tells that the behaviour of solutions of (31) contains all information about the behaviour of the solutions of (25).

Theorem 5

Suppose that the zero solution of (31) is stable (asymptotically stable) (unstable), then the zero solution of (25) is stable (asymptotically stable) (unstable) [2].

Now, (31) can be written as

$$\begin{aligned} \frac{d}{dt}\left( \begin{array}{cc} k_1 \\ k_2\\ \end{array} \right) = \left( \begin{array}{c@{\quad }c} 0&{}w\\ -w&{}0\\ \end{array}\right) \left( \begin{array}{cc} k_1 \\ k_2\\ \end{array} \right) +\left( \begin{array}{cc} g^1 \\ g^2\\ \end{array} \right) \!, \end{aligned}$$

(32)

where

$$\begin{aligned} g^1&= \frac{1}{D}\left( q_{11}{h_1}^{\prime }+q_{12}{h_2}^{\prime } +q_{13}{h_3}^{\prime }\right) +\hbox {h.o.t.,}\\ g^2&= \frac{1}{D}\left( q_{21}{h_1}^{\prime }+q_{22}{h_2}^{\prime }+q_{23}{h_3}^{\prime }\right) +\hbox {h.o.t.} \end{aligned}$$

and also the values of ${h_1}^{\prime }, {h_2}^{\prime }$ and ${h_3}^{\prime }$ are given below:

$$\begin{aligned} {h_1}^{\prime }&= -\frac{s}{L}(p_{11}k_1+p_{12}k_2)^2-\frac{sp_{13}Z}{L}(p_{11}k_1+p_{12}k_2) -\beta p_{21}k_1(p_{11}k_1+p_{12}k_2)\\&\quad \,\,- \frac{1}{2}\beta p_{13}p_{21}Z k_1-\frac{1}{2}\beta p_{23}Z(p_{11}k_1+p_{12}k_2)-\beta _1p_{21}k_1(p_{11}k_1+p_{12}k_2)^2\\&\quad \,\,-\beta _1I^*(p_{11}k_1\!+\!p_{12}k_2)^2 \!-\!\beta _1I^*p_{13}Z(p_{11}k_1\!+\!p_{12}k_2)\!-\!2\beta _1B^*p_{21}k_1 (p_{11}k_1+p_{12}k_2)\\&\quad \,\,-\beta _1B^*p_{23}Z(p_{11}k_1\!+\!p_{12}k_2)\!-\!\beta _1B^*p_{13}p_{21}k_1Z \!+\!\phi _1(p_{11}k_1\!+\!p_{12}k_2) (p_{31}k_1+p_{32}k_2)\\&\quad \,\,+\frac{1}{2}\phi _1p_{33}Z(p_{11}k_1\!+\!p_{12}k_2) \!+\!\frac{1}{2}\phi _1p_{13}Z(p_{31}k_1\!+\!p_{32}k_2) \!+\!\phi _2B^*p_{13}Z(p_{31}k_1\!+\!p_{32}k_2)\\&\quad \,\,+\phi _2T^*(p_{11}k_1+p_{12}k_2)^2\!+\!\phi _2T^*p_{13}Z(p_{11}k_1\!+\!p_{12}k_2) \!+\!\phi _2B^*p_{33}Z(p_{11}k_1\!+\!p_{12}k_2)\\&\quad \,\,+2\phi _2B^*(p_{11}k_1\!+\!p_{12}k_2)(p_{31}k_1\!+\!p_{32}k_2) \!+\!\phi _2(p_{11}k_1\!+\!p_{12}k_2)^2(p_{31}k_1\!+\!p_{32}k_2),\\ {h_2}^{\prime }&= \theta \beta p_{21}k_1 (p_{11}k_1+p_{12}k_2)+\frac{1}{2}\theta \beta p_{13}p_{21}Zk_1 +\frac{1}{2}\theta \beta p_{23}Z(p_{11}k_1+p_{12}k_2)\\&\quad \,\,+\theta _1\beta _1p_{21}k_1(p_{11}k_1\!+\!p_{12}k_2)^2 \!+\!\theta _1\beta _1I^*(p_{11}k_1\!+\!p_{12}k_2)^2 \!+\!\theta _1\beta _1I^*p_{13}Z(p_{11}k_1\!+\!p_{12}k_2)\\&\quad \,\,+2\theta _1\beta _1B^*p_{21}k_1(p_{11}k_1\!+\!p_{12}k_2) \!+\!\theta _1\beta _1B^*p_{23}Z(p_{11}k_1\!+\!p_{12}k_2) \!+\!\theta _1\beta _1B^*p_{13}p_{21}Zk_1\\&\quad \,\,-\theta _m{p_{21}}^2{k_1}^2-\theta _mp_{21}p_{23}k_1Z,\\ {h_3}^{\prime }&= 0, \end{aligned}$$

here

$$\begin{aligned} Z= \left( k_{11}k_1^2+2k_{12}k_1k_2+k_{22}k_2^2\right) . \end{aligned}$$

Now, the sign of the following quantity ‘$W$’ will determine the stability of limit cycle arising from Hopf-bifurcation:

$$\begin{aligned} W=\varGamma \hbox {Re}\left[ \frac{d\lambda _j}{d\phi _2}\right] _{\phi _2 ={\phi _2}_c}&= \frac{1}{w}[{g}^1_{12}({g}^1_{11}+{g}^1_{22})-{g}^2_{12} ({g}^2_{11}+{g}^2_{22})-{g}^1_{11}{g}^2_{11} +{g}^1_{22}{g}^2_{22}]\nonumber \\&-[{g}^1_{111}+{g}^2_{112}+{g}^1_{122}+{g}^2_{222}], \end{aligned}$$

(33)

here ${g}^1_{ij}$ denotes the partial derivative ${\partial ^2{g}^1}\ /{\partial k_ik_j}$ at the origin and the quantities with three subscripts represent third-order partial derivatives evaluated at origin. If $\varGamma > 0 \, (\varGamma < 0)$, then the Hopf-bifurcation is supercritical (subcritical). Further, if $W > 0 \, (W < 0)$, the bifurcating limit cycle is stable (unstable). Now, we find that

$$\begin{aligned} {g}^1_{11}&=\frac{1}{D}\left[ q_{11}\left( -\frac{2}{L}sp_{11}^2-2\beta p_{11}p_{21}-2\beta _1I^*p_{11}^2-4\beta _1B^*p_{11}p_{21}\right. \right. \nonumber \\&\left. \left. \quad \,\,+2\phi _1p_{11}p_{31}+2\phi _2T^*p_{11}^2+4\phi _2B^*p_{11}p_{31}\right) +q_{12}(2\theta \beta p_{11}p_{21}\right. \nonumber \\&\left. \quad \,\,+2\theta _1 \beta _1I^* p_{11}^2+4\theta _1 \beta _1B^* p_{11}p_{21}-2\theta _m p_{21}^2)\right] \!, \end{aligned}$$

(34)

$$\begin{aligned} {g}^2_{11}&=\frac{1}{D}\left[ q_{21}\left( -\frac{2}{L}sp_{11}^2-2\beta p_{11}p_{21}-2\beta _1I^*p_{11}^2-4\beta _1B^*p_{11}p_{21}\right. \right. \nonumber \\&\left. \left. \quad \,\,+2\phi _1p_{11}p_{31}+2\phi _2T^*p_{11}^2+4\phi _2B^*p_{11}p_{31}\right) +q_{22}(2\theta \beta p_{11}p_{21}\right. \nonumber \\&\left. \quad \,\,+2\theta _1 \beta _1I^* p_{11}^2+4\theta _1 \beta _1B^* p_{11}p_{21}-2\theta _m p_{21}^2)\right] \!, \end{aligned}$$

(35)

$$\begin{aligned} {g}^1_{12}&= \frac{1}{D}\left[ q_{11}\left( -\frac{2}{L}sp_{11}p_{12}-\beta p_{12}p_{21}-2\beta _1I^* p_{11}p_{12}-2\beta _1B^* p_{12}p_{21}\right. \right. \nonumber \\&\left. \left. \quad \,\,+\phi _1 p_{12}p_{31}+\phi _1p_{11}p_{32}+2\phi _2T^*p_{11}p_{12}+2\phi _2B^* p_{12}p_{31}+2\phi _2B^*p_{11}p_{32}\right) \right. \nonumber \\&\left. \quad \,\,+q_{12}(\theta \beta p_{12}p_{21}+2\theta _1 \beta _1I^* p_{11}p_{12}+2\theta _1 \beta _1B^* p_{12}p_{21})\right] \!,\end{aligned}$$

(36)

$$\begin{aligned} {g}^2_{12}&= \frac{1}{D}\left[ q_{21}\left( -\frac{2}{L}sp_{11}p_{12}-\beta p_{12}p_{21}-2\beta _1I^* p_{11}p_{12}-2\beta _1B^* p_{12}p_{21}\right. \right. \nonumber \\&\left. \left. \quad \,\,+\phi _1 p_{12}p_{31}+\phi _1p_{11}p_{32}+2\phi _2T^*p_{11}p_{12}+2\phi _2B^* p_{12}p_{31}+2\phi _2B^*p_{11}p_{32}\right) \right. \nonumber \\&\left. \quad \,\,+q_{22}(\theta \beta p_{12}p_{21}+2\theta _1 \beta _1I^* p_{11}p_{12}+2\theta _1 \beta _1B^* p_{12}p_{21})\right] \!,\end{aligned}$$

(37)

$$\begin{aligned} {g}^1_{22}&=\frac{1}{D}\left[ q_{11}\left( -\frac{2}{L}sp_{12}^2-2\beta _1I^* p_{12}^2+2\phi _1p_{12}p_{32}+2\phi _2T^*p_{12}^2\right. \right. \nonumber \\&\left. \left. \quad \,\,+4\phi _2B^*p_{12}p_{32}\right) +2q_{12}\theta _1\beta _1I^*p_{12}^2\right] , \end{aligned}$$

(38)

$$\begin{aligned} {g}^2_{22}&=\frac{1}{D}\left[ q_{21}\left( -\frac{2}{L}sp_{12}^2-2\beta _1I^* p_{12}^2+2\phi _1p_{12}p_{32}+2\phi _2T^*p_{12}^2\right. \right. \nonumber \\&\left. \left. \quad \,\,+4\phi _2B^*p_{12}p_{32}\right) +2q_{22}\theta _1\beta _1I^*p_{12}^2\right] \!, \end{aligned}$$

(39)

$$\begin{aligned} {g}^1_{111}&= \frac{1}{D}\left[ q_{11}\left( -\frac{6}{L}sp_{11}p_{13}k_{11}-3\beta p_{11}p_{23}k_{11}-3\beta p_{13}p_{21}k_{11}-6\beta _1p_{21}p_{11}^2\right. \right. \nonumber \\&\left. \left. \quad \,\,-6\beta _1I^*p_{11}p_{13}k_{11}-6\beta _1B^*p_{11}p_{23}k_{11}- 6\beta _1B^*p_{13}p_{21}k_{11}\right. \right. \nonumber \\&\left. \left. \quad \,\,+3\phi _1p_{13}p_{31}k_{11}+3\phi _1p_{11}p_{33}k_{11}+6\phi _2p_{11} ^2p_{31}+6\phi _2T^*p_{11}p_{13}k_{11}\right. \right. \nonumber \\&\left. \left. \quad \,\,+6\phi _2B^*p_{11}p_{33}k_{11}+6\phi _2B^*p_{13}p_{31}k_{11}\right) +q_{12}(3\theta \beta p_{13}p_{21}k_{11}\right. \nonumber \\&\left. \quad \,\,+3\theta \beta p_{11}p_{23}k_{11}+6\theta _1\beta _1p_{21}p_{11}^2+6\theta _1 \beta _1I^*p_{11}p_{13}k_{11}\right. \nonumber \\&\left. \quad \,\,+6\theta _1 \beta _1B^* p_{11}p_{23}k_{11}+6\theta _1 \beta _1B^* p_{13}p_{21}k_{11}-6\theta _m p_{21}p_{23}k_{11})\right] \!,\end{aligned}$$

(40)

$$\begin{aligned} {g}^2_{222}&=\frac{1}{D}\left[ q_{21}\left( -\frac{6}{L}sp_{12}p_{13}k_{22}-3\beta p_{12}p_{23}k_{22}-6\beta _1I^* p_{12}p_{13}k_{22}\right. \right. \nonumber \\&\left. \left. \quad \,\,-6\beta _1B^* p_{12}p_{23}k_{22}+3\phi _1p_{13}p_{32}k_{22}+3\phi _1p_{12}p_{33}k_{22} +6\phi _2p_{12}^2p_{32}\right. \right. \nonumber \\&\left. \left. \quad \,\,+6\phi _2T^*p_{12}p_{13}k_{22}+ 6\phi _2B^*p_{12}p_{33}k_{22}+6\phi _2B^*p_{13}p_{32}k_{22}\right) \right. \nonumber \\&\left. \quad \,\,+q_{22}(3\theta \beta p_{12}p_{23}k_{22}+6\theta _1 \beta _1I^* p_{12}p_{13}k_{22}+6\theta _1 \beta _1B^* p_{12}p_{23}k_{22})\right] \!,\end{aligned}$$

(41)

$$\begin{aligned} {g}^1_{122}&=\frac{1}{D}\left[ q_{11}\left( -\frac{4}{L}sp_{12}p_{13}k_{12}- \frac{2}{L}sp_{11}p_{13}k_{22}-\beta p_{13}p_{21}k_{22}-2\beta p_{12}p_{23}k_{12}\right. \right. \nonumber \\&\left. \left. \quad \,\,-\beta p_{11}p_{23}k_{22}-2\beta _1 p_{21}p_{12}^2-4\beta _1I^* p_{12}p_{13}k_{12}-2\beta _1I^* p_{11}p_{13}k_{22}\right. \right. \nonumber \\&\left. \left. \quad \,\,-4\beta _1B^* p_{12}p_{23}k_{12}-2\beta _1B^* p_{11}p_{23}k_{22}-2\beta _1B^* p_{13}p_{21}k_{22} +2\phi _1p_{12}p_{33}k_{12}\right. \right. \nonumber \\&\left. \left. \quad \,\,+\phi _1 p_{11}p_{33}k_{22}+2\phi _1 p_{13}p_{32}k_{12}+\phi _1 p_{31}p_{13}k_{22}+2\phi _2 p_{12}^2p_{31}+4\phi _2p_{11}p_{12}p_{32}\right. \right. \nonumber \\&\left. \left. \quad \,\,+4\phi _2T^*p_{12}p_{13}k_{12}+2\phi _2T^*p_{11}p_{13}k_{22} +4\phi _2B^*p_{12}p_{33}k_{12}+2\phi _2B^*p_{11}p_{33}k_{22}\right. \right. \nonumber \\&\left. \left. \quad \,\,+4\phi _2B^*p_{13}p_{32}k_{12}+2\phi _2B^*p_{13}p_{31}k_{22}\right) +q_{12}(\theta \beta p_{11}p_{23}k_{22}+2\theta \beta p_{12}p_{23}k_{12}\right. \nonumber \\&\left. \quad \,\,+\theta \beta p_{13}p_{21}k_{22}+2\theta _1\beta _1p_{21}p_{12}^2+4\theta _1 \beta _1I^* p_{12}p_{13}k_{12}+2\theta _1 \beta _1I^* p_{11}p_{13}k_{22}\right. \nonumber \\&\left. \quad \,\,+4\theta _1 \beta _1B^* p_{12}p_{23}k_{12}\!+\!2\theta _1 \beta _1B^* p_{11}p_{23}k_{22}\!+\!2\theta _1 \beta _1B^* p_{13}p_{21}k_{22}\!-\!2\theta _mp_{21}p_{23}k_{22})\right] \!,\end{aligned}$$

(42)

$$\begin{aligned} {g}^2_{112}&= \frac{1}{D}\left[ q_{21}\left( -\frac{2}{L}sp_{12}p_{13}k_{11}-\frac{4}{L}sp_{11} p_{13}k_{12}-2\beta p_{13}p_{21}k_{12}-\beta p_{12}p_{23}k_{11}\right. \right. \nonumber \\&\left. \left. \quad \,\,-2\beta p_{11}p_{23}k_{12}- 4\beta _1p_{11}p_{12}p_{21}-2\beta _1I^*p_{12}p_{13}k_{11}- 4\beta _1I^*p_{11}p_{13}k_{12}\right. \right. \nonumber \\&\left. \left. \quad \,\,- 2\beta _1B^*p_{12}p_{23}k_{11}- 4\beta _1B^*p_{11}p_{23}k_{12}- 4\beta _1B^*p_{13}p_{21}k_{12}+\phi _1 p_{12}p_{33}k_{11}\right. \right. \nonumber \\&\left. \left. \quad \,\,+2\phi _1 p_{11}p_{33}k_{12}+\phi _1 p_{13}p_{32}k_{11} +2\phi _1p_{13}p_{31}k_{12}+ 4 \phi _2 p_{11}p_{12}p_{31}+2\phi _2p_{32}p_{11}^2\right. \right. \nonumber \\&\left. \left. \quad \,\,+4\phi _2T^*p_{11}p_{13}k_{12}+2\phi _2T^* p_{12}p_{13}k_{11} +2\phi _2B^* p_{12}p_{33}k_{11}+4 \phi _2B^* p_{11}p_{33}k_{12}\right. \right. \nonumber \\&\left. \left. \quad \,\,+2\phi _2B^* p_{13}p_{32}k_{11}+4 \phi _2B^* p_{13}p_{31}k_{12}\right) +q_{22}(\theta \beta p_{12}p_{23}k_{11}+2\theta \beta p_{11}p_{23}k_{12}\right. \nonumber \\&\left. \quad \,\,+2\theta \beta p_{13}p_{21}k_{12}+ 4\theta _1 \beta _1 p_{11}p_{12}p_{21}+ 2\theta _1 \beta _1I^* p_{12}p_{13}k_{11}+4\theta _1\beta _1I^*p_{11}p_{13}k_{12}\right. \nonumber \\&\left. \quad \,\,+ 2\theta _1 \beta _1B^* p_{12}p_{23}k_{11}\!+\! 4\theta _1 \beta _1B^* p_{11}p_{23}k_{12}\!+\! 4\theta _1 \beta _1B^* p_{13}p_{21}k_{12}\!-\!4\theta _m p_{21}p_{23}k_{12})\right] . \end{aligned}$$

(43)

For finding the sign of $W$, we can evaluate the various quantities present in expression of $W$ in terms of the system parameters and substituting the resulting expression into Eq. (33).

Numerical Simulation

To check the feasibility of our analysis regarding existence of interior equilibrium and its stability conditions, we have conducted some numerical computation using MATLAB by choosing the following set of parameter values in model system (1):

$$\begin{aligned}&s=0.5, \, L=100, \, \beta =0.09, \, \beta _1=0.0001,\quad \nu =0.43,\quad \theta =0.02, \quad \theta _1=0.01, \nonumber \\&\theta _m=0.1 \quad \phi _1=0.02, \, \phi _2=0.001, \, \phi =0.01, \, \phi _0=0.03. \end{aligned}$$

(44)

The following equilibrium values are obtained for the above set of parameters:

$$\begin{aligned} B^* =49.2475,\qquad I^* = 15.0145,\qquad T^* = 16.9174. \end{aligned}$$

For the above set of parameter values, it may be checked that the stability conditions stated in theorem 1 are satisfied.

The eigenvalues of the Jacobian matrix $J_1$ corresponding to the equilibrium $E_1$ for the model system (1) are:

$-2.0952, \quad - 0.1668 + 0.1699{ i},\hbox { and } - 0.1668 -0.1699 i$.

We note that one eigenvalue of Jacobian matrix $J_1$ is negative and the other two eigenvalues are with negative real part. Hence, the interior equilibrium $E_1$ is locally asymptotically stable.

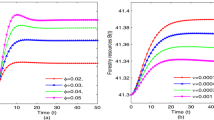
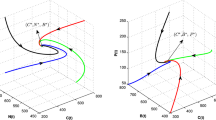
For the above set of parameter values, the critical value of $\phi _2$ (i.e. ${\phi _2}_c$) is 0.002. The variation of different variables with respect to time for $\phi _2=0.001$ and $\phi _2=0.0022$ has been shown in Figs. 1 and 2, respectively. From these figures, it is clear that for the value of $\phi _2$ less than ${\phi _2}_c$, the system get stabilized but for $\phi _2$ greater than ${\phi _2}_c$, sustained oscillations occur. Bifurcation diagrams of the model system (1) are drawn with respect to the parameter $\phi _2$ in Fig. 3. This figure clearly shows that as $\phi _2$ passes through a critical value, the system loses its stability and periodic solutions arise through Hopf-bifurcation. This means that the carrying capacity of forestry biomass can be increased only up to a certain level by applying suitable technological efforts. If we try to increase the carrying capacity of forestry biomass beyond a certain limit by using technological efforts, the system loses its stability. For the above given set of parameter values, the sign of $\varGamma$ and $W$ are calculated and found to be positive. Hence, in this case, supercritical Hopf-bifurcation occurs and bifurcating periodic solutions are stable. Figure 4 shows the periodic solutions are orbitally stable.

Fig. 1

Variation of forestry biomass, industrialization and technological efforts with respect to time for $\phi _2=0.001$

Fig. 2

Variation of forestry biomass, industrialization and technological efforts with respect to time for $\phi _2=0.0022$

Fig. 3

Bifurcation diagram of forestry biomass, industrialization and technological efforts with respect to $\phi _2$. The other parameters are same as given in (44)

Fig. 4

Stable limit cycle for $\phi _2=0.0022$

Conclusion

In this paper, a non-linear mathematical model is proposed and analyzed to study the depletion of forestry biomass due to industrialization and its conservation through suitable technological efforts, like genetically engineered plants. In the modeling process, we have assumed that the intrinsic growth rate as well as carrying capacity of the forestry biomass are depleted due to industrialization. It is also assumed that technological efforts are applied to increase the intrinsic growth rate and carrying capacity of forestry biomass. The model is analyzed using stability theory of differential equations. It is found that the proposed model exhibits one axial equilibrium and an interior equilibrium. Conditions for stability of interior equilibrium have been derived which are stated in Theorem 1. It is found that these conditions may be violated for higher values of $\phi _2$ implying that the growth rate coefficient of carrying capacity of forestry biomass due to technological efforts have destabilizing effect on the dynamics of the system. The Hopf-bifurcation analysis is performed by taking $\phi _2$ as a bifurcation parameter. It is shown that when $\phi _2$ passes through a critical value, the interior equilibrium $E_1$ loses its stability and periodic solutions arise through Hopf-bifurcation. The stability and direction of Hopf-bifurcation have also been discussed in detail by using the center manifold theorem. The obtained results reveal that with the help of technological efforts, we can increase the carrying capacity of forestry biomass only up to a certain level. Further attempts to increase the carrying capacity of forestry biomass results into the destabilization of the system i.e. the density of forestry biomass oscillates and does not settle down to its equilibrium level. Thus through applying technological efforts, it is not possible to increase the carrying capacity of forestry biomass up to any desired level.