Fractional lower order covariance-based estimator for bidimensional AR(1) model with stable distribution

Abstract

Real data modeling often requires the use of non-Gaussian models. A natural extension of the Gaussian distribution is the $\alpha$-stable one. The dependence structure description of the $\alpha$-stable-based models poses a substantial challenge due to the infinite variance. The classical second moment-based measures cannot be applied in this case. To overcome this issue one can use the alternative dependence measures. The measures of dependence can be applied to estimate the parameters of the model. In this paper, we propose a new estimation method for the parameters of the bidimensional autoregressive model of order 1. The procedure is based on fractional lower order covariance. The use of this method is reasonable from the theoretical point of view. The practical aspect of the method is justified by showing the efficiency of the procedure on the simulated data. Moreover, the new technique is compared with the classical Yule–Walker method based on the covariance function.

1 Introduction

The models based on the time series approach are considered to be the most natural for the modeling of discrete empirical data. An important class of univariate stationary time series which plays a pivotal role in the statistical analysis of time series data is the family of autoregressive models (AR), moving average models (MA) and general autoregressive moving average models (ARMA) combining both AR and MA parts [1,2,3,4,5]. However, many empirical data observed in practice should be rather considered as components of multivariate models with both internal dependence within each component and cross-dependence between different components. One of the most popular examples of the multivariate models is the vector autoregressive time series (VAR) generalizing the univariate autoregressive process to the multidimensional case [4, 6,7,8,9,10,11]. In the classical definition, the vector autoregressive model is assumed to be a second-order model because of the finite second moment of the innovations. Nevertheless, the common assumption of the Gaussian distributed innovations is not always reflected in real data analysis.

A lot of real phenomena exhibit non-Gaussianity which can be visible in the impulsive character of the time series. A useful class of distributions that can be applied to model the data manifesting impulsive behavior is a class of the heavy-tailed distributions for which the tails are not exponentially bounded [12,13,14,15,16,17,18]. One of the classical examples of a heavy-tailed distribution is the $\alpha$-stable one which can be considered as an extension of the Gaussian distribution. In most of the cases (with the exception of the Gaussian case) the second moment of an $\alpha$-stable distributed random variable is infinite. The models based on the $\alpha$-stable distribution are present in many applications both for one-dimensional and multi-dimensional data [19,20,21,22,23,24]. Because of the infinite variance, the analysis of the $\alpha$-stable-based models poses an important challenge to the researchers. The application of such processes requires the use of non-classical methods for statistical investigation and estimation [25,26,27,28,29,30,31,32]. In particular, the structure of dependence for the $\alpha$-stable-based models cannot be described by the covariance or correlation functions which are based on the second moment of the given process. However, in the literature, one can find the alternative measures that can replace the classical ones in the case of infinite variance. The most popular are: codifference, covariation and fractional lower order covariance, see [33,34,35,36,37,38,39,40,41,42,43,44].

In this paper, we propose a new estimation procedure for the parameters of the bidimensional autoregressive model of order 1 with $\alpha$-stable distributed noise. The classical Yule–Walker method used to estimate the parameters of the vector autoregressive models are based on covariance [4, 45,46,47,48]. As it was mentioned, the covariance function is not defined for the infinite variance models and for that reason we propose to replace it by one of the measures adequate for $\alpha$-stable-based models. In the literature this type of approach, based on the covariation function, was applied to the univariate time series, see [29, 49]. In this paper, the novel estimation method is based on the fractional lower order covariance (also called FLOC). The measure, considered as an extension of the covariance function to the $\alpha$-stable case, has found many interesting applications, see [50,51,52]. It is important to mention that the estimators obtained on the basis of FLOC are given in an explicit form. The use of the introduced method is reasonable from the theoretical point of view. However, we are also going to present the practical aspect of the method by showing the efficiency of the procedure on the simulated data and by comparing the new technique with the classical Yule–Walker method. We are going to show that the method works more effective, especially for small data samples.

The rest of the paper is organized as follows. In Sect. 2 we recall the definition and main properties of the univariate and bivariate $\alpha$-stable distribution together with dependence measures for the infinite variance processes. In Sect. 3 we define the bidimensional $\alpha$-stable autoregressive model of order 1. A new estimation technique for the parameters of the considered process is presented in Sect. 4. The efficiency of the estimators is tested on simulated data using Monte Carlo simulations in Sect. 5. In Sect. 6 the performance of the procedure is compared with the classical Yule–Walker method. Section 7 contains the conclusions.

2 Stable distribution

In this section, we present the stable distribution (also called $\alpha$-stable) which can be considered as the extension of the classical Gaussian distribution. In the one-dimensional case, there are three equivalent definitions of the stable distributed random variables. Here, we present the definition which is based on the characteristic function. A random variable Z is said to have stable distribution if its characteristic function is given by [53]

$$\begin{aligned} {\mathrm {E}}[\exp {i\theta Z}]= \left\{ \begin{array}{ll} \exp \left\{ -\sigma ^{\alpha }|\theta |^{\alpha }\left\{ 1-i\beta \mathrm {sign}(\theta )\tan \left( \pi \alpha /2\right) \right\} +i\mu \theta \right\} &{} \text{ for } \alpha \ne 1,\\ &{}\\ \exp \left\{ -\sigma |\theta |\{1+i\beta \mathrm {sign}(\theta )\frac{2}{\pi }\log (|\theta |\}+i\mu \theta \right\} &{} \text{ for } \alpha =1. \end{array} \right. \end{aligned}$$

(1)

The parameters of the distribution are $\alpha \in (0,2]$—stability index, $\sigma >0$—scale parameter, $\beta \in [-1,1]$—skewness parameter and $\mu \in \mathbb {R}$—shift parameter. For $\beta =\mu =0$ the random variable Z has symmetric stable distribution. It is worth to mention that in most of the cases, except the Gaussian case with $\alpha =2$, the variance of Z is infinite, which leads to many problems in the estimation and statistical investigation of the $\alpha$-stable-based models.

In the multidimensional case, similary to the one-dimensional distribution, a stable random vector can be defined via chracteristic function. Let $S_{d}=\{\mathbf {s}:||s||=1\}$ be a unit sphere in $\mathbb {R}^d$. A random vector $\mathbf {Z}=(Z_1,Z_2,\ldots ,Z_d)$ is said to be stable if its characteristic function is given by [53]

$$\begin{aligned} & {\mathrm {E}}[\exp \{i\langle \varvec{\theta }, \mathbf {Z} \rangle \}]\nonumber \\ & \quad =\left\{ \begin{array}{ll} \exp \left\{ -\int _{S_d}{|\langle \varvec{\theta },\mathbf {s} \rangle |}^{\alpha }\left( 1-i\mathrm {sign}(\langle \varvec{\theta },\mathbf {s} \rangle )\tan \left( \frac{\pi \alpha }{2}\right) \right) \varGamma (ds)+i\langle \varvec{\theta },\mu _{\mathbf {0}} \rangle \right\} &{} \text{ for } \alpha \ne 1,\\ &{}\\ \exp \left\{ -\int _{S_d}{|\langle \varvec{\theta },\mathbf {s} \rangle |}(1+i\frac{2}{\pi }\mathrm {sign}(\langle \varvec{\theta },\mathbf {s} \rangle )\log (\langle \varvec{\theta },\mathbf {s} \rangle )))\varGamma (ds)+i\langle \varvec{\theta },\mu _{\mathbf {0}} \rangle \right\} &{} \text{ for } \alpha =1, \end{array} \right. \end{aligned}$$

(2)

where $\varGamma (\cdot )$ is a finite spectral measure on the unit sphere $S_d$, $\mu _{\mathbf {0}} \in \mathbb {R}^d$ is a shift vector and $\langle \cdot ,\cdot \rangle$ is the inner product. The information about the shape and scale of the multidimensional $\alpha$-stable distribution are included in the spectral measure $\varGamma (\cdot )$. It is important to mention that the pair $(\varGamma ,\mu _{\mathbf {0}})$ is unique and together with the stability parameter fully describes d-dimensional multivariate stable distribution. Moreover, a necessary and sufficient condition for a stable vector to be symmetric is that $\mu _{\mathbf {0}}=\mathbf {0}$ and $\varGamma (\cdot )$ is a symmetric measure on $S_d$. The characteristic function of a symmetric $\alpha$-stable vector takes the following form

$$\begin{aligned} {\mathrm {E}}[\exp \{i\langle \varvec{\theta }, \mathbf {Z} \rangle \}]= \exp \left\{ -\int _{S_d}{|\langle \varvec{\theta },\mathbf {s} \rangle |}^{\alpha }\varGamma (ds)\right\} . \end{aligned}$$

(3)

2.1 Depedence measures for stable distributed random variables

In the case of stable distribution, the classical dependence measures, known as covariance or correlation, cannot be applied to describe the dependence between random variables due to the infinite variance for $\alpha \ne 2$. In the literature, one can find the alternative measures that can replace the classical ones for the $\alpha$-stable-based models, like for example codifference, covariation and fractional lower order covariance. Here, we present the definitions of the covariation and the fractional lower order covariance. The second measure, applied to the estimation procedure later in this paper, can be considered as an extension of the covariation. For more details on the codifference function see [38, 40, 53,54,55].

2.1.1 Covariation

The definition of the covariation involves the spectral measure of a random vector (X, Y). Let us consider a bidimensional symmetric stable vector with the stability index $1<\alpha \le 2$ and the spectral measure $\varGamma (\cdot )$. The covariation of X on Y is defined as [53, 56]

$$\begin{aligned} \mathrm {CV}(X,Y)=\int _{S_2}s_1s_2^{\langle \alpha -1 \rangle }\varGamma (ds), \end{aligned}$$

(4)

where $a^{\langle p\rangle }$ is called the signed power and it is equal to

$$\begin{aligned} a^{\langle p\rangle }=|a|^p\mathrm {sign}(a). \end{aligned}$$

Let us notice that the covariation can be applied only for the symmetric stable random vectors with $1<\alpha \le 2$. In the Gaussian case it reduces to the classical covariance, namely $2\mathrm {CV}(X,Y)=\mathrm {Cov}(X,Y)$, and for independent random variables $\mathrm {CV}(X,Y)=0$. Moreover, the covariation is not symmetric in its arguments. It can be proven, see [53], that the covariation is related to the joint moment of (X, Y) and therefore Eq. (4) can be equivalently written as

$$\begin{aligned} \mathrm {CV}(X,Y)=\frac{{\mathrm {E}}(XY^{\langle p-1\rangle })}{{\mathrm {E}}(|Y|^{p})}\sigma _Y^{\alpha }, \end{aligned}$$

(5)

where $\sigma _Y$ is the scale parameter of the random variable Y and $1\le p<\alpha$.

Covariation function can be applied to measure the interdependence of a stochastic process $\{X(t)\}$, see [57,58,59] or to describe the spacio-temporal dependence structure of the bidimensional process $\{(X_1(t),X_2(t))\}$, see [60].

In the literature, one can find several methods to estimate the covariation function [29, 49, 61].

2.1.2 Fractional lower order covariance

The fractional lower order covariance is a natural extension of the classical covariance. For a bidimensional symmetric stable random vector (X, Y) the fractional lower order covariance is defined as follows [62]

$$\begin{aligned} \mathrm {FLOC}(X,Y,A,B)={\mathrm {E}}(X^{\langle A\rangle }Y^{\langle B \rangle }), \end{aligned}$$

(6)

with the parameters $A,B \ge 0$ satisfying $A+B<\alpha$. The measure can be applied to any symmetric stable vector, even with $0<\alpha <1$. It is worth mentioning that the value of the fractional lower order covariance depends on the choice of A and B. In the Gaussian case, it reduces to the classical covariance when $A=B=1$. For independent random variables $\mathrm {FLOC}(X,Y,A,B)=0$.

Note that for $1<\alpha <2$, $A=1$ and $B=p-1$, where $1\le p<\alpha$, we obtain the following relation between the fractional lower order covariance and the covariation function

$$\begin{aligned} \mathrm {FLOC}(X,Y,1,p-1)=\frac{\mathrm {CV}(X,Y){\mathrm {E}}(|Y|^{p})}{\sigma _Y^\alpha }. \end{aligned}$$

(7)

Fractional lower order covariance can be applied to describe the interdependence of a stochastic process $\{X(t)\}$, see [61]. However, it can be also used as a measure of the spatio-temporal dependence of the bidimensional process $\{(X_1(t),X_2(t))\}$. The estimator of the cross-fractional lower order covariance is similar to the auto-FLOC estimator given in [62] and it has the following form

$$\begin{aligned}&\widehat{\mathrm {FLOC}}(X_1(t),X_2(t+k),A,B)\nonumber \\&\quad =\frac{\sum _{n=L_1}^{L_2}|x_1(n)|^A|x_2(n+k)|^B\mathrm {sign}(x_1(n)x_2(n+k))}{L_2-L_1}, \end{aligned}$$

(8)

where $\{x_1(1),x_1(2),\ldots ,x_1(N)\}$ and $\{x_2(1),x_2(2),\ldots ,x_2(N)\}$ are sample trajectories of the length N corresponding to the bivariate process $\{(X_1(t),X_2(t))\}$ and $L_2=\mathrm {min}(N,N-k)$, $L_1=\mathrm {max}(0,-k)$.

3 Bidimensional autoregressive model of order 1

We start with the classical definitions of the second-order white noise and of the general bidimensional autoregressive model of order 1 (also called bidimensional AR(1) model).

Definition 1

The bidimensional time series $\{\mathbf {Z}(t)\}$ is called white noise with mean $\mathbf {0}$ and covariance matrix $\varSigma$ if $\{\mathbf {Z}(t)\}$ is weak-sense stationary with mean vector $\mathbf {0}$ and covariance matrix function given by [4]

$$\begin{aligned} \gamma \left( h\right)&={\mathrm {E}}\left[ \mathbf {Z}(t+h)\mathbf {Z}(t)^{ T }\right] =\left\{ \begin{array}{ll}\varSigma &{} \text{ if }\,h=0,\\ 0&{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

(9)

Definition 2

The time series $\left\{ \mathbf {X}\left( t\right) \right\} =\left\{ X_1\left( t\right) ,X_2\left( t\right) \right\}$ is a bidimensional AR(1) model if $\left\{ \mathbf {X}\left( t\right) \right\}$ is weak-sense stationary and if for every t it satisfies the following equation [4]

$$\begin{aligned} \mathbf {X}\left( t\right) -\varTheta \ \mathbf {X}\left( t-1\right) =\mathbf {Z}\left( t\right) , \end{aligned}$$

(10)

where $\{\mathbf {Z}\left( t\right) \}$ is a bidimensional white noise and $\varTheta$ is a $2 \times 2$ matrix of the coefficients given by

$$\begin{aligned} \varTheta = \left[ \begin{array}{cc} a_1 &{} a_2\\ a_3 &{} a_4 \end{array} \right] . \end{aligned}$$

(11)

Let us notice that the Eq. (10) can be equivalently written as the following system of recursive equations

$$\begin{aligned} X_1\left( t\right) -a_1\ X_1\left( t-1\right) -a_2\ X_2\left( t-1\right)&= Z_1\left( t\right) , \end{aligned}$$

(12a)

$$\begin{aligned} X_2\left( t\right) -a_3\ X_1\left( t-1\right) -a_4\ X_2\left( t-1\right)&= Z_2\left( t\right) . \end{aligned}$$

(12b)

In this paper, we extend Definition 2 by considering the infinite-variance noise instead of the classical white noise. We assume that the bidimensional noise $\{\mathbf {Z}(t)\}$ is a symmetric stable vector in $\mathbb {R}^2$ defined in Eq. (3) with stability index $\alpha <2$, shift vector $\mu _{\mathbf {0}}=\mathbf {0}$ and the spectral measure $\varGamma (\cdot )$. We additionally assume that $\mathbf {Z}(t)$ is independent from $\mathbf {Z}(t+h)$ for all $h\ne 0$. In the following part of the paper we call $\{\mathbf {Z}(t)\}$ a symmetric stable noise (called also a symmetric $\alpha$-stable noise).

Moreover, provided that all the eigenvalues of the matrix $\varTheta$ are less than 1 in absolute value, which is equivalent to the following condition

$$\begin{aligned} \text {det}(I-z\varTheta )\ne 0 \quad \text {for all}\ z \in \mathbb {C}\ \text {such that}\ |z| \le 1, \end{aligned}$$

the time series $\{\mathbf {X}\left( t\right) \}$ given in Eq. (10) can be presented in the following casual representation [4]

$$\begin{aligned} \mathbf {X}(t)=\sum _{j=0}^{+\infty }\varTheta ^j\mathbf {Z}\left( t-j\right) . \end{aligned}$$

(13)

By introducing the following notation for the matrix taken to the j-th power

$$\begin{aligned} \varTheta ^j= \left[ \begin{array}{cc} a_1^{\left( j\right) } &{} a_2^{\left( j\right) }\\ a_3^{\left( j\right) } &{} a_4^{\left( j\right) } \end{array} \right] , \end{aligned}$$

and by writing the Eq. (13) in vector notation we obtain the following

$$\begin{aligned} \left\{ \begin{array}{ll} X_1\left( t\right) = \sum \nolimits _{j=0}^{+\infty } \left( a_1^{\left( j\right) } Z_1\left( t-j\right) + a_2^{\left( j\right) } Z_2\left( t-j\right) \right) ,\\ X_2\left( t\right) = \sum \nolimits _{j=0}^{+\infty } \left( a_3^{\left( j\right) } Z_1\left( t-j\right) + a_4^{\left( j\right) } Z_2\left( t-j\right) \right) . \end{array} \right. \end{aligned}$$

(14)

4 Estimation of bidimensional AR(1) parameters based on FLOC

In this section, we present a new estimation method for the parameters of bidimensional AR(1) model with stable noise. This procedure can be considered as a modification of the Yule–Walker (Y-W) method presented in [4]. However, it is based not on the covariance function, as in the classical Y-W method, but on the fractional lower order covariance. The use of FLOC is supported by the fact that, on the contrary to the covariance function, FLOC is well defined for the stable distributed random variables and thus it can successfully substitute the covariance function in the case of the infinite second moment. The theorem below presents the estimators of the bidimensional AR(1) model’s parameters.

Theorem 1

Let us assume that$\{\mathbf {X}(t)\}=\{X_1(t),X_2(t)\}$is a bidimensional autoregressive model of order 1 defined as the system of recursive equations (12a) and (12b), where$\{\mathbf {Z}(t)\}$is a bidimensional symmetric stable noise with$\alpha >1$. The parameters of the matrix$\varTheta$given in Eq. (11) can be estimated using the following formulas

$$\begin{aligned} \widehat{a_1}&=\frac{N}{N-1}\frac{\sum _{n=1}^{N-1}x_1(n+1)|x_1(n)|^B\mathrm {sign}(x_1(n))}{\sum _{n=1}^{N}|x_1(n)|^{B+1}}\\&\quad -\widehat{a_2}\frac{\sum _{n=1}^{N}x_2(n)|x_1(n)|^B\mathrm {sign}(x_1(n))}{\sum _{n=1}^{N}|x_1(n)|^{B+1}} \\ \widehat{a_2}&=\left[ \frac{N}{N-1}\left( \frac{\sum _{n=1}^{N-1}x_1(n+1)|x_1(n)|^B\mathrm {sign}(x_1(n))}{\sum _{n=1}^{N}|x_1(n)|^{B+1}}\right. \right. \\&\quad \left. \left. -\frac{\sum _{n=1}^{N-1}x_1(n+1)|x_2(n)|^B\mathrm {sign}(x_2(n))}{\sum _{n=1}^{N}x_1(n)|x_2(n)|^B\mathrm {sign}(x_2(n))}\right) \right] \\&\quad \left( \frac{\sum _{n=1}^{N}x_2(n)|x_1(n)|^B\mathrm {sign}(x_1(n))}{\sum _{n=1}^{N}|x_1(n)|^{B+1}}\right. \\&\quad \left. -\frac{\sum _{n=1}^{N}|x_2(n)|^{B+1}}{\sum _{n=1}^{N}x_1(n)|x_2(n)|^B\mathrm {sign}(x_2(n))}\right) ^{-1} \\ \widehat{a_3}&=\left[ \frac{N}{N-1}\left( \frac{\sum _{n=1}^{N-1}x_2(n+1)|x_2(n)|^B\mathrm {sign}(x_2(n))}{\sum _{n=1}^{N}|x_2(n)|^{B+1}}\right. \right. \\&\quad \left. \left. -\frac{\sum _{n=1}^{N-1}x_2(n+1)|x_1(n)|^B\mathrm {sign}(x_1(n))}{\sum _{n=1}^{N}x_2(n)|x_1(n)|^B\mathrm {sign}(x_1(n))}\right) \right] \\&\quad \left( \frac{\sum _{n=1}^{N}x_1(n)|x_2(n)|^B\mathrm {sign}(x_2(n))}{\sum _{n=1}^{N}|x_2(n)|^{B+1}}\right. \\&\quad \left. -\frac{\sum _{n=1}^{N}|x_1(n)|^{B+1}}{\sum _{n=1}^{N}x_2(n)|x_1(n)|^B\mathrm {sign}(x_1(n))}\right) ^{-1} \\ \widehat{a_4}&=\frac{N}{N-1}\frac{\sum _{n=1}^{N-1}x_2(n+1)|x_2(n)|^B\mathrm {sign}(x_2(n))}{\sum _{n=1}^{N}|x_2(n)|^{B+1}}\\&\quad -\widehat{a_3}\frac{\sum _{n=1}^{N}x_1(n)|x_2(n)|^B\mathrm {sign}(x_2(n))}{\sum _{n=1}^{N}|x_2(n)|^{B+1}} \end{aligned}$$

where$\{x_1(1),x_1(2),\ldots ,x_1(N)\}$and$\{x_2(1),x_2(2),\ldots ,x_2(N)\}$are sample trajectories of the lengthNcorresponding to the bivariate process$\{(X_1(t),X_2(t))\}$andBis the estimation parameter satisfying$0\le B<\alpha -1$.

Proof

Let us take the following notation

$$\begin{aligned} S_i(t)=\mathrm {sign}(X_i(t))\quad \text {for} \quad i=1,2 \end{aligned}$$

and

$$\begin{aligned} \mathrm {FLOC}(X_i(t),X_j(s),A,B)={\mathrm {E}}\left[ X_i(t)^{\langle A\rangle }X_j(s)^{\langle B\rangle }\right] \quad \text {for} \quad i,j=1,2. \end{aligned}$$

At first, let us multiply the Eq. (12a) by $S_1(t)S_1(t-1)$. We obtain the following equation

$$\begin{aligned}&X_1(t)S_1(t)S_1(t-1)-a_1X_1(t-1)S_1(t)S_1(t-1)\\&\quad -a_2 X_2(t-1)S_1(t)S_1(t-1)= Z_1(t)S_1(t)S_1(t-1). \end{aligned}$$

Then, due to the fact that $X_1(t)S_1(t)=|X_1(t)|$ and $X_1(t-1)S_1(t-1)=|X_1(t-1)|$ the above equation takes a form given by

$$\begin{aligned}&|X_1(t)|S_1(t-1)-a_1|X_1(t-1)|S_1(t)\\&\quad -a_2 X_2(t-1)S_1(t)S_1(t-1)= Z_1(t)S_1(t)S_1(t-1). \end{aligned}$$

Let us multiply the above equation by $|X_1(t)|^{A-1}|X_1(t-1)|^B$ where $A,B\ge 0$ and $A+B<\alpha$. We obtain the following

$$\begin{aligned}&|X_1(t)|^{A}|X_1(t-1)|^{B}S_1(t-1)\\&\qquad -a_1|X_1(t-1)|^{B+1}|X_1(t)|^{A-1}S_1(t)\\&\qquad -a_2 X_2(t-1)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t)S_1(t-1)\\&\quad = Z_1(t)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t)S_1(t-1). \end{aligned}$$

Then, after multiplying the above equation by $S_1(t)$ and using the fact that $\left( S_1(t)\right) ^2=1$ we have

$$\begin{aligned}&|X_1(t)|^{A}|X_1(t-1)|^{B}S_1(t-1)S_1(t)\\&\qquad -a_1|X_1(t-1)|^{B+1}|X_1(t)|^{A-1}\\&\qquad -a_2 X_2(t-1)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t-1)\\&\quad = Z_1(t)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t-1). \end{aligned}$$

Now, by taking the expectations on the both sides of the above equation we obtain the following

$$\begin{aligned}&\mathrm {FLOC}(X_1(t),X_1(t-1),A,B)\nonumber \\&\qquad -a_1{\mathrm {E}}\left[ |X_1(t-1)|^{B+1}|X_1(t)|^{A-1}\right] \nonumber \\&\qquad -a_2{\mathrm {E}}\left[ X_2(t-1)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t-1)\right] \nonumber \\&\quad = {\mathrm {E}}\left[ Z_1(t)|X_1(t)|^{A-1}|X_1(t-1)|^BS_1(t-1)\right] . \end{aligned}$$

(15)

Let us notice that the right hand side of the above equation is equal to zero only for $A=1$. In this case, we have

$$\begin{aligned}&{\mathrm {E}}\left[ Z_1(t)|X_1(t-1)|^BS_1(t-1)\right] \\&\quad ={\mathrm {E}}\left[ Z_1(t)\right] {\mathrm {E}}\left[ |X_1(t-1)|^BS_1(t-1)\right] =0, \end{aligned}$$

since ${\mathrm {E}}[Z_1(t)]=\mu =0$ for $\alpha >1$. Let us consider $A=1$ and $0\le B<\alpha -1$ which simplifies the Eq. (15) as follows

$$\begin{aligned}&\mathrm {FLOC}(X_1(t),X_1(t-1),1,B)-a_1{\mathrm {E}}\left[ |X_1(t-1)|^{B+1}\right] \nonumber \\&\quad -a_2\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)= 0. \end{aligned}$$

(16)

Now, in the second step, we multiply the Eq. (12a) by $S_1(t)S_2(t-1)$. That leads to the following equation

$$\begin{aligned}&X_1(t)S_1(t)S_2(t-1)-a_1X_1(t-1)S_1(t)S_2(t-1)\\&\quad -a_2 X_2(t-1)S_1(t)S_2(t-1)= Z_1(t)S_1(t)S_2(t-1). \end{aligned}$$

Now, let us use the fact that $X_1(t)S_1(t)=|X_1(t)|$ and $X_2(t-1)S_2(t-1)=|X_2(t-1)|$. The above equation takes the following form

$$\begin{aligned}&|X_1(t)|S_2(t-1)-a_1X_1(t-1)S_1(t)S_2(t-1)\\&\quad -a_2 |X_2(t-1)|S_1(t)= Z_1(t)S_1(t)S_2(t-1). \end{aligned}$$

Then, after multiplying the above equation by $|X_1(t)|^{A-1}|X_2(t-1)|^B$, where $A,B\ge 0$ and $A+B<\alpha$, we obtain

$$\begin{aligned}&|X_1(t)|^{A}|X_2(t-1)|^{B}S_2(t-1)\\&\qquad -a_1X_1(t-1)|X_1(t)|^{A-1}|X_2(t-1)|^BS_1(t)S_2(t-1)\\&\qquad -a_2 |X_1(t)|^{A-1}|X_2(t-1)|^{B+1}S_1(t)\\&\quad = Z_1(t)|X_1(t)|^{A-1}|X_2(t-1)|^BS_1(t)S_2(t-1). \end{aligned}$$

Let us multiply the above equation by $S_1(t)$. By applying the fact that $\left( S_1(t)\right) ^2=1$ we have the following

$$\begin{aligned}&|X_1(t)|^{A}|X_2(t-1)|^{B}S_1(t)S_2(t-1)\\&\qquad -a_1X_1(t-1)|X_1(t)|^{A-1}|X_2(t-1)|^BS_2(t-1)\\&\qquad -a_2 |X_1(t)|^{A-1}|X_2(t-1)|^{B+1}\\&\quad = Z_1(t)|X_1(t)|^{A-1}|X_2(t-1)|^BS_2(t-1). \end{aligned}$$

Now, we take the expectations on the both sides of the above equation which leads to the following expression

$$\begin{aligned}&\mathrm {FLOC}(X_1(t),X_2(t-1),A,B)\nonumber \\&\qquad -a_1{\mathrm {E}}\left[ X_1(t-1)|X_1(t)|^{A-1}|X_2(t-1)|^BS_2(t-1)\right] \nonumber \\&\qquad -a_2{\mathrm {E}}\left[ |X_1(t)|^{A-1}|X_2(t-1)|^{B+1}\right] \nonumber \\&\quad = {\mathrm {E}}\left[ Z_1(t)|X_1(t)|^{A-1}|X_2(t-1)|^BS_2(t-1)\right] . \end{aligned}$$

(17)

Again, because of the fact that the right hand side of the above equation is equal to zero only for $A=1$, we consider $A=1$ and $0\le B<\alpha -1$ and the Eq. (17) simplifies to

$$\begin{aligned}&\mathrm {FLOC}(X_1(t),X_2(t-1),1,B)\nonumber \\&\quad -a_1\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)\nonumber \\&\quad -a_2{\mathrm {E}}\left[ |X_2(t-1)|^{B+1}\right] = 0. \end{aligned}$$

(18)

Then, using the analogous procedure for the Eq. (12b) we finally obtain the following system of four equations

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm {FLOC}(X_1(t),X_1(t-1),1,B)&{}-\ a_2\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)\\ {} &{}-\ a_1{\mathrm {E}}\left( |X_1(t-1)|^{B+1}\right) = 0,\\ \mathrm {FLOC}(X_1(t),X_2(t-1),1,B)&{}-\ a_1\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)\\ {} &{}-\ a_2{\mathrm {E}}\left( |X_2(t-1)|^{B+1}\right) = 0,\\ \mathrm {FLOC}(X_2(t),X_1(t-1),1,B)&{}-\ a_4\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)\\ {} &{}-\ a_3{\mathrm {E}}\left( |X_1(t-1)|^{B+1}\right) = 0,\\ \mathrm {FLOC}(X_2(t),X_2(t-1),1,B)&{}-\ a_3\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)\\ {} &{}-\ a_4{\mathrm {E}}\left( |X_2(t-1)|^{B+1}\right) = 0. \end{array} \right. \end{aligned}$$

(19)

By solving (19) for $a_1$, $a_2$, $a_3$ and $a_4$, we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} a_1=\frac{\mathrm {FLOC}(X_1(t),X_1(t-1),1,B)}{{\mathrm {E}}(|X_1(t-1)|^{B+1})}-{a_2}\frac{\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)}{{\mathrm {E}}(|X_1(t-1)|^{B+1})},\\ a_2=\left( \frac{\mathrm {FLOC}(X_1(t),X_1(t-1),1,B)}{{\mathrm {E}}(|X_1(t-1)|^{B+1})}-\frac{\mathrm {FLOC}(X_1(t),X_2(t-1),1,B)}{\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)}\right) \\ \ \ \ \ \ \ \ \left( \frac{\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)}{{\mathrm {E}}(|X_1(t-1)|^{B+1})}-\frac{{\mathrm {E}}(|X_2(t-1)|^{B+1})}{\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)}\right) ^{-1} ,\\ a_3=\left( \frac{\mathrm {FLOC}(X_2(t),X_2(t-1),1,B)}{{\mathrm {E}}(|X_2(t-1)|^{B+1})}-\frac{\mathrm {FLOC}(X_2(t),X_1(t-1),1,B)}{\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)}\right) \\ \ \ \ \ \ \ \ \left( \frac{\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)}{{\mathrm {E}}(|X_2(t-1)|^{B+1})}-\frac{{\mathrm {E}}(|X_1(t-1)|^{B+1})}{\mathrm {FLOC}(X_2(t-1),X_1(t-1),1,B)}\right) ^{-1},\\ a_4=\frac{\mathrm {FLOC}(X_2(t),X_2(t-1),1,B)}{{\mathrm {E}}(|X_2(t-1)|^{B+1})}-{a_3}\frac{\mathrm {FLOC}(X_1(t-1),X_2(t-1),1,B)}{{\mathrm {E}}(|X_2(t-1)|^{B+1})} \end{array} \right. \end{aligned}$$

(20)

After replacing the theoretical fractional lower order covariance and the theoretical fractional moments with their empirical equivalents we obtain the estimators. $\square$

5 Monte Carlo simulations

In this section, we verify the effectiveness of the estimators presented in Theorem 1 using the generated trajectory of bidimensional AR(1) model. We analyze the time series $\{\mathbf {X}(t)\}=\{X_1(t),X_2(t)\}$ satisfying the following system of equations

$$\begin{aligned} \left\{ \begin{array}{ll} X_1\left( t\right) -0.6\ X_1\left( t-1\right) -0.2\ X_2\left( t-1\right) = Z_1\left( t\right) ,\\ X_2\left( t\right) -0.7\ X_1\left( t-1\right) +0.3\ X_2\left( t-1\right) = Z_2\left( t\right) , \end{array} \right. \end{aligned}$$

(21)

where $\{\mathbf {Z}(t)\}=\{Z_1(t),Z_2(t)\}$ is the bidimensional sub-Gaussian noise with the characteristic function given by

$$\begin{aligned}&{\mathrm {E}}\left( \exp \left\{ i\theta _1 Z_1\left( t\right) +i \theta _2Z_2\left( t\right) \right\} \right) \nonumber \\&\quad =\exp \left\{ -\frac{1}{2}\left( \theta _1^2 R_{11}+2\theta _1\theta _2R_{12}+\theta _2^2R_{22}\right) \right\} , \end{aligned}$$

(22)

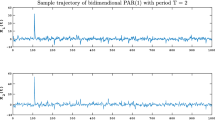
where $\alpha <2$, $R_{11}=0.1$, $R_{12}=0.05$ and $R_{22}=0.3$. We mention here that the sub-Gaussian vector is an example of a symmetric stable random vector presented in Sector 2. It is defined as a combination of a Gaussian vector and a totally skewed stable random variable, for more details we refer to [53]. Exemplary trajectory of $\{\mathbf {X}(t)\}$ given by Eq. (21) is presented in Fig. 1.

Fig. 1

Sample trajectory of time series given by Eq. (21) with $\alpha =1.8$

Fig. 2

Boxplots presenting 1000 estimated values of the parameters for bidimensional AR(1) model given in Eq. (21) with $\alpha =1.5$. The estimation parameter B is equal to 0.45

To test the proposed estimation procedure, we use the Monte Carlo method. We generate $M=10{,}000$ trajectories of time series of length N and for each trajectory we calculate the estimators $\widehat{a_1}$, $\widehat{a_2}$, $\widehat{a_3}$ and $\widehat{a_4}$ given in Theorem 1 performing the method for different values of B parameter. We consider the trajectories of length $N=100$, $N=500$ and $N=1000$ with $\alpha =1.5$. After performing the Monte Carlo simulations we obtain the vectors of estimated parameters, namely

$$\begin{aligned} \widehat{\mathbf {a}}_{1}= & {} (\widehat{a}_{1}^1,\widehat{a}_{1}^2,\widehat{a}_{1}^3,\ldots ,\widehat{a}_{1}^{M}),\\ \widehat{\mathbf {a}}_{2}= & {} (\widehat{a}_{2}^1,\widehat{a}_{2}^2,\widehat{a}_{2}^3,\ldots ,\widehat{a}_{2}^{M}),\\ \widehat{\mathbf {a}}_{3}= & {} (\widehat{a}_{3}^1,\widehat{a}_{3}^2,\widehat{a}_{3}^3,\ldots ,\widehat{a}_{3}^{M}),\\ \widehat{\mathbf {a}}_{4}= & {} (\widehat{a}_{4}^1,\widehat{a}_{4}^2,\widehat{a}_{4}^3,\ldots ,\widehat{a}_{4}^{M}). \end{aligned}$$

To find the parameter B which leads to the best estimate of theoretical parameters, we take into account both the center and the dispersion of the above vectors. Namely, we calculate the median of the vectors and the absolute value of the difference between the quantiles of order 0.95 ($q_{0.95}$) and 0.05 ($q_{0.05}$), which can be consider as the $90\%$ confidence interval. Moreover, we calculate the mean absolute error defined as

$$\begin{aligned} \mathrm {error} = \frac{1}{M}\sum _{m=1}^{M}\left| \widehat{a}_{i}^m-a_i\right| \quad \text {for} \quad i = 1, 2, 3, 4. \end{aligned}$$

(23)

Tables 1, 2 and 3 present the results obtained for the trajectories of the length $N = 100$, $N = 500$ and $N = 1000$, respectively. Regardless of the length of the data, for all the parameters it is clear that the medians are very close to the theoretical values and the empirical confidence intervals are getting narrower for larger values of B. Moreover, in Tables 1, 2 and 3 the results corresponding to the minimum mean absolute errors are highlighted. For all considered trajectory’s lengths, the calculated errors are getting smaller as B is getting closer to $\alpha -1$. The range of the estimated values is also visible on the boxplots presented in Fig. 2. It is important to mention that we applied the same procedure for the time series given by Eq. (21) with $\alpha = 1.2$ and $\alpha = 1.8$ considering the trajectories of the length $N=100$, $N=500$ and $N=1000$. In all the cases we obtain the same results indicating that the best choice of the estimation parameter is to take B very close to $\alpha -1$.

Table 1 The table presenting the results of the estimation method applied to the bidimensional AR(1) model given by Eq. (21) with $\alpha =1.5$

Table 2 The table presenting the results of the estimation method applied to the bidimensional AR(1) model given by Eq. (21) with $\alpha =1.5$

Table 3 The table presenting the results of the estimation method applied to the bidimensional AR(1) model given by Eq. (21) with $\alpha =1.5$

In the case of real data analysis we often do not know the theoretical value of the parameter $\alpha$ and thus we do not know how to choose parameter B to be close to $\alpha - 1$. In order to verify which value of B is the most suitable when the theoretical value of $\alpha$ is unknown, we carry out the following test. In the simulation procedure, we draw the parameter $\alpha$ from uniform distribution assuming that $1<\alpha <2$. Then, we generate the model given in Eq. (21) and we estimate the unknown parameters $a_1$, $a_2$, $a_3$ and $a_4$. As the best choice of the estimation parameter, we consider the value of B with the median corresponding to the vector of estimator’s values closest to the theoretical parameter. Moreover, we calculate the mean absolute error defined in (23). In the procedure, we performed 10,000 simulations and the length of the trajectory is equal to 1000. In Table 4 we present the medians and the errors corresponding to the best choice of parameter B. We also mention that for all choices of B between 0.6 and 0.95 the calculated errors normalized by the parameters’ theoretical values are smaller than $10\%$. Since the errors are small the proposed estimation method can be successfully used even in the case when we do not know the theoretical value of parameter $\alpha$.

Table 4 The table presenting the best choice of B parameter for the estimation method applied to the bidimensional AR(1) model given by Eq. (21) with $\alpha$ drawn from uniform distribution assuming $1<\alpha <2$

6 Comparison of FLOC-based estimators and classical Yule–Walker method

In this section, we compare FLOC-based estimators introduced in Theorem 1 with the Yule–Walker method. The classical Yule–Walker estimators (denoted also as Y-W estimators) are based on the covariance function and due to that they are defined only for the second-order models, see [4], and therefore the method should not be applied for the models that are based on the $\alpha$-stable distribution. For this reason, the use of the FLOC-based method is fully justified from a theoretical point of view. However, here we would also like to focus on the practical aspect by comparing the results corresponding to both the classical and the introduced method to emphasize the difference between these two approaches.

To perform the comparison we simulate $M=1000$ trajectories of the bidimensional sub-Gaussian AR(1) time series $\{\mathbf {X}(t)\}$ presented in the previous section in Eq. (21). Next, we estimate the parameters $a_1$, $a_2$, $a_3$ and $a_4$ using the Yule–Walker method and the introduced FLOC-based method. For the FLOC-based estimators, according to the results obtained in the previous section, we choose the parameter B to be close to $(\alpha -1)$, more precisely we take $B=\alpha -1.05$. By performing the simulations we obtain the following vectors of estimated parameters

$$\begin{aligned}&\widehat{\mathbf {a}}_{1,YW}=(\widehat{a}_{1,YW}^1,\ldots ,\widehat{a}_{1,YW}^{M}),\\&\widehat{\mathbf {a}}_{1,FLOC}=(\widehat{a}_{1,FLOC}^1,\ldots ,\widehat{a}_{1,FLOC}^{M}),\\&\widehat{\mathbf {a}}_{2,YW}=(\widehat{a}_{2,YW}^1,\ldots ,\widehat{a}_{2,YW}^{M}),\\&\widehat{\mathbf {a}}_{2,FLOC}=(\widehat{a}_{2,FLOC}^1,\ldots ,\widehat{a}_{2,FLOC}^{M}),\\&\widehat{\mathbf {a}}_{3,YW}=(\widehat{a}_{3,YW}^1,\ldots ,\widehat{a}_{3,YW}^{M}),\\&\widehat{\mathbf {a}}_{3,FLOC}=(\widehat{a}_{3,FLOC}^1,\ldots ,\widehat{a}_{3,FLOC}^{M}),\\&\widehat{\mathbf {a}}_{4,YW}=(\widehat{a}_{4,YW}^1,\ldots ,\widehat{a}_{4,YW}^{M}),\\&\widehat{\mathbf {a}}_{4,FLOC}=(\widehat{a}_{4,FLOC}^1,\ldots ,\widehat{a}_{4,FLOC}^{M}), \end{aligned}$$

and on the basis of these values, we calculate the statistics describing the error of the estimation defined in the following way

$$\begin{aligned} S_{YW}&=\frac{1}{4}\sum _{i=1}^{4}|\sqrt{N}(\overline{\widehat{\mathbf {a}}}_{i,YW}-a_i)|, \end{aligned}$$

(24)

$$\begin{aligned} S_{FLOC}&=\frac{1}{4}\sum _{i=1}^{4}|\sqrt{N}(\overline{\widehat{\mathbf {a}}}_{i,FLOC}-a_i)|, \end{aligned}$$

(25)

where $\overline{\widehat{\mathbf {a}}}_{i,YW}$ and $\overline{\widehat{\mathbf {a}}}_{i,FLOC}$ are the mean values of the vectors $\mathbf {a}_{i,YW}$ and $\mathbf {a}_{i,FLOC}$, respectively, and N is the length of the trajectory.

Fig. 3

Values taken by the statistics $S_{YW}$ (left panels) and $S_{FLOC}$ (right panels) corresponding to the trajectories of bidimensional sub-Gaussian AR(1) model given by Eq. (21) for different values of the parameter $\alpha$. Upper, middle and bottom panels correspond to the trajectories of length $N=100$, $N=500$ and $N=1000$, respectively. The statistics were calculated 100 times on the basis of $M=1000$ trajectories

Fig. 4

Values taken by the statistics $S_{YW}$ (left panels) and $S_{FLOC}$ (right panels) corresponding to the trajectories of bidimensional AR(1) model with $a_1=0.6$, $a_2=0.2$, $a_3=0.7$ and $a_4=-0.3$ with independent stable distributed noise components for different values of the parameter $\alpha$. Upper, middle and bottom panels correspond to the trajectories of length $N=100$, $N=500$ and $N=1000$, respectively. The statistics were calculated 100 times on the basis of $M=1000$ trajectories

For the simulated trajectories, we calculate the statistics given in Eq. (24) and in Eq. (25) 100 times and we presented their values on the boxplots in Fig. 3. The upper, middle and bottom panels correspond to the trajectories of length $N=100$, $N=500$ and $N=1000$, respectively. We consider the stability index $\alpha$ to be between 1.5 and 1.95 with the step equal to 0.05. One can observe that for all considered values of $\alpha$ and N the median of $S_{YW}$ is greater than the median of $S_{FLOC}$ which means that the FLOC-based method outperforms the Yule–Walker method in the sense of the considered statistics. The distinction between these two methods is the most visible for the trajectories of length N equal to 100 where the difference between the values taken by $S_{YW}$ are the values taken by $S_{FLOC}$ is the largest. To demonstrate that the tendency shown in Fig. 3 is general and both statistics behave in an analogous manner also for models other than models with sub-Gaussian noise we consider another time series. Namely, Fig. 4 presents the boxplots of 100 values taken by the statistics $S_{YW}$ and $S_{FLOC}$ corresponding to $M=1000$ trajectories of bidimensional AR(1) time series $\{\mathbf {X}(t)\}$ with $a_1 = 0.6$, $a_2 = 0.2$, $a_3 = 0.7$ and $a_4 = -0.3$ and the noise $\{\mathbf {Z}(t)\}$ consisting of two independent symmetric $\alpha$-stable distributed components $\{Z_1(t)\}$ and $\{Z_2(t)\}$ with the scale parameters $\sigma _1=0.1$ and $\sigma _2=0.5$, respectively. The results are analogous to the case of the sub-Gaussian noise.

Summarising, the graphs presented in Figs. 3 and 4 indicate that the FLOC-based method works better than the classical Yule–Walker method especially when we estimate the parameters with very little data available.

7 Conclusions

In this paper, we have introduced a new estimation method for the bidimensional AR(1) model with stable distribution. This method is based on the alternative measure of dependence adequate for infinite variance processes, namely fractional lower order covariance. The proposed technique is an extension of the classical Yule–Walker method, commonly used estimation algorithm based on the covariance function of the underlying process. The application of the FLOC measure is justified from the theoretical point of view in the considered case (the theoretical covariance does not exist) however by simulation study we have proved it is reasonable to use the new technique taking under account the practical aspects. Especially for small sample sizes, the FLOC-based technique is more effective in contrast to the classical Yule–Walker method. This paper is the continuation of the authors’ previous research where the alternative measures of dependence were applied to describe the dependence structure for heavy-tailed based processes.