Multi-Granulation-Based Graphical Analytics of Three-Way Bipolar Neutrosophic Contexts

Abstract

Recently, a three-way fuzzy concept lattice and its graphical structure analytics has given a mathematical way to deal with cognitive concept learning based on its truth, false, and uncertain regions, independently. In this process, a major problem was addressed while existence of bipolar information in a three-way decision space. To address this problem, the current paper aimed at introducing bipolar neutrosophic graph representation of concept lattice and its granular-based processing for cognitive concept learning. In addition, the proposed method is illustrated with an example for better understanding. Cognitive computing provides a way to mimic with human brain and its uncertainty beyond the binary values. To characterize these types of bipolar attributes based on its acceptation, rejection, and uncertain part, the three-way bipolar neutrosophic context and its concept lattice is introduced in this paper. In addition, another method is proposed to extract some of the bipolar cognitive concepts based on user required bipolar truth, bipolar indeterminacy, and falsity membership values, independently. This paper provides a graphical structure visualization of the three-way bipolar information at user defined granules. It is also shown that the extracted information from both of the proposed methods are concordant with each other. It is also shown that, the proposed method provides an adequate way to model the three-way bipolar cognitive concepts when compared to other available approaches. This paper introduces a method to model the three-way bipolar cognitive context using the properties of bipolar neutrosophic graph and its lattice structure. The line diagram is drawn based on their lower neighbors within O(|C| n² m³) time complexity. In addition, another method is proposed to refine the three-way bipolar neutrosophic cognitive concepts at user defined granulation within O(n⁶) or O(m⁶) time complexity with an illustrative example. However, the proposed method is unable to measure the changes in the three-way bipolar neutrosophic cognitive concepts at the given phase of time. Due to that, the author will focus on resolving this issue of bipolar neutrosophic context in near future.

Introduction

Recently, the calculus of neutrosophic set is introduced in [47] for graphical analytics of uncertainty in human cognition based on its acceptation, rejection, and uncertain parts, independently. It is one of the first kind of mathematical model which given a way to mimic with human cognition beyond a unipolar fuzzy space [48, 50]. In this direction, Prem Kumar Singh [43, 53] introduces the properties of bipolar fuzzy sets to measure the uncertainty and vagueness [52] in fuzzy attributes beyond the unipolar fuzzy space at given phase of time [18, 46]. In this process, a problem is addressed while dealing with positive and negative thought exists in human cognition. The first problem arises with its precise representation and the second problem arises with its graphical analytics for knowledge processing tasks. To approximate this problem, the mathematical algebra of interval valued [37, 49] and bipolar fuzzy [43, 44] set is introduced in applied lattice theory for cognitive concept learning [29, 34, 59]. Wille [65] develop a mathematical model called as concept lattice for knowledge discovery and representation tasks using the mathematics of applied abstract algebra [27]. This mathematical model is extended into the fuzzy space by Burusco and Fuentes-Gonzales [13] for computing with uncertainty and vagueness in attributes. This orientation given many ways to represent the fuzziness in attributes beyond the unipolar [9, 14] and bipolar space [5, 12, 43] for handling the heterogeneous [4] via multi-adjoint concept lattice [21, 38]. To measure the uncertainty and incompleteness in attributes by the three-way decision space [23, 25, 67, 68] at distinct multi-granulation [34, 45, 66] for handling multi-attributes cognitive contexts [56]. Some other distinct approaches are also introduced recently to handle the three-way cognitive concepts [29, 33, 74] using parallel computing [39]. In this process, one of the problems is addressed while representing the bipolar information in the three-way fuzzy space [26]. To deal with this problem, the current paper focuses on introducing the bipolar neutrosophic context and its compressed graphical structure visualization using the properties of bipolar neutrosophic graph.

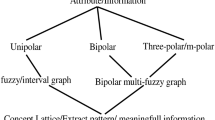
Figure 1 represents that the bipolar fuzzy attributes can be handled more precisely using the properties of the bipolar fuzzy set. To understand it more in a convinced way, the Table 1 represents that bipolar information exists in the three-way fuzzy space due to its corresponding relationship among objects and attributes. One of the suitable examples is an user wants to purchase a car for traveling with his/her family based on their acceptance, rejection, and uncertainty zone of given parameters. The user may purchase the car based on acceptation of its price list—the same time the user can reject the car based on its price list, whereas other cases the user may be uncertain about price list. The user can provide a positive or negative decision for purchasing the car based on his/her cognitive thought. The numerical representation of this type of human cognition is a mathematically expensive task, the reason representation of bipolarity requires mathematical representation beyond the unipolar space [17, 30]. The theory of fuzzy sets approximate the uncertainty and vagueness in attributes via a defined single fuzzy membership value between 0 and 1 [63, 71, 72]. This single-valued fuzzy membership includes both acceptation and rejection part of the attributes with respect to the given context, whereas the bipolarity is coexistence of true and false value at the same time. In this case, the properties of bipolar neutrosophic set is more helpful in precise representation of indeterminacy in fuzzy attributes as shown in Table 2.

Fig. 1

Graphical demonstration of the proposed study and its objective

Table 1 Understanding the existence of bipolarity in three-way decision attributes

Table 2 Comparison of fuzzy set and its extensive set theory

Let Z be a non-empty set then the bipolar fuzzy set J in Z contains a positive membership values μ^P(z) as well as negative membership values μ^N(z). The positive membership values used to represent the acceptation, whereas the negative membership values μ^N(z) used to represent the implicit counter-property J [1, 31]. It can be visualize using the properties of the bipolar fuzzy graph G = (I, J), where I = $({\mu ^{P}_{I}}, {\mu ^{N}_{I}})$ is a bipolar fuzzy set in V (vertices) and J=$({\mu ^{P}_{J}}, {\mu ^{N}_{J}})$ is a bipolar fuzzy set in E (edges) V ×V is extended in the three-way decision space [1, 73]:

$$ \begin{array}{@{}rcl@{}} &&{\mu^{P}_{J}}(\left\{ v_{1}, v_{2} \right\})\leq \min ({\mu^{P}_{I}}(v_{1}), {\mu^{P}_{I}}(v_{2})) (\forall (v_{1}, v_{2}) \in V \times V)\\ &&{\mu^{N}_{J}}(\left\{v_{1}, v_{2} \right\})\geq \max ({\mu^{N}_{I}}(v_{1}), {\mu^{N}_{I}}(v_{2})) (\forall (v_{1}, v_{2}) \in V \times V)~ \text{and}\\ &&{\mu^{P}_{J}}(\left\{ v_{1}, v_{2} \right\})={\mu^{N}_{J}}(\left\{v_{1}, v_{2}\right\})= 0 (\forall (v_{1}, v_{2}) \in V \times V-E). \end{array} $$

J={(z, μ^P(z), μ^N(z))|z ∈ Z} where μ^P:Z→[0, 1] and μ^N:Z → [-1, 0] are mappings [31].

The three-way decision space is a generalized representation of win, loss, and draw (neutral) conditions of any attributes based on its truth, indeterminacy, and falsity membership values, independently [3, 61]. One of the suitable examples is the state of mercury (Hg) that cannot be represented precisely in a unipolar or bipolar fuzzy space. The reason is its state is neither liquid nor solid in case of room temperature. Similarly, the semiconductors cannot be considered as conductors or isolators. Handling these type of information and their meaningful pattern is complex issue for the researchers of various fields. In this regard, recently, some of the researchers tried to represent them in the three-way decision space [34, 35, 70] for cognitive concept learning [7, 32, 60] based on their partial ordering [28] in m–dimension [19, 20]. In this case, the problem arises while processing bipolarity [58, 64] in multi-dimensional data sets [20, 42, 53]. Analysis of bipolar information in the three-way fuzzy space is a hotspot for the researchers [53, 62]. It means the bipolarity exists in each building blocks of the three-way decision space [22, 30, 69]. To deal with this problem, recently, properties of bipolar neutrosophic set [15] and its graphical properties [16] is studied for multi-attribute decision-making processing [22]. It is nothing but generalized algebra of neutrosophic set [61] and its logic theory [57] into the bipolar space which is recently utilized for knowledge processing tasks in [54]. This papers paid attention to deal with these type of multi-day data sets using the properties of bipolar neutrosophic graph and its partial ordering. The motivation is to extract some interesting information from the given bipolar neutrosophic context for knowledge processing tasks as shown in Fig. 1.

Recently, a method is introduced in [54] to deal with bipolar fuzzy attributes in the three-way decision space using the chosen subset of attributes. In this case, a problem is noted while dealing with large number of attributes. Some time processing the three-way bipolar fuzzy context at user required information granulation is another expensive task. To achieve this goal, two methods are proposed in this paper. The first method focuses on generating some of the useful pattern from the given bipolar neutrosophic context using the calculus of next neighbor algorithm [36]. The second method aimed at decomposition of the three-way bipolar fuzzy context at user required information granules. The motivation is to characterize the bipolar informations precisely via its acceptation, rejection, and uncertain parts, independently. The objective is to provide a mathematical model for dealing with three-way bipolar contexts for decision-making processes without any cognitive biases. In this way, the proposed method adds a significant analysis in the field of three-way data analysis.

Section “Preliminaries” provides some basic background about FCA in the three-way fuzzy setting and its connection with bipolarity is given in Section “Preliminaries.” Section “Proposed Methods” introduces a method for generating the three-way bipolar neutrosophic concepts based on user required subset of attributes with its illustration in Section “Illustration.” Section “Discussions” provides conclusions followed by acknowledgements and references.

Preliminaries

Formal Concept Analysis with Three-Way Fuzzy Setting

Definition 1

(Formal fuzzy context) [13]: A formal fuzzy context is a triplet K = (X, Y , $\tilde {R}$), where X is a set of objects, Y is a set of attributes and $\tilde {R}$ is an L-relation between X and Y , $\tilde {R}$: X×Y →L. Each relation $\tilde {R}(\textit {x},\textit {y})\in L$ represents the membership value at which the object x ∈ X has the attribute y ∈ Y in [0, 1] where L is a support set of some complete residuated lattice L.

Definition 2

(Three-way fuzzy context) [47] : A three-polar fuzzy context can be represented as K = (X, Y , $\tilde {R}$) where X represents set of objects, Y represents set of three-polar attributes and $\tilde {R}$ represents the three-polar relationship characterized by truth ($T_{\tilde {R}}(x,y)$), indeterminacy ($I_{\tilde {R}}(x,y)$), and false ($F_{\tilde {R}}(x,y)$) membership value at which the object x ∈ X has the attribute y ∈ Y in the three-polar space [0,1]³ where ($T_{\tilde {R}}(x,y)$),($I_{\tilde {R}}(x,y)$) and ($F_{\tilde {R}}(x,y)$) are real standard or non-standard subsets of ]0⁻,1⁺[. It means $\tilde {R}= \{ ((x,y), T_{\tilde {R}}(x,y), I_{\tilde {R}}(x,y), F_{\tilde {R}}(x,y): \forall x \in X, y \in Y \}$ where $0^{-} \leq T_{\tilde {R}}(x,y) + I_{\tilde {R}}(x,y)+ F_{\tilde {R}}(x,y) \leq 3^{+}$. It should be noted that 0⁻ = 0 − 𝜖 where 0 represents its standard part and 𝜖 represents its non-standard part [57]. Similarly, 1⁺ = 1 + 𝜖 (3⁺ = 3 + 𝜖) where 1 (or 3) represents standard part and 𝜖 represents its non-standard part. Hence, the real standard format (0, 1) or [0, 1] can be also used to represent the relationship among objects and attributes set using neutrosophic set [61].

Definition 3

(Residuated lattice) [40]: It is a basic structure of truth degrees L=(L, ∧, ∨, ⊗, →, 0, 1) where 0 and 1 represent least and greatest elements, respectively. L is a complete residuated lattice iff:

• (1) (L, ∧, ∨, 0, 1) is a complete lattice.

• (2) (L,⊗,1) is commutative monoid.

• (3) ⊗ and → are adjoint operators (called as multiplication and residuum, respectively), that is a ⊗ b ≤ c iff a ≤ b → c,∀a, b, c ∈ L. The operators ⊗ and → are defined distinctly by Lukasiewicz, Go$\ddot {}$del, and Goguen t-norms and their residua. In this paper, Go$\ddot {}$del t-norms and their residua is used as given below [9, 25]:

Go$\ddot {}$del:

• a ⊗ b = min(a, b),

• a → b = 1 if a ≤ b, otherwise b.

The L-set can be extended to finite set $\left \{ 0, \frac {2}{n}, \frac {3}{n}, \ldots , \frac {n-1}{n}, 1\right \}$ where n ∈ N⁺ to represent the acceptation part [43, 53]. Similarly, it can be defined for rejection n ∈ N⁻ as well as uncertain parts, independently as shown in [47] which is further extended for handling multi-valued logic [55] and Heyting algebra [74]. In this paper, it is used for handling the three-way bipolar fuzzy attributes.

Definition 4

(Formal fuzzy concepts) [9, 13]: For any L-set A∈ L^X of objects, and B∈ L^Y of attributes we can define L-set A^↑∈ L^Y of attributes and L-set B^↓ ∈ L^X of objects as follows [5]:

• (1) A$^{\uparrow } (y)=\wedge _{x\in \scriptsize {\textit {X}}}(\textit {A}(x) \rightarrow \tilde {R}(\textit {x},\textit {y}))$,

• (2) B$^{\downarrow } (x)=\wedge _{y\in \scriptsize {\textit {Y}}}(\textit {B}(y) \rightarrow \tilde {R}(\textit {x},\textit {y}))$.

A^↑(x) is interpreted as the L-set of attribute y ∈ Y shared by all objects from A. Similarly, B^↓(x) is interpreted as the L-set of all objects x ∈ X having the attributes from B in common. The fuzzy formal concept is a pair of (A, B) ∈ L^X × L^Y satisfy A^↑ = B and B^↓ = A, where fuzzy set of objects A called as extent and fuzzy set of attributes B called as intent.

Definition 5

(Three-polar concepts) [47, 49]: The pair (A, B) is called as three-polar formal concept iff B^↓ =(A,[T_A, I_A, F_A) and A^↑=(B,[T_B, I_B, F_B]). The ↓ is applied on three-polar set of attributes as follows:

$$\textit{B}^{\downarrow}= \left\{ y_{j}, (T_{B}(y_{j}), I_{B}(y_{j}), F_{B}(y_{j})) \in [0,1]^3: \forall y_{j} \in Y\right\}.$$

It provides the covering objects set as follows:

$$\textit{A}= \left\{ x_{i}, (T_{A}(x_{i}), I_{A}(x_{i}), F_{A}(x_{i})) \in [0,1]^3: \forall x_{i} \in X\right\}.$$

The obtained objects set includes maximal membership with respect to integrating the information by the given attributes set. Now, apply the ↑ on these constituted objects set which provide the three-polar attribute set with its membership value being maximal with respect to integrating the information from the constituted objects set. If the obtained pair make the three-polar fuzzy concepts then any extra attribute (or object) cannot be discovered which will make the maximum membership value of the obtained set of attributes (objects).

Definition 6

(Partial ordering of fuzzy concepts) [9, 24]: A formal fuzzy concept is a maximal rectangle of a given fuzzy context K filled with membership value between [0, 1], which is an ordered pair of two sets (A, B), where A ⊆ X called as fuzzy extent, and B ⊆ Y is called as fuzzy intent. The set of formal fuzzy concepts(C), generated from a given formal fuzzy context K, defines the partial ordering principle, i.e., (A₁, B₁) ≤ (A₂, B₂) ⇔ A₁ ⊆ A₂(⇔ B₂ ⊆ B₁) for every fuzzy formal concept.

Definition 7

(Partial ordering among three-way fuzzy concepts) [28]: Let C₁ and C₂ be two three-polar concepts generated from context K using the properties of neutrosophic set. Then, C₁ ⊆ C₂ iff $T_{C_{1}}(x) \leq T_{C_{2}}(x)$, $I_{C_{1}}(x) \geq I_{C_{2}}(x)$, $F_{C_{1}}(x) \geq F_{C_{2}}(x)$ for any x ∈ X. (C, ∧, ∨) is bounded lattice. Also, the structure (C, ∧, ∨, (1, 0, 0), (0, 1, 1), ¬) follows the De Morgan’s law.

Definition 8

(Complete lattice) [27] : In the complete lattice, there exist an infimum and a supremum for some formal concepts as given follows:

• ∧_{j∈ J}(A_j, B_j)=$(\bigcap _{j\in J} A_{j}, (\bigcup _{j\in J}B_{j})^{\downarrow \uparrow })$,

• ∨_{j ∈ J}(A_j, B_j)=$((\bigcup _{j \in J} A_{j})^{\uparrow \downarrow },\bigcap _{j\in J} B_{j})$.

The above mentioned definitions shows that three-way fuzzy concept lattice [47] given a way to mimic with human cognitive thought based on its acceptation, rejection, and uncertain parts [37, 49]. In this process, a problem exists when the human cognition contains bipolar information. To deal with this problem, recently, the mathematics of bipolar neutrosophic set [22], bipolar neutrosophic graph [16], and its extensive properties is studied [2] for computing with linguistics word [71, 72] in the three-way decision space. The current paper focuses on compact visualization of bipolar neutrosophic contexts via vertices and edges of a graph [10] and calculus of granular computing [41] for knowledge processing tasks. To achieve this goal, some of the useful and common properties among them is explained given in the next section.

Bipolar Neutrosophic Set, its Lattice and Graph

In this section, preliminaries properties of bipolar neutrosophic set, its graph and lattice structure is given to bridge it with the concept lattice structure as shown below:

Definition 9

(Bipolar neutrosophic set) [22] : Let x ∈ X and X is a space of points (objects) then a bipolar neutrosophic set N in X can be characterized by a bipolar truth-membership function T_N(x), a bipolar indeterminacy-membership function I_N(x) and a bipolar falsity-membership function F_N(x). The each point x inXT_N(x), I_N(x), and F_N(x) ⊆ [- 1, 1]. The bipolar neutrosophic set can be represented as follows:

$N= \{ x, (T^{+}_{N(x)}, T^{-}_{N(x)}), (I^{+}_{N(x)}, I^{-}_{N(x)}), (F^{+}_{N(x)}, F^{-}_{N(x)}): x \in X \}$ where T_N(x), I_N(x), F_N(x) ⊆ [- 1,1].

Example 1

Let us suppose, that an expert wants to characterize the product quality of a car company (x₁) based on its pollution controlling capacity y₁. In this case, the expert can write the product quality based on its acceptation, rejection and indeterminacy for the global environment as follows:

$$x_{1}= \frac{((0.4, -~0.6), (0.5, -~0.4), (0.3,-~0.5))}{y_{1}}.$$

Definition 10

(Intersection of bipolar neutrosophic set) [64] : Let N₃ defines intersection among two bipolar neutrosophic set N₁ and N₂ on a given universal set X, whose bipolar truth, indeterminacy, and falsity-membership can be computed as follows:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{N_{3}}(x)={\min} (T^{+}_{N_{1}}(x), T^{+}_{N_{2}}(x)),\\ &&T^{-}_{N_{3}}(x)={\max} [T^{-}_{N_{1}}(x), T^{-}_{N_{2}}(x)],\\ &&I^{+}_{N_{3}}(x)=(I^{+}_{N_{1}}(x) + I^{+}_{N_{2}}(x))/2,\\ &&I^{-}_{N_{3}}(x)=(I^{-}_{N_{1}}(x) + I^{-}_{N_{2}}(x))/2,\\ &&F^{+}_{N_{3}}(x)={\max}(F^{+}_{N_{1}}(x), F^{+}_{N_{2}}(x)),\\ &&F^{-}_{N_{3}}(x)={\min}(F^{-}_{N_{1}}(x), F^{-}_{N_{2}}(x)), \text{for all} ~x \in X\end{array} $$

This provides a way to discover an infimum among any given three-way bipolar concepts.

Definition 11

(Union of bipolar neutrosophic set) [58, 64] : Let N₃ defines union of two bipolar neutrosophic set N₁ and N₂ on a given universal set X, whose bipolar truth, indeterminacy and falsity-membership can be computed as follows:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{N_{3}}(x)={\max} (T^{+}_{N_{1}}(x), T^{+}_{N_{2}}(x)),\\ &&T^{-}_{N_{3}}(x)={\min}(T^{-}_{N_{1}}(x), T^{-}_{N_{2}}(x)),\\ &&I^{+}_{N_{3}}(x)=(I^{+}_{N_{1}}(x) + I^{+}_{N_{2}}(x))/2,\\ &&I^{-}_{N_{3}}(x)=(I^{-}_{N_{1}}(x) + I^{-}_{N_{2}}(x))/2,\\ &&F^{+}_{N_{3}}(x)={\min} (F^{+}_{N_{1}}(x), F^{+}_{N_{2}}(x)),\\ &&F^{-}_{N_{3}}(x)={\max} (F^{-}_{N_{1}}(x), F^{-}_{N_{2}}(x)), \text{for all}~ x \in X \end{array} $$

This provides a way to discover a supremum among any given three-way bipolar concepts.

Definition 12

(Bipolar neutrosophic graph) [15, 16]: Let G=(V, E) is a neutrosophic graph in which the vertices (V) can be characterized by a bipolar truth-membership $(T^{+}_{v_{i}}, T^{-}_{v_{i}})$, a bipolar indeterminacy-membership function $(I^{+}_{v_{i}}, I^{-}_{v_{i}})$ and a bipolar falsity-membership function $(F^{+L}_{v_{i}}, F^{-}_{v_{i}})$ such as follows:

$$\left\{(T_(v_{i}), I_(v_{i}), F_(v_{i})) \in [-1,1]^{3}\right\} for all v_{i} \in V.$$

Similarly, the edges (E) can be characterized by an interval-valued neutrosophic relations among them, i.e., {(T_E(V × V ), I_E(V × V ), F_E(V × V )) ∈ [− 1, 1]³} for all V × V ∈ E such as follows:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{E}(v_{i}v_{j}) \leq {\min} (T^{+}_{E}(v_{i}), T^{-}_{E}(v_{j})),\\ &&T^{-}_{E}(v_{i}v_{j}) \leq {\max} (T^{+}_{E}(v_{i}), T^{-}_{E}(v_{j})),\\ &&I^{+}_{E}(v_{i}v_{j}) \leq (I^{+}_{E}(v_{i}), I^{+}_{E}(v_{j}))/2,\\ &&I^{-}_{E}(v_{i}v_{j}) \leq (I^{-}_{E}(v_{i}), I^{-}_{E}(v_{j}))/2,\\ &&F^{+}_{E}(v_{i}v_{j}) \leq {\max} (F^{+}_{E}(v_{i}), F^{+}_{E}(v_{j})),\\ &&F^{-}_{E}(v_{i}v_{j}) \leq {\min}(F^{+}_{E}(v_{i}), F^{-}_{E}(v_{j})). \end{array} $$

The bipolar neutrosophic graph is complete iff:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{E}(v_{i}v_{j}) = {\min} (T^{+}_{E}(v_{i}), T^{-}_{E}(v_{j})),\\ &&T^{-}_{E}(v_{i}v_{j}) = {\max} (T^{+}_{E}(v_{i}), T^{-}_{E}(v_{j})),\\ &&I^{+}_{E}(v_{i}v_{j}) = (I^{+}_{E}(v_{i}), I^{+}_{E}(v_{j}))/2,\\ &&I^{-}_{E}(v_{i}v_{j}) =(I^{-}_{E}(v_{i}), I^{-}_{E}(v_{j}))/2,\\ &&F^{+}_{E}(v_{i}v_{j}) = {\max} (F^{+}_{E}(v_{i}), F^{+}_{E}(v_{j})),\\ &&F^{-}_{E}(v_{i}v_{j}) = {\min}(F^{+}_{E}(v_{i}), F^{-}_{E}(v_{j})). \end{array} $$

It is noted that {(T_E(v_iv_j), I_E(v_iv_j), F_E(v_iv_j))} = (0, 0, 0) ∀(v_i, v_i) ∈ (V × V ∖ E).

Example 2

Let us extend, the example 1 that the car company wants to analyze the three green suppliers based on pollution control (y₁). In this case, the three company can be represented using the vertices ({v₁, v₂, v₃}) of a bipolar neutrosophic graph as shown in Table 3. The corresponding bipolar neutrosophic relationship among them can be visualized using the edges E of a bipolar neutrosophic graph as shown in Table 4. The graphical structure is shown in Fig. 2.

Fig. 2

A bipolar complete neutrosophic graph representation of Tables 3 and 4

Table 3 A bipolar neutrosophic set representation of vertices v₁, v₂, v₃

Table 4 A bipolar neutrosophic edges (E) among the vertices of Table 3

In this way, the bipolarity in the three-way decision space can be visualized as discussed in [54]. However, for the graphical structure analytics, some pattern based on object and its common attribute based required. To achieve this goal, a method is proposed in the next section using the mathematical paradigm of next neighbor algorithm [6, 36] as well as granular computing [66].

Proposed Methods

In this section, two methods are proposed for analysis of bipolar neutrosophic context using the properties of next neighbor and granular computing.

A Next Neighbor-Based Method for Generating the Bipolar Neutrosophic Concepts

In this section, a method is proposed to find all the bipolar neutrosophic concepts using the properties of next neighbor algorithm:

Step 1

Let us suppose, a bipolar neutrosophic context F = (X, Y , $\tilde {R}$) where X is a set of objects, Y is a set of bipolar attributes, and $\tilde {R}$ is bipolar neutrosophic relationship among them as shown in Table 5.

Table 5 A bipolar neutrosophic context

Step 2

The proposed method find the attributes which covers the given objects set maximally as given below:

$$\left\{ \oslash \right\}^{\downarrow}=\left\{ x_{i}, (T^{+}_{A(x_{i})}, T^{-}_{A(x_{i})}), (I^{+}_{A(x_{i})}, I^{-}_{A(x_{i})}), (F^{+}_{A(x_{i})}, F^{-}_{A(x_{i})}) \right\}.$$

The bipolar neutrosophic membership value for the obtained objects set can be computed as follows:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{A_{s_{i}}}(x_{i}) = {\min}_{j \in T^{+}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{T^{+}}(x_{i},y_{j})),\\ &&T^{-}_{A_{s_{i}}}(x_{i}) = {\max}_{j \in T^{-}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{T^{-}}(x_{i},y_{j})),\\ &&I^{+}_{A_{s_{i}}}(x_{i}) = \frac{1}{2}_{j \in I^{L}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{I^{L}}(x_{i},y_{j})),\\ &&I^{-}_{A_{s_{i}}}(x_{i}) = \frac{1}{2}_{j \in I^{U}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{I^{U}}(x_{i},y_{j})),\\ &&F^{+}_{A_{s_{i}}}(x_{i}) = {\max}_{j \in F^{+}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{F^{+}}(x_{i},y_{j})),\\ &&F^{-}_{A_{s_{i}}}(x_{i}) = {\min}_{j \in F^{-}_{B_{s_{j}}}}(\mu^{\tilde{R}}_{F^{-}}(x_{i},y_{j})). \end{array} $$

Step 3

Now, discover the maximal covering attributes while integrating the information from above obtained objects set as follows:

$$\left\{x_{i}, (T^{+}_{A(x_{i})}, T^{-}_{A(x_{i})}), (I^{+}_{A(x_{i})}, I^{-}_{A(x_{i})}), (F^{+}_{A(x_{i})}, F^{-}_{A(x_{i})})\right\}^{\uparrow}.$$

This provides the maximal covering attributes. The membership value of the obtained attributes can be computed as follows:

$$ \begin{array}{@{}rcl@{}} &&T^{+}_{B_{s_{j}}}(y_{j}) = {\min}_{i \in T^{+}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{T^{+}}(x_{i},y_{j})],\\ &&T^{-}_{B_{s_{j}}}(y_{j}) = {\max}_{i \in T^{-}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{T^{-}}(x_{i},y_{j})],\\ &&I^{+}_{B_{s_{j}}}(y_{j}) = \frac{1}{2}_{i \in I^{+}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{I^{+}}(x_{i},y_{j})],\\ &&I^{-}_{B_{s_{j}}}(y_{j}) = \frac{1}{2}_{i \in I^{-}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{I^{-}}(x_{i},y_{j})],\\ &&F^{+}_{B_{s_{j}}}(y_{j}) = {\max}_{i \in F^{+}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{F^{+}}(x_{i},y_{j})],\\ &&F^{-}_{B_{s_{j}}}(y_{j}) = {\min}_{i \in F^{-}_{A_{s_{i}}}}[\mu^{\tilde{R}}_{F^{-}}(x_{i},y_{j})]. \end{array} $$

Step 4

This provides first bipolar neutrosophic concept ($A_{s_{i}}$, $B_{s_{j}}$).

Step 5

The lower neighbor of the first concept can be generated via combination of remaining attributes, i.e., :y_k = Y − y_j where j ≤ m and k ≤ m|.

Step 6

The maximal covering objects set for the newly obtained attributes can be investigated using the Galois connection and vice versa as shown in steps 2 and 3.

Step 7

In this way, all the lower neighbor can be generated for the first concept. However, the distinct lower neighbor having maximal bipolar neutrosophic membership value while integrating the information among objects and attributes set is considered as next neighbor.

Step 8

In similar way, other bipolar neutrosophic concepts can be generated.

Step 9

The bipolar neutrosophic concept lattice can be drawn using their obtained next neighbors.

Step 10

Interpret the obtain concept lattice for knowledge processing tasks. The pseudo code of the proposed algorithm is shown in Table 6.

Table 6 A proposed algorithm for generating the bipolar neutrosophic concepts using next neighbor

Complexity

Let us suppose, the number of objects and the number of attributes in the given bipolar neutrosophic context is n and m, respectively. The proposed method generates the lower neighbors using maximal ((1, 0) (0, 0), (0, 0)) acceptance of given bipolar neutrosophic attributes m which may take O(m²) time complexity for positive and negative membership values, respectively, i.e., gives O(m⁴). After that, it connects with corresponding covering objects set using the Galois connection which may take O(m⁴ ∗ n) time complexity for each lower neighbors (C), respectively. In this way, the proposed method may take maximum O(|C| n m⁴) time complexity where, C is lower neighbor. In the next section, another method is proposed to navigate the three-way bipolar fuzzy context at defined level of information granulation.

A Granular-Based Method for Decomposing the Bipolar Neutrosophic Context

It can be observed that the proposed method shown in Table 6 generates large as well as repeated bipolar neutrosophic concepts. This property of proposed method may decelerate the user or expert time in extracting some useful meaning from the given bipolar neutrosophic context. Reducing the size of concept lattice is one of the other concern for the researchers [8]. In this direction, the properties of granular computing has considered as one of the useful tool for knowledge reduction tasks [66]. The mathematical properties of granular computing is recently applied for navigation of the bipolar fuzzy context [44], the three-way fuzzy context [48], as well as interval-valued neutrosophic context [49] for processing the context using the defined information granules. The level of granulation can be decided by user or expert requirements to solve the complexity of particular problems [41]. In this way, it provides an effective way to modularize the complex problem into a series of well-defined sub problems (modules) in a given computation cost. To achieve this goal properties of granular computing is utilized for decomposition of an three-way bipolar neutrosophic context based on its bipolar truth, bipolar indeterminacy, and bipolar false membership value independently, at user defined ((α₊, α₋),(β₊, β₋),(γ₊, γ₋)))—cut.

Step 1

Let us suppose, a bipolar neutrosophic context K = (X, Y , $\tilde {R}$) where, |X| = n, |Y | = m and, $\tilde {R}$ represents the bipolar neutrosophic relationship among them, i.e., $((T^{+}_{\tilde {R}}, T^{-}_{\tilde {R}}), (I^{+}_{\tilde {R}}, I^{-}_{\tilde {R}}), (F^{+}_{\tilde {R}}, F^{-}_{\tilde {R}}))$.

Step 2

The decomposition of bipolar neutrosophic context is based on user requirements to solve the particular problem. The level of granulation can be kept based on bipolar truth, i.e., (α₊, α₋), indeterminacy, i.e., (β₊, β₋), and falsity membership value, i.e., (γ₊, γ₋).

Step 3

The decomposition based on chosen granulation can be done as follows:

The truth membership value belongs to the same decomposed context iff: K$^{T}_{(\alpha _{+}, \alpha _{-})}$ = $\{T_{\tilde {R}(x,y)}| \mu _{T_{\tilde {R}(x,y)}} \geq \alpha _{+} \land \mu _{T_{\tilde {R}(x,y)}} \leq \alpha _{-} \}$, where x_i is object, y_j is attribute. In this case, represent 1.0 (i.e., maximal acceptance of truth membership value) at the given bipolar neutrosophic relationship for the chosen (α₊, α₋)—cut otherwise 0.0.

The indeterminacy membership value belongs to the same decomposed context iff: K$^{I}_{(\beta _{+}, \beta _{-})}$ = $\{I_{\tilde {R}(x,y)}| \mu _{I_{\tilde {R}(x,y)}} \leq \alpha _{+} \land \mu _{I_{\tilde {R}(x,y)}} \geq \beta _{-} \}$, where x_i is object, y_j is attribute. In this case, represent 0.0 (i.e., maximal acceptance of indeterminacy value) at the given bipolar neutrosophic relationship for the chosen (β₊, β₋)—cut otherwise 1.0 (Table 7).

Table 7 A proposed algorithm for ((α₊, α₋),(β₊, β₋),(γ₊, γ₋)))—cut of bipolar neutrosophic context

The falsity membership value belongs to the same decomposed context iff: K$^{F}_{(\gamma _{+}, \gamma _{-})}$ = $\{F_{\tilde {R}(x,y)}| \mu _{F_{\tilde {R}(x,y)}} \leq \gamma _{+} \land \mu _{F_{\tilde {R}(x,y)}} \geq \gamma _{-} \}$, where x_i is object, y_j is attribute. In this case, represent 0.0 (i.e., maximal acceptance of indeterminacy value) at the given bipolar neutrosophic relationship for the chosen (γ₊, γ₋)—cut otherwise 1.0.

Step 4

The decomposed contexts K$_{((\alpha _{+}, \alpha _{-}), (\beta _{+}, \beta _{-}), (\gamma _{+}, \gamma _{-})))}$ at user defined granulation. It should be reconsidered as a couple of bipolar μ values which cannot be comparable with a real number and follows following property:

K= $\bigcup _{((\alpha _{+}, \alpha _{-}), (\beta _{+}, \beta _{-}), (\gamma _{+}, \gamma _{-}))}$ where, α is a defined granulation for the bipolar truth, β for the bipolar indeterminacy, and γ for bipolar falsity membership value.

Step 5

The decomposed context also satisfies the following properties, i.e., K$_{\alpha _{1}, \beta _{1}, \gamma _{1}}\subseteq$K$_{\alpha _{2}, \beta _{2}, \gamma _{2}}$ when α₁ ≥ α₂, β₁ ≤ β₂, γ₁ ≤ γ₂. It means number of concepts and size of neutrosophic concept lattice can be controlled using the defined granulation for the truth, indeterminacy, and falsity membership value.

Step 7

Similarly, it can be computed for each entries in bipolar neutrosophic context based on user required information granules.

Step 8

Write the obtained decomposed context for further processing. The pseudo code for this proposed algorithm is shown in Table 8.

Table 8 A bipolar three-way fuzzy context

Complexity

Table 8 shows the pseudo code for the decomposition of a given bipolar neutrosophic context having n number of objects and m number of attributes. The proposed method decomposed the context based on user defined granulation for the bipolar truth, bipolar indeterminacy, and bipolar falsity membership values, i.e., ((α₊, α₋),(β₊, β₋),(γ₊, γ₋))) (α, β, γ)—cut independently. It may take O(m⁶) or O(n⁶) time complexity either using extent or intent. In this way, the proposed method reduces the computational cost for processing the given bipolar neutrosophic context at user required information granules for precise analysis of knowledge processing tasks.

Illustration

This section illustrates the proposed methods shown in Tables 6 and 7 with an illustrative example in the consecutive sub-sections. The obtained results from them are also compared with the recently available approaches in FCA with bipolar fuzzy settings.

Next Neighbor-Based Three-Way Bipolar Neutrosophic Concept Lattice

Recently, the three-way concept lattice is studied in various research fields for knowledge processing tasks. In this direction, single-valued [47] and interval-valued neutrosophic [49] graph representation of concept lattices are studied for measuring the uncertainty in fuzzy attributes based on its truth, falsity, and indeterminacy membership values, independently. Other than that, some different orientations are also studied [34] to characterize the uncertainty and vagueness in attributes based on acceptation, rejection, and uncertain regions [67, 68]. The proposed method is distinct from each of the available approaches in many ways. It first provides a way to represent the bipolar information in the three-way fuzzy space and its navigation at distinct granules. To accomplish this goal, the current paper introduces an algorithm using the properties of bipolar neutrosophic set and granular computing in Section 3. In this section, the proposed method is illustrated with an example as given below:

Example 3

Let us consider, a decision-making problem given in [64] for the illustration of proposed method. A car company wants to analyze the most appropriate suppliers {x₁, x₂, x₃, x₄} based on the following parameters y₁ as product quality: y₂ as technology capability, y₃ as pollution control. The collected data set is represented using the bipolar neutrosophic context as shown in Table 8. The pattern from the given context can be generated using the proposed method shown in Table 6 for precise analysis of appropriate green suppliers.

• Step (1) The proposed method generates first concept using the attributes which covers each of the objects set as follows:

  $$\{\oslash\}^{\downarrow}= \{\frac{((1,0), (0, 0), (0, 0))}{x_{1}}+ \frac{((1,0), (0, 0), (0, 0))}{x_{2}}+\frac{((1,0), (0, 0), (0, 0))}{x_{3}}+\frac{((1,0), (0, 0), (0, 0))}{x_{4}}\}.$$

• Step (2) The covering bipolar fuzzy set of attributes for the obtained objects set can be discovered using the UP operator of Galois connection as follows:

  $$ \begin{array}{@{}rcl@{}}&&\{\frac{((1,0), (0, 0), (0, 0))}{x_{1}}+ \frac{((1,0), (0, 0), (0, 0))}{x_{2}}+\frac{((1,0), (0, 0), (0, 0))}{x_{3}}+\frac{((1,0), (0, 0), (0, 0))}{x_{4}}\}^{\uparrow}\\ &&\quad =\{\frac{((0.4, -0.2), (0.425, -0.45), (0.5, -0.7))}{y_{1}}+ \frac{((0.6, -0.1), (0.33, -0.25), (0.6, -0.5))}{y_{2}}+\frac{((0.6, -0.1), (0.425, -0.3), (0.5, -0.6)}{y_{3}}\}.\end{array} $$

This provides following three-way bipolar neutrosophic concepts:

• 1. Extent: $\{\frac {((1,0), (0, 0), (0, 0))}{x_{1}}+ \frac {((1,0), (0, 0), (0, 0))}{x_{2}}+\frac {((1,0), (0, 0), (0, 0))}{x_{3}}+\frac {((1,0), (0, 0), (0, 0))}{x_{4}}\}$.

  Intent: $\{\frac {((0.4, -~0.2), (0.425, -~0.45), (0.5, -~0.7))}{y_{1}}+ \frac {((0.6, -~0.1), (0.33, -0.25), (0.6, -~0.5))}{y_{2}}+\frac {((0.6, -~0.1), (0.425, -~0.3), (0.5, -~0.6)}{y_{3}}\}$.

• Step (3) The lower neighbor of this concept can be generated using the maximal acceptance of uncovered attributes y₁, y₂, and y₃ as follows:

• Step (3.(i)) Extent: $\{ \frac {((0.4, -~0.6), (0.5, -~0.4),(0.3,-~0.5))}{x_{1}}+\frac {((0.6, -~0.4), (0.4, -~0.5), (0.2,-~0.7))}{x_{2}}+\frac {((0.7, -~0.2), (0.2, -~0.6), (0.4, -~0.4))}{x_{3}}+\frac {((0.8, -~0.5), (0.6, -~0.3), (0.5, -~0.6))}{x_{4}}\}$.

  Intent: $\{\frac {((1, 0) (0, 0), (0,0))} {y_{1}}+ \frac {((0.6, -~0.1), (0.1, -~0.3), (0.2, -~0.5))}{y_{2}}+\frac {((0.6, 0.0), (0.6, -~1.0), (0.5, -~0.6))}{y_{3}}\}$.

• Step (3. (ii)) Extent: $\{ \frac {((0.6, -~0.4), (0.1, -~0.3), (0.2, -~0.2)}{x_{1}}+\frac {((0.6, -~0.5), (0.2, -~0.2), (0.3, -~0.3))}{x_{2}}+\frac {((0.9, -~0.2), (0.3, -~0.2), (0.6, -~0.5))}{x_{3}}+\frac {((0.6, -~0.1), (0.4, -~0.3), (0.3, -~0.4))}{x_{4}}\}$.

  Intent: {((0.4,− 0.2),(0.6,− 0.6),(0.5,− 0.7))/y₁ + ((1,0)(0,0),(0,0))/y₂ + ((0.6,0.0),(0.6,− 1.0),(0.5,− 0.6))/y₃}.

• Step (3. (iii)) Extent: $\{ \frac {((0.8, -~0.3), (0.6, -~0.2), (0.5, -~0.1))}{x_{1}}+\frac {((0.7, -~0.1), (0.4, -~0.3), (0.5, -~0.4))}{x_{2}}+\frac {((0.6, -~0.2), (0.1, -~0.4), (0.5, -~0.6))}{x_{3}}+\frac {((0.9, -~0.5), (0.6, -0.3), (0.4, -~0.6))}{x_{4}}\}$.

Intent: $\{ \frac {((0.4, -~0.3), (0.6, -~0.6), (0.5, -~0.7))}{y_{1}}+ \frac {((0.6, 0.0), (0.6, -~1.0), (0.5, -~0.6))}{y_{2}}+ \frac {((1, 0) (0, 0), (0,0))}{y_{3}}\}$.

All the above generated lower neighbors are distinct and can be considered as next neighbors as follows:

• 2. Extent: $\{ \frac {((0.4, -~0.6), (0.5, -~0.4),(0.3,-~0.5))}{x_{1}}+\frac {((0.6, -~0.4), (0.4, -~0.5), (0.2,-0.7))}{x_{2}}+\frac {((0.7, -~0.2), (0.2, -~0.6), (0.4, -~0.4))}{x_{3}}+\frac {((0.8, -~0.5), (0.6, -~0.3), (0.5, -~0.6))}{x_{4}}\}$.Intent: $\{\frac {((1, 0) (0, 0), (0,0))} {y_{1}}+ \frac {((0.6, -~0.1), (0.1, -~0.3), (0.2, -~0.5))}{y_{2}}+\frac {((0.6, 0.0), (0.6, -~1.0), (0.5, -~0.6))}{y_{3}}\}$.

• 3. Extent: $\{ \frac {((0.6, -~0.4), (0.1, -~0.3), (0.2, -~0.2)}{x_{1}}+\frac {((0.6, -~0.5), (0.2, -~0.2), (0.3, -~0.3))}{x_{2}}+\frac {((0.9, -~0.2), (0.3, -~0.2), (0.6, -~0.5))}{x_{3}}+\frac {((0.6, -~0.1), (0.4, -~0.3), (0.3, -~0.4))}{x_{4}}\}$.Intent: {((0.4,− 0.2),(0.6,− 0.6),(0.5,− 0.7))/y₁ + ((1,0)(0,0),(0,0))/y₂ + ((0.6,0.0),(0.6,− 1.0),(0.5,− 0.6))/y₃}.

• 4. Extent: $\{\frac {((0.8, -~0.3), (0.6, -~0.2), (0.5, -~0.1))}{x_{1}} + \frac {((0.7, -~0.1), (0.4, -~0.3), (0.5, -~0.4))}{x_{2}} + \frac {((0.6, -~0.2), (0.1, -~0.4), (0.5, -~0.6))}{x_{3}}+\frac {((0.9, -~0.5), (0.6, -~0.3), (0.4, -~0.6))}{x_{4}}\}$.Intent: $\{ \frac {((0.4, -~0.3), (0.6, -~0.6), (0.5, -~0.7))}{y_{1}}+ \frac {((0.6, 0.0), (0.6, -~1.0), (0.5, -~0.6))}{y_{2}}+ \frac {((1, 0) (0, 0), (0,0))}{y_{3}}\}$.

The concept lattice for this step is shown in Fig. 3.

• Step (4) Similarly, other next neighbors can be generated as follows:

• 5. Extent: $\{ \frac {((0.4, -~0.4), (0.3, -~0.35), (0.3, -~0.5))}{x_{1}}+\frac {((0.6, -~0.4), (0.3, -~0.5), (0.3, -~0.7))}{x_{2}}+\frac {((0.7, -~0.2), (0.25, -~0.4), (0.6, -~0.5))}{x_{3}}+\frac {((0.6, -~0.1), (0.5, -~0.3), (0.5, -~0.6))}{x_{4}}\}$.Intent: $\{ \frac {((0.4, -~0.3), ((1, 0) (0, 0), (0,0))}{y_{1}}+ \frac {((1, 0) (0, 0), (0,0))}{y_{2}}+ \frac {((0.6, -~0.1), (0.425, -~0.3), (0.5, -~0.6))}{y_{3}}\}$.

• 6. Extent: $\{ \frac {((0.4, -~0.3), (0.55, -~0.3), (0.5, -~0.5))}{x_{1}}+\frac {((0.6, -~0.1), (0.4, -~0.4), (0.5, -~0.7))}{x_{2}}+\frac {((0.6, -~0.2), (0.15, -~0.5), (0.5, -~0.6))}{x_{3}}+\frac {((0.8, -~0.5), (0.6, -~0.3), (0.5, -~0.6))}{x_{4}}\}$.Intent: $\{ \frac {((0.4, -~0.3), ((1, 0) (0, 0), (0,0))}{y_{1}}+ \frac {((0.6, -~0.1), (0.4, -~1.0), (0.6, -~1.0))}{y_{2}}+ \frac {((1, 0) (0, 0), (0,0))}{y_{3}}\}$.

• 7. Extent: $\{ \frac {((0.6, -~0.3), (0.35, -~0.3), (0.5, -~0.2))}{x_{1}}+\frac {((0.6, -~0.1), (0.3, -~0.3), (0.5, -0.4))}{x_{2}}+\frac {((0.6, -~0.2), (0.2, -~0.3), (0.6, -~0.6))}{x_{3}}+\frac {((0.6, -~0.1), (0.5, -~0.3), (0.4, -~0.6))}{x_{4}}\}$.Intent: {((0.4,− 0.3),((0.4,− 0.6),(0.6,− 0.6),(0.5,− 0.7))/y₁ + ((1,0)(0,0),(0,0))/y₂ + ((1, 0)(0, 0), (0, 0))/y₃}.

• 8. Extent: $\{ \frac {((0.4, -~0.3), (0.4, -~0.3), (0.5, -~0.5))}{x_{1}} + \frac {((0.6,\! -~\!0.5), (0.33, \!-~0.43), (0.5, -~0.7))/x_{2} + (\!(\!0.6, - 0.2), \!(0.2, ~ - 0.4), (0.6,\! -~\!0.6)\!)}{x_{3}}+\frac {((0.6, -~0.1), (0.53, -~0.3), (0.5, -~0.6))}{x_{4}}\}$.Intent: $\{ \frac {((0.4, -~0.3), ((1, 0) (0, 0), (0,0))}{y_{1}}+ \frac {((1, 0) (0, 0), (0,0)))}{y_{2}}+ \frac {((1, 0) (0, 0), (0,0))}{y_{3}}\}$.

Fig. 3

A bipolar neutrosophic concept lattice generated at step 2

The above generated bipolar neutrosophic concept and its graphical structure visualization is shown in Fig. 4. It shows the following ordering x₃ > x₄ > x₂ > x₁ which is concordant with Ulucay et al. [64] and Sahin et al. [58] method. Moreover, the proposed method provides a compressed graphical structure visualization to deal with bipolar neutrosophic contexts, in case the user or expert wants to navigate the bipolarneutrosophic context based on distinct granules to measure the suitable pattern. To achieve this goal, another method is proposed to decompose the three-way bipolar neutrosophic context using the mathematical algebra of granular computing as shown in Section 3.2. In the next section, the proposed method is illustrated using the same context to validate the results.

Fig. 4

A bipolar neutrosophic concept lattice representation of Table 8

Decomposition of Three-Way Bipolar Neutrosophic Context

Decomposition of fuzzy contexts and its navigation at user required granules is addressed as one of the major issues [8]. This problem continues for bipolar fuzzy context [44, 52] as well as other extensions of concept lattice [47]. To tackle this problem, one of the authors [48, 49] introduces granular computing in the three-way decision space to characterize the pattern based on user defined truth, falsity, and indeterminacy, membership values, independently. Toward this direction, some other researchers also tried to simulate the three-way decision space using multi-granulation [32]. The reason is calculus of granular computing given a way to navigate the context based on its small information or sub-modules [41]. Motivated from these studies, current paper introduces a method to simulate the bipolar neutrosophic context based on granular computing as shown in Section 3.2. In this section, the method is illustrated using the context shown in Table 8. The given context can be decomposed based on user required information granules as shown in Table 9. To illustrate the proposed method level 3: very interested, i.e., ((0.6, - 0.2), (0.3, - 0.6), (0.4, - 0.6)). This provides the cut as follows:

Table 9 Some of the interested granules based on user required preference

Example 4

Let us consider, the three-way bipolar neutrosophic context shown in Table 8 for the decomposition at granulation ((0.6, - 0.2), (0.3, - 0.6), (0.4, - 0.6)). To demonstrate the proposed method shown in Section 3.2 consider the matrix entry $\tilde {R}(x_{1}, y_{1})= ((0.4, -~0.6), (0.5, -~0.4), (0.3,-~0.5))$. In this case, α₊ = 0.6, $\alpha _{-} =-~0.2$, β₊ = 0.3, β₋ = 0.6, γ₊ = 0.4, γ₋ = 0.6. Now, the bipolar truth membership value of matrix entry $\tilde {R}(x_{1}, y_{1})$ 0.4 < α₊ and − 0.6 < α₋, then it can be represented as 0. The bipolar indeterminacy value of matrix entry $\tilde {R}(x_{1}, y_{1})0.5>\beta _{+}$ and − 0.4 > β₊ due to that it can be represented as 0. Similarly, the bipolar falsity membership value of matrix entry $\tilde {R}(x_{1}, y_{1})0.3<\gamma _{+}$ and − 0.5 > γ₋ due to that it can be represented as 1. It means the level 3 provides (0, 1, 0)—cut for the matrix entry $\tilde {R}(x_{1}, y_{1})$ of Table 8 as shown in Table 10. In a similar way, other three-way decomposed values can be obtained as shown in Table 10.

Table 10 Decomposition of bipolar neutrosophic context at level 3, i.e., ((0.6, − 0.2), (0.3, − 0.6), (0.4, − 0.6))

It can be observed that the object x₃ shows maximal acceptance for the chosen granulation as it contains maximal truth value in each entries. Similarly, the order in other preferences can be obtained as follows: x₃ > x₄ > x₂ > x₁. This ordering is resembled with its concept lattice shown in Fig. 4 as well as Ulucay et al. [64] and Sahin et al. [58] method. Moreover, the proposed method gives many ways to refine the given three-way bipolar neutrosophic context based on user required granules within O(m⁶) or O(n⁶) time complexity. In this way, the proposed method is useful for processing the bipolar neutrosophic context in precise way which will give more orientations to work in different fields [2, 46] for measuring the fluctuation in three-way fuzzy attributes [51]—the same time the application of the proposed method will be discussed in future with an illustrative example.

Discussions

Recently introduced, the three-way fuzzy concept lattice representation using neutrosophic set [47] is given a possible orientation to characterize the uncertainty based on its truth, falsity, and indeterminacy, independently in the three-way decision space when compared to other approaches [23, 35, 67, 68]. In this process, problem arises when the three-way fuzzy contains bipolar information [49, 53]. In this case, precise representation of bipolar truth, bipolar falsity, and bipolar indeterminacy membership values is major issues for the researchers—the same time defining their mathematical algebra and partial ordering is another tasks. To deal with this problem recently, the properties of bipolar neutrosophic sets [22] and its graphical structure [15] visualization is discussed with an illustrative example [64]. These available approaches motivated to analyze the bipolar neutrosophic contexts for knowledge processing tasks in limited time complexity. It can be observed that all of the available approaches just highlighted the distinct ways to represent the bipolarity in the three-way decision space without their super and sub-concept ordering as shown in Table 11. In the same time, these approaches does not provides any mathematical way to navigate the context at user or expert require granules to find some hidden pattern. To resolve this problem, the current paper aimed at graphical analytics of the three-way bipolar neutrosophic contexts and its decomposition at user required information granules with an illustrative example.

Table 11 Analysis of potential methods on three–way bipolar neutrosophic context

Table 12 represents the comparison of the proposed method while considering some of the recently available approaches. It shows that the proposed method provides a significant output in the field of the three-way decision space to deal with bipolar information within less computational time. In the same time, the proposed method gives an umbrella ways to zoom in or zoom out the three-way bipolar neutrosophic context for precise analysis of the hidden pattern. These two properties are distinct from the proposed method from any of the available methods in the three-way bipolar fuzzy setting. However, the proposed method unable to measure the fluctuation in bipolar neutrosophic context at given phase of time [2]. In the same time, it does not provide any information to process these types of dynamic data sets. To deal with these types of problems, the author will focus on introducing some other mathematical techniques [74] in this field [11, 46] to handle the complex bipolar attributes [55] at the given phase of time [18, 51].

Table 12 Comparison of the proposed methods with recently introduced methods

Conclusions

This paper aimed at analyzing the bipolar information based on its truth, falsity, and indeterminacy memberhship values and its graphical structure visualization for knowledge processing tasks. To achieve this goal, the bipolar neutrosophic set-based context and its hidden pattern is generated using the next neighbor algorithm which takes O(|C| n² m³) time complexity. It is observed that, the next neighbor algorithm provides repeated and maximal number of concepts in process of finding lower neighbors. To overcome this issues, another method is introduced to decompose the bipolar neutrosophic contexts at user defined information granules for its bipolar truth, falsity, and indeterminacy membership values, independently within O(m⁶) or O(n⁶) complexity. It is shown that the obtained results from both of the proposed methods are resembled with each other as well as Ulucay et al. [64], Sahin et al. [58], and subset-based [54] methods. In the near future, the author will try to focus on introducing some of the new mathematical techniques for processing the three-way bipolar fuzzy attributes and periodic changes.