Models for Computational Emotions from Psychological Theories Using Type I Fuzzy Logic

Abstract

Emotions have been subject of research and deliberation in philosophy and psychology mainstream for a long time. In contrast, emotions have only emerged in artificial intelligence research as a serious topic in the last two decades. Year 2000, in particular, experienced a shift in attitude towards emotions and their relationship to human reasoning and human–computer interaction. This shift continued slowly but surely over the years and computational emotions can be seen as a mainstream research topic within artificial intelligence and cognitive systems. In this paper, we attempt to contribute to the development of this area by interpreting psychological theories of emotions computationally and translating them into machine implementable models. These models are generic and application independent which most of the current computational emotions models lack. We have selected two psychological theories, namely Millenson (The psychology of emotion: theories of emotion perspective, vol 4. Wiley, New Jersey, pp 35–36, 1967) and Scherer (Soc Sci Inf 44(4):695–729, 2005), that lend themselves, with varying degrees of difficulty, to the computational interpretation. Fuzzy logic was utilised as a tool to keep the fidelity of psychological interpretation of emotion. The paper discusses in details the computational interpretation of these psychological models and presents a full theoretical formalism in fuzzy logic type 1, implementation and detailed analysis of this psychologically grounded generic computational models.

Introduction

The subject of accurately modelling the emotional state of an agent in such a fashion as to be both computationally advantageous and psychologically consistent is an area that has enjoyed consistent growth in interest over the years [1–3]. This work has varied in scope from the philosophical questions about why and how to make an emotional agent [4–7], to the sociological questions about what impact emotional agents have on human–computer interactions [2, 8–10].

While some authors focus on the overarching questions regarding the quantification of psychological concepts and phenomena [11], others direct their attention towards the ideas of emotions place within cognition and thought [12, 13]. By and large, however, the direction of such research has tended towards affective control systems [14–17], and rarely specifically upon the determination of the emotional state of an agent outside that somewhat narrow context [3, 18]. While some efforts have been made to introduce fuzzy logic to the field of emotion modelling [5], they have tended to discuss emotion in the context of deterministic behavioural architecture, rather than in the context of a psychological construct in its own right. Following on from work published in 2008 [19, 20] and in 2009 [21], we explore in greater depth this growing arena of scientific debate.

This paper shall present a brief overview of the psychology of emotion, and the historical application of fuzzy logic systems in this arena, to provide some measure of context to the ideas it proposes. It shall then discuss in detail two specific psychologically grounded models of emotion and outline several methods by which these models have been translated into fuzzy logic constructs. Implementations of these systems shall be presented in particular detail. The paper shall then conclude with a detailed result analysis from experimenting with the prototypes provided, which is freely available¹ to researchers for further experimentation and concrete application.

Background

Possibly more than any other multidisciplinary research area, the computational modelling of emotion requires some significant measure of preface, if only to outline the standpoint from which the researchers approach the issue. It is hoped that by outlining both the basic psychology of the work, including the historical research context in which the work fits, and the mathematics upon which the work is based, the overall aims and goals of the research might be better understood.

Psychology of Emotions

Within the various fields of psychological research, two schools of thought appear to dominate the debate regarding the nature of emotions, and how they are best modelled [22, 23]. From a philosophical perspective, the nature of their divergence and their theoretical differences is of great importance; from a computing sciences perspective, however, their differences lie entirely in the nature of the models they propose.

The view of emotions as an evolutionary construct was initially proposed by Darwin [24]. It was this work which postulated the idea of basic emotions, differing combined intensities of which might give rise to an overall emotional state. Over the past century, this has ultimately given rise to swathes of psychological research dedicated to determining both the number and nature of these basic emotions. The exact number of fundamental emotions given widely varies. Plutchik first proposed his system of emotion classification in 1980 [25], containing eight fundamental emotions. In contrast, Ekman proposed a system consisting of six fundamental, or basic, emotions in 1982 [22].

The maximum number of basic emotions is generally thought to be fourteen [26]. Following on from the definition of basic emotions comes the definition of more complex emotions. Occasionally, these categories are divided using nomenclature indicating primary and secondary emotions as in the structure proposed by Parrott [23]. Oftentimes, however, these more complex emotions are simply defined by the relative intensities of their parent emotions. In general terms, however, it is the view of this school of thought that the sum of human emotional experience can be defined as a function, or construct, of less than a dozen named emotions [27, 28]. An alternative to this view proposed by Wundt [29] suggested that emotions could be better defined in the context of experience than crisp linguistics. Research based on this principle has, as with the Darwinian view, given rise to many varied schools of thought following the same fundamental idea.

In Wundt’s original model, emotional state was represented in terms of three facets of experience which he labelled pleasantness, approach and arousal. He asserted that any individual emotion would be better modelled in the context of relative magnitudes of these facets of the emotional experience than through verbal labels. Subsequent to Wundts original work, significant research has been performed regarding this idea of a dimensional emotion model. In many cases, it is common for the third axis to be ignored and, instead, for proponents of this view to model emotions in the context of valence, which might be seen as a clearer definition of pleasantness and arousal. More recently, however, it has been suggested that these views are not necessarily mutually exclusive. Russell produced a circular model of emotions outlining the position of what he believed to be fundamental emotions in terms of relative values of what were effectively arousal and valence [30].

It is upon this idea of hybridised conceptual models that this work pitches its focus. Such models permit us to consider the emotional state as an output, or resultant, of disparate and seemingly unrelated contextual inputs. In particular, attention has been directed towards two such hybridised concepts. The first was proposed by Millenson [31]. The second is a more recent model called the Geneva Emotion Wheel, first presented by Scherer [26].

The Millenson Model

Millenson’s model of emotion, defined as a stand-alone model of emotion and not presented with its own psychological theory, was built upon Watson’s three-factor theory [32, 33]. Often considered the father of behaviourism [34], Watson proposed the connection between applied and withdrawn stimulus, and resultant emotional response. Millenson’s model took this idea and derived a three-axis system that associated certain applied and removed stimulus with different facets of emotional experience. Figure 1 shows an interpretation of his modular structure, where $S+$ represents an applied positive stimulus, $+ represents a removed positive stimulus, $S-$ represents an applied negative stimulus, and $- represents a removed negative stimulus.

Fig. 1

Millenson’s three-dimensional model of emotional intensity [31]

Along each axis, Millenson places an emotional archetype. He associates the x axis with anger, the y axis with anxiety and the z axis with pleasure. He acknowledges that three emotions do not account for the sum total of emotional experience and accounts for this in two ways. First, he posits that some emotions vary from each other only in terms of their intensity. Given the structure of his model, this is a linguistically ambiguous statement, with one of two meanings. The first possible meaning is that along a given axis, all named emotions are essentially the same emotion at varying levels of intensity. The second possible meaning is semantic inasmuch as it may be interpreted that his statement meant that emotions along a particular axis are only triggered by a more intensely felt application or removal of their associated stimulus. Both of these interpretations are explored in later discussions regarding mathematical transliteration of the model and subsequent implementation. Second, he suggests that some emotions are simply complex compounds of the basic emotions his model acknowledges. In this, his theory is consistent with many subsequent works suggesting the existence of basic emotions; that being that complex emotions, which might be linguistically recognised in popular language, are complex compounds of two or more basic emotions [28].

In terms of an applied example of Millenson’s theory in the context of compound emotional responses to stimulus, his own example was that of a child taking a cookie from a jar [31]. In this example, there is an associated applied positive stimulus with the action, that being to eat the cookie, and an associated applied negative stimulus, that being the fear of being caught. We can define this compound as guilt. We can also consider other combinations of more dramatically conflicting stimuli, such as behaviours that arise from neuroses.

As Fig. 1 outlines, his nine basic emotions are divided into three groups: those associated with the removal of positive stimulus; those associated with the application of negative stimulus; and, those associated with the conceptual combination of applied positive stimulus and removed negative stimulus. Listing these respectively, and subsequently in order of implied intensity, these emotions are as follows: (1) Annoyance, (2) Anger, (3) Rage, (4) Apprehension, (5) Anxiety, (6) Terror, (7) Pleasure, (8) Elation, (9) Ecstasy. Looking at Millenson’s model from a process sense and perspective, it fundamentally associates a given event with a composite of adding or removing two stimuli and their value impact. Any environmental stimulus will have a net addition or subtraction of positive and negative stimulus. Each stimulus has two possible quality values of positive and negative. Thus, an emotional response associated with the event is represented by nine basic emotions. These emotional responses to stimuli, over time, can be used to define an adaptive emotional state.

Scherer’s Geneva Emotion Wheel

Where Millenson’s model associates the stimulus of a given event with an emotional component, the Geneva Emotion Wheel adopts a more classical approach. Following on the principles outlined by Wundt over a century earlier, Scherer’s work associates the agent’s perceptions of its situation with a discrete emotional component. In his paper presenting the Geneva Emotion Wheel [26], Scherer discusses a perceived relationship between specific emotions, and relative experiences of valence and control. Through empirical analysis, informed by extensive experimentation, Scherer postulates that a structure featuring sixteen basic emotions might be generated, with each emotions position and intensity being determined by a vector relationship defined by these two input factors. Commenting on Russell’s original circumplex work [30], Scherer takes some of the conclusions drawn and uses them to tune his model. He also makes note of the comparable results obtained through separate empirical experimentation. At length, the Geneva Emotion Wheel is presented in the form shown in Fig. 2.

Fig. 2

A graphical depiction of the Geneva Emotion Wheel [26]

While Scherer admits that previous scholars suggested that, if basic emotions are the root of emotional experience, the maximum number of basic emotions would be fourteen, his circular model includes sixteen distinct emotions, each of which we may consider a basic emotion. These sixteen basic emotions are Pride, Elation, Happiness, Satisfaction, Relief, Hope, Interest, Surprise, Anxiety, Sadness, Boredom, Shame/Guilt, Disgust, Contempt, Hostility and Anger. We note that three of these basic emotions are directly comparable to the list proposed by Millenson: Anger, Anxiety and Elation. Indeed, these three emotions actually form the core of Millenson’s model, as they represent the conceptual mid-point on each axis of his system. We also note in particular that the example of a complex emotion provided by Millenson, that of Guilt, features as a basic emotion in the Geneva Emotion Wheel.

Considering further the graphical representation, we note that it also indicates varying degrees of intensity, showing that as the relative magnitudes of valence and control become greater, the emotions they engender are experienced in a more dramatic fashion. As these relative magnitudes of the two determining factors tend towards zero, so too does the emotional impact they generate. At the centre of the model lies an emotional white space to reflect this. Looking at the Geneva Emotion Wheel in a process sense, it connects an input based upon agent perception, specifically the agent’s perception of the valence and control it feels in a given situation. From this, it defines an emotional response associated with the event, represented by sixteen basic emotions. These emotional responses to stimuli, over time, can be used to define an adaptive emotional state.

Computational Emotions

While emotions have been extensively studied by philosophy and psychology mainstream researchers for a long time, as exemplified by Darwain’s work [24] and Sartre’s [35], it has only emerged in artificial intelligence research as a serious topic in the last two decades. Year 2000, in particular, experienced a shift in attitude towards emotions and their relationship to human reasoning and human–computer interaction [5, 8, 36–38]. This shift continued slowly but surely over the years [3, 4, 39–46] and now computational emotions can be seen as a mainstream research topic within artificial intelligence and cognitive systems [15, 47–50]. The computational emotions literature is growing at an impressive pace with raising number of applications in commercial consumer products, and yet it can be categorised into two main streams of research, namely detection and modelling, with fascinating differences.

Emotion Detection

Perhaps emotion detection was the key to the changing attitudes of computer technologists towards emotions and their applications. This could be contributed to three facts. The first and most important of these is that a ready-made physio-psychological system in the form of Ekman’s FACS [51] is readily available with practical applications prior to its’ computerisation and supported by growing literature surrounding its interpretation and uses [52–61].

The second fact is that this emotion detection in general and FACS in particular each lends itself naturally to the field of pattern recognition research that has a rich literature and a wide scope of techniques from the simple template-matching to multilayered neural nets and scores of classifiers, all of which gave researchers in computational emotions the basis to start developing emotion detection systems while dimensioning the importance of the question whether or not a machine can have emotions. Following the strands of pattern recognition research, a new strand of emotion categorisation investigations and models started to evolve [62, 63].

The importance of the philosophical question about machine abilities of holding emotions was diminished even further by the third fact that is contributing to the growth of this stream of computational emotions research, which is the immediate practical application of emotion detection without the burden of philosophical questions. This fact has also led to expansion in this stream beyond facial expression to other modalities including analysis of text [64], speech [65–67], audio and video [68–71], and images [72].

Internal Modelling of Emotions

The more relevant work to this paper is that done on modelling emotions in cognitive architectures to produce emotional agents [3, 4, 43, 73–75], which proved to be far more difficult technically, questionable to validate, and slow to progress generally.

The challenges faced in modelling emotions include but not limited to interpreting the semantics of an emotion construct. The importance of such interpretation becomes apparent in the debate on the relationship between emotions as discreet conscious points in which stimulus are evaluated and emotional state an agent may hold given his current emotional state, physical state, emotions associated with stimulus [3, 20], mood and personality of the agent [6, 74], i.e. the rate of the emotional swings and the duration of each swings.

We believe that if we wish for a generic emotion calculus independent of applications then a satisfactory answer to representing singular emotions and calculating emotional states should be found. This strand of thinking and approach is becoming more accepted as the way forward and more apparent in recent published work by other researchers of which the HourGlass Model is a good example [62]. In the HourGlass Model, the relation between affect states and emotions is an interact subject of investigation which also opens the door to new questions about the affect and emotional states, their interpretations and how they may relate.

Approach Adopted for Psychologically Grounded Models of Emotion

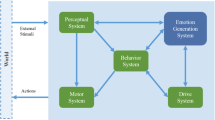
This work attempts to start from first principles and develop psychologically grounded computational models of emotion by taking established psychological theories of emotions and develop generic computational models that can be implemented in emotion-enabled machines. In doing so, we have selected two contrasting emotional theories, one of them supports the notions of behaviour-based school of thought on intelligence while the other relates more to the cognitive systems. Section “Psychology of Emotions” discusses these two theories, namely Millenson and Scherer, in sufficient details for the purpose of this paper. By looking at the emotion modelling research, interpretation of emotions in psychology and other related literature, it becomes evident that any generic models of emotion will require representational tool allowing for vagueness and shades of intensity to be present. Thus fuzzy logic (FL) [76, 77], which has been already used in modelling emotions [2, 5, 6, 18, 78], becomes an obvious candidate. Since we aim to calculate the emotional state and not merely provide data structures to represent emotions, we require inference mechanisms as well as ways of dealing with possible higher-order predicates. Considering the complexity of the emotional theories selected and their multidimensionality Type I of FL was selected as the modelling tool, which produced implementable generic models of computational emotions.

Fuzzy Computational Models of Millenson and Scherer

In this section of the paper is outlined the processes undertaken in constructing computational models of emotions based on the Millenson and Scherer models using fuzzy logic, while maintaining the integrity of their respective psychological standpoints. Representations of each model are presented. Due to their nature and possible interpretations, two computational models of Millenson were constructed while one model of Scherer. These models are presented here along with their derivative mathematics and discussion regarding their individual benefits. The Millenson model is addressed first, followed by subsequent discussion of the Geneva Emotion Wheel.

Fuzzifying the Millenson Model

As discussed previously, Millenson provides connective links between stimuli of differing valence and specific facets of emotional experience. As this link is contextual, we must first represent each axis as a conceptual relativistic sum of respective stimuli, with a crisp value between 0 and 1.

$$\begin{aligned} X&= \sum \{\$+\} [0,1]\end{aligned}$$

(1)

$$\begin{aligned} Y&= \sum \{S-\} [0,1]\end{aligned}$$

(2)

$$\begin{aligned} Z&= \sum \{S+,\$-\} [0,1] \end{aligned}$$

(3)

The nature of these variables, and the manner in which they are normalised into quantifiable values between 0 and 1, is naturally dependent upon the context in which they are applied and the setting in which they are being implemented. As an example, however, let us consider a mobile agent within a universe shared with two other objects: an item of food and a predator. Conceptually speaking, at a time $t$, the distance between the agent and the food we define as $r_t$, and the distance between the agent and the predator we define as $s_t$. The stimulus the agent receives between time $t$ and time $t+1$ may be derived through changes to these two variables. Thus, we might consider the agent to have received application of positive stimulus ($S+$) if $r_{t+1} < r_t$, informing the variable $Z$. Conversely, if $r_{t+1} > r_t$, we might consider this a removal of positive stimulus ($\$+$), informing the variable $X$. Similarly, we might consider the application of negative stimulus ($S-$), associated with the variable $Y$, to be influenced should $s_{t+1} < s_t$. Likewise, if $s_{t+1} > s_t$, we could consider this the removal of negative stimulus ($\$-$), and thus define an impact on the variable $Z$. Thus, we define the concept of an stimulus event $\mathbf {J}$. $\mathbf {J}$ is a column vector, defined by the variables $X$, $Y$ and $Z$ such that

$$\begin{aligned} \mathbf {J} = \left[ \begin{array}{c} X \\ Y \\ Z \end{array} \right] \end{aligned}$$

(4)

At this point, the manner in which we associate the stimulus event with emotional output conceptually bifurcates, as was briefly discussed during the psychological outline of the model. First, it is possible to infer from Millenson’s qualifications regarding multiple emotions that the differences between distinct emotions along a particular axis are solely defined in terms of experiential intensity. Alternatively, we might infer that the intensity he speaks of is explicitly the intensity of stimulus required to trigger individual emotions. Conceptually, and psychologically, these two interpretations each require an alternative representation through fuzzy logic. Both shall be discussed here, beginning with the first interpretation, published initially in 2008 [19]. Prior to expounding upon them, however, we are obliged to clarify in specific terms how the emotional state shall be defined through either representation of the Millenson Model.

Millenson’s model presents nine emotions that he describes as basic, whatever the interpretation of how they might be related to stimulus. It stands to reason, then, that in consideration of Millenson’s emotion model, the emotional state include representation of all nine of these elements. In explicit terms, this work defines the emotional state of an agent governed by the Millenon Model,

$$\begin{aligned} \mathbf {E}_\mathbf{M} = \left[ \begin{array}{c} \mu x_{1} [0,1]\\ \mu x_{2} [0,1]\\ \mu x_{3} [0,1]\\ \mu y_{1} [0,1]\\ \mu y_{2} [0,1]\\ \mu y_{3} [0,1]\\ \mu z_{1} [0,1]\\ \mu z_{2} [0,1]\\ \mu z_{3} [0,1] \end{array} \right] \end{aligned}$$

(5)

as an array of nine elements, and where $\mu$ in all cases represents the membership grade of the named emotion the variable is associated with, and where; $x_{1}$ represents $Annoyance$, $x_{2}$ represents $Anger$ and $x_{3}$ represents $Rage$; $y_{1}$ represents $Apprehension$, $y_{2}$ represents $Anxiety$ and $y_{3}$ represents $Terror$; $z_{1}$ represents $Pleasure$, $z_{2}$ represents $Elation$ and $z_{3}$ represents $Ecstasy$. These relative magnitudes seek to indicate the level to which the agent is experiencing each individual emotion at a given instant, and are informed by the systems we now outline.

Millenson A

Let us assume a given interpretation of Millenson’s model that connects the significance of applied and removed stimuli, of differing valence, with three emotional components. Let us explicitly define these connections of the form

$$\begin{aligned} X \rightarrow Anger \\ Y \rightarrow Anxiety \\ Z \rightarrow Pleasure \end{aligned}$$

where $X$, $Y$ and $Z$ are defined in Eqs. (1), (2) and (3), respectively, and their associated axes are clearly shown in Fig. 1. We assign variables to each of these emotional components, of the form

$$\begin{aligned} Anger \rightarrow x \\ Anxiety \rightarrow y \\ Pleasure \rightarrow z \end{aligned}$$

Each of these emotional components possesses three associated emotions, differing from each other in terms of the degree with which the component is experienced. Mirroring our merging of the stimulus components into a single variable, we define the emotional experience index $\mathbf {e}_\mathbf{J}$ associated with a discrete event J, to be a vector of these three values, and normalise them to crisp numbers between 0 and 1.

$$\begin{aligned} \mathbf {e}_\mathbf{J} = \left[ \begin{array}{c} x [0,1]\\ y [0,1]\\ z [0,1]\end{array} \right] \end{aligned}$$

(6)

Obtaining $e_J$ is a conceptual problem which this paper approaches from the perspective of fuzzy inferencing. Let us consider an individual component of $\mathbf {J}$, $X$. As has been previously stated, a given value assigned to $X$ is a number between 0 and 1, which conceptually represents the significance of removed positive stimulus from the system. Understanding that such a quantifier cannot crisply represent the nature of stimuli affecting the system, it is proposed that fuzzy linguistics be implemented in its interpretation. Thus, let us define $X$ as an input to a Mamdani fuzzy inferencing system, with linguistic variables describing “Low Significance”, “Medium Significance” and “High Significance”. Thus, we define $X$ in fuzzy terms as

$$\begin{aligned} (X,\mu ) = \begin{array}{l} \{\mu (\hbox {Low Significance})/\hbox {Low Sig.}, \\ \mu (\hbox {Medium Sig.})/\hbox {Medium Sig.}, \\ \mu (\hbox {High Sig.})/\hbox {High Sig.}\} \end{array} \end{aligned}$$

Millenson stipulates the correlation between stimulus and implied emotional output, and thus, we define $x$ as an output of a Mamdani fuzzy inferencing system, with linguistic variables describing “Low Response”, “Moderate Response” and “Extreme Response” describing the agent’s reaction to given behavioural stimuli in emotional terms. In mathematical terms, this redefines $x$ as

$$\begin{aligned} (x,\mu ) = \begin{array}{l} \{\mu (\hbox {Low Res.})/\hbox {Low Res.}, \\ \mu (\hbox {Moderate Res.})/\hbox {Mod. Res.}, \\ \mu (\hbox {Extreme Res.})/\hbox {Ext. Res.}\} \end{array} \end{aligned}$$

Let us ascribe three simple, fuzzy rules to this system:

• Rule 1: If $X$ is Low Significance, then $x$ is Low Response

• Rule 2: If $X$ is Medium Significance, then $x$ is Moderate Response

• Rule 3: If $X$ is High Significance, then $x$ is Extreme Response

Following from the Mamdani fuzzy inferencing system [76] and centroid defuzzifier, it is plain how this system can take a single, crisp variable defined as a component of $\mathbf {J}$, and provide a single, crisp variable which provides a component of $\mathbf {e}_\mathbf{J}$. Conceptually, this principle extends to all three axes in a similar fashion, with identical rules, thus providing all three elements of the emotional experience index $\mathbf {e}_\mathbf{J}$. It is not the purpose of this work simply to quantify in vague terms the emotional response to stimulus. Rather, it is to define an emotional state that may be informed and adapted through emotional response to environment. Having defined the emotional component of the stimulus $\mathbf {J}$, and clarified the means by which the two are connected, it is now obligatory to connect $\mathbf {e}_\mathbf{J}$ in some direct fashion with an as yet undefined emotional state. Before this undertaking, however, let us first associate the emotional component $\mathbf {e}_\mathbf{J}$ with the nine discrete emotions posited by Millenson. The numerical values within $\mathbf {e}_\mathbf{J}$ quantify the emotional component along the associated axis. Following Millenson’s literature, that component can then be used to determine which emotions along that axis are triggered by the stimulus changes presented by event $\mathbf {J}$. These emotions are, of course, linguistic terms, and as such inherently fuzzy [26, 79]; thus, it is not at all assumed that a binary state of active or inactive is inferred by the grade of the emotional component along a given axis. Rather, let us assume that each named emotion might be represented by a fuzzy set along its parent axis. In fuzzy set terminology, referencing our previous example discussing the variable $x$ in terms of a fuzzy set, this provides a new string of fuzzy relations. The axis with which $x$ is associated houses three named emotions: Annoyance, Anger and Rage. If we consider these emotions as linguistic variables, we can define their relationship with $x$ as

$$\begin{aligned} (x,\mu ) = \begin{array}{l} \{\mu (\hbox {Annoyance})/\hbox {Annoyance}, \\ \mu (\hbox {Anger})/\hbox {Anger}, \\ \mu (\hbox {Rage})/\hbox {Rage}\} \end{array} \end{aligned}$$

As with our interconnection of stimulus with emotional component, this relation between emotional component and named emotions can be extrapolated to all three variables. As such, $y$ and $z$ would take the form

$$\begin{aligned} (y,\mu )&= \begin{array}{l} \{\mu (\hbox {Apprehension})/\hbox {Apprehension}, \\ \mu (\hbox {Anxiety})/\hbox {Anxiety}, \\ \mu (\hbox {Terror})/\hbox {Terror}\} \end{array}\\ (z,\mu )&= \begin{array}{l} \{\mu (\hbox {Pleasure})/\hbox {Pleasure}, \\ \mu (\hbox {Elation})/\hbox {Elation}, \\ \mu (\hbox {Ecstasy})/\hbox {Ecstasy}\} \end{array} \end{aligned}$$

It should be stressed that this is not a preamble to the application of a second fuzzy inferencing system. Rather, the functions connecting the various values of $\mu$ to the named discrete emotions should be defined and employed in a more traditional, arithmetic manner. Millenson’s model gives us no reason to assume that the relations between a component and its associated discrete emotions are not uniform across individual components of equivalent scaling. That is to say that within his derivation, there is no reason to assume that the relationship associating $x$ with Rage is in any way different to the relationship associating $z$ with Ecstasy. That being the case, we define an array of equations associating the components of $\mathbf {e}_\mathbf{J}$ with values for discrete emotions associated with their respective axes.

$$\begin{aligned} \mu _\mathbf {J} x_{1}&= f_{1}(x) [0,1]\end{aligned}$$

(7)

$$\begin{aligned} \mu _\mathbf {J} x_{2}&= f_{2}(x) [0,1]\end{aligned}$$

(8)

$$\begin{aligned} \mu _\mathbf {J} x_{3}&= f_{3}(x) [0,1]\end{aligned}$$

(9)

$$\begin{aligned} \mu _\mathbf {J} y_{1}&= f_{1}(y) [0,1]\end{aligned}$$

(10)

$$\begin{aligned} \mu _\mathbf {J} y_{2}&= f_{2}(y) [0,1]\end{aligned}$$

(11)

$$\begin{aligned} \mu _\mathbf {J} y_{3}&= f_{3}(y) [0,1]\end{aligned}$$

(12)

$$\begin{aligned} \mu _\mathbf {J} z_{1}&= f_{1}(z) [0,1]\end{aligned}$$

(13)

$$\begin{aligned} \mu _\mathbf {J} z_{2}&= f_{2}(z) [0,1]\end{aligned}$$

(14)

$$\begin{aligned} \mu _\mathbf {J} z_{3}&= f_{3}(z) [0,1] \end{aligned}$$

(15)

where $\mu _\mathbf {J}$ represents explicitly the membership grade associated with the specified emotion for a given stimulus event $\mathbf {J}$, and where $x_{1}$, $x_{2}$ etceteras have the same meanings as outlined in Eq. 5. For the sake of succinctness, this relationship array condenses down to a single equation,

$$\begin{aligned} \mu _\mathbf {J} j_{i} = f_{i}(j) [0,1] \quad \quad \quad \quad for j = x, y, z\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad i = 1, 2, 3 \end{aligned}$$

Let us collect these nine membership grades into a single vector. We define this vector $\mathbf {E}_\mathbf{J}$, the emotional state component of an event $\mathbf {J}$.

$$\begin{aligned} \mathbf {E}_\mathbf{J} = \left[ \begin{array}{c} \mu _\mathbf {J} x_{1} \\ \mu _\mathbf {J} x_{2} \\ \mu _\mathbf {J} x_{3} \\ \mu _\mathbf {J} y_{1} \\ \mu _\mathbf {J} y_{2} \\ \mu _\mathbf {J} y_{3} \\ \mu _\mathbf {J} z_{1} \\ \mu _\mathbf {J} z_{2} \\ \mu _\mathbf {J} z_{3} \end{array} \right] \end{aligned}$$

(16)

The distinction between $\mathbf {E}_{\mathbf{J}}$ and $\mathbf {E}_\mathbf{M}$ is conceptually fundamental. $\mathbf {E}_\mathbf{M}$ is the emotional state of the agent. $\mathbf {E}_\mathbf{J}$ is the emotional impact of a given stimulus event $\mathbf {J}$; as such, $\mathbf {E}_\mathbf{J}$ informs $\mathbf {E}_\mathbf{M}$, but the two are not equivalent, as the distinctions in their notation emphasise. At this stage, the system can now inform the emotional state of the agent. How this emotional state is informed depends specifically upon the level of emotional memory it is desired that the agent experience; that meaning, how strongly the current emotional state mutes the impact of the stimulus event $\mathbf {J}$. Let us return to the emotional state $\mathbf {E}_\mathbf{M}$ as defined by Eq. 5. In merging $\mathbf {E}_\mathbf{M}(t)$ with $\mathbf {E}_\mathbf{J}$, to obtain $\mathbf {E}_\mathbf{M}(t+1)$, the simplest operator would be to take the mean of the two vectors, such that

$$\begin{aligned} \mathbf {E}_\mathbf{M}(t+1) = \frac{(\mathbf {E}_\mathbf{M}(t) + \mathbf {E}_\mathbf{J})}{2} \end{aligned}$$

(17)

However, this notation is inherently limiting and precludes study into the area of emotional memory and its impact on learning systems. As such, it is preferred to use alternative notation of the form

$$\begin{aligned} \mathbf {E}_\mathbf{M}(t+1) = \frac{(u\mathbf {E}_\mathbf{M}(t) + v\mathbf {E}_\mathbf{J})}{u+v} \end{aligned}$$

(18)

where $u$ and $v$ are constants introduced at the point of implementation, permitting the system to adjust the weightings of importance between a new event and an established emotional state. In behavioural simulation sense, $u$ and $v$ are emotion-change regulators dictating the degree of influence the current state and calculated emotional response have on the next cycle of derived behavioural responses. This allows the model to be flexible to accommodate the modelling of agents with varying degrees of emotional swings. Thus, those wishing to investigate cognitive systems where emotional memory makes up a large component have the freedom to do so with this notation, as do those who wish to study behaviour-based systems with a limited memory component where emotional state is based predominantly upon instantaneous stimulus.

Millenson B

Let us consider, from a psychological standpoint, the alternative interpretation of Millenson’s intensity statement. If one chooses to interpret it in the context of a more intense stimulus leads to a different triggered emotion along an axis, then one already has the fundamental basis for a complete fuzzy inferencing system, as shall now be outlined. Consider the stimulus event $\mathbf {J}$ in the context of its three components $X$, $Y$ and $Z$. Section “Millenson A” discussed these in terms of significance—the importance of the applied or withdrawn stimulus—and derived from this the intensity of the emotional response. If we linguistically define stimulus in terms of intensity, however, rather than context, the shape of the problem shifts somewhat. The intensity Millenson discussed in an emotional context might not specifically interconnect his basic emotions with each other, but rather define their connections with the stimulus itself. Let us return to the removed positive ($\$+$) stimulus variable, $X$. As before, we consider this an input to a fuzzy system. Let us define its linguistic variables as “No Intensity”, “Some Intensity”, “Particular Intensity” and “Extreme Intensity”. Thus, linguistically, our model particularly considers the idea of stimulus intensity and its impact on emotional reaction. In fuzzy set terms,

$$\begin{aligned} (X,\mu ) = \begin{array}{l} \{\mu (\hbox {No Intensity})/\hbox {No Int.}, \\ \mu (\hbox {Some Intensity})/\hbox {Some Int.}, \\ \mu (\hbox {Particular Int.})/\hbox {Part Int.}, \\ \mu (\hbox {Extreme Int.})/\hbox {Ext. Int.}\} \end{array} \end{aligned}$$

Further to that, if stimulus intensity is, as is implied by Millenson [31], the determining factor in which emotions are triggered along a particular axis, this system would require a redefinition of the previous interpretation’s definition of $x$ as a fuzzy set. Rather than discussing degrees of $x$, we instead consider $x$ to simply be a geometric construct indicating the relationship between three named emotions, Annoyance, Anger and Rage, and the removal of positive stimulus (represented through $X$). Thus, instead of associating $X$ with a single output variable, we associate $X$ with three output variables, each with their own linguistic definitions outlining the level to which they are triggered. The first, representing Annoyance, we define as $x_{1}$ and describe in fuzzy set terms as

$$\begin{aligned} (x_{1},\mu ) = \begin{array}{l} \{\mu (\hbox {Not Annoyed})/\hbox {Not Ann.}, \\ \mu (\hbox {Slightly Ann.})/\hbox {Slight. Ann.}, \\ \mu (\hbox {Annoyed})/\hbox {Annoyed}, \\ \mu (\hbox {Very Annoyed})/\hbox {Very Ann.}\} \end{array} \end{aligned}$$

Using comparable linguistic variables, we define the other two output variables associated with $X$, these being $x_{2}$ and $x_{3}$.

$$\begin{aligned} (x_{2},\mu )&= \begin{array}{l} \{\mu (\hbox {Not Angry})/\hbox {Not Ang.}, \\ \mu (\hbox {Slightly Ang.})/\hbox {Slight. Ang.}, \\ \mu (\hbox {Angry})/\hbox {Angry}, \\ \mu (\hbox {Very Angry})/\hbox {Very Ang.}\} \end{array}\\ (x_{3},\mu )&= \begin{array}{l} \{\mu (\hbox {Not Enraged})/\hbox {Not Enr.}, \\ \mu (\hbox {Slightly Enr.})/\hbox {Slight. Enr.}, \\ \mu (\hbox {Enraged})/\hbox {Enraged}, \\ \mu (\hbox {Very Enraged})/\hbox {Very Enr.}\} \end{array} \end{aligned}$$

This alternative architecture, connecting multiple outputs to a single inputs, generates rules which are significantly more complex. In the case of $X$, we create a list of rules of the form:

• Rule 1: If $X$ is No Intensity, then $x_{1}$ is Slightly Annoyed, and $x_{2}$ is Not Angry, and $x_{3}$ is Not Enraged

• Rule 2: If $X$ is Some Intensity, then $x_{1}$ is Very Annoyed, and $x_{2}$ is Slightly Angry, and $x_{3}$ is Not Enraged

• Rule 3: If $X$ is Particular Intensity, then $x_{1}$ is Annoyed, and $x_{2}$ is Very Angry, and $x_{3}$ is Slightly Enraged

• Rule 4: If $X$ is Extreme Intensity, then $x_{1}$ is Slightly Annoyed, and $x_{2}$ is Angry, and $x_{3}$ is Very Enraged

It should be clarified that these linguistic terms defining the level of the named emotions refer specifically to its level relative to the other emotions. One might say that to be Enraged one must be Very Angry by definition, but that would be the wrong context. Rather, when the agent is Very Enraged, but only Angry rather than Very Angry, this is because Anger and Rage are treated as two distinct basic emotions by Millenson, and the system is experiencing Rage to a greater degree than it is experiencing Anger. As we have with all other numerical variables, we apply limits of [0,1] to $x_{1}$, $x_{2}$ and $x_{3}$ in this context. That is to say that upon the conclusion of centroid defuzzification, as discussed in a previous section, the crisp output associated with each of the three named emotions shall be a value between 0 and 1. We explicitly label these outputs as $\mu x_{1}$, $\mu x_{2}$ and $\mu x_{3}$ explicitly as, for our purposes, they define membership of their associated emotion within the emotional component of the stimulus vector $\mathbf {J}$, $\mathbf {E}_\mathbf{J}$. Expanding this system to include the other two input variables, and their associated six basic emotions, permits us to generate a Mamdani fuzzy inferencing system which will absorb the numerical contents of the stimulus vector $\mathbf {J}$ and produce a value, between 0 and 1, for each of the nine named emotions in Millenson’s model. As these nine values represent the experiential level of the individual emotions, they are considered analogous to the emotional state generated by the previous implementation of Millenson’s model, and thus, we define a vector formed with these nine elements as $\mathbf {E}_\mathbf{J}$, taking the form outlined previously. At this stage, the system can now inform the emotional state of the agent. As we have kept our notation and vector structure consistent throughout both interpretations of the Millenson model, the manner in which it does this, with respect to the emotional state $\mathbf {E}_\mathbf{M}$ is analogous with that discussed in the previous subsection and, as such, has no need of explicit repetition.

Fuzzifying the Geneva Emotion Wheel

Scherer himself described emotions, and their surrounding linguistic conventions, in terms of fuzziness [26]. Indeed, were our interest entirely fixed on the implementation of a singular, emotionally informed cognitive engine, his work alone might provide a suitable basis for in-depth explanation. As the terms of this article reflect a broader topic, however, we are compelled to focus our interest upon specific aspects of his work. A major contrast between the Geneva Emotion Wheel and the Millenson model is Scherer’s inherent geometricalisation. Within the Millenson model, geometry was, to an extent, immaterial, primarily due to the independent nature of the variables. Within the Geneva Emotion Wheel, however, specific geometry and positional relativity enjoy significantly more prominence. Description of the Geneva Emotion Wheel as a concept was largely covered in our previous sections; here, we consider the wheel as a geometric construct and circumplex. Scherer provides us with two conceptual axes—the level of control experienced by the agent, ranging from ‘High’ to ‘Low’, and the valence (positivity or negativity) of the experience. Defined by these axes are two matters: the experienced emotion of the agent, and its intensity. In Scherer’s conceptual prototype, upon which our own prototyping is based, each named emotion had four represented degrees of intensity. In addition, each named emotion had a crisply defined occupational region in terms of relative magnitudes of control and valence. These are shown in Fig. 2. Each of the named emotions in Scherer’s prototype might be described in terms of a ratio of the control and experience magnitudes, irrespective of specific emotional intensity (though that is obviously important to our considerations). That is to say that one might assume a ‘prideful’ emotional state for any situation where the values of control and valence were positive, and the ratio of control to valence was significantly weighted in favour of control. Conceptually, this raised interesting questions regarding how best to represent the Geneva Emotion Wheel in fuzzy terms. When considering the output for a fuzzy system relating to the Geneva Emotion Wheel; therefore, Scherer has already provided us with two ‘fuzzy’ concepts. First, named emotions themselves, and second, intensity of those named emotions. The question comes in the manner in which we conceptually fuzzify the emotions, and in order to clarify that we must first define the inputs received by a system utilising the Scherer model of emotions, and the outputs our implementation of that system should provide. The inputs Scherer provides are the concepts of Control and Valence. We name these $x_\mathbf {J}$ and $y_\mathbf {J}$ for a given situation, and define them in the context of conceptual sums of experiential perceptions,

$$\begin{aligned} x_\mathbf {J}&= \frac{1}{n_u} \sum _{i=1}^{n} f_{u_{i}}(u_{i_{\mathbf {J}}}) [-1,1]\end{aligned}$$

(19)

$$\begin{aligned} y_\mathbf {J}&= \frac{1}{n_v} \sum _{i=1}^{n} f_{v_{i}}(v_{i_{\mathbf {J}}}) [-1,1] \end{aligned}$$

(20)

where $u_{i_{\mathbf {J}}}$ is an element of the agent’s environment which impacts its sense of valence, of which there are $n_u$ for any given $x_\mathbf {J}$, and whose individual impact is defined by an associated function $f_{u_{i}}$; and, $v_{i_{\mathbf {J}}}$ is an element of the agent’s environment which impacts its sense of control, of which there are $n_v$ for any given $y_\mathbf {J}$, and whose individual impact is defined by an associated function $f_{v_{i}}$; and, where the sums are normalised to a value between $-1$ and 1, to reflect the juxtapositions they represent. Usage of $\mathbf {J}$ with respect to Scherer is analogous to the usage of the variable with respect to Millenson, up to a point. Whereas Millenson permitted the explicit association of stimulus events with $\mathbf {J}$, Scherer’s model requires a more esoteric interpretation. Rather than an event, in this context $\mathbf {J}$ represents the agent’s perception of its situation at a given instant, in the context of valence and control. Thus, the input $\mathbf {J}$ is defined,

$$\begin{aligned} \mathbf {J} = \left[ \begin{array}{c} x\\ y \end{array} \right] \end{aligned}$$

(21)

As previously stated, the output of any system covered within this work should be that of an emotional state, defining at any given instant the discrete state of the agent in the context of experiential magnitudes of a given number of named emotions. Scherer’s model presents sixteen named emotions; thus, the desired output of any implementation is defined as a vector which indicates the relative magnitudes of each of these sixteen emotions, between values of 0 and 1. Numerically, this emotional state $\mathbf {E}_\mathbf{S}$ is written

$$\begin{aligned} \mathbf {E}_\mathbf{S} = \left[ \begin{array}{l} e_{\hbox {Pride}} \\ e_{\hbox {Elation}} \\ e_{\hbox {Happiness}} \\ e_{\hbox {Satisfaction}} \\ e_{\hbox {Relief}} \\ e_{\hbox {Hope}} \\ e_{\hbox {Interest}} \\ e_{\hbox {Surprise}} \\ e_{\hbox {Anxiety}} \\ e_{\hbox {Sadness}} \\ e_{\hbox {Boredom}} \\ e_{\hbox {Shame/Guilt}} \\ e_{\hbox {Disgust}} \\ e_{\hbox {Contempt}} \\ e_{\hbox {Hostility}} \\ e_{\hbox {Anger}} \end{array} \right] \end{aligned}$$

(22)

where $e$ represents the relative level with which a given emotion is being experienced, with that given emotion identified in explicit terms by its subscript. Having defined the generalist input and desired output of the system, one must now consider the best way to approach it from a fuzzy perspective. That is to say, whether to approach it from a fuzzified geometric perspective, or to approach it from a linguistic perspective. It should be clarified that by ‘linguistic perspective’, we mean description of inputs linguistically, rather than geometrically. For example, one could connect the concept of a ‘steep’ relationship between Valence and Control, and an intense experience, with a ‘high’ relative magnitude of Pride. The issue with such a system, however, is the inherently geometrical nature of Scherer’s model. While it might be possible to devise a multitude of adjectives to describe experienced level of Valence or Control, and thus map them in fuzzy terms, ultimately such linguistic variables would simply be geometric place-holders, not having any particular linguistic meaning, and thus defeating the purpose of their inclusion. It should also be borne in mind that the Geneva Emotion Wheel has inherently fuzzy, linguistic components already: the inputs themselves, and the conceptual intensities of the experienced emotions. As these are fuzzified in the method now outlined, it is felt the application of fuzzy logic is still wholly justified in this context. Shown in Fig. 2, the Geneva Emotion Wheel can be viewed from a geometric perspective. This means that rather than interpret inputs in the context of linguistic variables such as “Low”, “Medium” or “High”, we instead consider the inputs geometric coordinates, and fuzzify the emotions they represent. As with the Millenson model, it is possible to dissect this emotion representation in the context of its axes and associate each axis with one of the variables defined in $\mathbf {J}$. Let us consider first the axis associated with the variable $x$, that of Valence. Considering the model geometrically in the context of the $x$ axis, it is evident that all discrete regions therein can be conceptually represented by thirty-three unique sets. We say thirty-three, rather than the sixty-five unique regions indicated on the model, because the model is a geometrical mirror of itself, with only the emotional white space (the thirty-third unique set) crossing the intersection. Thus, is it possible to define the variable $x$, in fuzzy terms, as

$$\begin{aligned} (x,\mu ) = \begin{array}{l} \{\mu (x_{1})/x_{1},\mu (x_{2})/x_{2},\mu (x_{3})/x_{3}, \ldots , \\ \mu (x_{31})/x_{31},\mu (x_{32})/x_{32},\mu (x_{33})/x_{33} \} \end{array} \end{aligned}$$

These sets are described as unique, but it should be noted that many of the sets share elements; that is to say that many discrete values of $x$ are found in more than one set. It is necessary that the values assigned to these sets be geometrically consistent with the model, or the psychology upon which it is ground ceases to have meaning. The explicit limits that were defined for our particular implementation of the Geneva Emotion Wheel are included in the Implementation section. That said, it was reasoned that these sets should be defined such that their maxima coincide with the geometrically crisp regions defined by Scherer’s prototype at their widest points. The ranges defining alternative non-trivial memberships vary, dependent upon how broadly the implementation seeks to fuzzify the emotions. It is suggested, however, that the non-maximal, non-trivial bands remain proportionally consistent across different grades of the same emotion, thereby maintaining the ratio-based relationship that psychologically associates the conceptual inputs with the named emotions. Let us now consider the variable $y$, which we previously paired with the concept of control. As one compares the structure of $y$ to the structure of $x$, the near-identical, if tangential nature of their relationship coincides with the ideals of a circumplex representation. Again, each discrete grade of a named emotion can be represented by a single function, and thirty-three functions can be applied to represent the entire circumplex. As a fuzzy construct, we similarly define $y$ in terms of

$$\begin{aligned} (y,\mu ) = \begin{array}{l} \{ \mu (y_{1})/y_{1},\mu (y_{2})/y_{2},\mu (y_{3})/y_{3}, \ldots , \\ \mu (y_{31})/y_{31},\mu (y_{32})/y_{32},\mu (y_{33})/y_{33} \} \end{array} \end{aligned}$$

where the meanings are comparable with those espoused in the representation of $x$, and consistent with fuzzy principles as outlined in the preamble. It should be noted that, while linguistic variables are not employed in this case, the very nature of what each fuzzy function within the variables represents is inherently fuzzy, as shall become evident as the links between the input and output variables are explicitly clarified. Let us consider the output structure of a system informed by these two fuzzy input variables. As stipulated in the psychological outline of the Geneva Emotion Wheel, this system represents both the nature and intensity of sixteen named emotions, as a function of the variables we have outlined as $x$ and $y$. The output of such a system, then, should be a relative intensity of each of these sixteen emotions, individually. Let us consider a single emotion, Satisfaction, as a fuzzy construct, with its structure informed by the Geneva Emotion Wheel. We define Satisfaction, in this context, as $(e_{\hbox {Satisfaction}},\mu )$, and in specific terms as

$$\begin{aligned} (e_{\hbox {Satisfaction}},\mu ) = \begin{array}{l} \{ \mu (\hbox {N Int.})/\\ \hbox {N Int.}, \\ \mu (\hbox {Lo Int.})/\\ \hbox {Lo Int.}, \\ \mu (\hbox { Mid Int.})/\\ \hbox { Mid Int.}, \\ \mu (\hbox { Hi Int.})/\\ \hbox { Hi Int.} \\ \mu (\hbox { Ext Int.})/\\ \hbox { Ext Int.} \} \end{array} \end{aligned}$$

Let us introduce such a structure to the remaining discrete emotions, and thus define our system output. The links between input and output, however, have not yet been clarified. Let us return to our fuzzy construct $(e_{\hbox {Satisfaction}},\mu )$. The structure of $(e_{\hbox {Satisfaction}},\mu )$ is drawn from the geometric model, with a null membership function ascribed to the central emotional white space, and gradiated emotional intensities based upon the four discrete intensities shown in Fig. 2. Thus let us consider the fuzzy system rules which connect membership functions of our inputs to all of $(e_{\hbox {Satisfaction}},\mu )$’s membership functions. Such rules would be of the form,

• Rule 1: If $x$ is $x_{33}$, and $y$ is $y_{33}$, then $e_{\hbox {Satisfaction}}$ is Null Intensity

• Rule 2: If $x$ is $x_{17}$, and $y$ is $y_{24}$, then $e_{\hbox {Satisfaction}}$ is Low Intensity

• Rule 3: If $x$ is $x_{18}$, and $y$ is $y_{27}$, then $e_{\hbox {Satisfaction}}$ is Mid Intensity

• Rule 4: If $x$ is $x_{19}$, and $y$ is $y_{30}$, then $e_{\hbox {Satisfaction}}$ is High Intensity

• Rule 5: If $x$ is $x_{20}$, and $y$ is $y_{32}$, then $e_{\hbox {Satisfaction}}$ is Extreme Intensity

The minimum membership grade of each doublet of input-related fuzzy sets is projected onto their associated emotional grade. The centroid of all of these grades, for a given named emotion, determined its numerical output, between 0 and 1. In the case of $e_{\hbox {Satisfaction}}$, we call this discrete value $e_{\hbox {Satisfaction}}'$. Thus the structure of a geometrically conceptualised, fuzzy representation of the Geneva Emotion Wheel becomes clear. Any given values for $x$ and $y$ obtain membership grades for the thirty-three fuzzy functions that constitute their make up, and such memberships are compared to rules explicitly connecting combinations of these inputs with grades of specific output emotions. This will provide discrete values for the sixteen emotional outputs, between 0 and 1, thereby constructing an instantaneous emotional response $\mathbf {E}_{\mathbf{S}}'$, which is defined

$$\begin{aligned} \mathbf {E}_{\mathbf{S}}' = \left[ \begin{array}{l} e_{\hbox {Pride}}' \\ e_{\hbox {Elation}}' \\ \ldots \\ e_{\hbox {Anger}}' \end{array} \right] \end{aligned}$$

(23)

As discussed in the context of the Millenson representation, the instantaneous result of the fuzzy inferencing system informs the emotional state; that is to say, in this context, $\mathbf {{E}_{\mathbf{S}}'}$ informs $\mathbf {E}_{\mathbf{S}}$. Let us consider $\mathbf {E}_{\mathbf{S}}$ at time $t$ and time $t+1$, where the interval represents the time taken for the system to obtain a value for $\mathbf {E}_{\mathbf{S}}'$. As both $\mathbf {E}_{\mathbf{S}}$ and $\mathbf {E}_{\mathbf{S}}'$ are vectors of the same structure, the method of combining them is analogous to that used with respect to the Millenson model.

$$\begin{aligned} \mathbf {E}_\mathbf{S}(t+1) = \frac{(u\mathbf {E}_\mathbf{S}(t) + v\mathbf {E}_{\mathbf{S}}')}{u+v} \end{aligned}$$

(24)

where $u$ and $v$ are constants introduced at the point of implementation, permitting the system to adjust the weightings of import between the newly calculated emotional component $\mathbf {E}_{\mathbf{S}}'$ and the established emotional state $\mathbf {E}_{\mathbf{S}}$. In behavioural simulation sense, $u$ and $v$ are emotional regulators dictating the degree of influence the current state and calculated emotional response has on the next cycle of derived behavioural responses. Again, those wishing to investigate systems where emotional memory has significant influence on decision-making have the freedom to do so with this notation, as do those who wish to study systems with a limited memory component where emotional state is based predominantly newly obtained environment-driven emotional components.

FIS Prototyping of the Emotional Models

The MATLAB Fuzzy Inferencing System Editor (FISE) provides a stable, well-integrated platform through which to generate implementations of these psychologically grounded models of emotion. This section shall outline in specific detail the MATLAB implementations of the three mathematical mechanisms previously outlined. First, it shall address the representation of the initial Millenson model, followed by the alternative interpretation of Millenson’s literature. It shall then outline the process by which Scherer’s Geneva Emotion Wheel was implemented.

Millenson A in MATLAB

Within MATLAB’s FISE, a Mamdani fuzzy inferencing system was generated, three inputs to three outputs. This fuzzy inferencing system utilised the minimum ‘And’ operator as discussed in section “Internal Modelling of Emotions”, and the centroid method of defuzzification. This structure is illustrated by Fig. 3. As indicated in section “Fuzzifying the Millenson Model”, these inputs were declared so as to represent the elements of a stimulus event, $\mathbf {J}$. Each of the input elements $X$, $Y$ and $Z$ was, as a fuzzy construct, defined as having three associate fuzzy membership functions, representing quantified levels of associated stimulus in the context of significance to the agent. Within this implementation, those fuzzy membership functions were represented as triangular functions, with their geometric vertices given by Table 1. Figure 4 illustrates the membership functions described by Table 1, as applied to input variable $Z$. These structures were deemed to be conceptually uniform across all three axes and were applied thus. The output variables of the fuzzy inferencing system, $x$, $y$ and $z$, were described and outlined in section “Millenson A” as having three intrinsic membership functions. These were, explicitly, $Low \, Response, Moderate \, Response$ and $High \, Response$. Millenson’s model gives rise to direct equivalency across the input and output variables; thus, it was determined there should be equivalency in their description as triangular fuzzy membership functions. The geometric vertices of these three membership functions were applied uniformly across all three output variables. These are given in 2 and their application to the output variable $z$ is illustrated by Fig. 5.

Fig. 3

Millenson A: FIS structure

Table 1 Millenson A: input MFs

Fig. 4

Millenson A: MFs of input variable $Z$

Table 2 Millenson A: output MFs

Fig. 5

Millenson A: MFs of output variable $z$

Rules as outlined in section “Millenson A” in the context of variables $X$ and $x$ were defined the internal structure of the fuzzy inferencing system such that any vector $\mathbf {J}$ produced a suitable output $\mathbf {e}_\mathbf{J}$ where:

$$\begin{aligned} \mathbf {e}_\mathbf{J} = \left[ \begin{array}{c} x [0,1]\\ y [0,1]\\ z [0,1]\end{array} \right] \end{aligned}$$

The process by which the vector $\mathbf {e}_\mathbf{J}$ was processed to generate the desired output $\mathbf {E}_\mathbf{J}$ associated with a given stimulus $\mathbf {J}$ required more subtle analysis in order to be implemented. As a function of the usage of centroid defuzzification applied in this representation, coupled with the specific representation of the triangular membership functions, ensured that the minimum value for any output was 0.163. Conversely, the maximum output value for any output was 0.837. Returning to Millenson’s geometry, it was required that we suitably scale the named emotions along a given axis in accordance with his structure. That is to say that, along the axis, the maximum for the lowest grade would appear at 20 %, the next highest grade at 60 %, and the highest grade at 100 %. Thus, it was determined to scale these grades to fit the value range granted by the fuzzy inferencing system, when defining the fuzzy functions linking the output variables to the specific emotions they influenced. While the calculations that processed the individual outputs $x$, $y$ and $z$ into discrete grades of the nine named emotions were explicitly not a second fuzzy inferencing system, the nature of the associative functions was inherently fuzzy in nature. These functions were likewise triangular in structure, so as to maintain internal consistency within representations, though not symmetrical. Their vertices are presented in the context of output variable $z$ in Table 3, which is illustrated in Fig. 6.

Table 3 Millenson A: discrete emotions associated with $z$

Fig. 6

Millenson A: discrete emotions associated with $z$

These relations between variable and its associated discrete emotions were applied uniformly. For each vector $\mathbf {e}_\mathbf{J}$, a simple MATLAB M-File used these fuzzy relations to determine membership grades for each discrete emotion, producing the desired output for a given iteration, $\mathbf {E}_\mathbf{J}$. The interaction between $\mathbf {E}_\mathbf{J}$ and the emotional state $\mathbf {E}_\mathbf{M}$ is discussed in greater detail in the testing section, since it is an inherently customizable concept; for the basic implementation, however, a mean value of $\mathbf {E}_\mathbf{J}$ and the current $\mathbf {E}_\mathbf{M}$ was taken whenever a stimulus event $\mathbf {J}$ was applied to the system.

Millenson B in MATLAB

Within MATLAB’s FISE, a Mamdani fuzzy inferencing system was generated, three inputs to nine outputs. This fuzzy inferencing system utilised the minimum ‘And’ operator as discussed in section “Internal Modelling of Emotions”, and the centroid method of defuzzification. This structure is illustrated by Fig. 7. Implementation of this alternative representation of Millenson’s model through MATLAB was a simpler process than that listed above, primarily due to the removal of the intermediary layer of calculation associated with $\mathbf {e}_\mathbf{J}$. The structure of the input vector remained consistent, that being the stimulus event $\mathbf {J}$, although its context differs, as described earlier. Each of the input elements $X$, $Y$ and $Z$ was, as a fuzzy construct, defined as having four associate fuzzy membership functions, representing quantified levels of associated stimulus in the context of intensity with which the agent felt the stimulus. Within this implementation, those fuzzy membership functions were represented as triangular functions, with their geometric vertices given by Table 4. These are illustrated in the context of variable $X$ in Fig. 8. These membership functions were applied uniformly to the three input variables $X$, $Y$ and $Z$. The nine output variables, mathematically denoted as $x_{1-3}$, $y_{1-3}$ and $z_{1-3}$, were each associated with four membership functions as outlined in section “Millenson B”. In implementing them, these membership functions were represented as triangular functions; their vertices are given in Table 5, in the context of the output $x_{1}$, or the ‘Annoyed’ emotion. They are illustrated, again in the context of output $x_{1}$, in Fig. 9.

Fig. 7

Millenson B: FIS structure

Table 4 Millenson B: input MFs

Fig. 8

Millenson B: MFs of input variable $X$

Table 5 Millenson B: output MFs

Fig. 9

Millenson B: MFs of output variable $x_{1}$- annoyance

These membership functions were applied uniformly across all nine output emotions to maintain consistency across the target resultant, vector $\mathbf {E}_\mathbf{J}$, elements. Rules were input into the system reflecting those outlined in section “Millenson B”, where the mathematics of this model were discussed in depth. The rules were applied uniformly across input variables, connecting them each with their three associated output variables. An M-File obtained the nine discrete values, one for each output, and combined them into the desired iterative output vector $\mathbf {E}_\mathbf{J}$. In simple testing, $\mathbf {E}_\mathbf{J}$ was then aggregated with $\mathbf {E}_\mathbf{M}$ in order to construct an evolving emotional state; the specifics of this are discussed in the testing section of this paper.

The Geneva Emotion Wheel in MATLAB

Implementation of the Geneva Emotion Wheel through MATLAB proved to be a complex endeavour, both in terms of the geometric analysis required in order to maintain scientific consistency, and in terms of limitations of the MATLAB FISE. Within MATLAB’s FISE, a Mamdani fuzzy inferencing system was generated, two inputs leading to sixteen outputs. This fuzzy inferencing system utilised the minimum ‘And’ operator as discussed in section “Internal Modelling of Emotions” and the centroid method of defuzzification. This structure is illustrated by Fig. 10.

Fig. 10

Scherer: FIS structure

As outlined in section “Fuzzifying the Geneva Emotion Wheel”, the input vector to this system, $\mathbf {J}$, is defined in this context as

$$\begin{aligned} \mathbf {J} = \left[ \begin{array}{c} x\\ y \end{array} \right] \end{aligned}$$

where $x$ and $y$ represent a quantified determination of valence and control, respectively, within the value ranges of $-1$ to 1. As fuzzy constructs, it has already been determined that each of these input variables has thirty-three fuzzy functions associated with it; the matter of the implementation is to calculate in discrete terms and so encode these thirty-three functions. In this implementation, the nature of the fuzzy functions faced applied constraints. Firstly, that the fuzzy functions would be trapezoidal. Secondly, that the maxima of these trapezia would, along either axis, coincide with the discrete geometrical region determined by Scherer’s prototype. Thirdly, that each shoulder of a trapezium would be equal in width along its axis to the width of its maximum. Finally, that the absolute values of $-1$ and 1 along each axis would be determined by the edge of the maximum of the first and thirty-second membership functions for that axis (mindful that the thirty-third occurs out of sequence, and functionally occupies the origin 0). Following these constraints, and applying geometrical analysis to four significant figures of accuracy, a table was constructed from the vertices of each trapezoidal membership function. As the $x$ and $y$ axes on Scherer’s prototype mirrored each other, this table presents the membership functions of both the $x$ and $y$ variables, numericised according to the value of their first coordinate. These functions are naturally applied uniformly across both $x$ and $y$. A graphic representation of these membership functions as applied to the $x$ input variable is included as Fig. 11.

Fig. 11

Scherer: MFs of input variable $x$

Each of the sixteen outputs as described in section “Fuzzifying the Geneva Emotion Wheel” is required to have five membership functions describing its relative magnitude. These were described as $Null \, Intensity, Low \, Intensity, Middle \, Intensity, High \, Intensity$ and $Extreme Intensity$. The idea, as explained, was to map individual couplets of input membership functions to a specific grade of an individual output variable. Experimentation, however, revealed a weakness in the application of the centroid defuzzification mechanism. In this system, there were naturally instances where individual outputs would have membership of 0; in situations where Extreme Pride was triggered, for example, Anxiety would have no membership output. In such situations, MATLAB’s implementation of centroid defuzzification returns the median value of the output range. As such, in the above example $e_{\hbox {Anxiety}}$ would return membership of 0.5. The solution to this problem was to introduce a sixth output membership function. This function had a discernible membership area of $5 \times 10^{-5} \hbox {units}^2$ and would be the default state for all outputs unless one of their other rules was triggered. Regrettably, this introduced a potential error margin within obtained outputs. This error margin is factored into the results obtained from this implementation of the Geneva Emotion Wheel. As a result of this, the mathematical construct describing the emotion of satisfaction with respect to $\mu , e_{\hbox {Satisfaction}}$, given in section “Fuzzifying the Geneva Emotion Wheel” was amended to:

$$\begin{aligned} (e_{\hbox {Satisfaction}},\mu ) = \begin{array}{l} \{ \mu (\hbox { No Intensity})/\hbox { No Int.}, \\ \mu (\hbox { Null Intensity})/\hbox { Null Int.}, \\ \mu (\hbox { Low Intensity})/\hbox { Low Int.}, \\ \mu (\hbox { Middle Int.})/\hbox { Mid Int.}, \\ \mu (\hbox { High Int.})/\hbox { High Int.} \\ \mu (\hbox { Extreme Int.})/\hbox { Ext. Int.} \} \end{array} \end{aligned}$$

Table 6 Scherer: output MFs

Fig. 12

Scherer: MFs of output variable $e_{\hbox {Satisfaction}}$

Each of these fuzzy terms is represented by a trapezoidal membership function, the coordinates of which are given in Table 6. This table is illustrated by Fig. 12 in the context of the output $e_{\hbox {Satisfacton}}$. Whereas the rules required to represent both interpretations of the Millenson Model were self-explanatory in the context in which they were presented, the geometric representation of the Geneva Emotion Wheel is not so. Each rule in the implementation associated one membership function from each input variable with a specific membership function of one of sixteen output variables. An additional rule exists associating all outputs’ “Null” membership functions to $x_{33}$ and $y_{33}$, as has been suggested previously. Also, be necessity, all of the above couplets are also associated with the “No Intensity” error-correction membership function for all output emotions to which they are not explicitly connected. A simple M-File is used to generate the desired output vector $\mathbf {E}'_{\mathbf{S}}$ from the sixteen discrete numerical values generated by the fuzzy inferencing system outputs. In simple testing, $\mathbf {E}'_{\mathbf{S}}$ was then aggregated with $\mathbf {E}_\mathbf{S}$ in order to construct an evolving emotional state; the specifics of this are discussed in the testing section of this paper.

Models Testing and Evaluation

The testing segment of this paper will focus on broad examination of the effective and practical limitations of the implementations proposed, and comparison of their behaviours where appropriate. Undertaking an exhaustive experimental trial with a geometrically determined variety of inputs, we shall determine behavioural trends within the systems regarding their output structure.

Millenson A Testing

The Millenson A implementation was tested along its Elation-related axis, using the following input values: $-0.1$, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1. The uppermost and lowermost of these values were included to test the system’s behaviour when inputs were received that lay outside operational boundaries. As anticipated, these values, $-0.1$ and 1.1, returned warning errors. The remainder of the input values produced usable results which shall be further discussed in analysis. Specifically, these results are membership grades of the three named emotions that lie along the Elation-related axis. Our analysis shall focus upon these and their relationship with input magnitude. The reason for considering only one input variable for the purposes of this publication is a function of the structure of the model. Since each input variable, as has been discussed in both the psychological background and implementation sections, is associated solely with its single output variable and with no other, any single input–output pairing can be examined as a single entity without losing context. Furthermore, as all three axes are identical, numerically, in terms of their structure, analysis of any single input–output pairing provides equal insight into the two undiscussed input–output pairings. That said, in preliminary testing, all three input–output pairings in the implementation of Millenson A were tested to ensure complete consistency across them, and this was confirmed. The Analysis section, however, centres upon only the pairing discussed above.

Millenson B Testing

The Millenson B implementation was tested along its Elation-related axis, using the following input values: $-0.1$, 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1. The uppermost and lowermost of these values were included to test the system’s behaviour when inputs were received that lay outside operational boundaries. As anticipated, these values, $-0.1$ and 1.1, returned warning errors. The remainder of the input values produced usable results which shall be further discussed in analysis. Specifically, these results are membership grades of the three output variables (named emotions) associated with the $S+\$-$ input variable. Our analysis shall focus upon these and their relationship with input magnitude. The reason for considering only one input variable for the purposes of this publication is a function of the structure of the model, similar but naturally not identical to the justification with respect to Millenson A. Since each input variable, as has been discussed in both the psychological background and implementation sections, links exclusively to three output variables (named emotions lying along its representative axis) and with no other, any single input–output grouping may be treated as representing the entire structure. As with Millenson A, however, all three input–output groups in the model were tested to ensure complete consistency across them, and this was confirmed. The Analysis section centres upon only the $S+\$-$ grouping.

Scherer Testing

Unlike the Millenson model, neither of Scherer’s input variables enjoys exclusive impact with any of its output variables. Each of the sixteen emotional output variables is intrinsically associated with both the Control and Valence input variables. As such, exhaustive testing was required across the range of accepted input values, with no abstraction or extrapolation being possible. It was determined that 5 % incremental increases across the ranges, plus tests beyond the accepted extremities of both input variables, would be required to gain a true understanding of the model’s behaviour. These experiments were performed and the insight they provided into the capacities and limitations of this model are discussed in the next section.

Critical Analysis

Millenson A Analysis

Our analysis of the Millenson A fuzzy logic implementation centres upon the $S+\$-$ input variable and its associated named emotional outputs. Table 7 shows the data obtained within the functional boundaries of the model. Tests outside of these boundaries returned a warning error. This data can be represented visually as shown in Fig. 13. The graphical representation gives us a clearer view of the model’s behaviour as the numerical value of $S+\$-$ increases. We can see, in accordance with our expectations, there are no situations where all three emotions have nonzero membership grades.

Table 7 Millenson A test results

Fig. 13

Millenson A test results

The relative surface areas beneath the three named emotions were calculated based on the area beneath the chart. This information is useful in determining the relative membership magnitudinal probabilities of the three emotions, which is to say how ‘strongly’ they are represented within the boundaries of the system. In such terms, we choose to recognise the area under the Pleasure emotion as representing unity. The Elation emotion has a surface area, then, equal to 1.337 times unity. The Ecstasy emotion, similarly, has a surface area equal to 1.330 times unity. In terms of chance of firing for random data input, however, we must instead consider range of nonzero values. Again, we choose to recognise the operational range of the Pleasure emotion to represent unity. In this case, the Elation emotion’s active range is equal to unity, while the Ecstasy emotion’s active range is equal to 0.429 of unity. Taking both into consideration, the central emotion, Elation, which Millenson uses to describe the entire axis, is the most strongly represented for any given random input. By contrast Elation, which is considered the extremis emotion, while having very great membership when fired is the least likely to be so for any random input. The general shapes of the graphs display trends we anticipated on the basis of the two-tier nature of the Millenson A representation. In accordance with the limitations we sought to place upon the structure, lower-level emotions trail into higher-level emotions in terms of membership. That is to say that an Elation response is more likely to trigger residual Pleasure than a Pleasure response is likely to trigger residual Elation. Further discussion of this implementation shall occur in the context of its comparability with the alternative Millenson representation.

Millenson B Analysis

Our analysis of the Millenson B fuzzy logic implementation focuses on the $S+\$-$ input variable and associated named emotional outputs. Table 8 shows the data obtained within the functional boundaries of the model. As with Millenson A, tests outside of these boundaries returned a warning error. It is clear from the initial data that, importantly, there are no points within operational range of the system where all three named emotions do not provide nonzero results. We include a graphical representation of this data as Fig. 14. Again, the graphical representation can provide us with a clearer view of the behaviours of the model in terms of membership grades of the named emotions as the $S+\$-$ variable increases.

Table 8 Millenson B test results

Fig. 14

Millenson B test results

Again, we first consider the relative surface area beneath the curve. Taking the area under the Pleasure curve as unity, we can determine the area under the Elation curve to be 0.865 of unity, and the area under the Ecstasy curve to be 0.480 of unity. There can be no comparison of range of relevance when considering the results provided by the Millenson B implementation as nonzero results are provided for all three named emotions across the entire operational range of the system. Looking at the membership area, however, it is clear that the Millenson B implementation weights in favour of the lower-level emotions over the higher. In terms of trailing edges, this is visually apparent in the system when considering the length of the trailing edge of Pleasure relative to the leading edge of Ecstasy. It is also visible when comparing the descending trends of Elation with the ascending trends of Elation.

Millenson A versus Millenson B

In order to permit a clearer comparison of the two implementations of the Millenson theory, Fig. 15 demonstrates a superposition of Figs. 13 and 14. When comparing the behaviour of the models, it is appropriate that we consider their structural differences, in particular their rules structure. The key differences between the models come in two parts, rule structure and tier structure.

Fig. 15

Millenson A and B test results

In the Millenson A implementation, each rule in the fuzzy inferencing system makes a connection between a single input and a single output. That is to say association is drawn between a specific input membership function and a specific output membership function. In the Millenson B implementation, by contract, each rule in the fuzzy inferencing system connects a specific input to three associated outputs. Which is, again, to say that a connection is drawn between a specific input membership function and three output membership functions. Similarly, while the Millenson B fuzzy inferencing system has an output for every named emotion, Millenson A produces instead a three-part vector which is then converted, geometrically, to generate values for the nine named emotions. This is the role of its second tier. Taking these differences into consideration, the magnitude of variation in the results should not be considered surprising. A key and instantly discernible difference lies in the variety of compound emotional results presented by each implementation. While Millenson A never provides nonzero results for more than two named emotions, Millenson B provides nonzero results for all three named emotions at all times. Connected to this are the differences in membership surface area between the two models. Summing the membership surface area of all three named emotions, and defining the summed surface area of the Millenson A results as unity, the summed surface area of the Millenson B results equate to 2.281 of unity. This enables us to say that in average terms, Millenson B shall return a higher summed membership across the three named emotions for a given input value. Taking the global view, while both models have justification in Millenson’s theory, the broader-brush approach of Millenson B provides a more interesting psychological blend of emotions for a given emotional state, while the more targeted nature of Millenson A might be considered to have more use in terms of pedagogue system control. Indeed, the application of Millenson A as an agent controller in a pedagogic case is explored in associated work [21].

Scherer Analysis

An exhaustive list of results from the Scherer experimentation is impractical to present in print format, far moreso than is the case with either Millenson model. As such, discussion of these results will be more targeted and less abstract than in the prior cases. The first important result of experimentation with our implementation of the Scherer model was the revelation of a weakness in the system in cases of extremis. Specifically, in 4 % of cases, where both input variables approached $|1|$, errors were returned as though the input data lay outside the boundaries of the system. Investigation revealed that this error was an inherent function of the two-coordinate representation of the circumplex geometry. These aberrations aside, the fuzzy geometry used in the representation of the Geneva Emotion Wheel demonstrated interesting behaviour when considered across a range of named emotions with similar ratios of Valence to Control. Rather than discuss exhaustive results in the context of each named emotion, as is possible with Millenson, instead we focus upon four cross-sections and the implications of the non-trivial results each presents. In each case, the figures represent membership grades for the named emotions at the input values presented, with one input value remaining static while the other varies across the range. Figure 16 presents an example where Valence is fixed at 0.8, and Control varied from $-1.0$ to 1.0. Figure 17 presents its corrollary, Control fixed at 0.8 while Valence varies from $-1.0$ to 1.0. In an effort to provide additional evidence of the implementation’s behaviour, Fig. 18 presents emotion memberships where Valence is fixed at 0.5, with Control varied across the range of inputs. Similarly, Fig. 19 presents the corrollary, with Control fixed at 0.5 and Valence varied from $-1.0$ to 1.0.

Fig. 16

Geneva Emotion Wheel cross-section versus control, valence fixed @ 0.8

Fig. 17

Geneva Emotion Wheel cross-section versus valence, control fixed @ 0.8

Fig. 18

Geneva Emotion Wheel cross-section versus control, valence fixed @ 0.5

Fig. 19

Geneva Emotion Wheel cross-section versus valence, control fixed @ 0.5

The purpose of these figures is to demonstrate two things. Firstly, that the Scherer geometry is obeyed within the constraints of the model, and within the context in which the implementation is presented. Secondly, that the geometry is consistent inasmuch as behaviour is maintained across the operational region. Figure 16 presents a case where Valence is both positive and of high magnitude. That being the case, referring back to Fig. 2, and taking into account the trailing edges of our fuzzy geometry, we should expect the emotions triggered by a variance in Control across the range to be Elation, Happiness, Satisfaction, Relief, Hope and Interest. Figure 16 confirms that to be the case, in addition to several key features. Firstly, that the emotions triggered follow the Geneva Emotion Wheel geometry in abstract terms. That is to say, Interest, being the emotion in the above list associated with the lowest relative Control, is triggered at lower levels of Control than any other. Similarly, the order of triggering follows the geometry of the Geneva Emotion Wheel. Secondly, Fig. 16 demonstrates symmetrical membership relationships for emotions across the mid-point of the Control range. This is important from a consistency perspective. The Geneva Emotion Wheel is a circumplex and, as such, any attempt to represent it geometrically must adhere to the symmetry inherent in its structure. Lastly, the application of fuzzy logic, and the nature and structure of our particular implementation, should give rise to situations where multiple emotions have nonzero memberships simultaneously. Note that unlike Millenson, Scherer does not include as a function of the Geneva Emotion Wheel’s structure an intrinsic property of compound emotions. Rather, in this case, it is the fuzziness associated with environmental perception which gives rise to these complex solutions. Figure 16 demonstrates that the implementation provides such results, with over 80 % of samples providing nonzero results for two or more named emotions.

Considering Fig. 17, the important features are predominantly shared with Fig. 16, save that Fig. 17 demonstrates through it’s complete consistency with Fig. 16 that the symmetrical consistency is observed across both variables at the values presented. Once again, the named emotions triggered remain consistent with the structure outlined in Fig. 2, as is the order in which they are triggered. Moving on to consider Fig. 18, we present the case where Valence is both positive and of middling magnitude. In this case, we would anticipate across the range of Control values, all eight emotions associated with positive Valence to be triggered to a certain degree, which is to say Pride, Elation, Happiness, Satisfaction, Relief, Hope, Interest and Surprise. Figure 18 confirm this to be the case. Setting Valence as 0.5 prevents the prima facae analysis possible with Figs. 16 and 17 in terms of which emotions should be triggered at the highest intensity. As is shown when considering Surprise and Interest, it is Interest which enjoys a higher, earlier peak. This makes sense, however, when one considers the geometry of Fig. 2, whereby Interest more closely relates to a point of middling, positive Valence and extreme, negative Control.

Of particular interest are the membership spikes in Satisfaction and Relief, which occur when the point of input moves outside the third fuzzy region of each, while remaining within the extremes of the fourth, triggering a brief, sharp increase in membership. This is, again, a function of the squared membership functions that lie at the root of the aberrations discussed at the beginning of this subsection. That aside, Fig. 18 behaves much as we would expect. Unlike the case in Fig. 16, there are no positions within Fig. 18 which provide less than two emotions nonzero memberships at any given time. This is a result supported by the structure of the Geneva Emotion Wheel’s geometry, which demonstrates greater concentration of like emotions as input magnitude decreases. Similarly, in accordance with the geometry, membership of the named emotions behaves symmetrically about the Control mid-point. Figure 19, as with Fig. 17, provides useful information in the context that it supports all of the previous assertions regarding Fig. 18, while at the same time verifying that the symmetry of behaviour remains consistent across both input variables. Again, this is important as it demonstrates geometrical consistency with the Geneva Emotion Wheel upon which our implementation is based.

Future Work and Conclusions

Future work and exploration of these ideas will revolve around the application of one or more of the implementations presented here to influence the actions of an artificial agent in an effort to determine usefulness of these implementations in real-world behavioural simulation scenarios. Current work includes the exploration and expansion of all three of these implementations through type 2 fuzzy logic, an extension of fuzzy logic as it is presented in this paper. Following the conclusion of that work, comparisons and contrasts of behaviour between these type 2 implementations and the implementations presented here shall be made. This paper has presented fuzzy logic-based implementations of three mathematical models, based upon two thoroughly distinct psychological theories of emotion. It has provided a rationale for each mathematical interpretation, and an elementary overview of the psychology of the theories in question. The theories being wholly disparate in nature, direct comparison between them is not possible. That said, direct comparisons were provided in the context of the two implementations which shared a psychological basis. All three implementations were demonstrated to function from a numerical standpoint, with operational issues highlighted where appropriate. In addition, the behaviour of all three implementations was discussed in-depth, with graphical and numerical data provided where appropriate. It is envisioned that in future work the process of abstraction may be explored further. It by its nature implies a framework by which other psychologically ground theories of emotion might be explored. Developing such a framework requires a substantial effort but would provide an important contribution to computational emotions research.