Introduction

Along with the generation of uncertain data streams, more and more attention is paid to the mining of uncertain data streams. This need is due to the inherent uncertainties of data in many real-world applications, such as sensor network monitoring [1, 2] and moving object detection [3–5]. Since the intrinsic differences between uncertain and deterministic data streams, existing data mining algorithms on deterministic data streams cannot be applied to uncertain data streams. The mining tasks over uncertain data streams are much more complicated than mining task on deterministic data streams, because the possible world instances derived from the uncertain data stream expand exponentially.

Classification is considered as an important cognitive computation [6–10] task, which has drawn much attention. The objective is the creation of an target function, which maps each property set x to a predefined class label y. Due to inherent uncertainty and streams properties, the important challenge that classification over data streams mining is the uncertainty of data [11] and concept drift [12–16]. While the input data are uncertain, each uncertain tuple consists of several instances. These special properties of the uncertain data need to be considered in the process of classification, further complicating the classification process. Concept drift is the change of the data distribution, forcing changes in the classification model reflecting the drift. If the change in data distribution is ignored, inevitably, the accuracy of the classifier trained for the previous data will greatly decline. Therefore, the data streams classification algorithm research is focused on testing the new class and timely updating the classification model to adapt the new data distribution. Concept drift rate be loosely classified into two categories, namely emergent concept drift and gradual concept drift [17], in this paper, we only study gradual concept drift.

Motivation 1

(sensor data): Sensor networks are frequently used to monitor the surrounding environment. The monitoring range is covered by a number of individual sensors, each reporting its measurements to a central location. In the case of environmental monitoring sensor net, measurements may include temperature, humidity and air pressure. The true measured values cannot be accurately obtained due to limitations of the measuring equipment. Instead, sensor readings are send in order to approximate the true value, and a confidence in the measurement is often estimated based on its failure rate, leading to uncertain tuples, where multiple readings collected from a sensor at this location are instances of this uncertain tuple. An example of concept drift in this context includes the change of temperature due to the changes of the seasons.

Motivation 2

(stock data): Stock data streams come every day, which requires analyzing the data online with a timely manner. However, in order to protect the users’ privacy, the user’s data need to be blurred. Uncertain data streams are classified online, results are feeedback in time.

In the field of uncertain data mining, the presence of uncertainty can significantly affect the results of data mining [11]. Since the input data are uncertain, we should consider both the value and uncertainty of each uncertain tuple in the classification process. To the best of our knowledge, there is no existing method taking the uncertainty into account in the classification process for data mining in uncertain data streams.

Traditional classification algorithms are unable to deal with such challenges. In this paper, we investigate classification based on extreme learning machine (ELM) [18–28] of uncertain data streams. Our main contributions are:

  • We propose the weighted ensemble classifier based on ELM (WEC-ELM) algorithm, which can dynamically adjust the classifier and the weight of training data to solve the problem of concept drift.

  • Based on ELM and the uncertainty calculation method, we propose a two phase classification algorithm (UC-ELM) of uncertain data streams, which is able to balance the value and uncertainty of tuples, thus improving the effectiveness.

  • Because there is no real uncertain data set available, the data set we used in the experiments is synthesized from real data sets. We implement a series of experimental evaluations, showing that our methods are both effective and efficient.

The rest of the paper is organized as follows. We first introduce the ELM in “Brief of extreme learning machine” section. After that, “Problem definition” section defines our problem formally. We analyze the challenge of classification over uncertain data streams and develop the two algorithms, respectively, in “Classification algorithm” section. “Performance verification” section presents an extensive empirical study. In “Conclusions” section, we conclude this paper with directions for future work.

Brief of Extreme Learning Machine

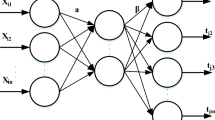
In this section, we present a brief overview of extreme learning machine (ELM), developed by Huang et al. [18, 28–31]. ELM is based on a generalized single-hidden-layer feedforward network (SLFN). In ELM, the hidden-layer node parameters are mathematically calculated instead of being iteratively tuned, providing good generalization performance at thousands of times higher speeds than traditional popular learning algorithms for feedforward neural networks [32]. The output function of SLFNs with L hidden nodes can be represented by

$$\begin{aligned} f_{L}(x)=\sum _{i=1}^{L}\beta _{i}g_{i}(x)=\sum _{i=1}^{L}\beta _{i}G(a_{i},b_{i},x),\quad x\in R^{d},\;\beta _{i}\in R^{m} \end{aligned}$$
(1)

where \(g_{i}\) denotes the output function \(G(a_{i},b_{i},x)\) of the ith hidden node. For additive nodes with activation function \(g,\,g_{i}\) is defined as

$$\begin{aligned} g_{i}=G(a_{i},b_{i},x)=g(a_{i}\cdot x+b_{i}),\quad a_{i}\in R^{d},\; b_{i}\in R \end{aligned}$$
(2)

For radial basis function (RBF) nodes with activation function \(g,\,g_{i}\) is defined as

$$\begin{aligned} g_{i}=G(a_{i},b_{i},x)=g(b_{i}\Vert x-a_{i}\Vert ),\quad a_{i}\in R^{d}, \; b_{i}\in R^{+} \end{aligned}$$
(3)

The above equation can be written compactly as:

$$\begin{aligned} H\beta =T \end{aligned}$$
(4)

where

$$\begin{aligned} H&= \left[ \begin{array}{c} h(x_1 ) \\ \vdots \\ h(x_N ) \\ \end{array} \right] = \left[ \begin{array}{c} G(a_1 ,b_1 ,x_1 ) \cdots G(a_L ,b_L ,x_1 ) \\ \vdots \\ G(a_1 ,b_1 ,x_N ) \cdots G(a_L ,b_L ,x_N ) \\ \end{array} \right] _{N \times L} \end{aligned}$$
(5)
$$\begin{aligned} \beta&= \left[ \begin{array}{c} \beta _1^T \\ \vdots \\ \beta _L^T \\ \end{array} \right] _{L \times m} \mathrm{and} \quad T = \left[ \begin{array}{c} t_1^T \\ \vdots \\ t_N^T \\ \end{array} \right] _{N \times m} \end{aligned}$$
(6)

\(H\) is called the hidden-layer output matrix of the \(SLFN\) [20, 32, 33]; the \(i\hbox {th}\) column of \(H\) is the ith hidden node output with respect to input \(x_{1},x_{2},\ldots ,x_{N}\ldots ,\,h(x)=G(a_{1},b_{1},x),\ldots ,\,g(a_{L},b_{L},x)\) is called the hidden-layer feature mapping. The ith row of \(H\) is the hidden-layer feature mapping with respect to the ith, input \(x_{i}:h(x_{i})\). It has been proved [31, 32] that from the interpolation capability point of view, if the activation function g is infinitely differentiable in any interval, the hidden-layer parameters can be randomly generated.

For the multiclass classifier with single output, ELM can approximate any target continuous function, and the output of the ELM classifier \(h(x)\beta\) can be as close as possible to the class labels in the corresponding regions [34]. The classification problem for the proposed constrained-optimization-based ELM with a single-output node can be formulated as

$$\begin{aligned} \mathrm{Minimize}:L_{P_\mathrm{ELM}}&= \frac{1}{2}\left\| \beta \right\| ^2 + C\frac{1}{2}\sum \limits _{i=1}^N {\xi _{i}^2} \nonumber \\ \mathrm{Subject\;to}:h(x_i )\beta&= t_i - \xi _i ,\quad i = 1, \ldots ,N \end{aligned}$$
(7)

where C is user-specified parameter. Based on the KKT theorem [35], training ELM is equivalent to solving the following dual optimization problem:

$$\begin{aligned} L_{D_\mathrm{ELM} } = \frac{1}{2}\left\| \beta \right\| ^2 + C\frac{1}{2}\sum \limits _{i = 1}^N {\xi _i^2 - \sum \limits _{i = 1}^N {\alpha _i (h(x_i )\beta - t_i + \xi _i)}} \end{aligned}$$
(8)

where each lagrange multiplier \(\alpha _{i}\) corresponds to the ith training sample. The KKT optimality conditions given in [35] are as follows:

$$\begin{aligned} \frac{\partial L_{D_\mathrm{elm}}}{\alpha \beta }&= 0\longrightarrow \beta =\sum _{i=1}^{N}\alpha _{i}h(x_{i})^{T}=H^{T}\alpha \end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial L_{D_\mathrm{elm}}}{\alpha \beta }&= 0\longrightarrow \alpha _{i}=C\xi _{i}, \; i=1,\ldots ,N \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial L_{D_\mathrm{elm}}}{\alpha \beta }&= 0\longrightarrow h(x_{i})\beta -t_{i}+\xi _{i}=0, \; i=1,\ldots ,N \end{aligned}$$
(11)

where \(\alpha =[\alpha _{1},\ldots ,\alpha _{N}]\).

For a multiclass classifier, ELM requires multioutput nodes instead of a single-output node. Under these conditions, the classification problem can be formulated as

$$\begin{aligned} \mathrm{Minimize}:L_{P_{ELM}}&= \frac{1}{2}\left\| \beta \right\| ^2 + C\frac{1}{2}\sum \limits _{i = 1}^N {\left\| \xi _{i} \right\| ^2 } \nonumber \\ \mathrm{Subject\;to}:h(x_i )\beta&= t_i^T - \xi _i^T ,\quad i = 1, \ldots ,N \end{aligned}$$
(12)

where \(\xi =[\xi _{i,1},\ldots ,\xi _{i,m}]^{T}\) is the training error vector of the \(m\) output modes with respect to the training sample \(x_{i}\). Similar as above, training ELM is equivalent to solving the following dual optimization problem:

$$\begin{aligned} L_{D_\mathrm{ELM} } = \frac{1}{2}\left\| \beta \right\| ^2 + C\frac{1}{2}\sum \limits _{i = 1}^N {\left\| {\xi _i } \right\| ^2 - \sum \limits _{i = 1}^N {\sum \limits _{j = 1}^m {\alpha _{i,j} (h(x_i )\beta _j - t_{i,j} + \xi _{i,j} )} } } \end{aligned}$$
(13)

where \(\beta _{j}\) is the vector of the weights linking hidden layer to the \(j\)-th output node and \(\beta =[\beta _{1},\ldots ,\beta _{m}]\).

There are many variants of ELM, such as Circular-ELM [36], which augments the standard ELM paradigm by introducing a structural enhancement derived from the CBP network. Circular-ELM proves effective in addressing the visual quality assessment problem, in which the input vector of a conventional multilayer perceptron (MLP) is augmented by one additional dimension, the circular input. Circular-ELM handles the actual mapping of visual signals into quality scores, successfully reproducing perceptual mechanisms. [37] proposed a novel model for ELMs, which exploits random projection (RP) techniques. A hidden layer performs an explicit mapping of the input space to a feature space; the mapping is not subject to any optimization, since all the parameters in the hidden nodes are set randomly. The output layer includes the only degrees of freedom, i.e., the weights of the links that connect hidden neurons to output neurons. The variants of ELM mentioned above all work on determine data.

[38] proposed classification algorithms based on ELM to conduct classification over uncertain data. Using a bound-based approach, they implemented the binary and multiclass classification over uncertain data objects. They also extended the proposed algorithms to classification over uncertain data in a distributed environment based on OS-ELM and Monte Carlo theory. However, this algorithm is suitable for static data. This means that the algorithm don’t have the ability to incremental updating. If there are changes in the underlying data objects, the algorithm must be executed from scratch, leading to performance degradation when operated on uncertain data streams.

Problem Definition

Uncertain Data Streams Model We assume that the uncertain data streams consist of a set of \(n\,d\)-dimensional uncertain tuples \(x_{1},\,x_{2},\,\cdots ,\,x_{i},\,\cdots ,\,x_{n}\), arriving with time stamp \(T_{1},\,T_{2},\,\cdots ,\,T_{i},\,\cdots ,\,T_{n}\), for any \(i<n,\,T_{i}<T_{n}\). Each uncertain tuple has \(m\) possible instances and existence probabilities i.e. \(x_{i}=\{(x_{i}^{1},p_{x_{i}^{1}}),(x_{i}^{2},p_{x_{i}^{2}}), \cdots , (x_{i}^{j},p_{x_{i}^{j}}), \cdots , (x_{i}^{m},p_{x_{i}^{m}})\}\), \(\sum _{j=1}^{m}p_{x_{i}^{j}}=1\), all instances are mutually independent. Each instance of uncertain tuple \(x_{i}\) is a \(d\)-dimensional vector. Thus each instance can be be viewed as a multi-dimension data that is input into ELM.

As an example, Table 1 shows partial uncertain tuples in streams, \(x_{1},\,x_{2},\,x_{3}\) and \(x_{4}\), the instances of each uncertain tuple are shown in column instances, and the probabilities of instances are shown in column probability. Figure 1 maps these uncertain tuples into a 2D coordinate. For simplicity, we only consider two attributes in the example. Let the shaded area and the white area represent two classes, respectively, and each of the instances of uncertain tuple is to be classified into the corresponding category. When all instances of the same uncertain tuple are classified into the same class, then the uncertain tuple should belong to that particular class, as \(x_{1},\,x_{2},\,x_{3}\). However, when instances in the same uncertain tuple are classified into different classes, then we will consider probability of each instance, as \(x_{4}\). For an uncertain dataset, we need to consider all instances to determine which class the uncertain tuple belongs to.

Concept drift: Comparing with the old dataset, in the new dataset, the related features are changed, which will lead to the concept of the characteristics to be different. Specially, the concept drift discussed in this paper refers that the classification disappears, new classification emerges, or the old classification shifts too much.

Table 1 Example of partial uncertain data tuple
Full size table
Fig. 1
figure 1

Mapping uncertain tuples to a 2D-space

Full size image

Binary Classification of ELM

For example in Fig. 1, instances in all uncertain tuples are learned using ELM to obtain binary classes.

Theorem 1

Let instance \(x_{i}^{j}\) denote the \(j\) -th instance of uncertain tuple \(x_{i},\,p_{x_{i}^{j}}\) is probability associated with \(x_{i}^{j}\) . Class set consists of two classes \(n\) and \(m\) . If \(p_{x_{i}^{j}}\ge 0.5\) and \(x_{i}^{j}\) belongs class \(n\) , then tuple \(x_{i}\) is in class \(n\) , otherwise, \(x_{i}\) belongs class \(m\).

For binary classification case, ELM needs only one output node (\(m=1\)), and the decision function of ELM classifier is:

$$\begin{aligned} f(x)=sign\left( \sum _{j=1}^{L}\beta _{i}G(a_{i},b_{i},x)\right) =sign(\beta \cdot h(x)) \end{aligned}$$

For an uncertain data tuple, its instances are classified into different classes, i.e., in tuple \(x_{4}\). Let \(c_{s}\) and \(c_{w}\) be class labels of the shaded area and the white area, respectively. \(x_{4}^{1}\) and \(x_{4}^{3}\) are in class \(c_{w},\,x_{4}^{2}\) is in class \(c_{s}\). The membership of class will be determined by the class, which has a high probability. To simplify this computing, we construct a function as follows:

$$\begin{aligned} f(x_{i})= \left\{ \begin{array}{l} 1,p_{x_{i}^{j}}\cdot sign(\beta \cdot h(x))\ge 0.5 \\ 0,p_{x_{i}^{j}}\cdot sign(\beta \cdot h(x))< 0.5 \\ \end{array} \right. \end{aligned}$$

Multiclass Classification of ELM

In this subsection, we introduce multiclass classification of ELM, the decision function is:

$$\begin{aligned} f(x)=sign\left( h(x)H^{T}\left( \frac{1}{C}+HH^{T}\right) ^{-1}T\right) \end{aligned}$$
(14)

The expected output vector is:

$$\begin{aligned} T=\left[ \begin{array}{l} t_{1} \\ \vdots \\ t_{L}\\ \end{array} \right] \end{aligned}$$

For multiclass cases, \(m\) is the number of classes and output nodes of hidden layer. The predicted class label of a given testing sample is the index number of the output node, which has the highest output value for the given testing sample. Let \(f_{k}(x_{i}^{j})\) denote the output function of the \(k\)-th \((1\le k\le m)\) output node, i.e., \(f(x_{i}^{j})=[f_{1}(x_{i}^{j}),\ldots , f_{ m}(x_{i}^{j})]\), then the predicted class label of sample \(x_{i}^{j}\) is:

$$\begin{aligned} label(x_{i}^{j})=arg \max \limits _{\tau \in (1,\ldots, m)} f_{\tau }(x_{i}^{j}) \end{aligned}$$

For multiclass classifier with multioutputs, it is obviously that the Theorem 1 cannot be applied to uncertain multiclass classification. For example, we assume that uncertain tuples are classified into three categories. If all probabilities in three classes are smaller than 0.5, Theorem 1 binary classification cannot be used for multiclass classification. Therefore, we revise Theorem 1 as follows:

Definition 1

(Probability of a classification instance) Let \(x_{i}^{j}\) denote the \(j\)-th instance of uncertain tuple \(x_{i},\,p_{x_{i}^{j}}\) is probability associated with \(x_{i}^{j}\). Given a number of classes \(L\), ELM can classify the instance \(x_{i}^{j}\) into \(L\) classes. If the instance \(x_{i}^{j}\) belongs to the class \(c_{l},\,(1\le l\le L),\,p_{x_{i}^{j}}^{c_{l}}\) is probability of instance \(x_{i}^{j}\) belonging to the class \(c_{l}\), then \(p_{x_{i}^{j}}^{c_{l}}=p_{x_{i}^{j}}\).

Definition 2

(Probability of classification uncertain tuple ) Let \(S_{x_{i}}\) be the set of instances of uncertain tuple \(x_{i}\), each uncertain tuple has m possible instances and existence probabilities, i.e., \(x_{i}=\{(x_{i}^{1},p_{x_{i}^{1}}),(x_{i}^{2},p_{x_{i}^{2}}),\,\ldots ,\,(x_{i}^{j},p_{x_{i}^{j}})\), \(\ldots ,\,(x_{i}^{m},p_{x_{i}^{m}})\},\,\sum _{j=1}^{m}p_{x_{i}^{j}}=1\), all instances are mutually independent. Let \(p_{x_{i}}^{c_{l}}\) be the probability of uncertain tuple \(x_{i}\) belonging to the class \(c_{l},\,p_{x_{i}}^{c_{l}}\) is sum of probabilities the instances which belong to class \(c_{l}\), then

$$\begin{aligned} p_{x_{i}}^{c_{l}}=\sum _{x_{i}^{j}\in S_{x_{i}}}p_{x_{i}^{j}}^{c_{l}} \end{aligned}$$

Definition 3

(Classification of uncertain data) Let \(S_{c}\) be the set of \(L\) classes, \(c_{l}\) be the class label, \((1\le l\le L)\). \(x_{i}\) is uncertain tuple. If \(p_{x_{i}}^{c_{l}}\ge \forall p_{x_{i}}^{c_{j}} (1\le j\le L,j\ne l)\), then uncertain tuple \(x_{i}\) belongs class \(c_{l}\).

For example, in Table 1, according to Definition 2 and Definition 3, let \(c_{s}\) and \(c_{w}\) be class labels of the shaded area and the white area, respectively. \(p_{x_{4}}^{c_{s}}=p_{x_{4}^{2}}^{c_{s}}=p_{x_{4}^{2}}=0.1\), and \(p_{x_{4}}^{c_{w}}=p_{x_{4}^{1}}^{c_{w}}+p_{x_{4}^{3}}^{c_{w}}=p_{x_{4}^{1}}+p_{x_{4}^{3}}=0.6+0.3=0.9\), then \(x_{4}\) belongs to class \(c_{w}\).

Theorem 2

Let \(x_{i}\) be an uncertain tuple, which consist of \(m\) instances and existence probabilities, i.e., \(x_{i}=\{(x_{i}^{1},p_{x_{i}^{1}}),(x_{i}^{2},p_{x_{i}^{2}}), \ldots , (x_{i}^{j},p_{x_{i}^{j}}), \ldots , (x_{i}^{m},p_{x_{i}^{m}})\},\,\sum _{j=1}^{m}p_{x_{i}^{j}}=1\) , and all instances are mutually independent. Let \(p_{x_{i}}^{c_{l}}\) be the probability of uncertain tuple \(x_{i}\) belongs to the class \(c_{l}\) . If \(p_{x_{i}}^{c_{l}}\ge 0.5\) , then uncertain tuple \(x_{i}\) belonging to the class \(c_{l}\).

According to the Theorem 2, when a calculated classification probability for a certain class exceeds 0.5, probabilities for the other classes do not need to be calculated. Thus, unnecessary calculations are then avoided, thereby enhancing efficiency. Based on the definition of classification of data stemming from uncertain data, we define the problem as follows:

Problem: Given uncertain data streams containing training data and testing data, output the class label for each uncertain data tuple while considering the risk of concept drift.

Classification Algorithm

In this section, we first introduce the weighted ensemble classifier based on ELM (WEC-ELM) algorithm, which is suitable for application in uncertain data and in the presence of concept drift. Secondly, we propose the uncertainty classifier based on ELM (UC-ELM) algorithm, which not only considers the value of the tuple, but also consider the uncertainty of the tuple.

Ensemble Classifier Based on ELM

In this section, a weighted ensemble classifier for uncertain data streams based on the ELM (WEC-ELM) algorithm is proposed. It consists of a number of component classifiers. The ordinary methods do not set the weights of training data; this section briefly describes the differences between existing methods. We use the ensemble classifier to distinguish the weighted training data, some tuples are classified correctly, and some are classified wrongly. The tuples that are classified incorrectly may represent the direction of the concept drift. These tuples need to be distinguished when the new classifier is created.

While concept drift occurs, a new component classifier needs to be trained and added to the ensemble classifier. If the number of component classifiers reached a preset maximum, the worst-performing component classifier is removed from the ensemble classifier, and a new component classifier is created by as trained by the new tuple. The standards to judge the classifier performance are accuracy of the previously classified data.

We first introduce the definition of the weight of a classifier and the weight of an instance which employs the idea of [39] as follows:

Definition 4

(Error rate) Let \(x_{i}^{j}\) be instance, \(C_{n}\) be the classifier label, \(Err_{C_{n}}^{x_{i}^{j}}\) is error rate of \(C_{n}\). If the instance \(x_{i}^{j}\) is classified incorrectly by classifier \(C_{n}\) then \(Err_{C_{n}}^{x_{i}^{j}}=1\), otherwise, \(Err_{C_{n}}^{x_{i}^{j}}=0\).

Definition 5

(Error of a classifier) Let \(W_{x_{i}^{j}}\) be the weight of uncertain instance \(x_{i}^{j},\,\lambda\) be the number of instances of current data chunk, \(E_{C_{n}}\) be the error of classifier \(C_{n}\), then

$$\begin{aligned} E_{C_{n}}=\frac{\sum _{i=1}^{\lambda }W_{x_{i}^{j}}\times Err_{C_{n}}^{x_{i}^{j}}}{\sum _{i=1}^{\lambda }W_{x_{i}^{j}}} \end{aligned}$$

Before the instance is classified, the weight of instance \(W_{x_{i}^{j}}\) is \(1\), so

$$\begin{aligned} E_{C_{n}}=\frac{\sum _{i=1}^{\lambda }Err_{C_{n}}^{x_{i}^{j}}}{\lambda } \end{aligned}$$

The number of instances which are classified incorrectly by classifier \(C_{n}\) is larger; the error of classifier \(C_{n}\) is larger. Otherwise, if the classifier \(C_{n}\) classify all instances correctly, then the error of classifier \(C_{n}\) is \(0\). If the classifier \(C_{n}\) classify all instances incorrectly, then the error of classifier \(C_{n}\) is \(1\), i.e., \(E_{C_{n}}=1\). The weight of each classifier is inversely proportional to the Error of classifier:

Definition 6

(Weight of classifier) Let \(W_{C_{n}}\) be the weight of classifier \(C_{n},\,MSE_{r}\) be random prediction mean square error of classifier and \(E_{C_{n}}\) be the error of classifier \(C_{n}\), then

$$\begin{aligned} W_{C_{n}}=MSE_{r}-E_{C_{n}} \end{aligned}$$

where \(MSE_{r}=\sum _{C_{n}}P(C_{n})(1-P(C_{n}))^{2},\,P(C_{n})\) is the proportion of each class in the data distribution. It follows that \(P(C_{n})\in (0,1)\). The idea of fuzzy math is imported to calculate the fuzzy rate of instance classification:

Definition 7

(Fuzzy instance classification) Let \(W_{C_{n}}\) be the weight of classifier \(C_{n},\,N\) be number of classifiers and \(f_{x_{i}^{j}}\) be the fuzzy classification, then

$$\begin{aligned} f_{x_{i}^{j}}=1-\frac{\sum _{n=1}^{N}W_{C_{n}}\times Err_{C_{n}}^{x_{i}^{j}}}{\sum _{n=1}^{N}W_{C_{n}}} \end{aligned}$$

We update the weight of instance based on the classified result.

Definition 8

(Weight of an instance) Let \(W_{C_{n}}\) be the weight of classifier and \(C_{n},\,f_{x_{i}^{j}}\) be the fuzzy classification, then

$$\begin{aligned} W_{x_{i}^{j}}= W_{x_{i}^{j}}\times (1-f_{x_{x}^{j}})= W_{x_{i}^{j}}\times \frac{\sum _{n=1}^{N}W_{C_{n}}\times Err_{C_{n}}^{x_{i}^{j}}}{\sum _{n=1}^{N}W_{C_{n}}} \end{aligned}$$

For each instance, the weight will be updated according to the fuzzy rate for correctly classified. The weight of the instance which is classified incorrectly is small, and the weight of instance which is classified wrongly is larger. We should pay attention to the instances which have larger weight, they may represent the direction of concept drift. When we need to retrain the classifier, the instances which have larger weight should be preferred. Figure 2 shows the framework of WEC-ELM, and the update is as follows:

Initialize: We assume that the data streams arrive within chunks, the number of tuples in each chunk is \(\lambda\). The first \(N\) chunks are selected to train \(N\) component classifiers based on ELM which form the ensemble classifier together.

Fig. 2
figure 2

Ensemble classifier framework

Full size image

Update: When the uncertain data chunk \(S_{N+1}\) arrives, the weight of each instance before being classified is \(1\). Each instance in data chunk \(S_{N+1}\) is classified using \(N\) existing component classifiers; the error rate \(E_{C_{n}}\) is computed according to the Definition 5. The maximum error rate is the maximum value of error rate of \(N\) Component Classifiers. If the maximum error rate is larger than a user-specified threshold \(E\), it means that the component classifier whose error rate is the maximum error rate which is not suitable for the current data, in other words, the concept drift may occur. The component classifier with the largest error rate will be deleted, and a new component classifier is created to take its place. The new weights of \(N\) classifiers \(W^{'}_{C_{n}}\,(1\le n\le N)\) are calculated according to the Definition 6. Next, the weight of each instance is updated according to the Definition 8. In order to get a better classifier, we use the instances in set \(S_{N+1}^{'}\) to train the new classifier. The set \(S_{N+1}^{'}\) consists of those instances whose weights are larger than a user-specified threshold \(W_{\rm instance}\). The new component classifier instead of being deleted is added to the integrated classifier, ready for classifying the next chunk uncertain data.

Uncertainty Classifier Based on ELM

In the field of uncertain data mining, tuple values are not the only issue to be considered. The presence of uncertainty can significantly affect the results of mining process [11]. The uncertainty classifier based on ELM (UC-ELM) takes both the value and the uncertainty of the tuple into account. Our method employs a two phase classification approach. First of all, according to the value of uncertain tuple, the K-classes set is composed, and next, it is decided which class absorbs the new tuple based on the uncertainty of the tuple. The definitions of instance uncertainty and tuple uncertainty [11] are as follows:

Definition 9

(Instance uncertainty) We assume that the uncertain tuple \(x_{i}\) consists of some possible instances; each possible instance consists of d-dimension value and probability of existence, i.e., \(x_{i}=\{(x_{i}^{1},p_{x_{i}^{1}}),(x_{i}^{2},p_{x_{i}^{2}})\), \(\ldots ,\,(x_{i}^{j},p_{x_{i}^{j}}), \ldots ,\,(x_{i}^{m},p_{x_{i}^{m}})\}\), where \(\sum _{j=1}^{m}p_{x_{i}^{j}}=1\), all instances are mutually independent. The instance uncertainty is defined are as follows:

$$\begin{aligned} U(x_{i}^{j})=\log _{2}\left( \frac{1}{p_{x_{i}^{j}}}\right) = -\log _{2}(p_{x_{i}^{j}}) \end{aligned}$$

Definition 10

(Tuple uncertainty) We assume that the uncertain tuple \(x_{i}\) has m possible instances and existence probabilities, where \(x_{i}=\{(x_{i}^{1}\), \(p_{x_{i}^{1}})\), \((x_{i}^{2},\,p_{x_{i}^{2}}), \ldots , (x_{i}^{j},p_{x_{i}^{j}}), \ldots , (x_{i}^{m},p_{x_{i}^{m}})\}\), and \(\sum _{j=1}^{m}p_{x_{i}^{j}}=1\), the uncertainty of tuple \(x_{i}\) is the expected value of its possible instance, denoted as follows:

$$\begin{aligned} U(x_{i})=-\sum _{i=1}^{m}p_{x_{i}^{j}}\times \log _{2}(p_{x_{i}^{j}}) \end{aligned}$$

The uncertainty of a class is determined by the uncertainties of the tuples belonging to that the class:

Definition 11

(Class uncertainty) We assume that the class \(c_{n}\) consists of \(\mu\) uncertain tuples, the uncertainty of class \(c_{n}\) is the average value of the uncertainty of each tuple in the class \(c_{n}\), defined as follows:

$$\begin{aligned} U(c_{n})=\frac{\sum _{i=1}^{\mu }U(x_{i})}{\mu } \end{aligned}$$

In order to avoid unnecessary computation, we will not compare all classes to decide which class will absorb the new tuple. Instead, we proposed a two phase method to handle this problem, choosing the optimal cluster.

Definition 12

(K-classes) We assume that there are L classes in the classes set, \(P_{x_{i}}^{c_{n}}\) denotes the probability of the tuple \(x_{i}\) belongs to the class \(c_{n}\,(1\le n \le L)\). Based on \(P_{x_{i}}^{c_{n}}\), the L classes in descending order select the top k classes as the K-classes set.

Figure 3 shows the framework for UC-ELM, which consists of two phases:

Initialize: The first N uncertain tuples to arrive are seen as the initialisation data set. The uncertain tuples in the initialization data set are used to train the ELM classifier.

Fig. 3
figure 3

Uncertainty classifier framework

Full size image

Update: When a new uncertain tuple \(x_\mathrm{new}\) arrives, the uncertainty of tuple \(x_\mathrm{new}\) is calculated by Definition 10. Each instance of tuple \(x_\mathrm{new}\) is classified by the ELM classifier. Using Definition 2, we obtain the probability of the new tuple \(x_\mathrm{new}\) belonging to each class. According to the Definition 12, the classes in descending order according to the probability of the new tuple \(x_\mathrm{new}\) belongs to each class select the top k classes as K-classes set; then, we retrieve the K-classes set for tuple \(x_\mathrm{new}\). According to the Definition 11, we select a class, which will reduce the uncertainty the most. In other words, the goal is to select one class with maximum value of \(\bigtriangleup U(c)=U(c)-U(c\bigcup \{x_{i}\})\), where c is any class in the K-classes set, then the tuple \(x_\mathrm{new}\) is absorbed by that class. The uncertainty of the class is updated after absorbing the new tuple \(x_\mathrm{new}\). In order to solve the concept drift, a counter n is initialized to 0. Furthermore, let \(p_{x_\mathrm{new}}^{c}\) denote the probability of \(x_\mathrm{new}\) belonging the class which absorbs the new tuple \(x_\mathrm{new}\), if \(p_{x_\mathrm{new}}^{c}<\varphi\), then \(n=n+1\), where \(\varphi\) is user-specified threshold. Until \(n=N\), where N is another user-specified threshold; we believe concept drift will occur, and the existing classifier is not suitable for current data; then, the classifier is deleted. Based on the recent training data set, a new classifier is trained.

Performance Verification

This section compares the performance of several algorithms (Support Vector Machine (SVM) [40], Dynamic Classifier Ensemble (DCE) [41], WEC-ELM, and UC-ELM,) in the real-world benchmark regression and multiclass classification data sets. We assume that all data arrive as chunks from a stream. All the evaluations are carried out in Windows 7, MATLAB R2012B, running on a Intel Core(TM) i5-2450M running at 2.50GHz and 4GB RAM.

Data Set and Experimental Setup

Because there is no real uncertain data set available, the data sets we used in the experiments are synthesized from real data sets. The values of each tuple of certain data set are fitted to four instances with four probabilities, respectively, and the expected value of the four values of instances is equal to the original value in the certain data set. All source data sets were taken from the UCI machine learning repository. Table 2 describe the data sets in detail.

Table 2 Uncertain data set
Full size table

  • Magic04: 3,000 uncertain tuples are synthesized, each of which consists of 4 instances; the probability of each instance is randomly generated where the sum of probabilities of the instances in the same tuple is 1. The first 500 tuples are used as training data and are divided into 5 chunks; each of which contains 100 tuples, to train 5 classifiers, respectively. The others are used as testing data and arrive in a stream pattern, where each chunk contains 100 tuples.

  • Waveform: 1,200 uncertain tuples are synthesized, each of which consists of 4 instances; the probability of each instance is randomly generated where the sum of probabilities of the instances in the same tuple is 1. The first 750 tuples are used as training data and are divided into 5 chunks; each of which contains 150 tuples, to train 5 classifiers, respectively. The others are used as testing data and arrive in a stream pattern, where each chunk contains 150 tuples.

  • Pendigits: 2,000 uncertain tuples are synthesized, each of which consists of 4 instances; the probability of each instance is randomly generated where the sum of probabilities of the instances in the same tuple is 1. The first 1,000 tuples are used as training data and are divided into 5 chunks; each of which contains 200 tuples, to train 5 classifiers, respectively. The others are used as testing data and arrive in a stream pattern, where each chunk contains 200 tuples.

  • Letter: 5,000 uncertain tuples are synthesized, each of which consists of 4 instances; the probability of each instance is randomly generated where the sum of probabilities of the instances in the same tuple is 1. The first 1,000 tuples are used as training data and are divided into 5 chunks; each of which contains 200 tuples, to train 5 classifiers, respectively. The others are used as testing data and arrive in a stream pattern, where each chunk contains 200 tuples.

  • Pageblocks: 1,300 uncertain tuples are synthesized, each of which consists of 4 instances; the probability of each instance is randomly generated where the sum of probabilities of the instances in the same tuple is 1. The first 500 tuples are used as training data and are divided into 5 chunks; each of which contains 100 tuples, to train 5 classifiers, respectively. The others are used as testing data and arrive in a stream pattern, where each chunk contains 100 tuples.

In the experiments, we employ SVM [40] and DEC [41] as a competitive method. DEC is a recently proposed classifier ensemble for uncertain data streams classification. In order to show the performance of the ELM classifier, we use three different activate the functions (sig, hardlim and sin) to execution algorithm in the experiments. The number of classes of Magic04 is too small to run UC-ELM, so the UC-ELM algorithm run on Waveform data set and Pendigits. The default parameter settings: \(E=70\,\%, K=2\).

Efficiency Evaluation

Firstly, we evaluate the efficiency of our methods. Table 3 shows the training time among SVM, DEC, WEC-ELM and UC-ELM. We can see that training time of WEC-ELM and UC-ELM is shorter than SVM and DEC. Table 4 shows the testing time for SVM, DEC, WEC-ELM and UC-ELM. As we expect, WEC-ELM and UC-ELM are faster than DEC.

Table 3 Training time comparison of SVM, DEC, WEC-ELM and UC-ELM
Full size table
Table 4 Testing time comparison of SVM, DEC, WEC-ELM and UC-ELM
Full size table

Accuracy Evaluation

Table 5 shows the accuracy rate for SVM, DEC, WEC-ELM and UC-ELM with five data sets. We adopt the traditional learning principle in the training phase. We compare the accuracy among SVM, DEC, WEC-ELM and UC-ELM as shown in Table 5. It can be seen that ELM can always achieve comparable performance as SVM and DEC. Seen from Table 5, different functions of ELM can be used in different data set in order to have similar accuracy in different size of data sets, although any output function can be used in all types of data sets. We can see that WEC-ELM and DEC performs as good as SVM.

Table 6 shows the number of updates among SVM, DEC, WEC-ELM and UC-ELM with five data sets. In WEC-ELM algorithm, since concept drift occurs, at least one component classifier is not suitable for the current data because of the concept drift. The worst-performing component classifier is deleted; the new component should be trained based on the current data and be added to ensemble classifier. In UC-ELM algorithm, when the counter is maximum value, the classifier should be deleted; we should train classifier according to current data. Due to the number of updates of WEC-ELM is more than UC-ELM algorithm, so UC-ELM is faster than WEC-ELM.

Table 5 Accuracy comparison for SVM, DEC, WEC-ELM and UC-ELM
Full size table
Table 6 Number of updates comparison of SVM, DEC, WEC-ELM and UC-ELM
Full size table

Uncertainty Evaluation

To the best of our knowledge, there is no existing standard for the evaluation of uncertain data streams classification. Due the nature of uncertain data, we propose the evaluation criteria of uncertain data classification based on [11]. Given a set of classes \(c_{l}\,(1\le l\le L)\) and corresponding uncertainty is \(U(c_{l}),\,UM\) denote the uncertainty of the result of classification, \(UM=\frac{1}{L}\sum _{1}^{L}U(c_{l})\). \(UM\) is a positive number that allows comparison of the variation of classes that have significantly different tuples. In general, the smaller the \(UM\) value is, the greater quality of the classification result, as the Table 7 shows that the UC-ELM performs better than the other methods. The UC-ELM takes into account the uncertainty of the data tuples in order to decide the assignment of uncertain tuples to classes.

Table 7 Uncertainty comparison of SVM, DEC, WEC-ELM and UC-ELM
Full size table

Conclusions

In this paper, we studied the problem of classification based on ELM over uncertain data streams. We first proposed a weighted ensemble classifier based on ELM (WEC-ELM), which can dynamic adjust the classifier and the weight of training uncertain data to solve the problem of concept drift. To get better classification results for uncertain data, an uncertainty classification based on ELM (UC-ELM) is proposed, which can balance the value and uncertainty of tuples. Finally, experiments were conducted on real data, which showed that the algorithms proposed in this paper are efficient and are able to deal with data streams in a real-time fashion.

An interesting direction for future work is classification on high-dimensional uncertain data. Another direction for future work is the classification for uncertain data streams in distributive environment.