Introduction

Recent advancements in communication technologies (i.e., Internet, mobile communication) permit easy intrusion to information communicated, and hence, important information has to be protected from threats and malicious actions. Steganography provides a high level of security for secret information transmitted over these communication channels. In steganography, secret messages are embedded in digital media files, such as images, video, or audio, by slightly modifying them. These digital media files are commonly referred to as cover objects, and the modified steganographic signal is statistically undetectable from the original cover signal.

Steganalysis is a powerful tool to detect the presence of secret hidden data in an object. The steganalysis problem can be formulated as a supervised classification problem and solved using machine learning approaches. The performance of machine learning approaches for steganalysis is highly influenced by the feature extraction and the nature of the classification algorithm. Earlier work uses higher order moments of coefficients obtained by transforming an image using quadratic mirror filters [8], 18 binary similarity metrics [1], 23 discrete cosine transform features [10], 27 higher order moments of wavelet coefficients [11], etc. However, for efficient steganalysis, using a higher dimensional feature vector becomes essential. The feature set designed for JPEG images described in [26] used 274 features and was later extended to twice its size [22] by Cartesian calibration, while 324- and 486-dimensional feature vectors were proposed in [42] and [4], respectively. Other higher dimensional feature extraction techniques for steganalysis can be found in [5, 23, 25, 43, 44].

The functional relationship between the features and class label can be approximated using machine learning approaches. The high dimensional features and growing image database require a machine learning approach which requires smaller training time with better generalization ability. The recently developed neural network learning algorithm, namely extreme learning machine (ELM) [14, 15], is computationally less intensive and has the better generalization ability. Hence, in this work, we use ELM for steganalysis. The ELM is a feed-forward neural network with a single hidden layer, where the input weights and bias are selected randomly, and the output weights are estimated analytically. ELM has been developed based on the earlier findings that a neural network with at most N hidden neurons is sufficient to learn a function with N samples [13, 16, 17, 20]. It has been shown that the learning mechanism in ELM is similar to brain learning without the need of knowing the actual activation function of living brain neurons [20].

Extreme learning machine [14, 15] is a single hidden-layer feed-forward neural network that assumes randomly generated input parameters, based on which the output weights are calculated analytically. Thus, ELM requires lesser training time and is hence computationally efficient. Several variants of the ELM algorithm are available in the literature, and an extensive review of the ELM methods is presented in [18]. The ELM classifiers available in the literature include the k-fold selection scheme ELM [31, 32] and the real-coded genetic algorithm ELM [31]. Similarly, a few fast-learning ELM classifiers have been developed in the complex domain, and they include the phase-encoded complex-valued ELM and the bilinear branch-cut complex-valued ELM [34], the fast-learning fully complex-valued neural classifier [35], the circular complex-valued ELM classifier [36], and meta-cognitive ELM [37]. Recently, it has been shown in [19] that ELM provides a unified learning platform with a widespread type of feature mappings and can be applied to solve both regression and multi-class classification applications directly. Regression and multi-class classification problems can be solved by using Fuzzy ELM [27] and incremental learning [9]. ELM is successfully used in intrusion detection [6], bioinformatics [29, 45], image/video processing [7, 31, 40], and control [28]. The generalization performance of the cognitive ensemble of ELM classifier is better than a single ELM classifier [38] for various applications.

In general, machine learning algorithm uses perception to extract the knowledge from the data. Proposed learning algorithm selects appropriate samples based on the current knowledge to learn efficiently. This process emulates the human metacognition. The proposed approach uses an ELM ensemble to learn the samples (knowledge representation using ELM classifier). The ensemble process uses appropriate sample/classifier selection based on the knowledge content in the current ELM classifier. The self-regulation in sample selection enables proposed classifier to perform better than other classifiers. Cognitive principals have been used for classification of social media affective information [12], of natural language concepts [2], of handwritten text [3], and offline–online personal photos [46].

However, as one would expect, owing to the random initialization of the input parameters, the performance of ELM algorithm is affected by the choice of the input parameters. Hence, there is a need for a cognitive machine learning algorithm with self-realization [21] that is capable of learning from observations of its own knowledge [39]. Moreover, it has been shown in the literature that the risk-sensitive hinge loss error function estimates the posterior probability more accurately than the mean-squared error function in classification problems. In this paper, we address the above requirements by developing a cognitive ensemble of ELM classifiers based on the risk-sensitive hinge loss error function and use the classifier to perform steganalysis. The input parameters of each individual ELM classifier in the cognitive ensemble are initialized in different regions of the domain considered. Thus, their performance varies widely. Samples that are repeatedly correctly classified are labeled as winning samples, and samples that are misclassified by the majority of the classifiers are labeled as losing samples. Based on the region of initialization, the losing samples are classified correctly only by a few classifiers. Hence, a cognitive ensemble of ELM classifiers combines the outputs of individual classifiers by obtaining the weighted sum of outputs of these classifiers for all the samples. In this process, the classifiers that classify only the winning samples correctly are discarded from the pool. Since the cognitive ensemble of ELM classifiers is capable of choosing the participating networks and their weights, it is referred to as, “cognitive ensemble of ELM classifier.” This cognition enables improved performance of the cognitive ensemble of ELM classifier compared to each individual ELM.

We study the performance of the cognitive ensemble of ELM classifiers on a set of benchmark binary classification problems from the UCI machine learning repository [41], in comparison with support vector machine classifier and ELM classifier. Next, we use the cognitive ensemble ELM to solve steganalysis problems. Here, the performance of the cognitive ensemble of ELM classifier is compared to SVM, ELM and the ensemble of base classifier that is the best performing classifier available in the literature for this data set. To understand the statistical significance of the classifiers, we also perform a binomial test using the cognitive ensemble of ELM classifiers as the base classifier. Performance study results also show that the cognitive ensemble of ELM classifiers outperforms the single ELM and ensemble of support vector machine classifier [24].

The paper is organized as follows. In “Cognitive Ensemble of Extreme Learning Machine Classifier” section, the algorithm of ELM classifier is presented and the hinge loss error based cognitive ensemble of ELM classifier is introduced. “Performance Study of Cognitive Ensemble of ELM Classifier” section presents the performance study of the cognitive ensemble ELM with other classifiers available in the literature on benchmark classification problems and steganalysis data sets. Finally, fourth section summarizes the main “Conclusions” from the study.

Cognitive Ensemble of Extreme Learning Machine Classifier

In this section, we first present the learning algorithm of ELM classifier and next describe the risk-sensitive hinge loss function-based cognitive ensemble ELM.

Extreme Learning Machine

ELM is a single hidden-layer feed-forward neural network. The input weights and bias of the hidden neurons in ELM are assigned randomly, and the output weights are computed analytically. ELM provides a unified framework to solve both regression and classification problems [19]. As steganalysis is solved as a classification problem, in this paper, ELM has been used as a classifier. The classification problem can be defined as follows: Given a training data set with N samples, \(\left\{ \left( {\mathbf{x}}^1,c^1\right) ,\ldots ,\left( {\mathbf{x}}^t,c^t\right) ,\ldots ,\left( {\mathbf{x}}^N,c^N\right) \right\}\), where \({\mathbf{x}}^t \in {\mathfrak{R}}^m\) are the m-dimensional real-valued input features of t-th observation and \(c^t \in \{1,2,\ldots ,C\}\) is its class label. The coded class label \({\mathbf{y}}^t\) are obtained using:

$$\begin{aligned} y_k^t = \left\{ \begin{array}{ll} 1, &{}\quad {\text{ if }}\; c_t=l, \\ -1, &{}\quad {\text{ otherwise}}, \\ \end{array} \right. \quad k=1,2,\ldots ,C \end{aligned}$$
(1)

Now, the classification problem can be viewed as approximating the decision function (\({\mathbb{F}}\)) that maps the input features to the coded class labels, i.e., \({\mathbb{F}}: {\mathfrak{R}}^m \rightarrow {\mathbb{C}}^{C}\) as close as possible, and then predicting the class labels of new, unseen samples with certain accuracy.

As there are m input features and C classes, the ELM used to solve the problem has m input neurons and C output neurons. Let the number of hidden neurons be L. The neurons in the input and output layer of the ELM are linear, while the neurons in the hidden layer of ELM employ Gaussian activation function. Thus, the response of the j-th hidden neuron for the t-th sample (\(h_j^t\)) is given by:

$$\begin{aligned} h_j^t= \exp\left( -\left( \frac{({\mathbf{x}}^t-{\mathbf{a}}_j)^T({\mathbf{x}}^t-{\mathbf{a}}_j)}{2b_j^2}\right) \right) \quad j=1,\ldots ,L \end{aligned}$$
(2)

where \({\mathbf{a}}_j\in {\mathfrak{R}}^m\) and \(b_j\in {\mathfrak{R}}\) are the center and width of the j-th hidden neuron, respectively.

Then, the predicted coded class label \(\hat{y}_k^t\) of the k-th hidden neuron of the t-th sample is computed as:

$$\begin{aligned} \hat{y}_{k}^t=\sum _{j=1}^{L}\beta _{kj}\cdot h_j^t, \quad k=1,\ldots ,C \end{aligned}$$
(3)

where \(\beta _{kj}\) is the weight connecting the j-th hidden neuron and the k-th output neuron.

The above equation can be written in the matrix form as

$$\begin{aligned} \hat{Y} = {\varvec{\beta}} H , \end{aligned}$$
(4)

where H is the hidden-layer output matrix as shown below:

$$\begin{aligned} H(A, B, X)=\left( \begin{array}{lll} G({\mathbf{a}}_1, b_1, {\mathbf{x}}_1^t) &{} \ldots &{} G({\mathbf{a}}_1, b_1, {\mathbf{x}}_N^t)\\ \vdots &{} \ldots &{} \vdots \\ G({\mathbf{a}}_L, b_L, {\mathbf{x}}_1^t) &{} \ldots &{} G({\mathbf{a}}_L, b_L, {\mathbf{x}}_N^t) \end{array}\right) \end{aligned}$$
(5)

The optimum output weight W can be computed analytically as:

$$\begin{aligned} W^* = YH^\dag \end{aligned}$$
(6)

From the predicted coded class labels, the class label of each sample can be estimated as:

$$\begin{aligned} \widehat{c}^t = \arg {\mathop{\max\limits_{k=1,\ldots ,C}}} {\widehat{y}}_k^t \end{aligned}$$
(7)

Thus, for a given training data set \(\left\{ \left( {\mathbf{x}}^1,{\mathbf{y}}^1\right) ,\ldots ,\left( {\mathbf{x}}^N,{\mathbf{y}}^N\right) \right\}\), and the number of hidden neurons L, the learning algorithm of ELM is summarized below:

  1. 1.

    Randomly generate hidden neuron centers, \(A \in {\mathfrak{R}}^{L\times m}\) and the Gaussian width of the hidden neurons, \({\mathbf{b}}\in {\mathfrak{R}}^{(L \times 1)}\)

  2. 2.

    Compute the hidden-layer output matrix H.

  3. 3.

    Calculate the output weights:

    $$\begin{aligned} \beta =YH^{\dag } \end{aligned}$$
    (8)

    where \(H^{\dag }\) is the Moore–Penrose generalization inverse of responses of the hidden neurons.

However, the generalization performance of the ELM is dependent on the randomly chosen centers and hidden neuron bias, especially in applications like steganalysis, where the dimension of the input feature is large. Hence, in this paper, we propose the cognitive ensemble of ELM classifiers using risk-sensitive hinge loss function.

Risk-Sensitive Hinge Loss Function-Based Cognitive Ensemble of ELM

In this section, we present a cognitive ensemble of ELM classifiers for steganalysis. The performance of the ensemble classifiers depends on the choice of classifiers and weightage of each classifier. First, we present the cognition for selection of classifiers. Next, we present gradient descent-based risk-sensitive hinge loss (RSHL) ensemble.

Cognition: Selection of Classifiers

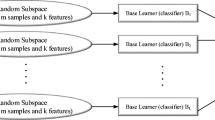
As the performance of the ELM classifier is affected by the random choice of centers and width, a cognition exploits the effect of initialization in the performance of ELM classifiers to develop a cognitive ensemble of ELM classifier. We train a pool of n ELM classifiers, each with initializations in different regions of the input space to ensure that Gaussian centers is distributed in the entire range of the input space. The cognition of the ensemble computes the outputs of these n classifiers on the N training samples, and the samples that are correctly classified are listed. Samples that are repeatedly correctly classified are labeled as winning samples, and samples that are misclassified by the majority of the classifiers are labeled as losing samples. The classifiers that classify only the winning samples correctly are discarded from the pool. Finally, the ensemble output is obtained as the weighted sum of the outputs of the participating classifiers for all the samples as shown in Fig. 1. The cognition in the ensemble of ELM classifier computes the weightage of each classifier using RSHL.

Estimation of Weights for Risk-Sensitive Hinge Loss Error Function-Based Cognitive Ensemble of ELM

In this section, we present the cognition that performs gradient descent-based estimation of the weights (\(v_l\)) for the participating classifiers of the ensemble obtained as shown in section “Cognition: Selection of Classifiers”. Let \(\widehat{{\mathbf{y}}}_1^t,\ldots ,\widehat{{\mathbf{y}}}_l^t,\ldots ,\widehat{{\mathbf{y}}}_n^t\) be the outputs of the n ELM classifiers in the pool for the t-th sample. Then, the total output is obtained as follows:

$$\begin{aligned} \widehat{{\mathbf{y}}}^t = v_1\widehat{{\mathbf{y}}}_1^t+\cdots +v_l\widehat{{\mathbf{y}}}_l^t+\cdots +v_n\widehat{{\mathbf{y}}}_n^t \end{aligned}$$
(9)

Thus, the overall performance of the cognitive ensemble of ELM classifier is better than each individual ELM classifier in the pool. The weights \({\mathbf{v}}^s=[v_1^s \cdots v_l^s \cdots v_n^s]^T\) are obtained by a gradient descent-based procedure as

$$\begin{aligned} {\mathbf{v}}^s_l&= {\mathbf{v}}^s_l + \eta {\mathbf{e}}^s_l \widehat{{\mathbf{y}}}_l^s + \beta \eta \delta _s;\,l=1,\ldots ,n\end{aligned}$$
(10)
$$\begin{aligned} {\text{ where, }} \delta _s& = \eta {\mathbf{e}}_l^{s-1} \widehat{{\mathbf{y}}}_l^{s-1} + \beta \eta \delta _{s-1} \end{aligned}$$
(11)

Here, \(\eta ,\,\beta\) are the learning rate constants, \(\delta _s\) is the adaptive factor for s-th iteration, which keeps the portion of updates \(\eta {\mathbf{e}}_l^{s-1} \widehat{{\mathbf{y}}}_l^{s-1}\) from the previous iteration, \(v_l^s\) is the weight of the l-th classifier for the s-th iteration, and \(e_l^s\) is the error of the l-th classifier for the s-th iteration.

Fig. 1
figure 1

Cognitive ensemble of ELM classifier

Full size image

It has been shown in [30, 48] that hinge loss function predicts the posterior probability better than mean square error. Further, it has also been shown in [30] that a hinge loss error function with a risk factor plays a vital role in minimization of error for classification problems by penalizing the misclassification heavily and by minimizing the effect of imbalance in the training set. Therefore, in this paper, we adapt the risk-sensitive hinge loss error function [30] with a constant risk factor of 2, as shown below:

$$\begin{aligned} e_{l_k}^t = \left\{ {\begin{array}{ll} 0 &{}\quad {\text { if }}\; \widehat{{y}}_{l_k}^t \cdot {y}_{l_k}^t > 1\\ {y}_{l_k}^t-\widehat{{y}}_{l_k}^t &{}\quad {\text { if }}\; 0<\widehat{{y}}_{l_k}^t \cdot {y}_{l_k}^t\le 1\\ 2\cdot ({y}_{l_k}^t -\widehat{{y}}_{l_k}^t ) &{}\quad {\text { if }}\; -1< \widehat{{y}}_{l_k}^t \cdot {y}_{l_k}^t \le 0\\ -2\cdot ({y}_{l_k}^t\cdot \hbox {sign}(\widehat{{y}}_{l_k}^t ))&{}\quad {\text {otherwise}} \end{array}}\right. \end{aligned}$$
(12)

The learning algorithm of the cognitive ensemble of ELM classifiers can be summarized as shown below:

  • Train n individual ELM classifiers:

    • Choose the number of hidden neurons (L), the center of Gaussian activation function (\({\mathbf{a}}_k\)) and the Gaussian width (\(b_k\)) randomly.

    • Estimate the output weight W using Eq. (6).

    • Obtain the hinge output of the network.

  • Develop the cognitive ensemble of ELM classifiers:

    • Define the samples that are correctly classified by most classifiers as winning samples.

    • If a network predicts only the winning samples correctly, delete the network.

  • Estimate using RSHL:

    • Obtain the weighted sum of the participating classifiers using Eq. (9).

    • Update the weights of the participating classifiers using Eqs. (10) and (11).

From the algorithm, it can be seen that the cognitive ensemble of ELM classifier positively exploits the effect of initialization on individual ELM classifiers to obtain a better performing classifier. In the next section, we use the cognitive ensemble of ELM classifiers for steganalysis and compare its performance to the performance of an individual ELM classifier and the best results available in the literature for this problem.

The computational complexity of proposed cognitive ELM ensemble is \(O(nL^3),\) where, n is the number of classifiers and L is the number of hidden neurons.

Performance Study of Cognitive Ensemble of ELM Classifier

In this section, we study the performance of the cognitive ensemble of ELM classifiers in comparison with other classifiers available in the literature. First, we evaluate the performance of the classifiers on benchmark binary classification problems and then use the classifier to solve a steganalysis problem. In our study, the number of hidden neurons in individual ELM classifier for all the problems considered in the study is chosen using the constructive–destructive procedure for selection of neurons, described in [33] and shown below.

  1. Step 1

    Select network with minimal configuration (\(L = m + C\)). Initialize the iteration count (\(\hbox{count} = 1\)).

  2. Step 2

    Train the network until \(\eta _{\rm tr} > \eta_{\rm desired}\).

  3. Step 3

    Calculate the testing efficiency (\(\eta_{\rm te}\)).

  4. Step 4

    If \(\eta_{\rm tr} < B\) (where B is a desired accuracy), then increase the number of hidden neurons and go to Step 2, else stop.

Performance Study on Benchmark Classification Problems

We first evaluate the performance of the cognitive ensemble ELM on benchmark binary classification problems from the UCI machine learning repository [41]. The details of the data sets including the number of features, the number of samples in training and testing, and the imbalance factor of these data sets are presented in Table 1. The imbalance factor (IF) is defined by:

$$\begin{aligned} {\text {IF}} = 1- \frac{C}{N} {\mathop{\min\limits_{k=1,\ldots ,C}}} N_k \end{aligned}$$
(13)

where \(N_k\) is the number of samples in the class k. From the table, it can be observed that all the data sets used in the study are unbalanced data sets.

Table 1 Description of benchmark data sets from UCI machine learning repository
Full size table

The results of the three classifiers, namely SVM, ELM, and a cognitive ensemble of ELM classifiers for the binary benchmark classification problems are presented in Table 2. From the table, it can be observed that the generalization ability of cognitive ensemble of ELM classifier is better than that of the SVM and ELM classifiers, although the training performance is better or almost similar to those of the SVM and ELM classifiers.

Table 2 Experiment results for benchmark data
Full size table

Hence, it is evident that the performance of a cognitive ensemble of ELM classifier is better than individual ELM classifier. Note that, for breast cancer and ionosphere problems, cognitive ensemble ELM does not show improvement ( see Table 2). Due to testing and training efficiencies close to 100 %, presented method discards all ELM networks except the one with the best performance. Thus, there is no room for further improvement using the cognitive ensemble of ELM. Next, we describe the steganalysis data set and present the performance study of the proposed classifier in solving steganalysis.

Steganalysis Using Cognitive Ensemble of ELM Classifier

In this section, we employ the cognitive ensemble of ELM classifier to perform steganalysis. We first discuss the data set used in steganalysis, followed by the performance study of steganalysis using the cognitive ensemble of ELM classifier in comparison with individual ELM classifier and an ensemble of baseline classifier [24].

Merge Steganalysis Feature Data Set

In general, steganalysis method is based on analyzing features extracted from JPEG images. The quality of the extracted features predefines the performance of the binary classifier. Extracted features have to be sensitive to modifications due to data hiding, then steganalysis may correctly identify the cover and stego images.

In our experiments, we used BCH-based steganographic method proposed by Zhang et al. [47] for data hiding, and steganalysis method based on 548 features [26, 24]. In our experiments, steganalysis is performed by modifying the image data set with the hiding message with a length of 0.2-bits per nonzero DCT coefficients (bnpc). Such an experiment is capable of hiding reasonable amount of data in respect of the number of available nonzero DCT coefficients. Thus, JPEG image with small number of nonzero DCT coefficients always contain small number of hidden bits and vice versa.

In this paper, we used popular 548-dimension merged feature set proposed by Pevny et al. [26] and improved by Kodovsky [24]. Merged feature set contains 7 features subsets, i.e., \(F_o=\{{\mathbf{f}}_1,\,{\mathbf{f}}_2,\,{\mathbf{f}}_3,\,{\mathbf{f}}_4,\,{\mathbf{f}}_5,\,{\mathbf{f}}_6,\,{\mathbf{f}}_7\}\) see Fig. 2:

  • \({\mathbf{f}}_1\): Global histogram \(H_l\) of all \(64\times n_b\) (\(n_b\) is the number of \(8 \times 8\) blocks of JPEG image).

  • \({\mathbf{f}}_2\): 5 Local histograms of the AC coefficients \(h^{ij}=\{h^{ij}_{L} ,\ldots , h^{ij}_{R}\}\) located in the five fist positions according to the zigzag scan, i.e., \((i,j) \in \{(1,2),\,(2,1),\) \((3,1),\) \((2,2),\) \((1,3)\}\).

  • \({\mathbf{f}}_3\): 11 Dual histograms.

  • \({\mathbf{f}}_4\): 6 Inter-block dependency coefficients.

  • \({\mathbf{f}}_5\): 2 Blockness coefficients.

  • \({\mathbf{f}}_6\): 3 Co-occurrence matrix of neighboring DCT coefficients.

  • \({\mathbf{f}}_7\): 81 Markov coefficients.

Fig. 2
figure 2

Features set

Full size image

Feature set \(F_o=\{{\mathbf{f}}_1,\,{\mathbf{f}}_2,\,{\mathbf{f}}_3,\,{\mathbf{f}}_4,\,{\mathbf{f}}_5,\,{\mathbf{f}}_6,\,{\mathbf{f}}_7\}\) has 274 features which is sufficient for efficient steganalysis. Later Kodovsky et al. [24] extended feature set by including another 274 features (i.e., \(F_c=\{{\mathbf{f}}^c_1,\,{\mathbf{f}}^c_2,\,{\mathbf{f}}^c_3,\,{\mathbf{f}}^c_4,\,{\mathbf{f}}^c_5,\,{\mathbf{f}}^c_6,\,{\mathbf{f}}^c_7\}\)) extracted from the cropped bitmap version of the examined JPEG image. Thus, resulted feature set \(F=\{F_o, F_c\}\) = \(\{{\mathbf{f}}_1,\,{\mathbf{f}}_2,\,{\mathbf{f}}_3,\,{\mathbf{f}}_4,\,{\mathbf{f}}_5,\,{\mathbf{f}}_6,\,{\mathbf{f}}_7,\,{\mathbf{f}}^c_1,\,{\mathbf{f}}^c_2,\,{\mathbf{f}}^c_3,\,{\mathbf{f}}^c_4,\,{\mathbf{f}}^c_5,\,{\mathbf{f}}^c_6,\,{\mathbf{f}}^c_7\}\) has 548 features. The image is cropped by 8 pixels in both vertical and horizontal directions. JPEG compression divides bitmap image into 8 by 8 blocks and processes each block separately. Thus, each JPEG block of the cropped image has four 4 by 4 sub-blocks from four neighboring noncropped JPEG blocks. Such design may amplify the artificial changes and may cause better detect-ability. For more details, refer to [26] and [24]. In the next section, we present a performance study of the proposed cognitive ensemble of ELM classifier for steganalysis.

Performance Study on Steganalysis

In this section, we study the steganalysis capability of the cognitive ensemble of ELM classifier, in comparison with the best performing classifier available in the literature for this data set. First, we perform a study based on the constructive–destructive procedure to fix the number of neurons in the hidden layer of the ELM. Table 3 presents the training and testing efficiencies of an ELM classifier for different number of hidden neurons. Although a wide range of neurons was chosen, we have presented the results only for six different numbers of hidden neurons. From the table, it can be seen that the best testing efficiency was obtained when \(L = 1{,}000.\) Hence, 1,000 hidden neurons employing Gaussian activation function are used at the hidden layer of each ELM of the cognitive ensemble of ELM classifier used in our experiments.

Table 3 Training and testing efficiency for various number of hidden neurons L
Full size table

Next, the performances of the different classifiers, namely ensemble classifier proposed by Kodovsky et al. [24], single ELM, and the cognitive ensemble of ELM are studied in the steganalysis data set using 75 % of the total samples in the training and the remaining 25 % of the samples in testing. To enable fair comparison, 7 trials were conducted, in each of which 75 % of the samples are randomly chosen for training and the remaining 25 % is used to test the trained classifier. The performance results of the 7 random trials of all the three classifiers are presented in Table 4. From the table, it can be observed that the cognitive ensemble of ELM classifier outperforms the ensemble classifier [24] and the single ELM classifier in all the 7 trials. Thus, it can be concluded that the cognitive ensemble of ELM classifier is capable of performing steganalysis much better than the single ELM and ensemble classifiers [24].

Table 4 Testing efficiency for tested classifiers and 7 different splits
Full size table

In our experiments, we found 48 classifiers achieve better performance. Beyond 48, there is no much improvement in results. We have conducted sevenfold validation. We found that the average performance is 65.22 % in terms of testing accuracy; standard deviation is 0.71.

Conclusions

In this paper, we have presented a risk-sensitive cognitive ensemble of ELM classifier for JPEG steganalysis. We have trained several ELM classifiers using the 548-dimensional merged feature set, and the cognitive ensemble of ELM classifier is then constructed by obtaining the weighted sum of the outputs of the individual ELM classifiers. The cognition in the classifier estimates the weight of individual ELM classifier through the gradient descent update based on RHSL. Thus, the cognitive ensemble of ELM classifier positively exploits the effect of randomness in each classifier to obtain the best results. The performance of the cognitive ensemble ELM is evaluated on 5 benchmark binary classification data sets from the UCI machine learning repository and a practical steganalysis data set. In all these problems, the performance of the proposed classifier is compared to that of a single ELM and SVM. In addition, the performance of the classifier in solving steganalysis is also compared with the best performing classifier available in the literature for this data set. Performance results obtained from the study show the superior classification ability of the cognitive ensemble of ELM classifier.