1 Introduction

The volumetric errors of machine tools decrease when geometric errors are identified and compensated, in turn reducing kinematic [1], stiffness-induced [2], and thermally induced [3] errors. Geometric errors can be identified via direct and indirect methods [4, 5]. Geometric errors are divided into position-independent geometric errors (PIGEs; also termed “location and orientation errors” [6] and “kinematic errors” [7]) and position-dependent geometric errors (PDGEs; also termed “error motions” [8]). PIGEs are defined using the averages of the PDGEs over the working range of linear and rotary axes, and thus affect volumetric error more significantly across the entire workspace [9]. Thirteen PIGEs are used to model the volumetric errors of five-axis machine tools, including three squareness errors between the three linear axes; two squareness errors and two offset errors for the rotary and tilting axes, respectively; and two squareness errors for the spindle axis [10, 11]. Although several methods of PIGE identification are available [6], it remains challenging to accurately determine the PIGEs of rotary axes; no method is optimal for identifying the errors.

PIGEs must be accurately identified to reduce workpiece geometric errors. However, PDGEs affect PIGEs because they are coupled. Thus, it is important to check the interdependencies of PIGEs and PDGEs, and to perform Monte Carlo simulations to investigate the effects of the interdependency [12]. Certain PIGEs are affected by the PDGEs [13], thermal errors [14] of linear axes, and PDGEs of both rotary and linear axes [15]. It is necessary to pre-identify and pre-compensate for PDGEs that affect rotary-axis PIGEs. However, this makes PIGE identification complex. Alternatively, as recommended here, PIGE identification can be optimized to minimize the effects of other errors (including PDGEs) on PIGEs.

Geometric errors affect workpiece geometric errors. The effects of PIGEs [7], and of PIGEs and PDGEs [16], on the machining geometric accuracy of a cone frustum have been investigated; the workpiece geometric errors were determined via simultaneous control of all five axes [17]. A cubic machining test was used to reveal the effects of geometric errors on the workpiece coordinate system [18]. A pyramidal testpiece was machined in a five-axis machine tool and measured using a coordinate measuring machine (CMM) to identify PIGEs alone [19], and both PIGEs and PDGEs [20, 21]. Three machining patterns were used, and CMM measurements were obtained; 11 PIGEs were identified on a single drive of a rotary axis and unwanted effects on the most sensitive direction were reduced, thereby enhancing accurate identification [22]. A cubic workpiece was subjected to five machining patterns via several large rotations of the rotary axes; a laser displacement sensor was employed to measure finished surface mismatches [23]. However, PIGEs identified via machining tests can be affected by errors in workpiece settings, cutting force, and tool parameters, which reduce the accuracy of the identified PIGEs [18]. Methods not affected by such errors have thus been developed. PIGEs are systematic deviations identified via double ball-bar (DBB) measurements of the eccentricity of three-axis circular motions [24]. An R-test using a device measuring three relative displacements has been applied to identify PIGEs after inducing circular-spherical movements [25]. DBB measurements on a single set-up have also been employed to identify PIGEs; down-time was reduced when the structural restrictions of machine tools were considered [26, 27]. To simplify measurements, one method identified PIGEs via single-axis control during a series of DBB measurements [28]. A DBB method with a single setup, single-axis control, and extension bar was used to identify PIGEs [29]. A reconfigurable mechanism model was employed to identify the PIGEs of machine tools using arbitrary combinations of linear and rotary axes [30]. All of the above methods are single-ball measurements derived using a DBB or the R-test device; in principle, a touch-trigger probe could also be employed. Other methods derive multi-ball [31] and square column measurements using a touch-trigger probe [32] to identify PIGEs. However, single-ball methods have the advantages of a simple set-up and cost-effective measurement; ISO standards employ such measurements [33]. Geometric errors are identified by optimizing the distribution of measurement points to reduce volumetric errors [34]. However, there are no optimized methods for workpiece geometric errors [24, 25, 33].

It is essential to consider the measurement uncertainties of identified PIGEs, where these uncertainties reflect a lack of precise knowledge of the measurand values [35]. In general, PIGEs are the sums of sensitivity coefficients multiplied by the measured data [9]. The sensitivity coefficients describe how output estimates vary as the input estimates change [36, 37]. During PIGE identification, the root-sum-square (RSS) values of sensitivity coefficients, which are affected by the measuring angle range for rotary axes, are used to determine the measurement conditions [38]; uncertainties in measured data are induced by both measuring devices and systematic and non-systematic errors of the controlled axes [32]. Measurement uncertainty can be improved by reducing the RSS values of the sensitivity coefficients and/or uncertainties in the measured data. However, such reduction of the measured data requires highly accurate (and thus expensive) measuring devices. Pre-measurement of other systematic errors should be performed using additional devices, again increasing costs. It is reasonable to seek to optimize measurement paths by reducing the effects of the RSS values of sensitivity coefficients on workpiece geometric errors; this is a cost-effective approach.

In summary, the PIGEs of rotary axes are identified using a number of methods to improve the volumetric errors of five-axis machine tools, and measurement uncertainties are analyzed via error budgeting; this reveals the confidence intervals of the PIGEs and the feasibility of the chosen methods. However, all methods to date have aimed to improve machine tool volumetric errors, rather than to directly improve workpiece geometric errors (Fig. 1a); the improvement is thus limited.

Fig. 1
figure 1

Strategies used to improve workpiece accuracy

Full size image

Here, we developed an adaptive method for identifying the PIGEs of rotary axes; this directly improves workpiece geometric errors (Fig. 1b) by optimizing the measurement processes. The processes are adaptively optimized for the workpiece rather than the machine tools. The measurement processes are optimized by determining the measurement paths that minimize the effects of PIGE sensitivity coefficients on workpiece geometric errors, whereas our previous method [38] used PIGE sensitivity coefficients to determine the measuring angle range for rotary axes without considering workpiece geometric errors. The method proposed in this study is shown in Fig. 2.

Fig. 2
figure 2

Adaptive method for identifying the PIGEs of rotary axes

Full size image

First, a workpiece coordinate \(\left( {x_{W,i} ,y_{W,i} ,z_{W,i} ,a_{W,i} ,c_{W,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) in the workpiece coordinate system \(\left\{ {\mathbf{W}} \right\}\) is assigned, and toolpath commands \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) in a reference coordinate system \(\left\{ {\mathbf{R}} \right\}\) are calculated for five-axis control. Then, the volumetric errors \({\mathbf{VE}}_{i}\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) for the toolpath commands are derived as functions of the commands and PIGEs, using an error synthesis model determined by the experimental machine configuration. The effects of the PIGE RSS values (which are affected by the measurement path) on workpiece geometric errors are analyzed, and an optimal path is determined to minimize such effects. In Sect. 2, a measurement path model concerned with the RSS values of the PIGE sensitivity coefficients is optimized for the cone-shaped ISO 10791–7, M3_15 testpiece [17]. We use this example because this is a representative workpiece that requires simultaneous five-axis control. We then identify the PIGEs using a R-test device. Equivalent DBB measurements (with PIGE compensation) are also performed, and demonstrate the validity of our approach based on the improvement in cone-shaped testpiece radial deviation (Sect. 3). The main contributions of this study are discussed in Sect. 4.

2 Optimal measurement path for workpiece geometric errors

2.1 Error synthesis model

To identify PIGEs, it is essential to establish an error synthesis model as a function of the nominal commands for the linear and rotary axes. Then, the relationships between the measured data and PIGEs are established using the model. The kinematic structure of our experimental machine tool is shown in Fig. 3 and the PIGEs of the rotary axes are listed in Table 1.

Fig. 3
figure 3

Kinematic structure of the experimental machine tool

Full size image
Table 1 PIGEs of the rotary axes of the experimental five-axis machine tool
Full size table

To identify the PIGEs, the ball positions on the workpiece table and tool nose are described using the homogeneous transformation matrices of Eq. (1). Here, \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) are the i-th toolpath commands corresponding to workpiece coordinate \(\left( {x_{W,i} ,y_{W,i} ,z_{W,i} ,a_{W,i} ,c_{W,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\). The terms \(ca_{TP,i}\), \(sa_{TP,i}\), \(cc_{TP,i}\), and \(sc_{TP,i}\) are \(\cos \left( {a_{TP,i} } \right)\), \(\sin \left( {a_{TP,i} } \right)\), \(\cos \left( {c_{TP,i} } \right)\), and \(\sin \left( {c_{TP,i} } \right)\), respectively. The reference coordinate system \(\left\{ {\mathbf{R}} \right\}\) is defined at the nominal crosspoint of rotary axes A and C; this allows for a simple description of the volumetric errors.

$$\begin{gathered} {{\varvec{\uptau}}}_{R}^{w} = {{\varvec{\uptau}}}_{R}^{Y} {{\varvec{\uptau}}}_{Y}^{A} {{\varvec{\uptau}}}_{A}^{C} {{\varvec{\uptau}}}_{C}^{w} \hfill \\ {{\varvec{\uptau}}}_{R}^{T} = {{\varvec{\uptau}}}_{R}^{X} {{\varvec{\uptau}}}_{X}^{Z} {{\varvec{\uptau}}}_{Z}^{T} \hfill \\ \end{gathered}$$
(1)

where:

(for the workpiece branch):

$${{\varvec{\uptau}}}_{R}^{Y} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & { - y_{TP,i} } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
$$\begin{gathered} {{\varvec{\uptau}}}_{Y}^{A} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {o_{ya} } \\ 0 & 0 & 1 & {o_{za} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & { - s_{za} } & {s_{ya} } & 0 \\ {s_{za} } & 1 & 0 & 0 \\ { - s_{ya} } & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {ca_{TP,i} } & {sa_{TP,i} } & 0 \\ 0 & { - sa_{TP,i} } & {ca_{TP,i} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \quad \,{\kern 1pt} = \left[ {\begin{array}{*{20}c} 1 & { - s_{za} ca_{TP,i} - s_{ya} sa_{TP,i} } & { - s_{za} sa_{TP,i} + s_{ya} ca_{TP,i} } & 0 \\ {s_{za} } & {ca_{TP,i} } & {sa_{TP,i} } & {o_{ya} } \\ { - s_{ya} } & { - sa_{TP,i} } & {ca_{TP,i} } & {o_{za} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], \hfill \\ \end{gathered}$$
$$\begin{gathered} {{\varvec{\uptau}}}_{A}^{C} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {o_{xc} } \\ 0 & 1 & 0 & {o_{yc} } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 & 0 & {s_{yc} } & 0 \\ 0 & 1 & { - s_{xc} } & 0 \\ { - s_{yc} } & {s_{xc} } & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {cc_{TP,i} } & {sc_{TP,i} } & 0 & 0 \\ { - sc_{TP,i} } & {cc_{TP,i} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \quad \,{\kern 1pt} = \left[ {\begin{array}{*{20}c} {cc_{TP,i} } & {sc_{TP,i} } & {s_{yc} } & {o_{xc} } \\ { - sc_{TP,i} } & {cc_{TP,i} } & { - s_{xc} } & {o_{yc} } \\ { - s_{yc} cc_{TP,i} - s_{xc} sc_{TP,i} } & { - s_{yc} sc_{TP,i} + s_{xc} cc_{TP,i} } & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], \hfill \\ \end{gathered}$$
$${{\varvec{\uptau}}}_{C}^{w} = \left[ {\begin{array}{*{20}c} {x_{W,i} } \\ {y_{W,i} } \\ {z_{W,i} } \\ 1 \\ \end{array} } \right],$$

(for the tool branch):

$${{\varvec{\uptau}}}_{R}^{X} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {x_{TP,i} } \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
$${{\varvec{\uptau}}}_{X}^{Z} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {z_{TP,i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
$${{\varvec{\uptau}}}_{Z}^{T} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

The volumetric errors \({\mathbf{VE}}_{i}\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) (positional deviations of the ball on the workpiece table from the nominal values) are defined by Eq. (2). Note that the volumetric errors \({\mathbf{VE}}_{i}\) are defined in the reference coordinate system \(\left\{ {\mathbf{R}} \right\}\), and thus can be used directly to compensate for the identified PIGEs via the G-code modification [39]. Here, \({\mathbf{VE}}_{coeff,i}\) refers to the sensitivity of the PIGEs to volumetric errors \({\mathbf{VE}}_{i}\).

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {{\mathbf{VE}}_{i} } \\ \hline 0 \\ \end{array} } \right] & = \left( {{{\varvec{\uptau}}}_{R}^{T} } \right)^{ - 1} \times {{\varvec{\uptau}}}_{R}^{w} - \left( {{{\varvec{\uptau}}}_{R}^{T} } \right)^{ - 1} \times {{\varvec{\uptau}}}_{R}^{Y} \times {\mathbf{AM}}_{A} \times {\mathbf{AM}}_{C} \times {{\varvec{\uptau}}}_{C}^{w} \\ & = \left[ {\begin{array}{*{20}c} {\left( {x_{W,i} sa_{TP,i} sc_{TP,i} + y_{W,i} sa_{TP,i} cc_{TP,i} + z_{W,i} ca_{TP,i} } \right)s_{ya} + \left( { - x_{W,i} ca_{TP,i} sc_{TP,i} - y_{W,i} ca_{TP,i} cc_{TP,i} + z_{W,i} sa_{TP,i} } \right)s_{za} + o_{xc} + z_{W,i} s_{yc} } \\ {o_{ya} + \left( {x_{W,i} cc_{TP,i} - y_{W,i} sc_{TP,i} } \right)s_{za} + o_{yc} ca_{TP,i} - \left( {x_{W,i} sa_{TP,i} sc_{TP,i} + y_{W,i} sa_{TP,i} cc_{TP,i} + z_{W,i} ca_{TP,i} } \right)s_{xc} + \left( {x_{W,i} sa_{TP,i} cc_{TP,i} - y_{W,i} sa_{TP,i} sc_{TP,i} } \right)s_{yc} } \\ {o_{za} + \left( { - x_{W,i} cc_{TP,i} + y_{W,i} sc_{TP,i} } \right)s_{ya} + o_{yc} sa_{TP,i} + \left( {x_{W,i} ca_{TP,i} sc_{TP,i} + y_{W,i} ca_{TP,i} cc_{TP,i} - z_{W,i} sa_{TP,i} } \right)s_{xc} + \left( { - x_{W,i} ca_{TP,i} cc_{TP,i} + y_{W,i} ca_{TP,i} sc_{TP,i} } \right)s_{yc} } \\ \hline 0 \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {{\mathbf{VE}}_{coeff,i} } \\ \hline 0 \\ \end{array} } \right] \times {\mathbf{PIGEs}} \\ \end{aligned}$$
(2)

where

$${\mathbf{VE}}_{i} = [\begin{array}{*{20}c} {x_{VE,i} } & {y_{VE,i} } & {z_{VE,i} } \\ \end{array} ]^{T} ,$$
$${\mathbf{AM}}_{a} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {ca_{TP,i} } & {sa_{TP,i} } & 0 \\ 0 & { - sa_{TP,i} } & {ca_{TP,i} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
$${\mathbf{AM}}_{c} = \left[ {\begin{array}{*{20}c} {cc_{TP,i} } & {sc_{TP,i} } & 0 & 0 \\ { - sc_{TP,i} } & {cc_{TP,i} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$
$${\mathbf{VE}}_{coeff,i} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ {x_{W,i} sa_{TP,i} sc_{TP,i} + y_{W,i} sa_{TP,i} cc_{TP,i} + z_{W,i} ca_{TP,i} } & 0 & { - x_{W,i} cc_{TP,i} + y_{W,i} sc_{TP,i} } \\ { - x_{W,i} ca_{TP,i} sc_{TP,i} - y_{W,i} ca_{TP,i} cc_{TP,i} + z_{W,i} sa_{TP,i} } & {x_{W,i} cc_{TP,i} - y_{W,i} sc_{TP,i} } & 0 \\ 1 & 0 & 0 \\ 0 & {ca_{TP,i} } & {sa_{TP,i} } \\ 0 & { - x_{W,i} sa_{TP,i} sc_{TP,i} - y_{W,i} sa_{TP,i} cc_{TP,i} - z_{W,i} ca_{TP,i} } & {x_{W,i} ca_{TP,i} sc_{TP,i} + y_{W,i} ca_{TP,i} cc_{TP,i} - z_{W,i} sa_{TP,i} } \\ {z_{W,i} } & {x_{W,i} sa_{TP,i} cc_{TP,i} - y_{W,i} sa_{TP,i} sc_{TP,i} } & { - x_{W,i} ca_{TP,i} cc_{TP,i} + y_{W,i} ca_{TP,i} sc_{TP,i} } \\ \end{array} } \right]^{{}}$$
$${\mathbf{PIGEs}} = \left[ {\begin{array}{*{20}c} {o_{ya} } & {o_{za} } & {s_{ya} } & {s_{za} } & {o_{xc} } & {o_{yc} } & {s_{xc} } & {s_{yc} } \\ \end{array} } \right]^{T}$$

2.2 General measurement path for PIGEs

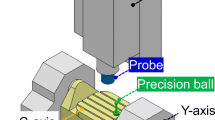
Two linear axes and a rotary axis are often controlled to identify PIGEs [33]. For the C-axis, it is easy to measure the positional deviations of the ball on the workpiece table along the full circle trajectory followed by the X, Y, and C axes. Thus, the measurement uncertainties are small. However, for the A-axis, the nominal measuring angle range is limited because the A-axis involves tilting only, i.e., not full rotation. Thus, the measurement path of the ball (followed by the Y, Z, A axes) on the workpiece table is limited to an arc, creating relatively large measurement uncertainties in the PIGEs. The measurement path can be changed in space (Fig. 4) depending on the initial position of the ball on the table, although the measuring angle range does not change. For example, Fig. 4a and b show the different measurement paths when the initial position of a ball on the table is changed. The measurement uncertainties of the PIGEs are affected by the measurement path determined by the initial position of the ball. In this case, the initial position is modeled using setting angle b, which must be optimized to minimize the effects of PIGE sensitivity coefficients on workpiece geometric errors.

Fig. 4
figure 4

Measurement paths according to the initial position of the ball on the workpiece table

Full size image

In Sect. 3, we measure the positional deviation of the ball on the workpiece table using a wireless Trinity probe (IBS Precision Engineering BV, Eindhoven, The Netherlands). In such a case, the ball position \(\left( {x_{W,i} ,y_{W,i} ,z_{W,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\), which remains the same during measurements, is given by Eq. (3). The set-up error \(\left( {\Delta x_{W} ,\Delta y_{W} ,\Delta z_{W} } \right)\) is unknown and fixed if the ball installation is not varied, and is used to describe the ball position in coordinate system \(\left\{ {\mathbf{C}} \right\}\). Here, \(cb\) and \(sb\) are \(\cos \left( b \right)\) and \(\sin \left( b \right)\), respectively. The nominal commands \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) for the linear and rotary axes are given by Eq. (4) for the A- and C-axis measurements, respectively. Note that the ball position \(\left( {x_{W,i} ,y_{W,i} ,z_{W,i} } \right)\) on the workpiece table does not change during measurements with a single set-up.

$$\left( {x_{W,i} ,y_{W,i} ,z_{W,i} } \right) = \left( {Rcb + \Delta x_{W} ,\Delta y_{W} ,Rsb + \Delta z_{W} } \right)$$
(3)
$$\begin{gathered} {\text{For A - axis}} \hfill \\ \left\{ \begin{gathered} x_{TP,i} = 0 \hfill \\ y_{TP,i} = Rc\left( { - a_{TP,i} + b} \right) \hfill \\ z_{TP,i} = Rs\left( { - a_{TP,i} + b} \right) \hfill \\ a_{TP,i} = [a_{\min } ,a_{\max } ], \, \left( {i = 1, \ldots ,n_{A} } \right) \hfill \\ c_{TP,i} = - 90^\circ \hfill \\ \end{gathered} \right. \hfill \\ {\text{For C - axis}} \hfill \\ \left\{ \begin{gathered} x_{TP,i} = Rcbcc_{TP,i} \hfill \\ y_{TP,i} = - Rcbsc_{TP,i} \hfill \\ z_{TP,i} = Rsb \hfill \\ a_{TP,i} = 0^\circ \hfill \\ c_{TP,i} = [c_{\min } ,c_{\max } ], \, \left( {i = 1, \ldots ,n_{C} } \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(4)

By substituting Eqs. (3) and (4) into Eq. (2), the volumetric errors \({\mathbf{VE}}_{i}\) are derived (along with the measurement paths) in Cartesian coordinates. However, it is essential to represent volumetric error \({\mathbf{VE}}_{i}\) in terms of cylindrical coordinates to minimize the effects of the main PDGEs (i.e., the angular positioning errors) of the rotary axes [38, 40]. In such a case, the relationships between the PIGEs and measured positional deviations \(\left( {x_{M,i} ,y_{M,i} ,z_{M,i} } \right)\) \(\left( {i = 1, \ldots ,n_{A} {\text{ for A - axis}};\quad i = 1, \ldots ,n_{C} {\text{ for C - axis}}} \right)\) of the ball along the measurement path, are derived as shown in Eq. (5).

$$\begin{gathered} {\text{For A - axis: Radial}} \hfill \\ \Delta R_{A,radial,i} = \sqrt {\left( {y_{TP,i} + y_{M,i} } \right)^{2} + \left( {z_{TP,i} + z_{M,i} } \right)^{2} } - R = c\left( { - a_{TP,i} + b} \right)o_{ya} + s\left( { - a_{TP,i} + b} \right)o_{za} + cbo_{yc} + cb\Delta x_{W} + sb\Delta z_{W} \hfill \\ \hfill \\ {\text{For A - axis: Axial}} \hfill \\ \Delta R_{A,axial,i} = x_{M,i} = Rs\left( { - a_{TP,i} + b} \right)s_{ya} - Rc\left( { - a_{TP,i} + b} \right)s_{za} + o_{xc} + Rsbs_{yc} - \Delta y_{W} \hfill \\ \hfill \\ {\text{For C - axis: Radial}} \hfill \\ \Delta R_{C,radial,i} = \sqrt {\left( {x_{TP,i} + x_{M,i} } \right)^{2} + \left( {y_{TP,i} + y_{M,i} } \right)^{2} } - Rcb = \left\{ {o_{xc} + R\left( {s_{ya} + s_{yc} } \right)sb} \right\}cc_{TP,i} - \left\{ {\left( {o_{ya} + o_{yc} } \right) - Rsbs_{xc} } \right\}sc_{TP,i} + \Delta x_{W} \hfill \\ \hfill \\ {\text{For C - axis: Axial}} \hfill \\ \Delta R_{C,axial,i} = z_{M,i} = - Rcbsc_{TP,i} s_{xc} - R\left( {s_{ya} + s_{yc} } \right)cbcc_{TP,i} + o_{za} + \Delta z_{W} \hfill \\ \end{gathered}$$
(5)

Equation (5) is formatted using the matrix notation of Eq. (6), and the PIGEs are identified using a least-squares approach at the given angle b. It is obvious that the coefficient matrices \({\mathbf{A}}_{i,j}\) \(\left( {i = A, \, C; \, j = radial, \, axial} \right)\) are affected by angle b.

$${\mathbf{A}}_{i,j} {\mathbf{x}}_{i,j} = \Delta {\mathbf{R}}_{i,j} \quad \left( {i = A,C;\quad j = radial,axial} \right)$$
(6)

2.3 Optimal measurement path using the RSS values

Pseudo-inversion of Eq. (6) yields Eq. (7). The PIGEs are identified by multiplying the rows of the pseudo-inverse matrix \({\mathbf{A}}_{i,j}^{ + }\) by the measured data \(\Delta {\mathbf{R}}_{i,j}\) [Eq. (8)]. Here, \(\Delta R_{i,j,k}\) \(\left( {i = A,C;\quad j = radial,axial;\quad k = 1, \ldots ,n_{A} \;{\text{for A - axis}};\;k = 1, \ldots ,n_{C} \;{\text{for C - axis}}} \right)\) refers to the k-th component of the measured data \(\Delta {\mathbf{R}}_{i,j}\) \(\left( {i = A,C; \, j = radial, \, axial} \right)\). Thus, the rows of the pseudo-inverse matrix \({\mathbf{A}}_{i,j}^{ + }\) constitute the set of sensitivity coefficients for the corresponding PIGEs.

$${\mathbf{x}}_{i,j} = \left( {{\mathbf{A}}_{i,j}^{T} \;{\mathbf{A}}_{i,j} } \right)^{ - 1} \;{\mathbf{A}}_{i,j}^{T} \;\Delta {\mathbf{R}}_{i,j} = {\mathbf{A}}_{i,j}^{ + } \;\Delta {\mathbf{R}}_{i,j}$$
(7)
$$PIGEs = f\left( {\Delta R_{i,j,k} } \right) = \sum\limits_{i,j,k} {\left\{ {\frac{\partial f}{{\partial \left( {\Delta R_{i,j,k} } \right)}}\Delta R_{i,j,k} } \right\}}$$
(8)

Next, the measurement uncertainties of the PIGEs, \(U\left( {PIGEs} \right)\), are calculated as the RSS values of the sensitivity coefficients, \(RSS_{PIGEs}\), multiplied by the measurement uncertainties \(U\left( {\Delta R_{i,j,k} } \right)\) [Eq. (9)] [36, 37]. The units for \(U\left( {PIGEs} \right)\), \(U\left( {\Delta R_{i,j,k} } \right)\) and \(RSS_{PIGEs}\) are summarized in Table 2. Here, it is assumed that the measurement uncertainties \(U\left( {\Delta R_{i,j,k} } \right)\) are identical over the measuring paths in Fig. 4, as the uncertainties are affected by the measuring devices and systematic and non-systematic errors of the controlled axes, as stated in Sect. 1.

$$U\left( {PIGEs} \right) = RSS_{PIGEs} \times U\left( {\Delta R_{i,j,k} } \right) = \sqrt {\sum\limits_{i,j,k} {\left\{ {\frac{\partial f}{{\partial \left( {\Delta R_{i,j,k} } \right)}}} \right\}^{2} } } \times U\left( {\Delta R_{i,j,k} } \right)$$
(9)
Table 2 Measurement uncertainty units for \(U\left( {PIGEs} \right)\), \(U\left( {\Delta R_{i,j,k} } \right)\), and the RSS values
Full size table

The measurement uncertainty \(U\left( {PIGEs} \right)\) is affected by both \(RSS_{PIGEs}\) and measurement uncertainty \(U\left( {\Delta R_{i,j,k} } \right)\). The \(RSS_{PIGEs}\) are a function of angle b. To improve workpiece geometric errors directly, it is essential to investigate the effects of measurement uncertainty \(U\left( {PIGEs} \right)\) on the measurement uncertainty \(U\left( {{\mathbf{VE}}_{i} } \right)\) along the toolpaths \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\). The measurement uncertainty \(U\left( {{\mathbf{VE}}_{i} } \right)\) is determined as shown in Eq. (10) [using Eq. (2)]. Here, the units for \(U\left( {{\mathbf{VE}}_{i} } \right)\) and \(RSS_{VE,j,i}\) \(\left( {j = x,y,z} \right)\) are μm and μm/μm, respectively.

$$U\left( {{\mathbf{VE}}_{i} } \right) = \left[ {\begin{array}{*{20}c} {U\left( {x_{VE,i} } \right)} \\ {U\left( {y_{VE,i} } \right)} \\ {U\left( {z_{VE,i} } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {RSS_{VE,x,i} } \\ {RSS_{VE,y,i} } \\ {RSS_{VE,z,i} } \\ \end{array} } \right] \times U\left( {\Delta R_{j,k,m} } \right)$$
(10)

where:

$$RSS_{VE,x,i} = \sqrt {\sum\limits_{n = 1}^{8} {{\mathbf{Q}}_{i}^{2} \left( {1,n} \right)} } ,$$
$$RSS_{VE,y,i} = \sqrt {\sum\limits_{n = 1}^{8} {{\mathbf{Q}}_{i}^{2} \left( {2,n} \right)} } ,$$
$$RSS_{VE,z,i} = \sqrt {\sum\limits_{n = 1}^{8} {{\mathbf{Q}}_{i}^{2} \left( {3,n} \right)} } ,$$
$${\mathbf{Q}}_{i} = {\mathbf{VE}}_{coeff,i} \times \left[ {\begin{array}{*{20}c} {RSS_{oya} } & {RSS_{oza} } & {RSS_{sya} } & {RSS_{sza} } & {RSS_{oxc} } & {RSS_{oyc} } & {RSS_{sxc} } & {RSS_{syc} } \\ \end{array} } \right]^{T}$$

The measurement uncertainty \(U\left( {{\mathbf{VE}}_{i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) is affected by both \(RSS_{VE,j,i}\) \(\left( {i = 1, \ldots ,n_{W} ;\quad j = x,y,z} \right)\) (which is in turn affected by angle b) and measurement uncertainty \(U\left( {\Delta R_{j,k,m} } \right)\) (which is constant). Thus, the measurement uncertainty \(U\left( {{\mathbf{VE}}_{i} } \right)\) can be improved by decreasing \(RSS_{VE,j,i}\) \(\left( {i = 1, \ldots ,n_{W} ;\quad j = x,y,z} \right)\); this is achieved in a cost-effective manner by determining the optimal angle b. The effect of angle b on \(RSS_{VE,j,i}\) along the toolpaths \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,n_{W} } \right)\) should be minimized for optimal adaptive identification. For example, we explored the effect of angle b on the \(RSS_{VE,j,i}\) along toolpaths of the ISO 10791-7 cone-shaped testpiece, and optimized angle b to minimize unwanted effects. The case study is described in Sect. 3.

3 Case study

3.1 Determination of the optimal measurement path

As an example, the optimal angle b is determined for the cone-shaped testpiece of ISO 10791-7, M3_15 [17]; this standard requires simultaneous control of five axes. The testpiece dimensions are shown in Fig. 5 and Table 3. In Sect. 3.3, DBB measurement (equivalent to machining) is performed to measure the radial deviation of the lower surface of the cone without and with PIGE compensation. The testpiece diameter D is 200 mm (not 80 mm in ISO 10791-7 [17]) because the nominal length of the experimental DBB is 100 mm. The spindle axis is constrained to lie tangential to the cone surface, and the toolpaths \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,720} \right)\) according to testpiece angle \(\psi\) are calculated as shown in Fig. 6. Here, \(n_{W} = 720\), because the toolpath is calculated as \(\psi\) is varied 0°–360° in steps of \(\Delta \psi = 0.5^\circ\).

Fig. 5
figure 5

Cone-shaped testpiece

Full size image
Table 3 Dimensions of the cone-shaped testpiece
Full size table
Fig. 6
figure 6

Toolpath commands for the cone-shaped testpiece

Full size image

The simulation sequence is summarized in Fig. 7. First, angle b in the range \(\left[ {0^\circ ,60^\circ } \right]\) with an interval \(\Delta b\) = 5° is chosen and \(RSS_{PIGEs}\) is calculated using Eq. (9) (Fig. 8). Note that \(RSS_{PIGEs}\) varies with angle b. As that increases, the \(RSS_{PIGEs}\) for \(\left\{ {o_{ya} ,o_{yc} ,s_{za} } \right\}\) (which reflects the sensitivity in the y-direction) decrease, and the measurement uncertainties of \(\left\{ {o_{ya} ,o_{yc} ,s_{za} } \right\}\) are thus reduced. In contrast, as angle b increases, the \(RSS_{PIGEs}\) for \(\left\{ {o_{za} ,o_{xc} ,s_{ya} ,s_{xc} ,s_{yc} } \right\}\) (which reflect sensitivity in the x- and z-directions) increase, and the measurement uncertainties of \(\left\{ {o_{za} ,o_{xc} ,s_{ya} ,s_{xc} ,s_{yc} } \right\}\) are thus increased. However, it is not essential to improve the \(RSS_{PIGEs}\) of all PIGEs. The reduction of workpiece geometric errors mainly requires an analysis of the effects of \(RSS_{PIGEs}\) on the volumetric error \({\mathbf{VE}}_{i}\) along testpiece toolpaths. As such, we used small (25°) and large (50°) angles of b to investigate the effect of this angle on volumetric error \({\mathbf{VE}}_{i}\) over the cone-shaped testpiece.

Fig. 7
figure 7

Simulation sequence to derive the optimal angle b

Full size image
Fig. 8
figure 8

Calculated \(RSS_{PIGEs}\) by the angle b

Full size image

\(RSS_{VE,i,j}\) \(\left( {i = x,y,z;\quad j = 1, \ldots ,720} \right)\) were calculated in Cartesian coordinates using Eq. (10) (Fig. 9a). The \(RSS_{VE,i,j}\) vary because the effects of \(RSS_{PIGEs}\) on volumetric error \({\mathbf{VE}}_{i}\) change with testpiece angle ψ. The peak-to-valley (PV) values of \(RSS_{VE,i,j}\) are greater at a large angle of b (50°) than at a small angle (25°). However, not all \(RSS_{VE,i,j}\) affect workpiece geometric errors, including the radial deviation of the cone lower surface; the radial deviations at that surface are critical for evaluating the cone-shaped testpiece because they reflect the lack of precise data on roundness. Thus, \(RSS_{VE,i,j}\) \(\left( {i = x,y,z;\quad j = 1, \ldots ,720} \right)\) in the Cartesian coordinate system are transformed into a cylindrical coordinate system, i.e., \(RSS_{VE,i,j}\) \(\left( {i = radial,tangential,axial;\quad j = 1, \ldots ,720} \right)\) (Fig. 9b). This yields PV values of \(RSS_{VE,i,j}\) \(\left( {i = radial;\quad j = 1, \ldots ,720} \right)\) of 0.3 and 0.2 μm/μm for angles of b of 25° and 50°, respectively. This reveals that testpiece radial deviation is further improved (by about 33%) when PIGEs are identified at b = 50° and compensated for, compared to the case when b = 25°. To determine the optimal angle b, the sum of the \(RSS_{VE,i,j}\) \(\left( {i = radial;\quad j = 1, \ldots ,720} \right)\) along toolpaths \(\left( {x_{TP,i} ,y_{TP,i} ,z_{TP,i} ,a_{TP,i} ,c_{TP,i} } \right)\) \(\left( {i = 1, \ldots ,720} \right)\) is calculated as shown in Fig. 10. The sum of the \(RSS_{VE,i,j}\) \(\left( {i = radial;\quad j = 1, \ldots ,720} \right)\) changes according to angle b; the minimum (optimal) value occurs when b = 50°. Note that the sum of \(RSS_{VE,i,j}\) \(\left( {i = tangential,axial;\quad j = 1, \ldots ,720} \right)\) increases with angle b, but this does not affect testpiece accuracy.

Fig. 9
figure 9

\(RSS_{VE,i,j}\) values at b angles of 25° and 50°

Full size image
Fig. 10
figure 10

Sum of \(RSS_{VE,i}\) \(\left( {i = radial,tangential,axial} \right)\) over the testpiece and the range of angle b

Full size image

3.2 Experiments

3.2.1 PIGE identification according to angle b

The PIGEs of an experimental machine tool (VMD 600/5AX; Doosan Machine Tools Co. Ltd., Republic of Korea) were identified at b angles of 50° (the optimal condition) and 25° using the wireless Trinity probe (Fig. 11). To identify the PIGEs, static data were collected over the range [− 90°, 30°] in steps of \(\Delta a\) = 15° (sample number \(n_{A}\) = 9) for the A-axis, and over the range [0°, 360°] in steps of \(\Delta c\) = 45° (sample number \(n_{C}\) = 9) for the C-axis.

Fig. 11
figure 11

Experimental set-up for different angles b

Full size image

The positional deviations \(\left( {x_{M,i} ,y_{M,i} ,z_{M,i} } \right)\) along all measurement paths exhibited large PVs (Fig. 12, in black) because the PIGEs were high. When the deviations \(\left( {x_{M,i} ,y_{M,i} ,z_{M,i} } \right)\) were inserted into Eqs. (5–8), the PIGEs shown in Fig. 13 were identified. The values differed, which was attributable to the various sensitivity coefficients of Eq. (8) that depend on angle b. By compensating the identified PIGEs using G-code modification, the positional deviations \(\left( {x_{M,i} ,y_{M,i} ,z_{M,i} } \right)\) were clearly improved at b angles of 25° and 50° (Fig. 12, in red), as was the measurement path. However, this does not guarantee direct improvements in workpiece geometric errors. Thus, we assessed how the PIGEs identified at b angles of 25° and 50° affected such errors.

Fig. 12
figure 12

Measured positional deviations without/with compensation

Full size image
Fig. 13
figure 13

PIGEs identified at angle b

Full size image

3.2.2 DBB measurement for the cone-shaped testpiece

We performed DBB measurements (equivalent to testpiece machining) to assess the radial deviation of the cone-shaped testpiece (Fig. 14). A DBB (QC20-w; Renishaw plc., Kingswood, UK) was used to measure radial deviations \(\Delta R_{i}\) \(\left( {i = 1, \ldots ,2132} \right)\) at a nominal length \(R\) = 100 mm along the bottom circular path of the testpiece without and with compensation of the PIGEs identified at b angles of 25° and 50°. For the DBB measurements, a ball was fixed on the workpiece table and another ball was fixed at the tool nose. Then, the distance between the two balls, along with the measurement path, were measured using a linear-variable-differential-transformer sensor. The ball on the workpiece table deviated from the nominal position in the coordinate system \(\left\{ {\mathbf{C}} \right\}\) due to two main factors: the PIGEs of the machine tool itself [41] and the set-up error caused by imperfection of the clamping device used for the ball. However, the set-up error of the experimental clamping device is negligible [42]. The deviation of the ball on the workpiece table was mainly affected by PIGEs and can be further reduced by compensating for the identified PIGEs. Thus, we used the raw measured deviation \(\Delta R_{i}\) as the radial deviation, without eliminating the eccentric center of the least squares circle [43], to investigate the PIGE effect for the cone-shaped testpiece.

Fig. 14
figure 14

DBB measurement set-up

Full size image

Without PIGE compensation (Fig. 15), the PV values were large, i.e., 94.8 and 95.5 μm in the counter-clockwise (CCW) and clockwise (CW) directions, respectively. Thus, the DBB measurements were repeated with PIGE compensation (Fig. 13). For angle b = 25° (Fig. 16a, b), in black], the PVs improved to 22.6 and 27.6 μm in the CCW and CW directions, respectively, showing the effectiveness of PIGE identification and compensation. However, this was achieved by improving the volumetric errors of the experimental machine tool, rather than by directly improving the workpiece geometric errors. Thus, the improvements were significant but limited. The PVs with compensation for the identified PIGEs at b = 50° (Fig. 16a, b), in red] were 16.4 and 22.9 μm in the CCW and CW directions, respectively. Thus, the radial deviation values were further improved by 27% and 17%, respectively, after compensating for the identified PIGEs at the optimal angle. Therefore, workpiece geometric errors can be reduced cost-effectively simply by using an optimal angle b, rather than by decreasing the uncertainties of measured data.

Fig. 15
figure 15

Measured radial deviations of the DBB measurements (without compensation)

Full size image
Fig. 16
figure 16

Measured radial deviations of the DBB measurements (with compensation)

Full size image

4 Summary and conclusion

The rotary axis PIGEs can be identified using the method in ISO 10791-6. However, the method is not optimized to reduce PIGE measurement uncertainties, associated with workpiece geometric errors. Thus, we proposed an adaptive identification method. The measurement paths for adaptive identification of rotary axis PIGEs described in ISO 10791-6 were modeled according to the initial angle of a precision ball installed on a workpiece table. PIGEs were calculated as the sum of the sensitivity coefficients multiplied by the measured deviations, and PIGE measurement uncertainties were defined as the RSS values of the sensitivity coefficients multiplied by the uncertainties of the measured data. The effects of the RSS values on workpiece geometric errors were explored using an error synthesis model. The effect of the summed RSS values on volumetric errors along the workpiece toolpath was calculated and used as the criterion for the optimal initial angle. Finally, PIGEs were identified using an optimized measurement path to reduce workpiece geometric errors. The main findings of our study are as follows:

  1. (1)

    To determine the PIGEs of rotary axes, ISO 10791-6 recognizes several methods using a DBB, R-test device, and touch-trigger probe, and defines the test conditions. Most approaches use PIGE measurements to reduce the volumetric errors of machine tools to, in turn, reduce workpiece geometric errors. However, such approaches are vague and indirect; although the improvements are significant, they are limited. It is essential to optimize the well-known method for PIGE measurements associated with workpiece geometric errors and reduce such errors directly.

  2. (2)

    An error-budgeting model is essential for calculating the measurement uncertainties of identified PIGEs, which reflect a lack of precise knowledge. Calculated measurement uncertainties are used to derive the PIGE-measuring capabilities of the various methods. Such approaches focus mainly on the effects of measuring devices, and systematic and non-systematic errors of the controlled axes, on the identified PIGEs. However, PIGE measurement uncertainties are also affected by the measurement path, which therefore cannot be ignored. PIGE measurements should be performed along an optimized path, i.e., a path that minimizes the effect of the RSS values of the PIGE sensitivity coefficients on workpiece geometric errors.

  3. (3)

    Identification of and compensation for the PIGEs of rotary axes may reduce workpiece geometric errors, because the PIGEs are the most significant errors of five-axis machine tools. Equivalent DBB experiments (without compensation) revealed that the radial deviation values of the ISO 10791-7 cone-shaped testpiece were 94.8 and 95.5 μm in the CCW and CW directions, respectively. However, the radial deviation values improved to 22.6 and 27.6 μm after compensation for the identified PIGEs along a common measurement path. Our strategy proved effective; the radial deviation values improved by 16.4 and 22.9 μm (27% and 17% improvements, respectively) when we adaptively identified and compensated for PIGEs along the optimal measurement path. Our method is also cost-effective. In addition, the improvements could be further increased by measuring and compensating the linear axis geometric errors.

  4. (4)

    Five-axis machine tools play a significant role in the machining of various complex-shaped workpieces; their application is not limited to the ISO 10791-7 cone-shaped testpiece used as an example in this study. The identification method in ISO 10791-6 should be optimized in terms of workpiece geometric error, to maximize error reduction in a direct manner. This can be done by analyzing the RSS values of the sensitivity coefficients. Measurements can then be optimized merely by adjusting the setting angle of a ball on the workpiece table (or the height of the ball from the table), without changing any methods of ISO 10791-6.