Extended High Gain Observer-Based Sliding Mode Control for an Electro-hydraulic System with a Variant Payload

Abstract

This paper presents a robust control regarding position control of an electro-hydraulic rotary actuator (EHRA) system under the presence of the lumped uncertainties such as the variant payload, the unknown friction, and the uncertain parameters. The proposed control is developed on a high order sliding mode control (HOSMC) and an extended high gain observer (EHGO). In detail, the HOSMC is derived to not only reduce the chattering effect but also guarantee the stability for the EHRA. In addition, the EHGO is used as a disturbance estimator to compensate the lumped uncertainties. Consequently, it helps to improve control performance. Furthermore, the stability and robustness of the whole system are theoretically proved by a Lyapunov approach. The proposed control is practically implemented through both the co-simulation between AMESIM and MATLAB, and the experiments. The results are compared to other controllers to exhibit the effectiveness of the proposed control with the lumped uncertainties.

1 Introduction

Recently, hydraulic systems play a crucial role in modern industry due to their fast responses and high power-to-weight ratios [1]. A conventional hydraulic system actuator is supplied with high-pressure oil from a hydraulic power unit. Control valves are usually used as the final control elements in the operation of the system to control the flow in and out of the hydraulic system from one or two chambers on either side of a working piston. Therefore, plant efficiency is directly affected by the performance of the valves. Energy consumption due to system losses may occur because of leakage or flow from the pump bypass valves. Losses also result from the energy that is transformed into heat because of throttle losses at the control valves [2]. An electrohydraulic actuator (EHA) is a combination of an electric motor, bi-directional pump, reservoir, and hydraulic circuit [3,4,5,6]. The system does not have control valves, which minimizes pressure losses and reduces heat generation in the fluid line. However, the dynamics of a pump-controlled EHA are complicated in control problems because dynamic behaviors of the pump supplied valves must be considered with the hydraulic actuator [7].

In order to achieve a position tracking for pump-controlled EHAs, several advanced controllers such as fuzzy PID [8], sliding mode control (SMC) [9,10,11,12,13], and adaptive backstepping control [7, 14, 15] have been developed. As a nonlinear control approach, the SMC exhibits good performance in resolving nonlinear system control problem against the uncertainties and external disturbance. The fundamental idea of the SMC is to use a discontinuous control term to drive the controlled system’s error state variables toward zero. Perron et al. [10] developed an SMC to overcome dynamic problems caused by the nonlinearities and parametric uncertainties in a pump-controlled EHA. Lin et al. [11] proposed a robust discrete-time SMC for a fluid power EHA system with the presence of vary friction parameters. Although the results proved the effectiveness of the SMC, they did not mention about the chattering problem caused by high-frequency control switching [16]. It may excite high-frequency dynamics and cause instability. In order to deal with this issue, a fuzzy logic system [9] was used to replace the discontinuous term. However, it involves low-pass filters thus weakening the steady-state error.

This paper presents an adaptive high order sliding mode control for position control of an EHA system with the presence of the variant payload, and unknown friction, and parametric uncertainties. Because the EHA system in this research uses a rotary actuator, this system is called an electro-hydraulic rotary actuator (EHRA) system in whole paper. The proposed control is constructed based on High order sliding mode control (HOSMC) and Extended high gain observer (EHGO). Different from the previous study [9], the HOSMC algorithm developed by Levant [17]. is to hide the discontinuity of control in its higher derivatives. It is a good candidate to deal with the chattering effect and preserve the main properties of the SMC. However, when the upper boundary of the uncertainties is large, then this SMC without a compensator can still cause serious chattering. The EHGO is a disturbance observer, which was developed by Han [18]. The merit of the extended state observer does not only possess the state observation capability but also provide a real-time estimation of lumped disturbance [19]. Comparing to the neural network [20,21,22,23] and fuzzy logic system [24, 25], the EHGO provide a simple approximator to estimate the lumped uncertainties. The observers have been employed to apply various EHGO-based controllers and verified in many applications [19, 26,27,28,29,30]. In this paper, the combination of EHGO and HOSMC is firstly applied into tracking control task of the EHRA system. The stability of the controlled system is theoretically proved by a Lyapunov stability theory. To verify the efficiencies of the proposed control, two case studies are analyzed. The first case is implemented by using co-simulation between MATLAB and AMESIM software. Other case is the experiments on the practical test bench.

This paper is organized as follows: Sect. 2 introduces the system modeling and problem statement. Section 3 presents the design details of the proposed control and stability proof by using the Lyapunov approach. Some results of proposed control which are implemented through both co-simulation and experiments are shown in Sect. 4. Finally, conclusions are produced in Sect. 5.

2 System Modeling and Problem Statement

2.1 Mechanical Dynamic

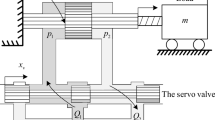
The considered EHRA in this paper includes a gear pump, supplement valves, and asymmetrical hydraulic rotary. The EHRA configuration is shown in Fig. 1.

Fig. 1

Structure of the pump-controlled electro-hydraulic rotary actuator

Using the second Newton’s law and principles of hydraulics system, the dynamics of the load shaft in loading rotary actuator (RA) can be described by the following state space [31]:

$$J\ddot{\theta } = (P_{1} - P_{2} )D_{R} - T$$

(1)

Here, $\ddot{\theta }$ is rotor angular acceleration of loading system, $J$ is the moment of inertia of load shaft, $P_{1}$ and $P_{2}$ are pressure values of two chambers respectively, $D_{R}$ is the displacement of the rotary actuator, $T$ is the reaction torque on the RA.

2.2 Hydraulic Dynamics

Base on the configuration of the EHRA system in Fig. 1, flow rates into two chambers are calculated as

$$\left\{ \begin{aligned} Q_{1} = Q_{P1} + Q_{v5} - Q_{v3} \hfill \\ Q_{2} = Q_{P2} + Q_{v6} - Q_{v4} \hfill \\ \end{aligned} \right.$$

(2)

where $Q_{Pi}$ is the flow rate from the pump supplying to the i^th chamber; $Q_{P1} = Q_{pump}$, $Q_{P2} = - Q_{P1}$; $Q_{pump}$ is the pump flow rate.

$$Q_{pump} = D\omega - k_{leakage} (P_{1} - P_{2} )$$

(3)

Here, k_leakage is the leakage constant, $D$ is the displacement of the pump, and $\omega$ is the speed of the pump system. The terms $Q_{vi} \left( {i = 3,..,6} \right)$ are flow rates through valves $v_{i} \left( {i = 3,..,6} \right)$, respectively.

In typical operation, the system pressure values: $P_{1} ,P_{2}$ should be kept under the setting value $P_{set}$ of the two relief valves: $v_{3}$, and $v_{4}$. It means the flow rates through the two relief valves: $Q_{v3}$, and $Q_{v4}$ maintain zero. Consequently, Eq. (3) can be rewritten as

$$\left\{ \begin{aligned} Q_{1} = Q_{P1} + Q_{v1} \hfill \\ Q_{2} = Q_{P2} + Q_{v2} \hfill \\ \end{aligned} \right.$$

(4)

Assume there is no external leakage, the dynamics of oil flow can be calculated as [32]

$$\left\{ \begin{aligned} \dot{P}_{1} = \frac{\beta }{{V_{01} + A\theta }}\left( {Q_{1} - A\dot{\theta } - C_{t} \left( {P_{1} - P_{2} } \right)} \right) \hfill \\ \dot{P}_{2} = \frac{\beta }{{V_{02} - A\theta }}\left( {Q_{2} + A\dot{\theta } + C_{t} \left( {P_{1} - P_{2} } \right)} \right) \hfill \\ \end{aligned} \right.$$

(5)

where $V_{01}$ and $V_{02}$ are original total volumes of two chambers respectively, $Q_{1}$ represents the supply flow rate to the chamber 1, $Q_{2}$ represents the supply flow rate to the chamber 2, $\dot{\theta }$ is the angular velocity of the loading system and $C_{t}$ is the coefficient of the internal leakage of the RA.

For the ease of calculation, let the system states be defined as

$$x = \left( {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right)^{T} = \left( {\theta ,\dot{\theta },P_{1} ,P_{2} } \right)^{T}$$

(6)

Then, the simplified mathematical model of the EHRA system can be described by employing (1), (2), (3), (4), and (5).

$$\left\{ \begin{array}{l} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = \frac{{D_{R} }}{J}\left( {x_{3} - x_{4} } \right) - \frac{T}{J} \hfill \\ \dot{x}_{3} = \frac{{\beta_{e} }}{{V_{01} + Ax_{1} }}\left( {D\omega - \left( {k_{leakage} + C_{t} } \right)\left( {x_{3} - x_{4} } \right) + Q_{v1} - Ax_{2} } \right) \hfill \\ \dot{x}_{4} = \frac{{\beta_{e} }}{{V_{02} - Ax_{1} }}\left( { - D\omega + \left( {k_{leakage} + C_{t} } \right)\left( {x_{3} - x_{4} } \right) - Q_{v2} + Ax_{2} } \right) \hfill \\ \end{array} \right.$$

(7)

To simplify the system (7), define

$$\begin{aligned} & x_{34} = \frac{{x_{3} - x_{4} }}{J}D_{R} ;\;d_{1} = - \frac{T}{J};k_{leak} = k_{leakage} + C_{t} ;\;\beta = \frac{{\beta_{e} }}{J} \\ & g\left( {x_{1} } \right) = \left( {\frac{\beta }{{V_{01} + Ax_{1} }} + \frac{\beta }{{V_{02} - Ax_{1} }}} \right)D_{R} D \\ & f\left( {x_{1} ,x_{2} } \right) = - \beta D_{R} Ax_{2} \left( {\frac{1}{{V_{01} + Ax_{1} }} + \frac{1}{{V_{02} - Ax_{1} }}} \right) \\ \end{aligned}$$

Obviously, system states are adjusted by the speed of the bi-directional pump that is driven by a DC motor. Given a bounded desired trajectory: $x_{1d}$, the objective of this paper is to determine the input speed command for the DC motor $\omega$ to control the output position $x_{1}$ track closely as possible to $x_{1d}$. Then the state space (7) can be rewritten in strictly feedback form as

$$\begin{aligned} & \dot{x}_{1} = x_{2} \\ & \dot{x}_{2} = x_{34} + d_{1} \left( t \right) \\ & \dot{x}_{34} = g\left( {x_{1} } \right)u + f\left( {x_{1} ,x_{2} } \right) + d_{2} \left( t \right). \\ \end{aligned}$$

(8)

Remark 1

In practical hydraulic systems with common working conditions, the pressure in two chambers are bounded by P_set and P_tank, and the function g(x1) is always a non-zero function.

Assumption 1

The matched and mismatched disturbances $d_{i} \left( t \right),i = 1,2$, their first derivatives and their second derivatives are bounded.

$$\left| {d_{i} \left( t \right)} \right| \le \kappa_{i} ,\left| {\dot{d}_{i} \left( t \right)} \right| \le \alpha_{i} ,\left| {\ddot{d}_{i} \left( t \right)} \right| \le \beta_{i} ,\quad i = 1,2$$

(9)

where $\kappa_{i}$, $\alpha_{i}$, and $\beta_{i}$ are positive constants.

3 Control Design

3.1 Design Model and Issues to be Address

In this paper, the estimated values of physical parameters are utilized in the observer and control design, and the parametric uncertainties are lumped to the unmodeled term, i.e., $d_{1} \left( t \right)$ in the second equation and $d_{2} \left( t \right)$ in the third equation of (8).

In practice, the inertial and friction load in mechanical dynamics, and hydraulic parametric uncertainties, such as bulk modulus, leakages always exist and changes with respect to time, and they can affect to control performances. They are considered as the main issue in the controlled system and should be handled and compensated in the observer and controller design.

To achieve the aforementioned design missions, the system state $\zeta$ is redefined as follows $\zeta = \left[ {\zeta_{1} ,\zeta_{2} ,\zeta_{3} ,\zeta_{4} } \right]^{T} = \left[ {x_{1} ,x_{2} ,\dot{x}_{2} ,\dot{d}_{1} \left( t \right) + \frac{{D_{R} }}{J}d_{2} } \right]^{T}$. The derivative of $d_{1} \left( t \right)$ and $d_{2}$ is defined as $\zeta_{4}$. Let $\delta \left( t \right)$ represent the time derivative of $\zeta_{4}$, the plant (8) can be rewritten as

$$\left\{ \begin{array}{l} \dot{\zeta }_{1} = \zeta_{2} \hfill \\ \dot{\zeta }_{2} = \zeta_{3} \hfill \\ \dot{\zeta }_{3} = f\left( {\zeta_{1} ,\zeta_{2} } \right) + g\left( {\zeta_{1} } \right)u + \zeta_{4} \hfill \\ \dot{\zeta }_{4} = \delta \left( t \right) \hfill \\ \end{array} \right..$$

(10)

Remark 2

Based on Assumption 1, the term, $\left| {\delta \left( t \right)} \right| \le \kappa_{1}$ is bounded.

Assumption 2

The desired trajectory belongs to $C^{3}$ and bounded.

Assumption 3

[27] The function $g\left( {\zeta_{1} } \right)$ is Lipschitz with respect to $\zeta_{1}$ in its practical range; $f\left( {\zeta_{1} ,\zeta_{2} } \right)$ is globally Lipschitz with respect to $\zeta_{1}$ and $\zeta_{2}$.

3.2 Extended High Gain Observer Design

This observer design is not only estimating the unmeasured system state ($\zeta_{2} ,\zeta_{3}$) but also approximate the lumped uncertainties for the controller compensation in real-time. The extended system (10) is represented in matrix form as follows:

$$\begin{aligned} &\dot{\zeta } = A\zeta + F\left( \zeta \right) + G\left( \zeta \right)u + \Delta \left( t \right) \hfill \\ &y = C\zeta \hfill \\ \end{aligned}$$

(11)

where $A = \left[ {\begin{array}{*{20}l} { 0} \hfill & {\quad 1} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ {0} \hfill & {\quad 0} \hfill & {\quad 1} \hfill & {\quad 0} \hfill \\ {0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 1} \hfill \\ {0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ \end{array} } \right]$, $F\left( \zeta \right) = \left[ \begin{array}{*{20}c} 0 \hfill \\ 0 \hfill \\ f\left( {\zeta_{1,} \zeta_{2} } \right) \hfill \\ 0 \hfill \\ \end{array} \right]$, $G\left( \zeta \right) = \left[ \begin{array}{c} 0 \hfill \\ 0 \hfill \\ g\left( {\zeta_{1} } \right) \hfill \\ 0 \hfill \\ \end{array} \right]$, $\Delta \left( t \right) = \left[ \begin{array}{c} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \delta \left( t \right) \hfill \\ \end{array} \right]$, $C = \left[ {\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$.

An extended high gain observer which is based on [27] and model (11) can be constructed as

$$\dot{\hat{\zeta }} = A\hat{\zeta } + F\left( {\hat{\zeta }} \right) + G\left( {\hat{\zeta }} \right)u + L\left( {\zeta_{1} - \hat{\zeta }_{1} } \right)$$

(12)

where $\hat{\zeta }$ denotes the estimate of $\zeta$, $F\left( {\hat{\zeta }} \right) = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {f\left( {\zeta_{1} ,\hat{\zeta }_{2} } \right)} \hfill & 0 \hfill \\ \end{array} } \right]^{T}$, $G\left( {\hat{\zeta }} \right) = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {g\left( {\zeta_{1} } \right)} \hfill & 0 \hfill \\ \end{array} } \right]^{T}$, $L = \left[ {\begin{array}{*{20}l} {\lambda_{1} \alpha_{0} } \hfill & {\lambda_{2} \alpha_{0}^{2} } \hfill & {\lambda_{3} \alpha_{0}^{3} } \hfill & {\lambda_{4} \alpha_{0}^{4} } \hfill \\ \end{array} } \right]^{T}$ is observer gain, and $\alpha_{0}$ is the bandwidth of the observer.

Let $\tilde{\zeta }$ derive the estimation error ($\tilde{\zeta } = \zeta - \hat{\zeta }$).

The dynamic of the state estimation error can be presented as

$$\begin{aligned} &\dot{\tilde{\zeta }} = A\tilde{\zeta } + F\left( \zeta \right) - F\left( {\hat{\zeta }} \right) + \left( {G\left( \zeta \right) - G\left( {\hat{\zeta }} \right)} \right)u \\ &\quad - L\left( {\zeta_{1} - \hat{\zeta }_{1} } \right) + \Delta \left( t \right) \\ \end{aligned}$$

(13)

Define $\tilde{F} = F\left( \zeta \right) - F\left( {\hat{\zeta }} \right)$,$\tilde{G} = G\left( \zeta \right) - G\left( {\hat{\zeta }} \right) = 0$, $\tilde{f} = f\left( {\zeta_{1} ,\zeta_{2} } \right) - f\left( {\zeta_{1} ,\hat{\zeta }_{2} } \right)$ and let $\varepsilon_{i} = \frac{{\tilde{\zeta }_{i} }}{{\alpha_{0}^{i - 1} }},i = 1,\ldots,4$ derive the scale estimation error. Then, (13) can be rewritten as

$$\dot{\varepsilon } = \alpha_{0} A_{0} \varepsilon + B_{1} \frac{{\tilde{f}}}{{\alpha_{0}^{2} }} + B_{2} \frac{\delta \left( t \right)}{{\alpha_{0}^{3} }}$$

(14)

where $\varepsilon = \left[ {\begin{array}{*{20}l} {\varepsilon_{1} } \hfill & {\varepsilon_{2} } \hfill & {\varepsilon_{3} } \hfill & {\varepsilon_{4} } \hfill \\ \end{array} } \right]^{T}$ and $B_{1} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} } \right]^{T}$, $B_{2} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]^{T}$, $A_{0} = \left[{\begin{array}{*{20}l} {-\lambda_{1} } \hfill & {\quad 1} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ {-\lambda_{2} } \hfill & {\quad 0} \hfill & {\quad 1} \hfill & {\quad 0} \hfill \\ {-\lambda_{3} } \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 1} \hfill \\ {-\lambda_{4} } \hfill & {\quad 0} \hfill & {\quad 0} \hfill & {\quad 0} \hfill \\ \end{array} } \right]$ in which $A_{0}$ is Hurwitz. Hence, there exists a positive definite matrix $P$ satisfying the following Lyapunov equation:

$$A_{0}^{T} P + PA = - 2I$$

(15)

Based on [27, 33], the dynamic of the scaled estimation error (14), and (15), it can be inferred that the state estimation error can be made arbitrarily small by increasing the bandwidth $\alpha_{0}$.

3.3 High Order Sliding Mode Control Design

The high order sliding mode surface is selected as follows:

$$\begin{aligned} &s_{1} = k_{1} e_{1} + k_{2} e_{2} + e_{3} \hfill \\ &s_{2} = \dot{s}_{1} + k_{3} s_{1} \hfill \\ \end{aligned}$$

(16)

where $k_{i} ,i = 1,2$ are positive constants and can be chosen to ensure that the polynomial $p^{2} + k_{2} p + k_{1}$ is Hurwitz; $k_{3}$ is arbitrary positive constant, $e_{i} = \zeta_{i} - \zeta_{id} ,\left( {i = 1,2,3} \right)$; and $x_{id}$ are desired displacement trajectories.

The control law is selected as follows:

$$u = g^{ - 1} \left( {\zeta_{1} } \right)\left( {u_{eq} + {\text{u}}_{\text{r}} } \right)$$

(17)

$$u_{eq} = - f\left( {\zeta_{1} ,\zeta_{2} } \right) - k_{3} s_{1} - k_{1} e_{2} - k_{2} e_{3} + \dot{\zeta }_{3d} - \hat{\zeta }_{4}$$

(18)

$$\dot{u}_{r} = - Tu_{r} + v$$

(19)

$$v = - \left( {\eta_{0} + \eta_{1} + \eta_{2} } \right)sign\left( {s_{2} } \right)$$

(20)

where $T \ge 0$ is positive constant; $\eta_{i} ,i = 1,2,3$ are positive constants.

The sliding variable $s_{2}$ yields as follows:

$$\begin{aligned} s_{2} = \dot{e}_{3} + \lambda_{2} e_{3} + \lambda_{1} e_{2} + k_{1} s_{1} \\ = f\left( {\zeta_{1} ,\zeta_{2} } \right) + g\left( {\zeta_{1} } \right)u + \zeta_{4} \\ - \dot{\zeta }_{3d} + k_{2} e_{3} + k_{1} e_{2} + k_{3} s_{1} \\ \end{aligned}$$

(21)

Replacing the control law (17) and (18) into (21), we have

$$s_{2} = u_{r} + \tilde{\zeta }_{4}$$

(22)

The derivative of the sliding variable, $s_{2}$, is expressed as

$$\dot{s}_{2} = \dot{u}_{r} + \dot{\tilde{\zeta }}_{4} = - Tu_{r} - \left( {\eta_{0} + \eta_{1} + \eta_{2} } \right)sign\left( {s_{2} } \right) + \dot{\tilde{\zeta }}_{4}$$

(23)

3.4 Control Stability

To prove the stability of the whole system, a Lyapunov function is selected as

$$V\left( {\varepsilon ,s_{2} } \right) = \frac{1}{2}\varepsilon^{T} P\varepsilon + \frac{1}{2}s_{2}^{2}$$

(24)

Taking the derivative of the Lyapunov function (24), the result is expressed as follows:

$$\begin{aligned} \dot{V}\left( {\varepsilon ,s_{2} } \right) &\le - \left( {\frac{{\sigma_{0} }}{2} - c_{1} } \right)\varepsilon^{T} \varepsilon - \left( {s_{2} Tu_{r} + \eta_{1} \left| {s_{2} } \right|} \right) \\ &\quad + \left( {\dot{\tilde{\zeta }}_{4} s_{2} - \eta_{2} \left| {s_{2} } \right|} \right) - \eta_{0} \left| {s_{2} } \right| \\ \end{aligned}$$

(25)

The control gains, $\eta_{i,i = 1,2}$, are chosen to

$$\eta_{1} \ge \left| {T\tilde{\zeta }_{4} } \right|,\eta_{2} \ge \left| {\dot{\tilde{\zeta }}_{4} } \right|$$

(26)

Equation (25) is represented as follows:

$$\dot{V}\left( {\varepsilon ,s_{2} } \right) \le - \left( {\frac{{\sigma_{0} }}{2} - c_{1} } \right)\varepsilon^{T} \varepsilon - \eta_{0} \left| {s_{2} } \right| \le 0$$

(27)

which can conclude that the system is asymptotically stable [34]. It means that the estimated state error will reach zero, and the system state will approach the sliding mode surfaces.

4 Numerical Simulation and Experimental Evaluation

In this paper, both simulations and experimental results are implemented under the presence of unknown payload and uncertainties. Then, they are compared with PID control, SMC, and SMC with EHGO to verify the effectiveness of the proposed control.

Remark 3

During the simulation and experimental procedure, the PID control is first implemented to guarantee the consistent performance of the system. Then, the proposed observer is applied to estimate the unmeasured states. The observer parameters are adjusted how the residual error between the estimated output state and the measured output state are bounded by the predetermined value. Finally, the HOSMC is carried out with the lumped disturbance which calculated by the observer.

4.1 Simulation Results

In this section, some simulations are described to demonstrate the efficiency of the proposed. These simulations are implemented by using a co-simulation between AMESIM 15.2 and MATLAB 2017a with a sampling time of 10 ms. The co-simulation structure which is shown in Fig. 2 includes two groups: one is the control group, and the other is the system dynamics group. In the system dynamics group, an S-function block is used to import the EHRA system dynamics which is set up in the AMESIM 15.2 as presented in Fig. 3.

Fig. 2

Simulation structure in MATLAB 2017a

Fig. 3

EHRA system in AMESIM

The parameters of the EHRA system are based on the parameters of the real test bench as presented in Table 1, $I = 1\;{\text{kg}}\,{\text{m}}^{2}$, $A = 0.0765\;{\text{cc/deg}}$, and under the presence of the lumped uncertainties such as measurement noise, viscous friction 10 Nm, leakages $\left( {C_{t} + k_{leakage} } \right) = 0.01\;{\text{l/min/bar}}$, and variant payload.

Table 1 Setting parameters for the EHRA system

Three simulations are carried out with the sine reference signal of 0.1 Hz, and 0.2 Hz. First, reference input is the sine signal of 0.1 Hz, and the payload is 50 N. Second, reference input is the sine signal of 0.2 Hz, and the payload is 50 N. Third, reference input is the sine signal of 0.1 Hz, and the payload is 1000 N.

Remark 4

In order to illustrate the effectiveness of the proposed control, the control parameters of the controllers are chosen in the first simulation case, then they are kept in other simulation cases.

The parameters of the controllers are chosen as follows: PID: $K_{p} = 500$, $K_{I} = 0$,$K_{D} = 50$; SMC: $k_{1} = 83.5$, $k_{2} = 280$,$k_{3} = 50$, $\sum\nolimits_{i = 0}^{2} {\eta_{i} } = 10^{3}$; EHGO: $\omega = 80$, $\lambda_{1} = 4$, $\lambda_{2} = 6$,$\lambda_{3} = 4$, $\lambda_{4} = 1$, the proposed control $T = 1$.

In the first simulation, Fig. 4 shows tracking performances of the PID, HOSMC, and the proposed control with a payload of 50 N. The results in Fig. 5 proved that the proposed control and the SMC with EHGO improved the accuracy more effectively than the PID, SMC. Figure 6, plots the pressures in two chambers with the proposed control. Figure 7, which is the control signals of the controllers showed that the proposed control reduced the chattering effect caused by the discontinuous term in the SMC. Base on Fig. 8, the remained fluctuations of the control signal are caused by the estimated lumped disturbance.

Fig. 4

Output performances of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz, and the payload of 50 N

Fig. 5

Error effort of PID, SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.1 Hz, and the payload of 50 N

Fig. 6

Pressure performances in two chambers of the proposed control with the sinusoidal signal of 0.1 Hz and the payload of 50 N

Fig. 7

Control signals of PID. SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.1 Hz and the payload of 50 N

Fig. 8

Estimated disturbance with the sinusoidal signal of 0.1 Hz and the payload of 50 N

In the second simulation, the frequency of the sinusoidal signal is changed from 0.1 Hz to 0.2 Hz. Figure 9 shows that the frequency of the references affects the accuracy of the controlled system with the PID, the SMC, and the SMC with EHGO. However, it is compensated by the extended high gain observer. Figure 10 plots the pressures in two chambers with the proposed control. Figures 11 and 12 are the control signals and the estimated lumped disturbance. The results also proved that the proposed control reduces the chattering effect, and the remained fluctuation in the control signal is caused by the estimated lumped uncertainties.

Fig. 9

Error effort of PID, SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.2 Hz and the payload of 50 N

Fig. 10

Pressure responses in two chambers with the proposed control with the sinusoidal signal of 0.2 Hz and the payload of 50 N

Fig. 11

Control signal of PID, SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.2 Hz and the payload of 50 N

Fig. 12

Estimated disturbance with the sinusoidal signal of 0.2 Hz and the payload is 50 N

In the third simulation, the payload is changed from 50 N to 1000 N, and the frequency of input reference is kept at 0.1 Hz. Figure 13 shows that the variant payload affected the performances of the controllers. In the proposed control and the SMC with EHGO, the EHGO compensated to enhance the accuracy performance. Figure 14 plots the pressures in two chambers with the proposed control. The results in Figs. 15 and 16 demonstrated that the proposed control reduce the chattering effect in the control signal. The remained fluctuation in the control signal is caused by the estimated lumped uncertainties.

Fig. 13

Error effort of PID, SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.1 Hz, and the payload of 1000 N

Fig. 14

Pressure performances in two chambers of the proposed control with the sinusoidal signal of 0.1 Hz and the payload of 1000 N

Fig. 15

Control signal of PID, SMC, SMC with EHGO, and the proposed control with the sinusoidal signal of 0.1 Hz, and the payload is 1000 N

Fig. 16

Estimated disturbance with the sinusoidal signal of 0.1 Hz and the payload of 1000 N

Fig. 17

Structure of the experiment test rig

Remark 5

The error efforts of the SMC with EHGO and the proposed control are close to each other, as presented in Figs. 5, 9, and 13, because the lumped uncertainties in the EHRA system are estimated and compensated by the EHGOs in these controllers. Other advantage of the proposed control is chattering reduction, which are presented in Figs. 7, 11, and 15.

4.2 Experimental Results

The experimental test rig is shown in Fig. 18. It includes an EHRA system, a vane rotary actuator, two pressure sensors, and a rotary encoder. The EHRA system is manufactured by Bosch Rexroth, which consists of a gear pump and supplement valves system. The vane RA is made from KNR system INC. The whole system is driven by a 24 V—20A DC motor. In this configuration, the movement of the RA is adjusted directly by the speed of the DC motor. One rotary encoder and two pressure transducers are installed to the system to measure the rotary position, the pressure in two chambers of main EHRA, respectively. The load simulator part is a gravity loading system which can adjust the loading force quickly by changing the attached mass. This setting is a simple yet efficient method to simulate the variation of the working condition for the EHRA system.

Fig. 18

Experimental apparatus with pressure sensors, a rotary actuator with encoder, hydraulic power unit, and load

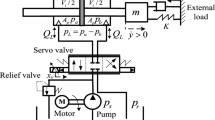
The developed controller is carried out on a personal computer within the Simulink environment combined and Real-time Windows Target Toolbox of MATLAB with the sampling time of 10 ms. One encoder Quad-04 Card from Measure Computing Corp. and multifunction data acquisition Advantech cards, NI6014 is installed on the PCI slots of the PC to perform the peripheral interfaces. Schematic diagram of the whole pump–controlled EHRA system is shown in Fig. 17, and setting parameters for the EHRA system are shown in Table 1.

Remark 6

The parameters in Table 1 are used to design the controllers. They are obtained by the device’s catalogs and hydraulic book [32].

Two experiments are employed on the EHRA system in 20 s. They are the sine reference signal of 0.1 Hz without payload and with a payload of 100 N. The parameters of the controllers are chosen as follows: PID: $K_{p} = 200$, $K_{I} = 10$,$K_{D} = 20$; SMC: $k_{1} = 40$, $k_{1} = 300$, $k_{2} = 25$, $\sum\nolimits_{i = 0}^{2} {\eta_{i} } = 500$; EHGO: $\lambda_{1} = 4$, $\lambda_{2} = 6$,$\lambda_{3} = 4$, $\lambda_{4} = 1$, $\omega = 70$; the proposed control T =0.1;

Remark 7

The controllers are designed without payload, and they are kept for the experiments with the payload of 100 N.

Figure 19 shows the output performances of the PID control, SMC, SMC with EHGO, and the proposed control without payload. The error results in Fig. 20 proved that the SMC with EHGO and the proposed control compensated the lumped uncertainties and improved the accuracy better than the PID control and the SMC. The control signals in Fig. 21 proved that the proposed control reduced the chattering effect better than the SMC with EHGO. The estimated lumped uncertainties are presented in Fig. 22.

Fig. 19

Output performances of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz and no payload

Fig. 20

Error effort of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz and no payload

Fig. 21

Control signal of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz and no payload

Fig. 22

Estimated disturbance with the sinusoidal signal of 0.1 Hz and without payload

Figure 23 shows the tracking error of the PID, SMC, SMC with EHGO, and proposed control with a payload of 100 N. The results also demonstrated that the SMC with EHGO and the proposed control improves the accuracy better than the PID and the SMC. The lumped uncertainties are estimated, as shown in Fig. 25. The control signals in Fig. 24 exhibited that the proposed control reduce the chattering effect more efficiency than the SMC with EHGO.

Fig. 23

Error effort of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz and payload of 100 N

Fig. 24

Control signal of PID, SMC, SMC with EHGO and the proposed control with the sinusoidal signal of 0.1 Hz and payload of 100 N

Fig. 25

Estimated disturbance with the sinusoidal signal of 0.1 Hz and payload of 100 N

5 Conclusion

This paper presented an EHRA system and a robust control regarding position control under the presence of the lumped uncertainties such as unknown friction, unknown leakages, and variant payload. Because the robust control is developed on a high order sliding mode control with an extended high gain observer, so it can inherit the advantages of both the HOSMC and the EHGO for improving the control performance and reducing chattering effect. The EHGO provided a simpler approximator than the fuzzy logic system and the neural network to estimate the lumped uncertainties. Additionally, the stability and robustness of the proposed control were theoretically proved by the Lyapunov approach. Some simulations and experiments were carried out by co-simulating two types of the simulation software of AMESIM 15.2 and MATLAB2017a and on the EHRA test bench. Comparative results were obtained to verify the efficiency of the proposed control.

However, the experimental results presented that the control performance was degraded when the system changed direction. Some intensive studies about this problem will be considered as future works of this paper.