1 Introduction

With the continuous development of modern manufacturing technology, the demand for high-precision NC machine tools is increasing. Machining accuracy is a significant performance index of NC machine tool, which directly influences the machining quality of the workpiece. How to improve the machining accuracy economically is a crucial issue, and researchers around the world have carried out in-depth studies on it [1,2,3,4]. Compared with the hardware compensation for machine tool error, error measurement and compensation as software technology to improve the machining accuracy have the advantages of wide applicability and low cost etc. [5,6,7], which has been widely used in the field of accuracy compensation of machine tool. In the machining process of workpiece, there exist many error factors, such as geometric error, thermal deformation error, cutting force error, clamping error etc., and these errors affect the final machining accuracy. Among these error factors, the geometric error is a major one [8,9,10,11,12]. It is relatively stable, and it is easy to be measured and compensated. Thus, the measurement and compensation for the geometric error of machine tool is one of the effective ways to improve the machining accuracy.

Currently, there are many methods for detecting the geometric error of machine tool, such as artifact standard measurement, laser ball bar measurement [13, 14], orthogonal grating measurement [15], laser interferometer measurement [16, 17], and so on. When the artifact standard is adopted, the operation is relatively easy, and the measurement is efficient. However, the measurement accuracy is lower due to the contact measurement adopted by this method. For laser ball bar measurement, the measurement can only be carried out within a certain range due to the limitation of the displacement sensor range, and the whole working space of machine tool can not be measured. Meanwhile, the identification of individual error is complex. For orthogonal grating measurement method, the measurement accuracy and efficiency is relatively high. However, the larger planar grating is challenging to be manufactured, and the cost is high. For laser interferometer measurement, the measurement accuracy is high. The corresponding optical accessories are needed for different geometric errors measurement. Meanwhile, the light adjustment is time-consuming in the measurement, so the measurement efficiency is inefficient.

Recently, laser tracker as a three-dimensional measuring instrument has been applied to the error calibration of the machine tool and the coordinate measuring machine [18,19,20,21,22,23]. Laser tracker is usually adopted spherical coordinate measurement principle, and its angle measurement error has a great influence on the coordinate measurement result [24]. For example, if the angle error is assumed as 1 arc seconds, the error will be amplified by about 5 µm each meter. [22] At present, the requirement of accuracy detection of machine tool is becoming higher and higher, and this measurement mode can not satisfy the accuracy demand. To further improve the measurement accuracy, a laser tracker is used to measure the target points successively at different base stations on the basis of GPS (Global positioning system) principle in Ref [18]. and [20], which is called‘multi-station and time-sharing measurement’. Only distance is involved in the measurement, and the influence of angle error on the measurement results can be effectively avoided. So, the measurement accuracy is greatly improved. However, this measurement has some shortcomings: (1) In order to identify the geometric error of machine tool, the machine tool should be controlled to feed in the 3D space, and the corresponding measurement trajectory is relatively complex. When the motion trajectory of machine tool is in a 2D plane or 1D line, the geometric error of machine tool can not be separated. (2) In the calibration of the base station, the calibration accuracy will be affected by the error of machine tool, which limits the further improvement of measurement accuracy. Given the problems mentioned above, a new method for geometric error calibration of the machine tool with laser tracker is proposed in the paper. A series of measuring points are set on the moving parts of the machine tool, and adjacent measuring points are connected to form a space vector. Then, the corresponding geometric errors can be identified by measuring the change of vector’s direction in the motion of machine tool, which is called‘space vector’s direction measurement’. For this new method, it does not require the motion area of the machine tool in a 3D space in the measurement, which simplifies the measurement trajectory. Meanwhile, the identification of angular displacement error and linear displacement error of each linear axis are separated, which reduces the complexity of error identification. In addition, a precision NC turntable is introduced to achieve the accurate calibration of base station, which overcomes the shortcoming of the calibration accuracy of the base station affected by the error of machine tool.

In this paper, a laser tracker is adopted the space vector’s direction measurement principle to achieve quick and accurate calibration of the geometric error of machine tool. The mathematical model of geometric error measurement of machine tool based on the principle of space vector’s direction measurement is established, and the corresponding measurement algorithm and geometric error identification algorithm are deduced respectively. The feasibility of this method is verified by simulations and experiments.

2 Space Vector’s Direction Deviation and Geometric Error

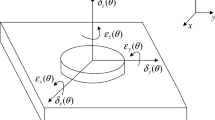
There are 6 degrees of freedom for object moving in space. Figure 1 shows the six geometric errors with the motion of machine tool along \(x{\text{-axis}}\). Here, \(\delta_{x} (x)\), \(\delta_{y} (x)\), \(\delta_{z} (x)\) are the linear displacement errors, and \(\varepsilon_{x} (x)\), \(\varepsilon_{y} (x)\), \(\varepsilon_{z} (x)\) are the angular displacement errors.

Fig. 1
figure 1

Six geometric errors with the motion of machine tool along \(x{\text{-axis}}\)

Full size image

Three measuring points \(A\), \(B\) and \(C\) are mounted on the moving part of machine tool in Fig. 1. Due to the motion error of the machine tool, the direction of three vectors \(\overrightarrow {AB}\), \(\overrightarrow {BC}\), \(\overrightarrow {CA}\) composed of measuring points \(A\), \(B\) and \(C\) would be changed during the motion as shown in Fig. 2.

Fig. 2
figure 2

The change of vectors’ direction composed of some measuring points

Full size image

At the initial position, three measuring points are assumed as \(A(x_{a0} ,y_{a0} ,z_{a0} )\), \(B(x_{b0} ,y_{b0} ,z_{b0} )\) and \(C(x_{c0} ,y_{c0} ,z_{c0} )\) respectively, and the corresponding vectors composed of these measuring points are:

$$\begin{aligned} \overrightarrow {AB} = (x_{a0} - x_{b0} ,y_{a0} - y_{b0} ,z_{a0} - z_{b0} ), \hfill \\ \overrightarrow {BC} = (x_{b0} - x_{c0} ,y_{b0} - y_{c0} ,z_{b0} - z_{c0} ), \hfill \\ \overrightarrow {CA} = (x_{c0} - x_{a0} ,y_{c0} - y_{a0} ,z_{c0} - z_{a0} ). \hfill \\ \end{aligned}$$
(1)

When the moving part is moved the distance \(L\) along the \(x{\text{-axis}}\) from the initial position, the measuring points \(A\), \(B\) and \(C\) will be reached at the position of \(A^{'}\), \(B^{'}\) and \(C^{'}\) respectively. During the motion, the theoretical homogeneous transformation matrix is defined as:

$$T = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & L \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(2)

The homogeneous transformation matrices caused by angular displacement error \(\varepsilon_{x} (x)\), \(\varepsilon_{y} (x)\) and \(\varepsilon_{z} (x)\) during the motion are: [12, 25]

$$\begin{aligned} T_{1} = &\, \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & {\cos \varepsilon_{x} (x)} & { - \sin \varepsilon_{x} (x)} & 0 \\ 0 & {\sin \varepsilon_{x} (x)} & {\cos \varepsilon_{x} (x)} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],\quad T_{2} = \left[ {\begin{array}{*{20}c} {\cos \varepsilon_{y} (x)} & 0 & {\sin \varepsilon_{y} (x)} & 0 \\ 0 & 1 & 0 & 0 \\ { - \sin \varepsilon_{y} (x)} & 0 & {\cos \varepsilon_{y} (x)} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], \\ T_{3} = &\, \left[ {\begin{array}{*{20}c} {\cos \varepsilon_{z} (x)} & { - \sin \varepsilon_{z} (x)} & 0 & 0 \\ {\sin \varepsilon_{z} (x)} & {\cos \varepsilon_{z} (x)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]. \\ \end{aligned}$$
(3)

The homogeneous transformation matrices caused by position error \(\delta_{x} (x)\), straightness error \(\delta_{y} (x)\) and \(\delta_{z} (x)\) are:

$$\begin{aligned} T_{4} = &\, \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {\delta_{x} (x)} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],\quad T_{5} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {\delta_{y} (x)} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], \\ T_{6} = &\, \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {\delta_{z} (x)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]. \\ \end{aligned}$$
(4)

The total error homogeneous transformation matrix is:

$$U = T_{1} T_{2} T_{3} T_{4} T_{5} T_{6} .$$
(5)

Then we can obtain

$$U = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{z} (x)} & {\varepsilon_{y} (x)} & {\delta_{x} (x)} \\ {\varepsilon_{z} (x)} & 1 & { - \varepsilon_{x} (x)} & {\delta_{y} (x)} \\ { - \varepsilon_{y} (x)} & {\varepsilon_{x} (x)} & 1 & {\delta_{z} (x)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right].$$
(6)

The total homogeneous transformation matrix during the motion is given as follows:

$$Q = TU = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{z} (x)} & {\varepsilon_{y} (x)} & {L + \delta_{x} (x)} \\ {\varepsilon_{z} (x)} & 1 & { - \varepsilon_{x} (x)} & {\delta_{y} (x)} \\ { - \varepsilon_{y} (x)} & {\varepsilon_{x} (x)} & 1 & {\delta_{z} (x)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right].$$
(7)

The coordinates of measuring point \(A^{'}\), \(B^{'}\) and \(C^{'}\) are assumed as \(A^{'} (x_{a1} ,y_{a1} ,z_{a1} )\), \(B^{'} (x_{b1} ,y_{b1} ,z_{b1} )\), \(C^{'} (x_{c1} ,y_{c1} ,z_{c1} )\), respectively. The following relation should be satisfied between measuring point \(A\) and \(A^{'}\).

$$\left[ {\begin{array}{*{20}c} {x_{a1} } \\ {y_{a1} } \\ {z_{a1} } \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{z} (x)} & {\varepsilon_{y} (x)} & {L + \delta_{x} (x)} \\ {\varepsilon_{z} (x)} & 1 & { - \varepsilon_{x} (x)} & {\delta_{y} (x)} \\ { - \varepsilon_{y} (x)} & {\varepsilon_{x} (x)} & 1 & {\delta_{z} (x)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{a0} } \\ {y_{a0} } \\ {z_{a0} } \\ 1 \\ \end{array} } \right].$$
(8)

From Eq. (8), the spatial coordinates of the measuring point \(A^{'}\) can be calculated. In the same way, the spatial coordinates of the measuring point \(B^{'}\), \(C^{'}\) can be also calculated in turn. Then, the direction of the vectors composed of \(A^{'}\), \(B^{'}\) and \(C^{'}\) are:

$$\begin{aligned} \overrightarrow {{A^{'} B^{'} }} = &\, (x_{a0} - x_{b0} - \varepsilon_{x} (x)(y_{a0} - y_{b0} ) + \varepsilon_{y} (x)(z_{a0} - z_{b0} ), \\ & y_{a0} - y_{b0} + \varepsilon_{z} (x)(x_{a0} - x_{b0} ) - \varepsilon_{x} (x)(z_{a0} - z_{b0} ), \\ & z_{a0} - z_{b0} + \varepsilon_{x} (x)(y_{a0} - y_{b0} ) - \varepsilon_{y} (x)(x_{a0} - x_{b0} )){\kern 1pt} , \\ \overrightarrow {{B^{'} C^{'} }} = &\, (x_{b0} - x_{c0} - \varepsilon_{x} (x)(y_{b0} - y_{c0} ) + \varepsilon_{y} (x)(z_{b0} - z_{c0} ), \\ & y_{b0} - y_{c0} + \varepsilon_{z} (x)(x_{b0} - x_{c0} ) - \varepsilon_{x} (x)(z_{b0} - z_{c0} ), \\ & z_{b0} - z_{c0} + \varepsilon_{x} (x)(y_{b0} - y_{c0} ) - \varepsilon_{y} (x)(x_{b0} - x_{c0} )){\kern 1pt} , \\ \overrightarrow {{C^{'} A^{'} }} = &\, (x_{c0} - x_{a0} - \varepsilon_{x} (x)(y_{c0} - y_{a0} ) + \varepsilon_{y} (x)(z_{c0} - z_{a0} ), \\ & y_{c0} - y_{a0} + \varepsilon_{z} (x)(x_{c0} - x_{a0} ) - \varepsilon_{x} (x)(z_{c0} - z_{a0} ), \\ & z_{c0} - z_{a0} + \varepsilon_{x} (x)(y_{c0} - y_{a0} ) + \varepsilon_{y} (x)(x_{c0} - x_{a0} )){\kern 1pt} {\kern 1pt} . \\ \end{aligned}$$
(9)

The direction deviations of vectors \(\overrightarrow {AB}\), \(\overrightarrow {BC}\), \(\overrightarrow {CA}\) during the motion of are:

$$\begin{aligned} \Delta \overrightarrow {AB} = &\, \overrightarrow {{A^{'} B^{'} }} - \overrightarrow {AB} \\ = &\, ( - \varepsilon_{x} (x)(y_{a0} - y_{b0} ) + \varepsilon_{y} (x)(z_{a0} - z_{b0} ), \\ & \varepsilon_{z} (x)(x_{a0} - x_{b0} ) - \varepsilon_{x} (x)(z_{a0} - z_{b0} ), \\ & \varepsilon_{x} (x)(y_{a0} - y_{b0} ) - \varepsilon_{y} (x)(x_{a0} - x_{b0} )), \\ \Delta \overrightarrow {BC} = &\, \overrightarrow {{B^{'} C^{'} }} - \overrightarrow {BC} \\ = &\, ( - \varepsilon_{x} (x)(y_{b0} - y_{c0} ) + \varepsilon_{y} (x)(z_{b0} - z_{c0} ), \\ & \varepsilon_{z} (x)(x_{b0} - x_{c0} ) - \varepsilon_{x} (x)(z_{b0} - z_{c0} ), \\ & \varepsilon_{x} (x)(y_{b0} - y_{c0} ) - \varepsilon_{y} (x)(x_{b0} - x_{c0} )){\kern 1pt} , \\ \Delta \overrightarrow {CA} = &\, \overrightarrow {{C^{'} A^{'} }} - \overrightarrow {CA} \\ = &\, ( - \varepsilon_{x} (x)(y_{c0} - y_{a0} ) + \varepsilon_{y} (x)(z_{c0} - z_{a0} ), \\ & \varepsilon_{z} (x)(x_{c0} - x_{a0} ) - \varepsilon_{x} (x)(z_{c0} - z_{a0} ), \\ & \varepsilon_{x} (x)(y_{c0} - y_{a0} ) + \varepsilon_{y} (x)(x_{c0} - x_{a0} )). \\ \end{aligned}$$
(10)

It can be seen from Eq. (10) that the direction deviations of \(\overrightarrow {AB}\), \(\overrightarrow {BC}\), \(\overrightarrow {CA}\) during the motion are only related to angular displacement error \(\varepsilon_{x} (x)\), \(\varepsilon_{y} (x)\), \(\varepsilon_{z} (x)\) rather than linear displacement error \(\delta_{x} (x)\), \(\delta_{y} (x)\), \(\delta_{z} (x)\). In the identification of geometric errors of machine tool, the angular displacement error can be firstly separated by measuring the direction changes of vectors composed of adjacent measuring points set on the moving part of machine tool, and then the linear displacement error can be separated in the end.

3 Measurement Principle and Algorithm

3.1 Measurement Principle

In order to reduce the influence of angle measurement error on the final coordinates measurement result, the multi-station and time-sharing measurement is adopted. A laser tracker is used to measure the direction of space vectors composed of a series of measuring points set on the machine tool, and then the geometric errors of machine tool can be identified by corresponding algorithms. Figure 3 shows its measurement principle. \(P_{1}\), \(P_{2}\), \(P_{3}\) and \(P_{4}\) represent the four positions of base station. Points \(ABC\) are the three initial measuring points, while points \(A'B'C'\), \(A^{\prime \prime } B^{\prime \prime } C^{\prime \prime }\),etc. represent the measuring points at other locations.

Fig. 3
figure 3

The principle of geometric error measurement of machine tool on the basis of space vector’s direction measurement

Full size image

Taking the motion error measurement of \(x{\text{-axis}}\) of machine tool for example, the corresponding measurement process is as follows. With the laser tracker at the first base station \(P_{1}\), the cat eye is successively moved to point \(A\), \(B\), \(C\), and the corresponding distances between base station \(P_{1}\) and point \(A\), \(B\), \(C\) are measured successively. Then the moving part is fed to next location along \(x{\text{-axis}}\), and the distances between the base station \(P_{1}\) and point \(A'\), \(B'\), \(C'\) are similarly measured. Repeat the above measurement at other locations, until the motion error measurement of moving part is accomplished at the first base station. After that, the laser tracker is moved to other base station \(P_{2}\), \(P_{3}\), \(P_{4}\), and the same measurement process is repeated just as the measurement at the base station \(P_{1}\) until the motion error measurement of machine tool is finished at all base stations.

In the actual measurement, in order to ensure the cat eye can move accurately to the measuring points \(A\), \(B\), \(C\) etc., a precision NC turntable is designed as shown in Fig. 4.

Fig. 4
figure 4

The precision NC turntable

Full size image

Manufactured with tight geometric tolerances, the radial and axial run outs of the turntable are less than \(0.3\;\upmu{\text{m}}\). Meanwhile, the position closed loop is constituted by a built-in motor and Renishaw circular grating, and its angular position accuracy is \(\pm\, 2^{''}\), with a repeat accuracy of \(\pm\, 1^{''}\). The axial and radial run out errors of this turntable are small, and its position accuracy and repeat accuracy are high. The cat eye is mounted on the turntable, and the turntable can drive the cat eye to rotate accurately with different angles. In addition, the position of base station can be accurately calibrated by measuring the motion of turntable. The turntable is fixed in the vicinity of the machine tool spindle as shown in Fig. 5.

Fig. 5
figure 5

The installation of precision turntable on the machine tool

Full size image

At the first base station \(P_{1}\), the position of \(P_{1}\) can be firstly calibrated by measuring the rotary motion of turntable. After that, the motion error of machine tool along each axis can be measured. The moving part of machine tool is controlled to move on the preset path, and some measurement locations are set on the path. At each measurement location, a series of measuring points can be set according to the different angles of turntable rotation. The corresponding distance between the base station \(P_{1}\) and each measuring point can be successively measured by laser tracker. When the measurement is finished at the base station \(P_{1}\), the laser tracker is moved to other base stations, and the above process is repeated until the motion measurement of machine tool is accomplished at all base stations.

3.2 Measurement Algorithm

With multi-station and time-sharing measurement by laser tracker, the measurement algorithms are mainly involved with base station calibration and measuring point determination, in which the base station calibration is a key issue that directly affects the final measurement accuracy. In order to accurately calibrate the base station, a precision NC turntable mentioned above is adopted, and the position of base station can be calibrated by measuring the motion of precision turntable.

3.2.1 Base Station Calibration

In the measurement, the distance between the center of cat eye and turntable is defined as \(R\). The measurement is carried out with rotating each \(\theta\) of turntable, and a series of measuring points such as \(M_{1} ,\;M_{2} ,\; \ldots M_{N}\) can be obtained, and the corresponding ranging data of laser tracker will be recorded. The rotary center \(O{}_{1}\) of turntable is defined as the origin of the coordinate system. The line \(O_{1} M_{2}\) is defined as \(Y_{1}\) axis, and the line perpendicular to the \(Y_{1}\) axis and through point \(O{}_{1}\) is defined as \(X_{1}\). Then according to the right-hand screw rule, the \(Z_{1}\) axis can be also determined, and the coordinate system of turntable will be established as shown in Fig. 6. Here, \(OXYZ\) is defined as the coordinate system of machine tool.

Fig. 6
figure 6

The establishment of the coordinate system of the turntable

Full size image

The coordinate of base station \(P_{1}\) is assumed as \(P_{1} (x_{p1} ,y_{p1} ,z_{p1} )\) in the coordinate system of turntable. With rotating each \(\theta\) of turntable, the corresponding ranging data of laser tracker is defined as \(l_{1i}\). The following equations concerning on the base station calibration can be obtained.

$$\left\{ \begin{array}{l} \sqrt {(x_{p1} - R\cos \theta_{1} )^{2} + (y_{p1} - R\cos \theta_{1} )^{2} + z_{p1}^{2} } = l_{11} \\ \sqrt {(x_{p1} - R\cos \theta_{2} )^{2} + (y_{p1} - R\cos \theta_{2} )^{2} + z_{p1}^{2} } = l_{12} \\ \vdots \\ \sqrt {(x_{p1} - R\cos \theta_{i} )^{2} + (y_{p1} - R\cos \theta_{i} )^{2} + z_{p1}^{2} } = l_{1i} \\ \end{array} \right..$$
(11)

Equation (11) is a nonlinear redundant equations, and it can be solved by least squares [26].

The residuals is defined as:

$$f_{i} = ((x_{p1} - R\cos \theta_{i} )^{2} + (y_{p1} - R\sin \theta_{i} )^{2} + z_{p1}^{2} )^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} - l_{1i} .$$
(12)

Suppose \(x_{p1}^{0} ,y_{p1}^{0} ,z_{p1}^{0} ,R^{0}\) are the approximations of \(x_{p1}^{{}}\), \(y_{p1}^{{}}\), \(z_{p1}^{{}}\) and \(R\) respectively, that is

$$x_{p1} = x^{0} + \Delta x,\quad y_{p1} = y^{0} + \Delta y,\quad z_{p1} = z^{0} + \Delta z,\quad R = R^{0} + \Delta R.$$
(13)

Equation (13) is expanded at \((x^{0} ,y^{0} ,z^{0} ,R^{0} )\) in accordance with Taylor series, and the terms over the first-order partial derivatives are omitted to eliminate the nonlinear terms, then the following Eq. (14) can be obtained

$$\begin{aligned} f_{i} = &\, \sqrt {(x^{0} - R^{0} \cos \theta_{i} )^{2} + (y^{0} - R^{0} \sin \theta_{i} )^{2} + z_{pi}^{2} } \\ & - l_{1i} + \frac{{\partial f_{i} }}{{\partial x_{p} }}\left| {_{0} \Delta x} \right. + \frac{{\partial f_{i} }}{{\partial y_{p} }}\left| {_{0} \Delta y} \right. + \frac{{\partial f_{i} }}{{\partial z_{p} }}\left| {_{0} \Delta z} \right. + \frac{{\partial f_{i} }}{\partial R}\left| {_{0} \Delta R} \right. \\ \end{aligned}$$
(14)

Let \(t_{i} = \sqrt {(x^{0} - R^{0} \cos \theta_{i} )^{2} + (y^{0} - R^{0} \sin \theta_{i} )^{2} + z_{pi}^{2} }\), then we can obtain

$$\begin{aligned} f_{i} = &\, t_{i} - l_{1i} + \frac{{x^{0} - r^{0} \cos \theta_{i} }}{{t_{i} }}\Delta x + \frac{{y^{0} - r^{0} \sin \theta_{i} }}{{t_{i} }}\Delta y \\ & + \frac{{z^{0} }}{{t_{i} }}\Delta z + \frac{{ - x^{0} \cos \theta_{i} - y^{0} \sin \theta_{i} + r^{0} }}{{t_{i} }}. \\ \end{aligned}$$
(15)

Let \(a_{xi} = \frac{{x^{0} - r^{0} \cos \theta_{i} }}{{t_{i} }}\), \(a_{yi} = \frac{{y^{0} - r^{0} \sin \theta_{i} }}{{t_{i} }}\), \(a_{zi} = \frac{{z^{0} }}{{t_{i} }}\), \(a_{ri} = \frac{{ - x^{0} \cos \theta_{i} - y^{0} \sin \theta_{i} + r^{0} }}{{t_{i} }}\), the following equations can be obtained

$$\left\{ {\begin{array}{*{20}c} {f_{1} = t_{1} - l_{11} + a_{x1} \Delta x + a_{y1} \Delta y + a_{z1} \Delta z + a_{r1} \Delta R} \\ {f_{2} = t_{2} - l_{12} + a_{x2} \Delta x + a_{y2} \Delta y + a_{z2} \Delta z + a_{r2} \Delta R} \\ \vdots \\ {f_{i} = t_{i} - l_{1i} + a_{xi} \Delta x + a_{yi} \Delta y + a_{zi} \Delta z + a_{ri} \Delta R} \\ \end{array} } \right..$$
(16)

Equation (16) is a linear redundant equations. According to least squares principle, the objective function is defined as:

$$H = \sum\limits_{i = 1}^{n} {(t_{i} } - l_{1i} + a_{xi} \Delta x + a_{yi} \Delta y + a_{zi} \Delta z + a_{ri} \Delta R)^{2} .$$
(17)

According to the maximum principle, it should satisfy following conditions to make \(H\) minimum,

$$\frac{\partial H}{\partial (\Delta x)} = 0,\quad \frac{\partial H}{\partial (\Delta y)} = 0,\quad \frac{\partial H}{\partial (\Delta z)} = 0,\quad \frac{\partial H}{\partial (\Delta R)} = 0.$$
(18)

Meanwhile,

$$\begin{aligned} \frac{{\partial^{2} H}}{{\partial \left( {\Delta x} \right)^{2} }} = 2\sum\limits_{i = 1}^{n} {a_{xi}^{2} } > 0,\quad \frac{{\partial^{2} H}}{{\partial \left( {\Delta y} \right)^{2} }} = 2\sum\limits_{i = 1}^{n} {a_{yi}^{2} } > 0 \hfill \\ \frac{{\partial^{2} H}}{{\partial \left( {\Delta z} \right)^{2} }} = 2\sum\limits_{i = 1}^{n} {a_{zi}^{2} } > 0,\quad \frac{{\partial^{2} H}}{{\partial \left( {\Delta R} \right)^{2} }} = 2\sum\limits_{i = 1}^{n} {a_{ri}^{2} } > 0. \hfill \\ \end{aligned}$$
(19)

From Eq. (19), the extreme value obtained by solving Eq. (18) is the minimum, and it can be deduced:

$$\left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {a_{xi}^{2} } } & {\sum\limits_{i = 1}^{n} {a_{yi} a_{xi} } } & {\sum\limits_{i = 1}^{n} {a_{zi} a_{xi} } } & {\sum\limits_{i = 1}^{n} {a_{ri} a_{xi} } } \\ {\sum\limits_{i = 1}^{n} {a_{yi} a_{xi} } } & {\sum\limits_{i = 1}^{n} {a_{yi}^{2} } } & {\sum\limits_{i = 1}^{n} {a_{zi} a_{yi} } } & {\sum\limits_{i = 1}^{n} {a_{ri} a_{yi} } } \\ {\sum\limits_{i = 1}^{n} {a_{zi} a_{xi} } } & {\sum\limits_{i = 1}^{n} {a_{zi} a_{yi} } } & {\sum\limits_{i = 1}^{n} {a_{zi}^{2} } } & {\sum\limits_{i = 1}^{n} {a_{ri} a_{zi} } } \\ {\sum\limits_{i = 1}^{n} {a_{ri} a_{xi} } } & {\sum\limits_{i = 1}^{n} {a_{ri} a_{yi} } } & {\sum\limits_{i = 1}^{n} {a_{ri} a_{zi} } } & {\sum\limits_{i = 1}^{n} {a_{ri}^{2} } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta x} \\ {\Delta y} \\ {\Delta z} \\ {\Delta R} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {(l_{1i} - t_{i} )a_{xi} } } \\ {\sum\limits_{i = 1}^{n} {(l_{1i} - t_{i} )a_{yi} } } \\ {\sum\limits_{i = 1}^{n} {(l_{1i} - t_{i} )a_{zi} } } \\ {\sum\limits_{i = 1}^{n} {(l_{1i} - t_{i} )a_{ri} } } \\ \end{array} } \right].$$
(20)

When \(\Delta x\), \(\Delta y\), \(\Delta z\), \(\Delta R\) are obtained, the position of the base station \(P_{1}\) and the distance between the center of cat eye and turntable can be determined from Eqs. (21) and (22) respectively,

$$\left[ {\begin{array}{*{20}c} {x_{p1} } \\ {y_{p1} } \\ {z_{p1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x^{0} } \\ {y^{0} } \\ {z^{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\Delta x} \\ {\Delta y} \\ {\Delta z} \\ \end{array} } \right].$$
(21)
$$R = R^{0} + \Delta R.$$
(22)

Repeat the above process, the position of base station \(P_{2}\), \(P_{3}\), \(P_{4}\) can be also calibrated.

3.2.2 Determining the Initial Value of Calibration Parameters of Base Station

In the base station calibration, the initial position of base station and the initial distance between the center of cat eye and the rotary center of turntable should be firstly selected. Meanwhile, the accuracy of the initial value selected may affect the calculation accuracy and efficiency. When the initial value is far from its true value, the iteration calculation can not converge. So how to accurately select the initial value of calibration parameters of base station is a crucial issue. The method of determining the initial distance and the initial position of each base station is given as follows:

3.2.3 Determining the Initial Distance Between the Center of Cat Eye and the Rotary Center of Turntable

The coordinates of a series of measuring points measured by laser tracker in the instrument coordinate system with different angles of turntable rotation are assumed as \(M_{i}^{'} (x_{mi}^{'} ,y_{mi}^{'} ,z_{mi}^{'} )\),and the space plane through these points can be determined by least squares fitting. The plane equation is assumed as \(z^{'} = Ax^{'} + By^{'} + C\), and the objective function is

$$F(A,B,C) = \sum\limits_{i = 1}^{N} {(Ax_{i}^{'} } + By_{i}^{'} + C - z_{i}^{'} )^{2} .$$
(23)

According to the maximum principle, it should satisfy following conditions to make \(F(A,B,C)\) minimum,

$$\frac{\partial F}{\partial A} = 0,\quad \frac{\partial F}{\partial B} = 0,\quad \frac{\partial F}{\partial C} = 0.$$
(24)

From Eq. (24), we can obtain

$$\left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {x_{i}^{'2} } } & {\sum\limits_{i = 1}^{n} {x_{i}^{'} y_{i}^{'} } } & {\sum\limits_{i = 1}^{n} {x_{i}^{'} } } \\ {\sum\limits_{i = 1}^{n} {x_{i}^{'} y_{i}^{'} } } & {\sum\limits_{i = 1}^{n} {y_{i}^{'2} } } & {\sum\limits_{i = 1}^{n} {y_{i}^{'} } } \\ {\sum\limits_{i = 1}^{n} {x_{i}^{'} } } & {\sum\limits_{i = 1}^{n} {y_{i}^{'} } } & N \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} A \\ B \\ C \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {x_{i}^{'} z_{i}^{'} } } \\ {\sum\limits_{i = 1}^{n} {y_{i}^{'} z_{i}^{'} } } \\ {\sum\limits_{i = 1}^{n} {z_{i}^{'} } } \\ \end{array} } \right].$$
(25)

Then, the equation of plane through these points can be obtained from Eq. (25)

The coordinate of the center of the space circle determined by three adjacent points \(M_{i}^{'} (x_{mi}^{'} ,y_{mi}^{'} ,z_{mi}^{'} )\), \(M_{i + 1}^{'} (x_{mi + 1}^{'} ,y_{mi + 1}^{'} ,z_{mi + 1}^{'} )\), \(M_{i + 2}^{'} (x_{mi + 2}^{'} ,y_{mi + 2}^{'} ,z_{mi + 2}^{'} )\) on the turntable in the instrument coordinate system is assumed as \(O^{'} (u^{'} ,v^{'} ,w^{'} )\), and point \(O^{'}\) is in the plane defined from Eq. (26) [27]. Then the following equation can be obtained

$$\left\{ {\begin{array}{*{20}l} {Au^{'} + Bv^{'} + C = w} \hfill \\ {(x_{mi}^{'} - u^{'} )^{2} + (y_{mi}^{'} - v^{'} )^{2} + (z_{mi}^{'} - w^{'} )^{2} = (x_{mi + 1}^{'} - u^{'} )^{2} + (y_{mi + 1}^{'} - v^{'} )^{2} + (z_{mi + 1}^{'} - w^{'} )^{2} } \hfill \\ {(x_{mi + 1}^{'} - u^{'} )^{2} + (y_{mi + 1}^{'} - v^{'} )^{2} + (z_{mi + 1}^{'} - w^{'} )^{2} = (x_{mi + 2}^{'} - u^{'} )^{2} + (y_{mi + 2}^{'} - v^{'} )^{2} + (z_{mi + 2}^{'} - w^{'} )^{2} } \hfill \\ \end{array} } \right..$$
(26)

The coordinates of the rotary center of turntable in the instrument coordinate system can be obtained by solving Eq. (26), and the corresponding radius determined by the series measuring points is

$$R^{0} = \sqrt {(x_{mi}^{'} - u)^{2} + (y_{mi}^{'} - v)^{2} + (z_{mi}^{'} - w)^{2} } .$$
(27)

From Eq. (27), the initial distance between the center of cat eye and turntable can be determined.

3.2.4 Determining the Initial Position of Base Station

In the measurement, the coordinates of a series of measuring points are given in the instrument coordinate system, and this coordinate system \(X^{'} Y^{'} Z^{'}\) is recorded as the old one. In order to determine the initial position of the base station, the coordinates of measuring point in the instrument coordinate system should be transformed into the turntable coordinate system, and this coordinate system \(O_{1} X_{1} Y_{1} Z_{1}\) is recorded as the new one. Figure 7 shows the coordinate systems transformation.

Fig. 7
figure 7

The coordinate systems transformation

Full size image

The coordinate system of instrument can be coincident with the coordinate system of turntable through the rotation and translation transformation. Assuming that the instrument coordinate system moving the distance \(\Delta x\) along \({\text{X-axis}}\), \(\Delta y\) along \({\text{Y-axis}}\), \(\Delta z\) along \({\text{Z-axis}}\), and rotating the angle \(\alpha\) around \({\text{X-axis}}\), \(\beta\) around \({\text{Y-axis}}\), \(\gamma\) around \({\text{Z-axis}}\), the two coordinate systems can be coincided, and the corresponding homogeneous transformation matrix is defined as \(W\). Here, \(x_{mi} = R^{0} \cos \theta_{i}\), \(y_{mi} = R^{0} \sin \theta_{i}\) and \(z_{mi} = 0\), let \(K^{'} = \left[ {\begin{array}{*{20}c} {x_{mi}^{'} } & {y_{mi}^{'} } & {z_{mi}^{'} } & 1 \\ \end{array} } \right]^{T}\), \(K = \left[ {\begin{array}{*{20}c} {x_{mi} } & {y_{mi} } & {z_{mi} } & 1 \\ \end{array} } \right]^{T}\).

The least square model concerning on the euclidean distance between the measuring points is established

$$F = \hbox{min} \frac{1}{N}\sum\limits_{i = 1}^{N} {\left\| {\left. {WK^{'} - K} \right\|^{2} } \right.} .$$
(28)

Six unknown parameters( \(\Delta x\), \(\Delta y\), \(\Delta z\), \(\alpha\), \(\beta\), \(\gamma\)) are involved in Eq. (28), and nonlinear least squares method can be used to solve these parameters. Then the coordinate homogeneous transformation matrix between the instrument coordinate system and turntable coordinate system can be determined, and the initial position of base station can be easily obtained.

3.2.5 Determining the Coordinates of Measuring Points

When the positions of four base stations are calibrated, the motion of machine tool can be measured. Then the redundant equation concerning on measuring point determination can be established, the actual coordinates of each measuring point with different angles of precision turntable rotation during the motion of machine tool can be determined by solving the equation, and the direction of vectors composed of adjacent measuring points can be calculated.

3.3 Geometric Error Separation for Machine Tool

Due to the motion error of machine tool, the direction of the vectors composed of adjacent measuring points on the moving part of machine tool will be changed. Meanwhile, the deviation of vector’s direction is only related to angular displacement error rather than linear displacement error. Based on the characteristic, the angular displacement error during the motion of machine tool can be firstly separated by measuring the direction change of vectors composed of adjacent measuring points, and then the linear displacement error can be identified. So, the identification of angular displacement error and linear displacement error of each linear axis of machine tool are separated, which reduces the complexity of error identification.

3.3.1 Angular Displacement Error Separation

At the initial position, three vectors are defined as \(\overrightarrow {AB} = \left[ {\begin{array}{*{20}c} {a_{1} } & {b_{1} } & {c_{1} } \\ \end{array} } \right]\), \(\overrightarrow {BC} = \left[ {\begin{array}{*{20}c} {a_{2} } & {b_{2} } & {c_{2} } \\ \end{array} } \right]\), \(\overrightarrow {CA} = \left[ {\begin{array}{*{20}c} {a_{3} } & {b_{3} } & {c_{3} } \\ \end{array} } \right]\) in Fig. 2. When the moving part of machine tool is moved the distance \(L\) along \(x{\text{-axis}}\), three new vectors \(\overrightarrow {{A^{'} B^{'} }} = \left[ {\begin{array}{*{20}c} {a_{1}^{'} } & {b_{1}^{'} } & {c_{1}^{'} } \\ \end{array} } \right]\), \(\overrightarrow {{B^{'} C^{'} }} = \left[ {\begin{array}{*{20}c} {a_{2}^{'} } & {b_{2}^{'} } & {c_{2}^{'} } \\ \end{array} } \right]\), \(\overrightarrow {{C^{'} A^{'} }} = \left[ {\begin{array}{*{20}c} {a_{3}^{'} } & {b_{3}^{'} } & {c_{3}^{'} } \\ \end{array} } \right]\) are obtained. There exists the following relation between vector \(\overrightarrow {AB}\) and \(\overrightarrow {{A^{'} B^{'} }}\)

$$\left[ {\begin{array}{*{20}c} {a_{1}^{'} } \\ {b_{1}^{'} } \\ {c_{1}^{'} } \\ 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & { - \varepsilon_{z} (x)} & {\varepsilon_{y} (x)} & 0 \\ {\varepsilon_{z} (x)} & 1 & { - \varepsilon_{x} (x)} & 0 \\ { - \varepsilon_{y} (x)} & {\varepsilon_{x} (x)} & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{1} } \\ {b_{1} } \\ {c_{1} } \\ 1 \\ \end{array} } \right].$$
(29)

Then, we can deduce

$$\left\{ {\begin{array}{*{20}c} {a_{1}^{'} = a_{1} - \varepsilon_{z} (x)b_{1} + \varepsilon_{y} (x)c_{1} } \\ {b_{1}^{'} = b_{1} - \varepsilon_{x} (x)c_{1} + \varepsilon_{z} (x)a_{1} } \\ {c_{1}^{'} = c_{1} - \varepsilon_{y} (x)a_{1} + \varepsilon_{x} (x)b_{1} } \\ \end{array} } \right..$$
(30)

Similarly, the relation between \(\overrightarrow {BC}\) and \(\overrightarrow {{B^{'} C^{'} }}\), and the relation between \(\overrightarrow {CA}\) and \(\overrightarrow {{C^{'} A^{'} }}\) can be also established, and then we can obtain

$$\left[ {\begin{array}{*{20}c} 0 & {c_{1} } & { - b_{1} } \\ { - c_{1} } & 0 & {a_{1} } \\ {b_{1} } & { - a_{1} } & 0 \\ {} & \vdots & {} \\ 0 & {c_{3} } & { - b_{3} } \\ { - c_{3} } & 0 & {a_{3} } \\ {b_{3} } & { - a_{3} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x} (x)} \\ {\varepsilon_{y} (x)} \\ {\varepsilon_{z} (x)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{1}^{'} - a_{1} } \\ {b_{1}^{'} - b_{1} } \\ {c_{1}^{'} - c_{1} } \\ \vdots \\ {a_{3}^{'} - a_{3} } \\ {b_{3}^{'} - b_{3} } \\ {c_{3}^{'} - c_{3} } \\ \end{array} } \right].$$
(31)

The direction of each vector in Eq. (31) can be calculated by the measuring point determined with laser tracker. Each angular displacement error of \(x{\text{-axis}}\) can be separated by solving Eq. (31) with least squares method. Compared with the method of identification of angular displacement error by using the deviation of one vector’s direction in Ref [22]., the amount of redundant data is increased, which will improve the identification accuracy.

3.3.2 Linear Displacement Error Separation

At the initial position, the middle point of the measuring point \(A\) and \(B\) is assumed as \(J\). When the moving part of machine tool is moved the distance \(L\) along \(x{\text{-axis}}\), the point \(J\) reaches the position of \(J_{1}^{'}\), and the corresponding motion errors are \(\Delta x_{J1} = x_{J1}^{'} - x_{J1}\), \(\Delta y_{J1} = y_{J1}^{'} - y_{J1}\), \(\Delta z_{J1} = z_{J1}^{'} - z_{J1}\),respectively. Here, \(\Delta x_{J1}\), \(\Delta y_{J1}\) and \(\Delta z_{J1}\) are composed of two parts: one part is the displacement error \(t_{x1}\), \(t_{y1}\), \(t_{z1}\) along \(x{\text{-axis}}\), \(y{\text{-axis}}\), \(z{\text{-axis}}\) caused by the angular displacement errors in the motion, the other part is the linear displacement error \(\delta_{x} (x)\), \(\delta_{y} (x)\), \(\delta_{z} (x)\). By using the identified angular displacement error \(\varepsilon_{x} (x)\), \(\varepsilon_{y} (x)\) and \(\varepsilon_{z} (x)\), the displacement errors \(t_{x1}\), \(t_{y1}\), \(t_{z1}\) along \(x{\text{-axis}}\), \(y{\text{-axis}}\), \(z{\text{-axis}}\) caused by these angular displacement error can be calculated. Then the following equation can be established

$$\left\{ {\begin{array}{*{20}c} {\Delta x_{J1} = t_{x1} + \delta_{x} (x)} \\ {\Delta y_{J1} = t_{y1} + \delta_{y} (x)} \\ {\Delta z_{J1} = t_{z1} + \delta_{z} (x)} \\ \end{array} } \right..$$
(32)

Similarly, the motion error equations concerning on the middle points of measuring point \(B\) and \(C\), \(C\) and \(A\) can also be established. Based on that, then the redundant equation can be obtained, and each linear displacement error can be separated by solving this redundant equation. In the above error identification, the motion trajectory of machine tool is not required in a 3D space, which simplifies the corresponding measurement trajectory.

4 Simulation for Measurement Algorithm and geometric Error Separation Algorithm

In order to verify the accuracy of the measurement algorithm derived based on the space vector’s direction measurement principle and the geometric error separation algorithm, the simulations are carried out as follows.

4.1 Simulation for Measurement Algorithm

The measurement algorithm derived based on the space vector’s direction measurement principle is involved with base station calibration and measuring point determination, and the corresponding simulations concerning on base station calibration and measuring point determination are given.

4.1.1 Simulation for Base Station Calibration

Firstly, the positions of each base station are assumed as follows: \(P_{1} (1200,\;800,\;600)\), \(P_{2} (1800,\;800,\;600)\), \(P_{3} (1200,\;1500,\;600)\), \(P_{4} (1800,\;1500,\;1600)\). \(A\) measuring point is set with turntable rotating each \(\theta = 30^{ \circ }\), and the distance between the center of cat eye and rotary center of turntable is 100 mm. The position of each base station can be determined by the base station calibration algorithm derived mentioned above. The simulations are carried out under two different conditions: with or without considering the motion error of turntable

4.1.2 Without Considering the Motion Error of Turntable

The calibration deviations of each base station are 0 with no deviation between the initial value of base station selected and its true value in calculation. When the deviation between the initial value of base station selected and its true value is 0.1 mm, the corresponding calibration deviations of four base stations are given in Table 1.

Table 1 Calibration deviations of four base stations mm
Full size table

It can be seen from Table 1 that the calibration deviations of each base station are very small. In the base station calibration, the initial value of base station selected has certain influence on the solving accuracy. Taking the calibration of base station \(P_{1}\) for example, the influence of the different initial values selected on the calculation results are analyzed. When the deviations between the initial value of base station \(P_{1}\) and its true value are 0.1 mm, 0.3 mm, 0.5 mm, 1 mm respectively, the corresponding calibration deviations are given in Table 2.

Table 2 The calibration deviation of base station \(P_{1}\) with different initial values selected in calculation mm
Full size table

From Table 2, the calibration deviations of base station with different initial values selected are relatively small. Meanwhile, the calibration deviation is becoming larger with increasing the deviation between the initial value selected and its true value increasing. In the actual calculation, the initial value of base station and the initial distance between the center of cat eye and the rotary center of turntable are calculated by a series of measuring points measured by laser tracker. Taking into account the measurement error of laser tracker and calculation error, the maximum deviation between the initial value of base station determined and its true value is generally within 0.3 mm. Then the corresponding calibration deviation of base station with this initial value can be generally within 10\(^{{{ - }4}}\) mm, and the calculation deviation is small. In addition, in order to further improve the calculation accuracy, the base station calibrated for the first time can be used as an approximate initial value again in calculation. After several iterative calculation, the satisfactory result can be generally obtained.

4.1.3 Considering the Motion Error of Turntable

In the measurement, the position error of the turntable has a certain influence on the calibration accuracy of base station. According to the different position errors of the turntable, the simulations are carried out under two conditions: (1) The position error of the turntable obeys a random normal distribution within[0, 5″]; (2)The position error of the turntable obeys a random normal distribution within[0, 10″]. Meanwhile, the ranging error of laser tracker is also considered, and the ranging error of the laser tracker obeys a random normal distribution within [0, 1 μm] in the simulations. Table 3 shows the calibration deviations of each base station under the first condition.

Table 3 The calibration deviations of each base station under the first condition mm
Full size table

It can be seen from Table 3 that the calibration deviations of each base station is small, so the base station calibration algorithm is feasible. Taking the calibration of base station \(P_{1}\) for example, Table 4 shows the calibration deviation of base station \(P_{1}\) under different conditions.

Table 4 Calibration deviations of base station \(P_{1}\) under the different conditions mm
Full size table

From Table 4, the calibration deviations of base station are becoming larger with increasing the position error of the turntable. To ensure measurement accuracy, the turntable should have a certain positioning accuracy requirement in the actual measurement.

In addition, the distance between the center of cat eye and the rotary center of turntable also has a effect on the calibration result. Assuming the distances between the center of cat eye and the rotary center of turntable 100 mm, 200 mm and 300 mm respectively, Table 5 shows the corresponding calibration deviations of base station \(P_{1}\) under the first condition.

Table 5 Calibration deviations of base station \(P_{1}\) with different distances between the center of cat eye and the rotary center of turntable mm
Full size table

It can be seen from Table 5 that, under the same error distribution of turntable, the calibration deviations of base station are becoming larger with increasing the distance between the center of cat eye and rotary center of turntable. So, the initial position of cat eye on the turntable can be set as close as possible to the rotary center of the turntable under the premise of guaranteeing no light block in the experiment in order to improve the calibration accuracy of base station.

4.1.4 Simulation for Measuring Point Determination

Firstly, some measuring points are presented as follows: \(A_{1} (400,\;200,\;150)\), \(A_{2} (200,\;400,\;150)\), \(A_{3} (400,\;200,\;500)\), \(A_{4} (200,\;400,\;500)\). The simulations are also carried out under two conditions: with or without considering the motion error of turntable.

Without considering the error in the measurement, the determination deviations of measuring points are generally within 10\(^{{{ - }4}}\) mm. The determination deviations are small, so the algorithm for measuring point determination is feasible. With considering the error in the measurement, the position error of the turntable obeys a random normal distribution within[0, 5″], and the ranging error of laser tracker obeys a random normal distribution within [0, 1 μm] in the simulation. Table 6 shows the coordinates of some measuring points under this condition.

Table 6 Coordinates of some measuring points mm
Full size table

4.2 Simulation for Geometric Error Separation

Taking the identification of geometric error of \(x{\text{-axis}}\) for example, the feasibility of error separation algorithm derived is verified as follows. Firstly, each geometric error at the position of \(x = 200\) are assumed as follows:

$$\begin{aligned} \delta_{x} (x) = &\, 0.015\;{\text{mm,}}\quad \delta_{y} (x) = 0.010\;{\text{mm,}}\quad \delta_{z} (x) = 0.005\;{\text{mm,}} \\ \varepsilon_{x} (x) = &\, 3 \times 10^{ - 5} {\text{rad}},\quad \varepsilon_{y} (x) = 1.5 \times 10^{ - 5} \;{\text{rad,}}\quad \varepsilon_{z} (x) = 2.5 \times 10^{ - 5} \;{\text{rad,}} \\ \end{aligned}$$

Each geometric error can be identified by measuring the direction change of vectors composed of a series of measuring points set on the moving part of machine tool. The simulations are carried out under two different conditions: with or without considering the effect of random error during the machine tool motion. In addition, the number of vectors composed (as shown in Fig. 8) in the measurement also has a certain effect on the identification results.

Fig. 8
figure 8

The distribution of measuring points; a triangle, b square, c pentagon, d hexagon, e heptagon, f octagon

Full size image

Under the first condition, each geometric error at the position of \(x = 200\) are identified with three vectors measured (as shown in Fig. 8a) as follows:

$$\begin{aligned} \delta_{x} (x) = &\, 0.0 1 50,\quad \delta_{y} (x) = 0.0 100,\quad \delta_{z} (x) = 0.00 50 \\ \varepsilon_{x} (x) = &\, 3.0 \times 10^{ - 5} ,\quad \varepsilon_{y} (x) = 1.5 \times 10^{ - 5} ,\quad \varepsilon_{z} (x) = 2.5 \times 10^{ - 5} , \\ \end{aligned}$$

The simulation shows that each identified geometric error is very close to the assumed one, and the maximum identification deviation is 1.9 × 10\(^{ - 14}\) mm for \(\delta_{x} (x)\), so the identification deviation is very small.

Under the second condition, a random error is added to the theoretical motion error at each measuring point. The random error obeys a random normal distribution within [0, 3 μm], [0, 5 μm], respectively. Table 7 shows the identification results of each geometric error at the position of \(x = 200\) with different random error distributions.

Table 7 Identification results of each geometric error at the position of \(x = 200\) mm
Full size table

From Table 7, the maximum identification deviation is 0.0001 mm for \(\delta_{y} (x)\) under the first condition; the maximum identification deviation is 0.0002 mm for \(\delta_{y} (x)\) on the second condition. The identification deviation is small, so the error separation algorithm is feasible.

The effect of different number of vectors composed on the identification accuracy is also analyzed. Taking the identification of straightness error \(\delta_{y} (x)\) for example, Table 8 shows the corresponding identification deviations with different number of vectors mentioned in Fig. 8 under the first condition.

Table 8 Identification deviations of straightness error \(\delta_{y} (x)\) with different distribution of measuring points mm
Full size table

From Table 8, it can be seen that the identification deviations of straightness error \(\delta_{y} (x)\) is decreasing gradually with increasing the number of measured vectors. However, the reduction is not large. Considering the measurement accuracy and efficiency, the number of the measured vectors is about 3–4.

5 Experimental Verification

Based on the space vector’s direction measurement, a laser tracker is adopted to detect the geometric error of the NC milling machine as shown in Fig. 9.

Fig. 9
figure 9

Geometric error detection of the NC milling machine

Full size image

The motion region of the milling machine is 450 mm × 550 mm × 350 mm, and the measurement will be carried out with the movement distance 50 mm. At each measurement location, the motion of the milling machine is controlled to stop, and the corresponding ranging data of laser tracker are recorded with rotating each \(120^{ \circ }\) of precise turntable fixed on the spindle. The total measuring time is about 2.5 h, and the measurement efficiency is high. Each geometric error of milling machine can be identified by the measurement algorithm and error separation algorithm derived. Figure 10 shows the part error curves of \(x{\text{-axis}}\) of milling machine.

Fig. 10
figure 10

Part error curves of \(x{\text{-axis}}\); a straightness error of \(x{\text{-axis}}\), b pitch error of \(x{\text{-axis}}\)

Full size image

In order to verify the effectiveness of the proposed method, taking the detection of position error of \(x{\text{-axis}}\) for example, the identification result obtained by this method is compared with that by laser interferometer measurement as shown in Fig. 11.

Fig. 11
figure 11

Comparison of the results of two measurement methods

Full size image

It can be seen from Fig. 11 that the change trend of the position error curves obtained by these two methods are basically consistent, and the deviations of the identified results at different measuring points are small, so the method based on the principle of space vector’s direction measurement is feasible.

6 Conclusions

  1. 1.

    Based on the space vector’s direction measurement principle, a laser tracker is adopted to achieve quick and accurate calibration of the geometric error of machine tool.

  2. 2.

    The mathematical model of geometric error measurement of machine tool based on the principle of space vector’s direction measurement is established, and the base station calibration algorithm by measuring the motion of the designed precise turntable, the measuring point determination algorithm and geometric error separation algorithm are derived respectively. Meanwhile, the method of determining the initial position of base station in its calibration is also given. The simulations verify the feasibility and accuracy of these derived algorithms.

  3. 3.

    Taking the detection of the position error of milling machine for example, the identification results obtained by the proposed method and laser interferometer measurement are compared and analyzed, which further verifies the feasibility of this method.