Abstract
In this paper, a new design approach for aerostatic bearing spindles (ABS) is firstly proposed which takes into account of the interactions between the mechanical and the servo subsystems, including the integration of electromagnetic effects, static pressure characteristics, servo control and mechanical characteristics. According to the air bearing design principle, the geometry of the spindle rotor is designed. The fluid software is used to analyze the influence of the bearing capacity and stiffness on the stability of the spindle. The simulation shows when the air film thickness is 12 μm, the bearing has good load carrying capacity and rigidity. In addition, the influence of motor harmonics on the spindle shaft modes is considered to avoid the resonance of ABS, and to ensure ABS anti-interference capability, proper inertia of ABS is calculated and analyzed. Finally, ABS has a good follow-up effect on the servo control and machining performance through the experimental prototype. The electromechanical coupling design approach for ABS proposed in this paper, can achieve a peak value better than 0.8 μm (surface size: 9 mm × 9 mm) and a surface roughness better than 8 nm in end face turning experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aerostatic bearing spindle (ABS) is a major component of the ultra-precision machine tools, and its dynamic performance determines the machining performance of ultra-precision machine tools. ABS is a complex electromechanical system, which contains both the mechanical and servo subsystems [1], so dynamic characteristics of ABS are more complex, which are compared with conventional spindles. It is necessary for engineers to thoroughly realize the influences of the system parameters to the ABS dynamics with considering the multi-physics coupling property [2]. The detail structures of ABS are shown in Fig. 1, which is mainly composed by a permanent magnet synchronous motor (PMSM) and aerostatic bearings. ABS can is divided into three parts: the grating ruler, the motor and the air bearings. In ABS, an air bearing system is directly connected with the motor, which cancel the intermediate transmission links. Because the spindle shaft of the ABS is directly driven by a motor, ABS can achieve high speed and precision which drastically increase productivity and reduce production cost [3, 4]. However, the direct drive mechanism causes ABS very sensitive to the variation of the work load. It also causes a strong feedback coupling between the machining process and the servo system.
In common, the mechanical system and the servo system of ultra-precision machine tools are separately designed. Generally, there would be inevitable matching problems between the mechanical system and the servo system, which dynamically affect the system performance, especially in the ultra-precision machine requirements. Accordingly, to maintain the processing stability and reduce external interference on ABS, the electromechanical coupling design should be considered. At present, many scholars have considered dynamic characteristics [5, 6], thermal characteristics [7], and static pressure characteristics [8, 9] during designing spindle systems, but rarely considered the integrated design for ABS. With the increasing requirements of high precision and high efficiency for the ultra-precision machining, the design method for the electromechanical integration is becoming more and more urgent. The traditional experience separation or step-by-step design method is facing great challenge, because the coupling factors in the design have been already inevitable problems [10]. To meet the needs of the machining development, many scholars have studied the impacts of servo systems for improving movement accuracy of the mechanical and electrical systems [11,12,13,14]. In addition, to study servo control system research, a PID controller to stabilize the system is adopted adaptive feed forward cancellation to effectively compensate for the process of driving the system of vibration [15]. Also, a three-loop servo system of the permanent magnet motor is studied [16]. In order to improve the control performance of the servo system, the control parameters are optimized and the three-loop feedback is designed to enhance stability and fast performance of the spindle system. Besides, to increase motor performance, an electromechanical integrated harmonic piezodrive system is proposed, and analyzed that the size parameters of the stator had a certain influence on the natural frequency of the drive system [17]. The mechanical and electrical integration to design the static pressure rail is proposed, containing the mechanical parts and the servo parts [18]. Moreover, to further study the dynamic characteristics of the spindle, the machined surface topography in the ultra-precision machining process is obviously affected by the aerostatic bearings [19, 20]. Therefore, machining workpiece surface is an effective method for detecting the dynamic performance of a spindle system. The above studies only consider the relationship between the mechanical and servo systems and do not take into account the influence of the electromagnetic effects of the motor on its performance, or just study one of the factors in electromechanical systems.
As ABS is a complex electromechanical coupling system, the interaction of various factors affects the dynamic performance. Coupling analysis of ABS is an inevitable problem, so the traditional single research method has faced enormous challenges. Nowadays, numerous of scholars have studied the effect of servo system on improving the motion accuracy of electromechanical systems. However, these studies mainly discuss the relationship between the mechanical system and the servo system, but seldom consider the motor characteristics. In fact, because the motor acts as a direct drive source, its performance directly affects system performance. In addition, the electromagnetic vibration of the motor acts on the mechanical mode of ABS, which is easy to generate resonance and affect the dynamic performance of the spindle system. As the air film of ABS is used to support the spindle shaft, the static pressure stiffness of ABS also has a certain influence on the dynamic characteristics, which affect the resonance frequency of the spindle shaft. Moreover, the inertia of the spindle shaft has a certain influence on the servo system of ABS, which affects the stability. However, the inertia of the spindle shaft is determined by its own volume, and the volume is affected by the stiffness and load carrying capacity. Therefore, the mechanical structure, the motor, the air supply and the servo control interact with each other, and the coupling relationship between them is shown in Fig. 2. In order to further improve dynamic performance of the direct drive system, it is very important to consider the coupling effects of the three parts, because the three complements influence each other, and only a comprehensive consideration can enable the electromechanical system to achieve better performance.
In this paper, an electromechanical coupling design approach for an aerostatic bearing spindle system is proposed, and the multi-factor dynamic studies of ABS are shown in Fig. 2. It considers the static pressure characteristics, mechanical characteristics, electromagnetic characteristics and servo characteristics as a whole, and takes into account the electromechanical coupling effects. According to the design specifications of ABS, the motor, the mechanical dimensions, the air bearing system and control parameters of the spindle shaft are designed. The harmonic frequency spectrum of the driven motor and the mechanical characteristics of the spindle are analyzed. To introduce the generic design approach, the following sessions will be implantation of the approach through a design case. As an important part of ultra-precision machine tools, this article will take an ABS as a research object to illustrate the design, and the dynamic characteristics of the ABS are evaluated by experiments.
2 Electromechanical Coupling Analysis
Before designing the spindle system, it should ensure that the spindle system has the sufficient stability, rapid response capability, and high positioning accuracy. Therefore, the spindle system should have lighter quality, but it must ensure that it has a certain degree of stiffness and inertia, which can resist external interference. In addition, the spindle system uses a motor to directly drive the spindle shaft. The electromagnetic harmonics generated by the motor also have a certain influence on the mechanical structure, which should be considered.
2.1 Selection of Film Thickness
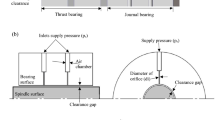
The servo stiffness of ABS ensures the smoothness of the rotation, but it cannot withstand the axial and radial interference from the outside. The axial and radial ant interference ability requires thrust and radial bearing guarantee. Considering that the air bearing system has sufficient resistance to external disturbances, it is necessary to determine the axial and radial stiffness and bearing capacity of the air bearing. In this paper, the throttling form of the small orifices is used in the air bearings. The working principle is that air is pressed into the air gap of the air bearings by each orifice, and the throttling principle of orifice restrictors embedded in the air bearing is adopted. The radial and axial loads are balanced by the radial bearing pressure difference and the thrust bearing pressure difference, respectively. The air bearing acts to support the rotation of the spindle shaft, ensuring the spindle system has sufficient bearing capacity, radial and axial stiffness. Since the air film size and air supply pressure directly affect its stiffness, it is necessary to analyze its air film and supply pressure.
2.1.1 Film Simplification of Thrust Bearings
Computational fluid dynamics (CFD) is the common analytical software for analysis of fluid dynamics. This paper will use Fluent to simulate the air films of the air bearings. ABS adopts two-way thrust bearings, both sides of the air film structures are symmetrical, and the air film structure of air bearings is a circumferential symmetry distribution. The one-side thrust bearing is evenly distributed with 12 orifices, thus 1/12 model of one-side thrust bearing can be calculated, which can reflect the characteristics of the overall thrust bearings. The detail parameters of the air film are shown in Fig. 3, where Fig. 3a shows an orifice enlargement. According to design manuals of air bearings, the structural parameters of air bearings are shown in Table 1.
ANSYS Meshing is used to mesh a single air film. Before air film meshing, the air film is sliced by the slicing method. This can reduce the difference between the length and thickness of the air model, reducing the grid aspect ratio to be too large, increasing the accuracy of the calculation. Besides, when using Fluent to simulate the air film, the boundary conditions of the model need to be defined. The boundary conditions are used to determine the calculation area and the initial setting range, and the boundary conditions in air film such as the inlet pressure inlet, the pressure outlet, and the wall are included. The structure of the air film in the extracted air bearing and boundary conditions are defined as shown in Fig. 4.
To simulate the single orifice air film of the thrust bearing, the model of the single throttle unit is built by SOLIDWORK and imported into ANSYS WORKBENCH, as shown in Fig. 5a. Before meshing the air films, it is necessary to refine mesh to the orifice, the throttle groove and the abrupt change of the air film structure, and divide the air film into 5 layers. The air film division process is shown in Fig. 5, the air intake mesh is shown in Fig. 5d. The air film finite element model is imported into Fluent for calculation. The double precision solver is used to define the air film as laminar flow due to the small Reynolds number and Mach number in the bearing. For the convenience of calculation, the pressure inlet is set to 0.5 MPa after setting the boundary, and the outlet pressure is defined as 0 MPa. The SIMPLE method is selected as the solution algorithm. This method is beneficial to the stable convergence solution, and the convergence criterion is set to 1 × 10−5. This value satisfies the calculation convergence condition. In addition, it can detect whether the simulation converges by setting the pressure change of the monitoring point. According to the combination of the convergence criterion and the detection result, it can be determined whether the calculation result converges. As the thrust film is very thin, to simulate the actual flow state of the air, the turbulence model is selected according to the Reynolds average N–S equation. The finite element simulation of the air film is carried out, and the simulated pressure distribution cloud diagram of the single orifice is shown in Fig. 5e.
2.1.2 Film Thickness
The small orifice diameter of the thrust air bearings is set to 0.2 mm, 12 rows are evenly distributed in each row, and the radial position is 78 mm. Under different film thicknesses, the bearing capacity and stiffness curve of the air supply pressure to the air bearings are shown in Figs. 6 and 7. Bearing capacity of the air bearing decreases with the increase of the air film thickness, and the bearing capacity decreases rapidly with the increase of the air gap spacing. Figure 6 shows the bearing capacity curve of the air bearing with the film gap. In addition, under different inlet pressures, the bearing capacity of air bearings is different. As the inlet pressure increases, the bearing capacity of the bearing increases continuously, and the load capacity changes greatly in the range where the inlet pressure film gap is small. The stiffness calculation of the air bearing is carried out, and the calculation result is shown in Fig. 7. With the increase of the air gap, the bearing stiffness increases first and then decreases. The bearing stiffness reaches a peak at a film thickness of 12 μm. This value is the ideal thickness value for this thrust bearings. In addition, the supply pressure also has a certain influence on the stiffness. As the supply pressure increases, the bearing stiffness increases, and the peak point reached by the bearing stiffness also increases. In summary, a suitable film gap can increase bearing stiffness and reduce air supply. When designing an aerostatic bearing, the given range of the supply pressure should be taken into account, and the fluctuation of the supply pressure should be reduced to ensure the performance of the designed bearing.
2.1.3 Air Supply Pressure
Bearing capacity and stiffness of the air bearings are calculated under different air supply pressures. The results are shown in Figs. 8 and 9. The film thickness is set to (a) 14 μm, (b) 15 μm and (c) 16 μm. It can be seen from the calculation results that as the supply pressure decreases, the bearing capacity of the air film decreases. As the air bearing capacity increases, the air bearing stiffness decreases. In addition, the flow rate under different supply pressures is calculated. As the pressure increases, the air flow also increases correspondingly, which is shown in Fig. 10. Through analysis of the air films and the inlet pressure of the air bearings, the design of the air bearing can obtain the proper film thickness and supply pressure, which not only ensures the bearing capacity and rigidity, but also reduces the air consumption.
2.2 Spindle Shaft Geometry
The bearings are characterized by the geometric configurations, so the restriction parameters and the optimization values of the bearings are significant in the dynamic characteristics of ABS [21]. As shown in Fig. 1, the spindle shaft adopts an integral structure of the journal and axial bearings, and all the bearings adopt the small orifice throttles. The spindle shaft structure uses two series of journal bearings to increase the journal bearing capacity and stiffness, and adopts two opposing axial bearings, which can be subjected to loads coming from two directions, forward and reverse. Although two axial bearings, which have the same sizes, reduce the load capacity of the spindle in the axial direction, it can increase the axial stiffness. In addition, in order to reduce the spindle shaft deformation caused by the temperature rise of the drive motor, the axial bearing of the spindle system adopts the front type, that is, the axial bearing is installed at the end of the machining workpiece, and the motor is installed the other end of the spindle shaft. Under this layout condition, when the motor becomes heat, the spindle deformation moves away from the axial bearing, avoiding the influence on the machining shaft end. In addition, in order to achieve the electromechanical optimization, the control system of the spindle system requires the drive component weight as little as possible. However, if the drive component weight is too little, the spindle system could not guarantee the system’s anti-interference. In order to study the performances of the spindle shaft, the detail requirements for the mechanical structure are put forward. To ensure ABS has good thrust and radial anti-interference capability, the thrust stiffness is better than 300 N/μm, and the journal stiffness is better than 300 N/μm.
It can be seen from Fig. 1, the axial length of the spindle shaft is selected taking into account the Grating ruler, motor and air bearings. According to the axial length required for the three parts, the influence of these factors should be considered in the design of the spindle shaft. To ensure good response and a certain anti-interference ability, the spindle shaft needs to be optimized. The outline dimensions of the spindle shaft are shown in Fig. 11. L0 represents the total length of the spindle shaft, L1 represents the axial bearing length, L3 represents the axial length of the mounting motor (L3 < L2), L4 represents the axial size of the circular grating, L5 represents the axial bearing thickness (L5 < L6), and L7 represents the internal bore length (L7 < L1). Besides, D0 represents the outer diameter of the axial bearing. D1 represents the diameter of the spindle shaft end, and this end can be used to install a vacuum chuck or a three grasping chuck for fixing the workpiece. D2 represents the journal bearing diameter, and D3 represents the bore diameter, which is used to vacuum and reduce the spindle mass. In order to ensure the sufficient strength of the spindle shaft, the general diameter of the spindle meets D3 ≤ D1 and D3 ≤ (1/2)D2. The spindle shaft length to diameter ratio is L1/D2 = 0.75, the throttle position meets L8/L1 = 1/4. To improve the control performance of the spindle system, and reduce the spindle shaft quality, the geometric sizes of the spindle shaft should meet L1 + L2 + L4 + L6 ≤ L0.
The journal and thrust air bearings are used for the spindle shaft, and its features should be considered. Hence, the design of the journal bearing is analyzed, which uses the double-row air supply and the load capacity coefficient CJ = 0.25, and the corresponding calculations are expressed as Eqs. (1–3).
where P0 = 1×105 Pa is atmospheric pressure, ε denotes the eccentricity, WJ denotes the bearing capacity, KJ denotes the stiffness, and Kα denote the angular rigidity.
The axial bearings adopt the annular porous air supply, and the structure performances meet the following requirements, which are calculated as Eqs. (4–6).
where r1 represents the inner radius, r2 represents the outer radius, Wt represents the bearing capacity, Kt represents the stiffness, Kα represents the angular rigidity, h0 represents the bearing air gap size, and Ct represents the load capacity coefficient, respectively. After above calculations, in order to ensure the spindle system has sufficient strengths, the main dimensions of the spindle shaft are shown in Table 2.
2.3 Mechanical Modal
Relative oscillations in the drive system, generated by the mechanical structure, may cause the feedback position to oscillate [22]. Therefore, considering the performance of the spindle system, it can be seen that the servo width of the spindle system should satisfy less than the minimum width value of those systems. Thus, the vibration of the servo system and the mechanical harmonic can be avoided, which can improve and the control accuracy. Through the above analysis, the performance of the spindle system can be improved by adjusting the servo parameters or changing the mechanical system, which allows the complementarities between the servo system and mechanical system to achieve optimizations.
The harmonic frequencies caused by the motor directly act on the mechanical system of ABS, and the mechanical vibrations caused by the harmonics and other outside interferences also directly affect the motor performance, which produces the electromechanical couplings in the direct driven system [23]. Therefore, the mechanical modal characteristics of the spindle shaft should be studied. The solid model of the spindle shaft is simplified and calculated by ANSYS. Firstly, to reduce the amount of computation and improve the accuracy of the calculation, the rotating spindle shaft is simplified as a solid. In addition, some bores in the entity and small removal parts are ignored. Secondly, according to its actual material, the material of the spindle shaft is defined as 38CrMoAl, and the model is meshed, which is shown in Fig. 12. Then, the aerostatic supports of the spindle system are simplified, and some springs are used to instead of the airfoil elasticity. The springs are arranged in the position of the feed air hole according to the solid structure, and the corresponding grid nodes are connected to the nodes of the corresponding entity. The simplified model is simulated, the first four-order modes of the simulation are shown in Table 3, and the mode shapes are shown in Fig. 13.
2.4 Harmonic Analysis of the Motor
Because an ABS is mainly composed by a motor and an aerostatic bearing, the characteristics of the motor and spindle shaft have a significant influence on the spindle system performance. In this ABS, the PMSM (10 poles/12 slots) and the spindle shaft are directly connected, all the intermediate transmission components are canceled, and the harmonics generated by the motor directly affects the dynamic characteristics of the spindle system. The harmonics and other disturbances act on the mechanical system, and then cause mechanical vibrations with multi-modes [24]. Therefore, it is necessary to study the motor harmonics. Based on motor theory, the software of Ansoft Maxwell is useful for calculating motor harmonics, which considers the impacts of the saturation factor and current waveform, and specifically emulates motor characteristics [25]. To simplify the motor model and increase the calculation efficiency, the permeability between stator and rotor is assumed to be infinite. The motor model is simulated, and the inner circle of motor rotor and the stator outer circle are selected as the boundary, which has no leakage magnetic. At a load condition, the motor windings have a rated current of 6 A and 3 phases, rated speed 1000 rpm, and Table 4 lists the detailed motor parameters. After the simulation, Fig. 14 shows the electromagnetic density cloud diagram of the motor, and the maximum electromagnetic density is 1.3313 T.
The magnetic density in the air gap is extracted from the simulation model, as shown in Fig. 15. Then, the space harmonics spectra in the air gap at t = 0.005 s are analyzed by Fast Fourier transformation (FFT), which is shown in Fig. 16. Because the fundamental frequency of the supply current is 50 Hz, it can be noted from Fig. 16 that the electromagnetic force is mainly affected by the five times (V = 5) fundamental frequency (250 Hz), and the second obvious interference is the harmonic frequency (750 Hz, V = 15). Hence, the harmonic frequency should be considered when the motor is analyzed, which may cause ABS resonance. Consequently, when the mechanical structure of ABS is designed, the natural frequency of the mechanical system should be far from the harmonic frequency for avoiding resonance.
The frequency of the maximum harmonic peak of PMSM is 250 Hz and 750 Hz, which is different from the modal value of the spindle shaft, as shown in Table 3. It can be known that the spindle rotor has sufficient rigidity, and the resonance phenomenon of the spindle system can be avoided effectively after the spindle rotor has enough stiffness. At the same time, during the machining process, the spindle rotation speed tries to avoid the fundamental wave and harmonic maximum component of the motor, which helps to improve the processing quality.
2.5 Servo Control of the Spindle System
In ABS, because a PMSM directly drives the spindle shaft rotating, the interference caused by mechanical structure would react to the servo system and affect stability of ABS, so the electromechanical coupling between the mechanical system and servo system should be considered together. Meanwhile, in order to improve the servo performances of the spindle system and reduce the coupling effects, a current loop, a speed loop and a position loop are used in the electromechanical system, but each loop has different roles. The current loop increases the reaction speed of the drive system and suppresses the interference of the current loop, and the system has enough large acceleration torque. The speed loop improves the performance of the spindle system against the load disturbance, and suppresses the speed fluctuations [26, 27]. The position loop ensures that the drive system has good static accuracy and dynamic tracking performance. Therefore, the three-loop servo system can ensure the spindle system has good follow-up performance and anti-jamming performance, as shown in Fig. 17.
2.6 Servo Response Simulation
The servo model of the spindle system takes into account the various aspects of the spindle system, including the control link of the position, the current loop, the drive model, the motor model and the mechanical motion model. The related parameters of the rotating motor are shown as follows: the rotating motor inductance Lm is 9.1 mH, the resistance R is 1.66 Ω, and the force constant KF is 1.49 N/A. The mechanical structure and the control system (controller and current regulator) have the characteristics of the multivariable, the strong coupling and the non-linearity, so the servo system is more complex. In order to meet the anti-interference force and stability of the spindle system, the inertia of the spindle shaft is set to more than 0.045 kg m2. Then, the closed-loop flow chart of the spindle system built by the Matlab/Simulink is calculated. The servo model of the spindle system is tested by the step signal, and the step signal result is shown in Fig. 20.
The servo system of the spindle system is simulated with different inertias, and a random disturbance force of 10 N is applied to the spindle system at time t = 0.04 s. The simulation results are shown in Fig. 18. Figure 18a shows the result of the spindle inertia is set to 0.045 kg m2. If the spindle system is too heavy, the inertia of the spindle system is set to 0.08 kg m2. As shown in Fig. 18b, it can be seen that the control reaction speed is slow, but it has strong anti-interference ability. If the spindle system is too light, the inertia is set to 0.02 kg m2, and the simulation is shown in Fig. 18c. At this time, the reaction speed is faster, but the anti-interference ability is weak, so it is easy to be disturbed the external interference.
3 Experiments
To verify the superiority of the optimized spindle system, an ABS is designed and mounted on an ultra-precision turning machine, which is shown in Fig. 19, rotation accuracy of ABS is controlled better than 80 nm, and the characteristics experiments of ABS are carried out. Firstly, the tracking performance of the spindle system is tested, which detect the follow-up performance. The sinusoidal motions are used to detect the following errors of the spindle system. The input signal cycle is set to T = 1000 ms, the amplitude is set to A = 60 μm and the experimental results are shown in Fig. 20. The detection method is explained as follows: the matching adjustments between the mechanical system and servo system are carried and optimized according above analysis. The following response errors of ABS are detected, the result is shown in Fig. 20, and the maximum following error is 0.08 μm.
The designed ABS is used for single-point turning, and AL7075 is used as the turning material. The single-crystal diamond tool is used, the tool radius is 3 mm, and the radius of the arc cutting edge is better than 50 nm. The spindle speed is arbitrarily given, the turning speed is set to 926 r/min, the turning feed is set to 8 μm/r, and the cutting depth is set to 6 μm. The machined workpieces are tested using Phase Cam 6000 (4Sight™ interferometer, 4D Technology Corporation, USA). It can be seen from the result Fig. 21 that the detection end face size can reach the range of 9.1 mm × 9.1 mm, the surface roughness quality can reach Ra = 46.585 nm, and the face turning has a good peak value (PV), which can reach 0.8 μm. In addition, it can be seen from the figure that if the influence of the turning error of the workpiece center is neglected, the surface PV can be better than 0.4 μm. The test results can reflect that the static thrust bearing has good thrust stiffness and can ensure a good flatness for turning. When the radius R = 4 mm is selected to analysis the end face quality, the Y maximum assignment change of the end face detection is 55.2 nm, which can been seen from Fig. 22. The surface roughness at this position can reach Ra = 8 nm, which has high processing quality. It can be seen that the spindle system has good servo anti-interference ability during the turning process, and it can effectively avoid the influence of external interference on the turning process.
4 Conclusions
In this article, a new electromechanical coupling design approach for ABS has been proposed, which considers the relationship among the mechanical, servo and electromagnetic subsystems, and which is important to improve the performance of the direct driven system. When designing the spindle system, the influence of the electromagnetic harmonics of the motor on the mechanical modal of ABS should be taken into consideration. Besides, the transfer function of the spindle system is simulated, and the following characteristics of the spindle system are carried out, and the following error of the spindle system is reduced by the electromechanical coupling design method, which is proved that the method is an effective way to improve the dynamic characteristics of ABS. The main conclusions are as follows:
-
1.
The effectiveness of the electromechanical coupling design method is proposed, which contains the mechanical, servo and electromagnetic subsystem. In the design process of electromechanical system, the mechanical structure, motor, air supply and servo control are integrated for the first time, and it is applied to the design of ultra-precision spindle.
-
2.
To improve the dynamic performance of the work spindle, the motor harmonic frequency and mechanical mode frequency should be considered together. The mechanical frequency is designed to avoid the possible driving excitation frequency when the mechanical component is designed.
-
3.
Considering the performance of the spindle system, the shaft inertia of the spindle system is not as small as possible. Although the inertia of the spindle system is small, the inertia is easy to control, but the anti-interference ability is weakened. The mechanical structure, servo control and the motor should be comprehensively considered in the spindle system.
-
4.
This method can also be applied to the design and application of linear motor drive systems, because they have similar drive principles.
References
Chen, G. D., Sun, Y. Z., Zhang, F. H., An, C. H., Chen, W. Q., & Su, H. (2017). Influence of ultra-precision flycutting spindle error on surface frequency domain error formation. The International Journal of Advanced Manufacturing Technology, 88, 1–9.
Liu, J. F., & Chen, X. A. (2014). Dynamic design for motorized spindles based on an integrated model. The International Journal of Advanced Manufacturing Technology, 71, 1961–1974.
Abele, E., Altintas, Y., & Brecher, C. (2010). Machine tool spindle units. CIRP Annals - Manufacturing Technology, 59(2), 781–802.
Lin, C. W., Tu, J. F., & Kamman, J. (2003). An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation. International Journal of Machine Tools and Manufacture, 43(10), 1035–1050.
Jiang, S., & Zheng, S. (2010). Dynamic design of a high-speed motorized spindle-bearing system. Journal of Mechanical Design, 132(3), 1–5.
Chen, G. D., Sun, Y., An, C. H., Zhang, F. H., Sun, Z. J., & Chen, W. Q. (2018). Measurement and analysis for frequency domain error of ultra-precision spindle in a flycutting machine tool. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 232(9), 1501–1507.
Li, H., & Shin, Y. C. (2004). Analysis of bearing configuration effects on high speed spindles using an integrated dynamic thermo-mechanical spindle model. International Journal of Machine Tools and Manufacture, 44(4), 347–364.
Gao, S., Cheng, K., Chen, S., Ding, H., & Fu, H. Y. (2016). Computational design and analysis of aerostatic journal bearings with application to ultra-high speed spindles. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 231(7), 1205–1220.
Cui, H., Wang, Y., Yue, X., Huang, M., & Wang, W. (2017). Effects of manufacturing errors on the static characteristics of aerostatic journal bearings with porous restrictor. Tribology International, 115, 246–260.
Chen, X., Yuan, S. H., & Peng, Z. X. (2015). Nonlinear vibration for PMSM used in HEV considering mechanical and magnetic coupling effects. Nonlinear Dynamics, 80, 541–552.
Huo, D. H., Cheng, K., & Wardle, F. (2010). Design of a five-axis ultra-precision micro-milling machine—UltraMill. Part 2: Integrated dynamic modelling, design optimization and analysis. International Journal of Advanced Manufacturing Technology, 47, 879–890.
Zhong, G. L., Shao, Z. Z., Deng, H., & Ren, J. L. (2017). Precise position synchronous control for multi-axis servo systems. IEEE Transactions on Industrial Electronics, 64(5), 3707–3717.
Jeong, S. K., & You, S. S. (2008). Precise position synchronous control of multi-axis servo system. Mechatronics, 18(3), 129–140.
Chen, C. S., & Chen, L. Y. (2012). Robust cross-coupling synchronous control by shaping position commands in multiaxes system. IEEE Transactions on Industrial Electronics, 59(12), 4761–4773.
Kim, J. H., & Lee, S. K. (2016). Micro-patterning technique using a rotating cutting tool controlled by an electromagnetic actuator. International Journal of Machine Tools and Manufacture, 101, 52–64.
Yang, S. M., & Lin, K. W. (2016). Automatic control loop tuning for permanent-magnet AC servo motor drives. IEEE Transactions on Industrial Electronics, 63(3), 1499–1506.
Xu, L., & Li, H. (2012). Resonant responses for an electromechanical integrated harmonic piezodrive system. Journal of Bacteriology, 169(5), 2245–2250.
Liang, Y. C., Chen, W. Q., Sun, Y. Z., Luo, X. C., & Liu, H. T. (2014). A mechanical structure-based design method and its implementation on a fly-cutting machine tool design. International Journal of Advanced Manufacturing Technology, 70, 1915–1921.
Cui, H. L., Wang, Y., Yang, H., Zhou, L., Li, H., Wang, W., et al. (2018). Numerical analysis and experimental research on the angular stiffness of aerostatic bearings. Tribology International, 120, 166–178.
Gao, S., Cheng, K., Chen, S., Ding, H., & Fu, H. Y. (2015). CFD based investigation on influence of orifice chamber shapes for the design of aerostatic thrust bearings at ultra-high speed spindles. Tribology International, 92, 211–221.
Chen, C., Kang, Y., & Huang, C. (2004). The influences of capillary restriction and journal eccentricity on the stability of the rigid rotor-hybrid bearing system. Tribology International, 37(1), 227–234.
Guan, C. L., Dai, Y. F., Xie, X. H., & Yin, Z. Q. (2009). Investigation on feedback control of linear motors in ultraprecision-machine feed-drive systems. Journal of Vacuum Science & Technology B Microelectronics & Nanometer Structures Processing Measurement & Phenomena, 27(3), 1351–1354.
Yang, X. J., Lu, D., Liu, H., & Zhao, W. H. (2018). Integrated modeling and analysis of the multiple electromechanical couplings for the direct driven feed system in machine tools. Mechanical Systems and Signal Processing, 106, 140–157.
Yang, X. J., Lu, D., & Zhao, W. H. (2018). Decoupling and effects of the mechanical vibration on the dynamic precision for the direct-driven machine tool. International Journal of Advanced Manufacturing Technology, 95, 3243–3258.
Shi, H., Niguchi, N., & Hirata, K. (2017). Characteristic analysis of surface permanent magnet vernier motor according to pole ratio and winding pole number. IEEE Transactions on Magnetics, 53(11), 821104.
Lee, Y., Shin, D., Kim, W., & Chung, C. C. (2016). Proximate In-phase current estimator to reduce torque ripple in permanent-magnet stepping motor. IEEE Transactions on Industrial Electronics, 63(3), 1707–1716.
Xia, C. L., Ji, B., & Yan, Y. (2015). Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional–integral–resonant controller. IEEE Transactions on Industrial Electronics, 62(4), 2123–2134.
Acknowledgements
The authors gratefully acknowledge financial support of the International Science & Technology Cooperation Program of China (No. 2015DFA70630), the National Natural Science Foundation of China (Grant No. 51505107), and China Scholarship Council.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wu, Q., Sun, Y., Chen, W. et al. An Mechatronics Coupling Design Approach for Aerostatic Bearing Spindles. Int. J. Precis. Eng. Manuf. 20, 1185–1196 (2019). https://doi.org/10.1007/s12541-019-00098-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12541-019-00098-w