Stress State Analysis of Radial Stress Superposed Bending

Abstract

Radial stress superposed bending is a sheet metal bending process, which superposes predetermined radial stresses. Stress superposition is mandatory to enable the reduction of the triaxiality in bending, resulting in delayed damage evolution and an improved product performance. The knowledge of the stress state is essential for damage-controlled bending as the triaxiality is the driving force for the void evolution. To control the stress state in radial stress superposed bending, an additional counter force responsible for the pressure in the outer fiber is applied. To predict the effect of the counter force on the radial stress and the triaxiality an analytical model is proposed. The prediction of the reaction forces in the system is required for the process design and for the calculation of the stress superposition. The stress state for plane strain bending with stress superposition is derived, and pressure calculations are made using the theory of Hertz. The model and the assumptions are verified in numerical and experimental studies for various counter pressures and bending ratios. Finally, a discussion of the load path depending on the transient counter pressure is carried out and experimental evidence for a inhibited damage evolution due to stress superposition is given.

1 Introduction

A key approach to achieve weight reduction in automotive industry is the usage of high-strength metals with a low density-to-strength ratio. This advocates the use of advanced high-strength steels (AHSS) since they offer a high specific strength with a reasonable formability. A representative steel of this group is the dual-phase steel, which consists of a ductile ferrite matrix and embedded hard martensite islands. In the forming process, failure typically occurs via ductile damage mechanisms, whereby voids nucleate at inhomogeneities in the material and then grow and coalescence. McClintock firstly investigated the growth of voids in low triaxiality fields [1]. Rice and Tracey later showed the strong stress triaxiality dependency of fracture [2]. Bao et al. gave a comprehensive overview of the relationship between the stress state and the equivalent plastic strain at fracture [3]. In a later study a fracture locus is introduced to correlate the fracture initiation to the current stress states and is derived through various models and material tests [4]. Descriptors of the stress state include the stress triaxiality η and the lode angle parameter $\bar{\theta }$.

Anderson et al. [5]. and Roth and Mohr [6] showed that for DP780 the fracture strain at lower triaxialities is significantly higher than at higher triaxialities at constant lode parameter, for example for a load path near shear (η = 0.027 and $\bar{\theta }$ = 0.069: ε_f = 0.86) and plane strain bending (η = 0.57 and $\bar{\theta }$ = 0: ε_f = 0.58) (Fig. 1).

Fig. 1

(Adopted from [6])

Equivalent plastic strain to fracture depending on the stress state according to the Hosford–Coulomb model.

In bending an inhomogeneous multi-axial stress and strain state evolves. In general, the outer fiber of the bent specimen experiences maximum tensile stresses, whereas stresses in the inner fiber are compressive. As the stress state is inhomogeneous, the resulting properties are a function of the position over the sheet thickness. Damage and also failure is usually triggered by the maximum tensile stress and therefore takes place at the outer area of the bent part [7]. Kaupper and Merklein showed that for the DP780 severe voids and microscopic damage appear before the onset of necking [8].

Rice and Tracey [2] suggested that a superposition of hydrostatic tensile stresses leads to higher void growth rates. In the past, many attempts have been carried out to superpose compressive stresses in order to lower the value of the bending stresses. The aim of this superposition was to increase the formability and to reduce springback, since additional compressive stresses lower the required bending moment and therefore the springback.

In four roll bending an additional pressure roll is used for applying a stress superposition during bending (Fig. 2). The superposition leads to a reduction of the tensile stresses in the outer fibre and therefore the formability is increased [9]. It focuses on the increased formability for thick sheet with t > 6 mm and corresponding bending radii > 250 mm of AlMg₃.

Fig. 2

Four roll bending

Another solution is the bending with a solid counterpunch [10]. A solid counter punch is inserted into a conventional air bending die and applies counter pressure on the plastic zone while bending. The superposition also leads to improved formability and decreased springback, but flattens the outer fibre.

One solution to supply compressive stresses without flattening the outer fibre is bending with an elastomer cushion, which facilitates the compressive stress superposition during the entire plastic deformation. For the complex phase steel CP1000 an improved formability by the use of compressive stresses is shown experimentally and numerically in [11].

A study on the effect of elastomer bending on damage evolution and the resulting product properties is carried out for a DP1180 steel in Tekkaya et al. [12]. This study showed that by using the elastomer-bending the stress triaxiality is lowered and therefore the void evolution is delayed, without macroscopic failure. Additionally, the delayed damage evolution caused an improved performance characteristics determined by multiple-step cyclic tests [12].

Despite the positive effect on the bent product, the reproducibility by the application of elastomer-bending is not fulfilled, which is often a required criterion for the industrial usage. Also, the predictability of the stress state and damage evolution is limited due to the evolving properties of the elastomer. For superposing predetermined compressive stresses a novel bending technology has been introduced, which is designed for the forming of advanced high strength steels [13].

The missing key to facilitate a damage controlled bending is the knowledge and predictability of the resulting stress state with adaptable compressive stress superposition. Therefore, the process principle and technological implementation of the so-called radial stress superposed bending (RSS-bending), which is capable of applying predetermined pressure, is shown. Then an analytical model for plastic bending with radial stress superposition is presented. With the proposed model the stress state can be described by the stress triaxiality and the lode angle parameter, which are values that allow for determining the void evolution. The additional radial stress applied in RSS-bending is derived by the pressure distribution according to Hertz [14]. For the calculation of the resulting pressure, the static equilibrium for the determination of the forces responsible for the stress superposition is required. The model is validated by numerical simulations and the load path variation in RSS-bending is discussed. Finally, the effect of the reduced triaxiality on the damage evolution is revealed by SEM-micrographs.

2 RSS-Bending

In this section the process principle of RSS-bending and the technological implementation with the most important geometry and process data is presented.

2.1 Process Principle

RSS-bending superposes predetermined radial stresses during bending. Additional compressive radial stresses are utilized by an additional counter punch and rotating tool segments (Fig. 3). During the bending process, radial stresses are applied by a force N_r, which acts in the instantaneous bending zone. The bending moment is applied by the force N_b and reaches its maximum in the contact area of punch force N_p. The bending moment remains constant between the punch forces and therefore the forming zone is moving along the circumference and a constant plastic strain distribution develops [15]. So the curvature is created by the maximum bending moment. The value of the counterforce N_r can be adjusted during the process to influence the stress state while bending.

Fig. 3

Process principle at initial state (left) and during bending (right)

The technological set-up consists out of two rotating tools to apply the bending moment with superposed compressive stresses (Fig. 4). A groove is inserted in the rotating tool for the introduction of radial stresses (Fig. 4). The contact area between the round surface of the rotating tool and the sheet is the area where the stress superposition is applied. Additionally, the lower rotating tools guide the sheet from underneath and rotate in a bearing shell, which moves axially. The axially moveable bearing shell is supported by a hydraulic cylinder, which applies a counter pressure force N_cp. By changing the counter pressure force, the radial stress superposition is adjusted. The upper punch is divided and rotatable so that the punch indentation is lower. Previous studies also showed that the adaptable stress superposition with RSS-bending is technologically possible and leads to delayed void area fraction in the outer fiber of RSS-bent products compared to air bending [15].

Fig. 4

Technological implementation of RSS-bending

2.2 Tool Set-Up

The tool set-up of RSS-bending technology is given in Fig. 5. The geometry and process data used in the following anaylsis are given in Table 1 referring to Fig. 4.

Fig. 5

Tool set-up of RSS-bending

Table 1 Geometry and process data

The material used is a dual phase DP800 steel bent parallel to the rolling direction and consisting of multiple phases for increased strength with a comparably high ductility. The tools are made of a tool steel 42CrMo4 + QT. Different bending operations are carried out with different punch geometries and different counter pressures.

The various punch radii lead to maximum equivalent plastic strains ε_max in the range of 0.24 < ε_max < 0.36. The hydraulic force is controlled by a PID-control implemented in a LabVIEW program [16], which decreases the hydraulic force with increasing punch displacement. The hydraulic force is directly measured under the bearing shell and for the validation of the numerical model the punch force is directly measured above the upper bearing shell. For a constant stress superposition during the whole process, the counter pressure force has to be monotonically reduced. A simplified model for the required counter force N_cp for a nearly constant radial stress superposition as a function of the punch displacement h is given in [16]. A reduction of 30% of the initial counter force N_cp,0 at h_max leads to a nearly constant stress superposition for the given experimental setup over the bending stroke. Therefore, the counter force is reduced by

$$N_{\text{cp}} (h) = N_{\text{cp,0}} \cdot \left(1 - \frac{h}{{h_{\hbox{max} } }} \cdot 0.3\right)$$

(1)

over the bending stroke h.

3 Analytical Model

An analytical model is developed to determine the effect of the stress superposition on the stress state in terms of stress triaxiality and lode angle parameter. Also, the bending angle as a function of the punch movement is derived. The forces responsible for the additional pressure are determined by the static equilibrium.

3.1 Approach

For the detailed strain and stress distribution over the sheet thickness, the bending theory proposed by Wolter is used [17]. The stress distribution is applied to plane strain bending and superposed with radial stresses. The used approach to estimate the contact pressure between a sphere and a surface is the analytical model of Hertz [14]. For the process design and the calculation of the contact force responsible for the pressure, all contact and friction forces as well as the moments between the bending tools have to be taken into account. Therefore, free body diagrams (FBD) for all external and internal forces are constructed. The variables of the whole system are the tool geometries, the applied counter pressure, the bending ratio and the material properties

3.2 Simplifications

In the beginning of the last century Ludwik [18] developed the basis of the analytical descriptions of the plastic bending, the elementary bending theory. In this theory the following simplifications are made:

• Pure bending moment (constant bending radius)

• Plane strain condition

• Plane sections remain flat

• The influence of shear forces is neglected

• The sheet thickness remains constant during the bending process

• The neutral fiber remains in the geometric center of the sheet

• An isotropic material behavior is present

• The flow behavior is identic under tensile and compressive load

Within the force calculations, force and moment equilibrium are assumed. It is presupposed, that the dominant surface loads operate as point loads, at predefined point of tool contacts. The bending tools are assumed rigid. Because the Hertz’ian pressure is conventionally used for the purely elastic state, the plastic deformation in thickness direction in the contact zone is assumed to be small in contrast to the plastic deformation in circumferential direction. The friction coefficient has to be estimated.

3.3 Bending Angle

The ideal loaded bending angle α is a function of the punch displacement h. For a given punch displacement h the pivot point T of the rotating system moves to T′ (Fig. 6).

Fig. 6

Process parameters for the determination of the bending angle α in function of the punch displacement h

The nominal bending angle is only dependent on the tool geometry and the punch displacement h and can be derived as following:

$$\alpha (h) = 2 \cdot \left[{\arctan \left({\frac{{s_{6}}}{{\sqrt {(h - s_{6}) + s_{8}}}}} \right) + \arctan \left({\frac{{h - s_{6}}}{{s_{8}}}} \right)} \right]$$

(2)

where s₆ and s₈ are constants given the Appendix 2.

3.4 Estimation of the Bending Stress and Bending Moment for Pure Bending

The strain distribution in pure bending (Fig. 7) is obtained by the model developed by Wolter [17].

Fig. 7

Definition of parameters for describing a bent segment and Strain and stress state during bending of sheets with b/t > 10

With the use of the Bernoulli hypothesis and neglecting elastic strains, the maximum plastic strain in the outer fiber is determined by:

$$\varepsilon_{1,\hbox{max} } = \ln (1 + \frac{t}{{2 \cdot (R_{\text{bo}} - t/2)}})$$

(3)

The strain in a fiber ε₁(y) is given in terms of the maximal outer fibre strain ε_1,max as by Wolter [17]. The model takes the shift of the fibres due to volume constancy into account and is therefore nonlinear:

$$\varepsilon_{1} (y) = - 1 + \sqrt {1 + \varepsilon_{1,\hbox{max} }^{2} + 4 \cdot \varepsilon_{1,\hbox{max} } \cdot \frac{y}{t}}$$

(4)

When bending wide sheets with a large width-to-thickness ratio (b/t > 10), plane strain can be assumed within the bulk of the sheet. So the strain along the bending axis is $\varepsilon_{2} = 0$. In air bending the radial stress is assumed to be zero, $\sigma_{3} = 0$.

During RSS-bending only the tensile fibers (upper part of bent part, Fig. 7) is important, so no case study for compressive fibers have been done.

3.5 Stress State with Radial Stress Superposition

A model to determine the resulting stress state for bending with stress superposition is necessary. In bending with radial stress superposition, the radial stress is not equal to zero (Fig. 7). Due to volume constancy, the ratio between the strains for a constant sheet thickness and assuming no thickness reduction is:

$$\varepsilon_{1} = - \varepsilon_{3}$$

(5)

With this ratio and the use of the Levy–Mises flow rule for the plastic region of the bent sheet

$$d\varepsilon_{\text{ij}} = d\lambda \cdot \sigma_{\text{ij}}^{{\prime }}$$

(6)

A principle stress relationship can be derived, whereas σ₃ represents the radial stress:

$$\sigma_{2} = \frac{1}{2} \cdot (\sigma_{1} + \sigma_{3} )$$

(7)

Thus, the mean stress can be calculated as:

$$\sigma_{\text{m}} = \frac{1}{2} \cdot (\sigma_{1} + \sigma_{3} )$$

(8)

By assuming plane strain, the third invariant J₃ of the deviatoric stress tensor is always 0, as the second deviatoric stress components $\sigma_{22} '$ is equal to zero. With equation for the calculation of the third normalized stress invariants (Fig. 1) the lode angle parameter is zero.

With the von Mises flow condition, Eq. (7) and the flow stress, the tensile stress σ₁ can be estimated:

$$\sigma_{1} = \sigma_{3} + \frac{2}{\sqrt 3 } \cdot \sigma_{\text{f}}$$

(9)

The strain at which the stress superposition is at its maximum is assumed reached (Fig. 24, Strain at minimum triaxiality). It is assumed that the first 50% of the plastic bending is with stress superposition and that at 50% of the strain in superposed bending the maximum of the stress superposition is. Therefore, the strain at the stress superposition ε_S is empirically assumed to:

$$\varepsilon_{S} = 0.25 \cdot \varepsilon_{1,\hbox{max} }$$

(10)

With the three principal stress values the triaxiality and the lode angle parameter can be calculated for the description of the stress state, which will allow for the determination of the void evolution.

The compressive stress σ₃ is determined by the use of a model which calculates contact stresses out of contact forces. As the rotating tool has a round tool shape for controlling the area of contact, the pressure distribution of Hertz is used [14] (Fig. 8).

Fig. 8

Pressure distribution between rotating tool and sheet

The distribution describes the maximum pressure between two surfaces in contact. For a round and a flat surface with a given poisons ratio ν, contact radius r_c, contact length b and contact force N_r the following maximum pressure p_r,max results:

$$p_{\text{r,max}} = - \sqrt {\frac{{N_{\text{r}} \cdot E}}{{2 \cdot \pi \cdot (1 - \nu^{2} ) \cdot r_{\text{c}} \cdot b}}}$$

(11)

The average Young’s-modulus E is a function of the two young’s modulus E₁ and E₂ of the contact partners

$$E = \frac{{2 \cdot E_{1} \cdot E_{2} }}{{E_{1} + E_{2} }}$$

(12)

Also with this model the width of the pressure zone d_r can be derived:

$$d_{\text{r}} = 2 \cdot \sqrt {\frac{{\frac{8}{\pi } \cdot (1 - \nu^{2} ) \cdot N_{\text{r}} \cdot r_{\text{c}} }}{b \cdot E}}$$

(13)

To obtain the pressure distribution in relation to the sheet thickness, the pressure distribution is given by [14]:

$$\sigma_{z} (x) = p_{\text{r,max}} \cdot (1 + \frac{{y^{2} }}{{(d_{\text{r}} /2)^{2} }})^{ - 1}$$

(14)

For the calculation of the stress superposition an average pressure p_r,ave is used, which is defined as the following and assumed to be the superposed stress σ₃ in the outer fiber of the bending zone:

$$p_{r,ave} = \frac{{p_{\text{r,max}} }}{{d_{\text{r}} \cdot b}} = \sigma_{3}$$

(15)

This model facilitates the control of the stress state by adjusting the counter force for different superposed processes.

4 Force Calculation

For the adjustment of the stress state by controlling the counter pressure and for the tool design all acting forces need to be calculated. The analytical prediction of all acting forces is derived by applying the equilibrium state for all free body diagrams. All forces with N_i represent normal forces, all forces with T_i represent tangential forces out of friction, which are acting against the movement of the tools (see Appendix 1 for the declaration of friction coefficients).

The static equilibrium leads to 11 variable forces, moments and angles within the five FBD’s and therefore 11 independent equations need to be stated.

The equilibrium of vertical forces acting on the system can be derived from Fig. 4:

$$N_{\text{M}} = N_{\text{cp}} + 2 \cdot N_{\text{d}} \cdot (\cos (\alpha /2) + \sin (\alpha /2) \cdot \mu_{2} )$$

(16)

In Fig. 9 the FBD of the lower (a) and upper (b) bearing shell is shown. The force N_cp is controllable over the punch displacement through a hydraulic cylinder and acts in the center of the bearing shell.

Fig. 9

Forces acting on the lower (a) and upper (b) bearing shell

The equilibrium of the vertical forces leads to the equation:

$$N_{\text{cp}} = 2 \cdot N_{\text{bs}} \cdot (\cos (\varphi_{1} ) - \sin (\varphi_{1} ) \cdot \mu_{1} )$$

(17)

The angle φ₁ is not a geometric variable since it is dependent on the equilibrium of forces of the rotating tools.

The equilibrium of vertical forces on the punch bearing results in:

$$N_{\text{M}} - 2 \cdot N_{\text{ps}} \cdot (\cos (\varphi_{2} ) + \sin (\varphi_{2} ) \cdot \mu_{5} = 0$$

(18)

The angle φ₂ is only dependent on the tool geometry since the rotating punch is tilting and therefore the force N_ps acts on the outer contact area.

The resulting equations for the upper and lower rotating tools are given in the Appendix 3. The whole system rotates around point C and this mimics an apparent punch radius r_p (Fig. 10).

Fig. 10

Forces acting on the rotating punch tools

Because the lower rotating tools are identical, only one tool is shown in Fig. 11.

Fig. 11

Forces acting on one rotating tool and the important distances (for further variable declaration refer to Figs. 9 and 10)

N_r is the contact force responsible for the stress superposition in radial direction. The forces acting on the sheet are shown in Fig. 12.

Fig. 12

Forces acting on the sheet (variable declaration given in Figs. 10 and 11)

The forces N_p and N_r are not collinear. Therefore, N_r also applies a bending moment on the bending zone (Fig. 13). The influence of the friction forces is neglected as the lever arm of the half sheet thickness t/2 is much smaller than the lever arms of the bending forces.

Fig. 13

Course of the bending moment over the circumference of the sheet

The bending takes place where the bending moment is the highest and the material is not strain hardened (Fig. 13, Point M). Hence, at first there is bending is under adjustable pressure and then bending under a conventional stress state without superposition takes place.

The required bending moment for plastic bending is calculated by the elementary bending theory.

$$M_{\text{b}} = \frac{1}{2 \cdot \sqrt 3 } \cdot \sigma_{\text{f}} \cdot b \cdot t^{2}$$

(19)

When the nonlinear strain hardening according to Gosh is taken into account, the flow stress σ_f is estimated by the extrapolated flow curve. For plastic bending, the bending moment has to be created by the normal forces acting on the sheet:

$$\begin{aligned} M_{b} & = N_{\text{b2}} \cdot s_{2} - N_{\text{l}} \cdot (s_{4} - s_{5} ) \\ & \quad + N_{\text{b1}} \cdot s_{4} + N_{\text{r}} \cdot s_{1} = \frac{1}{2 \cdot \sqrt 3 } \cdot \sigma_{\text{f}} \cdot b \cdot t^{2} \\ \end{aligned}$$

(20)

As the static system static indefinite, one equation of the elastic deflections is used. The approach and the equations are given in Appendix 4.

By solving the system of equations via the substitution method, all internal and external forces and moments can be computed. Equations (17) and (32) are not solvable in a closed-form because the angle φ₁ appears in several angular functions. Contrary to other occurring angles, φ₁ is not geometrically predefined, but derives from the force and moment equilibrium. Consequently, the angle must be changed iteratively by 0.001° until the equilibrium condition is accomplished. Likewise, the deflection equations are not closed-form solvable since several angular relationships prevail simultaneously (39). In a similar manner to φ₁, the deflection is adjusted iteratively by 0.001 mm steps until the state of equilibrium is reached. Even though a closed-form solution is not available, all forces, moments and stresses can be determined explicitly and are found to comply with force and moment equilibrium. All forces, moments and stresses can then be determined from this system of equations, and the solution verifies a state of equilibrium for every given input. With the knowledge of the force responsible for the radial stress superposition, the resulting stress state can be derived.

5 Numerical Model

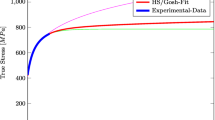
In this section the material characterization of the used DP800 steel, the numerical model and the comparison of the computed punch force and the experimental punch force is given. The flow curve is derived from uniaxial tensile tests in the transversal direction and extrapolated using the Gosh-approximation (Fig. 14).

Fig. 14

Flow curve of DP800 (HCT780X), (n = 3)

For numerical modelling of the RSS-bending, the elastic–plastic FEM is applied (ABAQUS 2016/implicit 2D) (Fig. 15). Beyond the planar symmetry, a plane strain condition is assumed in order to reduce the computational effort. The sheet is modelled by an isotropic elastic–plastic material behavior with isotropic hardening using the gosh model in Fig. 14. The rotating parts are modelled to be purely elastic and the bearing shells are rigid. In the prediction of the pressure and contact stress distribution, a small element size is required. So the element side length in the bending zone is 0.05 mm. In the elastic part of the sheet it is 0.3 mm (Element type: CPE4R, 4-node bilinear with reduced integration and hour glass control). This results in 30 elements over the sheet thickness in the forming zone and five elements over the thickness in the bending leg.

Fig. 15

Numerical model of RSS-bending

The friction between the tools, the sheet, the lower rotating part, and the lower shell is modelled by the means of Coulomb friction law (µ = 0.02, as it is well lubricated in this contact area). The contact between the tool and the die as well as the upper tool and the bearing shell is modelled with µ = 0.1. The used contact method is surface to surface with fine sliding. Slave adjustment only takes place to remove overclosure. The force is applied as a point load, whereas the punch stroke is defined by a predetermined displacement.

The resulting punch force during bending is taken as a reference to validate the simulation. The maximum force deviation between numerical and experimental punch force is lower than 4% (Fig. 16).

Fig. 16

Punch force comparison of the experimental, numerical and analytical analysis

6 Results

6.1 Prediction of Punch Force

In order to validate the force prediction of the analytical model, the directly measured punch force is compared to the analytical results (Fig. 16).

The load curves show a maximum deviation of < 7%. At the beginning of the process the analytical result overestimates the forces, as the tools are assumed to be rigid in the analytics.

6.2 Stress State Analysis over the Sheet Thickness

In order to analyze the damage evolution during plastic bending only the outer fiber of the profile is modelled as damage is triggered by the tensile stress state. The analytical and numerically predicted normalized radial stress distribution in the maximum point of stress superposition is shown in Fig. 17. With increasing counter force, the value of the radial stress superposition also increases.

Fig. 17

Comparison of the normalized radial stresses in analytical and numerical analysis for two counter forces (h = 15 mm)

In conventional air bending, the radial stress superposition at the outer fiber is zero since there is no tool contact. Due to inner moments and the compressive bending zone, an intrinsic radial stress arises (Fig. 18). These compressive stresses explain the deviation of the analytically predicted radial stresses around the middle fiber for N_cp/b = 0.3, as intrinsic compressive stresses are not considered.

Fig. 18

Numerical radial stresses distribution in air bending

These radial stresses are neglected since they are more than 3-times smaller than the applied radial stress superposition and act from the middle to the inner fiber.

Furthermore, the impact of various counter pressures and bending ratios on the analytical and numerical prediction of the bending stress is analyzed (Fig. 19).

Fig. 19

Normalized bending stress prediction for different equivalent plastic strains and counter forces (h = 15 mm)

The prediction of bending stresses for different counter pressures is more accurate for higher counter pressures. This is due to the lower deflection when applying a higher pressure. In conventional air bending the normalized bending stress is 1.15 according to Eq. (25), so the normalized bending stresses can be reduced by 60% through a counter force of 0.6 kN/mm.

With the knowledge of the flow stress, the pressure value and the bending stress, the course of the triaxiality over the sheet thickness can be derived (Fig. 20)

Fig. 20

Triaxiality distribution for different counter forces (h = 15 mm)

The stress triaxiality has a similar distribution as the bending and radial stress. The stress triaxiality is the lowest at the outer fiber because the radial stress is the most compressive there. In comparison the triaxiality of air bending at the outer fiber reaches the theoretically derived value of 0.57 (Fig. 21) and is therefore more than 500% higher than in compressive stress superposed bending.

Fig. 21

Triaxiality distribution in air bending of the outer fiber

The analytical prediction of the minimum stress triaxiality (Fig. 22) shows a deviation of 17% to 4% depending on the force and can therefore be used to estimate the damage evolution. Recall the values for pure bending, or no counter pressure, is η = 0.57.

Fig. 22

Triaxiality depending on the bending ratio and the stress superposition (h = 15 mm)

6.3 Load Paths in RSS-Bending

Damage evolution depends significantly on the degree of plastification as well as the corresponding stress state; therefore, both must be observed simultaneously. Only if the superposition of stress occurs concurrently with the plastification, it is possible to influence the damage evolution and the product properties. Hence, one characteristic feature of the developed process is the movement of the forming zone (Fig. 23) due to the bending moment distribution. Therefore, the plastic zone evolves around the circumference with the movement of the tool, and every point on the circumference experiences the same stress superposition with the same plastification. The highest strain rates appear in the zone where the stress superposition is applied.

Fig. 23

Maximum principal strain rate in RSS-bending

For the analysis of the whole load path of a single point on the outer fiber numerical investigations are carried out. (Figure 24).

Fig. 24

Triaxiality and plastic equivalent strain evolution at the outer fiber during RSS-Bending (DP800, t = 1.5 mm)

Hence, a bending with radial stress superposition and then a bending operation without stress superposition takes place. The moving forming zone is the reason for the constant equivalent plastic strain, after a punch displacement of 14 mm for this point on the circumference.

The width of the stress superposition and the value of the superposition can be adjusted by setting the counter force. The radial stress superposition is proportional to the acting force at the contact area. By increasing the radial stress superposition, the course of triaxiality is lowered, and the equivalent plastic strain at the end of the process remains constant. The stress triaxiality is not constant, since the rotating tool is moving around the analyzed point. A higher counter force reduces the triaxiality in the whole load path and will not be higher than in a load path with lower compressive stress superposition.

The stress superposition is assumed to be hydrostatic in the analytical model. Hence the deviatoric stress state needs to be similar for a given curvature, and only the hydrostatic stress state is influenced. The deviatoric and hydrostatic stress tensors of various stress superposition reveals that this assumption is valid for the range of stress superposition (Table 2).

Table 2 Deviatoric and hydrostatic stress state for maximum stress superposition at the outer fibre for two counter pressures

By lowering the maximum principal stress and the stress triaxiality, an inhibition of voids is expected. The influence of the lowered triaxiality on the void evolution for the same product produced by air bending and RSS-bending can be estimated by SEM-micrographs (Fig. 25).

Fig. 25

SEM-Micrographs of products produced by air bending and RSS-bending

The air bending process is adopted by the adjustment of the die width to produce parts with a comparable curvature in air bending and RSS-bending. For each air bending and RSS-bending product four samples are used, and in every specimen a number of four micrographs are taken of the outer fiber. The voids are separated by a black and white histogram from the matrix. The number of voids and the void area fraction in air bending is higher than in RSS-bending. The calculated void area fraction at the outer fiber for the given bending ratio and given counter force is on average 0.3% for air bending and 0.15% for RSS-bending. The standard deviation of these two values is 0.028 for air bending and 0.026 for RSS-bending. In the inner fiber nearly no voids are detected. The RSS-bending with the reduced triaxiality leads to delayed void evolution as the curvature and therefore the plastic strains are identical.

7 Conclusion

The superposition of stresses is mandatory for influencing the stress state and therefore influencing the product properties without changing the strain path in bending. A new process is designed, which facilitates controlled superposed radial stresses and meets the requirements of reproducibility. For the stress state control an analytical model is introduced, that is capable of predicting all acting forces and is therefore suitable for the tool design. Also, the course of the triaxiality over the sheet thickness, which is the driving force for damage evolution, for different stress superposition is determined. The analysis reveals that an increasing stress superposition leads to a reduced triaxiality during superposed bending. The reduced triaxiality leads to a lower void area fraction in RSS-bending. Therefore, the triaxiality can be used as an indicator for the accumulated damage in the material. Hence, the radial stress superposed bending manifests the potential for controlling the load path. For this purpose, the adjustment of the counter pressure is necessary, which in turn controls the damage evolution.

Appendices

Appendix 1

1.1 Friction Coefficient Declaration

• µ₁ Friction between lower bearing sheet and rotating tool

• µ₂ Friction between sheet and rotating tool

• µ₃ Friction between sheet and die

• µ₄ Friction between upper tools and sheet

• µ₅ Friction between upper tools and shell

Appendix 2

2.1 Determination of the Bending Angle

Determination of applied distances:

$$s_{6} = r_{\text{g}} + s_{3} + t + r_{\text{p}}$$

(21)

$$s_{7} = h - s_{6}$$

(22)

$$s_{8} = g/2 + r_{g}$$

(23)

$$s_{9} = \sqrt {s_{7}^{2} + s_{8}^{2} }$$

(24)

$$s_{10} = \sqrt {s_{6}^{2} - s_{9}^{2} }$$

(25)

Determination of resulting angles:

$$\beta_{1} = \arctan \,\,\,\,\,\left( {\frac{{s_{6} }}{{s_{9} }}} \right)$$

(26)

$$\beta_{2} = \arctan \,\,\,\,\,\left( {\frac{{s_{7} }}{{s_{8} }}} \right)$$

(27)

$$\alpha = 2 \cdot (\beta_{1} + \beta_{2} )$$

(28)

Appendix 3

3.1 Upper Rotating Tools

The equilibrium of moments at the apparent punch center point C of one upper rotating parts (Fig. 10) leads to equation:

$$(N_{\text{l}} + N_{\text{p}} ) \cdot r_{\text{b}} \cdot \mu_{4} + N_{\text{ps}} \cdot r_{\text{up}} \cdot \mu_{5} - N_{\text{l}} \cdot (s_{4} - s_{5} ) = 0$$

(29)

The two rotating upper parts can be considered as one FBD for the equilibrium of vertical forces as they are connected in a cylindrical bearing (Fig. 10). This leads to equation:

$$\begin{aligned} 2 \cdot (N_{\text{l}} + N_{\text{ps}} ) \cdot (\cos (\alpha /2) - \sin (\alpha /2) \cdot \mu_{4} ) \\ & \quad - 2 \cdot N_{\text{ps}} \cdot (\cos (\varphi_{2} ) + \sin (\varphi_{2} ) \cdot \mu_{5} = 0 \\ \end{aligned}$$

(30)

3.2 Lower Rotating Tools

The sum of the vertical forces leads to Eq. 31 and the sum of horizontal forces to Eq. 32

$$\begin{aligned} & N_{\text{b1}} + N_{\text{b2}} + N_{\text{r}} - N_{\text{d}} \\ & \quad - N_{\text{bs}} \cdot \cos (\varphi_{2} ) + T_{\text{bs}} \cdot \sin (\varphi_{2} ) = 0 \\ \end{aligned}$$

(31)

$$\begin{aligned} & T_{\text{b1}} + T_{\text{b2}} + T_{\text{r}} - T_{\text{d}} \\ & \quad - T_{\text{bs}} \cdot \cos (\varphi_{1} ) - N_{\text{bs}} \cdot \sin (\varphi_{1} ) = 0 \\ \end{aligned}$$

(32)

The equation for the equilibrium of moments around the apparent punch center point is given in equation:

$$\begin{aligned} & N_{\text{b1}} \cdot s_{4} + T_{\text{b1}} \cdot (t + r_{\text{p}} ) + N_{\text{b2}} \cdot s_{2} + T_{\text{b2}} \cdot (t + r_{\text{p}} ) \\ & \quad + N_{\text{r}} \cdot s_{1} + T_{\text{r}} \cdot (t + r_{\text{p}} ) - N_{\text{d}} \cdot s_{7} - T_{\text{d}} \cdot (t + r_{\text{p}} ) \\ & \quad + T_{\text{bs}} \cdot r_{\text{rt}} = 0 \\ \end{aligned}$$

(33)

Sheet

The equilibrium of vertical forces of the sheet leads to the equation:

$$\begin{aligned} & 2 \cdot N_{\text{b1}} \cdot (\cos (\alpha /2) + \sin (\alpha /2) \cdot \mu_{3} ) + 2 \cdot N_{\text{b2}} \cdot (\cos (\alpha /2) \\ & \quad + \sin (\alpha /2) \cdot \mu_{3} ) + 2 \cdot N_{\text{r}} \cdot (\cos (\alpha /2) + \sin (\alpha /2) \cdot \mu_{3} ) \\ & \quad - 2 \cdot N_{\text{l}} \cdot (\cos (\alpha /2) - \sin (\alpha /2) \cdot \mu_{4} ) \\ & \quad - 2 \cdot N_{\text{p}} \cdot (\cos (\alpha /2) - \sin (\alpha /2) \cdot \mu_{4} ) = 0 \\ \end{aligned}$$

(34)

Appendix 4

As the static system static indefinite, one equation of the elastic deflections is used. The groove in the rotating tool (Fig. 11, magnification) concentrates the force N_r to a pre-defined position, causing an elastic deformation within the bending legs (Fig. 26).

Fig. 26

Deflection of the sheet for individual loads (Deflection is exaggerated)

The forces N_b1 and N_b2 cause an elastic deflection in the bending direction, whereas the force N_l,n operates diametrically opposite. Contact points A and B, located between the sheet and the tool, are predetermined by the position in which the lower and upper tools lock the metal sheet. These are the locations in which the elastic deflections f_A and f_B are determined. The elastic deformation depends on the attacking forces at the metal sheet, the Young’s Modulus, the geometrical moment of inertia and the lever arms, leading to Eq. 38.

$$f_{\text{A}} = g(N_{\text{b1}} ,N_{\text{b2}} ,N_{\text{l}} ,E, \, I , { }s_{\text{i}} )$$

(35)

$$f_{\text{B}} = g(N_{\text{b1}} ,N_{\text{b2}} ,N_{\text{l}} ,E, \, I , { }s_{\text{i}} )$$

(36)

Through the preset tool geometry, the deflections f_A and f_B are predefined in such a way that they are situated on a line ${0\bar{A}B}$ (Fig. 26). With the given lever arms, the following equation arises:

$$(s_{2} - s_{1} ) \cdot f_{\text{A}} \,\, = \,\,\,(s_{4} - s_{1} ) \cdot f_{\text{B}}$$

(37)

4.1 Calculation of the Deflections

I = Area moment of Inertia

Deflection in Point A:

$$\begin{aligned} f_{A} & = N_{l} \cdot \left[{\frac{{(s_{4} - s_{5} - s_{1})}}{3 \cdot E \cdot I} \cdot \left({1 - 1.5 \cdot \frac{{s_{4} - s_{5} - s_{2}}}{{s_{4} - s_{5} - s_{1}}} + 0.5 \cdot \left({\frac{{s_{4} - s_{5} - s_{2}}}{{s_{4} - s_{5} - s_{1}}}} \right)^{3}} \right)} \right] \\ & \quad - N_{b1} \cdot \left[{\frac{{(s_{4} - s_{1})}}{3 \cdot E \cdot I} \cdot \left({1 - 1.5 \cdot \frac{{s_{4} - s_{2}}}{{s_{4} - s_{1}}} + 0.5 \cdot \left({\frac{{s_{4} - s_{2}}}{{s_{4} - s_{1}}}} \right)^{3}} \right)} \right] - N_{b2} \cdot \frac{{(s_{2} - s_{1})}}{3 \cdot E \cdot I} \\ \end{aligned}$$

(38)

Deflection in Point B:

$$\begin{aligned} f_{\text{B}} & = \frac{{N_{\text{l}} \cdot (s_{4} - s_{5} - s_{1})}}{3 \cdot E \cdot I} - \frac{{N_{\text{b1}} \cdot (s_{4} - s_{1})}}{3 \cdot E \cdot I} - \frac{{N_{\text{b2}} \cdot (s_{2} - s_{1})}}{3 \cdot E \cdot I} \\ & \quad - \tan \left({\frac{{N_{\text{b2}} \cdot (s_{4} - s_{1})}}{2 \cdot E \cdot I}} \right) \cdot (s_{4} - s{}_{2}) + \tan \left({\frac{{N_{\text{l}} \cdot (s_{4} - s_{5} - s_{1})}}{2 \cdot E \cdot I}} \right) \cdot (s_{4} - s_{5}) \\ \end{aligned}$$

(39)