1 Introduction

It is difficult to measure hot ductility considering various chemical composition ranges and continuous casting conditions of all commercially produced steels [1,2,3], so a more efficient hot ductility prediction method is required. As an alternative to existing physics-based and simple regression method, data-driven approach is significant interest to steel fields [4,5,6,7,8,9,10] by providing correlations among chemical composition, operation conditions, and mechanical properties. It helps to find out the properties of the material without performing any experiments. To analyze hot ductility, traditional forward simulation models [3, 11,12,13] including dynamic simulation models and state-space models simulate the physical behavior of steel by equations based on heat transfer/material transfer. These forward models require a lot of input variables and expertise to build a model. Uncertainty is also accompanied by assumptions and simplifications in the model construction.

On the other hand, data-based inverse models have been tried to analyze the existing ductility behavior [14, 15]. The inverse model implements a model using the observed input and output data. Data-driven inverse models have received a lot of attention in the field of model predictive control [16] because they are easy to build. The advantage of this approach is that the model can be flexibly constructed only by the input and output variables selected by the simulation performer. The inverse model is largely divided into a regression model and a machine learning (ML) models [16]. In particular, the ML method to search for the optimal model based on the learning algorithm is used like pattern recognition and data mining in various fields including steel and material, and can approximate nonlinear behavior.

Machine learning (ML) models use learning algorithms like pattern recognition to identify the relationship between the dependent and independent variables [16, 17]. ML models can describe systems that are have strong nonlinearities [18] and can extract knowledge from large datasets [19, 20]. Supervised learning is a method of ML in which the algorithm is provided input data (e.g., casting conditions), and a clear statement of the output (e.g., ‘cracked’ or not), so it has a clear objective when it derives the model and predictions future response. The properties of a steel depend on its chemical composition and the manner in which it is processed. These parameters are numerous and complex.

Various ML models have been used in attempts to predict the mechanical properties from these parameters. Examples include a random forest model (RF) [4] to predict the physical features of reduced activation ferritic/martensitic (RAFM) steels [21], a Gaussian Process (GP) [5] meta-model to predict the tensile yield strength of Ferrium® PH48S [5], a Support Vector Machine (SVM) [6, 7] to predict the tensile properties and yield strength of RAFM steels [6], and a Neural Network (NN) [8,9,10] to model the effects of elemental composition and thermal conditions concerning tensile strength of low carbon steels, and to assess the strength and particle size of hot strip mill products [8].

However, few studies have been conducted to predict reduction of area (RA). Examples include regression model [ 22, 23] and a back-propagation NN [14, 15]. These methods have the limitation that the prediction and judgment were made using one algorithm under a narrow range of conditions. It is difficult to generalize that the proposed methods are the best or optimal. Therefore, this study builds four ML models (RF, GP, SVR, NN) that analyze literature data related to hot ductility, and compares their prediction accuracy, then explains the characteristics and accuracy of each model and selects the optimal ML model for hot ductility analysis.

2 Materials and Methods

2.1 Dataset

Data sets on hot ductility had been collected using a web-based academic database. The terms such as hot ductility and high temperature ductility had been employed to find out from online scientific literature databases like ScienceDirect, Scopus, and Springer. Hits were pruned to leave only data from steel production. Then data that were incomplete, were duplicates, or were of unknown origin were deleted. This process left 4050 measurements of ductility according to temperature with steel composition and experimental variables. A total of 4420 experimental data were collected by adding 370 data obtained with the tensile test. The hot ductility-prediction models, the dependent variables are the ductility values according to temperature at 600 ≤ T ≤ 1200 °C; independent parameters such as 16 compositions and five process conditions (Table 1).

Table 1 Parameters considered in gathered data
Full size table

2.2 Data Preprocessing

The ranges of variables were standardized using the MinMaxScaler [24]; this process avoids parameter distortion that may occur in modeling due to different scales of variables. The MinMaxScaler changes the data so that all the attributes range between 0 and 1. In an n-dimensional dataset, all data are contained within a hyper-rectangle on a Cartesian hyperplane, between the origin and 1 on all axes. First, the raw data in vector x = (x1, x2, …, xn) are normalized as

$$x_{i}^{\prime } = \frac{{x_{i} - Min(x_{i} )}}{{Max(x_{i} ) - Min(x_{i} )}}$$
(1)

where \(x_{i}^{\prime }\) represents the normalized value of xi, Max(xi) is its highest value, and Min(xi) is its lowest value.

The goal of this study is to confirm thermal conditions that do not put cast steels in the bending/unbending area of the casting machine when their ductility has a low value. For the most part of steel grades, RA is a U-shaped or V-shaped style. Thus, even if the hot ductility follows a Gaussian curve, the low-ductility region can be predicted easily. However, even under the same thermal conditions, RA at each temperature cannot be predicted using literature data because they include variations depending on the researcher and the experimental apparatus. However, the overall trend of RA is the same even if the accrual values different, Gaussian fitting can be used to predict low-ductility regions. Therefore, to convert the observed RA values into a Gaussian curve, Gaussian fitting [25] is applied to convert them to low temperature limit (LTL), center temperature (CT) and high temperature limit (HTL). HTL represents the median of the maximum RA values, and LTL is the median of the minimum values, and CT indicates the mean of the Gaussian distribution. The ranges of LTL, CT, and HTL calculated in this study were 510.7–918.9 °C, 677.2–977.1 °C, 740.3–1149.3 °C respectively.

3 Data-Driven Models

3.1 RF

RF is an ensemble learning model that combines multiple models, and combines multiple random decision trees [26]. The RF selects n data sets in a bootstrap manner that allows random redundancy in a given learning data, then selects d variables without allowing duplicates in the selected data sample. d is usually the square root of the total number of variables in the given data [27]. The process of generating a decision tree from the selected data samples is repeated k times. Then the mean or multiple predictions are selected of the results from the decision trees created in this way; this is called an ensemble technique. Bootstrap Aggregating uses an ensemble technique that combines multiple bootstrap samples into one classifier; this method is called ‘bagging’.

Each decision tree node t is divided into a left child node tL and a right child node tR. The optimal node segmentation criterion S that derives the prediction value is calculated as

$$S = \arg max\Delta \hat{i}\left( {s, t} \right) = \hat{i}\left( t \right) - \left[ {\hat{p}\left( {t_{L} } \right)\hat{i}\left( {t_{L} } \right) + \hat{p}\left( {t_{R} } \right)\hat{i}\left( {t_{R} } \right)} \right],$$
(2)

where \(\hat{p}\left( t \right)\) is the conditional probability at node, \(n_{t}\) is the data size at node t, and \(\overline{{z_{t} }}\) is the average of the output values at node t. Then the impurity function \(\hat{i}\left( t \right)\) at node t is determined as Mean Squared Error (MSE)

$$\hat{i}\left( t \right) = \frac{1}{{n_{t} }}\mathop \sum \limits_{{x_{i} \in t}} \left( {y_{i} - \overline{{z_{t} }} } \right)^{2} .$$
(3)

The important hyper-parameters in the RF model are the number of decision trees used for bagging, and the depth of decision trees. In general, the learning model's accuracy increases as the increase in the number and depth of decision trees [26]. RF works well without much parameter tuning and is not sensitive to the scale of the data. RF can calculate the importance of independent variables [28]. RF can obtain the type of independent variables used in all nodes of the RF model and the increase in the amount of information obtained from those nodes. The relative importance of each independent variables can be obtained by comparing the average increase in the amount of information that each of them contributes [16].

3.2 GP

Gaussian process assumes that the observed values appear with a unique normal distribution at all-time series points.[29]. GP studies interrelation with mean and covariance for input and output variables. GP represents the set \(f\left( X \right) = { }\left\{ {(x_{i} ),{ } \ldots ,{ }\left( {x_{n} } \right)\} } \right.\) of the output function \(f\left( {x_{i} } \right)\) for the set X of the input values \({ }x_{i}\). In this case, each \(f\left( {x_{i} } \right)\) follows a Gaussian distribution. GP is expressed as

$$f\left( X \right) \sim GP\left( {m\left( X \right), k\left( {X, X} \right)} \right),$$
(4)

where \(m\left( X \right)\) is the mean function of the set of output functions, \(k\left( {X,{ }X} \right)\) is the covariance function of X and X, The average function of the output function set is

$$m\left( X \right) = E\left[ {f\left( X \right)} \right],$$
(5)

and the covariance function is

$$k\left( {X, X} \right) = { }E[\left( {f\left( X \right) - m\left( X \right)} \right)\left( {f\left( X \right) - m\left( X \right))^{T} } \right],$$
(6)

which can also be obtained by the covariance matrix

$$k\left( {X, X} \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} { k\left( {x_{1} , x_{1} } \right)} & {k\left( {x_{1} , x_{2} } \right) \cdots } & {k\left( {x_{1} , x_{n} } \right)} \\ {k\left( {x_{2} , x_{1} } \right)} & {k\left( {x_{2} , x_{2} } \right) \cdots } & {k\left( {x_{2} , x_{n} } \right)} \\ \vdots & \vdots & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {k\left( {x_{n} , x_{1} } \right)} & {k\left( {x_{n} , x_{2} } \right) \cdots } & {k\left( {x_{n} , x_{n} } \right)} \\ \end{array} } \\ \end{array} } \right),$$
(7)

where \(k\left( {x_{i} ,{ }x_{k} } \right)\) is the covariance kernel function of \(x_{j} \left( {j = 1:n} \right)\) and \(x_{k} \left( {k = 1:n} \right)\), or the Matern kernel

$$k_{Matern} \left( {x_{i} ,{ }x_{k} } \right) = \frac{{2^{1 - \nu } }}{{{\Gamma }\left( \nu \right)}}\left( {\frac{{\sqrt {2\nu } \left| {x_{i} - x_{k} } \right|}}{l}} \right)^{\nu } K_{\nu } \left( {\frac{{\sqrt {2\nu } \left| {x_{i} - x_{k} } \right|}}{l}} \right)$$
(8)

Hyper-parameters r and λ determine the amplitude and twist of the model, respectively. In this study, the maximum likelihood estimation (MLE) method is applied to estimate r and λ. The GP model has the advantage of being able to express the probabilistic attributes of the model by the covariance function. However, as the number of training data increases, computation time and computer memory usage increase exponentially [29].

3.3 SVM

SVM is a classification algorithm [30] that finds an optimal hyperplane that maximizes the size of the margin between categories and that includes as much data as possible within the distance between support vectors [31]. This study uses least-squares SVM [32]. The objective function was

$$\begin{gathered} \arg min \left( {\vartheta , e} \right) = \frac{1}{2}\left| {\left| \vartheta \right|} \right|^{2} + \frac{1}{2}\gamma \mathop \sum \limits_{i = 1}^{n} e_{i}^{2} \hfill \\ {\text{subject}}\;{\text{to}}\;y_{i} = \vartheta^{T} \emptyset \left( {x_{i} } \right) + b + e_{i} ,\quad i = 1, \ldots , n, \hfill \\ \end{gathered}$$
(9)

where \(\vartheta\) is a weight vector that determines the size of the margin, \(\gamma\) is a normalization constant, \(e\) is the error between the measured value and the predicted value, \(\emptyset \left( x \right)\) is a nonlinear function that links the input space of the input variable x into a high-dimensional feature space, and b is a bias value.

Kernel SVM is a form of SVM that uses kernels such as Polynomial, Sigmoid, and RBF to compute in a high-dimensional feature space without needing to calculate the coordinates of the data in that space, but rather by easily operating the inner product spaces [16]. Important parameters in the kernel SVM are C and gamma. C determines the number of data samples that can be placed in different classes. The RBF kernel has one γ parameter, which is the inverse of the Gaussian kernel width. Both γ and C adjust the complexity of the model, and must be adjusted together. SVM can simulate high-dimensional nonlinear systems by using a small number of data. However, the process of mapping data to a high-dimensional plane requires a large amount of computation time and memory [32]. SVM has the disadvantage of requiring careful preprocessing of and setting of parameters.

3.4 NN

NN is a structure that computers are adopting to solve problems in a way similar to how humans handle problems through the brain. In this study, a basic multilayer perceptron model [33, 34] is used. It comprises an input layer that accepts stimuli, an output layer that expresses response, and a hidden layer that processes input to yield output. Each layer consists of several nodes and is joined by weighted connections to nodes in other layers [35, 36]. Input to the input layer passes through an activation function to the hidden layer, which processes the input and sends it to the output layer. NN model has two main processes. The first is a feed-forward process that uses a series of input variables, the hidden layer’s variables, the relationships (Connectivity, Weight) between each pair of variables, and Transfer Functions. The second process is a backpropagation process, which can increase the accuracy of calculations by responding to the difference between the calculated value and the true value.

The objective function of the NN is to reduce the difference between the output values N(ω, xi) and the measured value yi of NN by adjusting the weight ω between nodes:

$${\text{argmin }}E\left( {\omega} \right) = \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} \left( {N\left( {\omega , x_{i} } \right) - y_{i} } \right)^{2} ,$$
(10)

where n is the number of data and x is the input value. In this study, the backpropagation learning algorithm was applied to find the optimal ω [37].

The main hyper-parameters of NN model are the type of output function, the learning rate, the number of hidden-layers, and the number of hidden-layer nodes [38, 39]. The advantage of NN is that they can capture information embedded in large amounts of data and create very complex models [40, 41]. However, data preprocessing is important because all features work relatively well on homogeneous data that have the same meaning. The parameters of NN must be tuned carefully to avoid local optimization and overfitting [42].

4 Evaluation

In this paper, the accuracy of each model is calculated by Root Mean-Squared Error (RMSE) [19, 43,44,45]

$$RMSE = { }\sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {z_{i} - { }y_{i} } \right)^{2} }}{N}}$$
(11)

where zi is the ith real RA, yi is the i-tth predicted RA, and N is the number of test data. The RMSE is applied to estimates of LTL, CT, and HTL for all four algorithms.

The evaluation results of ML models lead to the hyper-parameter settings that control its complexity. Therefore, the hyper-parameter setting should be optimized for each model before they are compared. In this study, k-fold cross validation [19, 46] is used to optimize each model. This method randomly divides the training data into k equal subsets, then uses k-1 of them as training data and to predict the rest of the data. The final average accuracy is calculated by averaging the evaluation results obtained by repeating this process for all k subsets.

This study used k = 10 for 80% of the training data. The cross-validation was performed with varying hyper-parameters for each ML model, then they were applied to quantify their ability to predict the remaining 20% of the data. For each ML method, the model with the highest average accuracy was identified as the model with the optimal hyper-parameter setting for each ML method. Finally, optimized model was evaluated by calculating its RMSE in predictions of test data. All analyzes in this study used Scikit-learn, Python's ML library.

5 Result

5.1 Model Training

5.1.1 RF

The important hyper-parameters in an RF model are the number of decision trees and the highest depth of each decision tree that is used for bagging. Typically, increasing the number of trees and the depth of the tree improves model accuracy. In this study, the RMSE error of tenfold cross-validation decreased as the depth of decision tree was increased; the average RMSE reached the saturation point when the number of decision trees was 204 and the highest depth was 24. Therefore, subsequent tests used 204 decision trees and a model with a maximum depth of 24. Changes in RMSE were also observed while changing parameters such as the minimum number of samples needed to separate an inner node and the lowest number of samples that should be in the leaf node, the changes were not significant, so but the default values 2 and 1 were used respectively.

5.1.2 GP

The Gaussian-Process-Regressor API supports several kernel combinations, each of which describes several attributes of the data. This paper tested all combinations of kernels supported by the API, and a white kernel that describes noise in the data. The Matern kernel provided the best accuracy. The optimal hyper-parameter of each kernel was found in the same way, and the noise level of the white kernel was optimized to 0.0001. The Matern kernel showed the best accuracy when the length scale of the kernel was 40 and the parameter ν that controls the smoothness of the learned function was 2.5.

5.1.3 SVM

In this study, the RBF kernel was used for the SVR. Polynomial and sigmoid kernels were tested, but the RBF kernel showed the best accuracy (Table 2). To optimize the accuracy of the SVR model, tenfold cross-validation was performed while adjusting the hyper-parameter values C and γ. The highest accuracy was achieved with C = 2.0 and γ with a “scale” option. We tested other hyper-parameters in kernels, but all showed the best accuracy at the default values. Another hyper-parameter used in the RBF kernel is epsilon, with a default of 0.1. It associates the epsilon tube with no penalty in the training loss function with the estimated point within the epsilon distance from the real value.

Table 2 Evaluation result of four machine learning models in terms of accuracy
Full size table

5.1.4 NN

NN model used in this study is a multi-layered perceptron containing an input layer, hidden layers, and an output layer. The main hyper-parameters of this model are the number of hidden-layers, the number of hidden-layer nodes, the activation function, the initializer, the learning rate, the dropout probability, and the batch size. The number of hidden layers was increased from 2, and the average accuracy was calculated by tenfold cross-validation while rising the node number in each layer. Accuracy was highest with four hidden layers and 64 nodes. Higher numbers of hidden layers or nodes resulted in overfitting. The activation function used leaky relu (α = 0.2) because it showed better accuracy than other activation functions. The He Initializer was selected, because it is suitable for leaky-Relu. Optimized learning rate was 0.0001 and optimal batch size was 32. For regularization, early stopping using Dropout (keep probability = 0.75) and Test Set Accuracy were used.

5.2 Accuracy of the Models

This study compared the accuracy of RF, GR, SVM, and NN four ML algorithms to predict LTL, CT, and HTL of steels (Table 2). The evaluation results of the three indicators in the NN model indicated the best accuracy. RMSE of NN were: LTL = 20.6 °C, CT = 15.2 °C, and HTL = 27.6 °C. The model of RF was the next most-accurate; it has a lower accuracy according to the correlation between input variables than other models, which is considered to be influenced by the characteristics of randomly selecting input variables. RMSE of RF were: LTL = 32.7 °C, CT = 24.8 °C, and HTL = 44.8 °C. The SVM and GP model had lower evaluation result. RMSE of SVM were: LTL = 44.1 °C, CT = 39.8 °C, and HTL = 68.3 °C. RMSE of GP were: LTL = 46.6 °C, CT = 43.7 °C, and HTL = 80.1 °C. NN seems best to predict the hot ductility value, but all were evaluated in a case study.

6 Case Study

6.1 Experimental Procedure

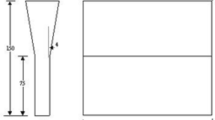
To test the accuracy of the four RA-prediction models, additional high-temperature tensile tests were performed on three steels not included in the previous training and testing (Table 3). The test specimen was fabricated using steel obtained by continuous casting (Fig. 1a). Tensile tests were conducted by a Caster and Thermo-mechanical simulator (40,334, Fuji Electronic Industrial, Saitama). Temperature was elevated to 1673 K (1400 °C) at 10 K/s, kept for 300 s at 1673 K, then reduced to 873–1273 K at 0.5 K/s (Fig. 1b). They were kept at the temperature for 60 s, then subjected to tensile strain of 5 × 10−4 until they broke. RA was gauged for each fractured specimen.

Table 3 Elemental composition (wt%) of steel
Full size table
Fig. 1
figure 1

a Specifications of test specimen, and b heat-treatment conditions of tensile test

Full size image

6.2 Analysis of Four Models

The models showed different accuracies in prediction of the ductility troughs of three steels. Steel 1 is an unalloyed steel that typically exhibits a trough shape with the lowest RA at 1073 K (800 °C) (Fig. 2a). For this steel, all four models predict new experimental values well. Steel 2 has a small amount of added alloying elements, and has a wider ductility trough (Fig. 2b) than Steel 1; all models predicted this tendency, although their predictions differ slightly. Steel 3 contains a large amount of alloy metals, and a wide ductility trough (Fig. 2c); only the NN predicted new data adequately.

Fig. 2
figure 2

Comparison of experimental (points) and modeling results (lines) of a Steel 1, b Steel 2 and c Steel 3

Full size image

These results suggest that the NN model is more accurate than the other models for prediction of complex cases that can occur when a large amount of alloy is added. A current trend in steelmaking is to increase the content and diversity of alloying elements to meet the changing requirements of steels. The NN model seems able to anticipate the ductility behavior of these novel steels.

7 Conclusion

This paper has presented development, optimization, and evaluation of four ML models (RF, GP, SVM, and NN) to estimate hot ductility of steel grades from its content and thermal history. Each model was optimized by tuning its hyper-parameters by preprocessing the data. First, all variables in the data were scaled to the range [0, 1], then the experimentally-measured RA values were changed to LTL, CT and HTL by applying Gaussian distribution. Then the most accurate version of each type of ML model was obtained by optimizing their hyper-parameters.

All four models predicted test data well after tenfold cross-validation, although the NN model showed better accuracy than RF, GP, and SVM in all three indicators of LTL, CT and HTL. However, in tests on three steels that had not been used for training and testing, only the NN model predicted all three the ductility troughs well. The difference in results can occur due to the non-linearity of the data and of hot ductility. We infer that the results are influenced by the high-diversity of the data sets, and by the large number of characteristics compared to the number of data. Secondly, RA varies depending on the steel composition and operating conditions, so the correlation between the input and output parameters is very complex. Therefore, the model of NN that best expresses complex nonlinearity is most suitable for predicting hot ductility from steel composition and thermal history. The proposed ML model in this study is more accurate than the physics-based models. This result shows that the ML model is a viable method to predict hot ductility, and to guide optimal control of secondary cooling conditions during continuous casting.