Microstructure Evolution Modeling and Simulation for Dynamic Recrystallization of Cr12MoV Die Steel During Hot Compression Based on Real Metallographic Image

Abstract

In this work, microstructure evolution of dynamic recrystallization (DRX) behavior in Cr12MoV die steel was investigated via experiments and simulations systematically. Firstly, hot compression tests were performed to obtain the true stress–strain curves. Based on the experimental results, the flow stress model was established, and Avrami equation was developed to model the kinetics of DRX. Then, the cellular automaton (CA) model was established to describe DRX behavior. In order to obtain more accurate simulation results, a microstructure enhancement, extraction and conversion program based on fingerprint image enhancement algorithm was developed to generate real initial microstructure which could be directly used in CA simulation. With real initial microstructure generation, good agreement between simulated and experimental results was achieved, indicating the high accuracy of the established CA model. Finally, the CA model was employed to investigate the hot deformation behavior of Cr12MoV die steel under multiple thermomechanical conditions. It could be found that a lower strain rate was beneficial to the occurrence of DRX. When the strain rate was beyond 1.0 s⁻¹, the DRX fraction was very small. This work would provide a significant guidance to optimize the hot working process of Cr12MoV die steel or some other similar steels.

1 Introduction

Due to high hardenability, hardness as well as excellent wear resistance at 600–700 K, Cr12MoV alloyed steel is widely used in die industry [1], especially for cold working die with complex shape and large sections, such as trimming die, punching die, piping die, deep drawing die, and thread rolling die [2]. As these dies usually work under large cyclic impact load situations, it puts forward higher requirement on mechanical properties of material itself aiming at ensuring the safety and stability of production. For most metals or alloys, thermomechanical processing is an efficient way to control the microstructure for achieving good mechanical properties [3,4,5]. Therefore, it is of great significance to study the law, mechanisms and models of the microstructure evolution of Cr12MoV die steel during hot deformation.

Dynamic recrystallization (DRX) is a dominant mechanism for grain refinement during the hot working process of metallic material. It is an important method to improve microstructure and properties since fine and homogenous grains can be obtained [6,7,8]. However, DRX behavior is sensitive to the deformation conditions, such as deformation temperature and strain rate. Therefore, it is of great importance to clarify the kinetics and microstructure evolution caused by DRX to make hot working process effectively. So far, DRX behavior of metals or alloys has been extensively studied, and several models for the recrystallization kinetics and microstructure evolution have been proposed [9,10,11,12]. Generally, the kinetics of DRX can be described by the Avrami equation [13], whose parameters can be identified based on experimental results. Phenomenological models were widely proposed to evaluate DRX grain size which was expressed as a function of the Zener–Hollomon parameter [14]. However, there are two obvious limitations of phenomenological models [15]. One is that the physical mechanism of DRX has not been considered sufficiently. Another is that the microstructure evolution cannot be observed dynamically, which makes it quite difficult to deeply analyze the law of DRX.

In recent years, cellular automaton (CA) has been extensively applied to investigate the hot deformation behavior and microstructure evolution of metals and alloys due to its high efficiency and flexibility [16,17,18]. It cannot only be able to predict general average microstructure performance, but also provide visualizations of the microstructure evolution. In addition, CA method can be calibrated more readily to time and length scale compared to other mesoscale simulation methods, such as Monte Carlo and Phase Field methods [19, 20]. It has been widely proved that CA method can simulate DRX behavior with satisfactory results, such as for carbon and alloy steels [21, 22], aluminum alloys [23], magnesium alloys [15, 24], copper and its alloys [25, 26], titanium alloys [27], and Ni-based superalloys [28]. Although considerable efforts are devoted to the behavior of different alloys and metals, there is less experimental and simulated information available on the DRX behavior of Cr–Mo–V die steel. What’s more, most simulated approaches were applied with insufficient consideration of the real material and its structural feature. Therefore, the DRX process of Cr12MoV die steel needs to be further investigated since it is beneficial for understanding and optimizing the hot working process. And, it will be also of significance to understand DRX behavior of some other similar steels.

The aim of this work is to establish a CA model to predict the microstructure evolution of Cr12MoV die steel during hot deformation process. Firstly, hot compression tests were performed to obtain the material parameters and the flow stress model. Then, the CA model was established to describe the DRX behavior. Meanwhile, a microstructure enhancement, extraction and conversion program based on fingerprint image enhancement algorithm was developed to generate real initial microstructure which can be directly used in CA simulation to obtain more accurate simulation results. Finally, the CA model was applied to study the hot deformation behavior of Cr12MoV die steel under different thermomechanical conditions. The influences of process parameters involving strain, strain rate and deformation temperature on the microstructure evolution of DRX were analyzed reasonably.

2 Hot Compression Experiment and Results

2.1 Experimental Material and Hot Compression Procedure

In order to obtain the material parameters which would be used in the CA model, a series of uniaxial hot compression tests of Cr12MoV steel were performed on a Gleeble-3500 thermomechanical simulator. The chemical compositions of the tested Cr12MoV die steel in this work are listed in Table 1. The cylindrical specimens were machined with a diameter of 8 mm and a height of 12 mm. Before the compression test, thin graphite flakes were laid between the punch heads and the specimen heads for the sake of reducing the friction between the die and specimens.

Table 1 Chemical compositions of the tested Cr12MoV die steel

The scheme of hot compression tests is illustrated in Fig. 1. The specimens were firstly heated to 1473 K at the heating rate of 10 K/s and held for 3 min to acquire a homogeneous and equiaxed microstructure. After that, the specimens were cooled down to the forming temperature at the cooling rate of 2 K/s and held for 1 min to eliminate the thermal gradients. Three different forming temperatures (1323 K, 1373 K, and 1423 K) and four different strain rates (0.01 s⁻¹, 0.1 s⁻¹, 01 s⁻¹ and 10 s⁻¹) were used in hot compression tests. When the true strain reached 0.8, the specimens were immediately quenched by cold water to retain the original microstructure formed at the high temperature. It should be noted that the characteristic of DRX can be fully observed when the true strain reached 0.8 in this study.

Fig. 1

Experimental procedure of hot compression tests

The specimens for metallographic observations were sectioned along the compression axis. After mechanical polishing, the specimens were chemically etched in a solution of saturated picric acid to reveal the microstructures. Optical micrographs of the specimens were observed by using Axiovert 200MAT metallographic microscope. The average grain sizes were obtained from optical micrographs by utilizing a linear intercept method [29].

2.2 Experimental Results and Discussions

The true stress–strain curves of Cr12MoV die steel at the same strain rate and different deformation temperatures are shown in Fig. 2. Due to the friction between specimens and fixtures during hot compression, these curves were corrected with the friction correction methods [30]. It can be seen that under the same deformation condition, the stress increased sharply at first with increasing the strain. Then, the increasing rate of the stress slowed down and the stress reached a peak value. Finally, the stress decreased and approached to a relatively steady value when the strain was beyond a certain value. It also can be found that under the same strain rate, the stress was higher at the temperature of 1323 K than that of 1423 K. When the strain rate was less than 0.1 s⁻¹, the flow stress decreased evidently, especially at the lower deformation temperature. On the whole, it indicated that there existed obvious dynamic recrystallization characteristics of Cr12MoV die steel in the thermomechanical processing.

Fig. 2

True stress–strain curves at strain rates of: a 0.01 s⁻¹; b 0.1 s⁻¹; c 1 s⁻¹; d 10 s⁻¹

During the hot compression process, there are three typical behaviors, i.e., work hardening (WH), dynamic recovery (DRV) and dynamic recrystallization (DRX). WH will increase the dislocation density to harden the material, while DRV and DRX can soften the material. According to the dynamic softening mechanisms during hot deformation, the true stress–strain curves for Cr12MoV die steel can be divided into two types, i.e., dynamic recovery and dynamic recrystallization, respectively, as shown in Fig. 3. Generally, the true stress–strain curves with the characteristic of DRX contain four stages: (I) working hardening stage, (II) transition stage, (III) softening stage and (IV) steady stage.

Fig. 3

Schematic diagram of the true stress–strain curve for DRX

At the first stage, WH and DRV occur together. Even though DRV caused by dislocation movement (i.e., climbing, sliding) and rearrangement in the interior of the grains can soften the matrix, WH resulted from dislocation multiplication is still dominant. At this stage, the stress increases from the initial stress ($\sigma_{0}$) to the critical stress ($\sigma_{c}$). As the strain increasing, DRX begins to take place leading to the material softening, which slows down the increase of stress. However, it still cannot counteract the hardening effect caused by WH. The stress will increase to the peak stress ($\sigma_{p}$) rapidly in a small range [31]. Then, after the peak strain ($\varepsilon_{p}$), DRX occurs in quantity, which makes the softening effect be greater than the hardening effect caused by WH, and thus the true stress decreases [32]. At last, the softening and hardening effects reach a dynamic balance. The true stress will be stable at a constant value, namely steady-state stress ($\sigma_{ss}$). If DRX does not occur in the interior of the material, the flow stress will continuously increase to a certain stress level after the critical strain ($\varepsilon_{c}$). The balance will stabilize at the saturation stress ($\sigma_{s}$) [25].

3 Flow Stress Model

3.1 Characteristic Parameters

In order to establish the kinetics model of DRX, characteristic parameters have to be firstly determined. The peak stress ($\sigma_{p}$), peak strain ($\varepsilon_{p}$) and steady stress ($\sigma_{ss}$) can be directly obtained from the true stress–strain curves. However, it is quite difficult to determine the critical stress ($\sigma_{c}$) directly. In general, the curve of work hardening rate versus stress can be used to obtain these eigenvalues more accurately, as shown in Fig. 4 [15, 27]. The work hardening rate ($\theta$) represents the flow stress with the change of strain, that is $\theta = d\sigma /d\varepsilon$ [33]. The critical stress ($\sigma_{c}$) can be attained when the value $\left| {d\sigma /d\varepsilon } \right|$ reaches the minimum, where is an inflection point involving stage I and II. Then, the saturation stress ($\sigma_{s}$) can be obtained depending on the intersection of the stress axis and the tangent line of $\theta - \sigma$ curve through the inflection point. The peak stress ($\sigma_{p}$) and steady stress ($\sigma_{ss}$) can be obtained when the work hardening rate is equal to zero as shown in Fig. 4. Finally, all the corresponding strain values can be obtained while placing above stress values back to the true stress–strain curves. The values of characteristic parameters for the occurrence of DRX of Cr12MoV die steel are listed in Table 2.

Fig. 4

Typical curve of work hardening rate versus stress ($\theta - \sigma$)

Table 2 The values of characteristic parameters of Cr12MoV die steel

Considering that the above parameters are affected by the strain rate and deformation temperature simultaneously, the Zener–Hollomon parameter is usually used to describe the regular changes. So the above characteristic parameters can be expressed as a function of the Zener–Hollomon parameter, which could be illustrated as [34]:

$$Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right)$$

(1)

where Q is the thermal deformation activation energy, $\dot{\varepsilon }$ is the strain rate, T is the temperature, and R is the gas universal constant.

3.2 Calculation of Activation Energy

In order to utilize the Zener–Hollomon parameter to describe above characteristic parameters, the activation energy of Cr12MoV die steel, which is the only unknown parameter in Eq. (1), should be determined at first. We combined the relational expressions of high temperature plastic flow stress [35], flow stress under low stress level [36], and flow stress under the high stress level [37]. They are expressed as follows:

$$\dot{\varepsilon } = \left\{ {\begin{array}{*{20}l} {A_{0} \left[ {\sinh \left( {\alpha \sigma } \right)} \right]^{{n_{0} }} \exp \left( { - \frac{Q}{RT}} \right) } \hfill &\quad {for \,all \, \sigma } \hfill \\ {A_{1} \sigma^{{n_{1} }} \exp \left( { - \frac{Q}{RT}} \right) } \hfill &\quad {\alpha \sigma < 0.8} \hfill \\ {A_{2} \exp \left( {\beta \sigma } \right)\exp \left( { - \frac{Q}{RT}} \right)} \hfill &\quad {\alpha \sigma > 1.2} \hfill \\ \end{array} } \right.$$

(2)

where $A_{0}$, $A_{1}$, $A_{2}$, α, $\beta$, $n_{0}$ and $n_{1}$ are the material constants, and $\sigma$ usually represents characteristic stresses, such as the peak stress and steady stress. Here, the peak stress ($\sigma_{p}$) is used to calculate the deformation activation energy.

When the deformation temperature T is a constant value, the curve of $\ln \dot{\varepsilon } - \ln \sigma_{p}$ and $\ln \dot{\varepsilon } - \sigma_{p}$ could be drawn, as presented in Fig. 5. The slope in the $\ln \dot{\varepsilon } - \ln \sigma_{p}$ curve and $\ln \dot{\varepsilon } - \sigma_{p}$ curve can represent $n_{1}$ and $\beta$, respectively. We calculated the average value of the slope selected at different temperatures to obtain $n_{1}$ and $\beta$. Then, the value of α can be calculated by $\alpha = \beta /n_{1}$. In order to determine Q, the first equation in Eq. (2) can be converted into the formula as Eq. (3):

Fig. 5

Linear fitting curves of a$\ln \dot{\varepsilon } - \ln \sigma_{p}$ and b$\ln \dot{\varepsilon } - \sigma_{p}$ curves

$$\ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right] = \frac{1}{{n_{0} }}\ln \dot{\varepsilon } - \frac{1}{{n_{0} }}\ln A_{0} + \frac{Q}{{n_{0} R}}\frac{1}{T}$$

(3)

It is quite obvious that $\ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right]$ is a linear function of $\ln \dot{\varepsilon }$ and $1/T$. Hence, the curves of $\ln \dot{\varepsilon } - \ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right]$ and $\ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right] - 1000/T$ were made in Fig. 6. Then, $n_{0}$ and $Q/n_{0} R$ can be obtained by the slopes. Specific values are showed in Tables 3 and 4. The value of activation energy (Q) was eventually obtained as 458.069 kJ/mol.

Fig. 6

Linear fitting curves of a$\ln \dot{\varepsilon } - \ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right]$ and b$\ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right] - 1000/T$ curves

Table 3 Material constants of Cr12MoV die steel

Table 4 Activation energy of Cr12MoV die steel

Combining with Table 2 and the Zener–Hollomon parameter, the linear relationships between $\ln \sigma_{c}$, $\ln \varepsilon_{p}$, $\ln \left[ {\sinh \left( {\sigma_{s} } \right)} \right]$, $\ln \left[ {\sinh \left( {\sigma_{ss} } \right)} \right]$ and $\ln Z$ could be obtained in Fig. 7. Accordingly fitting the curves, the expressions of critical stress ($\sigma_{c}$), peak strain ($\varepsilon_{p}$), steady state stress ($\sigma_{ss}$) and saturated stress ($\sigma_{s}$) with the Zener–Hollomon parameter were achieved as follows:

Fig. 7

Linear fitting curves of a$\ln \sigma_{c} - \ln Z$, b$\ln \varepsilon_{P} - \ln Z$, c$\ln \left[ {\sinh \left( {\alpha \sigma_{ss} } \right)} \right] - \ln Z$ and d$\ln \left[ {\sinh \left( {\alpha \sigma_{s} } \right)} \right] - \ln Z$ curves

$$\begin{aligned} \sigma_{c} & = 0.2345Z^{0.15821} \\ \varepsilon_{p} & = 0.0090Z^{0.08356} \\ \sigma_{ss} & = 114.15 \times \sinh^{ - 1} \left( {3.3490 \times 10^{ - 4} Z^{0.20733} } \right) \\ \sigma_{s} & = 114.15 \times \sinh^{ - 1} \left( {2.7024 \times 10^{ - 4} Z^{0.21702} } \right) \\ \end{aligned}$$

(4)

3.3 Calculation of $k_{1}$, $k_{2}$ and $X_{DRX}$

The stress required for hot plastic deformation is mainly affected by the propagation of dislocations and the resistance between dislocations. The relationship between the flow stress and the dislocation density can be described as follows [38]:

$$\sigma = \alpha \mu b\sqrt \rho$$

(5)

where α is a constant, called the dislocation interaction coefficient. It takes 0.5 for most metals [18]. $\mu$ is the shear modulus, b is the Burger’s vector, and $\rho$ is the dislocation density. At present, the evolution of dislocation density can be predicted by the KM model [39], as presented in Eq. (6). It contains two parts: work hardening and softening by the recovery.

$$\frac{d\rho }{d\varepsilon } = k_{1} \sqrt \rho - k_{2} \rho$$

(6)

where $k_{1}$ is the work hardening coefficient, and $k_{2}$ is the softening coefficient. These two terms represent the dislocation storage via work hardening and dislocation annihilation via recovery, respectively, which can be calculated by $k_{1} = 2\theta_{0} /\left( {\alpha \mu b} \right)$ and $k_{2} = 2\theta_{0} /\sigma_{s}$ [17], where $\theta_{0}$ is the initial work hardening rate. When the dislocation density within a grain reaches the saturated state, $d\rho /d\varepsilon$ equals to zero. Then, the saturated dislocation density can be obtained by:

$$\rho_{s} = \left( {\frac{{k_{1} }}{{k_{2} }}} \right)^{2}$$

(7)

Substituting Eqs. (5) and (7) into Eq. (6) after integrating, the stress–strain equation of the WH–DRV stage can be obtained, as shown in Eq. (8):

$$\sigma_{WH} = \sigma_{s} + \left( {\sigma_{0} - \sigma_{s} } \right)e^{{ - \frac{{k_{2} }}{2}\varepsilon }} \left( {\varepsilon < \varepsilon_{c} } \right)$$

(8)

In order to facilitate the subsequent verification analysis, the expressions of $k_{1}$ and $k_{2}$ are also described by Zener–Hollomon parameter. Based on the linear fitting method, the expressions of $k_{1}$ and $k_{2}$ were obtained, as shown in Eq. (9):

$$\begin{aligned} k_{1} & = 63.2528Z^{0.08765} \\ k_{2} & = 965.2045Z^{ - 0.06388} \\ \end{aligned}$$

(9)

In the case of the occurrence of dynamic recrystallization, the dynamic recrystallization fraction (X_DRX) needs to be taken into account. Hence, the flow stress can be expressed by:

$$\sigma = \sigma_{WH} - \left( {\sigma_{s} - \sigma_{ss} } \right)X_{DRX} \left( {\varepsilon > \varepsilon_{c} } \right)$$

(10)

As the dynamic recrystallization process is similar to the ordinary phase transition with a nucleation and growth process, the JMAK model can be used to characterize this process [40], as shown in Eq. (11). In addition, dynamic recrystallization fraction can also be described by Eq. (12) [41].

$$X_{DRX} = 1 - \exp \left[ { - k_{D} \left( {\frac{{\varepsilon - \varepsilon_{c} }}{{\varepsilon_{p} }}} \right)^{{n_{D} }} } \right]$$

(11)

$$X_{DRX} = \frac{{\sigma_{WH} - \sigma }}{{\sigma_{s} - \sigma_{ss} }}$$

(12)

By consolidating Eqs. (11) and (12), and using linear fitting method, $n_{D}$ and $k_{D}$ can be obtained. The DRX fraction model of Cr12MoV die steel was eventually expressed as:

$$X_{DRX} = 1 - \exp \left[ { - 0.979\left( {\frac{{\varepsilon - \varepsilon_{c} }}{{\varepsilon_{p} }}} \right)^{1.394} } \right]$$

(13)

At last, the flow stress model of Cr12MoV die steel with WH, DRV and DRX behaviors during hot deformation was established as Eq. (14):

$$\left\{ {\begin{array}{*{20}l} {\sigma_{WH} = \sigma_{s} + \left( {\sigma_{0} - \sigma_{s} } \right)e^{{ - \frac{{k_{2} }}{2}\varepsilon }} } \hfill &\quad {\varepsilon \le \varepsilon_{c} } \hfill \\ {\sigma = \sigma_{WH} - \left( {\sigma_{s} - \sigma_{ss} } \right)\left\{ {1 - \exp \left[ { - 0.979\left( {\frac{{\varepsilon - \varepsilon_{c} }}{{\varepsilon_{p} }}} \right)^{1.394} } \right]} \right\}} \hfill &\quad {\varepsilon > \varepsilon_{c} } \hfill \\ \end{array} } \right.$$

(14)

3.4 Model Validation

According to the flow stress model established above, Fig. 8 demonstrates comparisons of the experimental and calculated flow stress curves of Cr12MoV die steel at different deformation temperatures with various strain rates. We found that the calculated results are in good agreement with the experimental ones, which indicates that the flow stress model is capable of describing the hot deformation behavior of Cr12MoV die steel. On the whole, the model and parameters have extremely satisfactory accuracy and can be summarized as a basis for the simulation.

Fig. 8

Comparisons of the experimental and calculated flow stress curves: a 0.01 s⁻¹; b 0.1 s⁻¹; c 1 s⁻¹; d 10 s⁻¹

4 CA Modeling and Simulation of DRX

The DRX models are often used to describe the dislocation density evolution, nucleation and growth of dynamically recrystallized grain. To simplify the CA model of Cr12MoV die steel, the following assumptions were proposed in this study [18]: (1) The dislocation density of the parent phase was uniformly distributed. The initial dislocation density was set to 0.45 × 10⁻¹⁰ μm². (2) Nucleation of dynamic recrystallization occurred only when the internal dislocation density reached the critical value. The number of recrystallization was unlimited. (3) Nucleation of dynamic recrystallization took place only on the grain boundaries.

4.1 Model Description of DRX

4.1.1 Model of Dislocation Density Evolution

During the process of hot deformation, the evolution of material dislocation density is determined by work hardening and dynamic recovery together. Work hardening can lead to the dislocation increasing, while dynamic recovery and dynamic recrystallization are the opposite. Their relationship can be described as:

$$\frac{d\rho }{d\varepsilon } = \left( {\frac{d\rho }{d\varepsilon }} \right)_{hard} + \left( {\frac{d\rho }{d\varepsilon }} \right)_{soft}$$

(15)

where $\rho$ is the dislocation density, and $\varepsilon$ is the true plasticity strain. According to the model proposed by Kocks and Mecking in Eq. (6), the accumulation of dislocation density is proportional to $\sqrt \rho$. However, the annihilation of dislocation density is proportional to $\rho$. By integrating Eq. (6), the following expression of dislocation density and strain can be obtained:

$$\rho = \left( {\frac{{k_{1} }}{{k_{2} }} - \frac{{k_{1} }}{{k_{2} }}e^{{ - \frac{{k_{2} }}{2}\varepsilon }} + \sqrt {\rho_{0} } e^{{ - \frac{{k_{2} }}{2}\varepsilon }} } \right)^{2}$$

(16)

where $\rho_{0}$ means the initial dislocation density value when the strain ($\varepsilon$) is equal to zero. The relationship between high temperature flow stress and average dislocation density can be described as $\sigma = \alpha \mu b\sqrt {\bar{\rho }}$, as shown in Eq. (5). In the CA model, the average dislocation density can be calculated by:

$$\bar{\rho } = \frac{{\sum \rho_{i,j} }}{N}$$

(17)

where N is the total number of cells in the simulated region. Calculation of $k_{1}$, $k_{2}$ and other parameters have been introduced in the previous section.

4.1.2 Model of DRX Nucleation

The initiation of nucleation is closely associated with the accumulation of dislocations. As mentioned above, nucleation of DRX occurs only when the internal dislocation density reaches a critical value ($\rho_{c}$). It can be calculated by Eq. (18) [42]:

$$\rho_{c} = \left( {\frac{{20\gamma_{m} \dot{\varepsilon }\sigma }}{{3b^{2} K_{1} \mu M\tau^{2} }}} \right)^{1/3}$$

(18)

$$\gamma_{m} = \frac{{\mu b\theta_{m} }}{{4\pi \left( {1 - \nu } \right)}}$$

(19)

where $\gamma_{m}$ is the large angle grain boundary energy, seen as Eq. (19) [19]. b is the Burger’s vector. $K_{1}$ is a constant and it was taken 10 in this study. M is the grain boundary mobility ratio, seen as Eq. (22). $\tau$ is the dislocation line energy, which can be calculated by $\tau = 0.5\mu b^{2}$. $\nu$ is Poisson’s ratio.

As the nucleation of DRX takes place only at grain boundaries, a continuous nucleation model is assumed to treat the nucleation event in this study. The nucleation rate per unit grain boundary area can be expressed as a function of deformation temperature and strain rate, shown as [18]:

$$\dot{n} = C\dot{\varepsilon }^{m} \exp \left( { - \frac{{Q_{act} }}{RT}} \right)$$

(20)

where C is a constant. It can be determined by experimental value or anti-analytic method. m is constant and it was taken 1 in this study. $Q_{act}$ is dynamic recrystallization deformation activation energy. R is the ideal gas constant. T is the deformation temperature.

4.1.3 Model of DRX Growth

The driving force of recrystallized grain growth is determined by the difference between the dislocation density of the two phases. The growth rate of grain (V) can be described by Eq. (21) [18]:

$$V = {{MF} \mathord{\left/ {\vphantom {{MF} {\left( {4\pi r^{2} } \right)}}} \right. \kern-0pt} {\left( {4\pi r^{2} } \right)}}$$

(21)

where F is the driving force of grain growth. M is the grain boundary mobility, which can be calculated by Eq. (22) [21]:

$$M = \frac{{\delta D_{ob} b}}{KT}\exp \left( { - \frac{{Q_{b} }}{RT}} \right)$$

(22)

where $D_{ob}$ is the grain boundary diffusion coefficient at absolute zero temperature, $Q_{b}$ is the diffusion activation energy, $\delta$ is the grain boundary thickness, K is Boltzmann’s constant. The driving force of the spherical grain can be deduced by the change of energy [26], as shown in Eq. (23):

$$dW = 8\pi r\gamma dr + 4\pi r^{2} \tau \left( {\rho_{d} - \rho_{m} } \right)dr$$

(23)

where $\rho_{m}$ is the dislocation density in the matrix, and $\rho_{d}$ is the dislocation density of the dynamic recrystallized grain. The first term on the right side represents the surface energy, and the second term represents the volume energy. Therefore, the driving force of the recrystallized grain can be calculated by Eq. (24):

$$F_{i} = - \frac{{dW_{i} }}{{dr_{i} }} = 4\pi r_{i}^{2} \tau \left( {\rho_{m} - \rho_{d} } \right) - 8\pi r_{i} \gamma_{i}$$

(24)

where $r_{i}$ is the radius of the recrystallized grain, $\gamma_{i}$ is the interface energy, which can be obtained by the Read–Shockley equation shown as Eq. (25) [43]:

$$\gamma_{i} = \left\{ {\begin{array}{*{20}l} {\gamma_{m} \frac{{\theta_{i} }}{{\theta_{m} }}\left( {1 - \ln \frac{{\theta_{i} }}{{\theta_{m} }}} \right)} \hfill &\quad { \theta_{i} \le 15^\circ } \hfill \\ {\gamma_{m} } \hfill &\quad {\theta_{i} > 15^\circ } \hfill \\ \end{array} } \right.$$

(25)

where $\theta_{i}$ is the orientation difference between the recrystallized grain and the adjacent grain, and $\theta_{m}$ is the large angle orientation difference, which was taken 15 in this study.

4.2 Real Initial Microstructure Generation

At present, the initial microstructure for CA simulation is usually obtained by random nucleation and growth. However, it cannot reflect the distribution of actual grain size. In order to obtain more accurate simulation results, the real microstructure is better to be adopted as the initial microstructure for simulation. As we know, there is always blurred area between the boundary and grain in the real metallographic image which is not available for CA simulation directly. So a microstructure enhancement, extraction and conversion program was developed based on real metallographic image to reduce the error of acquiring microstructure.

Firstly, the real image was filtered and de-noised using fingerprint image enhancement algorithm [44] which can enhance the structural contrast between the boundary and grain. And some noise can be suppressed, shown in Fig. 9a which was acquired by quenching the specimens before hot compression. In order to accommodate different boundary thickness and different chromatic aberration between the boundary and grain, some filters with different frequencies were set for different regions of the image. Secondly, microstructure extraction was performed on the previous enhanced image. Boundary region was defined by a local adaptive threshold. What’s more, it was also necessary to partition the image and set different thresholds for each partition to obtain accurate results of the environment in which the boundary is located. Figure 9b shows the extracted grain boundary from enhanced metallographic image. Thirdly, the entire image region was digitized. The boundary region was defined as 1, while the grain region (non-boundary area) was defined as 0. Then these binary data can be used as the initial microstructure, shown in Fig. 9c. Finally, the grain orientation of each region was randomly assigned, and assuming that there were no grains with the same orientation in adjacent regions which have a same boundary. The initial grain distribution utilized CA simulation is shown in Fig. 9d.

Fig. 9

The real initial microstructure generation for CA simulation: a real microstructure; b extracted grain boundary; c digitized microstructure; d initial grains with orientation

4.3 Procedures of Simulation

In the CA model, the simulation area was 400 × 400 μm, and the cell was square with the length of $L_{CA}$ = 1 μm. Von Neumann’s neighboring rule and periodic boundary conditions were applied. The following five variables were assigned to each cell according to the initial microstructure. (1) Dislocation density variable in each cell was set as the initial value first. (2) Orientation variable was used to distinguish different grains in the range of 0–180. (3) Recrystallization times variable identified the times of the grain recrystallized. It was also used to distinguish parent and recrystallization grain, where 0 represented the parent phase. (4) Recrystallization fraction variable was used to decide the recrystallization transition only when it was greater than 0. It can be calculated by $l = \int_{t}^{t + \Delta t} {vdt/L_{CA} }$. (5) Crystal boundary variable indicated the boundary or interior of the grain, where 0 represented the grain boundary and 1 represented the interior of the grain.

During the simulation, an un-recrystallized cell would be changed into the recrystallized one when meeting the following rules simultaneously: (1) The driving force F_i > 0. (2) Recrystallization fraction variable l ≥ 1. (3) There were cells of high-order dynamic recrystallization grains existed in the neighbor cells. (4) Under the above conditions, the cells would begin to transform according to the probability of P = a/4, where a represented the number of cells with the same orientation value in the Von Neumann’s neighbors.

The realization process of the dynamic recrystallization CA model of Cr12MoV die steel is shown in Fig. 10. It includes the following main steps:

Fig. 10

Simulation flow chart for DRX by CA model

• (1) The first step was to read the real initial grain distribution, initialize each cell variables and assign the material parameters. Table 5 shows the parameters we used in the CA model.

  Table 5 Parameters used in the CA modeling

• (2) The second step was to determine the time step, and the total step number of the simulation, which can be calculated by Eq. (26) [23] and Eq. (27), respectively.

  $$\Delta t = \frac{{L_{CA} }}{{v_{max} }} = \frac{{2k_{2}^{2} L_{CA} }}{{k_{1}^{2} M\mu b^{2} }}$$

  (26)
  $$N_{CA} = \frac{\varepsilon }{{\dot{\varepsilon }\Delta t}}$$

  (27)

• (3) The third step was to calculate the cellular dislocation density variable and nucleation. All the cellular space was scanned to update the dislocation density value of each cell in turn depending on the KM model. Then whether the cellular dislocation density reached the critical value or not was estimated. If the critical value reached and the cell was located in the grain boundary, the cell would begin to nucleate according to the nucleation probability, which can be calculated by $P = \dot{n} \times \Delta t \times L_{CA}^{2}$.

• (4) Then the growth of recrystallized grains could be handled. Each cell was evaluated with the cellular rules of grain growth. If all the rules can be satisfied, the cell transformed to be the target recrystallized grain. Its orientation, dislocation density and recrystallization times values would be consistent with that of the target grain.

• (5) This step was to update the cellular state variables and save the results file of each step, including cell state, recrystallization fraction, average dislocation density and average grain size of recrystallization.

• (6) Repeat step (3)–(5) until the total simulation step was achieved.

5 Simulation Results and Discussion

5.1 Validation of CA Model on Microstructure Evolution

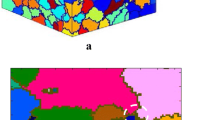
In order to verify the accuracy of the CA model for DRX of Cr12MoV die steel, some simulations were conducted under different deformation conditions. Figure 11 shows the microstructure comparisons between the simulation and experiment. The row above is the metallographic photographs, and the row below is the simulation results. The color regions of simulated microstructure are dynamic recrystallized grains with different orientations. It can be observed that the simulation results were in good consistent with the microstructure in the distribution of the grains. At the same temperature, the greater the strain rate was, the smaller the average grain size can be achieved. Meanwhile, the deformation temperature was positively correlated with the recrystallized grain size at the same strain rate.

Fig. 11

Comparisons of the microstructure between experimental and simulated results: aT = 1423 K, $\dot{\varepsilon }$ = 0.1 s⁻¹; bT = 1373 K, $\dot{\varepsilon }$ = 0.01 s⁻¹; cT = 1373 K, $\dot{\varepsilon }$ = 0.1 s⁻¹

To further substantiate the accuracy of the simulation results quantitatively, the average grain size measured by the transversal method was compared to that calculated by the CA method, as shown in Table 6. The results present that the relative error was within 4.7%, which is acceptable in the means of simulation. Comparisons of predicted DRX fractions between experimental and simulated results are shown in Fig. 12. It can be seen that there was a good agreement between predicted DRX fraction and the experimental one. In addition, the results indicate that predicted kinetic of DRX using CA simulation also follows the Avrami equation characteristic. Therefore, on the basis of the results we have obtained, it can be naturally concluded that the established CA model can accurately describe the kinetics of DRX and predict microstructure evolution of the Cr12MoV die steel during hot compression.

Table 6 Comparison of the recrystallized grain size between the experimental and simulated results

Fig. 12

Comparisons of the predicted DRX fractions between experimental and simulated results: a T = 1423 K, $\dot{\varepsilon }$ = 0.1 s⁻¹; b T = 1373 K, $\dot{\varepsilon }$ = 0.01 s⁻¹; c T = 1373 K, $\dot{\varepsilon }$ = 0.1 s⁻¹

5.2 The Influences of Strain on the Microstructure Evolution

We conducted a simulation using the established CA model at the deformation temperature of 1373 K and the strain rate of 0.01 s⁻¹. The microstructure at different strains is demonstrated in Fig. 13, in which the colored areas represent recrystallized grains, the white areas represent the parent phase, and the red lines represent the initial austenite grain boundaries. The colors of recrystallized grains with different orientations are different. As can be seen from the microstructure, the new nuclei appeared at the austenite grain boundary when the dislocation density in the matrix reached the critical value. With increasing the strain, the new nuclei continuously grew up and the DRX fraction increased. The original parent grains were almost all replaced by the dynamic recrystallized equiaxed grains when the strain is 0.5.

Fig. 13

The simulated microstructure at the deformation temperature of 1373 K, the strain rate of 0.01 s⁻¹ and the strains of: a 0.21; b 0.31; c 0.41; d 0.51

The relationship between DRX fraction and average recrystallized grain size with the change of strain is shown in Fig. 14. Since it contains some other curves that would be further discussed in the next subsection, we just take the curves at the strain rate of 0.01 s⁻¹ to analyze the influences of the strain. As can be seen from the curves, it is confirmed that the DRX phenomenon occurred only after the strain reached the critical value, 0.15 for the strain rate of 0.01 s⁻¹. Then, the DRX fraction increased with increasing the strain. When the strain reached 0.6, the DRX fraction was nearly stable.

Fig. 14

The relationship between DRX fraction and average recrystallized grain size (T = 1373 K)

Furthermore, it is interesting to find that the recrystallized grain size increased rapidly firstly. Then it reached a peak value of 16.3 μm. Finally, it decreased slowly and remained at a steady value of 12.0 μm. This is mainly because the recrystallized grains had enough space to grow up at the low strain. But with increasing the recrystallized grains, the retarding effect between different grains became more evident. The growth rate of recrystallized grains cannot keep up with the increase of the grain number. Besides, more new nucleation grains made the total average grain size drop. Therefore, the recrystallized grains became smaller, leading to the decrease of average grain size.

5.3 The Influences of Strain Rate on Microstructure Evolution

In order to make it clearer to analyze the influences of strain rate on the microstructure evolution, we chose the same initial microstructure to conduct the simulations. Figure 14 shows the relationship between DRX fraction and average recrystallized grain size. Figure 15 shows the microstructure obtained by CA simulation at the deformation temperature of 1373 K when the strain reached 0.5, where the corresponding values of the average recrystallized grain size were 3.18, 5.63, 5.91 and 12.0 μm, respectively, and the relevant DRX fractions were 4.7%, 6.9%, 79.2% and 97.1% in sequence.

Fig. 15

The simulated microstructure at the deformation temperature of 1373 K, the strain of 0.5, strain rates of: a 10 s⁻¹; b 1.0 s⁻¹; c 0.1 s⁻¹; d 0.01 s⁻¹

As shown in Fig. 14, when the strain rate was equal or greater than 1.0 s⁻¹, the proportion of DRX was rather small. This is mainly because the deformation process was so quick that few recrystallized grains were generated. However, when the strain rate decreased to 0.1 s⁻¹, the DRX fraction increased to 79.2% when the strain was 0.5. And the DRX fraction at the strain rate of 0.01 s⁻¹ was 97.1%. It indicates that a low strain rate is beneficial to the occurrence of DRX at a constant deformation temperature. In addition, it also can be found that an incubation period was required before the occurrence of DRX. And the strain rate was positively correlated with the time of incubation, since the length of the incubation period was mainly affected by the critical dislocation density and the accumulation rate of dislocation. This is mainly because the critical dislocation density increases with the increase of the strain rate. If the increase of the dislocation accumulation rate cannot keep up with the increase of the critical dislocation density when the strain rate increases, the incubation period would become longer.

Additionally, for the average recrystallized grain size, it can be seen that the higher the strain rate was, the smaller the size of the recrystallized grain would be. This is mainly because the nucleation rate of the recrystallization increases when the strain rate increases, which leads to more and more grains beginning to nucleate. However, these new nucleation grains cannot fully grow up at high strain rate. So the higher the strain rate is, the smaller the recrystallized grain size is. As to Cr12MoV die steel, the DRX fraction was very low and can be negligible under the high strain rate, which means the recrystallization nearly did not occur.

5.4 The Influences of Deformation Temperature on Microstructure Evolution

In order to investigate the influences of deformation temperature on the microstructure evolution, we conducted several simulations at temperatures of 1323 K, 1373 K, and 1423 K, where the strain was 0.4 and strain rate was 0.01 s⁻¹. The simulation results are demonstrated in Fig. 16, where the average recrystallized grain sizes are 5.78, 6.21 and 18.32 μm, respectively. Meanwhile, the relationship between DRX fraction and average recrystallized grain size is shown in Fig. 17. It can be found that at a fixed strain rate, both the DRX fraction and the average recrystallized grain size increased with increasing the temperature at the strain range of 0.2 to 1.0.

Fig. 16

The simulated microstructure at the strain of 0.4, strain rate of 0.01 s⁻¹; and defamation temperatures of: a 1323 K; b 1373 K; c 1423 K

Fig. 17

The relationship between DRX fraction and average recrystallized grain size ($\dot{\varepsilon }$ = 0.01 s⁻¹)

It is also obvious to see that the increase of the deformation temperature would shorten the incubation period of DRX. This suggests that the influences of deformation temperature on DRX behavior are reflected at two sides. On the one hand, the higher temperature provides necessary energy to the nucleation and growth of recrystallized grains. On the other hand, too high temperature will coarsen the grains, leading to a large size. On the whole, when the strain is constant, the lower the strain rate or the higher the temperature, the easier the occurrence of DRX phenomenon.

6 Conclusions

The DRX behavior of Cr12MoV die steel has been investigated via experiments and CA modeling systematically. The main conclusions are summarized as follows:

• (1) The characteristic parameters of the true stress–strain curves, including critical stress ($\sigma_{c}$), peak stress ($\varepsilon_{p}$), steady stress ($\sigma_{ss}$) and saturated stress ($\sigma_{s}$), have been expressed as a function of the Zener–Hollomon parameter. The flow stress model of Cr12MoV die steel was established. The predicted results were in good agreement with the experimental results, indicating the flow stress model was capable of describing the DRX behavior of Cr12MoV die steel.

• (2) Work hardening coefficient ($k_{1}$) and softening coefficient ($k_{2}$) in CA model have been expressed as a function of the Zener–Hollomon parameter. The activation energy for hot deformation of Cr12MoV die steel was determined as 458.096 kJ/mol. The kinetics of DRX behavior of Cr12MoV die steel can be represented by the Avrami equation: $X_{DRX} = 1 - \exp \left[ { - 0.979\left( {\frac{{\varepsilon - \varepsilon_{c} }}{{\varepsilon_{p} }}} \right)^{1.394} } \right]$.

• (3) The CA model was established to describe the DRX behavior of Cr12MoV die steel. A microstructure enhancement, extraction and conversion program was developed based on real metallographic image to acquire real initial microstructure used in CA simulation to obtain more accurate simulation results. The good agreement between the simulated and experimental results indicates that the established CA model can accurately describe the kinetics of DRX and predict microstructure evolution of the Cr12MoV steel during hot compression.

• (4) The influences of the strain, strain rate and deformation temperature on the microstructure evolution of DRX of Cr12MoV die steel were analyzed. It can be found that a lower strain rate was beneficial to the occurrence of DRX. When the strain rate was 10 s⁻¹ or 1.0 s⁻¹, the DRX nearly did not occur. Moreover, both the DRX fraction and the average recrystallized grain size increased with the increase of temperature at the strain range of 0.2 to 1.0.