Block splitting for distributed optimization

Abstract

This paper describes a general purpose method for solving convex optimization problems in a distributed computing environment. In particular, if the problem data includes a large linear operator or matrix $A$, the method allows for handling each sub-block of $A$ on a separate machine. The approach works as follows. First, we define a canonical problem form called graph form, in which we have two sets of variables related by a linear operator $A$, such that the objective function is separable across these two sets of variables. Many types of problems are easily expressed in graph form, including cone programs and a wide variety of regularized loss minimization problems from statistics, like logistic regression, the support vector machine, and the lasso. Next, we describe graph projection splitting, a form of Douglas–Rachford splitting or the alternating direction method of multipliers, to solve graph form problems serially. Finally, we derive a distributed block splitting algorithm based on graph projection splitting. In a statistical or machine learning context, this allows for training models exactly with a huge number of both training examples and features, such that each processor handles only a subset of both. To the best of our knowledge, this is the only general purpose method with this property. We present several numerical experiments in both the serial and distributed settings.

1 Introduction

We begin by defining a canonical form called graph form for convex optimization problems. In graph form, we have two sets of variables $x$ and $y$, related by $y=Ax$, where $A$ is a linear operator, and an objective function that is separable across these two sets of variables. We can think of the variables $x$ as input variables and of $y$ as output variables, and the corresponding objective terms represent costs or constraints associated with different choices of the inputs and outputs. This form arises naturally in many applications, as we discuss in Sect. 2.

We then introduce an operator splitting method called graph projection splitting to solve graph form problems. Its main characteristic is that it separates the handling of the nonlinear objective terms from the handling of the linear operator $A$. The algorithm is an operator splitting method that proceeds by alternating the evaluation of the proximal operators of the objective terms with the projection of the input and output variables onto the graph of the linear operator $A$. There are at least two major benefits of this approach:

• 1. Re-use of computation. In many problems, there are trade-off or regularization parameters that are provided exogeneously by the modeler. It is typically desirable to solve the problem for many different values of the tuning parameters in order to examine the behavior of the solution or performance of the model as the parameter varies. In graph projection splitting, if a direct method is used to solve the linear systems in which $A$ appears, the factorization of the coefficient matrix can be computed once, cached, and then re-used across all these variations of the original problem. This can enable solving $k$ variations on the original problem in far less time than it would take to solve $k$ independent instances. In fact, the factorization can be re-used across completely different problems, as long as $A$ remains the same. In a statistical context, this allows for fitting, e.g., multiple different classification models to the same dataset in far less time than would be needed to fit the models independently.

• 2. Distributed optimization. In Sect. 4, we extend graph projection splitting to obtain a distributed block splitting algorithm that allows each block of $A$ to be handled by a separate process or machine. This permits the method to scale to solve, in principle, arbitrarily large problems by using many processes or computers. In a statistical context, for example, $A$ is the feature matrix, so block splitting allows for decomposing parameter estimation problems across examples and features simultaneously. To the best of our knowledge, this is the first algorithm with this property that is widely applicable. (For example, the distributed algorithms described in [1] permit decomposing problems by either examples or features, but not both, while other techniques often rely on $A$ being very sparse.)

We discuss three classes of applications, at different levels of generality: cone programming, parameter estimation problems in statistics and machine learning, and intensity modulated radiation treatment planning. We also present a number of numerical experiments and discuss implementation issues in detail.

2 Problem

Throughout this paper, we consider the problem

$$\begin{aligned} \begin{array}{ll} \hbox {minimize}&{}\, f(y) + g(x)\\ \hbox {subject to}&{}\, y = Ax, \end{array} \end{aligned}$$

(1)

with variables $x \in \mathbf{R}^n$ and $y \in \mathbf{R}^m$, where $f : \mathbf{R}^m \rightarrow \mathbf{R}\cup \{+\infty \}$ and $g : \mathbf{R}^n \rightarrow \mathbf{R}\cup \{+\infty \}$ are closed proper convex functions. We sometimes refer to $x$ as the input variables and to $y$ as the output variables. Since $f$ and $g$ can take on extended values, they can include (convex) constraints on $y$ and $x$: If $f$ or $g$ is an indicator function of a closed nonempty convex set, then the corresponding objective term simply represents a constraint on $y$ or $x$, respectively.

We call this problem type graph form because the variables $x$ and $y$ are constrained to lie in the graph $\{ (x,y) \in \mathbf{R}^{n+m} \mid y = Ax \}$ of the linear operator $A$. We emphasize that here and throughout the paper, ‘graph’ refers to the graph of a function or operator, not to graphs in the sense of graph theory.

2.1 Examples

A wide variety of convex optimization problems can be expressed in the form (1); we describe some examples in this section.

Cone programming.    If $\mathbf{K}$ is a convex cone, then the problem

$$\begin{aligned} \begin{aligned} \hbox {minimize}&\,\, c^T x \\ \hbox {subject to}&\,\, Ax = b \\&\,\, x \in \mathbf{K}, \end{aligned} \end{aligned}$$

(2)

is called a cone program in standard form. To express this in graph form, let

$$\begin{aligned} f(y) = I_{\{b\}}(y), \qquad g(x) = c^T x + I_\mathbf{K}(x), \end{aligned}$$

where $I_{\fancyscript{C}}$ is the indicator function of the convex set ${\fancyscript{C}}$, i.e., $I_{\fancyscript{C}} (x) = 0$ for $x \in {\fancyscript{C}}, I_{\fancyscript{C}} (x) = \infty$ for $x \not \in {\fancyscript{C}}$. The term $f(y)$ simply enforces $y=b$; the term $g(x)$ includes the linear objective $c^{T}x$ and the conic constraint $x\in \mathbf{K}$.

When $\mathbf{K}$ is the nonnegative orthant $\mathbf{R}_{+}^{n}$, the second-order cone $\mathbf{Q}^{n}$, or the semidefinite cone $\mathbf{S}_{+}^{n}$, the problem (2) is called a linear program (LP), second-order cone program (SOCP), or semidefinite program (SDP), respectively. When $\mathbf{K}$ is a (Cartesian) product of these three cone types, it is called a symmetric cone, and (2) is called a symmetric cone program. A very wide variety of convex optimization problems can be expressed as symmetric cone programs; see, e.g., [2–5]. (Though the algorithms we will discuss do not require $\mathbf{K}$ to be symmetric, we limit ourselves to the symmetric case and refer to symmetric cone programs simply as cone programs.) See, e.g., [6] for a recent discussion of the use of ADMM for semidefinite programming.

Regularized loss minimization.    Many problems in statistics and machine learning are naturally expressed in graph form. In regularized loss minimization, we fit a parameter vector $x$ by solving

$$\begin{aligned} \begin{array}{ll} \hbox {minimize}&l(Ax - b) + r(x), \end{array} \end{aligned}$$

where $l$ is a loss function and $r$ is a regularization function. Here, $A$ is a feature matrix in which each row corresponds to a training example and each column corresponds to a feature or predictor, and $b$ is a response vector, i.e., $A$ and $b$ comprise the training set. To express this in graph form, let

$$\begin{aligned} f(y) = l(y-b), \qquad g(x) = r(x). \end{aligned}$$

(3)

As an example, we obtain the lasso [7] by setting $l(u) = (1/2)\Vert u\Vert _2^2$ and $r(x) = \lambda \Vert x\Vert _1$, where $\lambda >0$ is a regularization parameter chosen by the modeler to trade off model complexity with quality of fit to the training set. More generally, given a linear model $b_i = a_i^T x + v_i$, where $a_i$ is the $i$th feature vector and the noise terms $v_i$ are independent with log-concave densities $p_i$, the negative log-likelihood function is

$$\begin{aligned} l(Ax - b) = \sum _{i=1}^m l_i(a_i^T x - b_i), \end{aligned}$$

where $l_i(u) = -\log p_i(-u)$. If $r = 0$, then the solution to this problem gives the maximum likelihood estimate of $x$. If $r_i$ is the negative log prior density of $x_i$, then the solution is the maximum a posteriori (MAP) estimate. For example, the lasso corresponds to MAP estimation of a linear model with Gaussian noise and a Laplacian prior on the parameters. Thus we can carry out maximum likelihood and MAP estimation in exponential families.

In classification problems, the loss function is sometimes written as a function of the margin $b_i(a_i^T x)$. In this case, we can let $f(y) = \sum _{i=1}^m l_i(b_i y_i)$. For example, if $l_i(u) = (1 - u)_+$ (where $(\cdot )_+ = \max \{0,\cdot \}$) and $r(x) = \lambda \Vert x\Vert _2^2$, we recover the support vector machine. For background on this formulation, see, e.g., [1, §8.1].

Intensity modulated radiation treatment planning.    Many design and planning problems have the form (1), with $x$ representing an action or design, $y$ representing an outcome or result, and $y=Ax$ giving our (linear) model of how the action maps to a result. The functions $f$ and $g$ express the constraints or costs associated with the outcome or action.

Here, we describe one typical example that we revisit throughout the paper. In intensity modulated radiation treatment planning (IMRT) [8, 9], radiation is delivered to a patient with the goal of killing or damaging the cells in a tumor while carrying out minimal damage to other tissue. The radiation is delivered in beams, each of which has a known pattern; the intensity of each beam can be adjusted up to a given maximum level. The variable $x_j$ is the intensity of beam $j$, and $y_i$ is the radiation dosage delivered to voxel $i$ in the exposure area; the constraint $y=Ax$ relates the beam intensities to the delivered dosages. The coefficients in $A$ depend on the geometry of the beam and possibly the patient (when scattering is taken into account). The goal is to find beam intensities that deliver a sufficient dosage to voxels in the tumor, but not too high a dosage to voxels outside the tumor. This cannot be achieved perfectly, so the choice involves trade-offs between these two goals.

To formulate a typical IMRT problem in graph form, we let $g$ be the indicator function of $[0,I^{\mathrm{max}}]^{n}$, where $I^{\mathrm{max}}$ is the maximum possible beam intensity, so the term $g(x)$ simply expresses the constraints $0 \le x_i \le I^{\mathrm{max}}$. The objective is expressed in $f$ as

$$\begin{aligned} f(y) = w^T(d^{\mathrm{min}}-y)_+ + v^T(y-d^{\mathrm{max}})_+, \end{aligned}$$

where $d^{\mathrm{min}}_i$ is the target minimum dosage for the voxel $i, d_{i}^{\mathrm{max}}$ is the target maximum dosage for the voxel $i$, and $w$ and $v$ are positive weights chosen (by a radiation oncologist) to trade off dosage delivered to the tumor with damage to other tissue. A simple choice for the target dosages would be $d^{\mathrm{min}}_{i} = d^{\mathrm{max}}_i = 0$ for a voxel not in the tumor, and $d^{\mathrm{min}}_i = \alpha , d^{\mathrm{max}}_i = \infty$ for a voxel in the tumor, where $\alpha$ is a dosage level high enough to damage or kill tumor cells.

3 Graph projection splitting

3.1 Operator splitting

We now describe a standard operator splitting method known as the alternating direction method of multipliers (ADMM) or Douglas–Rachford splitting [1] for the generic convex constrained minimization problem

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{}\, \varphi (z)\\ \hbox {subject to} &{}\, z \in \mathbf{C}, \end{array} \end{aligned}$$

where $\varphi$ is closed proper convex and $\mathbf{C}$ is closed nonempty convex. The algorithm is

$$\begin{aligned} \begin{array}{r@{\quad }l@{\quad }l} z^{k+1/2} &{}:=&{} \mathbf{prox}_\varphi (z^k-\tilde{z} ^k) \\ z^{k+1} &{}:=&{} \Pi _\mathbf{C}(z^{k+1/2}+\tilde{z} ^k)\\ \tilde{z}^{k+1} &{}:=&{} \tilde{z}^k + z^{k+1/2}-z^{k+1}, \end{array} \end{aligned}$$

(4)

where $k$ is an iteration counter, $\Pi _\mathbf{C}$ denotes (Euclidean) projection onto $\mathbf{C}$, and

$$\begin{aligned} \mathbf{prox}_{\varphi }(v) = {\mathop {\hbox {argmin}}_{x}} \left( \varphi (x) + (\rho /2)\Vert x - v\Vert _2^2 \right) \end{aligned}$$

is the proximal operator of $\varphi$ with parameter $\rho > 0$ [10]. We suppress the dependence on $\rho$ to lighten notation. It is important to note, however, that while the algorithm will converge with any choice of $\rho$, the choice can affect its rate of convergence.

We emphasize that while ADMM algorithms can take many forms, the particular form used here is key to the subsequent discussion. This algorithm splits the handling of the objective function $\varphi$ (which happens in the first step) and the handling of the constraint set $\mathbf{C}$ (which happens in the second step). The third step, which is called the dual update step, coordinates the two other steps, resulting in convergence to a solution of the original problem. This algorithm is guaranteed to converge to optimality (when a solution exists); see [1, §3.2], for details.

There are many variations on the basic algorithm described here, including variations in the order of the proximal and projection steps, over-relaxation, and varying the proximal parameter $\rho$ in each step. All of these, which are surveyed in [1, §3.4], can be employed in what follows, but we limit our discussion to the simplest case.

3.2 Algorithm

Applying the algorithm above to (1), with $z = (x,y)$ and $\varphi (z) = f(y) + g(x)$, yields

$$\begin{aligned} x^{k+1/2}&:= \mathbf{prox}_g(x^k - \tilde{x}^k) \nonumber \\ y^{k+1/2}&:= \mathbf{prox}_f(y^k - \tilde{y}^k) \nonumber \\ (x^{k+1},y^{k+1})&:= \Pi _A(x^{k+1/2} + \tilde{x}^k, y^{k+1/2} + \tilde{y}^k) \\ \tilde{x}^{k+1}&:= \tilde{x}^k + x^{k+1/2} - x^{k+1} \nonumber \\ \tilde{y}^{k+1}&:= \tilde{y}^k + y^{k+1/2} - y^{k+1}, \nonumber \end{aligned}$$

(5)

where $\Pi _A$ denotes projection onto $\{ (x,y) \in \mathbf{R}^{n+m} \mid y = Ax \}$. We typically initialize all the variables to zero.

We refer to $\Pi _A$ as a graph projection operator because it projects onto the graph of the linear operator $A$, and to (5) as the graph projection splitting algorithm as a result. Graph projection can be seen to be a linear operator that can be expressed explicitly as

$$\begin{aligned} \begin{bmatrix} c \\ d \end{bmatrix} \mapsto \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix}^{-1} \begin{bmatrix} I&\quad A^T \\ 0&\quad 0 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix}, \end{aligned}$$

(6)

as shown in Appendix A, where we also describe several methods that can be used to implement graph projection efficiently. Briefly, when a direct method is used to evaluate graph projection, we can cache the matrix factorizations involved, a simple but important technique we refer to as factorization caching. After the first iteration, subsequent graph projections can be carried out using only forward-solve and back-solve steps, which can be much faster than the original factorization.

Because of the way the form of ADMM in Sect. 3.1 applies to graph form problems, the objective terms $f$ and $g$ never interact directly with the matrix $A$. This implies that we can solve multiple graph form problems with the same matrix $A$ but different $f$ and $g$ more quickly than solving them all independently, because they can all re-use the same cached factorization used to evaluate $\Pi _A$. In the context of machine learning, for example, this applies whenever we wish to fit two different models to the same dataset (either completely different models or versions of the same model with different settings of the regularization parameters). In IMRT, this permits the radiation oncologist to evaluate results quickly under different choices of the weights $w_i$. In general, this is very useful whenever there are parameters in the problem that need to be tuned by hand or via an external procedure like cross-validation.

Evaluating the proximal operators $\mathbf{prox}_f$ and $\mathbf{prox}_g$ involves solving convex optimization problems, and so may seem to be onerous. In many applications, however, $f$ and $g$ are simple or structured enough that their proximal operators can be evaluated very efficiently, either via closed-form expressions or simple linear-time algorithms. See [11, Chapter 6], for a discussion of many common examples of proximal operators and efficient ways to evaluate them.

Finally, we note that the first two (proximal evaluation) steps in graph projection splitting can be executed independently in parallel; similarly, the dual update steps can also be carried out in parallel. If in addition $f$ or $g$ is separable, i.e., is a sum of functions of disjoint subsets of the variable components, then the proximal steps for $f$ and $g$ split into proximal steps for each subset of variables, which can all be carried out in parallel (separability of $f$ and $g$ is discussed in detail in Sect. 4.)

Stopping criterion.    As discussed in [1, §3.3], the values

$$\begin{aligned} r^{k+1} = z^{k+1/2} - z^{k+1}, \quad s^{k+1} = -\rho (z^{k+1} - z^{k}), \end{aligned}$$

where $z^{k+1/2} = (x^{k+1/2}, y^{k+1/2})$ and $z^k = (x^k, y^k)$, can be viewed as primal and dual residuals in the algorithm. We can use a termination criterion that requires that both residuals are small, i.e.,

$$\begin{aligned} \Vert r^k\Vert _2 \le \varepsilon ^{\mathrm{pri}} \quad \hbox {and} \quad \Vert s^k\Vert _2 \le \varepsilon ^{\mathrm{dual}}, \end{aligned}$$

where $\varepsilon ^{\mathrm{pri}}>0$ and $\varepsilon ^{\mathrm{dual}}>0$ are feasibility tolerances for the primal and dual feasibility conditions. These tolerances can be chosen using an absolute and relative criterion, such as

$$\begin{aligned} \varepsilon ^{\mathrm{pri}}&= \sqrt{n}\; \varepsilon ^{\mathrm{abs}} + \varepsilon ^{\mathrm{rel}} \max \{ \Vert z^{k-1/2}\Vert _2, \Vert z^{k}\Vert _2\},\\ \varepsilon ^{\mathrm{dual}}&= \sqrt{n}\; \varepsilon ^{\mathrm{abs}} + \varepsilon ^{\mathrm{rel}} \Vert \rho \tilde{z}^k\Vert _2, \end{aligned}$$

where $\varepsilon ^{\mathrm{abs}}>0$ is an absolute tolerance and $\varepsilon ^{\mathrm{rel}}>0$ is a relative tolerance. A reasonable value for the relative stopping criterion might be in the range of $10^{-2}$ to $10^{-4}$, depending on the application. The choice of absolute stopping criterion depends on the scale of the typical variable values. We emphasize that this criterion is not heuristic and refer the reader to [1, §3.3], for a more detailed theoretical discussion.

Convergence in practice.    Simple examples show that ADMM can be very slow to converge to high accuracy. However, it is often the case that ADMM converges to modest accuracy—sufficient for many applications—within a few tens of iterations. This behavior makes ADMM similar to algorithms like the conjugate gradient method, for example, in that a few tens of iterations will often produce acceptable results of practical use. However, the slow convergence of ADMM also distinguishes it from algorithms such as Newton’s method (or, for constrained problems, interior-point methods), where high accuracy can be attained in a consistent amount of time. While in some cases it is possible to combine ADMM with a method for producing a high accuracy solution from a low accuracy solution [12], in the general case ADMM will be practically useful mostly in cases when modest accuracy is sufficient.

Fortunately, for the types of large-scale problems that are our primary concern here, this is typically the case. Also, in statistical and machine learning problems, solving a parameter estimation problem to very high accuracy often yields little to no improvement in actual prediction performance, the real metric of interest in applications. Indeed, in these fields, problems are often solved only to modest accuracy even when it is possible to obtain high accuracy solutions.

We mentioned previously that we typically initialize the algorithm by setting all variables to zero (this is the case for all the numerical experiments discussed later). It has been shown elsewhere in the literature that ADMM-based methods are not particularly sensitive to changes in the choice of starting point; see, e.g., [13] for a discussion of extensive numerical experiments with ADMM.

4 Block splitting

4.1 Block partitioned form

We now build on the graph projection splitting algorithm to obtain a distributed block splitting algorithm. Suppose that $f$ and $g$ are block separable, i.e.,

$$\begin{aligned} f(y) = \sum _{i=1}^M f_i(y_i), \quad g(x) = \sum _{j=1}^N g_j(x_j), \end{aligned}$$

where

$$\begin{aligned} y = (y_1, \ldots , y_M), \quad x = (x_1, \ldots , x_N), \end{aligned}$$

with $y_i \in \mathbf{R}^{m_i}, x_j \in \mathbf{R}^{n_j}$, so $\sum _{i=1}^M m_i = m$ and $\sum _{j=1}^N n_j = n$. When all subvector sizes are one, we say that $f$ or $g$ is fully separable.

We then partition $A$ conformably with the partitioning of $x$ and $y$, giving

$$\begin{aligned} A = \begin{bmatrix} A_{11}&\quad A_{12}&\quad \cdots&\quad A_{1N} \\ A_{21}&\quad A_{22}&\quad \cdots&\quad A_{2N} \\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ A_{M1}&\quad A_{M2}&\quad \cdots&\quad A_{MN} \end{bmatrix}, \end{aligned}$$

where $A_{ij} \in \mathbf{R}^{m_i \times n_j}$. In other words, if $f$ and $g$ are fully separable (down to the component), then there is no restriction on partitioning. As a convention, $i$ will index block rows and $j$ will index block columns. We can express the problem (1) in terms of the variable components as

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{} {\mathop \sum \limits _{i=1}^M} f_i(y_i) + {\mathop \sum \limits _{j=1}^N} g_j(x_j)\\ \hbox {subject to} &{} y_i = {\mathop \sum \limits _{j=1}^N} A_{ij} x_j, \quad i=1,\ldots , M. \end{array} \end{aligned}$$

(7)

In some cases, either $M = 1$ or $N = 1$. We refer to these cases as column splitting and row splitting, respectively.

The goal is to solve this block partitioned problem in a way that (a) allows for each block $A_{ij}$ to be handled by a separate process and (b) does not involve transfer of the block matrices $A_{ij}$ among processes.

4.2 Examples

Cone programming.    Consider a symmetric cone program (2) with

$$\begin{aligned} \mathbf{K} = \mathbf{K}_1 \times \cdots \times \mathbf{K}_N. \end{aligned}$$

The problem can then be written in the form (7), where $f_i$ is the indicator of $\{b_i\}$ and $g_j(x_j) = c_j^T x_j + I_{\mathbf{K}_j}(x_j)$. In other words, $f$ is fully separable and $g$ is block separable conformably with the product structure of $\mathbf{K}$, i.e., row splitting is always possible, but column splitting relies on $\mathbf{K}$ being a product cone. Put another way, $y$ can be arbitrarily split, but $x$ must be split comformably with the cones $\fancyscript{K}_j$.

Regularized loss minimization.    Here, $A$ is the training data, so row splitting splits the problem by examples, column splitting splits the problem by features, and block splitting splits by both examples and features.

Typically, the examples are assumed to be statistically independent, so the loss function $l$ is fully separable and row splitting is straightforward. If the regularization function $r$ is, e.g., $\ell _1$ or squared $\ell _2$ loss, then it is also fully separable. However, suppose $r(x)$ is $\sum _{j=1}^N \Vert x_j\Vert _2$, where $x_j \in \mathbf{R}^{n_j}$. Here, the regularizer is separable with respect to the partition $(x_1, \dots , x_N)$ but not fully separable (when $n_j > 1$). This extension of $\ell _1$ regularization is called the group lasso [14], or, more generally, sum-of-norms regularization [15]. In this case, we can split the columns of $A$ conformably with the blocks of variables in the same regularization group.

Intensity modulated radiation treatment planning.    In the IMRT problem, both $f$ and $g$ are fully separable, so $x$ and $y$ can be split into subvectors arbitrarily.

4.3 Algorithm

Problem transformation.    We first introduce $M\!N$ new variables $x_{ij} \in \mathbf{R}^{n_j}$ and $MN$ variables $y_{ij} \in \mathbf{R}^{m_i}$ to reformulate (7) in the equivalent form

$$\begin{aligned} \begin{array}{lll} \hbox {minimize} &{} {\mathop \sum \limits _{i=1}^M} f_i(y_i) + {\mathop \sum \limits _{j=1}^N} g_j(x_j)\\ \hbox {subject to} &{} x_j = x_{ij}, &{} i=1,\ldots , M\\ &{} y_i = {\mathop \sum \limits _{j=1}^N} y_{ij}, &{} i=1, \ldots , M\\ &{} y_{ij} = A_{ij} x_{ij}, &{} i=1, \ldots , M, \quad j=1,\ldots , N. \end{array} \end{aligned}$$

Here, $x_{ij}$ can be viewed as the local opinion of the value of $x_j$ only using row block $i$, and $y_{ij}$ can be viewed as partial responses only using local information $x_{ij}$ and $A_{ij}$.

We then move the partial response constraints $y_{ij} = A_{ij} x_{ij}$ into the objective:

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{} {\mathop \sum \limits _{i=1}^{M}} f_i(y_i) + {\mathop \sum \limits _{j=1}^N} g_j(x_j) + {\mathop \sum \limits _{i=1}^{M}}\, {\mathop \sum \limits _{j=1}^{N}} I_{ij} (y_{ij},x_{ij})\\ \hbox {subject to} &{} x_j = x_{ij}, \quad i=1,\ldots , M\\ &{} y_i = {\mathop \sum \limits _{j=1}^{N}} y_{ij}, \quad i=1, \ldots , M, \end{array} \end{aligned}$$

(8)

where $I_{ij}$ is the indicator function of the graph of $A_{ij}$. The three objective terms now involve distinct sets of variables, and the two sets of constraints involve distinct sets of variables, which will simplify a number of computations in the sequel.

Algorithm.    Applying the ADMM algorithm (4) to (8) gives

$$\begin{aligned} y_i^{k+1/2}&:= \mathbf{prox}_{f_i} (y_i^k-\tilde{y}_i^k) \\ x_j^{k+1/2}&:= \mathbf{prox}_{g_j} (x_j^k-\tilde{x}_j^k) \\ (x_{ij}^{k+1/2},y_{ij}^{k+1/2})&:= \Pi _{ij} (x_{ij}^{k}-\tilde{x}_{ij}^{k},y_{ij}^{k}- \tilde{y}_{ij}^{k}) \\ (x_j^{k+1}, \{ x_{ij}^{k+1} \}_{i=1}^M)&:= \mathbf{avg}(x_j^{k+1/2} + \tilde{x}_j^{k}, \{x_{ij}^{k+1/2} + \tilde{x}_{ij}^{k}\}_{i=1}^M) \\ (y_i^{k+1}, \{ y_{ij}^{k+1} \}_{j=1}^N)&:= \mathbf{exch}(y_i^{k+1/2} + \tilde{y}_i^{k}, \{y_{ij}^{k+1/2} + \tilde{y}_{ij}^{k}\}_{j=1}^N) \\ \tilde{z}^{k+1}&:= \tilde{z}^k + z^{k+1/2} - z^{k+1}, \end{aligned}$$

where $\tilde{z}$ is the collection of all the dual variables corresponding to $x_j, y_i, x_{ij}$, and $y_{ij};\, \Pi _{ij}$ is graph projection for $A_{ij};\, \mathbf{avg}$ is elementwise averaging; and $\mathbf{exch}$ is an exchange operator, defined below. By abuse of notation, we write $\mathbf{avg}$ as having multiple output arguments to denote that all these variables are set to the elementwise average of the inputs, i.e., $x_{ij}^{k+1} = x_j^{k+1}$ for $i = 1, \dots , M$.

The exchange projection $\mathbf{exch}(c, \{c_j\}_{j=1}^N)$ is given by

$$\begin{aligned} y_{ij} :&= c_j + \Big ( c - {\mathop \sum \limits _{j=1}^{N}} c_{j} \Big ) \Big / \left( N+1 \right) , \quad y_{i} := c - \Big ( c - {\mathop \sum \limits _{j=1}^{N}} c_{j} \Big ) \Big / \left( N+1 \right) . \end{aligned}$$

We will sometimes refer to $\mathbf{avg}$ and $\mathbf{exch}$ as consensus and exchange operators, respectively, since they project onto the constraint sets for $x_j = x_{ij}$ and $y_i = \sum _j y_{ij}$, respectively. See [1, §7], for background on the origin of these names.

Simplified algorithm.    The form of the consensus and exchange projections, together with the dual updates, can be used to obtain a simpler form for the algorithm:

$$\begin{aligned} \begin{array}{r@{\quad }l@{\quad }l} y_i^{k+1/2} &{}:=&{} \mathbf{prox}_{f_i} (y_i^k-\tilde{y}_i^k) \\ x_j^{k+1/2} &{}:=&{} \mathbf{prox}_{g_j} (x_j^k-\tilde{x}_j^k) \\ (x_{ij}^{k+1/2},y_{ij}^{k+1/2}) &{}:=&{} \Pi _{ij} (x_j^{k}- \tilde{x}_{ij}^{k}, y_{ij}^{k}+\tilde{y}_{i}^{k}) \\ x_j^{k+1} &{}:=&{} \mathbf{avg}(x_j^{k+1/2}, \{x_{ij}^{k+1/2}\}_{i=1}^M) \\ (y_i^{k+1}, \{y_{ij}^{k+1}\}_{j=1}^N) &{}:=&{} \mathbf{exch}(y_i^{k+1/2}, \{y_{ij}^{k+1/2}\}_{j=1}^N) \\ \tilde{x}_j^{k+1} &{}:=&{} \tilde{x}_j^k + x_j^{k+1/2} - x_j^{k+1} \\ \tilde{y}_i^{k+1} &{}:=&{} \tilde{y}_i^k + y_i^{k+1/2} - y_i^{k+1} \\ \tilde{x}_{ij}^{k+1} &{}:=&{} \tilde{x}_{ij}^k + x_{ij}^{k+1/2} - x_{j}^{k+1}. \end{array} \end{aligned}$$

(9)

Here, the $x_{ij}^{k+1}$ and $\tilde{y}_{ij}$ variables have been eliminated. The solution can be obtained via $x^\star = (x_1^{k+1/2}, \dots , x_N^{k+1/2})$. See Appendix B for details on how to obtain this simplified form from the original algorithm. In the sequel, we refer to (9) as the block splitting algorithm.

4.4 Parallel implementation

Parallelism.    Several of the steps in (9) can be carried out independently in parallel. The first three steps can all be performed in parallel: Each of the $M$ $y_i^{k+1/2}$’s, the $N$ $x_j^{k+1/2}$’s, and the $MN$ ($x_{ij}^{k+1/2}, y_{ij}^{k+1/2}$) pairs can all be updated separately. Similarly, each of the $N$ averaging and $M$ exchange operations can be carried out independently in parallel, and the final three steps can also be carried out independently in parallel. Overall, the algorithm thus involves three distinct stages, each of which corresponds to one of the three updates in ADMM. Intuitively, the $\mathbf{avg}$ and $\mathbf{exch}$ operations coordinate the local variables to move towards the global solution.

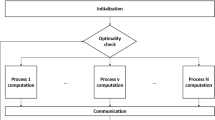
Communication.    We use a total of $MN$ processes split across some number of machines. For example, we may want each process on a separate machine, in which case $MN$ machines are required; alternatively, each process may use a distinct core, in which case multiple processes would run on the same machine. Only the averaging and exchange steps require communication. The averaging step communicates within each block column (but not across columns), and the exchange step communicates within block rows (but not across rows). This is portrayed diagrammatically in Fig. 1. The main collaborative component in computing both is summing a set of vectors, so both can be implemented via reduce operations in parallel programming frameworks like MPI; averaging involves $N$ reduce steps run in parallel and exchange involves $M$ reduce steps.

Fig. 1

Diagram of which nodes perform computations in which steps in each iteration. Red is $x$ and blue is $y$; the extra column on the right is for $y_i$ and the extra row at the bottom is for $x_j$ (square rather than circular dots). The only omitted step, the dual update, splits completely (color figure online)

Allreduce.    The only communication step needed is computing the elementwise sum of a set of vectors and depositing the result on each of a set of processes. This functionality is provided by a function often referred to as Allreduce. Explicitly, suppose each of $m$ processes has a local copy of a variable $x \in \mathbf{R}^n$. Then calling Allreduce with argument $x$ in each of the $m$ processes will (efficiently) compute the elementwise sum of the $m$ copies of $x$ and then deposit the result on each of the $m$ processes. The function Allreduce is a standard MPI primitive, but an implementation of Allreduce compatible with Hadoop clusters is also available in Vowpal Wabbit [16].

4.5 Block sparsity

Suppose an entire block $A_{ij}$ is zero, i.e., that $A$ is block sparse. In this case, we can use a slightly modified problem transformation that introduces fewer auxiliary variables; the approach can be viewed as a form of general form consensus [1, §7.2]. In other words, each subsystem should handle only its block of data and only the subset of variables that are relevant for that block of data. It is also possible to exploit other types of structure at the block level, though we focus on this case here.

Let $\mathbf{M}_j$ and $\mathbf{N}_i$ be the sets of indices of nonzero blocks in block column $j$ and block row $i$, respectively. In other words, $|\mathbf{M}_j| = M$ if block column $j$ has no zero blocks, and $|\mathbf{N}_i| = N$ if block row $i$ has no zero blocks. We assume that each $\mathbf{M}_j$ and $\mathbf{N}_i$ is nonempty, since otherwise $A$ itself has zero rows or columns.

The problem (1) can be written

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{} {\mathop \sum \limits _{i=1}^M} f_i(y_i) + {\mathop \sum \limits _{j=1}^N} g_j(x_j)\\ \hbox {subject to} &{} y_i = {\mathop \sum \limits _{j \in \mathbf{N}_i}} A_{ij} x_j, \quad i=1,\ldots , M. \end{array} \end{aligned}$$

Introducing auxiliary variables $x_{ij}$ and $y_{ij}$, the problem can then be written

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{}{\mathop \sum \limits _{i=1}^M} f_i(y_i) + {\mathop \sum \limits _{j=1}^N} g_j(x_j) + {\mathop \sum \limits _{i=1}^M} {\mathop \sum \limits _{j \in \mathbf{N}_i}} I_{ij}(x_{ij}, y_{ij}) \\ \hbox {subject to} &{} x_j = x_{ij}, \quad i=1,\ldots , M, \quad j \in \mathbf{N}_i, \\ &{} y_i = {\mathop \sum \limits _{j \in \mathbf{N}_i}} y_{ij}, \quad i=1, \ldots , M, \end{array} \end{aligned}$$

where $I_{ij}$ is defined as above. This means that we only introduce auxiliary variables $x_{ij}$ and $y_{ij}$ for each nonzero block $A_{ij}$, rather than $MN$ many as before. The consensus constraint $x_j = x_{ij}$ now only constrains the $x_{ij}$ for each nonzero block in column $j$ to equal $x_j$, and the exchange constraint only requires the nonzero $y_{ij}$ in a given block row to sum to $y_i$.

The resulting algorithm looks the same as before, but there are fewer arguments to the averaging and exchange operators. In particular, for fixed $j$, the averaging operator only averages together $|\mathbf{M}_j|+1$ rather than $M+1$ entries, and for fixed $i$, the exchange operator only aggregates $|\mathbf{N}_i|+1$ rather than $N+1$ entries.

5 Numerical experiments

In this section, we report numerical results for several examples. The examples are chosen to illustrate a variety of the ideas discussed above, including caching matrix factorizations for re-use of computation across iterations and multiple problem instances, using iterative solvers for the updates, and using block splitting to solve distributed problems. The implementations are written to be as simple as possible, with no special implementation-level optimization or tuning.

In the serial cases, we compare solving a problem with graph projection splitting to solving the problem with CVX [17], a MATLAB-based parser-solver for convex optimization. CVX reformulates a given problem into a symmetric cone program amenable to solution by interior-point solvers like SeDuMi [18] and SDPT3 [19].

All the experiments other than the distributed examples were run on a machine with one (quad-core) Intel Xeon E3-1270 3.4 GHz CPU and 16 GB RAM running Debian Linux. The examples were run with MATLAB version 7.10.0.499. Unless otherwise specified, all the serial examples were run with $\varepsilon ^{\mathrm{abs}} = 10^{-4}, \varepsilon ^{\mathrm{rel}} = 10^{-2}$, and $\rho = 1$. More details on the distributed example are provided in Sect. 5.2.

5.1 Cone programming

We implement a symmetric cone solver based on (5), where

$$\begin{aligned} f(y) = I_{\{b\}}(y), \qquad g(x) = c^T x + I_\mathbf{K}(x). \end{aligned}$$

The proximal operators of $f$ and $g$ are

$$\begin{aligned} \mathbf{prox}_f(v) = b, \quad \mathbf{prox}_g(v) = \Pi _\mathbf{K}(v - c/\rho ). \end{aligned}$$

Projection onto a product cone $\mathbf{K} = \mathbf{K}_1 \times \cdots \times \mathbf{K}_N$ involves projecting the relevant components onto each $\mathbf{K}_i$; expressions for the individual projections are in [11, §6.3].

Since CVX is able to reformulate a wide range of convex optimization problems as symmetric cone programs, we implement our solver as a (MATLAB-based) backend to CVX and, to provide a point of reference, provide similar results for SeDuMi, an interior-point solver. We emphasize, however, that the two are not really comparable: ADMM is a first-order method intended to provide solutions of low to medium accuracy, while the interior-point method implemented in SeDuMi is second-order and is capable of returning high-accuracy solutions reliably. For this reason, we omit SeDuMi’s iteration counts in Table 1; though they are all in the 20–40 iteration range, the iteration counts are not comparable to the ADMM ones.

Table 1 Summary of timings for single block cone programs

ADMM will mainly be of interest in the large-scale or distributed setting or in cases where solutions of low to medium accuracy suffice. For a thorough discussion of using ADMM for semidefinite programming, see [6], which also discusses some cone program-specific modifications to the basic method that are out of scope here.

We discuss two examples; the results are summarized in Table 1. The solution accuracy relative to SeDuMi is summarized in Table 2. The ‘error in $p^\star$’ is the relative error in objective value attained, treating the SeDuMi solution as the truth, and the infeasibility is the relative primal infeasibility of the ADMM solution, measured by

$$\begin{aligned} \frac{\Vert Ax^\star - b\Vert _2}{1 + \Vert b\Vert _1}. \end{aligned}$$

The attained values of these two metrics depend on $\varepsilon ^{\mathrm{abs}}, \varepsilon ^{\mathrm{rel}}$, and $\rho$.  For these examples, we used tolerance settings of $\varepsilon ^{\mathrm{abs}} = 10^{-4}$ and $\varepsilon ^{\mathrm{rel}} = 10^{-3}$. We note that while we used generic ADMM stopping criteria here, if one is really interested in cone programming in particular, it can be worthwhile to use cone program-specific stopping criteria instead; see, e.g., [6, §3.4].

Table 2 Relative solution accuracy for single block cone programs

In these examples, unlike some of the later experiments, the matrix $A$ is typically very sparse. In addition, while the original form of these problems is unconstrained, they are transformed into and solved as constrained cone programs.

The Huber fitting problem is

$$\begin{aligned} \begin{array}{ll} \hbox {minimize}&\varphi _{\mathrm{huber}}(Ax - b), \end{array} \end{aligned}$$

with variable $x \in \mathbf{R}^n$ and problem data $A \in \mathbf{R}^{m \times n}, b \in \mathbf{R}^m$, where

$$\begin{aligned} \varphi _{\mathrm{huber}}(x) = {\left\{ \begin{array}{ll} \Vert x\Vert _2^2 &{} \Vert x\Vert _2 \le 1 \\ 2\Vert x\Vert _2 - 1 &{} \Vert x\Vert _2 \ge 1. \end{array}\right. } \end{aligned}$$

CVX transforms this problem into a (dual) constrained cone program with $m+7$ variables, $n+5$ equality constraints, and a cone constraint with $\mathbf{K} = \mathbf{R}_+^4 \times \mathbf{Q}^{m+1} \times \mathbf{S}_+^2$. (We note that we could also solve the original unconstrained problem directly with graph projection splitting, using $f(y) = \varphi _{\mathrm{huber}}(y - b)$ and $g = 0$.)

We also consider a matrix fractional minimization problem, given by

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{}\, (Ax + b)^T (I + B \mathbf{diag}(x) B^T)^{-1} (Ax + b) \\ \hbox {subject to} &{}\, x \ge 0, \end{array} \end{aligned}$$

with variable $x \in \mathbf{R}^n$ and problem data $A,B \in \mathbf{R}^{m \times n}$ and $b \in \mathbf{R}^m$. CVX transforms this into a (dual) constrained cone program with $(m+1)^2 + n$ variables, $n+1$ equality constraints, and a cone constraint with $\mathbf{K} = \mathbf{R}_+^n \times \mathbf{S}_+^{m+1}$. For example, if $m = 200$ and $n = 100$, this is a symmetric cone program with 20,401 variables, 101 equality constraints, and $\mathbf{K} = \mathbf{R}_+^{100} \times \mathbf{S}_+^{201}$.

We can see from Table 1 that for some problems, this form of ADMM outperforms SeDuMi, while for other problems, it can be far slower to produce a solution of reasonable quality. There are a few points worth highlighting about this. First, if it is possible to solve a given cone program serially using SeDuMi or an interior-point method, it is usually best to do so; replacing SeDuMi is not our goal. Second, these results depend greatly on the precise way in which ADMM is used to solve the problem, and the one shown here is not ideal for serial solutions; see Wen et al. [6] for an example of much better results with ADMM for cone programs. Finally, recall that the reason we use this form of ADMM is solely because it is a stepping stone to block splitting, which lets us solve (albeit with modest accuracy) large problems that cannot be solved at all by traditional methods.

We mention that we have also tested this (general-purpose) cone solver on a large variety of other problems from the CVX example library [20] and the results shown here are representative; for brevity, we have highlighted the two examples above, since their conic formulations have sufficiently complex constraints to be interesting.

5.2 Regularized loss minimization

We solve several instances of the lasso in different regimes. Recall that in the lasso,

$$\begin{aligned} f(y) = l(y - b), \quad g(x) = \lambda \Vert x\Vert _1, \end{aligned}$$

where $l = (1/2)\Vert \cdot \Vert _2^2$, and the proximal operators of these functions are simple elementwise operations given in [11, §6.1.1 and §6.5.2].

Serial dense example.    We first solve instances of the lasso serially using graph projection splitting. We generate the data as follows. We first choose the entries of $A \in \mathbf{R}^{1,000 \times 3,000}$ independently from a standard normal distribution and then normalize the columns to have unit $\ell _2$ norm. A ‘true’ value $x^{\mathrm{true}} \in \mathbf{R}^n$ is generated with 10 nonzero entries, each sampled from a $\mathbf{N}(0,1)$ distribution. We emphasize that while $x^{\mathrm{true}}$ is sparse, the data matrix $A$ is dense. The labels $b$ are then computed as $b = Ax^{\mathrm{true}} + v$, where $v \sim \mathbf{N}(0,10^{-3}I)$, which corresponds to a signal-to-noise ratio $\Vert Ax^{\mathrm{true}}\Vert _2^2/\Vert v\Vert _2^2$ of around 60.

We first discuss results for a MATLAB implementation of graph projection splitting. Because the prox operators for the lasso are so efficient to evaluate, the bulk of the work is in carrying out the graph projection, which we carry out using (11) because $m < n$. We summarize some computational results in Table 3. They are in line with our expectations: The interior-point method reliably converges in a small number of iterations, but each iteration is much more expensive. Without caching the computation of $AA^T$, graph projection splitting took 18.5 s; while still much faster than CVX, this underscores the benefit of being able to cache computations.

Table 3 Summary of timings for single block dense lasso example

Regularization path.    We now solve a sequence of lasso problems for ten different values of the regularization parameter $\lambda$ logarithmically spaced from $0.01 \lambda ^{\mathrm{max}}$ to $\lambda ^{\mathrm{max}}$, where $\lambda ^{\mathrm{max}} = \Vert A^Tb\Vert _\infty$ is the critical value of $\lambda$ above which the solution of the lasso problem is $x^\star =0$. In this case, we also set $\rho = \lambda$ to solve each instance. This example illustrates how the form of the graph projection splitting algorithm enables us to use cached factorizations to solve different problems more quickly.

We use the same implementation as above, but with $A \in \mathbf{R}^{5,000 \times 8,000}$ (substantially larger problem instances). We compute $AA^T$ and the Cholesky factorization $L$ of $I + AA^T$ once, and then re-use these cached computations across all the solves. We are able to solve the 10 instances in 22.5 s total. The computation of $AA^T$ and $L$ took 5.4 s, and the solve times for the individual instances ranged from 1.18 s (14 iterations) to 2.2 s (26 iterations). By comparison, solving the 10 instances without sharing $A$ and $L$ across instances (but still caching them within each instance) takes 71.5 s. In this setting, clearly, the vast majority of the time is spent computing $AA^T$ and $L$ once per instance. Finally, we note that 22.5 s is still substantially less time than needed to solve a single problem instance with CVX.

Distributed example.    We now solve three distributed instances of the lasso with the block splitting algorithm. We implemented block splitting above as written (with factorization caching) in C using MPI and the GNU Scientific Library linked against ATLAS [21]; the computations were done on Amazon EC2. We used Cluster Compute instances, which have 23 GB of RAM, two quad-core Intel Xeon X5570 ‘Nehalem’ chips, and are connected to each other with 10 Gigabit Ethernet. We used hardware virtual machine images running CentOS 5.4. Each node had 8 cores, and all the examples were run with a number of processes equal to the number of cores; for example, the experiment with 40 cores was run with 40 processes spread across 5 machines. The data was sized so all the processes on a single machine could work entirely in RAM. Each node had its own attached Elastic Block Storage (EBS) volume that contained only the local data relevant to that machine, so disk throughput was shared among processes on the same machine but not across machines. This is to emulate a scenario where each machine is only processing the data on its local disk, and none of the dataset is transferred over the network.

The results are summarized in Table 4. Here, the ‘factorization step’ refers to forming $A_{ij}A_{ij}^T$ and factoring $I + A_{ij}A_{ij}^T$ once, and the ‘main loop’ refers to all the iterations after the factorization has been cached. We take the $A_{ij}$ to be dense $3{,}000 \times 5{,}000$ blocks and then set $M$ and $N$ as needed to produce problems at different scales. For example, if $M = 4$ and $N = 2$, the total $A$ matrix is $12{,}000 \times 10{,}000$ and contains 120 million nonzero entries. Again, we use $MN$ processes spread across $MN$ processor cores to solve each problem instance. In general, larger problems do not necessarily require more iterations to solve, so in some cases, it is possible that larger problems can be solved with no increase in total solve time.

Table 4 Summary of timings for distributed lasso example

5.3 Intensity modulated radiation treatment planning

Recall that in the IMRT problem, $f$ is given by

$$\begin{aligned} f(y) = w^T(d^{\mathrm{min}}-y)_+ + v^T(y-d^{\mathrm{max}})_+ \end{aligned}$$

and $g$ is the indicator function of $[0, I^{\mathrm{max}}]^n$. The proximal operator of $f$ is given by

$$\begin{aligned} \left( \mathbf{prox}_f(y)\right) _i&= y_i - (y_i - d_i^{\mathrm{max}})_+ + (d_i^{\mathrm{min}} - y_i)_+\\&+\, (y_i - d_i^{\mathrm{max}} + v_i/\rho )_+ - (d_i^{\mathrm{min}} - w_i/\rho - y_i)_{+} \end{aligned}$$

and the proximal operator of $g$ is a simple projection that involves thresholding each entry of the argument to lie in $[0, I^{\mathrm{max}}]$. Both prox operators are fully separable, and so in principle they could be evaluated using the generic methods in [11, §6.1.4]; in any case, each component can be evaluated independently in parallel, so these operators can be evaluated in microseconds. As in the lasso example, then, the main computational effort will be in evaluating the graph projection, and as before, factorization caching provides substantial benefit. Indeed, in IMRT, the matrix often does not change across trials because the same hardware configuration is used repeatedly.

We require tumor regions to have a minimum dose of 0.9 units of radiation and a maximum dose of 1.5. Critical regions have a maximum dose of 0.1, while noncritical regions have a maximum dose of 0.5. We chose the weights $w = v = \mathbf 1$ to be uniform for all pixels. There are 20 parallel beams directed through the slice every 18 degrees, and the task is to adjust the beam strengths to minimize the total sum-of-violations in the slice. The maximum beam strength is $I^{\mathrm{max}} = 1$. Here, $m = 3,969$ and $n = 400$; the matrix $A$ is sparse, with 35,384 nonzero entries and a density of around 0.02. Figure 2 shows the radiation treatment plan solved using a standard cone solver compared to the ADMM solver. The cone solver took 66.6 s (25 iterations) to solve, while the ADMM solver completed in 0.5 s (153 iterations). As mentioned earlier, it would also be possible to change the weights in the objective and re-solve even more quickly by exploiting factorization caching and warm starting of the algorithm.

Fig. 2

Radiation treatment results. Left CVX solution. Right ADMM solution

6 Conclusion

We introduced a canonical problem form called graph form, in which we have two sets of variables $x$ and $y$ that are related by a linear operator $A$, such that the objective function is separable across these two sets of variables. We showed that this form arises naturally in many applications.

We then introduced an operator splitting method, graph projection splitting, to solve graph form problems in such a way that the linear and nonlinear components of the problem are handled separately. The main benefits of this approach are its amenability to scaling to very large-scale distributed optimization problems and the way in which it permits re-use of computation in handling the linear component.

There are some important issues not explored here. For example, it is not always clear how best to partition $A$ in practice. If $f$ and $g$ are fully separable, then in principle one can have separate machines handling each component of $A$. Of course, this would be extremely inefficient in practice, so it would be preferable to select larger blocks of $A$ to process on each machine, but it is not obvious how to select these. As a related point, it is not obvious how to select which subset of rows and columns are best to process together rather than on separate machines.

Sometimes a natural partitioning is clear. For example, if $A$ is so large that different blocks are already stored (or even collected) on separate machines, then one would likely just use this partitioning as given. In a machine learning problem, it is useful to have each block contain independent subsamples of the dataset; in this case, each local estimate of the parameters will be fairly close to the global solution even in the early iterations, and the method will converge to consensus more quickly.

Appendices

Appendix A: Implementing graph projections

Evaluating the projection $\Pi _A(c,d)$ involves solving the problem

$$\begin{aligned} \begin{array}{ll} \hbox {minimize} &{} (1/2)\Vert x - c\Vert _2^2 + (1/2)\Vert y - d\Vert _2^2 \\ \hbox {subject to} &{} y = Ax, \end{array} \end{aligned}$$

with variables $x \in \mathbf{R}^n$ and $y \in \mathbf{R}^m$.

This can be reduced to solving the KKT system

$$\begin{aligned} \begin{bmatrix} I&\quad 0&\quad A^T \\ 0&\quad I&\quad -I \\ A&\quad -I&\quad 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ \lambda \end{bmatrix} = \begin{bmatrix} c \\ d \\ 0 \end{bmatrix}, \end{aligned}$$

where $\lambda$ is the dual variable corresponding to the constraint $y = Ax$. Substituting $\lambda = y - d$ into the first equation and simplifying gives the system

$$\begin{aligned} \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} c + A^T d \\ 0 \end{bmatrix}. \end{aligned}$$

(10)

Indeed, we can rewrite the righthand side to show that solving the system simply involves applying a linear operator, as in (6):

$$\begin{aligned} \Pi _A(c,d) = \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix}^{-1} \begin{bmatrix} I&\quad A^T \\ 0&\quad 0 \end{bmatrix} \begin{bmatrix} c \\ d \end{bmatrix}. \end{aligned}$$

The coefficient matrix of (10), which we refer to as $K$, is quasidefinite [22] because the (1,1) block is diagonal positive definite and the (2,2) block is diagonal negative definite. Thus, evaluating $\Pi _{ij}$ involves solving a symmetric quasidefinite linear system. There are many approaches to this problem; we mention a few below.

1.1 A.1 Factor-solve methods

Block elimination.    By eliminating $x$ from the system above and then solving for $y$, we can solve (10) using the two steps

$$\begin{aligned} \begin{aligned} y&:= (I + AA^T)^{-1}(Ac + AA^T d)\\ x&:= c + A^T (d - y). \end{aligned} \end{aligned}$$

(11)

If instead we eliminate $y$ and then solve for $x$, we obtain the steps

$$\begin{aligned} \begin{aligned} x&:= (I + A^T A)^{-1} (c + A^T d) \\ y&:= Ax. \end{aligned} \end{aligned}$$

(12)

The main distinction between these two approaches is that the first involves solving a linear system with coefficient matrix $I + AA^T \in \mathbf{R}^{m \times m}$ while the second involves the coefficient matrix $I + A^T A \in \mathbf{R}^{n \times n}$.

To carry out the $y$-update in (11), we can compute the Cholesky factorization $I + AA^T = LL^T$ and then do the steps

$$\begin{aligned} \begin{aligned} w&:= L^{-1}(Ac + AA^T d) \\ y&:= L^{-T} w, \end{aligned} \end{aligned}$$

(13)

where $w$ is a temporary variable. The first step is computed via forward substitution, and the second is computed via back substitution. Carrying out the $x$-update in (12) can be done in an analogous manner.

When $A$ is dense, we would choose to solve whichever of (11) and (12) involves solving a smaller linear system, i.e., we would prefer (11) when $A$ is fat ($m < n$) and (12) when $A$ is skinny ($m > n$). In particular, if $A$ is fat, then computing the Cholesky factorization of $I + AA^T$ costs $O(nm^2)$ flops and the backsolve (13) costs $O(mn)$ flops; if $A$ is skinny, then computing the factorization of $I + A^T A$ costs $O(mn^2)$ flops and the backsolve costs $O(mn)$ flops. In summary, if $A$ is dense, then the factorization costs $O(\max \{m,n\} \min \{m,n\}^2)$ flops and the backsolve costs $O(mn)$ flops.

If $A$ is sparse, the question of which of (11) and (12) is preferable is more subtle, and requires considering the structure or entries of the matrices involved.

$\mathbf{LDL}^{T}$ factorization.    The quasidefinite system above can also be solved directly using a permuted $\hbox {LDL}^\mathrm{T}$ factorization [22–24]. Given any permutation matrix $P$, we compute the factorization

$$\begin{aligned} PKP^T = LDL^T, \end{aligned}$$

where $L$ is unit lower triangular and $D$ is diagonal. The factorization exists and is unique because $K$ is quasidefinite.

Explicitly, this approach would involve the following steps. Suppose for now that $P$ is given. We then form $PKP^T$ and compute its $\hbox {LDL}^\mathrm{T}$ factorization. In order to solve the system (10), we compute

$$\begin{aligned} \begin{bmatrix} x \\ y \end{bmatrix} = P^T L^{-T} D^{-1} L^{-1} P \begin{bmatrix} c + A^T d \\ 0 \end{bmatrix}, \end{aligned}$$

(14)

where applying $L^{-1}$ involves forward substitution and applying $L^{-T}$ involves backward substitution, as before; applying the other matrices is straightforward.

Many algorithms are available for choosing the permutation matrix; see, e.g., [25–27]. These algorithms attempt to choose $P$ to promote sparsity in $L$, i.e., to make the number of nonzero entries in $L$ as small as possible. When $A$ is sparse, the number of nonzero entries in $L$ is at least as many as in the lower triangular part of $A$, and the choice of $P$ determines which $L_{ij}$ become nonzero even when $A_{ij}$ is zero.

This method actually generalizes the two block elimination algorithms given earlier. In block form, the $\hbox {LDL}^\mathrm{T}$ factorization can be written

$$\begin{aligned} LDL^T&= \begin{bmatrix} L_{11}&\quad 0 \\ L_{21}&\quad L_{22} \end{bmatrix} \begin{bmatrix} D_1&\quad 0 \\0&\quad D_2 \end{bmatrix} \begin{bmatrix} L_{11}^T&\quad L_{21}^T \\ 0&\quad L_{22}^T \end{bmatrix}\nonumber \\&= \begin{bmatrix} L_{11} D_1 L_{11}^T&\quad L_{11}D_1 L_{21}^T \\ L_{21} D_1 L_{11}^T&\quad L_{21} D_1 L_{21}^T + L_{22} D_2 L_{22}^T \end{bmatrix}\!, \end{aligned}$$

where $D_i$ are diagonal and $L_{11}$ and $L_{22}$ are unit lower triangular.

We now equate $PKP^T$ with the $\hbox {LDL}^\mathrm{T}$ factorization when $P$ is the identity, i.e.,

$$\begin{aligned} \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix} = \begin{bmatrix} L_{11} D_1 L_{11}^T&\quad L_{11}D_1 L_{21}^T \\ L_{21} D_1 L_{11}^T&\quad L_{21} D_1 L_{21}^T + L_{22} D_2 L_{22}^T \end{bmatrix}. \end{aligned}$$

Since $I = L_{11} D_1 L_{11}^T$, it is clear that both $L_{11}$ and $D_1$ are the identity. Thus this equation simplifies to

$$\begin{aligned} \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix} = \begin{bmatrix} I&\quad L_{21}^T \\ L_{21}&\quad L_{21} L_{21}^T + L_{22} D_2 L_{22}^T \end{bmatrix}. \end{aligned}$$

It follows that $L_{21} = A$, which gives

$$\begin{aligned} \begin{bmatrix} I&\quad A^T \\ A&\quad -I \end{bmatrix} = \begin{bmatrix} I&\quad A^T \\ A&\quad AA^T + L_{22} D_2 L_{22}^T \end{bmatrix}. \end{aligned}$$

Finally, rearranging $-I = AA^T + L_{22} D_2 L_{22}^T$ gives that

$$\begin{aligned} I + AA^T = -L_{22} D_2 L_{22}^T. \end{aligned}$$

In other words, $L_{22} D_2 L_{22}^T$ is the negative of the $\hbox {LDL}^\mathrm{T}$ factorization of $I + AA^T$.

Now suppose

$$\begin{aligned} P = \begin{bmatrix} 0&\quad I \\ I&\quad 0 \end{bmatrix}. \end{aligned}$$

Then $P\!K\!P^T$ is given by

$$\begin{aligned} PKP^T = \begin{bmatrix} -I&\quad A \\ A^T&\quad I \end{bmatrix}. \end{aligned}$$

Equating this with the block $\hbox {LDL}^\mathrm{T}$ factorization above, we find that $L_{11} = I, D_1 = -I$, and $L_{21} = -A^T$. The $(2,2)$ block then gives that

$$\begin{aligned} I + A^T A = L_{22} D_2 L_{22}^T, \end{aligned}$$

i.e., $L_{22}D_2 L_{22}^T$ is the $\hbox {LDL}^\mathrm{T}$ factorization of $I + A^T A$.

In other words, applying the $\hbox {LDL}^\mathrm{T}$ method to $PKP^T$ directly reduces, for specific choices of $P$, to the simple elimination methods above (assuming we solve those linear systems using an $\hbox {LDL}^\mathrm{T}$ factorization). If $A$ is dense, then, there is no reason not to use (11) or (12) directly. If $A$ is sparse, however, it may be beneficial to use the more general method described here.

Factorization caching.    Since we need to carry out a graph projection in each iteration of the splitting algorithm, we actually need to solve the linear system (10) many times, with the same coefficient matrix $K$ but different righthand sides. In this case, the factorization of the coefficient matrix $K$ can be computed once and then forward-solve and back-solves can be carried out for each righthand side. Explicitly, if we factor $K$ directly using an $\hbox {LDL}^\mathrm{T}$ factorization, then we would first compute and cache $P, L$, and $D$. In each subsequent iteration, we could simply carry out the update (14).

Of course, this observation also applies to computing the factorizations of $I + AA^T$ or $I + A^T A$ if the steps (11) or (12) are used instead. In these cases, we would first compute and cache the Cholesky factor $L$, and then each iteration would only involve a backsolve.

This can lead to a large improvement in performance. As mentioned earlier, if $A$ is dense, the factorization step costs $O(\max \{m,n\} \min \{m,n\}^2)$ flops and the backsolve costs $O(mn)$ flops. Thus, factorization caching gives a savings of $O(\min \{m,n\})$ flops per iteration.

If $A$ is sparse, a similar argument applies, but the ratio between the factorization cost and the backsolve cost is typically smaller. Thus, we still obtain a benefit from factorization caching, but it is not as pronounced as in the dense case. The precise savings obtained depends on the structure of $A$.

1.2 A.2 Other methods

Iterative methods.    It is also possible to solve either the reduced (positive definite) systems or the quasidefinite KKT system using iterative rather than direct methods, e.g., via conjugate gradient or LSQR.

A standard trick to improve performance is to initialize the iterative method at the solution $(x^{k-1/2}, y^{k-1/2})$ obtained in the previous iteration. This is called a warm start. The previous iterate often gives a good enough approximation to result in far fewer iterations (of the iterative method used to compute the update $(x^{k+1/2}, y^{k+1/2})$) than if the iterative method were started at zero or some other default initialization. This is especially the case when the splitting algorithm has almost converged, in which case the updates will not change significantly from their previous values.

See [1, §4.3], for further comments on the use of iterative solvers, and various techniques for improving speed considerably over naive implementations.

Hybrid methods.    More generally, there are methods that combine elements of direct and iterative algorithms. For example, a direct method is often used to obtain a preconditioner for an iterative method like conjugate gradient. The term preconditioning refers to replacing the system $Ax = b$ with the system $M^{-1}Ax = M^{-1}b$, where $M$ is a well-conditioned (and symmetric positive definite, if $A$ is) approximation to $A$ such that $Mx = b$ is easy to solve. The difficulty is in balancing the requirements of minimizing the condition number of $M^{-1}A$ and keeping $Mx = b$ easy to solve, so there are a wide variety of choices for $M$ that are useful in different situations.

For instance, in the incomplete Cholesky factorization, we compute a lower triangular matrix $H$, with tractable sparsity structure, such that $H$ is close to the true Cholesky factor $L$. For example, we may require the sparsity pattern of $H$ to be the same as that of $A$. Once $H$ has been computed, the preconditioner $M = HH^T$ is used in, say, a preconditioned conjugate gradient method. See [28, 29] and [30, §10.3], for additional details and references.

Alternatively, we may use a direct method, but then carry out a few iterations of iterative refinement to reduce inaccuracies introduced by floating point computations; see, e.g., [30, §3.5.3], and [31, 32].

Appendix B: Derivations

Here, we discuss some details of the derivations needed to obtain the simplified block splitting algorithm. It is easy to see that applying graph projection splitting to (8) gives the original block splitting algorithm. The operators $\mathbf{avg}$ and $\mathbf{exch}$ are obtained as projections onto the sets $\{ (x, \{x_i\}_{i=1}^M) \mid x = x_i,\ i = 1, \dots , M\}$ and $\{ (y, \{y_j\}_{j=1}^N \mid y = \sum _{j=1}^N y_j \}$, respectively.

To obtain the final algorithm, we eliminate $\tilde{y}_{ij}^{k+1}$ and $x_{ij}^{k+1}$ and simplify some steps.

Simplifying y variables.    Substituting for $y_{ij}^{k+1}$ in the $\tilde{y}_{ij}^{k+1}$ update gives that

$$\begin{aligned} \textstyle \tilde{y}_{ij}^{k+1} := - \Big ( y_i^{k+1/2} + \tilde{y}_i^{k} - \sum \limits _{j=1}^N (y_{ij}^{k+1/2} + \tilde{y}_{ij}^{k}) \Big )/\left( N+1\right) , \end{aligned}$$

and similarly,

$$\begin{aligned} \textstyle \tilde{y}_{i}^{k+1} := \Big ( y_i^{k+1/2} + \tilde{y}_i^{k} - \sum \limits _{j=1}^N (y_{ij}^{k+1/2} + \tilde{y}_{ij}^{k}) \Big )/\left( N+1\right) . \end{aligned}$$

Since $\tilde{y}_i^{k+1} = -\tilde{y}_{ij}^{k+1}$ (for all $j$, for fixed $i$) after the first iteration, we eliminate the $\tilde{y}_{ij}^{k+1}$ updates and replace $\tilde{y}_{ij}^{k+1}$ with $-\tilde{y}_i^{k+1}$ in the graph projection and exchange steps. The exchange update for $y_i^{k+1}$ simplifies as follows:

$$\begin{aligned} y_{i}^{k+1}&:= \textstyle y_i^{k+1/2} + \tilde{y}_i^{k} - \Big ( y_i^{k+1/2} + \tilde{y}_i^{k} - \sum \limits _{j=1}^N (y_{ij}^{k+1/2} + \tilde{y}_{ij}^{k}) \Big ) / \left( N+1 \right) \\&= \textstyle y_i^{k+1/2} - \Big ( y_i^{k+1/2} - \sum \limits _{j=1}^N y_{ij}^{k+1/2} \Big ) / \left( N+1 \right) \\&= \mathbf{exch}(y_i^{k+1/2}, \{y_{ij}^{k+1/2}\}_{j=1}^N), \end{aligned}$$

i.e., there is no longer any dependence on the dual variables.

Simplifying x variables.    To lighten notation, we use $x_{ij}$ for $x_{ij}^{k+1/2}, x_{ij}^+$ for $x_{ij}^{k+1}, \tilde{x}_{ij}$ for $\tilde{x}_{ij}^k$, and $\tilde{x}_{ij}^+$ for $\tilde{x}_{ij}^{k+1}$. Adding together the dual updates for $\tilde{x}_{ij}^+$ (across $i$ for fixed $j$) and $\tilde{x}_j^+$, we get

$$\begin{aligned} \textstyle \tilde{x}_j^+ + \sum \limits _{i=1}^M \tilde{x}_{ij}^+ = \tilde{x}_j + x_j + \sum \limits _{i=1}^M \left( \tilde{x}_{ij} + x_{ij} \right) - \sum \limits _{i=1}^M \left( x_j^+ + \sum \limits _{i=1}^M x_{ij}^+ \right) . \end{aligned}$$

Since $x_{ij}^+ = x_j^+$ after the averaging step, this becomes

$$\begin{aligned} \textstyle \tilde{x}_j^+ + \displaystyle \sum \limits _{i=1}^M \tilde{x}_{ij}^+ = \tilde{x}_j + x_j + \displaystyle \sum \limits _{i=1}^M \left( \tilde{x}_{ij} + x_{ij} \right) - (M+1)x_j^+. \end{aligned}$$

Plugging

$$\begin{aligned} \textstyle x_j^+ = \Big (\tilde{x}_j + x_j + \sum \limits _{i=1}^M (\tilde{x}_{ij} + x_{ij}) \Big ) / \left( M+1 \right) \end{aligned}$$

into the righthand side shows that $\tilde{x}_j^+ + \sum _{i=1}^M \tilde{x}_{ij}^+ = 0$. Thus the averaging step simplifies to

$$\begin{aligned} (x_j^{k+1}, \{x_{ij}^{k+1}\}_{i=1}^M) := \mathbf{avg}(x_j^{k+1/2}, \{x_{ij}^{k+1/2}\}). \end{aligned}$$

Since $x_{ij}^{k+1} = x_j^{k+1}$ (for all $i$, for fixed $j$), we can eliminate $x_{ij}^{k+1}$, replacing it with $x_j^{k+1}$ throughout. Combined with the steps above, this gives the simplified block splitting algorithm given earlier in the paper.