1 Introduction

Distributed and parallel algorithms to solve optimization problems have gained more and more attention in the last decades. These have acquired an even larger importance since the amount of data available has grown exponentially. Beyond the evident effectiveness from a computational time perspective, some of these also allow the distribution of the data. Partitioning the data in blocks and assigning those blocks to separate processes is key not only for speeding up the computation, but also e.g. for privacy reasons [7, 11, 20, 37,38,39,40].

Unfortunately, only a small subset of the optimization algorithms in the literature presents the desirable property of being distributable. Moreover, such distributed algorithms usually assume that the feasible set is representable as a cartesian product of feasible sets, so that the variables are block-separable and each block has a private feasible set independent from the other blocks, even if the objective function depends on all the blocks [6, 8, 18]. However, these assumptions are not satisfied in many real big data applications like, e.g., support vector machines training. In particular, in the dual formulation of the training problem of support vector machines the presence of a linear equality constraint (i.e. a coupling constraint) over all the variables makes the distribution of the data uneasy [26, 28, 30, 31, 33].

A solution to the problem of the coupling constraints is to employ methods that allow including such constraints in the objective function, thus making the feasible set block-separable. The most well-known of such methods is probably the augmented Lagrangian method [5, 12, 13, 27]. We must mention that there are other efficient decomposition methods, like column generation and Frank-Wolfe methods, which use fast subsolvers and have been effectively employed in machine learning applications [19, 21, 23, 24, 29, 32].

Thanks to Lagrangian duality theory the coupling constraints can be included in the objective function and the problem solved by alternating a minimization over the primal variables and a maximization step over the Lagrangian multipliers [5, 6]. Augmented Lagrangian methods, although much used in practice, need solving (at least inexactly) a subproblem over the primal variables at each iteration. Solving a subproblem by using an iterative scheme at each iteration may be really inefficient. In these regards, one may think to modify the standard version of the augmented Lagrangian method [5] by employing a single minimization step instead of performing a minimization with respect to the primal variables. We show that this is not viable in general and we provide a counterexample showing the ineffectiveness of such naive modification.

To fill this gap, we propose a modified augmented Lagrangian method to solve convex problems with linear coupling constraints. This new method turns out to be distributable and at every iteration performs a single gradient projection step with respect to the primal variables. We give a formal convergence proof to at least \(\varepsilon \)-approximate solutions of the problem, namely points that have an objective value better or equal than the optimal one and violate the equality constraints by a quantity lower or equal than \(\varepsilon \). A detailed analysis of how the parameters of the algorithm influence the value of the approximation \(\varepsilon \) is also included. Furthermore, we sketch a distributed version of the algorithm, underlining how the data can be partitioned and assigned to separate processes that perform the computations independently, with minimal communication at the end of each iteration.

In Sect. 2 we detail the motivation for this work, in particular we define a general distributed scheme and we show how standard augmented Lagrangian methods can hardly be distributed; in Sect. 3 we present Algorithm 2 and we state the main convergence results in Theorem 1. In Sect. 4 we explore some technical results that are fundamental for the proof of Theorem 1. In particular we define a nonsmooth function \(\phi \) whose properties are explored in Propositions 1 and 2; in Proposition 3 we show that any minimal point of \(\phi \) is an \(\varepsilon \)-approximate solution of the problem; in Proposition 4 we show a strategy for updating the parameters of the algorithm leading to optimal solutions of the problem. In Sect. 5 we give the proof of Theorem 1. Finally, in Sect. 6 we sketch a distributed version of the algorithm and we discuss some conclusions in Sect. 7.

2 Motivation

We define the general formulation of the convex programming problem with linear coupling constraints:

$$\begin{aligned} \begin{array}{rl} \text {minimize } &{} f(x)\\ \text {s.t. } &{} h(x) \triangleq Ax - b = 0 \\ &{} x \in X, \end{array} \end{aligned}$$
(1)

where \(f \ \in \ C^{1,1}\) is convex with Lipschitz constant of \(\nabla f\) equal to \({\overline{L}}\), \(A \ \in \ {\mathbb {R}}^{m \times n}\), \(b \ \in \ {\mathbb {R}}^m\), and \(X \subseteq {\mathbb {R}}^n\) is convex, compact and encompasses a structure that is separable in N blocks, namely

$$\begin{aligned}X \triangleq \prod _{\nu = 1}^{N} X_{\nu },\end{aligned}$$

where \(X_{\nu } \subseteq {\mathbb {R}}^{n_{\nu }}\), with \(n \triangleq n_1 + \cdots + n_N\). For the sake of notational simplicity we denote the feasible set of Problem (1) with S. We observe that the set S is in general not separable due to the presence of the constraints h that may tie together variables of different blocks. For this reason we refer to h as the coupling constraints. We underline that the case with linear inequality constraints can be included in the above framework by simply adding slack variables.

We assume that S is non-empty. Therefore there exists an optimal solution \(x^{\star }\) such that

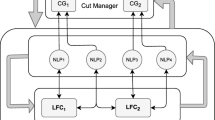
$$\begin{aligned} x^{\star }\ \in \ S, \qquad f(x^{\star }) \le f(x) \quad \forall \ x \ \in \ S. \end{aligned}$$

To compute \(x^{\star }\) one can resort to several numerical methods. We concentrate on (synchronous) distributed algorithms which structure is described in Fig. 1. Namely, in a distributed algorithm at every iteration the computation is split into N independent blocks that can be performed by different parallel processes, and a final communication phase allows synchronization among the processes.

Fig. 1
figure 1

General distributed algorithmic scheme

Full size image

Such a distribution of the computation is even more relevant when it makes it possible to partition the data defining the problem into N blocks that need to be known only by the respective processes. This is the case when the data comes from several sources and can not be stored in a unique place, for example when there exist privacy issues or the dimension of the data is huge.

One of the most well-known methods to solve Problem (1) is the classical gradient projection algorithm, see e.g. [4]:

$$\begin{aligned} x^{k+1} = {\mathscr {P}}_S \left[ x^k - \alpha _k \nabla f(x^k) \right] , \end{aligned}$$
(2)

where \(\alpha _k\) is a positive stepsize and \({\mathscr {P}}_S (z)\) denotes the projection of z over the convex set S. To guarantee the convergence of the algorithm defined by iteration (2), one can compute \(\alpha _k\) by employing a linesearch procedure, a diminishing stepsize rule, or by using a fixed, sufficiently small, stepsize \(\alpha _k = \alpha \ \in \ \left( 0,(2 / {\overline{L}}) \right) \) [2]. Unfortunately this method does not fall into the class of distributed algorithms because the projection on S, in general, cannot be decomposed with respect to the N blocks, see “Appendix A”.

Note however that in the special case in which there are no coupling constraints (i.e. \(m = 0\)) this task is easier. In fact in this case the projection can be performed in a distributed fashion and this scheme is a proper distributed algorithm, since the projection on S turns out to be a projection on the N sets \(X_{\nu }\) that are separate. With the additional assumption that the objective function \(f(x) = \frac{1}{2} x^T Q x + c^T x\) is quadratic, then the situation is even more favourable since also the data can be partitioned. Specifically, referring to the general scheme in Fig. 1, the vector of variables \(x \ \in \ {\mathbb {R}}^n\) can be partitioned into N blocks: \(x = \left( x_{(\nu )} \right) _{\nu = 1}^{N}\), with \(x_{(\nu )} \ \in \ {\mathbb {R}}^{n_{\nu }}\), \(\nu = 1,\ldots ,N\). Accordingly, \(\nabla f(x) = \left( \nabla f(x)_{(\nu )} \right) _{\nu = 1}^{N}\). In the situation cited above where \(m = 0\) and f is quadratic, the generic process \(\nu \) performs the following steps at any iteration k:

  1. (i)

    compute \(\nabla f(x^k)_{(\nu )} = \sum \limits _{\xi = 1}^N a^{\xi ,k}_{(\nu )} + c_{(\nu )}\) (where all the \(a^{\xi ,k}_{(\nu )}\) come from the communication phase at step (iii));

  2. (ii)

    compute \(x^{k+1}_{(\nu )} = {\mathscr {P}}_{X_{\nu }} \left[ x^k_{(\nu )} - \alpha \nabla f(x^k)_{(\nu )} \right] \);

  3. (iii)

    compute \(a^{\nu ,k+1} = Q_{*(\nu )} \ x^{k+1}_{(\nu )}\) and broadcast.

We observe that in this scheme the stepsize is fixed, and the computations up to process \(\nu \) are independent from those of the other blocks. Process \(\nu \) only needs to know the columns \(Q_{*(\nu )}\) of the matrix Q corresponding to the \(\nu \)-th block of variables, the \(\nu \)-th block \(c_{(\nu )}\) of vector c, and the set \(X_{\nu }\). Thus the data defining the problem can be partitioned and then distributed to the processes in the initialization phase. This plays a fundamental role in applications where either different pieces of information are available only to different processes or if the knowledge of such data requires significant computational burdens. The latter is the case of support vector machines training, because in its dual quadratic formulation a column of the matrix Q requires in general \({\mathscr {O}}(n^2)\) nonlinear calculations [28, 30]. Nonetheless, we underline that the above scheme is not directly applicable to the support vector machines quadratic formulation due to the presence of a coupling linear constraint (\(m = 1\)) [31].

In the general case where \(m > 0\), as explained above and in “Appendix A”, such simple distributed scheme with partitioned data cannot be employed due to the presence of the coupling constraints, which make S non-separable. One possible solution is to move the coupling constraints from the feasible set to the objective function, thus making the feasible set S separable since it reduces to X. This can be done by employing a Lagrangian method (see e.g. [4,5,6]). The well-known augmented Lagrangian function can be defined for Problem (1) as

$$\begin{aligned} {\mathscr {L}}_{\rho }(x,\mu ) \triangleq f(x) + \mu ^T h(x) + \frac{1}{2} \rho \Vert h(x)\Vert ^2, \end{aligned}$$
(3)

where \(\mu \ \in \ {\mathbb {R}}^m\) is the vector of Lagrangian multipliers, \(\rho > 0\) is the parameter of the penalty term, and \(\Vert \cdot \Vert \) denotes the euclidean norm. We recall that, in our framework, assuming the second-order sufficient conditions to hold at the optimal point of the problem with multipliers \(\mu ^*\), then a finite \(\rho ^*\) exists such that, for all \(\rho \ge \rho ^*\), the augmented Lagrangian with \(\mu = \mu ^*\) turns out to be an exact penalty function, see [34]. In a general augmented Lagrangian method (see e.g. [5] for an efficient version of such method) a solution of Problem (1) can be found by using the scheme described in Algorithm 1.

figure a

Algorithm 1 performs: at step 2 a minimization of the augmented Lagrangian function over X with respect to the variables x, at step 3 an ascent step for the augmented Lagrangian function with respect to \(\mu \) using the stepsize \(\beta _k\) with a projection over a nonempty convex compact set C, and at step 4 a possible increase of the penalty parameter \(\rho \). Convergence of such general scheme can be obtained by suitably choosing the sequence of positive steplengths \(\beta _k\) or by updating the penalty parameter \(\rho \) according to certain rules usually tied to the violation of the coupling constraints given by h. Actually, the minimization at step 2 can be also performed inexactly by computing \(x^{k+1}\) such that \({\mathscr {L}}_{\rho _k}(x^{k+1},\mu ^k) \le {\mathscr {L}}_{\rho _k}(x,\mu ^k) + \varepsilon _k\), for all \(x \ \in \ X\), with \(\varepsilon _k \downarrow 0\), maintaining convergence properties.

We notice that any single (inexact) minimization at step 2 of Algorithm 1 could be distributed by employing a scheme similar to the one described above for the case with \(m = 0\). In fact in this setting one can use e.g. a gradient projection method over X that is separable in N blocks. Therefore, the overall Algorithm 1, executing iteratively a distributed minimization over the variables x, can be viewed itself as a distributed algorithm (see e.g. [31, 37]). Nevertheless, solving an (inexact) optimization problem at each iteration may be numerically inefficient. The alternating direction method of multipliers suffers from the same inefficiency since it relies on a similar scheme where an (inexact) minimization with respect to the primal variables x must be performed at each iteration (see e.g. [6, 22]). One may try to substitute the (inexact) minimization at Step 2 of Algorithm 1 with one single gradient projection step and a stepsize updating rule such that the descent of the objective function at each iteration is guaranteed (a tipical choice is to set the stepsize equal to the inverse of the Lipschitz constant of the gradient with respect to x of the Lagrangian function). The following counterexample shows how this does not work in general.

Example 1

Let us consider the problem

$$\begin{aligned} \begin{array}{rl} \text {minimize } &{} x_1\\ \text {s.t. } &{} h(x) = x_1 - x_2 = 0 \\ &{} x \in [-1,1]^2, \end{array} \end{aligned}$$

which unique solution is \(x^{\star }= \left( \begin{array}{c} -1 \\ -1 \end{array} \right) \).

It is proved in [5] that Algorithm 1, with \(C = \{0\}\) and an updating rule for the penalty parameter \(\rho _{k+1} = 2 \rho _k\) if \(\Vert h(x^{k+1})\Vert ^2 > \tau \Vert h(x^k)\Vert ^2\), \(\rho _{k+1} = \rho _k\) otherwise, where \(\tau \ \in \ \left( 0,1 \right) \), globally converges to a solution of the problem. In this case \(\mu \) vanishes and the Lagrangian function is

$$\begin{aligned}{\mathscr {L}}_{\rho _k}(x) = x_1 + \frac{\rho _k}{2} \Vert x_1-x_2\Vert ^2,\end{aligned}$$

while its gradient can be written as

$$\begin{aligned} \nabla {\mathscr {L}}_{\rho _k}(x) = \left( \begin{array}{c} 1 + \rho _k (x_1-x_2) \\ \rho _k (x_2-x_1) \end{array} \right) . \end{aligned}$$

Let us see what happens by substituting step 2 with only one gradient projection step and a stepsize updating rule guaranteeing the descent of the objective function at each iteration. The modified version of the algorithm is then the following, for any iterate \(k \ge 0\):

  1. (i)

    \(\alpha _k = \frac{1}{{\overline{L}} + \rho _k \Vert A\Vert ^2} = \frac{1}{2 \rho _k}\);

  2. (ii)

    \(x^{k+1} = {\mathscr {P}}_{[-1,1]^2}\left[ x^k - \alpha _k \nabla {\mathscr {L}}_{\rho _k}(x^k) \right] \);

  3. (iii)

    \(\rho _{k+1} = 2 \rho _k\) if \(\Vert h(x^{k+1})\Vert ^2 > \tau \Vert h(x^k)\Vert ^2\); \(\rho _{k+1} = \rho _k\) otherwise.

In particular we choose \(\tau \ \in \ \left( 0,\frac{1}{4} \right) \), \(\rho _0 = 2\) and \(x^0 = \left( \begin{array}{c} 0 \\ \frac{1}{2} \end{array} \right) \). By simple calculations, we have, for any k, that condition \(\Vert h(x^{k})\Vert ^2 > \tau \Vert h(x^{k-1})\Vert ^2\) is always satisfied and:

$$\begin{aligned} \rho _{k}= & {} 2 \rho _{k-1} = 2^{k+1},\\ \nabla {\mathscr {L}}_{\rho _k}(x^k)= & {} \left( \begin{array}{c} 0 \\ 1 \end{array} \right) ,\\ x^k= & {} \left( \begin{array}{c} 0 \\ \frac{1}{2^{k+1}} \end{array} \right) ,\\ h(x^k)= & {} -x_2 = -\frac{1}{2^{k+1}}. \end{aligned}$$

But this implies

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } x^k = \left( \begin{array}{c} 0 \\ 0 \end{array} \right) \ne x^{\star }, \end{aligned}$$

that is, this modified version of the algorithm does not converge to a solution of the problem. \(\square \)

To fill this gap, in Sect. 3 we propose a nontrivial and globally convergent modification of Algorithm 1 to solve Problem (1) that is still distributable, but requires only a single gradient projection step with respect to the variables x at any iteration. The main idea underlying this new algorithm consists in avoiding the possible out of control growth of the penalty parameter \(\rho \), that is evident in Example 1, by introducing an upper bound on this parameter. Thus, in case the penalty parameter reaches its upper limit, the algorithm computes an approximate solution of the problem by performing gradient-like minimization steps for a suitable merit function that is introduced in Sect. 4.

3 A gradient projection method for the augmented Lagrangian reformulation

In this section we propose Algorithm 2, that is a gradient projection algorithm to solve the augmented Lagrangian reformulation of Problem (1). Algorithm 2 is characterized by two parameters, \({\widehat{\mu }} > 0\), used to define the compact set for the multipliers \(\mu ^k\), and \({\widehat{\rho }} > 0\), the upper bound for \(\rho _k\), which will play a key role in the effectiveness of computing a solution of Problem (1).

figure b

Algorithm 2 enjoys the following two nice properties:

  • the computation can be distributed and, moreover, if f is quadratic the data can be distributed too (see Sect. 2);

  • at each iteration k, only a gradient projection step over x is performed.

At step 2 the stepsize \(\alpha _k\) is updated, exploiting the value of \({{\widehat{k}}}\), such that:

  1. (i)

    on the one hand, whenever \({{\widehat{k}}} = k\) (i.e. \(\rho _k < {\widehat{\rho }}\)), it dynamically estimates the quantity \(1 / L_{\mathscr {L}}^k\), where \(L_{\mathscr {L}}^k = {\overline{L}} + \rho _k \Vert A\Vert ^2\) (with \({\overline{L}}\) being the Lipschitz constant of \(\nabla f\)) is the Lipschitz constant of \(\nabla _{x} {\mathscr {L}}_{\rho _k}(x^k,\mu ^k)\) over X;

  2. (ii)

    on the other hand, when \({{\widehat{k}}} < k\) (i.e. \(\rho _k = {\widehat{\rho }}\)), it ensures that \(\alpha _k \downarrow 0\) and \(\alpha _k\) is squared summable, but not summable, namely

    $$\begin{aligned} \sum _{k=0}^{\infty } \alpha _k^2 < \infty , \quad \sum _{k=0}^{\infty } \alpha _k = \infty . \end{aligned}$$
    (4)

It will be clear by the following sections that the convergence of the algorithm is based on the stepsize updating rule property defined in (4).

At step 3 a single gradient projection step is performed to update \(x^k\). The multipliers vector \(\mu ^k\) is updated either at step 5 if \(\rho _k < {\widehat{\rho }}\), or at step 8 otherwise. We observe that in the former case \(\mu ^{k+1}\) can be any element in the compact set \(M_{{\widehat{\mu }}} \triangleq \left[ -{\widehat{\mu }},{\widehat{\mu }}\right] ^m\), i.e. \(\mu ^k\) can be updated like in Algorithm 1. In the latter case, \(\mu ^{k+1}\) is such that

$$\begin{aligned} \mu ^{k+1} \in \arg \max _{\mu \in M_{{\widehat{\mu }}}} {\mathscr {L}}_{\rho _k}(x^{k+1},\mu ). \end{aligned}$$

Throughout the paper we will equivalently refer to the set \(M_{{\widehat{\mu }}}\) with the abbreviation M when the dependence on \({\widehat{\mu }}\) will not be of interest. Finally, at step 10 the penalty parameter \(\rho _k\), bounded above by \({\widehat{\rho }} > 0\), is increased if a sufficient decrease in the violation of the equality constraints is not achieved.

We observe that such an iterative scheme implies the boundedness of the generated sequence \(\{(x^k,\mu ^k,\rho _k)\}\). In Theorem 1 we show that Algorithm 2 converges in the worst case to an \(\varepsilon \)-approximate solution of Problem (1), i.e. a point \({\overline{x}}\) such that

$$\begin{aligned} {\overline{x}} \ \in \ X, \ \Vert h({\overline{x}})\Vert \le \varepsilon , \qquad f({\overline{x}}) \le f(x) \quad \forall \ x \ \in \ S. \end{aligned}$$

On the other hand, if \({\widehat{\rho }}\) is large enough, in the sense that the penalty parameter remains strictly below \({\widehat{\rho }}\), the algorithm provably converges to a solution \(x^{\star }\) of Problem (1), that is a 0-approximate solution. We underline that \(f({\overline{x}}) \le f(x^{\star })\), namely the value of the objective function at \({\overline{x}}\) is a lower bound of the optimal value. Furthermore, we can theoretically show (see Theorem 1) that the value of the feasibility relaxation parameter \(\varepsilon \) can be controlled by suitably choosing the parameters \({\widehat{\mu }}\) and \({\widehat{\rho }}\). It is expedient to define the following finite quantities:

$$\begin{aligned} f^{min} \triangleq \min \limits _{x \in X} f(x), \qquad f^{max} \triangleq \max \limits _{x \in X} f(x). \end{aligned}$$

Theorem 1

Let \(\{(x^k,\mu ^k,\rho _k)\}\) be the sequence generated by Algorithm 2 and \((\overline{x},{\overline{\mu }},{\overline{\rho }})\) be any of its limit points. Then we have two cases:

  1. 1.

    if \({\overline{\rho }} < \widehat{\rho }\), then \(\overline{x}\) is a solution of Problem (1);

  2. 2.

    otherwise, \({{\overline{\rho }}} = {\widehat{\rho }}\) and \(\overline{x}\) is an \(\varepsilon \)-approximate solution of Problem (1) with \(\varepsilon = \min \left\{ \frac{f^{max}-f^{min}}{\widehat{\mu }},\sqrt{\frac{f^{max}-f^{min}}{\widehat{\rho }}}\right\} \).

The proof of Theorem 1 is postponed to Sect. 5 since it requires some further theoretical developments, which are described in Sect. 4. In the light of Theorem 1, we observe that Algorithm 2 is in general inexact and the quality of the produced solution depends on the values of \({\widehat{\mu }}\) and \({\widehat{\rho }}\).

In Example 2 we show that the problem given in Example 1 is actually solved by employing Algorithm 2.

Example 2

Consider again the problem in Example 1. Let us assume again that the updating rule for the penalty parameter is \(\rho _{k+1} = 2 \rho _k\) if \(\Vert h(x^{k+1})\Vert ^2 > \tau \Vert h(x^k)\Vert ^2\), where \(\tau \ \in \ \left( 0,\frac{1}{4} \right) \), \(\rho _{k+1} = \rho _k\) otherwise. In this case we employ Algorithm 2 and we choose \({\widehat{\mu }} = 0\), \({\widehat{\rho }} = 2\), \(\gamma = \frac{1}{10}\), \(\delta = 1\). The Lagrangian function and its gradient are the same of Example 1.

Algorithm 2 performs the following updates for \(k \ge 0\):

  1. (i)

    \(\alpha _k = \dfrac{1}{{\overline{L}} + \rho _k \Vert A\Vert ^2 + \gamma (k-{{\widehat{k}}})} = \dfrac{1}{2 \rho _k + \gamma (k-{{\widehat{k}}})}\);

  2. (ii)

    \(x^{k+1} = {\mathscr {P}}_{[-1,1]^2}\left[ x^k - \alpha _k \nabla {\mathscr {L}}_{\rho _k}(x^k) \right] \);

  3. (iii)

    \(\rho _{k+1} = \min \{2 \rho _k, {\widehat{\rho }} \}\) if \(\Vert h(x^{k+1})\Vert ^2 > \tau \Vert h(x^k)\Vert ^2\), \(\rho _{k+1} = \rho _k\) otherwise.

We choose again \(\rho _0 = 2\) and \(x^0 = \left( \begin{array}{c} 0 \\ \frac{1}{2} \end{array} \right) \), that is the same starting point of Example 1 and for which the naive modification of Algorithm 1 does not converge. Then, by simple calculations, we have \(x^1 = \left( \begin{array}{c} 0 \\ \frac{1}{4} \end{array} \right) \) and, for any \(k \ge 1\), that \(\rho _k = {\widehat{\rho }} = 2\), \({{\widehat{k}}} = 0\) and \(\alpha _k = \frac{10}{40 + k}\). The sequence produced by the algorithm for \(k = 2,\dots ,9\) is the following:

$$\begin{aligned} x^k = \left( \begin{array}{c} -\frac{1}{2} \sum _{i=1}^{k-1} \alpha _i \\ \frac{1}{4}-\frac{1}{2} \sum _{i=1}^{k-1} \alpha _i \end{array} \right) . \end{aligned}$$

In \(k = 10\), \(x_1\) reaches its lower bound:

$$\begin{aligned} x^{10} = \left( \begin{array}{c} -1 \\ \frac{1}{4}-\frac{1}{2} \sum _{i=1}^{9} \alpha _i \end{array} \right) . \end{aligned}$$

For \(k \ge 11\),

$$\begin{aligned} x^k = \left( \begin{array}{c} -1 \\ \left( \frac{1}{4}-\frac{1}{2} \sum _{i=1}^{9} \alpha _i \right) \left( \prod _{i=10}^{k-1} \left( 1 - 2 \alpha _i \right) \right) - \sum _{i=10}^{k-1} 2 \alpha _i \left( \prod _{j=i+1}^{k-1} \left( 1 - 2 \alpha _j \right) \right) \end{array} \right) . \end{aligned}$$

Such sequence \(\left\{ x^k \right\} \) converges (from above) to the optimal solution \( x^{\star }= \left( \begin{array}{c} -1 \\ -1 \end{array} \right) \). \(\square \)

We remark that the new method presented in this work is a subgradient-type scheme for which the convergence speed depends strongly on the stepsize. In particular, if the Lipschitz constant \({\overline{L}}\) or the parameter \({\widehat{\rho }}\) are large, the stepsize can be very small. E.g. in the presented Example 2 the convergence is slow.

4 Technical results

In order to prove part 2 of Theorem 1, we introduce and analyze a nonsmooth value function \(\phi _{\widehat{\mu },\widehat{\rho }}\) that is related to the Lagrangian function (3) and to Problem (1):

$$\begin{aligned} \phi _{\widehat{\mu },\widehat{\rho }}(x) \triangleq f(x) + \widehat{\mu } \Vert h(x)\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(x)\Vert ^2. \end{aligned}$$
(5)

Notice that it depends on the same parameters \(\widehat{\mu }\) and \(\widehat{\rho }\) defined in Algorithm 2, and is useful for the subsequent analysis.

First of all we analyze the properties of the nonsmooth value function \(\phi _{\widehat{\mu },\widehat{\rho }}\).

Proposition 1

Let \(\widehat{\mu },\widehat{\rho } \ge 0\). The function \(\phi _{\widehat{\mu },\widehat{\rho }}\) is convex and locally Lipschitz continuous.

Proof

It is well known that a sum of convex functions is convex. Thus the proof follows by noticing that f is convex by assumption, \(\Vert h(x)\Vert _1 = \Vert Ax - b\Vert _1 = \sum \limits _{i=1}^m |A_{i *}x - b_i| = \sum \limits _{i=1}^m \max \{ A_{i *}x - b_i, - A_{i *}x + b_i \}\) is convex, and \(\Vert h(x)\Vert ^2 = x^TA^TAx - 2b^TAx + b^Tb\) is convex. The proof of the local Lipschitz continuity follows by recalling that any convex function is locally Lipschitz continuous, see e.g. [10, Proposition 2.2.6]. \(\square \)

Note that the role of the linearity of h is fundamental for the convexity of the nonsmooth function \(\phi _{\widehat{\mu },\widehat{\rho }}\).

Proposition 2

The subdifferential \(\partial \phi _{\widehat{\mu },\widehat{\rho }}(x)\) is non-empty and

$$\begin{aligned} \nabla f(x) + {\widehat{\mu }} \sum \limits _{i=1}^m \xi _i + {\widehat{\rho }} \nabla h(x) h(x) \in \partial \phi _{\widehat{\mu },\widehat{\rho }}(x), \end{aligned}$$

with

$$\begin{aligned} \xi _i \ \in \ {\left\{ \begin{array}{ll} \{A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i > 0, \\ \{-A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i < 0, \\ conv\{-A_{i *}^T,A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i = 0, \end{array}\right. } \end{aligned}$$

where \(conv\{x,y\}\) denotes the convex hull of the vectors \(x,y \ \in \ {\mathbb {R}}^n\).

Proof

From [10, Corollary 3], the subdifferential of the sum of convex functions equals the sum of the subdifferentials of the functions. Therefore we can write

$$\begin{aligned} \partial \phi _{\widehat{\mu },\widehat{\rho }}(x) = \partial f(x) + \widehat{\mu } \partial \Vert h(x)\Vert _1 + \frac{{\widehat{\rho }}}{2} \partial \Vert h(x)\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \partial f(x)= & {} \nabla f(x), \qquad \partial \Vert h(x)\Vert ^2 = 2 \nabla h(x) h(x) = 2A^T (Ax - b),\\ \partial \Vert h(x)\Vert _1= & {} \left( \sum \limits _{i=1}^m \partial |A_{i *} x - b_i| \right) = \left( \sum \limits _{i=1}^m \partial \max \{A_{i *} x - b_i,- A_{i *} x + b_i\} \right) \ni \sum \limits _{i=1}^m \xi _i, \end{aligned}$$

with

$$\begin{aligned} \xi _i \ \in \ {\left\{ \begin{array}{ll} \{A_{i *}^T\}, &{} A_{i *} x - b_i > 0, \\ \{-A_{i *}^T\}, &{} A_{i *} x - b_i < 0, \\ conv\{-A_{i *}^T,A_{i *}^T\}, &{} A_{i *} x - b_i = 0, \end{array}\right. } \end{aligned}$$

(see e.g. [35, Exercise 8.31]). \(\square \)

The following proposition proves that minimal points of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) over X are \(\varepsilon \)-approximate solutions of Problem (1) with \(\varepsilon = \min \left\{ \frac{f^{max}-f^{min}}{\widehat{\mu }},\sqrt{\frac{f^{max}-f^{min}}{\widehat{\rho }}}\right\} \).

Proposition 3

Given \(\widehat{\mu } > 0\) and \(\widehat{\rho } > 0\), for any minimal point \(\overline{x}\) of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) over X, it holds that:

  1. 1.

    \(f(\overline{x}) \le f(x^{\star }),\)

  2. 2.

    \(\Vert h(\overline{x})\Vert \le \min \left\{ \frac{f^{max}-f^{min}}{\widehat{\mu }},\sqrt{\frac{f^{max}-f^{min}}{\widehat{\rho }}}\right\} ,\)

where \(x^{\star }\) is a solution of Problem (1), \(f^{min} = \min \limits _{x \in X} f(x)\) and \(f^{max} = \max \limits _{x \in X} f(x)\).

Proof

We first show the first inequality. It holds that

$$\begin{aligned} f(\overline{x}) \le f(\overline{x}) + {\widehat{\mu }} \Vert h(\overline{x})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(\overline{x})\Vert ^2 \le f(x^{\star }) + {\widehat{\mu }} \Vert h(x^{\star })\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(x^{\star })\Vert ^2 = f(x^{\star }), \end{aligned}$$

by recalling that \({\widehat{\mu }} \Vert h(\overline{x})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(\overline{x})\Vert ^2 \ge 0\), that \(x^{\star }\ \in \ X\) and that \(h(x^{\star }) = 0\). This proves the first assertion of this proposition.

Let us now prove the second assertion. Let \({\widetilde{x}} \ \in \ X\) such that \(h({\widetilde{x}}) = 0\), namely \({\widetilde{x}}\) is any feasible point of Problem (1). Then we can write

$$\begin{aligned} f^{min} \le f(\overline{x}) \quad \text {and} \quad f({\widetilde{x}}) + {\widehat{\mu }} \Vert h({\widetilde{x}})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h({\widetilde{x}})\Vert ^2 = f({\widetilde{x}}) \le f^{max}. \end{aligned}$$

From the two inequalities above, we can write

$$\begin{aligned}&f^{min} + \widehat{\mu } \Vert h(\overline{x})\Vert _1 \le f(\overline{x}) + \widehat{\mu } \Vert h(\overline{x})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(\overline{x})\Vert ^2 \le f({\widetilde{x}}) + \widehat{\mu } \Vert h({\widetilde{x}})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h({\widetilde{x}})\Vert ^2 \\&\quad \le f^{max}, \end{aligned}$$

implying

$$\begin{aligned} \Vert h(\overline{x})\Vert \le \Vert h(\overline{x})\Vert _1 \le \frac{f^{max}-f^{min}}{\widehat{\mu }}. \end{aligned}$$

On the other hand,

$$\begin{aligned}&f^{min} + \frac{\widehat{\rho }}{2} \Vert h(\overline{x})\Vert ^2 \le f(\overline{x}) + \widehat{\mu } \Vert h(\overline{x})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h(\overline{x})\Vert ^2 \le f({\widetilde{x}}) + \widehat{\mu } \Vert h({\widetilde{x}})\Vert _1 + \frac{\widehat{\rho }}{2} \Vert h({\widetilde{x}})\Vert ^2 \\&\quad = f({\widetilde{x}}) \le f^{max}, \end{aligned}$$

from which

$$\begin{aligned} \Vert h(\overline{x})\Vert ^2 \le \frac{f^{max}-f^{min}}{\widehat{\rho }}, \end{aligned}$$

which completes the proof. \(\square \)

Furthermore, if a minimal point of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) is also feasible for Problem (1), then it is a solution of Problem (1).

Corollary 1

Let the same setting of Proposition 3 applies. Then, if \(\overline{x}\) is such that \(\Vert h(\overline{x})\Vert = 0\), \(\overline{x}\) is a solution of Problem (1).

Proof

From Proposition 3, it holds that

$$\begin{aligned} f(\overline{x}) \le f(x^*), \end{aligned}$$

where \(x^*\) is a solution of Problem (1). The proof follows by recalling the hypothesis, from which we have \(h(\overline{x}) = 0\). \(\square \)

We now want to provide a counterexample of how an \(\varepsilon \)-approximate solution of Problem (1) may not be a solution of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) over X, that is, the vice versa of Proposition 3 does not hold in general.

Example 3

Let us consider the problem

$$\begin{aligned} \begin{array}{rl} \text {minimize } &{} x^2 \\ \text {s.t. } &{} h(x) = x - 1 = 0 \\ &{} x \in [0,2], \end{array} \end{aligned}$$

which trivial solution is \(x^{\star }= 1\). By definition, this is an \(\varepsilon \)-approximate solution for any \(\varepsilon > 0\).

The corresponding \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) if we fix \(\widehat{\mu } = 1, \widehat{\rho } = 0\) is

$$\begin{aligned} \phi _{1,0}(x) = x^2 + |x-1|, \end{aligned}$$

which unique solution over [0, 2] is \(\overline{x} = \frac{1}{2}\), that is different from \(x^{\star }\).

Note that by letting \(\widehat{\mu }\) grow to infinity, the solution of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) gets closer and closer to the minimizer of \(|x-1|\), which is the solution of the original problem. This will be better formalized in the next proposition. \(\square \)

Proposition 3 shows that a minimizer of \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) is an \(\varepsilon \)-approximate solution of Problem (1). Specifically, the bigger the parameters \({\widehat{\mu }}\) and \({\widehat{\rho }}\) are, the smaller the value of the feasibility relaxation parameter \(\varepsilon \) is. The next proposition formally states that if one of the parameters goes to infinity, then \(\varepsilon \) goes to zero.

Proposition 4

Let \(\{\overline{x}^k\}\) be a sequence of minimizers of \(\phi _{\widehat{\mu }^k,\widehat{\rho }^k}(x)\) over X. If either \(\lim \limits _{k \rightarrow \infty } \widehat{\mu }^k = \infty \) or \(\lim \limits _{k \rightarrow \infty } \widehat{\rho }^k = \infty \), then any accumulation point \(\overline{x}\) of the sequence \(\{\overline{x}^k\}\) is a solution of Problem (1).

Proof

Let us assume, without loss of generality, that the first limit applies. By Proposition 3, it holds for any k that

$$\begin{aligned} \overline{x}^k \ \in \ X, \quad f(\overline{x}^k) \le f(x^*), \quad \Vert h(\overline{x}^k)\Vert \le \frac{f^{max}-f^{min}}{\widehat{\mu }^k}. \end{aligned}$$

By the continuity of \(\Vert h(\overline{x}^k)\Vert \), we can write

$$\begin{aligned} \Vert h(\overline{x})\Vert = \lim \limits _{k \rightarrow \infty } \Vert h(\overline{x}^k)\Vert \le \lim \limits _{k \rightarrow \infty } \frac{f^{max}-f^{min}}{\widehat{\mu }^k} = 0 \end{aligned}$$

and therefore \(h(\overline{x}) = 0\). Similarly, by recalling that \(x^{\star }\) is a solution of Problem (1), we can write \(f(\overline{x}) \le f(x^{\star })\). \(\square \)

We are now ready to give the proof of Theorem 1.

5 Proof of Theorem 1

In this section we give the proof of Theorem 1.

Proof

We start by proving the first assertion of the theorem, namely that if \({{\overline{\rho }}} < {\widehat{\rho }}\) then \({\overline{x}}\) is a solution of Problem (1).

Recalling step 10 of Algorithm 2, if \({{\overline{\rho }}} < {\widehat{\rho }}\) then a \(\overline{k} \ge 0\) exists such that for all \(k \ge \overline{k}\)

$$\begin{aligned} \Vert h(x^{k+1})\Vert \le \tau \Vert h(x^k)\Vert < \Vert h(x^k)\Vert , \end{aligned}$$
(6)

by recalling that \(\tau \ \in \ (0,1)\). This yields, together with the positiveness of the sequence \(\{\Vert h(x^k)\Vert \}\), that

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } \Vert h(x^k)\Vert = \overline{h} \ge 0. \end{aligned}$$

Taking the limit for \(k \rightarrow \infty \) in (6), we get

$$\begin{aligned} \overline{h} \le \tau \overline{h}, \end{aligned}$$

which, since \(\tau \ \in \ (0,1)\), is true only if \(\overline{h} = 0\). Therefore, by the continuity of h, we have proved that

$$\begin{aligned} h({\overline{x}}) = 0. \end{aligned}$$
(7)

Moreover, recalling a well-known property of the projection operator, it holds for all \(z \ \in \ {\mathbb {R}}^n\)

$$\begin{aligned} \left( y - {\mathscr {P}}_X[z] \right) ^T \left( z - {\mathscr {P}}_X[z] \right) \le 0 \quad \forall y \ \in \ X. \end{aligned}$$

Therefore we can write

$$\begin{aligned}&\left( x^k - {\mathscr {P}}_X[x^k - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)] \right) ^T \left( x^k - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k) - {\mathscr {P}}_X[x^k \right. \\&\quad \left. - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)] \right) \le 0, \end{aligned}$$

and by expanding the products

$$\begin{aligned}&\left\| x^k - {\mathscr {P}}_X[x^k - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)] \right\| ^2 \\&\quad + \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)^T \left( {\mathscr {P}}_X[x^k - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)] - x^k \right) \le 0,\end{aligned}$$

from which, by recalling that \(x^{k+1} = {\mathscr {P}}_X[x^k - \alpha _k \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)]\), we get

$$\begin{aligned} \nabla _x {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)^T \left( x^{k+1} - x^k \right) \le -\frac{1}{\alpha _k} \left\| x^{k+1} - x^k \right\| ^2. \end{aligned}$$
(8)

The descent lemma [4, Lemma 2.1] and (8) therefore yield

$$\begin{aligned} {\mathscr {L}}_{{{\overline{\rho }}}}(x^{k+1},\mu ^k) - {\mathscr {L}}_{{{\overline{\rho }}}}(x^k,\mu ^k)&\le \nabla _x {\mathscr {L}}_{\rho _k}(x^k,\mu ^k)^T (x^{k+1} - x^k) + \frac{L_{\mathscr {L}}^k}{2} \Vert x^{k+1} - x^k\Vert ^2 \\&\le - \left( \frac{1}{\alpha _k} - \frac{L_{{\mathscr {L}}}^k}{2} \right) \Vert x^{k+1} - x^k\Vert ^2 \end{aligned}$$

and consequently

$$\begin{aligned}&f(x^{k+1}) - f(x^k) + {\mu ^k}^T(h(x^{k+1}) - h(x^k)) + \frac{{\overline{\rho }}}{2}(\Vert h(x^{k+1})\Vert ^2-\Vert h(x^k)\Vert ^2) \\&\quad \le -\frac{\overline{L} + {\overline{\rho }} \Vert A\Vert ^2}{2} \Vert x^{k+1}-x^k\Vert ^2. \end{aligned}$$

By taking the limit for \(k \rightarrow \infty \) of the above inequality we get

$$\begin{aligned}&\lim \limits _{k \rightarrow \infty } (f(x^{k+1}) - f(x^k)) + \left( \lim \limits _{k \rightarrow \infty } \mu ^k\right) ^T (\overline{h} - \overline{h}) + \frac{{\overline{\rho }}}{2}(\Vert \overline{h}\Vert ^2-\Vert \overline{h}\Vert ^2)\\&\quad \le -\frac{\overline{L} + {\overline{\rho }} \Vert A\Vert ^2}{2} \lim \limits _{k \rightarrow \infty } \Vert x^{k+1}-x^k\Vert ^2, \end{aligned}$$

from which we can write

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } \left( f(x^{k+1}) - f(x^k) \right) \le 0. \end{aligned}$$

This yields

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } f(x^{k}) = f({\overline{x}}) = {\overline{f}}, \end{aligned}$$

because f is continuous and bounded from below over X. It follows that

$$\begin{aligned} \lim \limits _{k \rightarrow \infty } \Vert x^{k+1}-x^k\Vert ^2 = 0. \end{aligned}$$

Focusing on step 3 of the algorithm, by the limit above and since \(\alpha _k = {{\overline{\alpha }}} = \frac{1}{{\overline{L}} + {{\overline{\rho }}} \Vert A\Vert ^2}\) for all \(k \ge {\overline{k}}\), this yields

$$\begin{aligned} \nabla _x {\mathscr {L}}_{{\overline{\rho }}}(\overline{x},{\overline{\mu }}) ^T (x - \overline{x}) \ge 0 \qquad \forall \ x \ \in \ X. \end{aligned}$$
(9)

Let us suppose by contradiction that \({\overline{f}}\) is greater than the optimal value of Problem (1). Therefore a point \({{\widetilde{x}}} \in X\) exists such that \(h({{\widetilde{x}}}) = 0\) and \(f({{\widetilde{x}}}) < {\overline{f}} = f({\overline{x}})\). We can write

$$\begin{aligned} 0 \le \left( \nabla f({\overline{x}}) + A^T {\overline{\mu }} \right) ^T ({{\widetilde{x}}} - {\overline{x}}) = \nabla f({\overline{x}})^T ({{\widetilde{x}}} - {\overline{x}}) \le f({{\widetilde{x}}}) - f({\overline{x}}) < 0, \end{aligned}$$

where the first inequality comes from (9), the equality is a consequence of the fact that \(h({{\widetilde{x}}}) = 0\) and (7), the second inequality is due to the convexity of f and the last inequality comes from the hypotheses that \({\overline{x}}\) is not optimal and \({{\widetilde{x}}}\) is optimal. But this is impossible. Finally, \({\overline{x}}\) is a solution of Problem (1) and this completes the proof of the first part.

We now prove the second assertion, i.e. if \({{\overline{\rho }}} = {\widehat{\rho }}\) then \({\overline{x}}\) is an \(\varepsilon \)-approximate solution of Problem (1) with \(\varepsilon = \min \left\{ \frac{f^{max}-f^{min}}{\widehat{\mu }},\sqrt{\frac{f^{max}-f^{min}}{\widehat{\rho }}}\right\} \). First we need to prove that the updates at steps 3 and 8 of Algorithm 2 are eventually equivalent to employ a gradient projection method to minimize the nonsmooth function \(\phi _{\widehat{\mu },\widehat{\rho }}(x)\), defined in (5), over X. In Proposition 2 we proved that the subdifferential of \(\phi \) satisfies for all \(x \ \in \ X\)

$$\begin{aligned} \nabla f(x) + {\widehat{\mu }} \sum \limits _{i=1}^m \xi _i + {\widehat{\rho }} \nabla h(x) h(x) \in \partial \phi _{\widehat{\mu },\widehat{\rho }}(x), \end{aligned}$$

with

$$\begin{aligned} \xi _i \ \in \ {\left\{ \begin{array}{ll} \{A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i > 0, \\ \{-A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i < 0, \\ conv\{-A_{i *}^T,A_{i *}^T\}, &{} \text {if } A_{i *} x - b_i = 0. \end{array}\right. } \end{aligned}$$

The gradient of \({\mathscr {L}}_{{\widehat{\rho }}}(x^k,\mu ^k)\) with respect to x is

$$\begin{aligned} \nabla {\mathscr {L}}_{{\widehat{\rho }}}(x^k,\mu ^k) = \nabla f(x^k) + A^T \mu ^k + {\widehat{\rho }} \nabla h(x) h(x), \end{aligned}$$

where, recalling the update rule of \(\mu ^k\) at step 8 of Algorithm 2, \(A^T \mu ^k\) can be rewritten as

$$\begin{aligned} A^T \mu ^k = \sum \limits _{i=1}^m \mu ^k_i A_{i *}^T = {\widehat{\mu }} \left( \sum \limits _{i:h_i(x^k) \ge 0} A_{i *}^T + \sum \limits _{i:h_i(x^k) < 0} -A_{i *}^T \right) = {\widehat{\mu }} \sum \limits _{i=1}^m \psi _i, \end{aligned}$$

where

$$\begin{aligned} \psi _i = {\left\{ \begin{array}{ll} A_{i *}^T, &{} \text {if } A_{i *} x - b_i \ge 0, \\ -A_{i *}^T, &{} \text {if } A_{i *} x - b_i < 0, \end{array}\right. } \end{aligned}$$

which yields

$$\begin{aligned} \nabla _x {\mathscr {L}}_{{\widehat{\rho }}}(x^k,\mu ^k) \in \partial _x \phi _{\widehat{\mu },{\widehat{\rho }}}(x^k), \qquad \forall \ k \ge {{\widehat{k}}}. \end{aligned}$$

We just proved that step 3 of Algorithm 2 is eventually equivalent to employ a gradient projection method to minimize the nonsmooth function \(\phi _{\widehat{\mu },\widehat{\rho }}(x)\), which is a convex and Lipschitz-continuous function by Proposition 1. About the stepsize, since \({{\widehat{k}}}\) is fixed and finite, we get

$$\begin{aligned} \sum _{k=0}^\infty \alpha _k = \sum _{k=0}^{{{\widehat{k}}}} \frac{1}{\overline{L} + \rho _k \Vert A\Vert ^2} + \frac{1}{\gamma } \sum _{k=1}^{\infty } \frac{1}{k+\left( \frac{\overline{L} + {\widehat{\rho }} \Vert A\Vert ^2}{\gamma }\right) } \ge \frac{1}{\gamma } \sum _{k=\Bigl \lceil \frac{\overline{L} + {\widehat{\rho }} \Vert A\Vert ^2}{\gamma } \Bigr \rceil + 1}^{\infty } \frac{1}{k} = \infty , \end{aligned}$$

and

$$\begin{aligned} \sum _{k=0}^\infty \alpha _k^2= & {} \sum _{k=0}^{{{\widehat{k}}}} \left( \frac{1}{\overline{L} + \rho _k \Vert A\Vert ^2} \right) ^2 + \frac{1}{\gamma ^2} \sum _{k=1}^{\infty } \left( \frac{1}{k+\left( \frac{\overline{L} + {\widehat{\rho }} \Vert A\Vert ^2}{\gamma }\right) } \right) ^2 \\\le & {} \left( {{\widehat{k}}}+1 \right) \left( \frac{1}{\overline{L} + \rho _0 \Vert A\Vert ^2} \right) ^2 + \frac{1}{\gamma ^2} \sum _{k=1}^{\infty } \frac{1}{k^2} < \infty . \end{aligned}$$

Therefore the rule in (4) is fulfilled. This implies that \(\overline{x}\) is a minimizer for \(\phi _{\widehat{\mu },{\widehat{\rho }}}\) over X, see e.g. [3, Theorem 3.2.6]. The proof follows by Proposition 3. \(\square \)

We remark the following facts:

  1. (i)

    the updating rule for the stepsize \(\alpha _k\) defined in step 2 of Algorithm 2 can be modified, as long as it satisfies (4) when \(\rho _k = {\widehat{\rho }}\), namely it must be squared summable, but not summable;

  2. (ii)

    as long as \(\rho _k < {\widehat{\rho }}\), the update rule for the multipliers at step 5 does not play any role and therefore any bounded \(\mu _k\) is acceptable; this can be useful in the first phase of Algorithm 2 where different updating rules for \(\mu _k\) can be developed;

  3. (iii)

    Algorithm 2, with \({\widehat{\mu }} = 0\), can be viewed as a modified version of a sequential penalty algorithm and therefore the above theoretical analysis can be directly applied also to such framework.

6 A distributed version of Algorithm 2

In this section we want to sketch a distributed version of Algorithm 2 similar to the one described in Sect. 2. Our aim in particular is to consider the case of a quadratic objective \(f(x) = \frac{1}{2} x^T Qx + c^T x\), which will allow distribution of the data too. Namely, we want to be able to perform Algorithm 2 in a distributed fashion where each process, indexed by \(\nu = 1,\ \ldots ,\ N\),

  • acts only on a block of variables \(x_{(\nu )} \ \in \ {\mathbb {R}}^{n_{\nu }}\),

  • stores only its own data, i.e. the columns \(Q_{*(\nu )} \ \in \ {\mathbb {R}}^{n \times n_{\nu }}\) of the matrix \(Q \ \in \ {\mathbb {R}}^{n \times n}\), \(c_{(\nu )}\), \(X_{\nu }\) and \(A_{*(\nu )}\), and does not need to know the data blocks of the other processes,

  • communicates with the other processes in order to get convergence to a (\(\varepsilon \)-approximate) solution of Problem (1).

In this framework, we recall that we can write the gradient of the objective function f as \(\nabla f(x) = \left( \nabla f(x)_{(\nu )} \right) _{\nu = 1}^{N}\). A possible distributed implementation is the following, where the generic process \(\nu \) performs the following steps at any iteration k:

  1. (i)

    compute \(\alpha _k = \frac{1}{\overline{L} + \rho _k \Vert A\Vert ^2 + \gamma (k-{\widehat{k}})}\)

  2. (ii)

    compute \(h(x^k) = \sum \limits _{\xi = 1}^N h^{\xi ,k} - b\) (where all the \(h^{\xi ,k} = A_{*(\xi )} \ x^{k}_{(\xi )}\) come from the communication phase at step (ix))

  3. (iii)

    compute \(\mu _i^k = \max \left\{ -{\widehat{\mu }}, \min \left\{ {\widehat{\mu }}, \mu _i^{k-1} + \frac{1}{\Vert A\Vert } h_i(x^{k}) \right\} \right\} \) if \(\rho _{k-1} < {\widehat{\rho }}\), and \(\mu _i^k = {\left\{ \begin{array}{ll} -\widehat{\mu }, &{} i \ : \ h_i(x^k) < 0, \\ \widehat{\mu }, &{} otherwise, \end{array}\right. }\) otherwise, for all \(i = 1,\ \dots ,\ m\);

  4. (iv)

    compute \(\rho _k = {\left\{ \begin{array}{ll} \min \{\rho _{k-1} + \delta , \ \widehat{\rho }\}, &{} \Vert h(x^k)\Vert > \tau \Vert h(x^{k-1})\Vert , \\ \rho _{k-1}, &{} otherwise; \end{array}\right. }\)

  5. (v)

    compute \(\nabla {\mathscr {L}}_{\rho _k}(x^k,\mu ^k)_{(\nu )} = \sum \limits _{\xi = 1}^N a^{\xi ,k}_{(\nu )} + c_{(\nu )} + A_{*(\nu )}^T \mu ^k + \rho _k A_{*(\nu )}^T h(x^k)\) (where all the \(a^{\xi ,k} = Q_{*(\xi )} \ x^{k}_{(\xi )}\) come from the communication phase at step (viii));

  6. (vi)

    compute \(x^{k+1}_{(\nu )} = {\mathscr {P}}_{X_{\nu }} \left[ x^k_{(\nu )} - \alpha _k \nabla {\mathscr {L}}_{\rho _k}(x^k,\mu ^k)_{(\nu )} \right] \);

  7. (vii)

    compute \({\widehat{k}} = {\left\{ \begin{array}{ll} k + 1, &{} \rho _k < \widehat{\rho }, \\ {\widehat{k}}, &{} otherwise; \end{array}\right. }\)

  8. (viii)

    compute \(a^{\nu ,k+1} = Q_{*(\nu )} \ x^{k+1}_{(\nu )}\) and broadcast;

  9. (ix)

    compute \(h^{\nu ,k+1} = A_{*(\nu )} \ x^{k+1}_{(\nu )}\) and broadcast.

We observe that the above algorithm needs the communication of the vectors \(a^{\nu ,k+1}\) and \(h^{\nu ,k+1}\) at Steps (viii) and (ix). This communication is not too heavy from a computational performance point of view, although it can slow down the algorithm if the number of processes N is big. Beyond this communication phase, any process \(\nu \) works only on its block of variables \(x_{(\nu )}\) and needs only to know its data block \(Q_{*(\nu )}\), \(A_{*(\nu )}\), \(c_{(\nu )}\), \(X_{\nu }\) and b. As explained in Sect. 2, such possible distribution of the data can be beneficial, and sometimes is necessary, in many applications like e.g. support vector machines training. At step (i), any process \(\nu \) performs the computation of the stepsize \(\alpha _k > 0\) in a way that, as described in Sect. 3, it is squared summable but not summable for all k such that \(\rho _k = {\widehat{\rho }}\). Furthermore, such update allows that \(\alpha _k = 1 / L^k_{\mathscr {L}}\) for all \(k: \ \rho _k < {\widehat{\rho }}\) (see Sect. 3). At step (iii) each process \(\nu \) updates the multipliers vector \(\mu ^k\) as in Algorithm 1 if \(\rho _{k-1}<{\widehat{\rho }}\), or, otherwise, such that it is the maximum of the function \({\mathscr {L}}_{\rho _k}(x^k,\mu )\) over \(M_{{\widehat{\mu }}}\) with respect to \(\mu \). At step (iv) the penalty parameter is increased if a sufficient descent in the violation of the coupling constraints defined by h is not achieved. Finally, at steps (v–vi) every process \(\nu \) updates its block of variables \(x_{(\nu )}\) by a gradient projection step over \(X_{\nu }\). We want to stress that such update does not require any approximate solution of the subproblem in \(X_{\nu }\), like instead is required in Algorithm 1.

Fig. 2
figure 2

Objective relative error (full line) and constraints violation (dotted line) versus iterations

Full size image

We are ready to report some preliminary tests on the proposed distributed method. We consider the following problem setting: \(n=1000\), \(m=100\), Q positive definite and \(\Vert Q\Vert =1\) (i.e. \({\overline{L}} = 1\)), c equal to the vector of all ones, \(\Vert A\Vert = 1\), \(b=0\), \(X = [-10,10]^n\). We focus on the following setting for Algorithm 2: \(\gamma = 1\), \(\delta = 0.5\), \(\tau = 0.9\), \(x^0 = 0\), \(\mu ^0 = 0\), \(\rho _0 = 1\). We generated 4 experiments by considering different values for \({\widehat{\mu }}\) and \({\widehat{\rho }}\): exp1 with \({\widehat{\mu }} = \)1e-1 and \({\widehat{\rho }} = \)1e3, exp2 with \({\widehat{\mu }} = \)1e1 and \({\widehat{\rho }} = \)1e3, exp3 with \({\widehat{\mu }} = \)1e-1 and \({\widehat{\rho }} = \)1e4, exp4 with \({\widehat{\mu }} = \)1e1 and \({\widehat{\rho }} = \)1e4. In our tests we used: PC Windows with CPU Intel Core i7-8650U - 4 core (base frequency 1.9 GHz, turboboost up to 4.2 GHz) and RAM 16 GB, Python 3.6.3, and MPI 3.0.

In Fig. 2, for all the 4 experiments, we report: with a full line the objective relative error (i.e. \(\max \{ \)1e-4\(, (f(x^k)-f^*)/f^* \}\), where \(f^*\) is the optimal value of the problem), and with a dotted line the coupling constraints violation (i.e. \(\Vert h(x^k)\Vert /\sqrt{n}\)), versus iterations (we report the first 120k iterations). In all the experiments the algorithm returns an \(\varepsilon \)-approximate solution of the problem, i.e. a point \({\overline{x}} \in X\) such that \(f({\overline{x}}) \le f(x^*)\) and \(\Vert h({\overline{x}})\Vert \le \varepsilon \). As theoretically observed in Theorem 1, Fig. 2 confirms that the larger \({\widehat{\mu }}\) and \({\widehat{\rho }}\), the smaller \(\varepsilon \). Moreover, our experiments make it evident that Algorithm 2 is faster in the first phase (when \(\rho _k < {\widehat{\rho }}\)) than in the second one. The slower convergence in exp1 and exp2 with respect to the one in exp3 and exp4 is due to the fact that we get \(\rho _k = {\widehat{\rho }}\) quite early in exp1 and exp2 (around iteration 2k), while in exp3 and exp4 the algorithm switches to phase 2 later (around iteration 20k). For this reason it is important to set carefully the parameters \({\widehat{\rho }}\), \(\delta \), and \(\tau \) to grant many iterations to phase 1 of the algorithm: while \({\widehat{\rho }}\) must be reasonably large, \(\delta \) should be small, and \(\tau \) close to 1. Another key issue is the value of \({\widehat{\mu }}\): large values of \({\widehat{\mu }}\) on the one hand yield small values of the approximation \(\varepsilon \), as stated in Theorem 1, but on the other hand can make phase 2 of the algorithm really different from phase 1 thus spoiling the joint convergence of the objective relative error and the constraints violation that is obtained in phase 1. In our experiments we considered reasonable values for \({\widehat{\mu }}\) (up to 10), and we get good convergence behaviours. However in the figure of both exp3 and exp4 it is possible to see that, when the algorithm switches from phase 1 to phase 2 (around iteration 20k), the lines make a small jump.

We tested the algorithm with \(N = 1\), 2, and 4 parallel processes, every process takes care of 1000 / N variables. While the iterations clearly remain exactly the same, we observed a speedup in terms of CPU time that is almost ideal. Specifically, to execute 200k iterations we notice around 700 s with \(N=1\), around 360 s with \(N=2\), and around 190 s with \(N=4\), for all the experiments.

7 Conclusions and directions for future research

In this paper we propose an augmented Lagrangian method to solve convex problems with linear coupling constraints. The proposed method employs only one gradient projection step at any iteration and therefore both the data and the computation can be easily distributed. This can be beneficial (or necessary) in many practical situations, like e.g. when privacy concerns exist.

Convergence to (at least \(\varepsilon \)-approximate) solutions of the problem and a detailed analysis on the influence of the parameters to the effectiveness of the method are given. Furthermore, a parallel, distributed implementation is presented in the case where the function f is quadratic. Such case is of particular interest for many applications, e.g. support vector machines training.

In future work, we aim at testing such method on real applications like support vector machines training, in order to find out how to determine the parameters such that the quality of the solution and the convergence speed are acceptable. In such kind of problems the computation of the kernel matrix Q represents a large part of the computational burden [9]. Computing such matrix in a distributed fashion by the parallel processes may lead to substantial computational savings, especially if the available memory of each process is enough to allow pre-computation of the entire matrix offline.