1 Introduction

The widely used clustering techniques may use different kind of distances to measure the separation between data samples. The well-known Euclidean distance is currently the most frequently used metric space for the established clustering algorithms (MacQueen 1967; Fukunaga and Hostetler 1975). Other metric spaces, using the Mahalanobis (McLachlan 1999), city block, Hamming, Minkowski types of distances, etc., are also widely used in different clustering algorithms for different purposes. It is often the case that clustering algorithms employing divergences, i.e. pairwise dissimilarity, which does not obey all the properties of distances (e.g. cosine similarity), could generate meaningless conclusions.

One problem the traditional distance metrics are facing is the so-called “curse of dimensionality” (Domingos 2012; Aggarwal et al. 2001). Many clustering techniques, which use the traditional distance metrics work well in low dimensional space, however, become intractable for high dimensional problems. Research results have shown that in high dimensional space, the concept of distance may not even be qualitatively meaningful (Aggarwal et al. 2001; Beyer et al. 1999). Under certain reasonable conditions, it has been found that the distances of the nearest and farthest neighbours to a given data sample are the same for a number of distance metrics in high dimensional space (Beyer et al. 1999). This phenomenon is frequently seen in the cases that some dimensions of the data are highly irrelevant. This is not hard to understand because our intuitions come from a three-dimensional world only, which may not be applicable to high dimensional ones.

Compared with the commonly used distance metrics including the Euclidean, Mahalanobis, Minkowski distances, etc., which measure the magnitude of vector difference, cosine similarity focuses much more on the directional similarity. Therefore, it is more often used in the natural language processing (NLP) problems (Allah et al. 2008; Dehak et al. 2010, 2011; Setlur and Stone 2016; Senoussaoui et al. 2013). In NLP problems, machine learning algorithms, for example, k-means (Allah et al. 2008; Setlur and Stone 2016), mean shift (Senoussaoui et al. 2013), etc., are used to cluster very high dimensional vectors representing the documents together based on the cosine similarity. Nonetheless, the cosine similarity is a pseudo metric because it does not obey the triangle inequality [it obeys the Cauchy–Schwarz inequality (Callebaut 1965)]. Consequently, the cosine similarity between two vectors can be misleading and hides information, especially in cases where the vectors are sparse or orthogonal.

In this paper, a new “direction-aware” distance is introduced. This new metric space is a combination of a distance (in this paper, we consider Euclidean), and an angular/directional component, which is based on the cosine similarity. Therefore, it takes the advantages of the both components while still obeys all the properties of a distance metric (McCune et al. 2002) as we will demonstrate.

The proposed distance in this paper is applicable to various machine learning algorithms including the recently published ones (Angelov et al. 2014; Rong et al. 2006, 2011; Precup et al. 2014; Lughofer et al. 2015) as an alternative distance measure and can enhance the ability of the algorithms to handle high dimensional problems. A new evolving clustering algorithm is also proposed for streaming data processing. This algorithm employs the new direction-aware distance only and is able to start “from scratch”. Therefore, it is very suitable for handling the high dimensional data streams.

Numerical examples using benchmark datasets demonstrate the potential of the direction-aware distance against many traditional metrics in high dimensional problems. It is also shown that the proposed clustering algorithm is able to produce top quality clustering results on various problems with high computational efficiency.

The remainder of this paper is organised as follows. Section 2 describes the newly proposed direction-aware distance and provides the proof for the proposed distance to be a full metric. Section 3 introduces the application of the newly proposed direction-aware distance to traditional clustering algorithms. The new evolving clustering algorithm based on the proposed distance is presented in Sect. 4. Section 5 presents numerical examples. The paper is concluded by Sect. 6.

2 Direction-aware distance and proof of metric axioms

2.1 The new direction-aware distance

In this section, we introduce the direction-aware distance, and prove that it is a distance over the space of real numbers. If no specific declaration is provided, all the derivations in this paper are conducted over the real numbers.

First of all, let us define a metric space, \({\mathbf{R}^m}\), \({\varvec{x}}\)and \({\varvec{y}}\) are two data points within the space, \(m\) is the dimensionality of the metric space \({\mathbf{R}^m}\). The newly introduced direction-aware distance, \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) consists of two terms:

  1. 1.

    A Euclidean component, \({d_M}\left( {{\varvec{x}},{\varvec{y}}} \right)\), and

  2. 2.

    A direction-aware component, \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)\), and is expressed as:

    $${d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {\lambda _{M}^{2}{{\left( {d_{M}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)} \right)}^2}+\lambda _{A}^{2}{{\left( {d_{A}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)} \right)}^2}} ,$$
    (1)

    where \({\varvec{x}}={\left[ {{x_1},{x_2},...,{x_m}} \right]^\text{T}}\) and \({\varvec{y}}={\left[ {{y_1},{y_2},...,{y_m}} \right]^\text{T}}\), \({\varvec{x}},{\varvec{y}} \in {\mathbf{R}^m}\); \({\lambda _M}\),\(\lambda _{A}^{{}}\) are a pair of scaling coefficients and \({\lambda _M}>0\), \({\lambda _A}>0\); \(d_{M}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) denotes the Euclidean distance between \({\varvec{x}}\) and \({\varvec{y}}\), \(d_{M}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {{{\left( {{\varvec{x}} - {\varvec{y}}} \right)}^\text{T}}\left( {{\varvec{x}} - {\varvec{y}}} \right)} =\sqrt {\sum\limits_{i=1}^m {{{\left( {{x_i} - {y_i}} \right)}^2}} } .\)

    The direction-aware component \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)\) is derived based on the cosine similarity expressed by:

    $${d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {1 - \cos \left( {{\varTheta _{xy}}} \right)} ,$$
    (2)

    where \({\varTheta _{xy}}\) is the angle between \({\varvec{x}}\)and \({\varvec{y}}\). In the Euclidean space, since \(\left\langle {{\varvec{x}},{\varvec{y}}} \right\rangle =\sum\limits_{i=1}^m {{x_i}{y_i}}\) and \(\left\| {\varvec{x}} \right\|=\sqrt {\left\langle {{\varvec{x}},{\varvec{x}}} \right\rangle }\), thus \(\cos \left( {{\varTheta _{xy}}} \right)=\frac{{\left\langle {{\varvec{x}},{\varvec{y}}} \right\rangle }}{{\left\| {\varvec{x}} \right\|\left\| {\varvec{y}} \right\|}}.\) Therefore, the directional component \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)\) can be rewritten as:

    $${d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {1 - \frac{{\left\langle {{\varvec{x}},{\varvec{y}}} \right\rangle }}{{\left\| {\varvec{x}} \right\|\left\| {\varvec{y}} \right\|}}} =\sqrt {1 - \frac{{\sum\limits_{i=1}^m {{x_i}{y_i}} }}{{\left\| {\varvec{x}} \right\|\left\| {\varvec{y}} \right\|}}} =\sqrt {\frac{{\sum\limits_{i=1}^m {x_{i}^{2}} }}{{2{{\left\| {\varvec{x}} \right\|}^2}}}+\frac{{\sum\limits_{i=1}^m {y_{i}^{2}} }}{{2{{\left\| {\varvec{y}} \right\|}^2}}} - \frac{{\sum\limits_{i=1}^m {{x_i}{y_i}} }}{{\left\| {\varvec{x}} \right\|\left\| {\varvec{y}} \right\|}}} =\sqrt {\frac{1}{2}\sum\limits_{i=1}^m {{{\left( {\frac{{{x_i}}}{{\left\| {\varvec{x}} \right\|}} - \frac{{{y_i}}}{{\left\| {\varvec{y}} \right\|}}} \right)}^2}} } =\frac{1}{{\sqrt 2 }}\left\| {\frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}} - \frac{{\varvec{y}}}{{\left\| {\varvec{y}} \right\|}}} \right\|.$$
    (3)

One can notice that, if \({\varvec{x}}\) or \({\varvec{y}}\) is equal to \(0\), \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)=0.\)

2.2 Proof of metric axioms

In this subsection, we will prove that the proposed distance is a full metric. For a distance \(d\left( {{\varvec{x}},{\varvec{y}}} \right)\) in the space to be a full metric, \({\mathbf{R}^m}\), it is required to satisfy the following properties for \(\forall {\varvec{x}},{\varvec{y}}\) (13):

  1. 1.

    Non-negativity:

    $$d\left( {{\varvec{x}},{\varvec{y}}} \right) \geqslant 0;$$
    (4)
  2. 2.

    Identity of indiscernibles:

    $$d\left( {{\varvec{x}},{\varvec{y}}} \right)=0\,\,iff\,\,{\varvec{x}}={\varvec{y}}{;}$$
    (5)
  3. 3.

    Symmetry:

    $$d\left( {{\varvec{x}},{\varvec{y}}} \right)=d\left( {{\varvec{y}},{\varvec{x}}} \right);$$
    (6)
  4. 4.

    Triangle inequality:

    $$d\left( {{\varvec{x}},{\varvec{z}}} \right)+d\left( {{\varvec{z}},{\varvec{y}}} \right) \geqslant d\left( {{\varvec{x}},{\varvec{y}}} \right).$$
    (7)

In this paper, we propose a new theorem as follows:

Theorem

\({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) is a distance within the metric space over the domain R m.

In the rest of this subsection, we will prove this theorem by proving that \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) obeys the four distance axioms stated in Eqs. (5–6) and inequalities (4) and (7) one by one.

Lemma 1

\(\forall {\varvec{x}},{\varvec{y}} \in {\mathbf{R}^m}\), \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right) \geqslant 0\)

Proof

It can be seen directly from the Eq. (5) that \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) is always non-negative.

Lemma 2

\(\forall {\varvec{x}},{\varvec{y}} \in {\mathbf{R}^m}\), \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=0\) iff \({\varvec{x}}={\varvec{y}}.\)

Proof

It is clear that if \({\varvec{x}}={\varvec{y}}\), then \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {1 - 1} =0\), \({d_M}\left( {{\varvec{x}},{\varvec{y}}} \right)=0\) and \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=0.\)

The directional component \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)\) alone does not obey this property because as we can see from equations (2) and (3), if \({\varvec{x}}\) and \({\varvec{y}}\) are nonzero and orthogonal, \({d_A}\left( {{\varvec{x}},{\varvec{y}}} \right)=0,\) so it is not true. However, in this case, due to the fact that if \({\varvec{x}} \ne {\varvec{y}}\), \({d_M}\left( {{\varvec{x}},{\varvec{y}}} \right) \ne 0\), \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) will still be non-zero as \({\lambda _M},{\lambda _A}>0.\) Therefore, one can still conclude that \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=0\) if and only if \({\varvec{x}}={\varvec{y}}\).

Lemma 3

\(\forall {\varvec{x}},{\varvec{y}} \in {\mathbf{R}^m}\),\({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=\) \({d_{DA}}\left( {{\varvec{y}},{\varvec{x}}} \right)\)

Proof

For the Euclidean metric, it is true that:

$${d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)=\sqrt {\lambda _{M}^{2}{{\left\| {{\varvec{x}} - {\varvec{y}}} \right\|}^2}+\frac{{\lambda _{A}^{2}}}{2}{{\left\| {\frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}} - \frac{{\varvec{y}}}{{\left\| {\varvec{y}} \right\|}}} \right\|}^2}} =\sqrt {\lambda _{M}^{2}{{\left\| {{\varvec{y}} - {\varvec{x}}} \right\|}^2}+\frac{{\lambda _{A}^{2}}}{2}{{\left\| {\frac{{\varvec{y}}}{{\left\| {\varvec{y}} \right\|}} - \frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}}} \right\|}^2}} ={d_{DA}}\left( {{\varvec{y}},{\varvec{x}}} \right).$$
(8)

Therefore, \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)={d_{DA}}\left( {{\varvec{y}},{\varvec{x}}} \right).\)

Lemma 4

\(\forall {\varvec{x}},{\varvec{y}},{\varvec{z}} \in {\mathbf{R}^m}\),\({d_{DA}}\left( {{\varvec{x}},{\varvec{z}}} \right) \leqslant\) \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) \(+\) \({d_{DA}}\left( {{\varvec{y}},{\varvec{z}}} \right)\)

Proof

Firstly, let us assume that there is a triplet data samples \({\varvec{x}},{\varvec{y}},{\varvec{z}}\), which make \({d_{DA}}\) break the triangle rule, namely:

$${d_{DA}}\left( {{\varvec{x}},{\varvec{z}}} \right)>{d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)+{d_{DA}}\left( {{\varvec{y}},{\varvec{z}}} \right).$$
(9)

By including Eq. (3) in Eq. (2), the direction-aware distance \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) can be rewritten as:

$$\begin{aligned} {d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right) & =\sqrt {\lambda _{M}^{2}{{\left( {d_{M}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)} \right)}^2}+\lambda _{A}^{2}{{\left( {d_{A}^{{}}\left( {{\varvec{x}},{\varvec{y}}} \right)} \right)}^2}} =\sqrt {\lambda _{M}^{2}{{\left\| {{\varvec{x}} - {\varvec{y}}} \right\|}^2}+\frac{{\lambda _{A}^{2}}}{2}{{\left\| {\frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}} - \frac{{\varvec{y}}}{{\left\| {\varvec{y}} \right\|}}} \right\|}^2}} \\ & =\sqrt {\lambda _{M}^{2}\sum\limits_{i=1}^m {{{\left( {{x_i} - {y_i}} \right)}^2}} +\frac{{\lambda _{A}^{2}}}{2}\sum\limits_{i=1}^m {{{\left( {\frac{{{x_i}}}{{\left\| {\varvec{x}} \right\|}} - \frac{{{y_i}}}{{\left\| {\varvec{y}} \right\|}}} \right)}^2}} } =\left\| {\varvec{\chi} - \varvec{\psi}} \right\|={d_M}\left( {\varvec{\chi},\varvec{\psi}} \right), \\ \end{aligned}$$
(10)

where, \(\varvec{\chi}={\left[ {{\lambda _M}{{\varvec{x}}^\text{T}},\frac{{{\lambda _A}{{\varvec{x}}^\text{T}}}}{{\sqrt 2 \left\| {\varvec{x}} \right\|}}} \right]^\text{T}}={\left[ {{\lambda _M}{x_1},{\lambda _M}{x_2}, \ldots ,{\lambda _M}{x_m},\frac{{{\lambda _A}{x_1}}}{{\sqrt 2 \left\| {\varvec{x}} \right\|}},\frac{{{\lambda _A}{x_2}}}{{\sqrt 2 \left\| {\varvec{x}} \right\|}}, \ldots ,\frac{{{\lambda _A}{x_m}}}{{\sqrt 2 \left\| {\varvec{x}} \right\|}}} \right]^\text{T}}\) and \(\varvec{\psi}={\left[ {{\lambda _M}{{\varvec{y}}^\text{T}},\frac{{{\lambda _A}{{\varvec{y}}^\text{T}}}}{{\sqrt 2 \left\| {\varvec{y}} \right\|}}} \right]^\text{T}}={\left[ {{\lambda _M}{y_1},{\lambda _M}{y_2}, \ldots ,{\lambda _M}{y_m},\frac{{{\lambda _A}{y_1}}}{{\sqrt 2 \left\| {\varvec{y}} \right\|}},\frac{{{\lambda _A}{y_2}}}{{\sqrt 2 \left\| {\varvec{y}} \right\|}}, \ldots ,\frac{{{\lambda _A}{y_m}}}{{\sqrt 2 \left\| {\varvec{y}} \right\|}}} \right]^\text{T}}.\)

Similarly, for \(\varvec{\varsigma}={\left[ {{\lambda _M}{{\varvec{z}}^\text{T}},\frac{{{\lambda _A}{{\varvec{z}}^\text{T}}}}{{\sqrt 2 \left\| {\varvec{z}} \right\|}}} \right]^\text{T}}\), we can see that \({d_{DA}}\left( {{\varvec{x}},{\varvec{z}}} \right)={d_M}\left( {\varvec{\chi},\varvec{\varsigma}} \right)\), \({d_{DA}}\left( {{\varvec{y}},{\varvec{z}}} \right)={d_M}\left( {\varvec{\psi},\varvec{\varsigma}} \right).\)

Considering an auxiliary algebraic data space \({\mathbf{R}^{2m}}\), for \(\varvec{\chi},\varvec{\psi},\varvec{\varsigma}\), it follows that:

$${d_M}\left( {\varvec{\chi},\varvec{\varsigma}} \right) \leqslant {d_M}\left( {\varvec{\chi},\varvec{\psi}} \right)+{d_M}\left( {\varvec{\psi},\varvec{\varsigma}} \right).$$
(11)

As we can see from inequalities (9) and (11), the two equations have the same algebraic form, but there are different signs (\(>\) and \(\leqslant\)). For Euclidean distance in \({\mathbf{R}^{2m}}\), the triangle rule is always conformed, therefore, we can conclude that \({d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)\) always satisfies the triangle inequality: \({d_{DA}}\left( {{\varvec{x}},{\varvec{z}}} \right) \leqslant {d_{DA}}\left( {{\varvec{x}},{\varvec{y}}} \right)+{d_{DA}}\left( {{\varvec{y}},{\varvec{z}}} \right).\)

Based on the proofs of the four Lemmas, the proposed Theorem is proven. Therefore, we can conclude that the proposed direction-aware distance, d DA is a full distance in the Euclidean space.

2.3 The property of the proposed distance

The proposed direction-aware distance metric is a combination of two components: (1) the traditional Euclidean distance and (2) an angular/directional divergence, derived from the cosine similarity. It defines a metric space as a combination of Euclidean metric space and cosine similarity pseudo-metric space, and consequently, can effectively combine information extracted from both spaces and takes into account both spatial and angular divergences. Therefore, the direction aware distance can serve as a more representative distance metric than the traditional distance metric.

3 The application of the proposed distance to traditional clustering approaches

In this section, we will describe the applications of the proposed distance to the traditional offline clustering approaches. First of all, let us define the dataset in the metric space as \({\left\{ {\varvec{x}} \right\}_N}=\left\{ {{{\varvec{x}}_1},{{\varvec{x}}_2},...,{{\varvec{x}}_N}} \right\} \in {\mathbf{R}^m}\), \({{\varvec{x}}_i}=\) \({\left[ {{x_{i,1}},{x_{i,2}},...,{x_{i,d}}} \right]^\text{T}}\) \(\in {\mathbf{R}^d}\), \(i=1,2,...,N\), where \(N\) is the number of data samples in the dataset.

The newly proposed direction-aware distance can be used in various clustering, classification as well as regression approaches. For example, the k-means (Allah et al. 2008; Setlur and Stone 2016), mean-shift clustering (Comaniciu and Meer 2002), k nearest neighbour classification (Keller and Gray 1985) algorithms may use the newly introduced direction-aware distance to enhance the ability in dealing with high dimensional data.

Since the traditional offline algorithms have been studied well for many years, in this paper, we will not focus on the algorithm themselves. Instead, we will look at the direction-aware distance and introduce the strategy of using the proposed distance in the algorithms for different purposes.

The direction-aware distance has a pair of scaling factors, the values of which can be adjusted for various problems. For example, if without losing generality, we want to allocate the same importance to the Euclidean and directional components, \({\lambda _M}\) and \(\lambda _{A}^{{}}\) can be set as the inverse of average \({d_M}\) and \(d_{A}^{{}}\), respectively (the data is taken without pre-processing):

$${\lambda _M}=\frac{1}{{\sqrt {\frac{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^N {d_{M}^{2}\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right)} } }}{{{N^2}}}} }},$$
(12a)
$$\lambda _{A}^{{}}=\frac{1}{{\sqrt {\frac{{\sum\limits_{i=1}^N {\sum\limits_{j=1}^N {d_{A}^{2}\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right)} } }}{{{N^2}}}} }}.$$
(12b)

Alternatively, if the data has been re-scaled to the range \(\left[ {0,1} \right]\) in advance, the values of \({d_M}\) and \({d_A}\) are within the ranges \(\left[ {0,\sqrt m } \right]\) and \(\left[ {0,1} \right]\), respectively, thus, the pair of the scaling coefficients within the proposed distance can be set to \({\lambda _M}=\frac{1}{{\sqrt m }}\)and \({\lambda _A}=1\) if we aim to allocate the same importance to each component.

While for some problems like NLP, where the directional similarity plays a more important role compared with magnitude differences, we can enhance the importance of the directional component in the distance measures by increasing the value of \({\lambda _A}\), and vice versa. The scaling factors \({\lambda _M}\) and \({\lambda _A}\) that allow the clustering approaches to achieve the best performance with the proposed direction-aware distance are always problem-specific, which incorporates the prior knowledge of the problem. We believe that this choice is out of the scope of this paper.

4 The applications of the proposed distance to evolving clustering

Similarly, the direction-aware distance can also be employed in the evolving clustering approaches. In this section, we propose a new evolving clustering approach with the direction-aware distance. This algorithm is able to “start from scratch” and consistently evolves its system structure and updates the meta-parameters based on the newly arrived data samples.

The main procedure of the proposed algorithm is described as follows. In this section, we consider \({\left\{ {\varvec{x}} \right\}_k}=\left\{ {{{\varvec{x}}_1},{{\varvec{x}}_2}, \ldots ,{{\varvec{x}}_k}} \right\} \in {\mathbf{R}^m}\) as a data stream and the subscript indicates the time instance that the data sample arrives.


Stage 1 Initialization


The first data sample \({{\varvec{x}}_1}\) in the data stream is used for initializing the system and its meta-parameters. In the proposed algorithm, the system has the following initialized global meta-parameters:

  1. 1.

    \(k \leftarrow 1\), the current time instance;

  2. 2.

    \(C \leftarrow 1\), the number of exiting clusters;

  3. 3.

    \({\varvec{\mu}_M} \leftarrow {{\varvec{x}}_1}\), the global mean of \({\left\{ {\varvec{x}} \right\}_k};\)

  4. 4.

    \({X_M} \leftarrow {\left\| {{{\varvec{x}}_1}} \right\|^2}\), the global average scalar product of \({\left\{ {\varvec{x}} \right\}_k};\)

  5. 5.

    \({\varvec{\mu}_A} \leftarrow \frac{{{{\varvec{x}}_1}}}{{\left\| {{{\varvec{x}}_1}} \right\|}}\), the global mean of \({\left\{ {\frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}}} \right\}_k}\), which is also the normalized global mean of \({\left\{ {\varvec{x}} \right\}_k}\).

  6. 6.

    \({X_A} \leftarrow {\left\| {\frac{{{{\varvec{x}}_1}}}{{\left\| {{{\varvec{x}}_1}} \right\|}}} \right\|^2}=1\), the global average scalar product of \({\left\{ {\frac{{\varvec{x}}}{{\left\| {\varvec{x}} \right\|}}} \right\}_k}\), which is always equal to 1.

The local meta-parameters of the first cluster are initialized as follows:

  1. 1.

    \({\varvec{\Xi}^1} \leftarrow \left\{ {{{\varvec{x}}_1}} \right\}\), the first cluster;

  2. 2.

    \({\varvec{f}}_{M}^{1} \leftarrow {{\varvec{x}}_1}\), the centre of the first cluster, which is also the mean of \({\varvec{\Xi}^1}\);

  3. 3.

    \(X_{M}^{1} \leftarrow {\left\| {{{\varvec{x}}_1}} \right\|^2}\), the average scalar product of \({\varvec{\Xi}^1}\);

  4. 4.

    \({\varvec{f}}_{A}^{1} \leftarrow \frac{{{{\varvec{x}}_1}}}{{\left\| {{{\varvec{x}}_1}} \right\|}}\), the normalized mean of \({\varvec{\Xi}^1}\);

  5. 5.

    \(X_{A}^{1} \leftarrow 1\), the normalized average scalar product of \({\varvec{\Xi}^1}\), which is always equal to 1 as well;

  6. 6.

    \({S^1} \leftarrow 1\), the support (population) of the first cluster.

After the initialization of the system, the proposed algorithm updates the system structure and meta-parameters with the arrival of each new data samples.


Stage 2 System structure and meta-parameters update

With each newly arrived data sample, the system’s global meta-parameters, \({\varvec{\mu}_M}\), \({X_M}\) and\({\varvec{\mu}_A}\) are updated using the following equations (Angelov et al. 2017):

$${\varvec{\mu}_M} \leftarrow \frac{k}{{k+1}}{\varvec{\mu}_M}+\frac{1}{{k+1}}{{\varvec{x}}_{k+1}},$$
(13a)
$${X_M} \leftarrow \frac{k}{{k+1}}{X_M}+\frac{1}{{k+1}}{\left\| {{{\varvec{x}}_{k+1}}} \right\|^2},$$
(13b)
$${\varvec{\mu}_A} \leftarrow \frac{k}{{k+1}}{\varvec{\mu}_A}+\frac{1}{{k+1}}\frac{{{{\varvec{x}}_{k+1}}}}{{\left\| {{{\varvec{x}}_{k+1}}} \right\|}},$$
(13c)
$$k \leftarrow k+1.$$
(13d)

Then, the condition A is checked to see whether the new data sample denoted by \({{\varvec{x}}_k}\) is associated with a new cluster:

$${Condition \; A}:\begin{array}{*{20}{c}} {IF\,\,\left( {{d_{DA}}\left( {{{\varvec{x}}_k},{\varvec{\mu}_M}} \right)>\mathop {\max }\limits_{j=1,2,...,C} \left( {{d_{DA}}\left( {{\varvec{f}}_{M}^{j},{\varvec{\mu}_M}} \right)} \right)} \right)\,\,OR\,\,\left( {{d_{DA}}\left( {{{\varvec{x}}_k},{\varvec{\mu}_M}} \right)<\mathop {\min }\limits_{j=1,2,...,C} \left( {{d_{DA}}\left( {{\varvec{f}}_{M}^{j},{\varvec{\mu}_M}} \right)} \right)} \right)} \\ {THEN\,\,\left( {{{\varvec{x}}_k}\,creates\,\,a\,\,new\,\,cluster} \right)} \end{array}.$$
(14)

Based on the previous subsection, without a loss of generality, we use the inverse of the average \({d_M}\) between the existing data samples as \({\lambda _M}\) and the inverse of the average \({d_A}\) as \(\lambda _{A}^{{}},\) correspondingly. However, for streaming data processing, it is less efficient to keep all the observed data samples in the memory and recalculate \({\lambda _M}\) and \(\lambda _{A},\) every time when a new data sample is observed. Therefore we introduce the recursive forms for calculating the pair of scaling coefficients as follows (Angelov et al. 2017):

$${\lambda _M}=\frac{1}{{\sqrt {\frac{{\sum\limits_{i=1}^k {\sum\limits_{j=1}^k {d_{M}^{2}\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right)} } }}{{{k^2}}}} }}=\frac{1}{{\sqrt {2\left( {{X_M} - {{\left\| {{\varvec{\mu}_M}} \right\|}^2}} \right)} }},$$
(15a)
$$\lambda _{A}^{{}}=\frac{1}{{\sqrt {\frac{{\sum\limits_{i=1}^k {\sum\limits_{j=1}^k {d_{A}^{2}\left( {{{\varvec{x}}_i},{{\varvec{x}}_j}} \right)} } }}{{{k^2}}}} }}=\frac{1}{{\sqrt {1 - {{\left\| {{\varvec{\mu}_A}} \right\|}^2}} }}.$$
(15b)

If condition A is satisfied, a new cluster is added with \({{\varvec{x}}_k}\) as its centre:

  1. 1.

    \(C \leftarrow C+1\), the number of existing clusters;

  2. 2.

    \({\varvec{\Xi}^C} \leftarrow \left\{ {{{\varvec{x}}_k}} \right\}\), the new cluster;

  3. 3.

    \({\varvec{f}}_{M}^{C} \leftarrow {{\varvec{x}}_k}\), the centre of the new cluster/ mean of \({\varvec{\Xi}^C}\);

  4. 4.

    \(X_{M}^{C} \leftarrow {\left\| {{{\varvec{x}}_k}} \right\|^2}\), the average scalar product of \({\varvec{\Xi}^C}\);

  5. 5.

    \({\varvec{f}}_{A}^{C} \leftarrow \frac{{{{\varvec{x}}_k}}}{{\left\| {{{\varvec{x}}_k}} \right\|}}\), the normalized centre of the new cluster/ normalized mean of \({\varvec{\Xi}^C}\);

  6. 6.

    \(X_{A}^{C} \leftarrow 1\), the normalized average scalar product of \({\varvec{\Xi}^C}\),

  7. 7.

    \({S^C} \leftarrow 1\), the support of the new cluster.

In contrast, if condition A is not met, \({{\varvec{x}}_k}\) is assigned to the cluster with the nearest centre, denoted by \({\varvec{f}}_{M}^{n}\) as:

$${\varvec{f}}_{M}^{n}=\mathop {\arg \min }\limits_{i=1,2,...,C} \left( {{d_{DA}}\left( {{{\varvec{x}}_k},{\varvec{f}}_{M}^{i}} \right)} \right).$$
(16)

The meta-parameters of the cluster with the nearest centre are updated as follows (Angelov et al. 2017):

$${\text {1.}} \quad{\varvec{\Xi}^n} \leftarrow {\varvec{\Xi}^n} \cup \left\{ {{{\varvec{x}}_k}} \right\},$$
(17a)
$${\text {2.}}\quad{\varvec{f}}_{M}^{n} \leftarrow \frac{{{S^n}}}{{{S^n}+1}}{\varvec{f}}_{M}^{n}+\frac{1}{{{S^n}+1}}{{\varvec{x}}_k},$$
(17b)
$${\text {3.}}\quad X_{M}^{n} \leftarrow \frac{{{S^n}}}{{{S^n}+1}}X_{M}^{n}+\frac{1}{{{S^n}+1}}{\left\| {{{\varvec{x}}_k}} \right\|^2},$$
(17c)
$${\text {4.}}\quad{\varvec{f}}_{A}^{n} \leftarrow \frac{{{S^n}}}{{{S^n}+1}}{\varvec{f}}_{A}^{n}+\frac{1}{{{S^n}+1}}\frac{{{{\varvec{x}}_k}}}{{\left\| {{{\varvec{x}}_k}} \right\|}},$$
(17d)
$${\text {5.}}\quad{S^n} \leftarrow {S^n}+1.$$
(17e)

After the update of the global and local meta-parameters, the system is ready for the arrival of the next data sample and begins a new processing cycle.


Stage 3 Clusters adjusting


In this stage, all the existing clusters will be examined and adjusted to avoid the possible overlap. For each existing cluster \({\varvec{\Xi}^i}\) (\(i=1,2,...,C\)), firstly, we find its neighbouring clusters, denoted by \(\left\{ \varvec{\Xi} \right\}_{{neighbour}}^{i}\) based on the following condition:

$${Condition\;B}:\begin{array}{*{20}{c}} {IF\,\,\left( {{d_{DA}}\left( {{\varvec{f}}_{M}^{i},{\varvec{f}}_{M}^{j}} \right)>\frac{{\sum\limits_{p=1}^C {\sigma _{{DA}}^{p}} }}{C}} \right)}&{THEN\,\,\left( {\left\{ \varvec{\Xi} \right\}_{{neighbour}}^{i} \leftarrow {\varvec{\Xi}^j} \cup \left\{ \varvec{\Xi} \right\}_{{neighbour}}^{i}} \right)} \end{array},$$
(18)

where \({\left( {\sigma _{{DA}}^{p}} \right)^2}=\frac{{\sum\limits_{{\varvec{x}} \in {\varvec{\Xi}^p}} {\sum\limits_{{\varvec{y}} \in {\varvec{\Xi}^p}} {d_{{DA}}^{2}\left( {{\varvec{x}},{\varvec{y}}} \right)} } }}{{S_{p}^{2}}}=2\left( {X_{M}^{p} - {{\left\| {{\varvec{f}}_{M}^{p}} \right\|}^2}} \right)+\left( {1 - {{\left\| {{\varvec{f}}_{A}^{p}} \right\|}^2}} \right)\) is the average square direction-aware distance between all the members within the \({p^{th}}\) cluster.

For each cluster centre, \({\varvec{f}}_{M}^{i}\) (\(i=1,2,...,C\)), we calculate its weighted unimodal density as (Angelov et al. 2017):

$${D^W}\left( {{\varvec{f}}_{M}^{i}} \right)={S^i}\frac{{\sum\limits_{l=1}^C {\sum\limits_{j=1}^C {d_{{DA}}^{2}\left( {{\varvec{f}}_{M}^{l},{\varvec{f}}_{M}^{j}} \right)} } }}{{2C\sum\limits_{j=1}^C {d_{{DA}}^{2}\left( {{\varvec{f}}_{M}^{i},{\varvec{f}}_{M}^{j}} \right)} }},$$
(19)

and we also compare \({D^W}\left( {{\varvec{f}}_{M}^{i}} \right)\) with the \({D^W}\) of its neighbouring clusters denoted by \(\left\{ {{D^W}\left( {{\varvec{f}}_{M}^{{}}} \right)} \right\}_{{neighbour}}^{i}\), to identify the local maxima of the weighted unimodal density,\({D^W}\):

$${Condition\; C}:~\begin{array}{*{20}{c}} {IF\,\,\left( {{D^W}\left( {{\varvec{f}}_{M}^{i}} \right)>\max \left( {\left\{ {{D^W}\left( {{\varvec{f}}_{M}^{{}}} \right)} \right\}_{{neighbour}}^{i}} \right)} \right)} \\ {THEN\,\,\left( {{\varvec{f}}_{M}^{i}\,\,is\,\,one\,\,of\,\,the\,\,local\,\,maxima\,\,of\,\,{D^W}} \right)} \end{array}.$$
(20)

By identifying all the local maxima, denoted by \({\left\{ {{\varvec{f}}_{M}^{{}}} \right\}_o}\) and assigning each data sample to the cluster with the nearest centre using Eq. (16), the whole clustering processing is finished. The parameters of the clusters can be extracted post factum.

The main procedure of the algorithm is summarised in the form of pseudo code as follows.

figure a

5 Numerical examples and analysis

In this section, a number of numerical experiments are conducted to demonstrate the performance of the newly proposed direction-aware distance for high dimensional problems. Analysis based on the numerical examples will be provided.

Firstly, we use the standard k-means algorithm as a benchmark. We consider the following problems to test the performance of the k-means algorithm with different type of distance/similarity including Euclidean distance, cosine similarity, cityblock distance and the proposed direction-aware distance:

  1. 1.

    Dim256 dataset (22);

  2. 2.

    Dim512 dataset (22);

  3. 3.

    Dim1024 dataset (22);

  4. 4.

    Dim15 dataset (22);

  5. 5.

    Steel plate faults dataset (23);

  6. 6.

    Pen-based recognition of handwritten digits dataset (24);

  7. 7.

    Optical recognition of handwritten digits dataset (25);

  8. 8.

    Cardiotocography dataset (26);

The dim256, dim512, dim1024 and dim15 datasets are sampled from Gaussian distributions, and, thus, the four datasets are ideal for testing the ability of the algorithms in separating high dimensional data samples from different classes. The other five datasets are real benchmark problems and we use them to evaluate the performance of the algorithms on real, non-Gaussian problems. The details of the benchmark datasets are given in Table 1.

Table 1 Details of the datasets
Full size table

Because of the complexity of the high-dimensional problems, the clustering results of the k-means algorithm may exhibit some degree of randomness, for each dataset and each type of distance/similarity, we did 100 Monte Carlo experiments and tabulated the average values of the five different measures in Table 2. The algorithms used in this paper were implemented within MATLAB 2015b; the performance was evaluated on a PC with dual core Intel i7 processor with clock frequency 3.4 GHz each and 16 GB RAM. In the experiment, without loss of generality, the pair of the scaling parameters of the direction-aware distance is set by Eq. (12) and we consider the Calinski-Harabasz (CH) index (Caliński and Harabasz 1974) to evaluate the quality of the clustering results. Higher Calinski-Harabasz (CH) index indicates a better clustering quality.

Table 2 Experimental results
Full size table

As we can see from Table 2, in the previous section, the performance of the k-means algorithm is largely influenced by the choice of the type of distance/similarity. Based on the Calinski-Harabasz (CH) indexes of the clustering results, one can see that the k-means algorithm with the proposed direction-aware distance can produce higher quality clusters compared with the one with traditional distances/dissimilarities.

Then, numerical experiments for the same benchmark problems as tabulated in Table 1 are conducted to evaluate the performance of the evolving algorithm employing the direction-aware distance. To better demonstrate the performance of the evolving algorithm using the direction-aware distance, we involve the following algorithms for comparison:

  1. 1.

    Subtractive clustering algorithm (Chiu 1994);

  2. 2.

    Mean-shift clustering algorithm (Comaniciu and Meer 2002);

  3. 3.

    DBScan clustering algorithm (Ester et al. 1996);

  4. 4.

    Mode identification based clustering algorithm (Li et al. 2007);

  5. 5.

    Random swap algorithm (Franti et al. 2008);

  6. 6.

    Density peak algorithm (Rodriguez and Laio 2014).

As the k-means algorithm exhibits certain degree of randomness, we exclude it from the comparison. In the experiments, due to the insufficient prior knowledge, we use the recommended settings of the free parameters from the published literature. The experimental setting of the free parameters of the algorithms are presented in Table 3.

Table 3 Experimental settings of the algorithms
Full size table

To objectively compare the performance of different algorithms, we consider the following measures:

  1. 1.

    Number of clusters (C), which should be equal or larger than the number of classes in the dataset. However, if C is too large (in our paper, we consider \(C>0.1 \times Number{ }of{ }Samples\) as too large) or is smaller than the number of classes in the dataset, the clustering result should be considered as an invalid one. The former case indicates that there are too many trivial clusters generated which are hard for users to understand. The latter case implies that the clustering algorithm fails to separate the data samples from different classes.

  2. 2.

    Calinski Harabasz index (CH) (Caliński and Harabasz 1974), the higher the Calinski Harabasz index is, the better the clustering result is;

  3. 3.

    Purity (P) (Dutta Baruah and Angelov 2012), which is calculated based on the result and the ground truth:

    $$P=\frac{{\sum\limits_{i=1}^N {S_{D}^{i}} }}{K},$$
    (21)

    where \(S_{D}^{i}\) is the number of data samples with the dominant class label in the ith cluster. The higher purity the clustering result has, the stronger separation ability the clustering algorithm exhibits.

  4. 4.

    Davies–Bouldin (DB) index (Davies and Bouldin 1979), the lower Davies–Bouldin index is, the better the clustering result is.

  5. 5.

    Time: the execution time (in seconds) should be as small as possible.

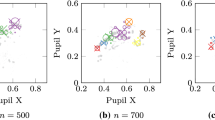
The experiment results obtained by the proposed evolving algorithm as well as other clustering algorithms are given in Table 4. The clustering results of the dim15, Pen-based recognition and Cardiotocography datasets obtained by the proposed algorithm are depicted in Fig. 1, where dots in different colours represent data samples in different clusters.

Table 4 Experimental results
Full size table

From Table 4 one can see that the subtractive clustering algorithm is able to produce high quality clustering results on the datasets with Gaussian distribution. However, for the more complex benchmark datasets, it fails to give valid results. The mean-shift clustering algorithm is one of the most efficient algorithms, but it can only perform high-quality clustering with low dimensional datasets. The DBScan algorithm is very efficient as well, but the quality of its clustering results is very limited in terms of the three clustering quality measures. Mode identification based clustering algorithm is a so-called “non-parametric” clustering algorithm. Nonetheless, its performance is very limited on high dimensional problems; its computational efficiency is also not very good. The quality of the clustering results obtained by the random swap algorithm is also very limited. In addition, this algorithm requires the number of classes to be known in advance in order to perform valid clustering results; its computational efficiency is also relatively lower. The density peak clustering algorithm is highly efficient, however, based on the recommended input selection, the algorithm failed to separate data samples from different classes in many cases. In addition, with the growth of the number of data samples, the difficulty of deciding the input selection for the users is also increasing.

Fig. 1
figure 1

Visualization of clustering results

Full size image

In contrast, the proposed evolving clustering algorithm consistently produces the top quality clustering results on various problems. In the core of the method is the idea to incorporate into the direction-aware distance both the spatial divergence and the angular similarity. Its computational efficiency does not deteriorate with the increase of dimensionality. Therefore, one can conclude that the proposed evolving clustering algorithm is the top one in the comparison. Nonetheless, we have to admit that the computational complexity of some clustering algorithms using the direction-aware distance will be inevitably higher compared with the same ones using the traditional distance/dissimilarity.

6 Conclusion

In this paper, a new type of distance, named “direction-aware”, is proposed and proved to be a full metric. The proposed distance is defined as a combination of two components: (1) the traditional Euclidean distance and (2) a cosine similarity based angular/directional divergence. Therefore, it is able to consider both spatial and angular divergences. It is using the advantages of one of them to compensate for the disadvantages of the other. The proposed distance is applicable to various traditional machine learning algorithms as an alternative distance measure. A new direction-aware distance based evolving clustering algorithm is also proposed for streaming data processing. Numerical examples demonstrate that the proposed distance can improve the clustering quality of the k-means algorithm for high dimensional problems. They also show the validity and effectiveness of the proposed evolving algorithm for handling high dimensional streaming data.

As future work, we will apply the proposed distance to various high dimensional problems including, but not limited to, the NLP, image processing problems, etc. We will also study the convergence of the evolving clustering algorithm.