Enhanced evolving participatory learning fuzzy modeling: an application for asset returns volatility forecasting

Abstract

Evolving participatory learning (ePL) modeling joins the concepts of participatory learning and evolving fuzzy systems. It uses data streams to continuously adapt the structure and functionality of fuzzy models. This paper suggests an enhanced version of the ePL approach, called ePL+, which includes both an utility measure to shrink rule bases, and a variable cluster radius mechanism to improve the cluster structure. These features are useful in adaptive fuzzy rule-based modeling to recursively construct local fuzzy models with variable zone of influence. Moreover, ePL+ extends ePL to multi-input, multi-output fuzzy system modeling. Computational experiments considering financial returns volatility modeling and forecasting are conducted to compare the performance of the ePL+ approach with state of the art fuzzy modeling methods and with GARCH modeling. The experiments use actual data of S&P 500 and Ibovespa stock market indexes. The results suggest that the ePL+ approach is highly capable to model volatility dynamics, in a robust, flexible, parcimonious, and autonomous way.

1 Introduction

Real-world problem solving and decision making relies on information management, involving high-volume and complex non-stationary data streams. When handling streaming data, data processing systems must extract meaningful knowledge on line. In practice it is virtually impossible to store all data and batch methods may become unsuitable (Angelov and Zhou 2006). In the last decade, data-driven rule/knowledge extraction methods have emerged as a complementary approaches to develop intelligent systems to deal with data streams (Attar et al. 2010; Shaker and Hüllermeier 2012). They assemble a class of adaptive data processing and modeling systems (Yager and Filev 1994; Kasabov 1996; Ljung 1999). Evolving fuzzy systems (eFS) are an advanced form of adaptive systems because they have the ability to simultaneous learn the model structure and functionality from flows of data. eFS have been useful to develop adaptive fuzzy rule-based models, control systems, neural fuzzy, and fuzzy regression and classification trees.

Typically, eFS consider functional rule-based systems in which the structure (number of rules and antecedents/consequent components) evolves continuously using clusters created/excluded by recursive clustering algorithms (Lemos et al. 2011). After a pioneering approach for online learning of evolving Takagi-Sugeno (eTS) models (Angelov and Filev 2004) and its extensions, Simpl_eTS (Angelov and Filev 2005), and eXtended eTS (xTS) (Angelov and Zhou 2006); Angelov (2010) proposed the eTS+, an approach in which the antecedent parameters and rule-base structure are updated using criteria such as age, utility, local density and zone of influence, comprising a robust, flexible and autonomous technique (can start from scratch and does not use thresholds or user-specific parameters).

Dovzan and Skrjanc (2011a, b) suggest an alternative method for online identification of Takagi-Sugeno fuzzy functional models. To learn rule antecedents, they use a recursive fuzzy c-means (rFCM) algorithm. Distinctively from eTS (Angelov and Filev 2004), in which cluster centers can only be data samples with the largest potential, in rFCM the cluster centers depend on a weighted mean of the data (Dovzan and Skrjanc 2011a, b). They also suggest a recursive Gustafson–Kessel (rGK) method to capture the shapes of the clusters in the data set (Dovzan and Skrjanc 2011a, b). Combining the rGK algorithm and adaptation mechanisms such as adding, removing, splitting and merging, an evolving fuzzy model, called eFuMo (Dovzan et al. 2012), was constructed and shown to be effective for online identification of fuzzy rule-based models.

A distinct, but conceptually similar approach for adaptive TS modeling is the dynamic evolving neural-fuzzy inference system model (DENFIS) (Kasabov 2002). This approach uses a distance-based recursive clustering method to adapt the rule base structure, and a weighted recursive least squares with forgetting factor algorithm to update rules consequent parameters. A recursive clustering algorithm derived from a modification of the vector quantization technique, called evolving vector quantization, is another significant methodology to construct flexible fuzzy inference systems (FLEXFIS) (Lughofer 2008). More recent examples of eFS in the realm of neuro-fuzzy type-2 are the self-organizing fuzzy modeling and modified least-squares network (SOFMLS) (Rubio 2009), and the sequential adaptive fuzzy inference system (SAFIS) (Rong et al. 2006). SOFMLS employs an evolving nearest neighborhood clustering algorithm, whereas SAFIS uses a distance criterion in conjunction with an influence measure of the new rules created to construct and update the rule base.

The fuzzy self-organizing neural network (Leng et al. 2005) is another alternative evolvable system that adopts an error criterion to measure the generalization performance of the network. Similarly, Tung et al. (2011) suggest a self-adaptive fuzzy inference network (SaFIN) with categorical learning-induced partitioning as a clustering algorithm. The idea is to avoid the need for prior knowledge regarding the number of clusters in the input–output space. This model also shows the flexibility to incorporate new knowledge in the system. There exist other online techniques for TS fuzzy models identification considering similar mechanisms to construct and adapt their structure as the above-mentioned methods, such as the self-organizing fuzzy neural network (SOFNN) (Qiao and Wang 2008), the self-constructing fuzzy neural network (SCFNN) (Lin et al. 2001) and the generalized adaptive neuro-fuzzy inference system (GANFIS) (Azzem et al. 2003).

As reported in Lemos et al. (2011), a weakness of the recursive clustering algorithms adopted by most eFS approaches is the lack of robustness due to noise or outliers. In these situations, the algorithms may create new clusters instead of rejecting or smoothing noisy data or outliers. A method to improve robustness was suggested by Lima et al. (2010), namely, evolving participatory learning (ePL) fuzzy modeling. This approach joins the concept of participatory learning (PL) (Yager 1990) with the idea of evolving fuzzy modeling (Angelov and Filev 2004). Participatory learning induces an unsupervised clustering algorithm and is a natural candidate to develop rule base structures in dynamic environments. Similarly as in eTS modeling, structure identification and self-organization in ePL estimates the focal points of the rules, except that ePL uses PL fuzzy clustering instead of scattering, density, or information potential, as eTS does.

Alternatively Hartert et al. (2010) propose a validation phase in an adaptive fuzzy K-nearest neighbors (FKNN) method to delete non-representative groupings (outliers) and to merge similar clusters. In the eTS+ model, this problem is coped with the use of monitoring measures such as age and utility. The eFuMo approach uses the method of Hartert et al. (2010) to adapt the rule base and to handle outliers. A pruning criterion evaluates if a cluster was added due to an outlier. If the cluster does not gather enough support samples after a certain period of time, then it is removed.

In this paper, we introduce an enhanced version of the evolving participatory learning model, namely ePL+, which incorporates in ePL an utility measure and a variable zone of influence of clusters. The utility measure allows shrinking of fuzzy rule bases by removing rules that have low utility (the data pattern shifts away from the focal point of the rules), endowing rule bases with rules of higher summarization power. Unlike the original version of the ePL, ePL+ modeling adapts the cluster radius, an important parameter to determine the dispersion of membership functions, and hence, to govern the zone of influence and activation level of the fuzzy rules. Furthermore, ePL+ modeling gives multi-input, multi-output (MIMO) system models.

We evaluate ePL+ considering asset returns volatility modeling and forecasting. Volatility plays a central role in asset pricing, portfolio allocation and risk management. Despite the widespread use of GARCH models (Engle 1982) to address volatility forecasting, GARCH methodologies have been criticized for failing to capture dynamics of asset returns in highly unstable environments, as during financial crisis (Kung and Yu 2008; Tseng et al. 2008). To overcome this limitation, the idea is to use evolving fuzzy modeling to avoid the high computational effort needed to process data stored in databases, and to take advantage of the inherent adaptability of evolving models, an essential requirement to handle nonlinear and non-stationary behavior such as in volatility dynamics.

Recent literature reveals several applications of evolving fuzzy rule-based models in finance and economics. Examples include: Value-at-Risk modeling and forecasting (Ballini et al. 2009a), sovereign bonds modeling (Ballini et al. 2009b), exchange rates forecasting (McDonald and Angelov 2010), fixed income option pricing (Maciel et al. 2012a, b, c), interest rate term structure forecasting (Maciel et al. 2012a, b, c), financial volatility forecasting (Luna and Ballini 2012a, b), and stochastic volatility prediction (Luna and Ballini 2012a, b).

Methods based on fuzzy set theory have been also developed to explain complex dynamics such as financial time series volatility (Chang et al. 2011; Helin and Koivisto 2011; Hung 2011a, b). Basically, these methods construct hybrid models combining fuzzy systems and GARCH models whose structure addresses both, time-varying volatility and volatility clustering. For example, Popov and Bykhanov (2005); Chang et al. (2011); Helin and Koivisto (2011); Hung (2011a, b) combine fuzzy and GARCH models to handle volatility modeling and forecasting. These modeling methods require high computational effort because they estimate the parameters of the model using all data available in the database. This may be troublesome in situations in which forecasts are needed whenever new data arrive. Therefore, current hybrid modeling methods may be prohibitive in dynamic environments which involve volatility forecasting, immunization strategies, portfolio allocation, and risk management.

Computational results reported in this paper include comparison of ePL+ modeling with state of the art evolving fuzzy modeling methods, and with GARCH modeling as benchmark. Simulations were done using actual data of S&P 500 (US) and Ibovespa (Brazil) stock market indexes from January 2000 to September 2011. Comparisons consider goodness of fit and statistical tests.

After this introduction, the paper proceeds as follows. Section 2 details ePL+ modeling, that is, a recursive scheme to learn the model structure and its parameters. Section 3 summarizes the computational results for assets returns volatility forecasting. Section 4 concludes the paper and suggests issues for further investigation.

2 Enhanced evolving participatory learning modeling (ePL+)

Evolving functional fuzzy participatory learning (ePL) modeling adopts the same philosophy as the classical evolving Takagi–Sugeno (eTS) methodology (Angelov and Filev 2004). After the initialization phase, data processing is performed at each step to verify if a new cluster must be created, if an old cluster should be modified to account for the new data, or if redundant clusters must be eliminated, in an online-like mode. Cluster centers are the focal points of the rules, and to each cluster corresponds a fuzzy rule. Parameters of the consequent functions are computed using the local recursive least squares method.

The main difference between ePL and eTS concerns the procedure to update the rule base structure. Differently from eTS, ePL uses a fuzzy similarity measure to determine the proximity between new data and the existing rule base. The rule base structure is isomorphic to the cluster structure once each rule is associated with a cluster. Participatory learning assumes that model learning depends on what the system already knows about the model (Yager 1990). Therefore, in ePL the current model is part of the evolving process itself and influences the way in which new observations are used for self-organization. An essential property of participatory learning is that the impact of new data in causing self-organization or model revision depends on its compatibility with the current rule base structure, or equivalently, on its compatibility with the current cluster structure.

In this paper, we suggest an enhanced version of the evolving participatory learning model, called ePL+. There are essentially three main additions in ePL+ that enhances ePL. First, in ePL, clusters radiuses, which represent the zone of influence of membership functions, are fixed and defined by expert knowledge. All membership functions of the fuzzy rules have the same dispersion, and hence they have the same shape in the input–output data space. In contrast, ePL+ adopts an adaptive mechanism to compute the zone of influence of each rule. Therefore, cluster radiuses are different and their values modify during learning. Because dispersion affects the activation degree of the fuzzy rules, the mechanism to determine their values has a major impact in the performance of the model. Second, the participatory learning clustering algorithm of ePL eliminates redundant clusters whenever the compatibility measure between cluster centers are greater than a user selected threshold, and no adaptive mechanism to evaluate the rule base quality is provided. On the contrary, ePL+ includes an utility measure to evaluate, recursively, the quality of the cluster structure, similar to eTS+ (Angelov 2010). The utility measure allows rule base shrinking by removing low utility rules, keeping only rules with high summarization power. Third, ePL modeling was developed for online identification of multi-input-single-output (MISO) fuzzy systems, whereas ePL+ models multi-input-multi-output (MIMO) systems as well. Therefore, ePL+ provides a more effective methodology than ePL because it is computationally efficient, requires less prior knowledge about the modeling environment, and enhances applicability in handling multivariable systems.

Next section describes the structure and parameter learning mechanisms of ePL+ modeling, emphasizing the points that differ from ePL. Details of the ePL modeling approach can be found in Lima (2008); Lima et al. (2010); Maciel et al. (2012a, b, c).

2.1 The structure of ePL+ models

ePL+ modeling assumes fuzzy rule-based systems whose rule consequents are functions of the rule antecedent variables. They form local models called local fuzzy functional models. From now on we consider, without loss of generality, Takagi–Sugeno (TS) type of fuzzy models with linear functions as rule consequents. More specifically, an ePL+ model is a set of functional fuzzy rules of the following form:

$$\begin{aligned} R^i:& {\mathbf{IF}} \ x_1 \ \mathrm{is} \ \Upgamma^i_1 \ {\mathbf{AND}} \ \ldots \ {\mathbf{AND}} \ x_n \ \mathrm{is} \ \Upgamma^i_n \ {\mathbf{THEN}}\\ & y_1^i = \gamma_{0,1}^i + \sum_{j=1}^n{\gamma_{j,1}^ix_j} \ {\mathbf{AND}} \ \ldots \ {\mathbf{AND}} \ y_m^i = \gamma_{0,m}^i + \sum_{j=1}^n{\gamma_{j,m}^ix_j} \end{aligned}$$

(1)

where R ⁱ is the ith fuzzy rule ($i=1,2,\ldots,R$), $x_j \in \Re$ is the j th input variable ($j=1,2,\ldots,n$), $\Upgamma^i_j$ is the fuzzy set associated with the j th input variable of the i th fuzzy rule, $y^i_t \in \Re$ is the output of the i th rule ($t = 1,2,\ldots,m$) ¹, and γ ⁱ_0,t and γ ⁱ _j,t are the parameters of the consequent of the i th rule.

TS models are developed for fuzzy domains identified by clusters, and to each cluster corresponds a linear local model. Overall, it forms a nonlinear model composed by a collection of loosely (fuzzily) coupled multiple local linear models. The contribution of a local linear model to the model output is proportional to the activation degree of each rule. We assume fuzzy sets of rule ancetedents with Gaussian membership functions to ensure generalization of the description (Angelov and Filev 2004):

$$\mu^i(x_j) = e^{\displaystyle{-\frac{(x_{j} - v_j^i)^2}{2(\sigma_j^i)^2}}}$$

(2)

where μ ⁱ(x _j ) is the membership degree of the input x _j in $\Upgamma^i_j, v^i_j$ corresponds to the cluster center (focal point), and $\sigma_j^i$ is the radius of $\Upgamma^i_j.$. The values of $\sigma_j^i$ define the zone of influence of the ith rule.

ePL assumes that the values $\sigma_j^i$ are the same and kept fixed for all fuzzy sets of all rules antecedents. Conversely, ePL+ assumes that radiuses σ ⁱ _j are different for each rule. σ ⁱ _j is an important parameter because it characterizes the dispersion of the membership functions, the zone of influence and the activation degree of the rules. Therefore, in stream data processing and dynamic environments, adaptation of σ ⁱ _j provides a more effective modeling framework and reduces the need of prior knowledge and user-specific parameter choices.

If the algebraic product t-norm is chosen to represent rule antecedents $\mathbf{AND},$ then the activation degree of the ith rule is:

$$\kappa^i (x) = \prod_{j=1}^{n}\mu^i(x_j) = \mu^i(x_1)\mu^i(x_2) \ \ldots \ \mu^i(x_n)$$

(3)

The output of the TS model at each step is the weighted average of the individual rule contributions:

$$y= \sum_{i=1}^R{\theta^i y^i}, \ \ \;\;\;\theta^i = \displaystyle{\frac{\kappa^i}{\sum_{l=1}^R{\kappa^l}}}$$

(4)

where θ ⁱ is the normalized activation degree of the ith rule, and R is the number of fuzzy rules.

As stated in Angelov and Filev (2004), identification of a TS model requires two sub-tasks: (1) learning the antecedent part of the model using e.g. a fuzzy clustering algorithm, and (2) learning the parameters of the linear rule consequent functions. In this paper, we focus on the evolving fuzzy participatory clustering algorithm for antecedent learning, and on the recursive least squares algorithm to estimate the consequent parameters.

2.2 Participatory learning clustering

The ePL+ modeling approach adopts the same mechanism to construct the rule base as ePL, i.e., the participatory learning clustering algorithm. Generally speaking, participatory learning assumes that model learning depends on what the system already knows about the model. Therefore, in ePL+ the current model is part of the evolving process itself and influences the way in which new data are used for self-organization. An essential property of PL is that the impact of new data in inducing self-organization or model revision depends on its compatibility with the current rule base structure or, equivalently, its compatibility with the current cluster structure (Lima et al. 2010).

In online mode, rather than being a fixed set, training data are collected continuously (Angelov and Zhou 2008). Let $v^{i}_{k}=[v_{1k}^i,v_{2k}^i,\ldots,v_{nk}^i]^T$ be a vector that encodes the ith ($i = 1,\dots,R_k$) cluster center at step k. The aim of the participatory mechanism is to learn the value of v ⁱ _k using a stream of data $x_{k}=[x_{1k},x_{2k},\ldots,x_{nk}]^T.$ In other words, each $x_{k}, k = 1,2,\ldots,$ is used as a vehicle to learn about v ⁱ _k . We say that the learning process is participatory if the contribution of each data x _k to the learning process depends upon its acceptance by the current estimate of v ⁱ _k being valid. Implicit in this idea is that, to be useful and to contribute to the learning of v ⁱ _k , data x _k must somehow be compatible with current estimates of v ⁱ _k .

In ePL+, the main object of learning is the cluster structure. A cluster structure is formed by the collection of cluster centers (or prototypes) that assemble the input space partition. More formally, given an initial cluster structure $v^{i}_{0}, i = 1,\ldots,R_{0},$ a collection of cluster centers $v^{i}_{k}, i = 1,\ldots,R_{k},$ is constructed at each k using a compatibility measure $\rho^{i}_{k}\in[0,1]$ and an arousal index $a^{i}_{k}\in[0,1].$ While ρ ⁱ _k measures the extent to which data x _k is compatible with the current cluster structure, the arousal index a ⁱ _k acts as a reminder of when current cluster structure should be revised in face of new information contained in the data. Figure 1 shows the main constituents and functioning of PL clustering. If an initial cluster structure is not available beforehand, then the PL algorithm assumes the first data point as a cluster center.

Fig. 1

Participatory learning clustering

Due to its unsupervised, self-organizing nature, the PL clustering procedure may create a new cluster or modify existing ones at each step k. If the arousal index is greater than a threshold value $\tau\in [0,1],$ a new cluster is created. Otherwise, the ith cluster center, the one most compatible with x _k , is adjusted as follows:

$$v^{i}_{k+1} = v^{i}_{k} + G^{i}_{k}(x_{k} - v^{i}_{k})$$

(5)

where

$$G^{i}_{k} = \alpha(\rho^{i}_{k})^{1-a^{i}_{k}}$$

(6)

with $\alpha\in[0,1]$ as the learning rate and

$$\rho^{i}_{k} = 1 - \frac{||x_{k} - v^{i}_{k}||}{n}$$

(7)

with $||\cdot||$ a norm, n the dimension of input space, and

$$i = \arg{\displaystyle\max_{j}}\{\rho_{j}^{k}\}$$

(8)

Note that the ith cluster center is a convex combination of the input data x ^k and the closest cluster center.

The arousal index a ⁱ _k in (6) is updated as follows:

$$a^{i}_{k+1} = a^{i}_{k} + \beta(1-\rho^{i}_{k+1} - a^{i}_{k})$$

(9)

The value of $\beta\in[0,1]$ controls the rate of change of arousal: the closer β is to one, the faster the system is to sense compatibility variations. When a ⁱ _k  = 0, G ⁱ _k  = αρ ⁱ _k , which is the PL procedure with no arousal. If the arousal index increases, the similarity measure has a reduced effect. The arousal index can be interpreted as the complement of the confidence we have in the truth of the current belief, the rule base structure. The arousal mechanism monitors the performance of the system by observing the compatibility of the current model with the observations. Therefore learning is dynamic in the sense that (5) can be viewed as a belief revision strategy whose effective learning rate (6) depends on the compatibility among new data, the current cluster structure, and on model confidence as well.

Note that the learning rate is modulated by compatibility. Conventional learning models have no participatory considerations and the learning rate is usually set small to avoid undesirable oscillations due to spurious values of data far from cluster centers. While protecting against the influence of noisy data, low learning rate slow down learning. Participatory learning allows higher values of the learning rate, but the compatibility index lowers the effective learning rate when large deviations occur. On the other hand, high compatibility increases the effective rate and speeds up the learning process.

Whenever a cluster center is updated or a new cluster added, the PL clustering procedure verifies whether redundant clusters were created. Updating a cluster center using (5) can push a given center closer to another one and a redundant cluster may be formed. Thus, a mechanism to avoid redundancy is needed. One of such a mechanism is to verify if distinct rules produce similar outputs. In PL clustering, a cluster center is declared redundant whenever its similarity with another center is greater than or equal to a threshold value- $\lambda \in [0,1].$ If this is the case, then we can either maintain the original cluster center or replace it by the average between the new data and the current cluster center. Similarly as in (7), the compatibility index between cluster centers i and j is computed using:

$$\rho^{i,j}_{k} = 1 - \sum_{l=1}^{n}|v^{i}_{lk} - v^{j}_{lk}|$$

(10)

Therefore, if

$$\rho^{i,j}_{k}\geq\lambda$$

(11)

then the cluster i is declared redundant.

Participatory clustering requires the user to choose parameters α, β, λ and τ. The choice can be guided by the following consideration. If an input data is such that the arousal is greater than the threshold $\tau \in \left[0,1\right],$ then this data becomes the focal point of a new cluster (Lima 2008). If the cluster with the highest compatibility s is updated, then a ^s _k+1  < τ, and from (9) we get:

$$a^{s}_{k} + \beta(1-\rho^{s}_{k+1} - a^{s}_{k}) = (1 - \beta )a^{s}_{k} + \beta d^{s}_{k} < \tau \Rightarrow d^{s}_{k} < \frac{\tau - (1-\beta )a^{s}_{k}}{\beta}<\frac{\tau}{\beta}$$

(12)

where d ^s _k  = d(v ^s _k , x _k ) is the distance between cluster center s and input x _k at k.

For any two distinct cluster $i,j=1,\ldots,c^{k}, i\neq j,$ the compatibility measure ρ ^i,j _k is such that:

$$\rho^{i,j}_{k} = 1 - d^{i,j}_{k} < \lambda \Rightarrow d^{i,j}_{k} > 1 - \lambda$$

(13)

If d ^i,j _k  < 1 − λ, clusters i and j are considered redundant and become a single cluster. Here, d ^i,j _k  = d(v ⁱ _k , v ^j _k ) is the distance between clusters centers v ⁱ _k and v ^j _k .

To ensure that a new, non redundant cluster is added, (12) and (13) suggest to choose values of $\beta,\; \lambda$ and τ such that:

$$0< \frac{\tau}{\beta}\leq 1-\lambda\leq 1$$

where

$$\tau\leq \beta\;\;\;{\rm and} \;\;\; \lambda \leq 1-\tau$$

Analysis of the dynamic behavior of the participatory learning considering the compatibility and arousal mechanisms simultaneously with learning rate is discussed in Lima et al. (2010). The learning rate α is a small value, typically $\alpha \in \left[10^{-1},10^{-5}\right].$

Initial cluster structure can be chosen differently if data are available beforehand. In this case, we may consider the use of subtractive clustering (SC) algorithm (Chiu 1994) to obtain a corresponding initial rule base because SC does not require pre-specified number of clusters. This adds flexibility and increases PL clustering autonomy once the number of clusters and the clusters themselves are derived from data. The subtractive clustering proceeds as follows.

• (1) For all training data, select the one with the highest potential to be the first cluster center. The potential of a point is measured as the spatial proximity between all other data points computed by the Euclidean distance;

• (2) Reduce the potential of all other points by an amount proportional to the potential of the chosen point and inversely proportional to the distance to the current center;

• (3) Define two boundary (lower and upper) conditions as a function of the maximal potential. If a potential of data point is higher than the upper threshold, then create a new cluster center;

• (4) If the potential of a point lies between the boundaries and if this point is very close to some cluster center, then replace this cluster center by the current one.

See Chiu (1994) for further details.

2.3 Clusters quality measurement

Originally, the PL clustering algorithm removes redundant clusters, but gives no mechanism to recursively evaluate the summarization power of the rule base induced by the cluster structure. Differently, ePL+ uses an online monitoring scheme to evaluate the quality of a cluster structure based on the utility measure introduced in Angelov (2010). The utility measure is an indicator of the accumulated relative activation degree of a rule:

$$U^i_k = \frac{\sum_{l=1}^k{\theta^l}}{k-I^{i*}}$$

(14)

where I ^i* denotes the step at which an input data became the focal point of the ith fuzzy rule, that is, it indicates when the i-th fuzzy rule was generated.

The utility measure gives a clue about the extent to which a fuzzy rule is useful. The use of the quality measure U ⁱ _k aims at avoiding unused clusters in the cluster structure; that is, it eliminates fuzzy rules with steadily low activation degrees. For this purpose, the following principle for rule elimination is adopted (Angelov 2010):

$$\mathrm{IF} \ \ U^i_k < \epsilon \ \ \mathrm{THEN} \ \ \mathrm{delete} \ \ R^i, \ \ R_k \leftarrow R_k-1$$

(15)

where $\epsilon \in [0.03;0.1]$ is a threshold to control the utility of each cluster, and R _k is the number of rules in the rule base at step k.

This principle helps to underscore high quality rule bases because it emphasizes the rules which are relevant for the current structure of model. Angelov (2010) has suggested alternative quality measures such as age, support, zone of influence, and local density. This paper considers utility measure only because of it achieves good performance with low computational cost.

2.4 Adaptation of the zone of influence

A key parameter associated with Gaussian membership functions is its cluster radius σ ⁱ _j because it defines the spread of the membership function and influences the activation degree of the fuzzy rules (Angelov 2010). Similarly as in Angelov and Zhou (2006), ePL+ modeling considers variable radiuses to capture the distribution of data at each step. They are updated as follows:

$$\sigma_{jk}^i = \pi \sigma_{jk}^i + (1-\pi)\varrho_{jk}^i$$

(16)

where π is a learning rate (suggested values are in range [0.3, 0.5]) (Angelov 2010), and $\varrho_{jk}^i,\, j=1,2,\ldots,n,$ is called the local scatter:

$$(\varrho_{kj}^i)^2 = \frac{1}{S^i_k-1}\sum_{l=1}^{S^i_k-1}{(z_j^i - z_{lj})^2}$$

(17)

where z = [x ^T, y ^T]^T is an input/output pair and S ⁱ _k  = S ⁱ _k−1  + 1 is the support of the cluster $i, i=\max_{i=1}^{R_k} \kappa^i(x).$ Essentially, S ⁱ _k is the number of data samples associated with cluster i and gives and indication of the generalization power of the i-th fuzzy rule.

2.5 Parameter estimation

Estimation of the parameters of the linear rule consequent functions can be formulated as a least squared problem (Angelov and Filev 2004). Equation (4) can be put into vector form:

$$y = \Uplambda^T \Upphi$$

(18)

where $y=\left[y_1, y_2, \ldots, y_m\right]^T$ is the m-dimensional output of the MIMO ePL+ model, $\Uplambda = \left[\lambda_1x_e^T,\lambda_2x_e^T,\ldots,\lambda_nx_e^T\right]^T$ is the fuzzily weighted extended input vector, $x_e = \left[1 \ x^T\right]^T$ is the expanded data vector, $\Upphi = \left[\Uppsi_1^T,\Uppsi_2^T,\ldots,\Uppsi_R^T\right]^T$ is the matrix of rule base parameters, and

$$\begin{aligned} \Uppsi_i = \left[\begin{array}{lll} \gamma^i_{01}&\ldots&\gamma^i_{0m}\\ \ldots&\ldots&\ldots\\ \gamma^i_{n1}&\ldots&\gamma^i_{nm}\end{array} \right]^T \end{aligned}$$

(19)

is the matrix of consequent function parameters of the ith linear local model.

Since the actual output value is available at each step, the parameters of the consequents can be updated using either the local or global recursive least squares algorithm (Chiu 1994). In this paper we use the local recursive least squares whose purpose is to minimize local modeling errors:

$$\min{E_L^i} = \min{\sum_{l=1}^k{\theta^i(x_l)\left(y_l - x_{el}^T\Uppsi_l^i\right)^2}}$$

(20)

Thus, the parameters of the ith local model is updated as follows (Angelov and Filev 2004; Angelov and Zhou 2008; Angelov 2010):

$$\Uppsi^i_{k+1} = \Uppsi^i_k + \Upsigma^i_kx_{ek}\theta_k^i\left(y_k-x_{ek}^T\Uppsi_k^i \right), \ \Uppsi_1^i=0$$

(21)

$$\Upsigma^i_{k+1} = \Upsigma^i_k - \frac{\theta_k^i \Upsigma_k^i x_{ek} x_{ek}^T \Upsigma_k^i}{1+ \theta_k^i x_{ek}^T \Upsigma_k^ix_{ek}}, \ \Upsigma_1^i = \Upomega I_{(n+1)\times(n+1)}$$

(22)

where I is the (n + 1) × (n + 1) identity matrix; $\Upomega$ is a large number (usually $\Upomega = 1,000$); and $\Upsigma$ is the dispersion matrix.

Whenever a new fuzzy rule is added, the corresponding dispersion matrix is set as $\Upsigma_k^{R_k+1}=I\Upomega.$ Parameters of the new rule are estimated using the parameters of the existing R _k fuzzy rules as follows (Angelov 2010):

$$\Uppsi^{R_k+1}_k = \sum_{i=1}^{R_k}{\theta^i\Uppsi^i_{k-1}}$$

(23)

If no new rule is added, then their parameters are inherited from the previous step, and the dispersion matrices updated accordingly. Finally, after estimation of the consequent parameters values, the model output is produced using (4).

The use of the recursive least squares algorithm depends on the initial values of the parameters $\Uppsi_0,$ and on the initial values of the entries of the dispersion matrix $\Upsigma_0.$ These initial values may be chosen if previous information about the system is available and exploring a database to get an initial rule base and $\Uppsi_0$ and $\Upsigma_0.$ When no previous information is available we may proceed choosing large values for the entries of the matrix, as indicated above. In this paper, we assume the availability of a database to get the initial rule base and corresponding parameters.

2.6 ePL+ algorithm

The detailed steps of the ePL+ model are specified in pseudo-code form. All steps of the algorithm are non-iterative. The model can develop/evolve an existing model whenever the data pattern changes, and its recursive nature turns it computationally effective.

3 Computational experiments for volatility forecasting

The ePL+ model introduced in this paper is a flexible structure that can be employed to a range of problems such as regression, time series forecasting, classification, control, clustering, and novelty detection. In Maciel et al. (2012a, b, c), the ePL+ was used to forecast nonlinear benchmark problems such as Mackey–Glass time series and Box–Jenkins gas furnace data. The results have shown the efficiency of ePL+ to produce accurate time series forecasts.

This paper shows the effectiveness of ePL+ to model and forecast financial asset returns volatility. We compare the performance of ePL+ with state of the art evolving fuzzy system modeling approaches respectively, eTS, xTS, eTS+ and ePL, and with the GARCH model, a benchmark in the area of volatility modeling.

3.1 Data

To illustrate the performance of the ePL+ model in forecasting stock market volatility, we took the daily values of the S&P 500 (US) and the Ibovespa (Brazil) stock market indexes over the period from January 3, 2000 through September 19, 2011. The daily stock return series were generated by considering the differences in the natural logarithm of the daily stock index and the previous day stock index as follows:

$$r_t = ln(P_t) - ln(P_{t-1})$$

(24)

where r _t is the stock market return, and P _t is the stock index at t.

The data set was split into two subsets. The first is an in-sample set consisting of data from January 3, 2000 through September 21, 2007. The second is an out-of-sample set with data from September 24, 2007 through September 19, 2011. The second data set is used for forecasting. Data splitting is needed for the GARCH modeling only. The evolving fuzzy models learn recursively and do not require a pre-training phase.

S&P 500 and Ibovespa intra-day data were collected for the period from January 3, 2000 through September 19, 2011 to construct the realized volatility time series and use it as the ′true volatility′ ². Realized volatility RV _t at t is computed as the sum of squared high-frequency returns within a day. This mechanism conveniently avoids data processing complications while covering more information on daily transactions. Thus

$$RV_{t+1}(\Updelta) = \sum_{j=1}^{1/\Updelta}{r^2_{t+j\cdot \Updelta,\Updelta}}$$

(25)

where $r_{t,\Updelta}$ is the discretely sampled $\Updelta$-period returns.

The evolving fuzzy models inputs are previous lags of the realized volatility of each market index. The Bayesian information (BIC) and Akaike information (AIC) criteria were used to select lag values for the GARCH model (Akaike 1974; Schwarz 1978).

3.2 Performance assignment

Evaluation of the models was done considering the root mean square error (RMSE), and the non-dimensional error index (NDEI) which is the ratio between the RMSE and the standard deviation of the target data. They are computed as follows:

$$RMSE = \left( \frac{1}{N} \sum_{k=1}^{N}{(y_k - \hat y_k)^2} \right)^{\frac{1}{2}}$$

(26)

$$NDEI = \frac{RMSE}{\mathrm{std}(y_k)}$$

(27)

where y _k is the actual volatility, $\mathrm{std}(\cdot)$ is the standard deviation function, $\hat y_k$ is the model output, and N is the number of forecasts.

Model validation is an important task in system identification to access the goodness of fit of the model. As stated by Billings and Zhu (1994), nonlinear model validation can be approached using either correlation or model-comparison. Correlation based validation involves computing correlation functions of model residuals and system inputs, and testing if these lie within confidence intervals (Billings and Zhu 1994). Model-comparison based validation concerns the use of statistical tests to compare models pairwise to test whether they are equally accurate or not in terms of their accuracy. Since ePL+ and the state of the art evolving models considered in this paper do not assume any probability distribution of data or model residuals, model-comparison based validation appear to be the one most appropriate.

In this paper, we employ the (Diebold and Mariano 1995) statistic test assuming equal predictive accuracy as the null hypothesis. This statistic test is widely used for forecasting model validation, especially in economics and finance. If N is the sample size and $e_i^1, e_i^2 \,(i=1,2,\ldots,N)$ are the forecast errors of two models, the mean square error (MSE) loss functions are computed as:

$$L_1^{\mathrm{MSE}} (e_i^1)= (e_i^1)^2, \ L_2^{\mathrm{MSE}}(e_i^2) = (e_i^2)^2$$

(28)

The Diebold–Mariano test is based on the loss difference:

$$d_i^{\mathrm{MSE}} = L_1^{\mathrm{MSE}}(e_i^1) - L_2^{\mathrm{MSE}}(e_i^2)$$

(29)

Thus, the null hypothesis is $H_0: E(d_i^{\mathrm{MSE}})=0,$ meaning that both models are equally accurate. The alternative hypothesis $H_1: E(d_i^{\mathrm{MSE}}) \neq 0$ means that model 1 is more accurate than model 2. The Diebold–Mariano test statistic, $\mathrm{DM},$ is found as follows:

$$\mathrm{DM} = \frac{\bar{d}}{\sqrt{\hat V(\bar{d} )}}\sim {\mathcal{N}}(0,1)$$

(30)

where $\bar{d}=N^{-1} \sum_{i=1}^{N} d_{i}^{MSE}$ and $\hat V(\bar{d}) = N^{-1}\left[\hat \varphi_0 + 2 \sum\nolimits_{k=1}^{N-1}{\hat \varphi_k}\right],\;\varphi_{k} = cov(d_{i}, d_{i-k}).$

3.3 Control parameters

Control parameters were chosen based on simulation experiments, attempting to produce better performance in terms of RMSE and NDEI measures in-sample set. Table 1 shows the parameters values of all evolving fuzzy models for S&P 500 and Ibovespa indexes. The SC algorithm was employed to initialize the rule base of all evolving modeling approaches.

Table 1 Control parameters of the evolving fuzzy models for S&500 and Ibovespa data

3.4 Results and discussion

Table 2 summarizes the basic statistics of the return series. The average daily returns are negative for the S&P 500 and positive for Ibovespa. The daily returns display evidence of skewness and kurtosis. The return series is skewed toward the left and characterized by a distribution with tails that are significantly thicker than for a normal distribution. The Jarque–Bera test statistics further confirm that the daily returns are non-normally distributed. The Ibovespa index has a higher kurtosis than S&P 500, which explains the fact that emerging countries, generally, exhibit more leptokurtic behavior. Under the null hypothesis of no serial correlation in the squared returns, the Ljung–Box Q ² (10) statistics infer linear dependence for both, S&P 500 and Ibovespa series. Moreover, Engle’s ARCH test for the squared returns reveals strong ARCH effects, an evidence supporting GARCH effects (that is, heteroscedasticity).

Table 2 Descriptive statistics of S&P 500 and Ibovespa daily returns

The stock indexes are shown in Fig. 2 and the corresponding returns in Fig. 3. In particular, in Fig. 3 volatility clustering becomes clearer, especially when the context of the recent US subprime crisis is considered, which translates the idea of higher non-stationarity during unstable events.

Fig. 2

Daily closing stock price indexes for the S&P 500 and Ibovespa

Fig. 3

S&P 500 and Ibovespa daily returns

For the S&P 500 index, the inputs of the evolving fuzzy models are the previous five lags of actual volatility, measured as the realized volatility, while for the Ibovespa index the past three lags of actual volatility were chosen as inputs. Models outputs are one-step ahead forecasts. A GARCH (1,1) model was selected as benchmark.

Table 3 summarizes the performance of the models when forecasting the S&P 500 and Ibovespa stock indexes volatility in terms of error measures (RMSE and NDEI), final number of rules (Rules), processing time, and number of control parameters (CP). The ePL+ model performs better than the remaining models in terms of accuracy. All evolving fuzzy models achieve better performance than the GARCH model. The number of fuzzy rules and the processing time are similar for the evolving models. From the point of view of accuracy and model complexity, ePL+ performs best since it requires less rules to achieve comparable or better modeling error values.

Table 3 Volatility modeling performance for one-step ahead forecast

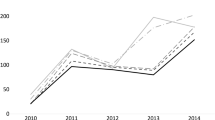
Figures 4 and 5 depict the continuous adaptation of the ePL+ model structure, i.e., the number of fuzzy rules in the rule base when modeling S&P 500 and Ibovespa stock market indexes, respectively. Notice that the number of rules increases for both indexes during 2007 and 2009, revealing the capability of ePL+ to capture instabilities due to crises. Interestingly, the 2007–2009 period corresponds to the US subprime mortgage crises.

Fig. 4

Number of fuzzy rules of ePL+ for S&P 500

Fig. 5

Number of fuzzy rules of ePL+ for Ibovespa

To illustrate the capability of the ePL+ model to deal with volatility forecasting, Figs. 6, 7 show the ″true volatility″, measured as the realized volatility, and the volatility forecasted using the ePL+ model for the S&P 500 and Ibovespa indexes, respectively. Periods of high volatility correspond to the volatility clustering behavior in the series of stock returns. The S&P 500 (Fig. 6) and Ibovespa (Fig. 7) indexes forecasts show that ePL+ successfully captures the instabilities suffered by the economies during the subprime crisis that started in the second semester of 2008.

Fig. 6

S&P 500 actual and volatility forecast using ePL+

Fig. 7

Ibovespa actual and volatility forecasts using ePL+

Figures 8 and 9 show how the values of the arousal index of ePL+ change during learning with out-of-sample data sets for both, S&P 500 and Ibovespa indexes, respectively. For S&P 500, out-of-sample learning starts with five fuzzy rules and ends with three rules for arousal threshold τ = 0.16 (Fig. 8). The Ibovespa index model starts with five rules and ends with four rules when arousal threshold τ = 0.02.

Fig. 8

Evolution of the arousal index of ePL+, out-of-sample learning for S&P 500 data

Fig. 9

Evolution of the arousal index of ePL+: out-of-sample learning for Ibovespa data

The statistical performance evaluated using the (Diebold and Mariano 1995) using MSE loss function are summarized in Table 4. Diebold–Mariano tests were done between pairs of models, e.g., ePL+ versus GARCH. The null hypothesis, the equal forecast accuracy, is rejected in all cases, assuming 5 % confidence level because |DM| > 1.96. Therefore, statistically evolving fuzzy forecast models are superior than GARCH. The eFS models can be viewed as equally accurate.

Table 4 Diebold–Mariano statistic for MSE loss function

4 Conclusion

This paper has introduced improvements of the evolving participatory learning fuzzy modeling (ePL), a method based on participatory learning and evolving systems paradigms to build adaptive fuzzy rule-based models. The enhanced version of ePL modeling, namelly ePL+, uses an utility measure to monitor the quality of the rule base and variable zone of influence of the clusters that form fuzzy rules.

Computational results concerning the evaluation of ePL+ modeling to forecast volatility were reported. The ePL+ was compared with evolving fuzzy modeling methods representative of the current state of the art, and with GARCH modeling, an approach commonly used in the economics and finance literature. Volatility forecasting plays a central role in many financial decisions such as asset allocation and hedging, option pricing, and risk analysis. Since volatility mirrors behavior of non-stationary nonlinear environments, evolving modeling have been shown to be very suitable. Empirical evidence based on S&P 500 and Ibovespa index market data illustrates the potential of the ePL+ to forecast volatility. ePL+ perform better than ePL models in terms of both, model accuracy and model structure because it achieves low modeling error with smaller number of fuzzy rules than its counterparts.

Future work will address the use of the ePL+ model in financial decision making under volatility such as in option pricing, portfolio selection, and risk analysis.