Introduction

Groundwater is an essential resource on earth for water requirements. Its quality and quantity are decreasing day by day; as a result, it is being polluted and has entered a dangerous state (Kumar et al. 2014, 2016a, 2016b). It is getting contaminated for many reasons, for instance, natural and human-caused pollution such as industrial, agricultural, and urban pollution (Karkra et al. 2016, 2017). The contaminated groundwater affects all the living organisms on earth directly or indirectly and causes several health issues and even death. Also, the treatment of groundwater against pollution is quite costly and clumsy. The pollution of groundwater in cultivation areas is having a global concern these days. Its availability as a crop irrigation resource is decreasing year by year. The organic and inorganic contaminants existing in groundwater used for irrigation can cause soil fertility loss and many health issues for humans and animals. Groundwater contamination is a topic that has gotten attention in recent years. The contamination of groundwater is a common problem all over the world.

Some countries tragically affected by this are Bangladesh, India, China, the USA, etc. (Islam 2007, Rodríguez-Lado et al. 2013; Adimalla et al. 2018; Rajmohan 2020). In Bangladesh, the condition is the worst in the history of groundwater poisoning from arsenic contamination. Some Indian states also have groundwater pollution issues such as Assam, West Bengal, Bihar, Jharkhand, Chhattisgarh, and Karnataka (Lalwani et al. 2004; Ckakraborty et al. 2007; Ghosh and Singh 2009; Umar et al. 2009; Gorai and Kumar 2013). Being the long-term use of these toxic contaminants, humans and other living beings face several problems such as hypertension, skin cancer, skin lesions, cardiovascular diseases, pulmonary diseases, neurological effects, and diabetes (Saha et al. 1999, Kile and Christiani 2008, Hendryx 2009). Therefore, it is necessary to check the vulnerability level of groundwater by producing vulnerability maps, protecting, and preserving groundwater from all kinds of contamination. By knowing the contamination level of groundwater at different places through a vulnerability map, the distribution of the areas for distinct purposes will be easy and very useful. For example, highly contaminated regions will not be used for agricultural purposes not to be affected. It will be less harmful to living beings, after knowing which area is rich in what kind of minerals the crop which has a high need of those minerals will be used there. Some remedies can also be applied in highly contaminated areas to reduce the pollution level as much as possible. Monitoring groundwater is a very scrupulous job, and also it is pretty pricey to represent a geographical degree of pollution satisfactorily on a large scale (Bai et al. 2012). So, groundwater vulnerability assessment must be economical and rapid to guard the resources and the land use management (Kumar et al. 2012; Shrestha et al. 2016).

To estimate the vulnerability level of groundwater, many models have been established as process-based models, statistical models, and index-based models. Index-based models are the most suitable ones as they do not lack proper data monitoring; they also use weights instead of parameter coefficients. In overlay and index models, the combination of spatial distributions of specific feature data (geology, depth to water, etc.) with maps gives an assigned numerical score for each feature. They are combined to produce a vulnerability score (Gogu and Dassargues 2000; Kumar et al. 2015; Lad et al. 2019; Rajasekhar et al. 2019). Among all index-based models, the DRASTIC model is the highly used model which was developed in 1987 (Aller et al. 1987). It is effortless and a rapid regional assessment tool to estimate the hydrogeologic parameter’s weights and ratings (Puri et al. 2014; Rana et al. 2014; Krishna et al. 2015; Muhammad et al. 2015; Neh et al. 2015; Pacheco et al. 2015; Hamutoko et al. 2016; Tiwari et al. 2016). However, the DRASTIC model has some limitations as weights are fixed here, and they do not need to meet the particularities of all the different study areas; also, it has human subjectivity issues as it uses the Delphi technique for assignments of weights and ratings that is why vulnerability indices estimated by this model are doubtful. Many distinctive factor weighting techniques have been developed to overcome this problem.

The weight of a parameter illustrates the significance of that parameter compared with the others. To eliminate the subjectivity of parameter weights and ratings, many modifications have been done in the fundamental DRASTIC model. Such methods are single-parameter sensitivity analysis (Pacheco et al. 2015), correlation analysis between parameter ratings and the nitrate concentrations of the study region (Panagopoulos et al. 2006), logistic regression method, or weight of evidence method (Antonakos and Lambrakis 2007). These methods were developed to calibrate the DRASTIC parameter weights and ratings, but they also had limitations and disadvantages. Another method of optimizing the DRASTIC weights and ratings was to use multi-criteria decision analysis techniques with a fundamental DRASTIC approach (Thirumalaivasan et al. 2003; Sener and Davraz 2013; Neshat et al. 2014; Kumar et al. 2019). Many MCDA techniques are developed like the analytic hierarchy process and analytic network process. These techniques give much better and optimized results than the above models, reducing subjectivity in some manner. Another modification is the inclusion of fuzzy logic in the approach to consider the uncertainty associated with the input data of study regions so that it can give us more realistic vulnerability maps (Shouyu and Guangtao 2003; Dixon 2005; Afshar et al. 2007; Pathak and Hiratsuka 2011; Rezaei et al. 2013). It sets the parameters as membership functions and assigns values between 0 and 1 instead of categorical variables with integer values in the interval 1–10. Many researchers have tried to optimize the weights and ranking of DRASTIC parameters using individual MCDA methods. There are very few studies wherein MCDA techniques have been compared vis-à-vis the optimized values of DRASTIC parameters.

This work aims to demonstrate the implementation of MCDA techniques for the optimization of weights and ranking of DRASTIC parameters and presents a critical analysis of most suitable method to get the most reliable values of DRASTIC parameters which can further be integrated with GIS to develop the groundwater vulnerability maps for any region. The analysis of the different models uncovers the impacts on vulnerability resulting from differences in the principles underlying the various weight adjustments.

Methodology

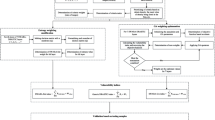
The paper deals with optimizing weights and ratings of DRASTIC parameters by using some modification techniques to make comparisons of the different models and see their accuracy levels. The novelty of the work lies in the fact that the authors have optimized both the ratings and the weights of the fundamental DRASTIC by using very comprehensive multi-criteria evaluation techniques for better accuracy assessment and fuzzy logic approach to include the fuzziness, i.e., the uncertainty of inputs. The schematic of the methodology is shown in Fig. 1.

Fig. 1
figure 1

Methodological steps of the research process

Full size image

The DRASTIC model is an index-based model proposed by Aller et al. (1987) to assess the vulnerability of groundwater to contamination. It is a rapid regional assessment tool. It is an acronym of seven important hydro-geological parameters, namely depth to water, net recharge, aquifer media, soil media, topography, impact of vadose zone, and hydraulic conductivity. It takes these parameters in terms of contamination as input and assigns weights and ratings to these parameters with the help of the Delphi network technique (Aller et al. 1987). The weights of parameters are fixed according to Aller et al., but the ratings may vary from region to region. After calculating weights and ratings, the final vulnerability index is calculated by using the below formula:

$$\mathrm{Vulnerability}\;\mathrm{Index}=\sum\limits_{i=1}^7W_i\ast R_i$$
(1)

\({W}_{\mathrm{i}}\) and \({R}_{\mathrm{i}}\) represent the weight and relative ratings, respectively, assigned to the \({\mathrm{i}}^{\mathrm{th}}\) factor of the DRASTIC formula.

The parameters, their weights, different ranges of each parameter, and their ratings established by Aller are shown in Table 1.

Table 1 DRASTIC weights and ratings by Aller (1987)
Full size table

There are many limitations in the DRASTIC model in terms of accuracy, such as lack of scientific basis, its performance significantly depending on local environmental conditions, and the assignment of weights and ratings being subjective based on Delphi technique. Thus, groundwater vulnerability assessment through the DRASTIC model does not give realistic results.

To improve DRASTIC’s performance, many modifications have been made to it; one uses multi-criteria decision analysis (MCDA) techniques. MCDA techniques are a constructive tool for solving complex decision problems (Malczewski 1999; Machiwal et al. 2011; Thokala et al. 2016; Jhariya et al. 2017; Salo et al. 2021). These techniques are helpful for complex problems where the solution to the problem depends on the number of criteria. It solves complex problems by breaking them into a hierarchy of smaller sub-problems shown in Fig. 2, which are way easier to understand and solve. It then analyzes each part and, in the end, integrates all the parts to build a meaningful solution to the problem (Malczewski 1999). The hierarchy structure of MCDA techniques is shown in Fig. 2. Its purpose is to operate a synthesis of the general contradictory features of objects, achieve a goal like choosing between the objects, rank wise ordering the objects or alternatives, organizing them into categories, etc. There are many MCDA techniques available such as AHP (analytic hierarchy process), ANP (analytic network process), best worst method (BWM), Brown-Gibson Model, etc. In this work, some MCDA techniques are used to optimize the weights and ratings of the DRASTIC parameters by employing experts’ knowledge of the particular field.

Fig. 2
figure 2

Hierarchy structure of MCDA techniques

Full size image

Optimization of DRASTIC parameters using AHP

Analytic hierarchy process (AHP) is a multi-criteria decision analysis technique given by Thomas L. Saaty (Saaty 1990a) for solving complex problems which are based on several criteria by splitting them into sub-problems (Saaty 1990b, 1994, 2000, 2001, 2008). AHP is a famous approach to solving many complex problems such as conflict resolution and any such issue, depending upon various criteria for unique alternatives. AHP is also helpful in calculating the vulnerability index of the DRASTIC model by optimizing the criteria weights and relative ratings. It also tries to eliminate the human subjectivity problem of the Delphi network technique used in the DRASTIC model in two ways:

  1. a)

    It does subjective and comparative evaluation (comparison matrices) of qualitative and quantitative views of all the existing criteria.

  2. b)

    It estimates and excludes inconsistencies in subjective valuation by calculating consistency ratios.

To calculate weights and ratings of different criteria and sub-criteria, a pairwise comparison matrix is created with comparable judgment scores obtained using “Saaty’s scale of importance,” and then the normalized principal eigenvectors are calculated. The “Saaty’s scale of importance” ranges from 1 to 9, where different levels have different meanings. The scale is represented in Table 2.

Table 2 Saaty’s scale of importance
Full size table

The whole hierarchy structure of the AHP-DRASTIC model has a goal, criteria, and sub-criteria shown in Fig. 3.

Fig. 3
figure 3

Hierarchy structure of AHP-DRASTIC model

Full size image

Here the consistency of relative weights and ratings is calculated by two terms, namely consistency index and consistency ratio. If any inconsistency remains, then reassignment of judgment values is performed.

$$\mathrm{Consistency}\;\mathrm{Index}=\left(\lambda_{max}-1\right)/\left(n-1\right)$$
(2)

where \({\lambda }_{max}\) is principal eigenvalue and n size of the comparison matrix.

It is acceptable if the estimated consistency ratio is less than or equal to 10%. Otherwise, it needs to revise the relative judgment of the criteria and sub-criteria. The consistency ratio is obtained as:

$$\mathrm{Consistency}\;\mathrm{Ratio}=\mathrm{CI}/\mathrm{RCI}$$
(3)

where RCI is standard random consistency index.

Implementation of AHP-DRASTIC model

First, a pairwise comparison matrix is obtained from all the criteria (for weights) and determines this matrix’s consistency index and ratio shown in Table 3.

Table 3 AHP-DRASTIC criteria pairwise comparison matrix for optimization of weights
Full size table

Further, pairwise comparison matrix and consistency indices are calculated for all the criteria’s sub-criteria as shown in tables (Appendix 1: Table 3a,  b, c, d, e, f, and g).

In AHP, the goal has the value of 1; also, in each level of the AHP hierarchy, total sum of criteria/sub-criteria values is 1. Here goal weight, i.e., 1, is distributed into all the criteria according to their importance, and again each criteria value is distributed into its sub-criteria as per their importance. Local values represent the importance of that criteria/sub-criteria with respect to its level, but the global values represent the importance of that criteria/sub-criteria concerning the goal. Here global values are calculated by multiplying local values with the criteria weight. The final calculated weights and ratings of DRASTIC parameters are shown in Table 4.

Table 4 Optimized weights and ratings of AHP-DRASTIC
Full size table

The limitations of AHP are that it does not include the interrelations of several parameters. Because of this, it is not much able to provide accurate results; also, it still has subjectivity issues in its weight and rating calculation process. Another limitation of AHP is that to reduce inconsistency in parameter weights and ratings, there is a need to reassign values in comparison matrices again and again to minimize inconsistency below 10%.

Optimization of DRASTIC parameters using ANP

Analytic network process is another MCDA technique that can be used in the optimization of DRASTIC parameters. ANP is a modified technique of AHP. It gives more relevant results than AHP because it recognizes the indescribable interrelationships and feedbacks between parameters and sub-parameters. The analytic network process (ANP) is a new concept that broadened the AHP by considering the dependence of parameters and the feedback between them. It introduced Thomas Saaty’s 1980 book’s supermatrix approach on the analytic hierarchy process (Wind and Saaty 1980, Khorrami et al. 2018, Thakur et al. 2021). ANP incorporates a holarchy structure rather than the hierarchy structure of AHP. In a holarchy structure, criteria, sub-criteria, and alternatives are all represented as nodes in a network of clusters. So, the ANP model has the main hierarchy having clusters with several elements, interrelations between elements, and among clusters. It has two types of feedback; first, feedback is among elements within the clusters called inner dependence, and the second is among clusters called outer dependence, as shown in Fig. 4. The cluster of elements can be connected to derive the priorities of elements by including the influence among components, i.e., clusters and elements.

Fig. 4
figure 4

A AHP structure, B ANP structure

Full size image

To perform the ANP model, the software is needed. It also creates the comparison matrices for criteria and sub-criteria based on their connections. After putting all these connection influences, a supermatrix is created, called an unweighted supermatrix of clusters with nodes. After this, the weighted supermatrix is created by multiplying the priority weights of their control criteria, i.e., normalization. Finally, a limiting matrix is created. Each matrix value resembles the connection between two nodes/clusters, i.e., priority. ANP shows each element’s significance and the complete vulnerability assessment on other elements. Here different characteristic matrices were obtained to enhance the parameter’s weight and rating prediction to assess the groundwater vulnerability.

Implementation of DRASTIC ANP model

First, the pairwise comparison matrices are formed between different parameters and sub-parameters inside and outside the cluster elements, likewise AHP. ANP compares the sub-parameters inside the parameter cluster and compares all the eight parameters and their interrelationship between the parameters and other parameters’ sub-parameters if there is a dependency. To validate the judgment criteria of matrices, C.R. is evaluated. Reconsidering the comparison matrix is necessary whenever the C.R. value beats the threshold value, which is 0.1. In ANP, inconsistency reduction is much easier than the AHP because it uses software like Super Decisions, which calculates inconsistency by itself directly. One can manipulate the values of comparison matrices at any time, and the software shows the inconsistency ratio. The comparison matrices adjusted in Super Decisions software for criteria comparison (for weights) is given in Table 5.

Table 5 ANP-DRASTIC criteria pairwise comparison matrix for optimization of weights
Full size table

Further, pairwise comparison matrix and consistency indices are calculated for all the criteria’s sub-criteria as shown below in tables (Appendix 2: Table 5a, b, c, d, e, f, and g).

The final optimized values obtained from the ANP model are given in Table 6.

Table 6 Optimized weights and ratings of ANP DRASTIC model
Full size table

Optimization of DRASTIC parameters using fuzzy logic

The fuzzy set theory concept came to solve the partial truth of values, i.e., not entirely true, not wholly false. Fuzzy set theory is a leading tool for managing imprecision or ambiguity in any system (Zadeh 1975; Rezaei et al. 2013; Hamamin and Nadiri 2018). The conventional way of quantifying values is not enough to convey complex situations, so there is a necessity to employ some other technique which is linguistic variables. The fuzzy set theory became very popular for many reasons, such as the power of working with linguistic variables, low computational cost, and easy to understand. The AHP and ANP DRASTIC models give better results than the fundamental DRASTIC. Still, they do not provide accurate results because they do not include the uncertainty or the input parameters’ fuzziness. For estimating the DRASTIC index, usually Boolean logic, i.e., the conventional quantifier, is used. Still, it may result in wrong conclusions, where values are rational numbers or near the classification boundaries. Because of the spectral and ambiguous nature of the DRASTIC parameters, if the classifications are based on Boolean logic, a slight variation in a point value may shift its rating up or down among categories and in case of points with clearly different values might have the same ratings because they are in a single category (range) together. All these difficulties cannot get resolved in the Boolean logic classification system. The only solution to these problems is the use of fuzzy logic. The fuzzy optimization model is presented to calculate the groundwater vulnerability risk by including fuzziness into the assessment. In the past, several models have been used to design fuzzy comparison matrices such as a fuzzy logarithmic least square model (LLSM) developed by (Van Laarhoven and Pedrycz 1983), which derived the triangular fuzzy weights from a triangular fuzzy comparison matrix. Similarly, other models were developed in this regard such as revised fuzzy LLSM (Wang et al. 2006) and geometric mean model employed by (Buckley 1985) to calculate fuzzy weights and many more.

The basic concept of fuzzy logic is simple: generally, the statements are not entirely “true” or “false.” They may have some degree of truth or falseness for each input. Membership functions characterize the fuzzy sets. The fuzzy optimization model is developed to estimate the risk associated with groundwater vulnerability by taking the standard value matrix of samples of the respected area. In the fuzzy logic models, pairwise comparison matrices have been constructed by utilizing linguistic evaluations concerning decision-makers’ judgments. The linguistic variables for making pairwise comparison for each criterion are given in Table 7.

Table 7 Fuzzified Saaty’s scale of importance
Full size table

Buckley’s fuzzy geometric mean model

In this research paper, the authors have implemented Buckley’s fuzzy GM model (Buckley 1985) to improve the optimization process of the ANP DRASTIC model by using the triangular membership function to give more accurate results. The following steps are to be performed:

  • Step 1: The fuzzy pairwise comparison matrix \(\tilde{D }=\left[\stackrel{\sim }{{a}_{ij}}\right]\) is constructed as

    $$\tilde{D }= \left[\begin{array}{ccc}\begin{array}{cc}(\mathrm{1,1},1)& \stackrel{\sim }{{a}_{12}}\\ \stackrel{\sim }{{a}_{12}}& (\mathrm{1,1},1)\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}\stackrel{\sim }{{a}_{1n}}\\ \stackrel{\sim }{{a}_{2n}}\end{array}\\ \begin{array}{cc}\vdots & \vdots \end{array}& \ddots & \vdots \\ \begin{array}{cc}\stackrel{\sim }{{a}_{n1}}& \stackrel{\sim }{{a}_{n2}}\end{array}& \cdots & (\mathrm{1,1},1)\end{array}\right]$$
    (4)

where \(\stackrel{\sim }{{a}_{ij}}\times \stackrel{\sim }{{a}_{ji}}\approx 1\) and i, j = 1, 2, …, n.

  • Step 2: For each criterion i, there is the fuzzy geometric mean value \(\stackrel{\sim }{{r}_{i}}\) is calculated by using the formula

    $$\stackrel{\sim }{{r}_{i}}{=({\tilde{A }}_{1}*{A}_{2}*{A}_{3}{\dots *A}_{n}\text{) }}^{\raisebox{1ex}{1}\!\left/ \!\raisebox{-1ex}{n}\right.}$$
    (5)

  • Step 3: Finally, for each criterion i the fuzzy weight \(\stackrel{\sim }{{w}_{i}}\) is calculated by

    $$\stackrel{\sim }{{w}_{i}}= {r}_{i}*{({r}_{1}+{r}_{2}+\dots +{r}_{n})}^{-1}$$
    (6)

  • Step 4: The fuzzy weights \(\stackrel{\sim }{{w}_{i}}=\left({l}_{i}, {m}_{i}, {u}_{i}\right)\) obtained from the previous step are de-fuzzified by using any method of defuzzification; here, Buckley used the COA (center of area) method, which is given below:

    $$\stackrel{\sim }{{\mathrm{w}}_{\mathrm{i}}}=\frac{\mathrm{l}+\mathrm{m}+\mathrm{u}}{3}$$
    (7)

This is how the final weights and ratings should be calculated from this fuzzy GM model.

Implementation of fuzzy geometric mean model

Here triangular fuzzy numbers are taken to obtain the pairwise comparison matrices for all the criteria and sub-criteria. After that fuzzy geometric mean, i. e., \(\stackrel{\sim }{{r}_{i}}\) is calculated by using Eq. (5), and then the fuzzy weights are calculated by using Eq. (6) Lastly, all the fuzzy weights and ratings are de-fuzzified using Eq. (7). The fuzzified criteria pairwise comparison matrix is shown in Table 8.

Table 8 Fuzzified criteria pairwise comparison matrix for optimization of weights
Full size table

The fuzzified sub-criteria pairwise comparison matrices are given below in tables (Appendix 3: Table 8a, b, c, d, e, f, and g).

The final calculated weights and rating values are shown in Table 9.

Table 9 Optimized weights and ratings of fuzzy DRASTIC model
Full size table

Results and discussion

Authentication of such kinds of experimental studies is quite difficult in the sense that vulnerability maps generated by these models, which consider the physical parameters, cannot always be very accurate due to the complex dynamics of groundwater. It is challenging to replace the cumbersome manual on-site physical investigations for ground truth. But DRASTIC provides relatively good approximate vulnerability maps, which can further be improved for more clarity and accuracy.

The weights and ratings of the DRASTIC model parameters assigned by Aller are called the fundamental DRASTIC model results. Now that it has some serious issues related to its accuracy, effectiveness, and the scientific proof of the model strategy, MCDA techniques are involved in resolving these problems. To optimize the weights and ratings of DRASTIC parameters, the authors have employed three models—AHP DRASTIC model, the ANP-DRASTIC model, and the fuzzy DRASTIC model.

AHP technique is quite useful in optimizing the weights and ratings of fundamental DRASTIC model parameters. It gives much more understandable outcomes, and it is easy to compare and analyze the importance of different criteria/sub-criteria by looking at their values. It reduces human involvement in the assignment process to some extent. Also, it has scientific proof and a methodology. To implement this technique, MATLAB software is used to calculate the results. It gives good approximate values, which can be further used for in-depth analysis. It has a limitation in that it does not provide many realistic values. To determine the accuracy at each level, the consistency index and consistency ratios are calculated for all pairwise comparison matrices, which shows the level of uncertainty present in the weights and ratings of DRASTIC parameters. So, this is not the best model to optimize the parameter values, but it sure gives a rough idea of the ranges of values.

To overcome some issues of the AHP technique, ANP technique is used. ANP gives more accurate results than the AHP technique because it includes the interrelations between parameters and the feedback between the criteria/sub-criteria, improving outcomes. Also, in ANP analysis, it is more direct and easier to reduce the uncertainty level of each parameter. In AHP, there is a need to calculate the uncertainty of pairwise comparison matrices by finding the principal eigenvector by coding in MATLAB or any other tool. Then by using an associated formula, uncertainty is calculated manually. To reduce the level of uncertainty, reassignment of the values in pairwise comparison matrices is necessary, and repeat the above process every time until the minimum possible uncertainty level is achieved, which is quite time-taking and somewhat complex. Though ANP does this much easier, it requires a software tool to estimate. This research paper uses Super Decisions software, which allows us to see uncertainty at every optimization level. It is easy to reduce it by simply changing the values of pairwise comparison matrices in the judgment tab. It recalculates the uncertainty itself, which is very useful and, more importantly, time-saving.

The following technique employed is fuzzy logic. Fuzzy logic is a beneficial technique to include when the information provided is linguistic. Fuzzy techniques included the fuzzy nature or, say, uncertain nature of the input parameters, which gives more accurate results in optimizing weights and ratings of the DRASTIC model parameters. Because of the spectral and ambiguous nature of the DRASTIC parameters, if the classifications are based on Boolean logic, a slight variation in a point value may shift its rating up or down among categories and in case of points with clearly different values might have the same ratings because they are in a single category (range) together. All these difficulties cannot get resolved in the Boolean logic classification system. The only solution to these problems is the use of fuzzy logic. This work has employed a triangular membership function instead of Gaussian or trapezoidal membership functions to obtain the best possible outcomes. The pairwise comparison matrix is converted into a fuzzy pairwise comparison matrix, and the final weights and rating get calculated. It gives the best results among the above three models.

The comprehensive comparison showing the optimized values of AHP-DRASTIC, ANP-DRASTIC, and fuzzy-DRASTIC is given in Table 10.

Table 10 Comparison of fundamental DRASTIC, AHP DRASTIC, ANP DRASTIC, and fuzzy DRASTIC parameter values
Full size table

AHP assigns parameter importance in the range of 0 to 1, through which the difference in importance values of parameters are easy to see and pretty straightforward. According to Aller, parameter D has the highest importance of value 5; however, in the case of AHP, it has an importance of 0.3221, which is the highest importance value in AHP. This optimised weight value of D parameter is improved in ANP with a value of 0.3080 because the consistency index of D parameter for weights in ANP is better than that of D parameter in AHP. Further, the fuzzy approach gives a value of 0.3086 for the weight of D parameter which includes the uncertainty present in available surface input data. Therefore, this value of 0.3086 as optimised weight of D parameter is more reliable and acceptable. T parameter has the lowest value in fundamental DRASTIC, while in case of AHP, it has a weight of 0.0245, which is lowest in AHP too, ANP improved it to be 0.0601, and fuzzy approach makes it 0.0262 again after improving. In ANP model results, parameter D and I have equal weights of value 0.3080, which shows equal importance; however, in AHP, this is not the case. In ANP, parameter A has the lowest weight with the value 0.0429, while in AHP, it has a moderate weightage of 0.0800 because, in AHP, the calculation of consistency index is very slow, manual, and complex. In fuzzy DRASTIC, parameter D and I also have an equal weightage of value 0.3086, and parameter T has the lowest weight with the value of 0.0262.

The fuzzy model gives more realistic values of optimized weights and the ratings of DRASTIC parameters by assigning the membership values as the weights and the ratings of DRASTIC parameters. Becasue in the case of fuzzy model, fuzzy numbers are used to determine the weights and ratings in contrast to crisp values which are used in AHP and ANP approaches. Then membership functions are selected to calculate the membership value. The triangular fuzzy membership function has been used in this research work. The obtained membership values are the corresponding weights and ratings of the DRASTIC parameters. The fuzzy DRASTIC approach reduces the fuzziness/ambiguity existing in the parameter inputs. For example, if the 0–5-m range of depth to water has the assigned rating of 6, instead of this, it is given a rating in a range of (5,6,7); in this case, for the whole range, the rating will not be the same for two different input values. Also, if the 0–5-m range of depth to water has the assigned rating of 6, the rating will be the same in the range from 0 to 4.9 m. But, for the range of 5 - 10m, the rating changes to 7. For example, up to 4.9m depth of water table, the rating is 6, but the rating suddenly changes to 7 for the depth of water table from 5.1 m onwards, which is a crisp jump in value. In fact, it should be gradual change. Further, for depth of water table corresponding to the depth exactly 5m, it is unclear that it should have the rating of 6 or 7. However, in the case of fuzzy approach for 0–5-m range, rating will be in the range of (5,6,7), and for 5–10-m range of depth to the water table, the rating will be in a range of (6,7,8), so the 5 m of depth to table value will have the membership value of both the ranges of (5,6,7) and (6,7,8), and that will be its rating. So fuzzy theory eliminates the ambiguity problem. Therefore, to avoid these situations, the fuzzy technique is useful. Overall, the fuzzy approach gives much more accurate and realistic results than AHP and ANP as found in the practical implementation of these optimized values of weights and ranking with GIS for study region Deccan Basaltic Province, Pune India (Lad et al. 2019). However, this is not the most precise model. It also has subjectivity issues remaining, as well as it is not a self-learning model; it cannot recognize the input patterns and use them in the future.

Conclusion

Optimization of the weights and ranking of DRASTIC parameters is a challenging task, and there have been several attempts to optimize the weights and the rankings of DRASTIC parameters, but no technique is a generic solution as every technique has its own sets of pros and cons. However, as far as the removal of human subjectivity is concerned in the assignment of values to weights and ranking of DRASTIC parameters, fuzzy system does perform better as discussed above. The work presented in this paper gives a detailed implementation of AHP, ANP, and fuzzy approach to optimize the weights and the ranking of DRASTIC parameters. The subtle nuances of building the pairwise comparison matrices in AHP and ANP and the selection of membership functions play a vital role in getting the most reliable optimized values of DRASTIC parameters which ultimately has a final role in building the groundwater vulnerability maps, and when these maps are validated against the ground truth values such as water quality parameters, it generates the most reliable map for the further analysis. As it is quite evident from Saaty’s scale of importance that in cases of trade-offs, values like 2, 4, 6, and 8, a slight different assignment of scale values can lead to a not very much optimized DRASTIC parameters values which will ultimately lead to a false groundwater vulnerability map thereby not matching with the ground truth values.

There is a need for further development and application of other decision optimization techniques depending upon the study area’s requirement and limitations of data availability. There is a need to find out one universal optimization technique used in any area, which can include all kinds of nonlinearity, and possesses the self-learning ability to bring results as accurately as possible. However, more research needs to be done on inconsistency calculation, subjectivity, uncertainty, correlation index, and accuracy for better and reliable results.