Introduction

Cautious investigations of the inherent stability of naturally occurring or man-made slopes are crucial to effective and successful engineering designs. The occurrences of slope failures are numerous and different, in such a manner that an effort to model mathematically the mechanism of slope failures presents a challenging task for the engineers. What is observed, yet, is that numerous forms of instability initiate, or advance, by sliding along critical surfaces located inside the soil mass. Thus, it is evident that for many of the engineering uses (and also for a number of others), simple sliding soil mass models are sufficient. These slope stability analysis methods mainly comprise limit equilibrium method (LEM) (Bishop 1955; Fellenius 1936; Fredlund and Krahn, 1977; Janbu 1973; Morgenstern and Price 1965; Sarma 1973; Spencer 1967), strength reduction technique (SRT) based on finite element method (FEM) (Griffiths et al. 2009; Griffiths and Fenton 2000, 2004; Griffiths and Lane 1999; Griffiths and Yu 2015) and limit analysis method (Drucker and Prager 1952; Gao et al. 2014; Wai and Chen 1975; Wu 2015). Among them, the LEM has gained immense popularity all over the world because of its robustness and simplicity of concept.

LEM for stability analysis of soil slopes works on the principle of determination of an index, which divides the strength of soil in order to bring the soil slope on the verge of failure. This index is popularly known as factor of safety Fs. A state of limiting equilibrium in soil is achieved when the shear strength of the soil along the slip surface just equates to the disturbing forces trying to destabilize the slope. The LEM deals with principles of static equilibrium only. Most of the real-life slope stability problems are generally indeterminate in nature. LEM starts with an assumption of pre-fixed shape of the failure surface, i.e., circular, logarithmic spiral, parabolic, etc. LEM for the analysis of stability of soil slopes basically follows three approaches. One approach consists of satisfying the moment equilibrium only (Bishop 1955; Fellenius 1936), and another consists of satisfying the force equilibrium of individual slices and one more approach which satisfies both the overall moment equilibrium as well as force equilibrium (Morgenstern and Price 1965; Sarma 1973; Spencer 1967). A simple approach considering a general slip surface satisfying all the conditions of equilibrium was proposed by Sarma (1973). A generalized approach for stability analysis which conglomerates all the important aspects of earlier discussed methods was proposed by Fredlund and Krahn (1977). This method can be applied to slip surface of any geometry.

Identification of critical failure surface (CFS) and the determination of the associated minimum Fs of the slope is an integral part of any slope design based on LEM. A grid-based technique can be utilized in which Fs values are determined by using various positions of center of the slip circle with different radius values and finally choosing the circle with minimum Fs as the CFS. This method is limited to circular failure surfaces. For non-circular failure surfaces, various optimization methods were suggested which works toward finding a global minimum value of Fs. Baker and Garber (1978) suggested the use of variational formulations for optimization. Chen and Shao (1988), Nguyen (1985) adopted the simplex method for optimization as it is suitable for the case when gradient of global minimum is zero. Celestino and Duncan (1981) made use of alternating variable approach. These methods were based on the approach that global minimum will be found where the gradient of objective function is zero. Cheng (2003) suggested that global minimum can exist within another domain. With the increasing application of computers in engineering field, various heuristic optimization methods gained popularity. Kirkpatrick et al. (1983) suggested an optimization algorithm based on the heat treatment process termed as simulated annealing algorithm. Holand (1975) used the concept of genetic evolution of living beings and gave the genetic algorithm method. Further developments in the field of meta-heuristic optimization methods by Kennedy and Eberhart (1995) gave birth to particle swarm optimization (PSO) which is based on simulation involving simplified social models of flocking of birds in search of food source. Geem et al. (2001) and Lee and Geem (2005) used the musical method of search for a perfect harmony state and developed a meta-heuristic algorithm known as simple harmony search method (SHM) of optimization. Cheng et al. (2007) improved the SHM method for application to complicated problems and developed the modified harmony search method. Dorigo (1992) used natural metaphors in solving optimization problems and is based on the optimization mechanism observed in Ants known as Ant-colony algorithm.

The traditional concept of Fs currently used by practicing geotechnical engineers is basically based on experience and has long been used in case of soil stability analysis. This Fs is applied to various problems of similar nature irrespective of the fact that every single one is different. It is basically a “one size fits all approach.” The deterministic approach of slope analysis does not take into account of the uncertainty of the input soil parameters which usually vary from one location to another. A better and more realistic approach would take into account the unpredictability of input parameters with respect to space. The unpredictability arises in the form of associated mathematical quantity termed as probability of failure (pf) which is a measure of the uncertainties related to our inability to properly quantify the spatial variation of various soil properties and also various inaccuracies involved during estimation of these properties. Probability of failure (pf) has become a very useful criterion for assessing the risk associated with an entity. The conflicting explanation of risk is a major cause of confusion and makes it difficult to quantify the acceptable risk. This acceptable risk means quantifying an acceptable pf for slope analysis. Probabilistic slope stability analysis of soil mass has long attracted the attention of many scientists. A number of literary works are found which have contributed to this field’s further evolution. Matsuo and Kuroda (1974) concluded that soil properties can be treated as random variables . Whitman (1984) supported the need for estimation of risk in early stages of project. Phoon and Kulhawy (1999) utilized the statistical parameters to quantify geotechnical unpredictability. Griffiths and Fenton (2004) derived the relationship between pf and Fs for undrained clay slope using the finite element method. Griffiths et al. (2009) determined the pf in case of two-dimensional slopes and three-dimensional slope by making use of random finite element method . Griffiths and Yu (2015) observed a linear increment in undrained shear strength with increasing deepness. But most of the study was limited to classical techniques incorporating limit equilibrium approaches in it. The impact of variation basically of spatial nature, of soil properties was ignored, also ambiguity was found in the location of CFS along with ignorance of local averaging.

Machine learning is the new computer-based approach to analyze the stability of soil slopes as it utilizes the input data in order to predict the future trends. In this process, programmable algorithms are used to predict the invisible patterns to make feasible decisions regarding design variables. A number of such algorithms such as SRLEM and BPNN have added to the realistic evaluation of soil slope stability problem. Chen et al. (2020) presented probabilistic evaluation of rock slope considering bi-planar sliding. BPNN is used to develop a surrogate model for factor of safety against bi-planar sliding. Zhang et al. (2021) presented the current geotechnical practices using deep learning algorithms. Extensive geotechnical applications of four major algorithms namely feedforward neural network (FNN), recurrent neural network (RNN), convolutional neural network (CNN), generative adversarial network (GAN) in the field of geotechnical engineering have been presented in recent literatures. Aladejare and Wang (2018) used Bayesian approach to indicate the correlation between c and φ and performed reliability-based slope stability analysis of rocks. Wang et al. (2020a, b) performed probabilistic slope stability analysis of Ashigong earth dam using a combination of MARS and GeoStudio software taking into account the uncertainty associated with soil parameters and water level fluctuation velocity. Wang et al. (2020a, b) performed stability analysis of Ashigong earth dam using XG-boost based reliability method and has been quite successful in predicting the failure probability. Further applications of machine learning algorithms in the field of slope stability analysis are highly warranted.

There have been numerous instances of catastrophes resulting from the failure of soil slopes. In most of the above cases, the design value of factor of safety was found to be greater than 1.5. One of the possible reasons could be the inability to take into account the uncertainty of input soil strength parameters. Modern mathematical tools of statistics and probability provide us with the arsenal to take into account the uncertainty of input variables. This study is a small initiative to use probabilistic tools to predict the failure probability and thus supplement the limit equilibrium method (LEM) based stability analysis of slopes. The procedure suggested in the paper can be utilized to improve and modify design codes for future slope stability analysis. In this study, the stability analysis of soil slope is carried out with special consideration toward the theoretical explanation of probabilistic approach of implementation procedure. This study aims at carrying out stability analysis of a cohesive soil slope and c – ϕ soil slope using classical techniques as well as using modern theories of statistics and probability. Single random variable approach is adopted in case of probabilistic analysis and the impact of using locally averaged soil properties on the is also studied. The pf versus Fs curve attains linearity with negative slope as soon as ν approaches unity and greater than unity.

Methodology

Background

In this part, the theories, mathematical analysis and associated terminologies relevant to the study of probabilistic slope stability analysis are discussed. First of all, the classical approach for slope stability analysis of cohesive soil slope devised by Skempton (1948) based on the limit equilibrium approach is illustrated. Here, undrained cohesion has been treated as a random variable. After that a simple probabilistic analysis is performed using a single random variable perspective. The dependency of pf with respect to coefficient of variation ν is also investigated in detail. The idea of local averaging is used to generate the random data. The effect of local averaging and spatial correlation length Θ on the desired output is also studied. In the next part, a c – ϕ soil slope is analyzed deterministically using the method of slices (Fellenius 1936). Further, probabilistic study of the c – ϕ slope is carried out and pf has been determined for various cases such as keeping cohesion c constant while angle of internal friction ϕ has been treated as random variable and vice versa. The effect of ν on the pf is also studied.

Random variable

In numerous analyses including components of arbitrariness, geotechnical engineers are regularly keen on some mathematical quantification related to the potential results instead of the actual results. So, to each entity in the sample space W a real number is allotted in a helpful manner in order to make estimate the probability of occurrence of the event under consideration. Mathematically, this approach deals with defining a real-valued function \(Y: \, U \, \to \, R\) which, when certain parameters are satisfied, is called a random variable. These are of two types:

  1. 1.

    Discrete random variable: The random variable, which can take at most a fixed number of distinct values, is termed as discrete random variable.

  2. 2.

    Continuous random variable: A continuous random variable is the one which takes an endless number of conceivable outcomes. A continuous random variable is not characterized at particular values. Instead, it is specified over an interval of numerical values.

Choice of distributions

In geotechnical engineering, most of the time, situations arise in which it is necessary to deal with stationary random fields. Therefore, it is necessary to choose a distribution that is truly sensible for the soil property which is going to be archetype. The Gaussian normal distribution, though a tremendously popular option, suffers from a huge disadvantage that its range varies from \(- \infty\) to \(+ \infty\). For majority of soil parameters, for example, \(c\) or elastic modulus \(\left( E \right)\), negative values are unacceptable. So, for nonnegative soil properties, one such candidate is lognormal distribution which perfectly shows the distribution only on the positive side. In the upcoming sections, we are going to use lognormal as principal distribution for soil properties being used here.

Lognormal distribution

This distribution is termed as distribution of those properties in engineering which are strictly nonnegative specific to geotechnical engineering for example \(E\), \(c\), etc. Lognormal distribution is obtained from normal distribution by carrying out a nonlinear transformation. If \(H\) is a normally scattered random variable lying in the range \(- \infty\) to \(+ \infty\), then \(Y = \exp \left\{ H \right\}\) will vary from \(0 \le y < \infty\). This implies that \(Y\) is lognormally distributed with mean \(\mu\) and standard deviation \(\sigma\). The probability density function of Y is given by

$$f(y)=\frac1{y\sigma_{\ln\;y}\sqrt{2\pi}}exp\left\{-\frac12\left(\frac{\ln\;y-\mu_{\ln\;y}}{\sigma_{\ln\;y}}\right)^2\right\}\mathrm{for} 0\leq\mathrm y<\infty$$
(1)

where \(\mu_{\ln y}\) and \(\sigma_{\ln y}^{2}\) are the mean and the variance of the normal distribution \(H\), respectively. They are obtained as follows

$$\sigma_{\ln y}^{2} = \ln \left( {1 + \frac{{\sigma_{y}^{2} }}{{\mu_{y}^{2} }}} \right)$$
(2)
$$\mu_{\ln y} = \ln (\mu_{y} ) - \frac{1}{2}\sigma_{\ln y}^{2} .$$
(3)

Correlation function

The covariance function explains a little regarding the linear dependence between Y(u′) and Y(u*). A more feasible alternative to it will be correlation function. It is also positive definite in nature. It is given by

$$\rho (u^{\prime},u^{*} ) = \frac{{C(u^{\prime},u^{*} )}}{{\sigma_{y} \left( {u^{\prime}} \right)\sigma_{y} \left( {u^{*} } \right)}}$$
(4)

where \(\sigma_{y} \left( {u^{\prime}} \right)\) is the standard deviation of Y at the position u′. A numerical value of ρ = ±1 indicates perfect linear correlation either on positive or negative side.

Markov correlation function

It is the simplest function of all the functions applicable in geotechnical engineering. This function is formulated on the principle that the future is dependent on the present. Most of the existing body of work in engineering adopts this principle, Markov property is well applicable in today’s era. The function is expressed in the form as defined below:

$$\rho (\tau ) = \exp \left\{ { - \frac{2\tau }{\theta }} \right\}.$$
(5)

The parameters \(\tau\) and \(\theta\) are the separation distance and correlation length, respectively. Correlation length is defined as the distance within which there exists a significant correlation between two points.

Variance function

Engineering properties generally consist of properties which are virtually local averages of some type. So, it is of significant interest for the engineers to study how the averages of random fields behave. A moving local average is expressed as

$$Y_{U} (u) = \frac{1}{U}\int\limits_{{u - \frac{U}{2}}}^{{u + \frac{U}{2}}} {Y(\eta )d\eta }$$
(6)

where \(Y_{U} (u)\) is the local average of \(Y\left( u \right)\) over a window of width \(U\) centered at \(u\). Local averaging generally influences the variances and the high-frequency components by reducing and damping out, respectively. But it preserves the mean of the random field. Now let us consider the variance part which is defined as

$$Var[Y_{U} (u)] = \sigma_{Y}^{2} \gamma (U)$$
(7)

where \(\gamma (U)\) is called the variance function, which tells how much variance is scaled down when \(Y\left( u \right)\) is averaged over the length \(U\). The variance function achieves a value of unity when the length \(U\) tends to \(0\). The variance function over an area \(U_{1} \times U_{2}\) in two dimensions is defined as

$$\gamma (U_{1} ,U_{2} ) = \frac{1}{{U_{1}^{2} U_{2}^{2} }}\int\limits_{{ - U_{1} }}^{{ + U_{1} }} {\int\limits_{{ - U_{2} }}^{{ + U_{2} }} {\left( {\left| {U_{1} } \right| - \left| {\tau_{1} } \right|} \right)\left( {\left| {U_{2} } \right| - \left| {\tau_{2} } \right|} \right)} } \times \rho (\tau_{1} ,\tau_{2} )d\tau_{2} d\tau_{1} .$$
(8)

Considering quadrant symmetry, the above equation can be simplified as follows:

$$\gamma (U_{1} ,U_{2} ) = \frac{4}{{U_{1}^{2} U_{2}^{2} }}\int\limits_{0}^{{U_{1} }} {\int\limits_{0}^{{U_{2} }} {\left( {\left| {U_{1} } \right| - \left| {\tau_{1} } \right|} \right)\left( {\left| {U_{2} } \right| - \left| {\tau_{2} } \right|} \right)} } \times \rho (\tau_{1} ,\tau_{2} )d\tau_{2} d\tau_{1} .$$
(9)

Now the two-dimensional variance function in terms of \(\theta\) is given as

$$\gamma (U_{1} ,U_{2} ) = \frac{{\theta_{1}^{2} \theta_{2}^{2} }}{{4U_{1}^{2} U_{2}^{2} }}\left[ {\frac{{2\left| {U_{1} } \right|}}{{\theta_{1} }} + \exp \left\{ { - \frac{{2\left| {U_{1} } \right|}}{{\theta_{1} }}} \right\} - 1} \right] \times \left[ {\frac{{2\left| {U_{2} } \right|}}{{\theta_{2} }} + \exp \left\{ { - \frac{{2\left| {U_{2} } \right|}}{{\theta_{2} }}} \right\} - 1} \right]$$
(10)

where the symbols have their usual meanings. Eq. 10 can be evaluated using Gaussian quadrature.

Slope stability analysis

In this part, the determination of factor of safety Fs for undrained cohesive soil slope as well as for \(c - \phi\) soil slope is discussed in brief. Stability analysis is carried out for both uniform soil as well as spatially varying soil. The expression of factor of safety for cohesive soil slope and for \(c - \phi\) soil slope has been presented following moment equilibrium approach and the corresponding expressions have been depicted in the following text.

Evaluation of factor of safety (F s):

Cohesive soil

The Fs is determined using the moment equilibrium approach. Let us consider a soil slope as shown in Fig. 1. For the slope shown in Fig. 1, Fs is determined using the moment equilibrium approach. The factor of safety of the cohesive soil slope is expressed as the ratio of resisting moment and the driving moment and is given by

$$F_{s} = \frac{{c_{u} L_{a} R}}{Wd}$$
(11)

where \(c_{u} =\) undrained cohesion \(L_{a} =\) Length of circular arc \(R =\) Radius of slip circle \(W =\) Weight of failure mass \(d =\) Lever Arm of the failure mass about center O of the slip circle.

Fig. 1
figure 1

Cohesive soil slope

Full size image

Cohesive frictional \(\left( {c - \phi } \right)\) Soil

One of the earliest methods of analysis generally adopted for the evaluation of \(c - \phi\) soil slope was ordinary method of slices. For the soil profiles where the effective \(\phi\) is not found to be constant over the considered failure surface, the friction circle methodology cannot be used. The ordinary method of slices is the most appropriate one.

A cohesive frictional soil slope is as shown in Fig. 2. The expression of Fs for the slice under consideration is given by

$$F_{S} = \frac{cl + w\cos \alpha \tan \phi }{{w\sin \alpha }}$$
(12)

w = weight of slice, α is the angle made by the normal with the vertical.

Fig. 2
figure 2

Cohesive frictional \(c - \phi\) soil slope

Full size image

Evaluation of probability of failure (p f)

Cohesive Soil

In this part, undrained cohesion \(c_{u}\) has been treated as random variable which leads to the following expression \(c_{u} L_{a} R\) as random variable having lognormal distribution with statistical properties denoted by mean \(\left( {\mu_{{c_{u} L_{a} R}} } \right)\) and standard deviation \(\left( {\sigma_{{c_{u} L_{a} R}} } \right)\). The pf value for the current case has been defined as the probability that the \(F_{s}\) value is less than 1. The pf value is defined as

$$p_{f} = P\left[ {F_{s} < 1} \right] = P\left[ {Z < \frac{{\ln \left( {Wd} \right) - \mu_{{ln\left( {c_{u} L_{a} R} \right)}} }}{{\sigma_{{ln\left( {c_{u} L_{a} R} \right)}} }}} \right].$$
(13)

The above expression denotes the expression for determination of pf value in case of cohesive soil, where \(Z\) is the standard normal variate. This Z value is used to express a random variable with distribution given by N (μ, σ2) to a standard form, i.e., having zero mean and unit variance using linear transformation.

Cohesive Frictional \(\left( {c - \phi } \right)\) Soil

In the present work, we are going to study how \(c\) and \(\phi\) are going to affect the Fs if each of them is considered separately. First of all, we investigate the impact of cohesion upon associated Fs by keeping the \(\phi\) value a constant and again the Fs is approximated using the following expression.

$$F_{s} = \frac{{\sum {cl} }}{{\sum {w\sin \alpha } - \sum {w\cos \alpha \tan \phi } }}.$$
(14)

Similarly, \(c\) to be constant, the expression for the Fs involved is given by

$$F_{s} = \frac{{\sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha } - \sum {cl} }}.$$
(15)

Also, the Fs is determined considering both \(c\) and \(\phi\) at a time using following expression and hence Fs is obtained.

$$F_{s} = \frac{{F_{R} }}{{F_{D} }} = \frac{{\sum {cl} + \sum {w\cos \alpha \tan \phi } }}{{\sum {w\sin \alpha } }}$$
(16)

where FR and FD represent the resisting/stabilizing and driving/destabilizing forces, respectively. Further, the value of pf is determined considering \(c\) as the random variable for the first case, and then \(\phi\) is treated as a random variable in the second case and further, both \(c\) and \(\phi\) are treated as random variables and corresponding associated pf is determined. The calculated pf versus Fs graph is plotted for each case.

When only cohesion \(\left( c \right)\) is only considered as variable

In this case, the \(c\) is assigned lognormal distribution. Further, the pf expression is derived as follows

$$p_{f} = P\left[ {F_{s} < 1} \right] = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {w\cos \alpha \tan \phi } } } \right) - \mu_{{\ln (\sum {cl} )}} }}{{\sigma_{{\ln (\sum {cl} )}} }}} \right].$$
(17)

Using Eq. 17, the pf value is determined.

When only angle of internal friction \(\left( \phi \right)\) is only considered as variable:

In this case, \(\phi\) is assigned lognormal distribution. Further, the pf expression is derived as follows

$$P\left[ {F_{s} < 1} \right] = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha - \sum {cl} } } \right) - \mu_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {w\cos \alpha \tan \phi } )}} }}} \right].$$
(18)

When both cohesion \(\left( c \right)\) and angle of internal friction \(\left( \phi \right)\) are considered as variables:

Javankhoshdel and Bathurst (2016) gave analytical solution of pf for cohesive soil by considering undrained strength \(S_{u}\) and unit weight \(\gamma\) as random variables. The analytical solution for \(c - \phi\) soil assuming both cohesion \(c\) and angle of internal friction \(\phi\) as lognormally distributed random variables doesn’t seem to be mathematically feasible. When logarithm is applied on the entire numerator term, i.e., \(\left( {F_{R} = \sum {cl} + \sum {w\cos \alpha \tan \phi } } \right)\) in Eq. 16, individual variation of \(c\) and \(\phi\) cannot be considered. A logical and simple alternative would be to apply the variation on the entire FR in Eq. 16 when the material parameters are assumed to vary lognormally. It should be kept in mind that the numerator term FR actually represents the shear strength of the soil along the considered slip surface. Therefore, if the variation is applied on the entire numerator term FR, it would include the effect of variation of the material parameters \(c\) and \(\phi\) in a crude but simple manner. When Javankhoshdel and Bathurst (2016) carried out probabilistic slope stability analysis for a purely cohesive soil slope, the variation was applied on the undrained shear strength \(S_{u}\) which only depends on the cohesion \(c_{u}\) of the soil. When \(c\) and \(\phi\) are both considered as lognormally distributed random variables, it seems logical to apply the variation on the shear strength along the slip surface. This simplification would allow us to obtain the design charts between Fs and pf when the randomness of both \(c\) and \(\phi\) is taken into consideration. Therefore, when both \(c\) and \(\phi\) are assigned lognormal distribution, the expression of pf expression becomes

$$P\left[ {F_{s} < 1} \right] = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha } } \right) - \mu_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}{{\sigma_{{\ln (\sum {cl} + \sum {w\cos \alpha \tan \phi } )}} }}} \right] = P\left[ {Z < \frac{{\ln \left( {\sum {w\sin \alpha } } \right) - \mu_{{\ln (F_{R} )}} }}{{\sigma_{{\ln (F_{R} )}} }}} \right].$$
(19)

Spatial variation of soil

The spatial variation of soil properties is taken into account using the concept of local averaging. Griffiths and Fenton (2004) advocated the use of local averaging subdivision method for developing random field involving single random variable. The method can be useful in creating random distribution of any interested parameter (such as \(c\) and \(\phi\)) over the domain of interest. Griffiths and Fenton (2004) have shown that the effect of local averaging on the lognormally distributed random variable can be mapped on a square element. Each element denotes a unique value of shear strength parameter \(\left( s \right)\). Now, the variance reduction factor for square element is determined by performing the numerical integration of variance reduction function. Now the expression of \(\gamma \left( A \right)\) as a result of local averaging over an area element having area \(A\) is given by

$$\gamma \left( A \right) = \left( {\frac{{\sigma_{{ln\left( s \right)_{a} }} }}{{\sigma_{ln\left( s \right)} }}} \right)^{2} .$$
(20)

Therefore, the locally averaged value of the variable of interest, \(\sigma_{{ln\left( s \right)_{a} }}\) in this case can be obtained as

$$\sigma_{{ln\left( s \right)_{a} }} = \sigma_{ln\left( s \right)} \sqrt {\gamma \left( A \right)}$$
(21)

and assuming for two-dimensional isotropic case with equal \(\theta\) in all directions, \(\rho \left( {\tau_{1} ,\tau_{2} } \right)\) is defined as

$$\rho \left( {\tau_{1} ,\tau_{2} } \right) = \exp \left\{ { - \frac{2}{{\theta_{\ln (s)} }}\sqrt {\left( {\tau_{1}^{2} + \tau_{2}^{2} } \right)} } \right\}$$
(22)

where \(\tau_{1}\) is the dissimilitude between the horizontal coordinates of two points \(\tau_{2}\) and is the disparity among the vertical coordinates of two points.

Considering a square-shaped element (refer to Fig. 3) having side length as a linear function of correlation length, let us denote a size parameter \(\alpha\) such that area is depicted by \(A = \alpha \theta_{\ln s} \times \alpha \theta_{\ln s}\). For square element, \(\gamma \left( A \right)\) as per Vanmarcke (1983) is given by

$$\gamma (A) = \frac{4}{{(\alpha \theta_{\ln (s)} )^{4} }}\int\limits_{0}^{{\alpha \theta_{\ln (s)} }} {\int\limits_{0}^{{\alpha \theta_{\ln (s)} }} {\left( {\alpha \theta_{\ln (s)} - x_{1} } \right)} } \left( {\alpha \theta_{\ln (s)} - x_{2} } \right) \times \exp \left\{ { - \frac{2}{{\theta_{\ln (s)} }}\sqrt {\left( {x_{1}^{2} + x_{2}^{2} } \right)} } \right\}dx_{1} dx_{2}$$
(23)

where the symbols have their usual meanings. Using the above expression, we can determine values of variance reduction function for different values of size parameter and is shown in Fig. 4. Eq. 23 can be integrated numerically using Gaussian quadrature method as suggested by Griffiths and Fenton (2008). The variance reduction function \(\gamma \left( A \right)\) can be calculated by discretizing the domain into square-shaped elements of size \(A\). For, e.g., if the slope geometry is discretized as shown in Fig. 4, it can be seen that there are 20 square elements corresponding to the dimension H where H represents the height of slope which results in side of each square element being equal to \(\frac{H}{20}\). While determining the variance reduction function for given size parameter \(\alpha\), we have considered square element with sides equal to \(\alpha \theta_{\ln s}\) where \(\theta_{\ln s}\) represents the spatial correlation length. Comparing these two parameters, the spatial correlation length is given by \(\theta_{\ln s} = \frac{0.05H}{\alpha }\) and expressing in non-dimensional form, i.e., \(\Theta = \frac{{\theta_{\ln s} }}{H} = \frac{0.05}{\alpha }\). Expressing spatial correlation length in dimensionless form adds to the simplicity of the problem and makes it possible to use the subsequent results to any size of the problem having same slope.

Fig. 3
figure 3

Discretization of slope geometry into square-shaped elements of size A

Full size image
Fig. 4
figure 4

Variance reduction function as a function of size parameter

Full size image

Using Eq. 23, the value of \(\gamma \left( A \right)\) is obtained. From Eq. 20, it is now possible to determine the locally averaged value of standard deviation \(\sigma_{{ln\left( s \right)_{a} }}\). This value is placed in the respective expressions for probability of failure pf. This results in different values of probability of failure. Spatial correlation length \(\Theta\) is obtained by comparing the no. of elements and the dimensions of the soil slope. A plot of pf against \(\Theta\) for diverse values of \(\nu\) is obtained.

Results and discussion

This section consists of two parts. In the first part, single random variable approach is used which corresponds to spatial correlation length \(\Theta = \infty\), i.e., uniform soil properties, while in the other part spatial variation of soil properties is considered through local averaging, i.e., smaller spatial correlation lengths \(\Theta\) are considered. The variation of pf with respect to \(F_{S}\) is studied for different values of coefficient of variation \(\nu\). The variability of the material parameter throughout the soil domain is represented by considering various values of \(\nu\). The obtained plots are useful to arrive at the design factor of safety \(F_{S}\) for any pre-fixed value of probability of failure (pf) of the soil slope.

Variation of p fvs. \({\varvec{F}}_{{\varvec{S}}}\) for uniform Soil \(\left( {\Theta = \infty } \right)\)

Cohesive Soil

For an undrained cohesive soil slope, Griffiths and Fenton (2004) have shown that the factor of safety \(F_{S}\) against failure increases linearly with increase in the value of the undrained cohesion \(c_{u}\). However, such deterministic estimation of \(F_{S}\) fails miserably to incorporate the effect of variability of \(c_{u}\) inside the slope. In case of soil domains where the properties show large variation, such incapability of considering the effect of variation of soil properties may lead to disastrous consequences. In such situations, it would be always desirable to take into consideration of the effect of soil variability in the slope analysis. In the present work, a cohesive soil slope of height \({\text{H = 5 m}}\), slope angle β=45°, saturated unit weight γsat = 18.0 kN/m3 (refer to Fig. 1) has been analyzed by considering undrained cohesion \(c_{u}\) to be lognormally distributed over the soil domain.

Fig. 5 shows the plot of probability of failure of pf versus \(F_{S}\) for diverse values of coefficient of variation \(\nu = \nu_{{c_{u} }}\) ranging between 0.0 and 8.0. Eq. 13 has been used to calculate pf for different values of \(F_{S}\) obtained by considering resisting moment \(c_{u} L_{a} R\) as the mean input value. The pf vs. \(F_{S}\) plots for \(\nu\) values are helpful in depicting the effect of variation of undrained cohesion \(c_{u}\) over the slope domain. The behavior observed at \(\nu = 0.00\) is interesting as \(\sigma_{{\ln c_{u} L_{a} R}} \to 0\) when \(\nu \to 0\) which causes pf to take only two extreme values either \(0\) or \(1\). Further, it is observed that with increasing \(F_{s}\) values after \(1\), the value of pf increases as \(\nu\) increases. If a certain pf is fixed as design requirement, the curves clearly depict that a higher \(F_{s}\) value must be achieved for a soil domain characterized by higher \(\nu\) signifying larger variation in its properties.

Fig. 5
figure 5

\(p_{f} \, vs \, F_{s}\) for undrained clay slope where \(c_{u}\) is a random variable

Full size image

Cohesive–frictional \(\left( {c - \phi } \right)\) soil

Effect of variation of cohesion \(\left( {\varvec{c}} \right)\)

Further, the study is carried forward by keeping \(\phi\) constant and providing statistical properties to \(c\) using lognormal distribution specified mathematically by associated mean and standard deviation values. The value of \(\phi\) is kept equal to \(35^{ \circ }\). Fs is determined by evaluating Eq. 14 and corresponding pf is found out by making use of Eq. 17. The results shown in Fig. 6 is similar to earlier case with curves turning out to be steeper demonstrating how the variation of \(c\) influences the pf versus Fs curves for \(c - \phi\) soil slopes.

Fig. 6
figure 6

\(p_{f} \, vs \, F_{s}\) in case of variation of cohesion \(c\)

Full size image

Effect of variation of angle of internal friction \(\left( \phi \right)\)

The variation in ϕ has been introduced by means of an allotment of statistical properties to it assuming it as a random variable. The angle of internal friction ϕ is assumed to follow lognormal distribution characterized by the mean and standard deviation, while c is kept fixed at a value of \(10{\text{ kN}}/m^{2}\). The obtained results are shown in Fig. 7. In this case, Fs has been determined using Eq. 15 and the associated probability of failure pf of the c – ϕ soil slope has been estimated by the use of Eq. 18. The curves depict how the variation of angle of internal friction ϕ affects the pf values when the variation of soil properties has been simulated by using different \(\nu = \nu_{\phi }\) values. Fig. 7 indicates that as ν increases, failure occurs at an inexorably more extensive range of Fs. This obtained result is further illustrated by the attainment of flat-shaped curves when ν increases gradually. For example, corresponding to ν value of 0.5, a Fs value of 1.3 yields a pf value of 0.38. In other words, if the slope is designed for a pf of 0.38, a minimum value of Fs = 1.3 is required.

Fig. 7
figure 7

pf vs Fs in case of variation of friction angle ϕ

Full size image

Variability of both c and ϕ

The variability of both c and ϕ is simulated by applying the variation on the shear strength FR appearing in Eq. 16 as shown in Fig. 8. In this figure, the symbol used to represent coefficient of variation of soil is \(\nu_{c\phi } \simeq \nu_{{F_{R} }}\). The factor of safety Fs of the slope is determined using Eq. 16 and corresponding pf is evaluated from Eq. 19. If two previous cases are considered, where both c and ϕ were varied individually (refer to Figs. 6 and 7), it can be seen that the nature of variation of pf vs. Fs follows similar trend. Although, the curves are comparatively less steep compared to the case when only c was treated as the random variable (refer to Fig. 6) as evident from the curves corresponding to coefficient of variation \(\nu = 0.5\) in Figs. 6 and 8.

Fig. 8
figure 8

\(p_{f} \, vs \, F_{s}\) in case of variation of both cohesion \(c\) and friction angle \(\phi\)

Full size image

Spatially varying soil \(\left( {\Theta < \infty } \right)\)

Cohesive soil

In this section, the effect of correlation length on the probability of failure pf of the soil slope is investigated for undrained cohesive soil slope characterized by material parameter \(c_{u}\). However, in order to express the results in non-dimensional form, a modified correlation length \(\Theta\) = \(\frac{{\theta_{\ln c} }}{H}\) is defined. The advantage of non-dimensional form is that the results become independent of the units being used during calculation. The variation of \(p_{f}\) with \(\Theta\) for different values of \(\nu\) is shown in Fig. 9. The \(\Theta\) is expressed in logarithmic form on abscissa and ordinate represents pf. With reference to Fig. 9, the curve corresponding to \(\nu = 0.42\) is almost a straight line, as not much change is observed in the value of pf with changing values of \(\Theta\). Apart from the straight line corresponding to \(\nu = 0.42\), two types of curves are observed in Fig. 9, one is below the curve corresponding to \(\nu = 0.42\) and the other above it. For the first set, that is below \(0.42\), positive slope of the curve is observed up to \(\Theta > 1\). With an increase in the value of \(\Theta\), pf value increases. On the other hand, the opposite nature is observed for the case when \(\nu > 0.42\), i.e., negative slope is observed for most of curves. It is also evident that \(p_{f}\) value decreases with an increase in \(\Theta\). Similar behavior of curve is observed when the values of \(\Theta > 1\) as the curves follow almost straight-line paths. The graph also depicts there is increase in \(p_{f}\) values with increase in \(\nu\) for different \(\Theta\) values.

Fig. 9
figure 9

\(p_{f} \, vs \, \Theta\) for different values of \(\nu\) in case of locally averaged statistics

Full size image

The variation of pf with Fs in case of using locally averaged statistics is illustrated in Fig. 10. This curve is plotted for constant value of \(\nu = 0.50\) for different values of \(\Theta\) ranging between \(0\) and \(\infty\). Most of the curves are similar except the one corresponding to \(\Theta = 0\). In this case, i.e., for \(\Theta = 0\), size parameter \(\alpha\)\(\to \infty\), which results in \(\gamma \left( A \right) \to 0\). In this case,\(\sigma_{{\ln (c_{u} L_{a} R)_{A} }} \to 0\), which makes the value of \(Z\) either \(- \infty\) or \(+ \infty\) and just provides scope for two values of \(p_{f}\) either \(0\) or \(1\). For other values of \(\Theta > 0\), most of the curves are coinciding with each other and not much difference is observed, i.e., the curves corresponding to \(\Theta = 10\) and that due to \(\Theta = \infty\) are quite similar and almost no difference is observed in specific values.

Fig. 10
figure 10

\(p_{f} \, vs \, F_{s}\) for different values of \(\Theta\) in case of local averaging

Full size image

Cohesive–frictional soil

Variation of \({\varvec{c}}\)

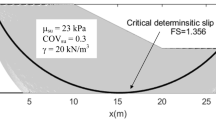
The effect of variation of \(\Theta\) on the pf is examined in the case of \(c\) assigned lognormal distribution having a mean value of \({7}{\text{.5 kN}}/m^{2}\) which corresponds to Fs value of \(1.36\). The value of \(\phi\) is kept fixed at \(35^{ \circ }\). With an increase in \(\Theta\), the effect on pf is not much pronounced due to the flattening of curves. As evident from the curves in Fig. 11, the pf values increase with an increase in \(\Theta\).

Fig. 11
figure 11

\(p_{f} \, vs \, \Theta\) considering local averaging

Full size image

The variation of pf with Fs in case of using locally averaged statistics is illustrated in Fig. 12. This curve is plotted for constant value of \(\nu = 0.50\) for different values of \(\Theta\) ranging between \(0\) and \(\infty\). Most of the curves are similar except the one corresponding to \(\Theta = 0\). In this case, i.e., for \(\Theta = 0\), size parameter \(\alpha\)\(\to \infty\), which results in \(\gamma \left( A \right) \to 0\). In this case,\(\sigma_{{\ln (c_{u} L_{a} R)_{A} }} \to 0\), which makes the value of \(Z\) either \(- \infty\) or \(+ \infty\) and just provides scope for two values of pf either \(0\) or \(1\). For nonzero values of spatial correlation length \(\Theta\), with increase in \(\Theta\) the curves start to coincide with each other.

Fig. 12
figure 12

\(p_{f} \, vs \, F_{s}\) for different values of \(\Theta\) in case of local averaging

Full size image

Variation of ϕ

The effect of variation of \(\Theta\) on the pf is examined in the case of ϕ assigned lognormal distribution having a mean value of \(34.9^{ \circ }\) which corresponds to Fs value of \(1.13\). The value of \(c\) is kept constant at \(10{\text{ kN}}/m^{2}\). With an increase in \(\Theta\), the effect on pf is not much pronounced due to the flattening of curves. As evident from the curves in Fig. 13, the pf values increase with an increase in \(\Theta\).

Fig. 13
figure 13

pf vs Θ considering local averaging

Full size image

The variation of pf with Fs in case of using locally averaged statistics is illustrated in Fig. 14. This curve is plotted for constant value of \(\nu = 0.50\) for different values of \(\Theta\) ranging between \(0\) and \(\infty\). Most of the curves are similar except the one corresponding to \(\Theta = 0\). In this case, i.e., for \(\Theta = 0\), size parameter \(\alpha\)\(\to \infty\), which results in \(\gamma \left( A \right) \to 0\). In this case,\(\sigma_{{\ln (c_{u} L_{a} R)_{A} }} \to 0\), which makes the value of Z either –∞ or +∞ and just provides scope for two values of pf either 0 or 1. For nonzero values of spatial correlation length Θ, with increase in Θ the curves start to coincide with each other.

Fig. 14
figure 14

pf vs Fs for different values of Θ in case of local averaging

Full size image

Conclusions

Stability analysis of 1:1 cohesive soil slope and 2:1 c – ϕ soil slope is carried out using probabilistic approach. The LEM is used in both cases. Skempton (1948) approach has been followed for the case of cohesive soil while Fellenius (1936) approach has been followed in case of c – ϕ soil. The Fs was determined following the above-mentioned respective cases. Expressions for the pf considering lognormal distribution of soil properties are also derived and pf value in each case is obtained. A plot of pf vs Fs is generated. Local averaging is performed over a square-shaped element and variance function is calculated using Markov correlation function for different values of scale of fluctuations/correlation length. Now the statistical soil parameters are modified after local averaging and using these modified values, pf value is again calculated. A plot of pf vs Θ and pf vs Fs is generated. From these plots, following observations are made.

In case of earlier approaches, the idea of declaring a particular slope safe was limited to the attainment of a particular value of Fs preferably above 1.0, which is a quite ambiguous approach as we have seen that even if a higher magnitude of Fs is achieved, there is always an existence of finite magnitude of pf. The variation of soil shear strength property is taken into cognizance by adopting the concept of \(\nu\) which is helpful in depicting soil strength as lognormal distribution specified by associated parameters \(\mu\) and \(\sigma\).

It is observed that with an increment in the coefficient of variation ν, respective pf increases for same value of Fs for both cohesive and c – ϕ soil slopes. Similarly, for smaller pf, Fs can be limited if value of ν is small, i.e., while designing for a given value of pf, Fs should be provided as per the variation of soil properties governed by ν. The impact of Θ upon the pf is discerned up to unit value of spatial correlation length after which their impact becomes negligible, i.e., not much change is observed in pf with increasing correlation lengths. The study highlights the need for adopting a pf based design approach of slopes. Such approach will drastically minimize the occurrences of frequent slope failures.

The limitations of the present study include a) the mathematical formulation for probabilistic analysis of soil slope has been able to well represent the separate effects of cohesion and friction, but the mathematical limitation to separate the cohesion and friction bound by logarithmic interpretation has hampered the initiative. However, when the probabilistic analysis of c – ϕ soil has been carried out, the material parameters have been considered to be uncorrelated. There has been inherent inability to develop a relationship between cohesion and angle of internal friction so as to define a factor of safety in terms of single soil strength parameter which represents the effect of both cohesion and angle of internal friction. Nevertheless, the future scopes of this study may include a) in this study, ordinary method of slice has been used to estimate factor of safety of the slope. More rigorous slope stability analysis methods such as Bishop’s method, Janbu’s method, Morgenstern–Price method, may be used to estimate factor of safety of a slope and its subsequent probabilistic analysis; b) the effect of pore water pressure and earthquake loads can be incorporated and probabilistic study may be performed; c) a formulation may be suggested where the correlation between strength parameters (i.e., c and ϕ) are considered; d) the present study is based on the consideration of a specific geometric configuration of the slope. If the slope angle changes or provisions of berms are considered, the design charts will change. Therefore, it may be interesting to develop design charts involving probability of failure and the factor of safety of slope for another geometric configuration; and e) application of different machine learning algorithms such as artificial neural network (Asteris et al. 2021; Jalal et al. 2021; Kardani et al. 2021b; Onyelowe et al. 2021), adaptive neuro-fuzzy inference system (Jalal et al. 2021; Kaloop et al. 2021), gene-expression programming (Jalal et al. 2021) and extreme learning machine (Kardani et al. 2021a) can be used to perform reliability analyses of soil slopes considering uncertainties in soil characteristics.