Introduction

In general, waterways have played a key duty in the development of civilizations. For example, major cities and industrial hubs have been historically created adjacent to the Yangtze, Nile, Mississippi, and Amazon rivers. The protection of the banks and riverbeds against erosion and scour is one of the most important issues in river engineering. There are several techniques used to protect riverbeds and banks against scour. The utilization of stone cross-section structures is considered a viable solution to protect the bed of canals and rivers. Scour is a three-dimensional phenomenon in which erodible materials such as gravel and sand are removed from around the structures. Commonly, scour is one of the most important reasons for the failure of infrastructures such as piers, road bridge piles, and abutments. Due to the complete consistency of stone with the structure of rivers, structures with stone cross-section are more popular than other riverbed protective structures. Using them, the fish pathway is fully maintained in all parts of the flow. Additionally, the construction reduction and saving costs compared with common structures are one of the most important advantages of cross-section structures. Thus, thanks to the significance of such protective constructions, numerous laboratory and theoretical investigations have been done on the flow pattern in their vicinity. For instance, some criteria for designing stone cross-vane structures with different forms such as U, W, and J shapes were suggested by Rosgen (2001). Using the shear stress concept, he put forward several equations for calculating the minimum dimension of aggregates. Also, Scurlock et al. (2011a) did a laboratory-analytical survey to assess energy drop occurring on U-shaped cross-vane structures. To simulate energy drop values, they utilized the HEC-RAS numerical model and verified the results of this model with their experimental model data. Besides, the scour pattern around these constructions with U, W, and A forms in straight channels was measured by Scurlock et al. (2011b). They proposed several formulae to predict the scour depth. Scurlock et al. 2011a, b through a laboratory investigation measured the scour values near the stone weirs sequentially installed at the bend locations of an open conduit. They evaluated the results and concluded several equations for computing maximum velocity variations at the inner bank, outer bank, and centerline of the conduit. Moreover, Pagliara et al. (2013a) measured scour hole dimensions near J-Hook vanes located in an open rectangular channel in clear-water conditions. They proposed several equations with reasonable accuracy to calculate the maximum scour depth. Subsequently, Pagliara and Kurdistani (2013) performed an experiment to measure scour values downstream of these constructions located in an open r channel. Through the conduction of dimensional analyses, they introduced the variables affecting the scour parameter and indicated that the sedimentary bed morphology changes by hydraulic conditions. Pagliara et al. (2013b) measured the dimensions of scour hole in the vicinity of W-shaped constructions through a laboratory program. Through a dimensional analysis, they suggested several relationships for estimating the maximum length and depth of the scour hole. Furthermore, the authors analyzed the obtained results by the above relationships with the laboratory measurements to exhibit their accuracy. Kurdistani and Pagliara (2017) through a laboratory investigation compared the scour values around different protective constructions such as Log-Deflectors and Log-Vanes. Using the Buckingham theorem, they manage to conduct a dimensional analysis on the variables affecting the scour values. In addition, Pagliara et al. (2015a) performed an experiment on the scour pattern around Log-Vanes made of wood. These authors scaled the scour hole depth in various geometric and hydraulic circumstances and stated that the tailwater depth was a significant hydraulic factor affecting the formation of the scour hole dimension. It is worth mentioning that Pagliara and Kurdistani (2015) assessed the scour hole values at the downstream of J-Hook constructions located in bending channels in clear-water conditions. They expressed that different types of morphologies are formed downstream of these structures according to flow hydraulic conditions. Besides, Pagliara et al. (2015b) carried out an experimental program to calculate scour values around log-deflectors installed in horizontal straight channels in clear-water conditions. They evaluated such protective structures for various geometric and hydraulic conditions. Furthermore, Pagliara et al. (2016) evaluated the scour resulted from the existence of rock sills in open horizontal and bending channels. They conducted several experiments in a horizontal channel in clear-water conditions. They proposed several useful empirical formulae for assessing the bed morphology. Furthermore, Pagliara and Kurdistani (2017) experimentally investigated scour values around log-frame deflectors. They measured the scour values near these structures for various layouts of protective structures. Subsequently, Kurdistani and Pagliara (2017) experimentally evaluated the scour pattern near U-shaped constructions installed in bending channels. By analyzing the experimental data, they divided the scour occurring in the vicinity of such structures into three different categories. Khosronejad et al. (2018) utilized a numerical model to simulate the flow pattern and the morphology of sedimentary beds in bending channels with rock vanes. To simulate the flow field, they used a model regarding the Reynolds-averaged Navier-Stokes principal in unsteady conditions. The authors validated the numerical results with the observational measurements.

Recently, various artificial intelligence (AI) algorithms have been employed to model various phenomena. Besides, such numerical models have noticeable abilities in estimating and simulating scour hole dimensions near different constructions such as piers, pipes, abutments, and submerged vanes (Azamathulla et al. 2009; Amini et al. 2011; Ebtehaj et al. 2015; Khoshbin et al. 2016; Shabanlou et al. 2018; Azimi et al. 2017, 2018, 2019a, b; Azimi and Shiri 2020). Azimi et al. (2020) simulated the scour depth around cross-vane structures through the outlier robust extreme learning machine (ORELM). The authors suggested a set of matrices to estimate the subject value.

Reviewing the literature reveals that due to the importance of the protection of banks and beds of rivers, different experimental and analytical investigations have been conducted on the scour modeling near cross-vane constructions with various forms. However, the scour depth around these constructions with I, J, and U forms installed in bending channels has not been investigated using the artificial intelligence approaches and soft computing techniques so far. So, in the current paper, the scour depth around cross-vane constructions with I, J, and U forms in bending channels is innovationally simulated by a modern artificial intelligence technique entitled “generalized structures group method of data handling (GSGMDH).” Compared to the group method of data handling (GMDH) method, this new technique has more flexibility and accuracy so that the middle nodes can receive inputs from non-adjacent nodes. By simulating the scour depth, the superior model is introduced and the most influencing inputs are detected. Eventually, a formula is presented for approximating the scour depth.

Method

The numerical models used in this study are described. Initially, the group method of data handling (GMDH) is expressed and then the new generalized structures group method of data handling (GSGMDH) is thoroughly assessed.

Group method of data handling

The GMDH model with one output and a set of inputs and is a subset of the base function elements expressed as follows:

$$ Y\left({x}_1,\dots, {x}_n\right)={a}_a\sum \limits_{i=1}^m\left({a}_i-{f}_{ij}\right) $$
(1)

where f denotes the initial function depending on different functions of the inputs, a represent factors, and m is the number of base function elements.

To solve the problem, the GMDH has several solutions called “partial models” or “partial derivatives.” The factors of this model are reckoned using the “least square” methodology. The GMSH algorithm enhances several partial models and finds a topology of GMDH with a desirable complication shown with at least one external criterion among them. The process is called the self-organizing model. It can be said that the GMDH method is considered a self-organizing methodology that gradually creates more sophisticated issues during the evaluation of the performance of output and input values. The GMDH algorithm is used to evaluate the environmental behaviors of highly complex nonlinear problems. The major idea of GMDH is to establish an analytic method based on a progressive network according to binomial transition functions. Its structure is in the form of a progressive multilayer network which is similar to artificial neural networks, except that, unlike neural networks, the number of neurons and layers are unknown and they are determined during the training process. Ivakhnenko (1976), using the Kolmogorov-Gabor polynomial, developed the GMDH theory and expressed the relationship between input and output parameters of each system using the Voltra series that is identical to the Kolmogorov-Gabor discrete polynomial.

Mathematical basis of GMDH algorithm

Suppose there are some m variables such as x1, x2, ..., xm and a parameter y as the objective parameter. There is also data for each of the xi and the objective variable y for each of training and test modes. It means that each factor is a vector containing different numbers associated with the parameter. The initial data required to be collected for the structure of the GMDH are a combination of n values represented by the following matrix:

figure a

In this matrix, the total number of data is represented by n, so that k (k<n) samples are used for learning data and n-k samples for testing data. To start the algorithm, we encounter two problems: (1) Identifying a relationship that produces the output variable based on the input variables. (2) Prediction of y for known parameters of xi, that is, model identification and the relationship between variables (simulated) is needed to model values of the target function from that model (prediction). The principal of the GMDH is the procedure of creating a high-order polynomial known as the Volterra functional series provided as follows:

$$ y={a}_0+\sum \limits_{i=1}^m{a}_i{x}_i+\sum \limits_{i=1}^m\sum \limits_{j=1}^m{a}_{ij}{x}_i{x}_j+\sum \limits_{i=1}^m\sum \limits_{j=1}^m\sum \limits_{k=1}^m{a}_{ij k}{x}_i{x}_j{x}_k+\dots $$
(2)

To this end, in the GMDH algorithm, initially, the Volterra functional series is decomposed into multivariate quadratic polynomials:

$$ y\left({x}_i,{x}_j\right)={a}_0+{a}_1{x}_i+{a}_2{x}_j+{a}_3{x}_i^2+{a}_4{x}_j^2+{a}_5{x}_i{x}_j $$
(3)

In this equation, the Volterra series is transformed into some chain recursive formulas, so that by the algebraic placement each of the recursive equations in that relationship (Volterra series) is created once again. So, the following equation:

$$ {y}_i=f\left({x}_{i1},{x}_{i2},{x}_{i3},\dots, {x}_{im}\right);i=1,2,3,\dots, n $$
(4)

is estimated by the function \( \hat{f} \):

$$ {y}_i=\hat{f}\left({x}_{i1},{x}_{i2},{x}_{i3},\dots, {x}_{im}\right);i=1,2,3,\dots, n $$
(5)

If the function \( \hat{f} \) is expressed as Eq. 2, the function \( \hat{f} \) is written as below:

$$ {\displaystyle \begin{array}{c}{\hat{y}}_k=G\left({u}_i,{u}_j\right)\kern1.32em i,j=1,2\;\left(i\ne j\right)\kern7.799994em k=1\\ {}{u}_k=G\left({s}_i,{s}_j\right)\kern1.32em i,j=1,2,K,{F}_1\;\left(i\ne j\right)\kern2.16em {F}_1\le {C}_{F_2}^2\kern2.16em k=2\\ {}{s}_k=G\left({p}_i,{p}_j\right)\kern1.08em i,j=1,2,K,{F}_2\;\left(i\ne j\right)\kern2.16em {F}_2\le {C}_{F_3}^2\kern2.16em k=3\\ {}\vdots \kern7.319995em \vdots \kern5.399997em \vdots \kern3.719998em \vdots \\ {}{z}_k=G\left({w}_i,{w}_j\right)\kern1.32em i,j=1,2,K,{F}_l\;\left(i\ne j\right)\kern1.92em {F}_l\le {C}_m^2\kern2.28em k={F}_{l-1}\\ {}{w}_k=G\left({x}_i,{x}_j\right)\kern1.32em i,j=1,2,K,m\;\left(i\ne j\right)\kern6.119996em k={F}_l\end{array}} $$
(6)

The order of these relationships from top to bottom is a display of the decomposition steps of Eq. 4 into quadratic polynomials. On the other hand, the order of these relationships from bottom to top indicates the completion of Eq. 4 using returning equations. Indeed, the aim of the algorithm is to detect the unknown factor “a” in the Volterra function series. The resulted partial models own a structure identical to the below function:

$$ \hat{f}\left({x}_i,{x}_j\right)={v}_0+{v}_1{x}_i+{v}_2{x}_j+{v}_3{x}_i^2+{v}_4{x}_j^2+{v}_5{x}_i{x}_j $$
(7)

Given that the purpose we pursue in this algorithm is nothing but the initial system modeling, thus through the combination of partial models and iteration of this process, the major model of the problem is calculated as below:

$$ \hat{f}={v}_0+\sum \limits_{i=1}^m{v}_i{x}_i+\sum \limits_{i=1}^m\sum \limits_{j=1}^m{v}_{ij}{x}_i{x}_j+\sum \limits_{i=1}^m\sum \limits_{j=1}^m\sum \limits_{k=1}^m{v}_{ij k}{x}_i{x}_j{x}_k+\dots $$
(8)

After the analysis of the problem into Cm2 partial systems, a function with two inputs is calculated for each of them. Thus, produced partial systems are combined in pairs resulting \( {C}_m^2\left({C}_m^2-1\right)/2 \) problems or new partial models with at least three or four inputs. However, the number of variables dependent on the model or in other words the number of problem inputs is not significant and only the actual precision of the problem estimation by produced systems is important. So, considering this rule to reduce redundant computations and increase the modeling performance and precision, several produced partial functions with acceptable precision and approximation over other functions are chosen and the rest are removed.

Secondly, partial functions are chosen and then the ideal function created in the earlier stage is combined in pairs similar to the first step and new partial functions with at least five and at most six inputs are generated.

In the same way, in the next steps, the combination procedure is repeated by choosing and eliminating a number of created partial functions to finally reach a perfect result.

The main aim of these steps is to achieve a function that almost all parameters are visible and have the lowest number of models (the provided model should be simple). The other purpose considered in performing iterative amalgamation is to reach a model with the lowest error compared to other models calculated in the previous steps.

To this end, the Corrected Akaike Information Criterion (AICC) is used which in addition to considering the means square error (MSE) for evaluating the model accuracy considers the number of parameters that exist in the model to provide the simplest model.

$$ AI{C}_C=n\times \log \left(\sum \limits_{i=1}^n{\left({y}_{pre}-{y}_{obs}\right)}^2\right)+2z+\frac{2z\left(2z+1\right)}{n-z-1} $$
(9)

Here, n is the number of observations, ypre and yobs are the predicted and observed values, respectively, and z is the number of tuned factors through the modeling by GMDH.

In each layer of the GMDH network, to estimate partial equations, binary choices are done among inputs of that layer of the neural network to create partial equations by means of partial equations. For example, the number of binary selections in the first layer is:

$$ {C}_m^2=\left(\begin{array}{c}m\\ {}2\end{array}\right)=\frac{m\left(m-1\right)}{2} $$
(10)

Given that the aim of the utilization of this algorithm is to model and estimate y, so the main equation (Eq. 4) is obtained by the amalgamation of partial systems and iterating this process.

Generalized structure of GMDH

Despite a good capability of convectional GMDH for modeling complex issues, GMDH owns some disadvantages like other techniques. Such disadvantages have a significant impact on results provided by this model so that sometimes significantly decreases the modeling accuracy. Some of the main important disadvantages of this technique are as follows:

  1. 1-

    The structure of the defined polynomial (Eq. 7). This is a second-order polynomial so that there are only two neurons in each polynomial.

  2. 2-

    Input neurons in each layer are only chosen from adjacent layers.

Therefore, for problems of great complexity, the use of second-order polynomials may not yield satisfactory results. Besides, considering two inputs for each neuron leads to an increase in the number of neurons in order to achieve an acceptable model. Using adjacent neurons increase the number of produced polynomials. Thus, the existence of such problems has a noticeable influence on the accuracy and simplicity of provided models. Hence, a model entitled “generalized structure of GMDH (GSGMDH)” is presented in this paper. GSGMDH has been coded by using MATLAB software. The presented model changes the global structure of convectional GMDH so that simultaneously evaluates all possible modes in achieving the best and simplest available model using second and third polynomials and also using two and three inputs in each neuron and finally chooses the best model by means of AICc.

In fact, four states can occur: (1) second-order polynomial with two inputs, (2) second-order polynomial with three inputs, (3) third-order polynomial with two inputs, and (4) third-order polynomial with three inputs. Among these states, the first case is exactly the same relationship provided for convectional GMDH (Eq. 7). Thus, the general form of the polynomial defined in this study is expressed as follows:

$$ y=v0+v1\ast xik+v2\ast xiq+v3\ast xip+v4\ast xiq\ast xik+v5\ast xip\ast xik+v6\ast xip\ast xiq+v7\ast xik\ast xik+v8\ast xiq\ast xiq+v9\ast xip\ast xip+v10\ast xip\ast xiq\ast xik+v11\ast xiq\ast xik\ast xik+v12\ast xiq\ast xiq\ast xik+v13\ast xip\ast xik\ast xik+v14\ast xip\ast xiq\ast xiq+v15\ast xip\ast xip\ast xik+v16\ast xip\ast xip\ast xiq+v17\ast xik\ast xik\ast xik+v18\ast xiq\ast xiq\ast xiq+v19\ast xip\ast xip\ast xip $$
(11)

Furthermore, GSGMDH has the ability to choose neuron inputs from a non-adjacent layer. In Fig. 1, a GSGMDH modeling sample in which the neuron input is from the non-adjacent layer is illustrated. It is seen that Neuron x6 has three inputs and the Neuron x7 has two inputs. Moreover, Neuron x8 as the output of the problem takes three inputs including x3, x6, and x7. It is clear that x3 is taken from a non-adjacent layer. The flowchart of GSGMDH is presented in Fig. 2.

Fig. 1
figure 1

An example of GSGMDH for a model with five inputs

Full size image
Fig. 2
figure 2

Flowchart of proposed GSGMDH

Full size image

Goodness of fit

In the present paper, for assessment of the introduced models, the correlation coefficient (R), variance accounted for (VAF), Root Mean Square Error (RMSE), the scatter index (SI), Mean Absolute Error (MAE), and the Nash-Sutcliffe efficiency coefficient (NSC) are employed as follows (Azimi and Shiri 2020a, b):

$$ R=\frac{\sum_{i=1}^n\left({F}_i-\overline{F}\right)\left({O}_i-\overline{O}\right)}{\sqrt{\sum_{i=1}^n{\left({F}_i-\overline{F}\right)}^2{\sum}_{i=1}^n{\left({O}_i-\overline{O}\right)}^2}} $$
(12)
$$ VAF=\left(1-\frac{\mathit{\operatorname{var}}\left({F}_i-{O}_i\right)}{\mathit{\operatorname{var}}\left({F}_i\right)}\right)\times 100 $$
(13)
$$ RMSE=\sqrt{\frac{1}{n}{\sum}_{i=1}^n{\left({F}_i-{O}_i\right)}^2} $$
(14)
$$ SI=\frac{RMSE}{\overline{O}} $$
(15)
$$ MAE=\frac{1}{n}\sum \limits_{i=1}^n\left|{F}_i-{O}_i\right| $$
(16)
$$ \mathrm{NSC}=1-\frac{\sum \limits_{i=1}^n{\left({O}_i-{F}_i\right)}^2}{\sum \limits_{i=1}^n{\left({O}_i-\overline{O}\right)}^2} $$
(17)

where Oi represents observational values, Fi is predicted values by AI models, \( \overline{O} \) is the average of experimental values, and n is the number of experimental values. In the following parts, initially, different activation functions are evaluated. Then, the superior model and the most significant inputs are ascertained through a sensitivity analysis. Moreover, the GSGMDH superior is compared with the GMDH model. Besides, an uncertainty analysis and a partial derivative sensitivity analysis (PDSA) are accomplished. Finally, a formula is proposed for estimating the scour depth near the cross-vane constructions with various forms placed in bending channels.

Experimental models

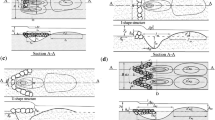
In order to validate the AI models, the experimental values conducted by Pagliara and Kurdistani (2015), Pagliara et al. (2016), and Kurdistani and Pagliara (2017) are used. The experimental models of cross-vane constructions with J, U, and I forms were used inside a bending channel with a rectangular cross-section with a length of 15 m, a height of 0.5 m, and a width (B) of 0.5 m. They measured the scour depth (Zm) near a structure with a height of hst and a width of b for densimetric Froude numbers equal to Fd. Additionally, the difference between the flow depths near the structure is Δy. The schematic of these experimental models is illustrated in Fig. 3.

Fig. 3
figure 3

Schematic of laboratory models of cross-vane constructions in bending channels (a) J-shaped, (b) U-shaped, (c) I-shaped (Pagliara and Kurdistani 2015; Pagliara et al. 2016; Kurdistani and Pagliara 2017)

Full size image

Scour near cross-vane constructions

Pagliara and Kurdistani (2015), Pagliara et al. (2016), and Kurdistani and Pagliara (2017) showed that the variables governing the scour near the structures are scour depth (Zm), height of the structure (hst), tailwater depth (htw), length of the cross-vane construction (l), channel width(B), the difference between flow depth at the downstream and the upstream of the structure (Δy), discharge (Q), viscosity of water and sediment (ρs, ρ), gravity (g), the average diameter of sediments (d50), and the radius of the channel bend (R) as follows:

$$ f\left({Z}_m,{h}_{st},{h}_{tw},l,B,\varDelta y,Q,{\rho}_s,\rho, g,{d}_{50},R\right)=0 $$
(18)

Through a dimensional analysis, they exhibited that the scour near the cross-vane constructions is a function of the below variables:

$$ {Z}_m/{h}_{st}=f\left(l/B,{h}_{tw}/{h}_{st},{F}_d,\varDelta y/{h}_{st},B/R\right) $$
(19)

In the studies accomplished by Pagliara and Kurdistani (2015), Pagliara et al. (2016), and Kurdistani and Pagliara (2017), the parameter l has not been reported. Furthermore, the shape factor of cross-vane constructions with J, I, and U shapes is also denoted byφ. Thus, Eq. 17 is rewritten as follows:

$$ {Z}_m/{h}_{st}=f\left({h}_{tw}/{h}_{st},{F}_d,\varDelta y/{h}_{st},B/R,\phi \right) $$
(20)

where Fd is the densimetric Froude number. So, the variables of Eq. 20 are assumed as the inputs. It means that six numerical models are developed through different combinations to detect the influencing factors. The developed models are depicted in Fig. 4. It is worth mentioning that 70% of the data are applied for learning the GMDH and GSGMDH models and 30% of this data are employed for testing these models.

Fig. 4
figure 4

Combinations of input parameters for developing different numerical models

Full size image

Result and discussion

GMDH models

All GMDH numerical models are examined. As discussed in the previous section, six different artificial intelligence models are defined using the input parameters to detect the superior GMDH and the most influencing input. All estimated indices for the GMDH models are illustrated in Fig. 5. GMDH1 simulates the scour parameter using all inputs(htw/hst, Fd, Δy/hst, B/R, ϕ). This model is more accurate than other GMDHs. As an example, the VAF, MAE, and NSC for GMSH1 in the training mode are respectively computed to be 74.451, 0.233, and 0.646. Furthermore, the RMSE and SI for this model in the testing stage are respectively reckoned to be 0.277 and 0.252. For GMDH2, the SI, RMSE, and MAE in the testing stage are respectively estimated to be 0.541, 0.594, and 0.511. Besides, the NSC and VAF in the training mode for this model are − 0.911 and − 11.517. On the other hand, for simulating the scour parameter by this model, the shape factor (ϕ) is eliminated and this model is a function of htw/hst, Fd, Δy/hst, B/R. Also, in the training mode, GMDH3 estimates MAE and RMSE equal to 0.582 and 0.439, respectively. Besides, this artificial intelligence model calculates VAF, SI, and NSC in the testing mode to be 9.343, 0.574, and − 0.384, respectively. GMDH3 forecasts the target values regarding the parameters htw/hst, Fd, Δy/hst, ϕand the effect of the parameter B/R is neglected, while for GMDH4 in the training mode, the VAF and RMSE are 31.384 and 0.502. Additionally, MAE and NSC in the testing situation are estimated to be 0.543 and − 0.594. For simulating the scour pattern by GMSH4, the dimensionless parameters htw/hst, Fd, B/R, ϕ are implemented and the effect of the Δy/hst is relinquished. For GMDH5, the RMSE, VAF, and SI in the testing stage are surmised 0.572, 6.507, and 0.529. Furthermore, the MAE and NSC in the testing situation are respectively yielded equal to 0.516 and − 0.941. To approximate the scour parameter by the GMDH5 model, the dimensionless parameters htw/hst, Δy/hst, B/R, ϕ are employed and the impact of the parameter Fd is neglected. Besides, GMDH6 simulates the target value using Fd, Δy/hst, B/R, ϕ and for this model the effects of the parameter htw/hst are removed. For this model, SI and MAE in the testing stage are respectively calculated to be 0.561 and 0.612.

Fig. 5
figure 5

Calculated indices for GMDH models

Full size image

In Figs. 6 and 7, the comparison of the scour values simulated by the GMDH models with the experimental measurements and their scatter diagrams is shown. GMDH1 owns the highest precision and the lowest error among these GMDHs. For GMDH1, the correlation coefficient (R) in the training and testing stage is obtained equal to 0.863 and 0.855, respectively. Also, the R values for GMDH2, GMDH3, and GMDH4 in the testing situation are computed 0.191, 0.425, and 0.409. In contrast, GMDH5 and GMDH6 estimate the R values in the training mode equal to 0.371 and 0.423. Therefore, GMDH2 has the lowest correlation and the highest error. Furthermore, GMDH1 is the best model estimating the objective function using all input parameters. In addition, the shape factor (ϕ) and also the densimetric Froude number are known as the most important inputs.

Fig. 6
figure 6

Comparison of scour values simulated by GMDH models with observed

Full size image
Fig. 7
figure 7figure 7

Scatter plots for GMDH models

Full size image

GSGMDH models

The accuracy of the GSGMDH models is assessed. The computed indices for these GSGMDH models are depicted in Fig. 8. Among all GSGMDHs, the GSGMDH1 model owns the highest accuracy and the lowest error. Additionally, the model calculated the RMSE, MAE, and SI in the training stage as 0.232, 0.166, and 0.214, respectively. For GSGMDH1, the VAF value in the training mode is improved by about 12% compared to the GMDH1 model. Moreover, the NSC value for this model in the testing mode is estimated to be 0.842. In the training mode, GSGMDH1 computes NSC and MAE equal to 0.397 and 0.263. The VAF in the testing mode of the GSGMDH model significantly increases compared to the GMDH2 model. Furthermore, for GSGMDH3 in the testing mode, the values of NSC, SI, and MAE are estimated to be 0.829, 0.186, and 0.155. The VAF index in the training mode of the GSGMDH 3 model is improved by about 41% compared to the GMDH3 model. Among all GSGMDHs, the GSGMDH4 model owns the maximum error and the lowest accuracy. In other words, the RMSE and MAE in the testing stage of this model are considered 0.335 and 0.279. However, the VAF index in the testing mode of this model is almost twice the GMDH4 model. Additionally, the NSC, MAE, and SI for the GSGMDH5 in the testing situation are 0.542, 0.231, and 0.298, respectively. Compared to the GMDH5 model, this model has a better performance so that the VAF index in the training mode increases about 11 times the GMDH5 model. For GSGMDH6, the SI, MAE, and RMSE in the testing situation are respectively estimated to be 0.235, 0.201, and 0.295. Furthermore, the VAF index in the training and testing phases for the GSGMDH6 model is approximated to be 78.427 and 76.429, respectively.

Fig. 8
figure 8

Computed indices for GSGMDH models

Full size image

Thus, according to the results of the GSGMDH models, the dimensionless parameters Δy/hst and ϕ are the most influencing inputs of the GSGMDH.

In Figs. 9 and 10, a comparison of the predicted and observed scour parameters and also the scatter plots of all GSGMDH models are depicted. the R values for the GSGMDH 1 in the training and testing modes are computed 0.913 and 0.930, respectively. Additionally, for the testing mode of GSGMDH2 and GSGMDH4, the R index values are estimated 0.821 and 0.924, respectively. Besides, the R values for GSGMDH4, GSGMDH5, and GSGMDH6 in the training stage are respectively obtained as 0.790, 0.860, and 0.886.

Fig. 9
figure 9

Comparison of scour values simulated by GSGMDH models with observed parameters

Full size image
Fig. 10
figure 10figure 10

Scatter plots for GSGMDH models

Full size image

Thus, all GSGMDH models have a better proficiency in comparison with the GMDH models and predict the objective function values with higher accuracy.

Moreover, among all numerical models, the GSGMDH1 is determined as the best model. This model surmises the scour parameters using all inputs.

Based on the analysis of the artificial intelligence models, the parameters ϕ, Δy/hst and the densimetric Froude number are considered the most effective inputs.

Uncertainty analysis

The performance of the best models is assessed through an uncertainty analysis. Generally, the uncertainty analysis is a beneficial aid for assessing the performance of GMDHs and GSGMDHs (Karbasi and Azamathulla 2016; Azimi et al. 2018, 2019a, b). In other words, this analysis is performed to measure the error computed by these models and assess their proficiency. The error predicted by a model equal to values predicted by the model (Pi) minus observed parameters (Oi)(ei = Pi − Oi). Besides, the average of the calculated error is surmised as \( \overline{e}={\sum}_{i=1}^n{e}_i \). Furthermore, the standard deviation of calculated error is in the form of \( {S}_e=\sqrt{\sum_{i=1}^n{\left({e}_i-\overline{e}\right)}^2/n-1} \). Also, the negative sign of \( \overline{e} \) shows an underestimated proficiency of this model, whereas its positive sign reveals the overestimated performance. In addition, by using the \( \overline{e} \) and Se, a confidence bound is created near the error values predicted by the Wilson score model without the continuity correction. Then, the utilization of ±1.96Se, approximately results in a 95% confidence bound (Azimi and Shiri 2021). These parameters of the uncertainty analysis are listed in Table 1. In this table, the width of the uncertainty bound and the 95% prediction error interval are denoted by WUB and 95% PEI, respectively. Both the GMDH1 and GSGMDH1 models own an underestimated performance. Furthermore, the width of the uncertainty bound for the GMDH1 and GSGMDH1 models are respectively calculated − 0.049 and − 0.038. Moreover, 95% PEI for the GMDH1 model is calculated from − 0.049 to 0.049. Also, 95%PEI for the GSGMDH1 model is approximated from − 0.038 to 0.038.

Table 1 Uncertainty analysis results for GMDH and GSGMDH
Full size table

Superior model

The GSGMDH1 is introduced as the superior GSGMDH in simulating the scour depth near cross-vane construction with different forms. For this model, a formula is presented for predicting the scour depth near these protective structures as follows:

$$ {Z}_m/{h}_{st}=0.296+-0.171\ast x6+3.056\ast B/R+0.1457\ast x7-3.393\ast B/R\ast x6+2.016\ast x7\ast x6-0.052\ast x7\ast B/R-0.140\ast x{6}^2-9.462\ast B/{R}^2-0.928\ast x{7}^2+0.188\ast x7\ast B/R\ast x6+0.502\ast B/R\ast x{6}^2+4.721\ast B/{R}^2\ast x6-0.219\ast x7\ast x{6}^2-2.686\ast x7\ast B/{R}^2-0.647\ast x{7}^2\ast x6+0.443\ast x{7}^2\ast B/R+0.117\ast x{6}^3+10.864\ast B/{R}^3+0.506\ast x{7}^3 $$
(20)
$$ x6=0.491-0.845\ast \varphi -2.979\ast \varDelta y/{h}_{st}+0.276\ast {F}_d+3.635\ast \varDelta y/{h}_{st}\ast \varphi -0.005\ast {F}_d\ast \varphi +2.347\ast {F}_d\ast \varDelta y/{h}_{st}+0.481\ast {\varphi}^2+7.610\ast {\left(\varDelta y/{h}_{st}\right)}^2-0.121\ast {F_d}^2-0.250\ast {F}_d\ast \varDelta y/{h}_{st}\ast \varphi -0.365\ast {\left(\varDelta y/{h}_{st}\right)}^2\ast {\varphi}^2-5.563\ast {\left(\varDelta y/{h}_{st}\right)}^2\ast \varphi -0.045\ast {F}_d\ast {\varphi}^2-2.770\ast {F}_d\ast {\left(\varDelta y/{h}_{st}\right)}^2+0.0496\ast {F_d}^2\ast \varphi -0.065\ast {F_d}^2\ast \varDelta y/{h}_{st}-0.027\ast {\varphi}^3+1.406\ast {\left(\varDelta y/{h}_{st}\right)}^3+0.004\ast {F_d}^3 $$
(1-20)
$$ x7=1.144-4.572\ast \varphi +0.348\ast {F}_d-1.235\ast {h}_{tw}/{h}_{st}+0.836\ast {F}_d\ast \varphi -2.468\ast {h}_{tw}/{h}_{st}\ast \varphi +0.571\ast {h}_{tw}/{h}_{st}\ast {F}_d+8.840\ast {\varphi}^2-0.278\ast {F_d}^2+0.135\ast {\left({h}_{tw}/{h}_{st}\right)}^2-0.194\ast {h}_{tw}/{h}_{st}\ast {F}_d\ast \varphi -0.547\ast {F}_d\ast {\varphi}^2+0.142\ast {F_d}^2\ast \varphi +1.379\ast {h}_{tw}/{h}_{st}\ast {\varphi}^2+0.027\ast {h}_{tw}/{h}_{st}\ast {F_d}^2+0.056\ast {\left({h}_{tw}/{h}_{st}\right)}^2\ast \varphi -0.046\ast {\left({h}_{tw}/{h}_{st}\right)}^2\ast {F}_d-3.188\ast {\varphi}^3-0.003\ast {F_d}^3-0.040\ast $$
(2-20)

Partial derivative sensitivity analysis

The PDSA is performed for GSGMDH1. Generally, PSDA is performed for identifying the influence of inputs on the objective parameter. In other words, PSDA is a method for identifying the variation pattern of the objective parameter according to input parameters. The positive PDSA shows that the scour parameter is enhancing, whereas the negative sign identifies that the objective function is reducing. The relative derivative of each input parameter is calculated regarding the target value (Azimi et al. 2017). For example, the PDSA values are negative for most of the htw/hst values. The impact of this input variable is decreasing, while the PDSA results for the input parameters Fd, Δy/hst, and B/R are positive. Conversely, a part of the PSDA results for the shape factor (φ) has a positive sign and the other part has a negative sign (Fig. 11).

Fig. 11
figure 11

PSDA results for superior model

Full size image

Conclusion

Thanks to the crucial role of rivers in maintaining the ecosystem of different areas and developing cities, the preservation of their bed and banks is quite significant. In general, different approaches such as submerged vanes, log-deflectors, and cross-vane structures are used to protect riverbeds. Thanks to the ease of protection, cost-saving, and consistency with the ecosystem, cross-vane structures are more popular. In the current paper, a modern AI method entitled “generalized structure group method of data handling (GSGMDH)” was employed for predicting the scour depth near cross-vane constructions with I, U, and J shapes installed inside bending channels for the first time. Compared to the classical GMDH method, this model has higher accuracy and greater flexibility for estimating the scour depth, because, in this technique, middle nodes can take inputs from a non-adjacent layer. To simulate the scour depth, through the inputs, six models were developed for the GMDH and GSGMDH methodologies. The analysis of the models exhibited that the proficiency of the GSGMDH was better. For instance, the RMSE, R, and NSC for the GMDH in the testing stage are calculated to be 0.277, 0.855, and 0.655, while for the GSGMDH are computed equal to 0.196, 0.930, and 0.842, respectively. The sensitivity analysis indicated that the shape factor (ϕ) of cross-vane structures, the ratio of the difference between the flow depths downstream and upstream of the structure to the structure height (Δy/hst), and the densimetric Froude number (Fd) are the most effective input parameters. In addition, the GMDH and GSGDMH models had underestimated performance. Subsequently, an equation for calculating the scour depth near cross-vane construction with various forms was proposed. Finally, the influence of the input parameters on the objective function was investigated by performing a PDSA.

The obtained results exhibited that the artificial intelligence (AI) approaches had a reasonable ability to predict the scour hole in the vicinity of the cross-vane structures in the curved flumes. It is worth noting that the suggested formula can be utilized in practical application particularly in the field of river engineering to approximate the scour hole depth around this type of structures. Even though the current study provides a good understanding of the simulation of scouring around cross-vane structures with different shapes by using the artificial intelligence (AI) models, further experimental and numerical investigations can be performed in the future.