Introduction

Rock mass contains many types of discontinuities like fault, fold, and joints. ISRM (1978) defines these discontinuities as having zero tensile strength. Among them, joint can be defined as a plane of weakness along which there is no visible displacement. It can be opened or filled with gouge material such as silt and clay. The presence of rock joints largely governs the mechanical properties of rock mass. In geotechnical engineering, the accurate assessment of joint shear strength is very essential for stability of rock mass. The shear strength is mostly controlled by the roughness of joint surface which is composed of first-order (waviness) and second-order (unevenness) asperities.

Due to very complex nature of roughness, the accurate prediction of joint shear strength is not an easy task. In literature, many constitutive models (Patton 1966; Ladanyi and Archambault 1970; Barton 1973; Plesha et al. 1989; Maksimović 1992, 1996; Jing et al. 1992; Huang et al. 1993; Wibowo et al. 1994; Kulatilake et al. 1995; Zhao 1997a, b; Amadei et al. 1998; Yang and Chiang 2000; Indraratna and Haque 2000; Homand et al. 2001; Wang et al. 2003; Grasselli and Egger 2003; Tatone 2009; Asadollahi and Tonon 2010; Ghazvinian et al. 2012; Xia et al. 2014) are developed to predict shear strength of rock joints under CNL condition. Among all constitutive models, Barton model (Eq. 1) is still widely used in practice due to its simplicity.

$$ {\tau}_B={\sigma}_n\tan \kern.1em \left[{\phi}_b+ JRC{\log}_{10}\left(\frac{JCS}{\sigma_n}\right)\right] $$
(1)

where ϕb is the basic friction angle, JRC is the joint roughness coefficient, and JCS is the joint wall strength which is equal to compressive strength of rock for fresh rock joints. JRC can be estimated either by back calculation of direct shear tests results or by visual comparison with ten standard profiles ranging from 0 to 20 (Barton and Choubey 1977).

In the field of rock engineering, the accurate determination of JRC remains an active area of research, and to quantify JRC, several methods like statistical (Tse and Cruden 1979; Yu and Vayssade 1991; Yang et al. 2001; Tatone and Grasselli 2010), fractal (Brown and Scholz 1985; Reeves 1985; Maerz et al. 1990; Milinverno 1990; Power and Tullis 1991; Sakellariou et al. 1991; Huang et al. 1992; Odling 1994; Kulatilake and Um 1999; Xie et al. 1999; Yang and Di 2001), and tilt tests (Barton et al. 1985) are used in literature.

Tse and Cruden (1979) proposed empirical statistical relationship between the JRC and Z2 (root mean square of first derivative of profile). In their study, ten standard profiles given by Barton and Choubey (1977) are enlarged by 2.5 times both in x and y coordinates. Then, new profile (25 cm long) digitized along its length and 200 discrete data points taken at equal interval of 1.27 mm. However, the enlargement of standard profiles seems incorrect because it changes the roughness of profile significantly, but Tse and Cruden’s relationship (Eq. 2) is still used as an alternate method to estimate JRC numerically.

$$ JRC=32.2+32.47{\log}_{10}{Z}_2 $$
(2)

where Z2 is given as:

$$ {Z}_2=\sqrt{\frac{1}{L}\underset{x=0}{\overset{x=L}{\int }}{\left(\frac{dy}{dx}\right)}^2 dx}=\sqrt{\frac{1}{L}\sum \limits_{i=1}^{i=N-1}\frac{{\left({y}_{i+1}-{y}_i\right)}^2}{\left({x}_{i+1}-{x}_i\right)}}\kern1em $$
(3)

In Eq. 3, L is length of profile and dy/dx is the slope of profile at fixed interval. The value of Z2 is not unique and it is sensitive to choice of sampling interval. The relationships between JRC and Z2 at different sampling interval are studied by many researchers as given in Table 1.

Table 1 Existing relationship of Z2 with JRC in literature
Full size table

In literature, fractal methods (Brown and Scholz 1985; Reeves 1985; Maerz et al. 1990; Milinverno 1990; Power and Tullis 1991; Sakellariou et al. 1991; Huang et al. 1992; Odling 1994; Kulatilake and Um 1999; Xie et al. 1999; Yang and Di 2001) are used for estimation of JRC. Odling (1994) determined the amplitude (A) and fractal dimension (D) of ten standard profiles and observed that with increase in JRC, amplitude (A) of profiles increases while fractal dimension (D) decreases. He showed that rough joints and smoother joints have D values close to 1 (self-similar fractal) and 1.5 (self-affine fractal), respectively. Khosravi et al. (2013) measures “D” for saw toothed joint samples with line segment method and establish power relationship between back calculated JRC and “D.” Li and Huang (2015) had done review of compass-walking, box-counting, and average height-base length (h–b) methods for determining “D” of ten standard profiles and discussed applicability of existing relationships of JRC and D in literature. They indicate that the fractal dimension estimated from compass-walking and h–b method more closely relate to JRC than box-counting methods.

Grasselli and Egger (2003) and Tatone (2009) developed new surface characterization parameters and shown that normalized potential contact area \( \left({A}_{\theta^{\ast }}\right) \)in specific shear direction is function of threshold dip angle (θ∗) as shown in Eq. 4.

$$ {A}_{\theta^{\ast }}={A}_0{\left(\frac{\theta_{max}-{\theta}^{\ast }}{\theta_{max}}\right)}^C $$
(4)

where A0 is the maximum potential contact area for specified shear direction which is found by putting threshold dip angle (θ∗) equal to zero, θmax is the maximum asperity angle in shear direction, and C is the dimensionless fitting parameters that characterize the distribution of apparent inclination angles over the joint surface in desired shear direction. Moreover, they postulated that parameters (A0, θmax, and C) are directional dependent, and the ratio of θmax/(C + 1) is capable to characterize the anisotropy in roughness of joint surface.

In literature, many empirical equations are available to find JRC based on statistical parameter and the fractal dimension. In these empirical equations, one of the major drawback is that JRC values are taken from Barton’s standard ten 2D profiles of 10 cm which subjective in nature. Moreover, it is almost impossible to compare a 3D joint surface with these standard profiles. Therefore, in this study, to eliminate subjectivity in estimation of JRC, a predictive model is proposed based on known morphological parameter of joint surface in desired shear direction.

The experimental shear stress or uncorrected shear stress (τ) is simply the shear force divided by nominal (fixed) area. Many researchers (Hencher and Richards 1989; Jing et al. 1992; Muralha et al. 2014) suggested that sample half that remains fixed during shearing should have greater diameter than the moving half sample so that nominal area remains constant throughout the test. If this procedure is not followed then nominal area or gross contact area reduction techniques should be carried out for estimation of correct shear stress. Moreover, due to complex nature of roughness, angle of shearing plane continuously changes during the direct shear tests. This leads to continuous change in dilation angle. Therefore, in this manuscript, experimental peak shear strength is corrected with gross contact area (AC) and incremental dilation angle (i) and a correct method to find peak dilation angle is also discussed.

Sample preparation

The natural rock joint samples are collected from different location and three different profiles of 90-mm diameter are selected visually on them. The joint roughness is transferred to silicon rubber mold with the help of room temperature vulcanizing (RTV) silicon rubber and catalyst. Further, ratio of cement, sand, and water in the ratio of 1:1.5:0.45 by weight is poured on silicon rubber mold, and finally, joint replicas (JR1, JR2, and JR3) are prepared. The detailed description of sample preparation is given by Kumar and Verma (2016).

The mechanical properties like uniaxial compressive strength, Brazilian tensile strength, and Poisson’s ratio of joint replicas are determined and reported in Table 2. The basic friction angle (ϕb) of replicas are determined on saw cut surface and found to be 35.83°.

Table 2 Mechanical properties of model material (Kumar and Verma 2016)
Full size table

Roughness quantification

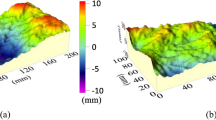
A 3D noncontact type rock surface profiler is used for roughness quantification of joint replicas (Fig. 1). It is a laser scanner and has least count of 0.5 mm in X and Y directions and 0.1 mm in Z direction. Each joint replica is scanned at 30° interval in only six directions (0°, 30°, 60°, 90°, 120°, and 150°) because in backward and forward directions, roughness measurement will remain same. In each shearing direction, for 90 mm replica, a total of 180 parallel lines at 0.5 mm spacing were obtained with X, Y, and Z data. These data are processed in MATLAB software to find joint roughness parameters (A0, θmax, and C) as suggested by Grasselli and Egger (2003).

Fig. 1
figure 1

3D noncontact type joint surface profiler used for roughness quantification of replicas

Full size image

To visualize the distribution of \( {A}_{\theta^{\ast }} \)with θ∗ of asperities (0°, 15°, 25°, 35°…) over joint surface in shear direction, plots between them are shown in Fig. 2a. These graphs depict maximum potential contact area for particular threshold dip angle before shearing. Further, to determine the value of C, the graph between \( {A}_{\theta^{\ast }} \) and (θmax − θ∗)/θmax is plotted and found that these are related in power function (Fig. 2b). Further, nonlinear regression analysis was performed to find the correct value of parameter C as described (Tatone 2009).The values of A0 and C for three joint replicas are reported in Table 3 and observed that these values are comparable with existing values in literature (Grasselli et al. 2002; Xia et al. 2014). It is observed that values of A0, C, and θmax change as shearing direction changes which show the capability to characterize the anisotropy of joint surface.

Fig. 2
figure 2

(a) Distribution of \( {A}_{\theta^{\ast }} \)with θ∗ (b) graph between \( {A}_{\theta^{\ast }} \) and (θmax − θ∗)/θmax

Full size image
Table 3 Estimated values of C, θmax, and A0 for joint replicas
Full size table

Direct shear tests

In this study, a total of 144 direct shear tests are performed using 4 normal stresses (0.25, 0.5, 1.0 and 1.5 MPa) under CNL condition. For particular profile and at each normal stress, twelve direct shear tests are performed at 30° apart in anticlockwise direction from direction 0° as shown in Fig. 1. This 0° is marked and kept constant for particular profile. The electro-mechanical direct shear apparatus is used for conducting all shear tests. The joint replicas of 90 mm diameter are put with necessary arrangements in square shear box of 10 cm. These tests are performed up to 10 mm of shear displacement at shearing rate of 0.2 mm/min (Muralha et al. 2014). The shear load, normal load, shear displacement, and vertical displacement are recorded by a personal computer equipped with a data acquisition system.

Results and discussion

Correcting shear stress with gross contact area (Ac)

It is observed that for any direct shear test, huge data points (around 2000 to 2500) are generated because data are recorded at 1 second interval. Among these data, it is also observed that for the same shear displacements, many close values of shear load and vertical displacement exist. These data are defined as “identical data” in this study. To overcome this issue, Origin Lab version 2018 is used in which these identical data are averaged to get one value of shear load and vertical displacement at particular shear displacement. This procedure reduced the data points (around 1000) which is quite easy for further calculation.

Among these data, the shear load and shear displacement are selected at interval of 0.2 mm with MATLAB program. The value of 0.2 mm shear displacement is so selected that there is minimum loss of data points. Then, corrected shear stress with gross contact area (τA) is calculated by dividing the shear force with the gross contact area (Ac). For shear displacement of “Δh” in mm, the gross contact area (Ac) is calculated with Eq. 5 (Hencher and Richards 1989).

$$ {A}_c=\pi {r}^2-\left(\frac{\Delta hr\sqrt{4{r}^2-{\left(\Delta h\right)}^2}}{2r}\right)-2{r}^2{\sin}^{-1}\left(\frac{\Delta h}{2r}\right)\kern1.5em $$
(5)

where "r” is the radius of sample in mm.

Correcting shear stress with incremental dilation angle (i)

If the shear plane has angle (i) from the horizontal, the normal stress (σn) and corrected shear stress with gross contact area (τA) can resolved tangentially and vertically to the plane of shearing. Then, dilation corrected shear stress (τi) and normal stress (σi) can be evaluated by following equations (Hencher et al. 2011).

$$ {\tau}_i=\left({\tau}_A\cos i-{\sigma}_n\sin i\right)\cos i $$
(6)
$$ {\sigma}_i=\left({\sigma}_n\cos i+{\tau}_A\sin i\right)\cos i $$
(7)

where i = tan−1(dv/dh) and dv and dh are vertical and horizontal displacements (0.2 mm), respectively. The Eq. (6) and Eq. (7) are for uphill movement of upper half of sample. The sign of these equations should be reverse in case of downhill movement.

In 0°direction of JR1, the dilation corrected shear stress (τi) and uncorrected shear stress (τexp) are compared for normal stress of 1.5 MPa (Fig. 3). It depicts that the trend of both plots is same, but in post-peak region, the τexp is less than τi. For this phenomenon, there may be two possible reasons. First is that the nominal area decreases sharply as the shearing progress and second is rate of dilation (dv/dh) which may be positive due to failure of asperities and production of gouge material during shearing. For comparison, uncorrected peak shear stress (τp) and dilation-corrected peak shear stress (τip) for 144 direct shear tests are reported in Table 4.

Fig. 3
figure 3

Comparison of dilation corrected shear stress (τi) and uncorrected shear stress (τexp) in 0° direction of JR1

Full size image
Table 4 Comparison of peak shear stress (τp) and dilation corrected peak shear stress (τip)
Full size table

Estimation of correct peak dilation angle

Peak dilation angle is mobilized at peak shear stress and there is no peak dilation prior to peak shear stress and it is determined by drawing tangent at a point corresponding to peak shear stress (τp) on plot of vertical displacement versus shear displacement (Barton 1973). Hencher et al. (2011) exhibit that Barton’s approach is based on empiricism and provides instantaneous peak dilation angle. They suggested that peak dilation angle can exist prior or post to peak shear stress depending upon the nature of roughness and applied normal stress.

Therefore, to extend our understanding and to remove existing ambiguity toward peak dilation angle, Barton and Hencher’s approach are analyzed. In this paper, plots between uncorrected shear stress (τ) versus shear displacement (h) (Fig. 4a), and vertical displacement (V) versus shear displacement (h) (Fig. 4b) are plotted. Then, peak dilation angle (dn) are determined as per Barton (1973). Moreover, the graphs between dilation-corrected shear stress (τi) versus shear displacement (h) (Fig. 4c) and dilation rate (dv/dh) versus shear displacement (h) (Fig. 4d) are drawn and actual peak dilation angle (dna) is determined. The values of dn and dna, are reported in Table 5 and observed that dna underestimate the dn at large extent. The reason for this phenomenon is that rate of dilation (dv/dh) gives incremental dilation angle at every 0.2 mm shear displacement which is always high.

Fig. 4
figure 4

Typical curves of direct shear test on JR2 in 0° direction

Full size image
Table 5 Peak dilation angle (dn) and actual peak dilation angle (dna)
Full size table

During analysis of data, multiple peaks of τi is observed in Fig. 4c. However, in this research paper, first τip is recorded for all 144 direct shear tests. It is also noticed that concept of dilation rate (dv/dh) provides easier way to find unique value of dna in any shearing direction which is quite essential for prediction of peak shear stress of rock joints.

Back calculated JRC

Over the years, the prediction of JRC remains a matter of research to predict shear strength of rock joint in Barton’s model. So, it is imperative to know JRC in each shearing direction. For four normal stresses (0.25, 0.5, 1, 1.5 MPa), τBarton is determined (Eq. 1) with one arbitrary value of JRC. Then, sum of square error (SSE) as given in Eq. (8) is minimized by altering the value of JRC in Solver add-in for Microsoft Excel. The value of JRC corresponding to minimum SSE is back calculated JRC in desire shear direction.

$$ SSE=\sum {\left({\tau}_{exp}-{\tau}_B\right)}^2\kern13em $$
(8)

As seen above, the back calculated JRC is determined after conducting direct shear tests at different normal stresses. But the ultimate aim is to find JRC in advance so that Baton’s model (Eq. 1) can be used in efficient way. Keeping this objective, efforts are made to predict back calculated JRC with known parameter of roughness (A0, θmax, and C) in desired shearing direction. Different combinations of these parameters are plotted with back calculated JRC but they did not provide good relationships. Finally, back calculated JRC is plotted with function \( \frac{1}{A_0}\times \frac{\theta_{max}}{\left(C+1\right)} \) as shown in Fig. 5 and found that JRC can be predicted with power function (R2 = 0.73) as given in Eq. (9). For JR3, the back calculated JRC and predicted JRC are compared in radar diagram (Fig. 6) which indicate that Eq. (9) provides the good approximation of JRC.

$$ JRC={\left[\frac{1}{A_0}\times \frac{\theta_{max}}{\left(C+1\right)}\right]}^{0.62} $$
(9)
Fig. 5
figure 5

Plot between JRC and \( \frac{1}{A_0}\times \frac{\theta_{max}}{\left(C+1\right)} \)

Full size image
Fig. 6
figure 6

Comparison between back calculated JRC and Predicted JRC for JR3

Full size image

Modified Barton’s peak shear strength criterion (τpre)

In order to develop peak shear strength criterion, it is assumed that shear behavior of rock joints replicas is similar to that of rock joints. Taking account this consideration, modified Barton’s peak shear strength criterion (Eq. 10) is developed by substituting Eq. (9) is in Eq.(1).

$$ {\uptau}_{\mathrm{pre}}={\upsigma}_{\mathrm{n}}\tan \kern.1em \left[{\phi}_{\mathrm{b}}+{\left[\frac{1}{{\mathrm{A}}_0}\times \frac{\uptheta_{\mathrm{max}}}{\left(\mathrm{C}+1\right)}\right]}^{0.62}\times {\log}_{10}\left(\frac{\mathrm{JCS}}{\upsigma_{\mathrm{n}}}\right)\right] $$
(10)

For all three joint replicas, dilation-corrected peak shear strength (τip) and modified Barton’s peak shear strength (τpre) are compared (Fig. 7). At each normal stress, mean square error (MSE) is calculated (Eq. 11) and the values of τip and τpre with mean square error are listed in Table 6. It is noticed that mean square error varies from 1.33 to 4.95% which is quite reasonable.

$$ MSE=\left[\frac{1}{N}{\sum}_{i=1}^N{\left({\tau}_{ip-}{\tau}_{pre}\right)}^2\right]\times 100 $$
(11)
Fig. 7
figure 7

Comparison between dilation corrected peak shear strength (τip) and predicted shear strength (τpre)

Full size image
Table 6 Dilation corrected peak shear strength (τip) and predicted peak shear strength (τpre) of joint replicas
Full size table

Comparison of modified Barton’s criterion with existing models

Modified Barton’s peak shear strength criterion is compared with Barton’s criterion as shown in Fig. 8. The mean square error (MSE) is calculated at normal stress of 0.25, 0.5, 1, and 1.5 MPa and found to be 0.24, 0.54, 1.22, and 1.93%, respectively, which is quite comparable.

Fig. 8
figure 8

Comparison of modified Barton’s peak shear strength criterion with Barton’s criterion

Full size image

Further, modified Barton’s peak shear strength criterion (τpre) is also compared with Grasselli’s experimental peak shear strength (τGE). For comparison, the input data like σn, ϕb, A0, θmax, C, and JCS are taken from the research paper of Grasselli and Egger (2003). It is found that for few experimental cases, τGE overestimates the τpre as shown in Fig. 9. The possible reason for overestimation may be that Grasselli and Egger (2003) calculated the joint roughness parameters A0, θmax, and C at accuracy of 0.05 mm, whereas in proposed modified Barton’s peak shear strength criterion, these parameters are calculated at accuracy of 0.10 mm. The another probable reason for this overestimation can be scale effect of joints because Grasselli and Egger (2003) have used joint size of 150 mm by 150 mm in lab experiments, whereas modified Barton’s peak shear strength criterion is proposed for joint sample of 90 mm diameter. However, the scale effect of joints is not studied in this manuscript.

Fig. 9
figure 9

Comparison of modified Barton’s peak shear strength with Grasselli’s experimental peak shear strength

Full size image

Conclusions

In this paper, 144 direct shear tests are performed on rock joint replicas of 90-mm diameter under constant normal load condition (CNL). In each shearing direction, experimental shear stress (τexp) is corrected using corrections like gross contact area (AC) and incremental dilation angle (i). The peak dilation angle (dn) and actual peak dilation angle (dna) are determined with Barton’s and incremental dilation (dv/dh) approach, respectively. It is concluded that mostly numerical value of dn is lower than the dna. Therefore, this research recommends that the actual peak dilation should be determined by incremental dilation (dv/dh) method.

A predictive model for JRC is developed based on morphological parameters like A0, θmax, and C. Finally, Barton’s model is modified and it is observed that modified peak shear strength criterion provides good approximation of dilation corrected peak shear strength (τip). The developed shear strength criterion has the advantage over existing models because it is independent of JRC. Modified Barton’s peak shear strength (τpre) is compared with Barton’s shear strength (τB) and found that τpre closely matches with τB. Moreover, τpre is also compared with Grasselli’s experimental shear strength (τGE) and it is found that few cases τGE overestimate the values of τpre. It is pointed out that the probable reasons of overestimation are scale effect and accuracy of joint roughness quantification in proposed model.

It should be noted here that parameters A0, θmax, and C are sensitive to measurement accuracy. Therefore, Eq. (9) is subjected to change at different measuring accuracy. The modified Barton’s peak shear strength criterion is formulated for joint replicas by conducting laboratory direct shear tests in range of σn/σc=0.006 to 0.036.