The propagation mechanism of an oblique straight crack in a rock sample and the effect of osmotic pressure under in-plane biaxial compression

Abstract

In this paper, the propagation mechanism of an oblique straight crack has been studied theoretically, which reveals its mechanical characteristics under in-plane biaxial compression. Firstly, the stress components away from the boundary are derived based on the superposition principle. The normal stress components are strengthened and shear stress component is restrained compared to the uniaxial condition. Then the relationship between stresses and stress intensity factors is analyzed, and the effect of stresses on the strength of cracked rocks is discussed. The analysis of wing crack growth shows that the reliable experimental results are very demanding for sample preparation. Based on Mohr-Coulomb criterion and Mohr’s stress circles, the failure mechanism of cracked rocks is analyzed, and the physical meaning of some formulas is vividly displayed. Moreover, we study the relationship between friction angle θ₀ and angle β, which determines the minimum compressive strength of cracked rocks. There are evidences that the increase of crack opening width leads to β₀ (a value of β) away from the theoretical value determined by sliding crack model, so that the role of stress σ_x can no longer be ignored. Theoretically speaking, for an initially closed crack, we find that, for the first time, both wing crack growth and shear compression failure are more likely to occur when the angle β between 22.5 and 45 degrees combining the statistical results of Barton and Choubey (Rock Mech Rock Eng 10:1–54, 1977). As for an initially open crack, the characteristics of stress intensity factors and circumferential stresses are also discussed, especially when σ₁ equals σ₃. Finally, we study the effect of osmotic pressure on stresses and stress intensity factors, the weakening of the properties of crack surfaces by water is also considered, and the mechanical behavior of a rock sample with an oblique straight crack changes dramatically.

Introduction

It is well known that the cracks in rock materials weaken their mechanical properties; for example, rock plates used in pavement construction are easily damaged due to stress concentration around the crack tips. In addition, cracks in walls and roofs of underground roadways/tunnels reduce their stability (Zhang et al. 2019). At present, the effect of cracks on mechanical properties of rocks is still a hot topic in the field of brittle materials.

So far, many achievements have been obtained through experiments (Cao et al. 2016; Wang et al. 2018, 2020; Wu et al. 2020; Cao et al. 2020). For example, Zhou et al. (2018a, b) conducted drop weight impact experiments, and the crack propagation velocity and crack initiation time were measured by using crack propagation gauges, which were applied in the determination of initiation toughness. Han et al. (2019) established the relationship between the electric dipole moment and the stress change rate at the crack tip and the crack propagation characteristics. The displacement fields obtained from experiments by digital image correlation (DIC) technique provided information on the evolution of the fracture process zone at the interface (Dong et al. 2017). Cheng et al. (2018) conducted physical similarity simulation experiments to obtain the crack propagation law of directional hydraulic fracturing (DHF) technology. For the Brazilian Disk specimen containing double pre-existing cracks, Zhou and Wang (2016) stated that the crack coalescence was mainly caused by the propagation of wing cracks emanating from the tips of the pre-existing cracks. In a word, the experimental results can show the characteristics of crack propagation as well as the influencing factors, and be helpful to preliminarily understand the law of its propagation (Pepe et al. 2018; Chen et al. 2019a, b; Undul et al. 2015; Fakhimi et al. 2018; Klichowicz et al. 2018; Huang et al. 2018a, b; Guo et al. 2018; Yin et al. 2018; Lee and Jeon 2011; Peng et al. 2019; Zhao et al. 2016; Cao et al. 2019).

Due to the limitation of monitoring technology, it is often difficult to obtain the required data, such as displacement field and stress field; therefore, numerical calculation is often needed after experiments (Wang et al. 2016a, b; Zhou et al. 2015; Guo et al. 2019; Huang et al. 2018a, b; Zhang et al. 2020a, b). At present, many achievements have been made by different numerical methods. For example, finite element method is widely used in fracture of rock materials (Zhou et al. 2018a, b; Jiang and Meng 2018; Liang et al. 2012; Taghichian et al. 2018; Xie et al. 2016; Zhou and Yang 2012; Chen and Liu 2015; Lin et al. 2019a, b, c). In recent years, discrete element method (DEM) is becoming more and more popular, which can be used to study the mechanism of crack propagation from a microscopic point of view (Li et al. 2017; Camones et al. 2013; Virgo et al. 2013; Duriez et al. 2016; Wang et al. 2014, Wang et al. 2016a, b; Cao et al. 2018a, b; Liu et al. 2018; Fan et al. 2018a, b, c; Lin et al. 2019a, b, c). In addition, crack propagation is also studied by other numerical methods, such as the finite difference method (Li et al. 2015; Kang et al. 2014), the element-free Galerkin (EFG) method (Tunsakul et al. 2018), and three-dimensional element partition method (3D-EPM) (Wang et al. 2013).

At present, numerical simulation methods are widely adopted; however, their results also have some defects; therefore, continuous optimization is always essential. For example, Xia and Zhao (2014) found that the uniaxial compressive strength (UCS), tensile strength (TS), and elastic modulus were overestimated when the conventional loading procedure was adopted in PFC2D/3D numerical calculation with the clump parallel-bond model (CPBM). Therefore, a newly proposed discontinuous loading procedure was adopted to simulate spontaneous crack generation phenomena (Zhao et al. 2007).

Theory is an important means of mechanics research (Wang et al. 2012; Lin et al. 2019a, b, c; Xie et al. 2020a, b; Zhao et al. 2019a, b; Zhang et al. 2020a, b), which can guide the analysis of experimental and simulation results. At present, the classical fracture criteria of rock materials mainly include the maximum circumferential stress criterion (Gao et al. 2017; Alneasan et al. 2018; Xeidakis et al. 1996; Sun 2001; Zou et al. 2018), the strain energy density factor criterion (Alneasan et al. 2018; Ayatollahi and Sedighiani 2012), the maximum energy release rate criterion (Alneasan et al. 2018; Wei and Bremaecker 1993), and the maximum tensile stress criterion (Zhu et al. 2013).

Nevertheless, at present, there are relatively few continuing studies of these criteria from a theoretical point of view; most of the results are based on numerical calculations or experiments. Therefore, in this paper, the propagation law of an oblique straight crack in a rock sample is studied theoretically based on the maximum circumferential stress criterion and sliding crack model; in addition, the effect of osmotic pressure is also considered.

Basic assumptions and cracks classification

Basic assumptions

The failure of rocks often occurs before compressive strength, mainly due to the existence of cracks in rocks, which are collectively called Griffith cracks. The structure of rocks is very complex, various kinds of cracks are unevenly distributed, and the failure process of rocks cannot be described by one or a limited number of cracks. However, if only a complex model is established to study the combined effect of crack groups, it may lead to the mutual concealment of some features. Therefore, the study of a single crack is helpful to obtain insight into the mechanism of crack propagation in rocks. In this paper, the shape of rock samples is square, their height and width are much larger than thickness, and there is an oblique crack in the middle of each sample, which is far away from the boundary. Some assumptions are listed as follows:

It is considered that the rock is an isotropic, continuous, and homogeneous material. The crack is an oblique straight one, which is considered infinitely far away from the boundary of the rock sample. Crack opening width is very small, and the curvature radius of crack tips can be considered to be zero. Considering that the sample thickness is much smaller than that of its height and width, the study can be regarded as a plane problem. In addition, the friction coefficient of crack surfaces is considered to remain unchanged in the shearing process without the influence of water.

Cracks classification

Irwin (1957) has divided the cracks into three types, that is, type I, II, and III cracks. The three typical cracks are shown in Fig. 1. More complex cracks can be formed through a combination of the three ones. Type I crack is most important in the field of engineering due to the fact that the tensile strength of rock materials is the lowest one relative to their compressive and shear strengths. Generally speaking, the oblique straight crack has the mechanical properties of both type I and type II cracks, where σ is the normal stress and τ is the shear stress; x, y, and z represent different coordinate axes.

Fig. 1

Three basic types of cracks. a A type I crack. b A type II crack. c A type III crack

Stress characteristics at a crack tip

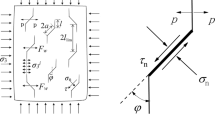
Figure 2 depicts the stress of a rock sample with an oblique straight crack which is far from the boundary of the model. In this paper, compressive stress is positive and tensile stress is negative. If the crack is only subjected to uniaxial compression stress β₀, the value of stress n is zero; therefore, by means of coordinate transformation, the stress components away from the boundary can be obtained, as shown in Eq. (1), where θ₀ is applied in the vertical direction; φ is applied in the horizontal direction; the x axis coincides with the crack strike; y axis is perpendicular to the crack plane; α and α^′ are the angle between normal direction of crack plane (y axis) and the direction of corresponding stresses (see Fig. 2), respectively; β and β^′ are the angle between the crack strike (x axis) and the direction of corresponding stresses (see Fig. 2), respectively; o is the origin of coordinates.

$$ \left\{\begin{array}{l}{\sigma}_x^{\infty }={\sigma}_1{\cos}^2\beta \\ {}{\sigma}_y^{\infty }={\sigma}_1{\sin}^2\beta \\ {}{\tau}_{xy}^{\infty }={\sigma}_1\sin \beta \cos \beta \end{array}\right. $$

(1)

where σ_x∞ and ${\sigma}_y^{\infty }$ are the normal stresses along the direction of x axis and y axis, respectively, and ${\tau}_{xy}^{\infty }$ represents the shear stress along the direction of crack inclination.

Fig. 2

Stress characteristics of an oblique straight crack under in-plane biaxial compression

As for a rock sample with an oblique straight crack, there is stress concentration at the crack tip under the action of stress β₀ and σ₃. According to fracture mechanics theory (Gross and Seelig 2011; Gao et al. 2017), the stress field near the crack tip can be obtained, as shown in Eq. (2).

$$ \left\{\begin{array}{c}{\sigma}_x=\frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)-\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\left(2+\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\right)\\ {}{\sigma}_y=\frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)+\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\\ {}{\tau}_{xy}=\frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}+\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\end{array}\right. $$

(2)

where σ_x and σ_y are the normal stresses near the crack tip; τ_xy is the shear stress near the crack tip; and K_I and K_II are the stress intensity factors of type I and II cracks, respectively.

Figure 3 depicts the stresses at the crack tip in polar coordinate system, and Eq. (3) can be obtained (Gao et al. 2017).

$$ \left\{\begin{array}{c}{\sigma}_r=\frac{1}{2\sqrt{2\pi r}}\left[{K}_{\mathrm{I}}\left(3-\cos \theta \right)\cos \frac{\theta }{2}+{K}_{\mathrm{I}\mathrm{I}}\left(3\cos \theta -1\right)\sin \frac{\theta }{2}\right]\\ {}{\sigma}_{\theta }=\frac{1}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[{K}_{\mathrm{I}}\left(1+\cos \theta \right)-3{K}_{\mathrm{I}\mathrm{I}}\sin \theta \right]\\ {}{\tau}_{r\theta}=\frac{1}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[{K}_{\mathrm{I}}\sin \theta +{K}_{\mathrm{I}\mathrm{I}}\left(3\cos \theta -1\right)\right]\end{array}\right. $$

(3)

where σ_r is the radial stress, σ_θ is the circumferential stress, τ_rθ is the shear stress, and θ is the angle in polar coordinate system.

Fig. 3

Stress components at the crack tip in polar coordinate system

If the value of stress σ₃ is zero for an open crack, K_I and K_II are determined by Eq. (4).

$$ \left\{\begin{array}{c}{K}_{\mathrm{I}}={\sigma}_{y_1}^{\infty}\sqrt{\pi a}={\sigma}_1\sqrt{\pi a}{\sin}^2\beta \\ {}{K}_{\mathrm{I}\mathrm{I}}={\tau}_{x{y}_1}^{\infty}\sqrt{\pi a}={\sigma}_1\sqrt{\pi a}\sin \beta \cos \beta \end{array}\right. $$

(4)

where a is the half the length of the long axis of the crack and equal to the distance from the crack tip to the crack center.

If the value of stress σ₃ is not zero, the oblique straight crack (see Fig. 2) will be in the joint action of σ₁ and σ₃. The superposition principle depicted in Fig. 2 can be used to determine the stress components away from the boundary of the sample. Under the action of stress σ₁, the following stress relations can be obtained:

$$ \left\{\begin{array}{l}{\sigma}_{x_1}^{\infty }={\sigma}_1{\cos}^2\beta \\ {}{\sigma}_{y_1}^{\infty }={\sigma}_1{\sin}^2\beta \\ {}{\tau}_{xy_1}^{\infty }={\sigma}_1\sin \beta \cos \beta \end{array}\right. $$

(5)

where ${\sigma}_{x_1}^{\infty }$ and ${\sigma}_{y_1}^{\infty }$ represent normal stresses determined by σ₁ and follow the direction of x axis and y axis, respectively, and ${\tau}_{xy_1}^{\infty }$ represents shear stress determined by σ₁ and follows the direction of crack inclination.

Under the action of stress σ₃, the following stress relations can be obtained:

$$ \left\{\begin{array}{l}{\sigma}_{x_3}^{\infty }={\sigma}_3{\cos}^2{\beta}^{\prime}\\ {}{\sigma}_{y_3}^{\infty }={\sigma}_3{\sin}^2{\beta}^{\prime}\\ {}{\tau}_{xy_3}^{\infty }={\sigma}_3\sin {\beta}^{\prime}\cos {\beta}^{\prime}\end{array}\right. $$

(6)

where ${\sigma}_{x_3}^{\infty }$ and ${\sigma}_{y_3}^{\infty }$ represent normal stresses determined by σ₃ and follow the direction of x axis and y axis, respectively, and ${\tau}_{xy_3}^{\infty }$ represents shear stress determined by σ₃ and follows the direction of crack inclination.

According to Fig. 2, the relationship between β and β^′ can be seen as follows:

$$ {\beta}^{\prime }={90}^{{}^{\circ}}-\beta $$

(7)

Therefore, by substituting Eq. (7) into Eq. (6), the following result is obtained:

$$ \left\{\begin{array}{l}{\sigma}_{x_3}^{\infty }={\sigma}_3{\sin}^2\beta \\ {}{\sigma}_{y_3}^{\infty }={\sigma}_3{\cos}^2\beta \\ {}{\tau}_{xy_3}^{\infty }={\sigma}_3\sin \beta \cos \beta \end{array}\right. $$

(8)

Considering the role of σ₃, according to the principle of superposition and consideration of the relationship between the stresses, the following results can be obtained:

$$ \left\{\begin{array}{l}{\sigma}_x^{\infty }={\sigma}_1{\cos}^2\beta +{\sigma}_3{\sin}^2\beta \\ {}{\sigma}_y^{\infty }={\sigma}_1{\sin}^2\beta +{\sigma}_3{\cos}^2\beta \\ {}{\tau}_{xy}^{\infty }=\left({\sigma}_1-{\sigma}_3\right)\sin \beta \cos \beta \end{array}\right. $$

(9)

In Eq. (9), it can be seen that the normal stresses ${\sigma}_x^{\infty }$ and ${\sigma}_y^{\infty }$ are strengthened under biaxial stress state, only when σ₃ is zero; the normal stresses obtain their minimum value and are equal to the ones in Eq. (1). Under biaxial stress, the shear stress ${\tau}_{xy}^{\infty }$ is restrained compared to the uniaxial condition. Due to the fact that the compressive strength of rock materials is far greater than their shear strength, therefore, compared with the uniaxial compression, a rock sample with a closed straight crack can withstand larger stress under in-plane biaxial compression. When the values of σ₁ and σ₃ are equal, ${\tau}_{xy}^{\infty }$ dramatically decreases to zero, at this moment, a cracked sample can have the greatest loading capacity according to the Mohr-Coulomb criterion. Based on Eq. (9), the stress intensity factors of a rock sample with an open straight crack under in-plane biaxial compression are as follows:

$$ \left\{\begin{array}{c}{K}_{\mathrm{I}}={\sigma}_y^{\infty}\sqrt{\pi a}=\sqrt{\pi a}\left({\sigma}_1{\sin}^2\beta +{\sigma}_3{\cos}^2\beta \right)\\ {}{K}_{\mathrm{I}\mathrm{I}}={\tau}_{xy}^{\infty}\sqrt{\pi a}=\left({\sigma}_1-{\sigma}_3\right)\sqrt{\pi a}\sin \beta \cos \beta \end{array}\right. $$

(10)

In Eq. (10), compared with uniaxial compression tests, the value of K_I is increased and K_II is decreased under in-plane biaxial compression. Although the shear strength is improved (see Eq. (9)) under biaxial stress conditions according to the Mohr-Coulomb criterion, the circumferential stress of an open straight crack tip increases dramatically as shown in Eq. (3); therefore, it is more likely to cause tensile failure of a sample with an open straight crack according to the maximum circumferential stress criterion (Gao et al. 2017). It is also found that the stress distribution formulas at the crack tip are the same whether under uniaxial or biaxial loading conditions (see Eq. (2) and Eq. (3)), except that the stress intensity factors are different.

According to the maximum circumferential stress criterion (Gross and Seelig 2011; Gao et al. 2017), the following relationship can be obtained from Eq. (3):

$$ {\left.\frac{\partial {\sigma}_{\theta }}{\partial \theta}\right|}_{\theta ={\theta}_0}=0 $$

(11)

Then the following equation can be obtained:

$$ {K}_{\mathrm{I}}\sin {\theta}_0+{K}_{\mathrm{I}\mathrm{I}}\left(3\cos {\theta}_0-1\right)=0 $$

(12)

where θ₀ is a value of angle θ, which corresponds to maximum circumferential stress, and it is also the initiation angle of wing crack growth.

Then Eq. (13) can be obtained by solving Eq. (12).

$$ {\theta}_0=\pm 2\arctan \frac{\sqrt{1+8{\left({K}_{\mathrm{I}\mathrm{I}}/{K}_{\mathrm{I}}\right)}^2}-1}{4\left({K}_{\mathrm{I}\mathrm{I}}/{K}_{\mathrm{I}}\right)} $$

(13)

The value of K_I and K_II in Eq. (12) is determined by Eq. (10), the tensile stresses are negative and compressive stresses are positive in this paper, and the following results should be met to obtain the direction of maximum circumferential stress:

$$ \left\{\begin{array}{c}{\left.\frac{\partial^2{\sigma}_{\theta }}{\partial^2\theta}\right|}_{\theta ={\theta}_0}={\left.\frac{\partial \left(\partial {\sigma}_{\theta}\right)}{\partial \left(\partial \theta \right)}\right|}_{\theta ={\theta}_0}<0\\ {}{\sigma}_1\ge 0;{\sigma}_3\ge 0;{\sigma}_1\ge {\sigma}_3\\ {}\frac{K_{\mathrm{I}\mathrm{I}}}{K_{\mathrm{I}}}>0;{K}_{\mathrm{I}\mathrm{I}}\ge 0;{K}_{\mathrm{I}}\ge 0\end{array}\right. $$

(14)

The negative solution in Eq. (13) can satisfy Eq. (14) by calculation, which indeed indicates the initial angle of wing crack growth in Fig. 2 and the direction of the maximum value of σ_θ. In fact, the positive value of θ₀ meets the requirements of tension stress state and crack II, as shown in Fig. 4, and crack I is symmetrical to crack II and the same as the one in Fig. 2. It should be pointed out that cracks I and II (see Fig. 4) are not in the same rock sample, but only to illustrate their mutual symmetry. It is important to be clear that θ₀ is set to zero in the positive direction of X-axis, and the direction of the negative solution under compressive stress is different from that under tensile stress. θ₀ is positive in a clockwise direction and negative in an anticlockwise direction as shown in Fig. 4 under the condition of compressive stress, where crack I is the same as that in Fig. 2, and crack II is a crack symmetrical to crack I; x^′ axis coincides with the crack strike, and y^′ axis is perpendicular to the crack plane; α^″ is the angle between y^′ axis and the stress σ₁, and β^″ is the angle between x^′ and the stress σ₁.

Fig. 4

Two symmetrical cracks

The comparison between Eq. (3) and Eq. (12) shows that τ_rθ is zero if σ_θ gets the maximum value ${\sigma}_{\theta_0}$; therefore, ${\sigma}_{\theta_0}$ is one of the principal stresses, which is the same as that under uniaxial stress conditions. In addition, Eq. (12) can be transformed into Eq. (15).

$$ \left\{\begin{array}{c}\frac{K_{\mathrm{I}\mathrm{I}}}{K_{\mathrm{I}}}=-\frac{\sin {\theta}_0}{\left(3\cos {\theta}_0-1\right)}\\ {}-\left|\operatorname{arccos}\frac{1}{3}\right|\le {\theta}_0\le 0\end{array}\right. $$

(15)

According to Eq. (15), when K_II is zero, K_II/K_I has its minimum value, and θ₀ is zero. When K_I approaches zero, K_II/K_I approaches infinity, and θ₀ is about − 70.53 degrees. In addition, the other values of θ₀ and the corresponding values of K_II/K_I can also be calculated, so that the relationship between θ₀ and K_II/K_I can be plotted as a curve (see Fig. 5) which is also the same as that under uniaxial stress conditions.

Fig. 5

The relationship between θ₀ and KII/KI

As shown in Fig. 5, the value of K_II/K_I grows slowly and the characteristics of type I crack are mainly displayed when the absolute value of θ₀ is relatively small, especially when θ₀ is zero, only the characteristics of type I crack are shown. After that, a slight increase of the absolute value of θ₀ will lead to a rapid increase of K_II/K_I, and the characteristics of type II crack will occupy the leading position. In addition, under uniaxial and biaxial loading conditions, the relationship between θ₀ and K_II/K_I is the same, only K_I and K_II are different.

Discussion on wing crack propagation

Wing crack is also called primary crack, as shown in Fig. 6, there is a test sample containing a pre-crack, and its slope is 45 degrees, two wing cracks are generated at both tips, which propagate under in-plane biaxial compression (σ₃ = 0). Figure 6 also shows that the initial angles of wing crack growth are different at both pre-crack tips, one is about − 48.00 degrees and the other is about − 68.00 degrees, and the corresponding values of K_II/K_I are about 0.74 and 7.49, respectively. If the pre-crack is an initially closed one, then the value of K_I is initially zero, and the initial angle of wing crack growth is about − 70.53 degrees. Therefore, it indicates that the pre-crack in Fig. 6 is not an initially closed one.

Fig. 6

Propagation characteristics of wing cracks

In addition, taking into account the symmetry of the stresses at both pre-crack tips, theoretically speaking, the values of θ₀ at both pre-crack tips should be the same, which is also verified by numerical calculations (Xie et al. 2016). However, there are differences in the initiation angle of wing cracks at both tips as shown in Fig. 6; on the one hand, this may be due to the discreteness of materials; on the other hand, the error caused by sample processing is also an important reason. It can be seen that reliable experimental results are very demanding for sample preparation.

However, after the initial stage of propagation, the growth direction of wing crack aligns with the direction of the most compressive load (Bobet and Einstein 1998; Sagong and Bobet 2002; Park and Bobet 2009, 2010; Sharafisafa and Nazem 2014; Bobet 2000; Tang et al. 2001); therefore, the growth angles of wing cracks at both pre-crack tips tend to be similar (about − 54.00 degrees), as shown in Fig. 6. It is well known that the propagation of wing cracks is caused by tensile stress; in general, wing crack surfaces are not affected by shear stress (Bobet and Einstein 1998; Chan et al. 1997). The previous studies concluded by Xie et al. (2016) have also showed that the typical propagation (type I) of wing cracks can be observed in most tests, while type II is only observed in few experiments. It can be concluded that wing cracks normally propagate along the direction of zero shear stress, where it has the maximum compressive load, and then the wing crack growth only shows the characteristics of type I crack. Although wing cracks propagate earlier than secondary cracks, they have a weaker effect on the bearing capacity of rock samples, and secondary cracks appear later and are responsible, in most cases, for sample failure (Bobet and Einstein 1998).

Application of the Mohr-Coulomb criterion

If the oblique straight crack is closed, its upper and lower surfaces contact each other, resulting in compressive shear stress. If contact occurs near the crack tip, the value of K_I is zero (Ribeaucourt et al. 2007); therefore, the characteristics of pure type II crack will be displayed.

The Mohr-Coulomb criterion is a macroscopic yield one for shear failure of rock materials. Due to the fact that the crack has been closed and subjected to compression shear stress, the Mohr-Coulomb criterion can be used to analyze its mechanical properties (Wu and Wong 2012). According to the Mohr-Coulomb criterion, the shear failure resistance of a closed crack is determined by material cohesive stress and crack face friction, as shown in Eq. (16).

$$ {\tau}_f={\tau}_0+{\sigma}_y^{\infty}\tan \varphi $$

(16)

where τ_f is the shear strength of a closed crack, τ₀ is the cohesive stress, and φ is the internal friction angle.

According to Eq. (16), taking into account the shear stress component ${\tau}_{xy}^{\infty }$ on the crack surfaces away from the boundary, the effective shear stress applied on the crack surfaces can be obtained as shown in Eq. (17).

$$ {\tau}_e={\tau}_{xy}^{\infty }-{\tau}_f={\tau}_{xy}^{\infty }-{\tau}_0-{\sigma}_y^{\infty}\tan \varphi $$

(17)

where τ_e is the effective shear stress.

In order to facilitate the application of Mohr-Coulomb criterion, Eq. (9) can be changed into Eq. (18).

$$ \left\{\begin{array}{l}{\sigma}_x^{\infty }=\frac{\sigma_1+{\sigma}_3}{2}+\frac{\sigma_1-{\sigma}_3}{2}\cos 2\beta \\ {}{\sigma}_y^{\infty }=\frac{\sigma_1+{\sigma}_3}{2}-\frac{\sigma_1-{\sigma}_3}{2}\cos 2\beta \\ {}{\tau}_{xy}^{\infty }=\frac{\sigma_1-{\sigma}_3}{2}\sin 2\beta \end{array}\right. $$

(18)

According to the Mohr-Coulomb criterion, Mohr’s stress circles under different stress conditions can be plotted in the σ − τ plane. The values of stresses in Eq. (18) are positive in this paper, and it represents only that the direction of the stresses is the same as the prescribed one. Three Mohr’s circles under different stress conditions are shown in Fig. 7.

Fig. 7

The analysis of Mohr-Coulomb failure criterion

where C₁, C₂, and C₃ are the center of Mohr’s circles; σ₁, ${\sigma}_1^{\hbox{'}}$, σ₃, and ${\sigma}_3^{\hbox{'}}$ are principal stresses; the abscissa represents the normal stress and the ordinate represents the shear stress; and α and β are shown in Fig. 2.

As shown in Fig. 7, if the cohesive stress τ₀ is not zero, the Mohr’s circle whose center is C₁ is just tangent to the curve of τ_f, and it indicates that a cracked sample has reached the critical state of shear failure. At this moment, the shear stress ${\tau}_{xy}^{\infty }$ is equal to τ_f and the effective shear stress τ_e is just 0. The Mohr’s circle whose center is C₂ shows that the shear failure of a cracked sample does not occur due to low value of ${\sigma}_1^{\hbox{'}}$, the threshold stress of crack propagation has not been reached, and ${\tau}_{xy}^{\infty }$ is less than τ_f. Nevertheless, even if the stress σ₁ reaches a higher value, the crack does not necessarily propagate; for example, an increase in stress σ₃ can indirectly increase the difficulty of crack propagation after the crack has been closed according to the theory of sliding crack model as shown in the Mohr’s circle whose center is C₃. These mechanical characteristics can also be seen from Eq. (9), Eq. (10), Eq. (2), and Eq. (18).

It is generally considered that the cohesive stress of an initially closed crack is not zero. If the crack is not an initially closed one, as for brittle materials such as rocks, the cohesive stress between crack surfaces can be almost negligible; therefore, the effect of cohesive stress cannot be considered, and Eq. (16) can be changed into Eq. (19).

$$ {\tau}_f={\sigma}_y^{\infty}\tan \varphi $$

(19)

According to Eq. (19), the effective shear stress (see Eq. (17)) can be changed into Eq. (20).

$$ {\tau}_e={\tau}_{xy}^{\infty }-{\sigma}_y^{\infty}\tan \varphi $$

(20)

The physical meaning of Eq. (19) can also be reflected in Fig. 7, which shows that the crack propagation is more likely to occur without the effect of cohesive stress. Take Mohr’s circle whose center is C₂ as an example, the threshold of crack propagation has already exceeded without considering the influence of cohesive stress. If the crack becomes a closed one, the value of K_I decreases to zero, and the stress field at the crack tip (see Eq. (2)) is changed to Eq. (21).

$$ \left\{\begin{array}{c}{\sigma}_x=-\frac{K_{\mathrm{II}}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\left(2+\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\right)\\ {}{\sigma}_y=\frac{K_{\mathrm{II}}}{\sqrt{2\pi r}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2}\\ {}{\tau}_{xy}=\frac{K_{\mathrm{II}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}\right)\end{array}\right. $$

(21)

If polar coordinates are adopted, the following equation can be obtained:

$$ \left\{\begin{array}{c}{\sigma}_r=\frac{K_{\mathrm{II}}}{2\sqrt{2\pi r}}\left(3\cos \theta -1\right)\sin \frac{\theta }{2}\\ {}{\sigma}_{\theta }=\frac{-3{K}_{\mathrm{II}}}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\sin \theta \\ {}{\tau}_{r\theta}=\frac{K_{\mathrm{II}}}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(3\cos \theta -1\right)\end{array}\right. $$

(22)

As for an initially closed crack, according to the maximum circumferential stress criterion, the theoretical value of the initial angle of wing crack propagation is − 70.53 degree. The same result can also be obtained, if an initially open crack is closed under compressive loading and the wing cracks have not yet propagated. When an open crack is closed, it will be affected by shear stress, the effective shear stress is determined by Eq. (20), at this moment, only the characteristics of pure type II crack is shown, and K_II is determined by Eq. (23). However, for an initially closed crack, the influence of cohesive stress τ₀ should also be considered in the determination of K_II.

$$ {\displaystyle \begin{array}{c}{K}_{\mathrm{II}}={\tau}_e\sqrt{\pi a}=\left({\tau}_{xy}^{\infty }-{\sigma}_y^{\infty}\tan \varphi \right)\sqrt{\pi a}\\ {}=\left[\left({\sigma}_1-{\sigma}_3\right)\left(\sin \beta \cos \beta +{\cos}^2\beta \tan \varphi \right)-{\sigma}_1\tan \varphi \right]\sqrt{\pi a}\end{array}} $$

(23)

Discussion on the value of angle β

Relationship between shear compression failure and angle β

According to the theory of sliding crack model, the shear stress on crack surfaces is the driving one for relative sliding. Therefore, according to the basic assumptions mentioned in the “Basic assumptions and cracks classification” section, if the friction coefficient between crack surfaces is kept constant, there must be a maximum value of effective shear stress which can lead to the relative sliding of crack surfaces more easily. According to Eq. (9) and Eq. (20), the effective shear stress τ_e can also be expressed as follows:

$$ {\tau}_e=\left({\sigma}_1-{\sigma}_3\right)\left(\sin \beta \cos \beta +{\cos}^2\beta \tan \varphi \right)-{\sigma}_1\tan \varphi $$

(24)

The first-order partial derivatives of β can be obtained by Eq. (24), and a method similar to the maximum circumferential stress criterion can be adopted, then Eq. (25) can be obtained.

$$ {\left.\frac{\partial {\tau}_e}{\partial \beta}\right|}_{\beta ={\beta}_0}={\cos}^2{\beta}_0-{\sin}^2{\beta}_0-2\sin {\beta}_0\cos {\beta}_0\tan \varphi =0 $$

(25)

where β₀ is a value of angle β and corresponds to the maximum effective shear stress.

Therefore, the following results can be obtained:

$$ {\beta}_0=\pm \left(\frac{\pi }{4}-\frac{\varphi }{2}\right) $$

(26)

In Eq. (26), φ is the friction angle between the crack surfaces. According to Eq. (24), the second-order partial derivatives of β can be obtained as shown in Eq. (27). The value of β₀ should satisfy the requirement of Eq. (27) to get the maximum value of τ_e.

$$ \left\{\begin{array}{l}{\left.\frac{\partial^2{\tau}_e}{\partial^2\beta}\right|}_{\beta ={\beta}_0}=-2\left(\sin 2{\beta}_0+\cos 2{\beta}_0\tan \varphi \right)\left({\sigma}_1-{\sigma}_3\right)<0\\ {}{\sigma}_1\ge {\sigma}_3\ge 0\end{array}\right. $$

(27)

Barton and Choubey (1977) have systematically studied the friction angle of rock joints, the results have indicated that the friction angle (φ) of various unweathered rock joints obtained from flat and residual surfaces is generally no more than 45 degrees; therefore, the absolute value of β₀ is between 22.5 and 45 degrees according to Eq. (26). It is found that the positive value of β₀ can satisfy Eq. (27), so that the final value of β₀ is as follows:

$$ {\beta}_0=\frac{\pi }{4}-\frac{\varphi }{2} $$

(28)

In fact, the negative value of β₀ in Eq. (26) satisfies the requirement of crack II (see Fig. 4) which is symmetrical to crack I and the crack in Fig. 2. The value of φ in Eq. (28) remains unchanged according to the basic assumptions stated in the “Basic assumptions and cracks classification” section; therefore, if the value of angle β is equal to β₀ (between 22.5 and 45 degrees), the maximum value of effective shear stress can be obtained and the shear failure of a rock sample with an oblique straight crack is more likely to occur, and it also shows that the rock sample has the lowest compressive strength. When σ₃ = 0, Eq. (28) can also be obtained, therefore, the range of β₀ corresponding to the maximum effective shear stress is the same as that of in-plane biaxial compression. The curve in Fig. 8 depicts the relationship between φ and β₀ (see Eq. (28)), which shows that the gradual increase of φ leads to a linear decrease of β₀ determined by Eq. (28).

Fig. 8

The relationship between friction angle φ and β₀ corresponding to the maximum effective shear stress

In addition, the positive direction of β₀ is the counterclockwise rotation starting from the positive direction of X-axis, which is just the opposite of θ₀ in the “Stress characteristics at a crack tip” section, the main reason is that the positive direction of β₀ is independent of stress. On the contrary, the positive direction of θ₀ is related to stress, so that the positive direction of θ₀ in Fig. 4 must be opposite to that under tension stress.

However, the above discussion on β₀ corresponding to the maximum effective shear stress is based on certain conditions; in fact, the effect of some factors should not be ignored, such as crack opening width and the radius of curvature of the crack tip. The study conducted by Muskhelishvili (1953) has indicated that the effect of transverse compressive stress σ_x (see Fig. 2) cannot be neglected when the crack opening width and the radius of curvature of the crack tip reach a certain value, then the sliding crack model will no longer be applicable in this case. Therefore, in this paper, it is assumed that the crack opening width is very small and the curvature radius of the crack tips can be considered to be zero (see the “Basic assumptions and cracks classification” section).

In order to verify the effect of crack opening width on the range of β₀, a simple test was carried out. Concrete is a brittle rock-like material and convenient for processing samples, and has mechanical properties similar to rocks; therefore, the concrete samples were adopted. The pre-cracks were made by inserting thin slices with 0.1-mm, 0.2-mm, 0.4-mm, and 0.8-mm thickness, respectively. The dimension of samples was 200 mm × 150 mm × 50 mm (height×width×thickness), the pre-crack length was 30 mm, and the angle β (see Fig. 2) of pre-cracks was 0, 15, 30, 45, 60, 75, and 90 degrees, respectively. The number of each type of samples including the one without pre-crack was 8; therefore, the total number of samples was 232. RMT-150B high-precision compression tester was employed in this study as shown in Fig. 9, the stress σ₃ was zero, and the loading rate was 200 N/S during the compression process.

Fig. 9

RMT-150B high-precision compression tester

Due to the fact that all samples are processed by the same method, it is considered that the friction coefficients between crack surfaces are similar. In addition, the pre-cracks also meet the requirements mentioned by Barton and Choubey (1977), that is to say, the crack surfaces are smooth and unweathered. Figure 10 depicts variations of the average value of the peak strength of pre-cracked samples under different opening width conditions. The results indicate that the larger the crack opening width is, the lower the peak strength of pre-cracked samples is, under the same angle β (see Fig. 2). When the crack opening width is 0.1 mm, the mean value of minimum peak strength of pre-cracked samples appears at angle β equal to 45 degrees, and it is just within the range of β₀ determined by Eq. (28). However, the increase of pre-crack opening width leads to the increase of β₀ value as shown in Fig. 10; thus, the value of β₀ gradually deviates from the range determined by Eq. (28). The reason is that the sliding crack model is no longer applicable, and the role of transverse compressive stress σ_x can no longer be ignored (Muskhelishvili 1953). Therefore, a very small crack opening width or a closed crack can ensure that the value of β₀ is within the theoretical range based on sliding crack model as shown in Eq. (28). In addition, there is a 15 degrees interval between angle β values of each group of samples; therefore, the values of β₀ are approximate ones in Fig. 10.

Fig. 10

The effect of crack opening width on peak strength of pre-cracked samples and the value of β₀ corresponding to the minimum peak strength values

Relationship between circumferential stress and angle β

The test results (see the “Discussion on the value of angle β” section) show that the value of β₀ is consistent with the one derived from sliding crack model only when the crack opening width is very small or the crack is an initially closed one. In addition, according to the maximum circumferential stress criterion, the maximum circumferential stress is also related to angle β, as shown in Eq. (3) and Eq. (22), and the values of K_I and K_II are determined by angle β. The relationship between the circumferential stress and the angle β will be studied in this section.

As for an initially closed crack, the stress field near the crack tip is calculated by Eq. (22), and if the effect of cohesive stress is considered, the stress intensity factor K_II can be calculated as follows:

$$ {\displaystyle \begin{array}{c}{K}_{\mathrm{II}}={\tau}_e\sqrt{\pi a}=\left({\tau}_{xy}^{\infty }-{\tau}_0-{\sigma}_y^{\infty}\tan \varphi \right)\sqrt{\pi a}\\ {}=\left[\left({\sigma}_1-{\sigma}_3\right)\left(\sin \beta \cos \beta +{\cos}^2\beta \tan \varphi \right)-{\tau}_0-{\sigma}_1\tan \varphi \right]\sqrt{\pi a}\end{array}} $$

(29)

The stress σ_θ (see Eq. (22)) at the crack tip can be changed to Eq. (30).

$$ {\sigma}_{\theta }=\frac{-3\cos \frac{\theta }{2}\sin \theta }{2\sqrt{2\pi r}}\left[\left({\sigma}_1-{\sigma}_3\right)\left(\sin \beta \cos \beta +{\cos}^2\beta \tan \varphi \right)-{\tau}_0-{\sigma}_1\tan \varphi \right]\sqrt{\pi a} $$

(30)

Because the crack is an initially closed one, therefore, theoretically speaking, the initial angle of wing crack propagation is about − 70.53 degrees. In addition, the cohesive stress τ₀ is considered to be a constant value, and the friction angle remains unchanged for the same crack surfaces in the shearing process according to the basic assumptions (see the “Basic assumptions and cracks classification” section). Therefore, if σ_θ obtains its maximum value, F(β, φ) in Eq. (31) also gets its maximum.

$$ F\left(\beta, \varphi \right)=\sin \beta \cos \beta +{\cos}^2\beta \tan \varphi $$

(31)

In Eq. (31), if the first-order partial derivatives of β are equal to zero, the following equation can be obtained:

$$ {\left.\frac{\partial F\left(\beta, \varphi \right)}{\partial \beta}\right|}_{\beta ={\beta}_0^{\prime }}={\cos}^2{\beta}_0^{\prime }-{\sin}^2{\beta}_0^{\prime }-2\sin {\beta}_0^{\prime}\cos {\beta}_0^{\prime}\tan \varphi =0 $$

(32)

where ${\beta}_0^{\prime }$ is a value of angle β and corresponds to the maximum circumferential stress σ_θ.

It can be found that Eq. (32) is the same as Eq. (25); therefore, the relationship between φ and ${\beta}_0^{\prime }$ is the same as the relationship between φ and β₀ in Eq. (28), and therefore, ${\beta}_0^{\prime }$ is equal to β₀. Due to the fact that φ is generally no more than 45 degrees, thus the absolute value of ${\beta}_0^{\prime }$ (equal to β₀) is also between 22.5 and 45 degrees. More importantly, it is theoretically demonstrated that the maximum value of effective shear stress is synchronous with the maximum value of circumferential stress. In a word, for cracks with smooth and unweathered surfaces, wing crack propagation and shear compression failure are more likely to occur when angle β is in the range of 22.5 to 45 degrees (φ≤ 45°); in this case, the minimum strength of a rock sample with an oblique straight crack can be obtained. If the opening width of a crack is very small, and wing crack propagation has not yet begun after the crack has been closed, the results are the same as those of an initially closed crack, and the only difference is that τ₀ is considered to be zero.

If wing crack propagation has occurred before the open crack is closed, then the results are different from those discussed above. In this case, the stress intensity factors K_I and K_II determined by Eq. (10) are not zero, then σ_θ in Eq. (3) can be changed into the following form:

$$ {\sigma}_{\theta }=\frac{\sqrt{\pi a}}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[\begin{array}{l}\left({\sigma}_1{\sin}^2\beta +{\sigma}_3{\cos}^2\beta \right)\left(1+\cos \theta \right)-\\ {}3\left({\sigma}_1-{\sigma}_3\right)\sin \beta \cos \beta \sin \theta \end{array}\right] $$

(33)

As shown in Eq. (33), it is theoretically feasible to determine the relationship between maximum circumferential stress and angle β; however, the calculation is very complicated. If σ₁ is equal to σ₃, a very interesting feature is that the stress intensity factor K_II is zero (see Eq. (10)), and the characteristics of a pure type I crack are shown. In this case, the sliding crack model is not applicable; however, the maximum circumferential stress criterion can be applied, and Eq. (33) can be changed to Eq. (34).

$$ \left\{\begin{array}{l}\begin{array}{l}{\sigma}_{\theta }=\frac{\sqrt{\pi \alpha}}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left[\left({\sigma}_1{\sin}^2\beta +{\sigma}_3{\cos}^2\beta \right)\left(1+\cos \theta \right)\right]\\ {}=\frac{\sigma_1\sqrt{\pi \alpha}}{2\sqrt{2\pi r}}\cos \frac{\theta }{2}\left(1+\cos \theta \right)\end{array}\\ {}{\sigma}_1={\sigma}_3\end{array}\right. $$

(34)

According to the maximum circumferential stress criterion (Gross and Seelig 2011; Gao et al. 2017), Eq. (35) can be obtained.

$$ {\left.\frac{\partial {\sigma}_{\theta }}{\partial \theta}\right|}_{\theta ={\theta}_0}=\frac{-3{\sigma}_1\sqrt{\pi \alpha}}{2\sqrt{2\pi r}}\sin \frac{\theta_0}{2}{\cos}^2\frac{\theta_0}{2} $$

(35)

If the value of Eq. (35) is equal to zero, then the following equation can be obtained:

$$ \sin \frac{\theta_0}{2}{\cos}^2\frac{\theta_0}{2}=0 $$

(36)

where θ₀ is a value of angle θ and corresponds to maximum circumferential stress, and it is also the initiation angle of wing crack growth.

Thus, θ₀ can be obtained as shown in Eq. (37).

$$ \left\{\begin{array}{l}{\theta}_0=0\\ {}{\theta}_0=\pm {180}^{{}^{\circ}}\end{array}\right. $$

(37)

In Eq. (37), the reliability of the values of θ₀ needs to be verified. As shown in Fig. 11, zero is the correct value of θ₀ which reflects the initial direction of wing crack growth and also shows the direction of maximum circumferential stress. The value of θ₀ that equals ± 180 degrees should be eliminated, which shows the opposite direction of initial growth of the wing crack in Fig. 11. In fact, the minimum absolute value (equal to zero) of the circumferential stress can be obtained when θ₀ is ± 180 degrees (see Eq. (34)). In addition, the circumferential stress is not related to angle β in this case as shown in Eq. (34); therefore, the maximum circumferential stress can be determined by Eq. (38).

$$ {\sigma}_{\theta }=\frac{\sigma_1\sqrt{\pi \alpha}}{\sqrt{2\pi r}} $$

(38)

Fig. 11

Determination of the value of θ₀

Of course, if σ₁ and σ₃ are equal and the crack is an initially closed one, then both stress intensity factors K_I and K_II are equal to zero; therefore, there will be no stress concentration at the crack tip.

Effect of osmotic pressure on crack propagation

Crack propagation is often affected by groundwater in nature, and osmotic pressure is one of the most important reasons. It has been assumed that the crack opening width is very small and the curvature radius of crack tips can be considered to be zero (see the “Basic assumptions and cracks classification” section); therefore, the effect of osmotic pressure along the crack strike is ignored, and osmotic pressure acts only on the upper and lower surfaces of cracks, which direction is parallel to the y axis, and as shown in Fig. 12, σ_o is the osmotic pressure. Under the action of osmotic pressure and in-plane biaxial compression, the stress components (see Eq. (9)) away from the boundary of a rock sample with an oblique straight crack can be changed to Eq. (39) which shows that only the normal stress ${\sigma}_y^{\infty }$ is affected, and ${\sigma}_x^{\infty }$ and ${\tau}_{xy}^{\infty }$ remain unchanged.

$$ \left\{\begin{array}{l}{\sigma}_x^{\infty }={\sigma}_1{\cos}^2\beta +{\sigma}_3{\sin}^2\beta \\ {}{\sigma}_y^{\infty }={\sigma}_1{\sin}^2\beta +{\sigma}_3{\cos}^2\beta -{\sigma}_o\\ {}{\tau}_{xy}^{\infty }=\left({\sigma}_1-{\sigma}_3\right)\sin \beta \cos \beta \end{array}\right. $$

(39)

Fig. 12

A rock sample with an oblique straight crack under in-plane biaxial compression and osmotic pressure

Osmotic pressure can affect the mechanical behavior of cracks, such as their closure and opening, and its influence is mainly manifested in three stages. In the first stage, ${\sigma}_y^{\infty }$ (see Eq. (39)) is still larger than zero despite the presence of osmotic pressure for a closed crack, and frictional stress still exists on crack surfaces. Due to the lubrication and weakening effect of water, the friction angle of crack surfaces decreases dramatically; therefore, the effective shear stress τ_e (see Eq. (17)) can be changed to Eq. (40).

$$ {\tau}_e=\left({\sigma}_1-{\sigma}_3\right)\left[\sin \beta \cos \beta +{\cos}^2\beta \tan \left( n\varphi \right)\right]-{\tau}_0-\left({\sigma}_1-{\sigma}_o\right)\tan \left( n\varphi \right) $$

(40)

where n is the weakening coefficient of friction angle, and its value is between 0 and 1.

It can be seen from Eq. (40) that the effective shear stress of an initially closed crack can be increased under osmotic pressure; therefore, the stress intensity factor K_II can also be increased according to Eq. (23). In addition, water has a negative effect on the fracture toughness of cracks, so that cracked rock samples affected by osmotic pressure are more easily destroyed under the same stress conditions. The first-order partial derivatives of β in Eq. (40) can be used to obtain the extreme value of τ_e, and Eq. (41) can be obtained.

$$ {\left.\frac{\partial {\tau}_e}{\partial \beta}\right|}_{\beta ={\beta}_0}={\cos}^2{\beta}_0-{\sin}^2{\beta}_0-2\sin {\beta}_0\cos {\beta}_0\tan \left( n\varphi \right)=0 $$

(41)

The results obtained by solving Eq. (41) are as follows:

$$ {\beta}_0=\pm \left(\frac{\pi }{4}-\frac{n\varphi}{2}\right) $$

(42)

According to Eq. (41), the second-order partial derivatives of β can also be obtained, and β₀ in Eq. (42) must satisfy the requirement of Eq. (43) to get the maximum value of τ_e.

$$ \left\{\begin{array}{l}{\left.\frac{\partial^2{\tau}_e}{\partial^2\beta}\right|}_{\beta ={\beta}_0}=-2\left[\sin 2{\beta}_0+\cos 2{\beta}_0\tan \left( n\varphi \right)\right]\left({\sigma}_1-{\sigma}_3\right)<0\\ {}{\sigma}_1\ge {\sigma}_3\end{array}\right. $$

(43)

Considering the value of φ determined by Barton and Choubey (1977) and the coefficient n, obviously, the positive value of β₀ can satisfy Eq. (43), so that the final value of β₀ is shown in Eq. (44). In fact, the negative value of β₀ in Eq. (42) satisfies the requirements of crack II (see Fig. 4) which is symmetrical to crack I and the one in Figs. 2 and 12.

$$ {\beta}_0=\frac{\pi }{4}-\frac{n\varphi}{2} $$

(44)

According to Eq. (44), the relationship between φ and β₀ can be obtained under different n values. In Fig. 13, the value of β₀ corresponds to the maximum effective shear stress, and it indicates that no matter what the value of n is, there is always a linear relationship between φ and β₀. The gradual decrease of n results in the β₀ approaching 45 degrees. When n is zero, β₀ remains at 45 degrees and has nothing to do with φ, as shown in Eq. (44).

Fig. 13

The relationship between φ and β₀determined by different n values

When osmotic pressure continues to increase, ${\sigma}_y^{\infty }$ will be equal to zero (see Eq. (39)), it shows that the second stage has arrived. At this moment, the stress intensity factor K_I is zero, and only the characteristics of type II crack are shown. If the cohesion is neglected due to the weakening effect of water, under the same stress condition, the effective shear stress τ_e reaches the maximum value τ_xy (see Eq. (45)) according to Eq. (17), the stress intensity factor K_II also reaches its maximum value (see Eq. (46)) according to Eq. (29). In addition, if σ₁ equals σ₃, K_I, and K_II are zero at the same time, so that there is no stress concentration at the crack tip.

$$ {\tau}_e={\tau}_{xy}=\left({\sigma}_1-{\sigma}_3\right)\sin \beta \cos \beta $$

(45)

$$ {K}_{\mathrm{II}}={\tau}_e\sqrt{\pi a}={\tau}_{xy}^{\infty}\sqrt{\pi a}=\left({\sigma}_1-{\sigma}_3\right)\sqrt{\pi a}\sin \beta cos\beta $$

(46)

If osmotic pressure continues to increase, the third stage begins, K_II maintains its maximum value, as shown in Eq. (23) and Eq. (46), and ${\sigma}_y^{\infty }$ does not equal zero and changes from compressive stress to tensile stress, and the absolute value of both ${\sigma}_y^{\infty }$ and K_I increases gradually, so that the characteristics of type I and II cracks are simultaneously displayed, and the value of K_II/K_I gradually decreases. In addition, the crack will open when osmotic pressure exceeds the crack opening resistance.

Conclusions

Compared to the uniaxial condition, a rock sample with a closed straight crack can withstand larger stress under in-plane biaxial compression; moreover, K_I is increased and K_II is decreased; however, the stress distribution formulas at the crack tip are the same under both conditions, and only the stress intensity factors are different. τ_rθ is zero when σ_θ gets the maximum value ${\sigma}_{\theta_0}$, so that the ${\sigma}_{\theta_0}$ is one of the principal stresses. The relationship between θ₀ and K_II/K_I is also discussed in this paper.

The results indicate that the reliable experimental results are very demanding for sample preparation. Based on Mohr-Coulomb criterion and Mohr’s stress circles, the failure mechanism of a rock sample with an oblique straight crack is analyzed, and the physical meaning of some formulas is vividly displayed, such as Eq. (3), Eq. (9), Eq. (10), and Eq. (19).

The friction angle (φ) of various unweathered rock joints obtained from flat and residual surfaces is generally no more than 45 degrees; therefore, β₀ is between 22.5 and 45 degrees in which the shear failure of a rock sample with an oblique straight crack is more likely to occur. The increase of pre-crack opening width leads to the increase of β₀; thus, it gradually deviates from the range determined by sliding crack model, and the role of stress σ_x can no longer be ignored.

As for an initially closed crack, both wing crack propagation and shear compression failure are more likely to occur when β = β₀. For an open crack, when σ₁ = σ₃, the stress intensity factor K_II is zero (see Eq. (10)), and the characteristics of a pure type I crack are shown. If σ₁ = σ₃ and the crack is an initially closed one, both K_I and K_II are equal to zero, and there will be no stress concentration at the crack tip.

Only ${\sigma}_y^{\infty }$ is affected under the effect of osmotic pressure, τ_e and K_II of a closed oblique straight crack are increased; therefore, the cracked rock samples are more easily destroyed. The decrease of n results in the β₀ approaching 45 degrees (see Fig. 13). Finally, the influence of osmotic pressure on the mechanical behavior of cracks can be divided into three stages.