Mechanisms of Anisotropy in Salt Rock Upon Microcrack Propagation

Abstract

Salt rock is a polycrystalline material of interest for geostorage because of its low permeability and potential to self-heal by pressure solution at favorable stress and temperature conditions. It is often assumed that microcrack propagation and healing lead to isotropic stiffness changes. The goal of this study is to check this assumption and to gain a fundamental understanding of the mechanisms that control the accumulation of damage and irreversible deformation. Cyclic axial loading tests are performed under a confining pressure of 1 MPa on synthetic salt rock generated by thermal consolidation. The stress–strain curves and the microstructure images taken at key stages of the cycles reveal the formation of a complex system of sliding and wing microcracks, the orientation of which is loading dependent. We interpret the mechanisms that control the coupled evolution of crack families by a discrete wing crack elastoplastic damage (DWCPD) model. Crack propagation is controlled by Mode I and Mode II fracture mechanics criteria. Sliding “main” cracks grow if a cohesive frictional criterion is met, while the wing cracks propagate in tension. Displacement jumps at crack faces are related to the deformation of the rock representative elementary volume (REV). The DWCPD model can capture the nonlinear stress–strain relationship and the degradation of stiffness during the loading cycles. Simulations show that microcracks occur following two stages: (1) wing cracks initiate and main cracks do not propagate; (2) wing cracks and main cracks then propagate simultaneously. Higher friction at the crack faces leads to higher strength. With a larger cohesion, salt rock strength increases, damage development is delayed and exhibits a stick-slip evolution. At higher confinement, the initiation of wing cracks is delayed, which results in an increase of strength. The damage rate is higher in specimens that are damaged prior to compression than in the ones that are not. The proposed DWCPD model can be extended to any polycrystalline semi-brittle material, and can be applied to understand the formation of crack patterns in geostorage facilities.

1 Introduction

Salt rock is an attractive host material for geological storage (e.g., $\hbox {CO}_2$ sequestration, waste isolation, and compressed air energy storage), due to its favorable creep properties, low gas permeability, and low porosity (Cosenza et al. 1999; Kwon and Wilson 1999; Chan et al. 2001; Zhu and Arson 2015). Under typical geotechnical stress conditions, rock energy is dissipated predominantly by the nucleation and propagation of microscopic cracks. At the macroscopic scale of a typical salt rock specimen, the occurrence of these microscopic defects leads to a nonlinear stress–strain relationship, a degradation of stiffness, and a decrease of strength. Continuum damage mechanics (CDM) provides a solid theoretical framework to model the effects microstructure on the mechanical behavior of a representative elementary volume (REV) (Yuan and Harrison 2006; Krajcinovic and Fanella 1986).

In phenomenological CDM, damage is a macroscopic internal state variable that is introduced in the expression of the free energy and thus influences the energy dissipation function at the REV scale.The expression of the free energy of the REV is postulated in such a way that the stress/strain relationship that derives from it is representative of the behavior of the damaged material, and also to ensure the symmetry and positivity of the damaged stiffness tensor. When damage increases, it is expected that both stiffness and strength decrease (Lemaitre and Desmorat 2005; Chaboche 1981; Simo and Ju 1987). The evolution of damage is controlled by phenomenological driving forces derived from the thermodynamic potential, often expressed in terms of stresses and strains, e.g., Mises-equivalent stresses and strains or tensile stresses and strains (Cicekli et al. 2007; Arson and Gatmiri 2011). When coupled to an elastoplastic framework, CDM can be used to predict the behavior of semi-brittle materials, including rocks that exhibit a transition from brittle to ductile behavior (crystal-plastic in the case of salt rock) (Chiarelli et al. 2003; Hayakawa and Murakami 1997; Salari et al. 2004). Damage can be a scalar equivalent to a crack volume fraction, a second-order tensor equivalent to a crack density tensor, or a higher-order tensor for more complex fabrics. If cracks do not interact, it is sufficient to formulate the model with the second-order crack density tensor to capture stress-induced anisotropy (Kachanov 1992; Zhu and Arson 2015; Halm and Dragon 1996).

In micromechanical CDM, the displacement jumps (opening and sliding) at crack faces are internal variables that each affect the loss of elastic potential energy of the REV. Stiffness is obtained by deriving the damaged elastic energy potential, which yields a direct relationship between microcrack distributions, the stiffness tensor and inelastic deformation. Crack closure is automatically accounted for, which allows one to predict the unilateral effects of damage on stiffness (Budiansky and O’connell 1976; Pensée et al. 2002). The effect of microscopic cracks that propagate in Mode I or Mode II in a homogeneous medium was studied by Gambarotta and Lagomarsino (1993). The development of microcracks in mixed-mode (e.g., wing cracks) was discussed based on fracture mechanics principles (Germanovich et al. 1994; Jin and Arson 2017b).

The effects of pre-existing small cracks on the propagation of a brittle fracture in a solid under compression was first discussed by Griffith (1924), who indicated that the magnitude of tensile stress increases and opening mode cracks initiate at the edges of pre-existing small cracks under axial compression. Following Griffith’s work, wing cracks were then defined as the tensile cracks that initiate at the tips of defects present in the rock matrix (Bobet and Einstein 1998; Lehner and Kachanov 1996). The evolution of wing cracks in solids under compression was studied theoretically (Dyskin and Salganik 1987), experimentally (Bobet 1998; Germanovich et al. 1994), and numerically (Scholtès and Donzé 2012).

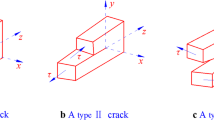
In this paper, we couple a micromechanical CDM model and an elastoplastic model to explain the formation of complex patterns of pre-existing cracks and wing cracks that develop in salt upon confined cyclic axial loading, and to understand the implication of anisotropic damage on stiffness, strength, and deformation. In the following, damage is defined as a crack density tensor, i.e., as a tensor that represents the volume fraction of cracks in each direction of space in the REV. Pre-existing cracks are referred to as main cracks. Main cracks are assumed to be penny shaped and to propagate in Mode I and Mode II. Wing cracks are tensile cracks that initiate at the tips of the main cracks. Typical crack patterns observed in the experiments discussed below are shown in Fig. 1.

In Sect. 2, we summarize the main observations made during an extensive experimental campaign that consisted in subjecting synthetic salt rock specimens obtained by thermal consolidation to confined cyclic axial loading, and in acquiring microstructure images at key stages of the stress path. In Sect. 3, we formulate a new model, called discrete wing crack elastoplastic damage (DWCPD) model, to explain the crack patterns observed. A micromechanical approach is proposed to capture the inelastic deformation induced by microscopic cracks. We explain the expression of the Gibbs free energy, damage criteria and flow rules, for both the main cracks and the wing cracks. Then, a plastic damage model is introduced to capture the accumulation of irreversible deformation. In Sect. 4, the cyclic loading tests are simulated with the DWCPD model, and the model is calibrated against the experimental results. The evolution of damage calculated by the model is commented on in detail. In Sect. 5, we discuss the influence of the friction and cohesion parameters, the confinement pressure, and the initial damage on the accumulation of damage and on the stress–strain relationship of salt rock.

2 Confined Axial Loading Tests and Microstructure Observations

A complete description of the materials, methods, results and interpretations of the tests conducted on salt rock is provided in Ding et al. (2016, 2017). Here, we summarize the main results of the experimental campaign to present what we aim to explain by the model presented in the following.

2.1 Materials and Methods

The synthetic salt rock specimens used in this study were fabricated through uniaxial consolidation of reagent-grade granular halite at the following conditions: grain size ranges between 0.3 and 0.355 mm; consolidation temperature of 150 °C; maximum axial stress of 75 MPa; displacement rate of 0.034 mm/s. After consolidation, the specimen was a right-circular cylinder with a diameter of 19.75 mm and a length of 42.67 mm, and the bulk porosity of the specimen was 5.6%. The specimen was kept dry throughout all stages of this study.

The synthetic salt rock specimens were deformed at room temperature, at a confining pressure of 1 MPa, and strain rate of $3\times 10^{-6}$$\hbox {s}^{-1}$ (Fig. 2). Axial and radial strains were measured by two rosette strain gauges of 6.35 mm gauge length and 350 ${\varOmega }$ resistance. Strain gauges were glued at opposing sides of the specimen, and the two strain measurements were averaged to account for specimen tilting during deformation tests. Differential force was measured through an internal force gauge that was in direct contact with specimen assembly and unaffected by the friction between the loading piston and the sealing stack. A total of eight unloading–reloading cycles were employed, in addition to initial loading and final unloading. One unloading–reloading cycle was applied in the elastic deformation regime. In the subsequent load cycles, the plastic yielding threshold was reached.

Using repeat experiments, synthetic salt rock specimens before, during, and at the end of cyclic loading were epoxy-saturated, cut, and polished to make petrographic sections. In Fig. 3a , the red triangles indicate each of the loading stages at which a specimen was taken out for analysis. A small sample of each specimen was then cut out for microstructure observation. These samples were chemically etched to allow observation of grain-scale features, including grain boundaries and microcracks. The sectioning and etching procedures followed the techniques developed by Spiers et al. (1986) with only minor modifications. Thin section images were taken from the center portion of the specimen using 20 $\times$ magnification, and stitched together to allow observation of more than 100 grains (Fig. 2). On the stitched image, salt grain boundaries were traced and opening-mode microcracks were interpreted based on the following two criteria: (1) there is clear separation between two salt grain boundaries; (2) the opposing sides of these two salt grain boundaries match well geometrically, which indicates that they were previously in contact.

2.2 Summary of the Results

At room temperature and 1 MPa confining pressure, synthetic salt rock exhibits a ductile mechanical response. The first unloading–reloading cycle nearly fully overlies the initial loading curve, which indicates dominant elastic behavior, as shown in Fig. 3b. After yielding, the specimen deforms plastically with slight work hardening. Each unloading cycle is taken to zero differential stress; subsequent reloading does not produce significant hysteresis. The specimen behavior first shows slight compaction (positive volumetric strain), followed by continuous dilation (negative volumetric strain). At the end of the test, the specimen increases in volume by about 0.6%.

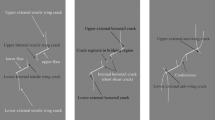
The synthetic salt rock produced from uniaxial consolidation at elevated temperature shows minor intragranular microcracking. Almost all of these intragranular microcracks are associated with fluid inclusions present in salt grains. These fluid inclusions are thought to act as stress concentrators and to promote microcracking. There is no evidence for separation at grain contacts, as all of them are tight, which results from crystal-plastic deformation of salt grains (Ding et al. 2016). As shown in Fig. 4, after cyclic triaxial loading to an axial strain of 7.3%, grain-boundary cracking becomes the dominant brittle deformation mechanism. These microcracks exhibit a preferred orientation that is sub-parallel to the axial loading direction. With further cyclic loading, dilatant grain-boundary microcracks increase in density as well as in separation. These grain-boundary microcracks, represented in red in Fig. 4, also display a clear tendency to link with neighboring cracks in the axial (loading) direction, as can be seen from the red lines oriented vertically that follow the boundaries of several neighboring grains.

2.3 Interpretation of the Results

Below, we propose a model to explain the following observed phenomena:

• (1) At room temperature and low confining pressure, grain-boundary microcracking is the dominant brittle deformation mechanism.

• (2) Wing cracks linked to main cracks propagate along grain boundaries.

• (3) Grain-boundary microcracks initiate preferably in the loading direction and tend to link with increasing deformation.

• (4) Cyclic loading leads to progressive lengthening of linked crack arrays.

• (5) Stiffness degradation is related to microscropic intergranular cracks and grain re-arrangement.

3 Theoretical Formulation of the Discrete Wing Crack Elastoplastic Damage (DWCPD) Model

3.1 The Evolution of Main Cracks

We consider a representative elementary volume (REV) of salt rock made of a homogeneous solid matrix that contains a dilute distribution of penny-shaped cracks, at the tips of which wing cracks propagate. These penny-shaped cracks, called main cracks in the following, can propagate in Mode I and Mode II. In Mode II, we postulate that the slipping of a main crack can trigger the Mode I initiation of wing cracks at its tips, perpendicular to the slipping main crack. By definition of a dilute distribution, main cracks do not interact mechanically with each other, i.e., the stress at the faces of a main crack only depends on the macroscopic stress applied at the boundaries of the REV—not on the stress at the faces of other main cracks.

We restrict our study to static conditions. Under the assumption that main cracks do not interact, the traction $\varvec{t}^m$ on the faces of the main cracks is induced by the macroscopic stress (noted $\varvec{\sigma }$) applied to the REV (Kachanov 1982). Hence, for each main crack (m), we get:

$$\begin{aligned} \varvec{t}^m= & {} \overrightarrow{n}\cdot \varvec{\sigma }, \end{aligned}$$

(1)

$$\begin{aligned} \sigma ^m_{\text {n}}= & {} \varvec{\sigma }:\left( \overrightarrow{n}\otimes \overrightarrow{n}\right) \end{aligned}$$

(2)

$$\begin{aligned} \varvec{\sigma }^m_{\text {t}}= & {} \varvec{\sigma }\cdot \overrightarrow{n} -\left( \overrightarrow{n}\cdot \varvec{\sigma }\cdot \overrightarrow{n}\right) \, \overrightarrow{n}, \end{aligned}$$

(3)

where $\overrightarrow{n}$ is the direction normal to the main crack plane, $\sigma ^m_{\text {n}}$ is the normal stress that is applied on the faces of the main crack (compression stress), and $\varvec{\sigma }^m_{\text {t}}$ is the tensor of tangential stresses that is applied on the faces of the main crack (shear stresses), as illustrated in Fig. 5.

Here, we introduce a linear frictional crack model (with friction coefficient $\mu$ and cohesion c), in which the main cracks can be subjected to five deformation mechanisms, listed in Table 1. $N^m$ and $B^m$ are the normal and frictional indices, respectively. They are introduced in the expressions of the crack displacements to distinguish the crack propagation micromechanisms, as explained in the following.

In mechanism 1, the main crack opens in pure Mode I, without slipping. In mechanism 2, the main crack does not propagate: it remains closed and does not slip. In mechanism 3, the main crack propagates both in Mode I (tensile opening) and Mode II (slipping). In mechanisms 4 and 5, the main crack is under compressive stress and does not propagate in Mode I. In mechanism 4, past loading history or current large shear stress led to inter-crystal bond breakage, and the main crack propagates in Mode II, producing frictional shear strain. In mechanism 5, although inter-crystal bonds are broken, slipping does not occur, due to the friction induced by the large normal stress on the crack face. The main crack propagation mechanisms are summarized in Fig. 6, in which main cracks do not slip in the gray region, while slipping of main cracks occurs in the blue region.

The deformation induced by main crack development is due to the occurrence of displacement discontinuities (so-called jumps) in directions that are either normal or tangential to the main crack planes. The main cracks of the same orientation are gathered in families. Since the main cracks are assumed to not interact, the mechanical behavior of the main cracks is that of cracks that are embedded in an infinite elastic medium. In the ith family, it is assumed that all main cracks have the same normal direction $\overrightarrow{n_i}$. Main cracks are assumed to be penny shaped with radius $a_{i}^{m}$. The volume fraction of the normal displacement jumps $\beta ^m_i$ and the volume fraction of shear displacement jumps $\varvec{\gamma }^m_i$ of the main cracks family i are expressed as follows (Kachanov 1992; Jin and Arson 2017b):

$$\begin{aligned} \beta ^m_i= & {} \rho ^m_is_{\text {o}}N^m_i\sigma ^m_{ni} ,\end{aligned}$$

(4)

$$\begin{aligned} \varvec{\gamma }^m_i= & {} \rho ^m_is_1B_i^m\varvec{\sigma }^m_{ti}, \end{aligned}$$

(5)

where $N^m_i$ is an index parameter used in the model to control the crack propagation mechanism in the normal direction; $B_i^m$ is an index parameter that controls the frictional mechanism in the tangential direction. $N^m_i$ (respectively, $B_i^m$) is zero when the main cracks do not propagate in Mode I (respectively, do not propagate in Mode II), as explained in Table 1. The main crack density $\rho ^m_i$ is calculated as:

$$\begin{aligned} \rho ^m_i=\frac{M_i\left( a^m_i\right) ^3}{V_{{\text {REV}}}}, \end{aligned}$$

(6)

where $V_{{\text {REV}}}$ is the actual volume of the REV and $M_i$ is the number of cracks in family i. The expressions of elastic compliances $s_{\text {o}}$ and $s_1$ were established by Kachanov (1992), as follows:

$$\begin{aligned} s_0= & {} \frac{16\left( 1-\nu _{\text {o}}^2\right) }{3E_{\text {o}}}, \end{aligned}$$

(7)

$$\begin{aligned} s_1= & {} \frac{32\left( 1-\nu _{\text {o}}^2\right) }{3\left( 1-2\nu _{\text {o}}\right) E_{\text {o}}}, \end{aligned}$$

(8)

where $E_{\text {o}}$ and $\nu _{\text {o}}$ are the Young’s modulus and Poisson’s ratio of the infinite elastic medium. The average strain induced by the displacement jumps of the main cracks in family i can be then calculated as:

$$\begin{aligned} \varvec{\epsilon }^m_i=\beta ^m_i\overrightarrow{n}_i \otimes \overrightarrow{n}_i+\frac{1}{2} \left( \varvec{\gamma }^m_i\otimes \overrightarrow{n}_i+ \overrightarrow{n}_i\otimes \varvec{\gamma }^m_i\right) . \end{aligned}$$

(9)

3.2 The Development of Wing Cracks

Based on the literature review presented in the introduction and the observations reported in the previous section, we assume that tensile wing cracks initiate at the tips of the main cracks that slip. The shear force that acts on the faces of the main cracks is viewed as the force that drives the propagation of wing cracks. Since salt rock is a polycrystalline material, and salt crystals are typically rhomboids, wing cracks are assumed to initiate in the direction perpendicular to the main crack plane, as shown in Fig. 5. The net tangential stress that is applied on the faces of the main crack in the direction $\overrightarrow{l}$ drives the tensile opening of wing crack planes perpendicular to $\overrightarrow{l}$.

The propagation of a wing crack is triggered by a tensile force, equal to the shear force $\overrightarrow{T}_i$ that is applied at the faces of the main crack. The norm of the latter is calculated as:

$$\begin{aligned} T_i=(a^m_i)^2\pi B_i^m\parallel \varvec{\sigma }^m_{ti}\parallel , \end{aligned}$$

(10)

where $a_i^m$ is the radius of the main cracks of the ith family and $\varvec{\sigma }^m_{ti}$ is tangential stress at the faces of the main cracks of the ith family. Note that if $B_i^m$ is equal to zero, the main crack does not slip, therefore $T_i=0$. As illustrated in Fig. 7, the normal stress that is applied on the faces of a wing crack of family i is the sum of the projection of the macroscopic stress on the direction normal to the wing crack ($\overrightarrow{l_i}$) and of the tensile stress induced by the main crack shear force:

$$\begin{aligned} \sigma ^w_{ni}=\frac{T_i}{{a^w_i}^2\pi }+ \varvec{\sigma }:\left( \overrightarrow{l_i}\otimes \overrightarrow{l_i}\right) . \end{aligned}$$

(11)

Substituting Eqs. (10) into (11), we have:

$$\begin{aligned} \sigma ^w_{ni}=\left( \frac{a^m_i}{a^w_i}\right) ^2 B_i^m\parallel \varvec{\sigma }^m_{ti}\parallel +\, \varvec{\sigma }:\left( \overrightarrow{l_i}\otimes \overrightarrow{l_i}\right) . \end{aligned}$$

(12)

Similar to main cracks, the volume fraction of the normal displacement jumps of a wing crack is obtained as follows:

$$\begin{aligned} \beta ^w_i=\rho ^w_is_{\text {o}}\sigma ^w_{ni}. \end{aligned}$$

(13)

The strain of the wing cracks in family i is calculated as:

$$\begin{aligned} \varvec{\epsilon }^w_i=\beta ^w_i\overrightarrow{l}_i\otimes \overrightarrow{l}_i. \end{aligned}$$

(14)

3.3 Micromechanics-Based Gibbs Free Energy

The Helmholtz free energy of the REV (noted $\varPsi ^*_{\text {s}}$) is the sum of the elastic deformation energy stored in the matrix and of the elastic deformation energy stored in the displacement jumps of the main cracks and wing cracks. $\varPsi ^*_{\text {s}}$ is expressed as follows:

$$\begin{aligned} \varPsi ^*_{\text {s}}=\frac{1}{2}\varvec{\epsilon }^e:\varvec{C}_{\text {o}}: \varvec{\epsilon }^e+\frac{1}{2}\varvec{\sigma }^m: \varvec{\epsilon }^m+\frac{1}{2}\varvec{\sigma }^w:\varvec{\epsilon }^w , \end{aligned}$$

(15)

where $\varvec{\epsilon }^e$ is the elastic strain of the matrix; $\varvec{C}_{\text {o}}$ is the elastic stiffness of the matrix; $\varvec{\sigma }^m$ and $\varvec{\sigma }^w$ are the stress fields that are applied at the main crack faces and wing crack faces, respectively. Since the main cracks do not interact and the traction stress on the faces of the main crack is induced by the macroscopic stress applied on the REV, we have:

$$\begin{aligned} \varvec{\sigma }^m\cdot \overrightarrow{n}=\varvec{\sigma }\cdot \overrightarrow{n}. \end{aligned}$$

(16)

The Legendre transformation allows expressing the free energy in terms of stress instead of elastic strain. Based on that transformation, the Gibbs free energy (free enthalpy, $G^*$) is expressed as:

$$\begin{aligned} G^*=\varvec{\sigma }:\varvec{\epsilon }^E-\varPsi ^*_{\text {s}}, \end{aligned}$$

(17)

where $\varvec{\epsilon }^E=\varvec{\epsilon }^e+\varvec{\epsilon }^w+\varvec{\epsilon }^m$ i s the REV total elastic strain. Substituting Eqs. (9), (15), and (16) into (17), we have (Jin and Arson 2017a):

$$\begin{aligned} G^*=\frac{1}{2}\varvec{\sigma }:\varvec{S}_{\text {o}}:\varvec{\sigma }+ \frac{1}{2}\varvec{\sigma }:\varvec{\epsilon }^m+ \varvec{\sigma }:\varvec{\epsilon }^w-\frac{1}{2}\varvec{\sigma }^w:\varvec{\epsilon }^w. \end{aligned}$$

(18)

Distributions of crack orientations appear in the expression of the free energy by substituting Eqs. (9) and (14) into (18). The Gibbs energy for Q main microcrack families of Q different orientations is obtained as follows:

$$\begin{aligned} G^*&=\frac{1}{2}\varvec{\sigma }:\varvec{S}_{\text {o}}:\varvec{\sigma }+\frac{1}{2}\displaystyle \sum _{i=1}^{Q} w_i\{ s_0\rho ^m_iN^m_i\left( \overrightarrow{n}_i\cdot \varvec{\sigma }\cdot \overrightarrow{n}_i\right) \left( \overrightarrow{n}_i\cdot \varvec{\sigma }\cdot \overrightarrow{n}_i\right) \nonumber \\&\quad +s_1\rho ^m_iB_i^m [\left( \varvec{\sigma }\cdot \varvec{\sigma } \right) : \overrightarrow{n}_i\otimes \overrightarrow{n}_i- \left( \overrightarrow{n}_i\cdot \varvec{\sigma }\cdot \overrightarrow{n}_i\right) \left( \overrightarrow{n}_i\cdot \varvec{\sigma }\cdot \overrightarrow{n}_i\right) ] \nonumber \\&\quad +2s_0\rho ^w_i\varvec{\sigma }: \sigma ^w_{ni}\overrightarrow{l}_i\otimes \overrightarrow{l}_i-\rho ^w_is_0 {\sigma ^w_{ni}}^2 \}, \end{aligned}$$

(19)

in which we used Baz̆ant’s discrete integration scheme, with a discrete set of $Q=74$ micro-crack families of 74 distinct crack orientations distributed on the unit sphere (Bažant and Oh 1986). The parameters $w_i$ are the weight coefficients for that integration scheme. The total strain of the REV (noted $\varvec{\epsilon }$) can be decomposed into the elastic strain $\varvec{\epsilon }^E$ and the plastic strain $\varvec{\epsilon }^p$ induced by the propagation of microscopic cracks, as follows:

$$\begin{aligned} \varvec{\epsilon }=\varvec{\epsilon }^{E}+\varvec{\epsilon }^{p}= \varvec{\epsilon }^e+\varvec{\epsilon }^{{\text {ed}}}+\varvec{\epsilon }^{p}, \end{aligned}$$

(20)

where the elastic strain $\varvec{\epsilon }^E$ is the partial derivative of Gibbs energy with respect to the macroscopic stress applied on the REV:

$$\begin{aligned} \varvec{\epsilon }^E=\frac{\partial G^*}{\partial \varvec{\sigma }}, \end{aligned}$$

(21)

where $\varvec{\epsilon }^e$ is the elastic strain of the matrix (which would exist in the absence of cracks under the given stress), and is determined by the elastic modulus $E_{\text {o}}$ and Poisson ratio $\nu _{\text {o}}$:

$$\begin{aligned} \varvec{\epsilon }^e=\frac{1+\nu _{\text {o}}}{E_{\text {o}}} \varvec{\sigma }-\frac{\nu _{\text {o}}}{E_{\text {o}}}\text {tr}\left( {\varvec{\sigma }}\right) \varvec{\delta }, \end{aligned}$$

(22)

where $\varvec{\epsilon }^{{\text {ed}}}$ is the additional recoverable strain induced by the loss of stiffness upon the development of the microcracks. Based on Eqs. (18), (20) and (21), $\varvec{\epsilon }^{{\text {ed}}}$ is expressed as:

$$\begin{aligned} \varvec{\epsilon }^{{\text {ed}}}&=\displaystyle \sum _{i=1}^{Q} w_i \rho ^m_i\left( s_1B_i^m {\mathbb {T}}_i:\varvec{\sigma }+ \frac{1}{2}s_1\frac{\partial B_{i}^{m}}{\partial \varvec{\sigma }} \varvec{\sigma }:{\mathbb {T}}_i:\varvec{\sigma }+s_0N^m_i{\mathbb {N}}_i: \varvec{\sigma }\right) \nonumber \\&+\displaystyle \sum _{i=1}^{Q} w_i\rho ^w_i s_0 \left\{ \frac{\partial \left( \varvec{\sigma }:\sigma ^w_{ni} \overrightarrow{l}_i\otimes \overrightarrow{l}_i\right) }{\partial \varvec{\sigma }}-\sigma ^w_{ni}\frac{\partial {\sigma ^w_{ni}}}{\partial {\varvec{\sigma }} }\right\} . \end{aligned}$$

(23)

In the equation above, the first term represents the recoverable strain induced by the propagation of main cracks, while the second term represents the recoverable strain induced by the propagation of wing cracks. The fourth-order operators ${\mathbb {N}}_{ijkl}$ and ${\mathbb {T}}_{ijkl}$ are defined as:

$$\begin{aligned} {\mathbb {N}}_{ijkl}= & {} n_in_jn_kn_{\text {l}}, \end{aligned}$$

(24)

$$\begin{aligned} {\mathbb {T}}_{ijkl}= & {} \frac{1}{4}\left( n_in_k \delta _{jl}+n_in_{\text {l}}\delta _{jk}+n_jn_{\text {l}}\delta _{ik}+n_jn_k\delta _{il}\right) -n_in_jn_kn_{\text {l}}, \end{aligned}$$

(25)

where ${\mathbb {N}}_{ijkl}$ can be thought of as a normal projection operator, and ${\mathbb {T}}_{ijkl}$ as a tangential projection operator. According to Fig. 6, when main cracks deform under mechanism 4 (pure Mode II), $\partial B_{i}^{m}/\partial \varvec{\sigma }$ in Eq. (23) is calculated by Eq. (26) (below); otherwise, $\partial B_{i}^{m}/\partial \varvec{\sigma }$ is equal to 0. We have:

$$\begin{aligned} \frac{\partial B_{i}^{m}}{\partial \varvec{\sigma }}= \frac{\mu }{\parallel \varvec{\sigma }^m_{ti}\parallel }\frac{\partial \sigma _{ni}^{m}}{\partial \varvec{\sigma }}-\frac{\mu \sigma _{ni}^{m}}{\parallel \varvec{\sigma }^m_{ti} \parallel ^2}\frac{\partial \parallel \varvec{\sigma }^m_{ti}\parallel }{\partial \varvec{\sigma }}, \end{aligned}$$

(26)

in which the effect of friction is accounted for in the first term, and the effect of cohesion is accounted for in the second term.

3.4 Damage Criterion and Flow Rule

The main cracks propagate if the following criteria are satisfied:

$$\begin{aligned} f^m_{{\text {I}}\,i}= & {} \sigma ^m_{ni}\sqrt{\pi a^m_i}-K_{{\text {Ic}}} , \end{aligned}$$

(27)

$$\begin{aligned} f^m_{{\text {II}}\,i}= & {} B_i^m\parallel \varvec{\sigma }^m_{ti}\parallel \sqrt{\pi a^m_i}-K_{{\text {IIc}}}, \end{aligned}$$

(28)

for Mode I and II, respectively. $K_{\text {c}}$ represents the hardening of crack toughness (Jin and Arson 2017a), as shown in Fig. 8; it is expressed as a hyperbolic function, as follows:

$$\begin{aligned} K_{\text {c}}=\frac{a^{3/2}}{\frac{1}{K_{\text {o}}}+\frac{a}{\varvec{\sigma }_{\text {c}}}}, \end{aligned}$$

(29)

in which a is the crack radius (we omitted the indices i and m for clarity). $K_{\text {o}}$ and $\varvec{\sigma }_{\text {c}}$ are constitutive parameters that respectively control the yield point and the peak stress. The values of $K_{\text {o}}$ and $\varvec{\sigma }_{\text {c}}$ in Mode I differ from those in Mode II.

Wing cracks are assumed to propagate in Mode I only, according to the following criterion:

$$\begin{aligned} f^w_{{\text {I}}\,i}=\sigma ^w_{ni}\sqrt{\pi a^w_i}-K_{{\text {Ic}}}. \end{aligned}$$

(30)

According to the consistency rule, when the damage criterion is reached, the damage function f is equal to zero and remains equal to zero, i.e., $f = 0$, $\hbox {d}f = 0$. The equation $\hbox {d}f = 0$ is solved for the radius of cracks of family i, as follows:

$$\begin{aligned} \text {d}a_i=\frac{\frac{\partial {f}}{{\varvec{\sigma }}}\text {d} \varvec{\sigma }}{\frac{\partial {f}}{\partial {a_i}}}, \end{aligned}$$

(31)

in which f is the damage function of the ith crack family. Several damage mechanisms can be active at the same time for a single crack family, so that f can denote any of the following criteria: $f^m_{{\text {I}}\,i}$ (main cracks opening in Mode I), $f^m_{{\text {II}}\, i}$ (main cracks propagating in Mode II), $f^w_{{\text {I}}\,i}$ (wing cracks propagating in Mode I). Each crack family comprises one main crack and two wing cracks. The radius of the main cracks ($a_i^m$) is calculated from Eq. (31), in which $f = f^m_{{\text {I}}\,i}$ if the main cracks of the ith family propagate in Mode I and $f = f^m_{{\text {II}}\, i}$ if they propagate in Mode II. The radius of the wing cracks ($a_i^w$) is also obtained from Eq. (31), in which $f = f^w_{{\text {I}}\,i}$. For each crack family, we calculate the main crack density and the wing crack density by using the following equation:

$$\begin{aligned} \text {d}\rho _i=\frac{3M_ia^2_i}{V_{{\text {REV}}}}\text {d}a_i, \end{aligned}$$

(32)

in which $a_i = a_i^m$ for the main crack density and $a_i = a_i^w$ for the wing crack density. The initial radius of the main cracks ($a_{{\text {mo}}}$) is set equal to 0.022 mm, which is about one-tenth of the mean grain size. Note that for each crack family i, we calculate a main crack density ($\rho ^m_i$) and a wing crack density ($\rho ^w_i$). The macroscopic damage variable of the REV ($\varvec{\varOmega }$) is defined as the sum of the crack density tensors of all crack families, as follows:

$$\begin{aligned} \varvec{\varOmega }=\displaystyle \sum _{i=1}^{Q} \rho ^m_i \overrightarrow{n}_i\otimes \overrightarrow{n}_i+ \displaystyle \sum _{i=1}^{Q} \rho ^w_i\overrightarrow{l}_i\otimes \overrightarrow{l}_i. \end{aligned}$$

(33)

3.5 Inelastic Deformation

The plastic deformation in Eq. (20) (noted $\varvec{\epsilon }^p$) is introduced to account for the inelastic strain that results from the rearrangement of crystals. A non-associated plastic flow rule is adopted. The plastic yield surface is a quadratic function, adopted in former rock mechanics models (Shao et al. 2006):

$$\begin{aligned} f_{\text {p}}(\varvec{\sigma },d,\varvec{\epsilon }^p)=q^2h^2(\theta )+\alpha _{\text {p}}(p-e) \end{aligned}$$

(34)

where q is the deviatoric stress; p is the mean stress; e is a constant describing the cohesion of the rock; $\alpha _{\text {p}}$ is the plastic hardening function; $h(\theta )$ is a function of Lode’s angle $\theta$. The yield surface is shown in Fig. 9. A simplified expression of $h(\theta )$ can be given as (Van Eekelen 1980):

$$\begin{aligned} h(\theta )= & {} 1-m_{\theta }\text {sin}(\theta ) \end{aligned}$$

(35)

$$\begin{aligned} \text {sin}(\theta )= & {} -\frac{J_3}{2}{\left( \frac{3}{J_2}\right) }^{\frac{3}{2}}, \end{aligned}$$

(36)

where $J_2$ and $J_3$ are the second and third stress invariants, respectively, and $m_\theta$ is a material parameter, controlling the effect of Lode’s angle. The plastic function $\alpha _{\text {p}}$ couples damage and plasticity, and depends both on the volumetric part of the damage tensor (d = tr$\left( \varvec{\varOmega }\right)$) and on the plastic hardening variable (noted $\omega _{\text {p}}$). The expression of $\alpha _{\text {p}}$ is the following:

$$\begin{aligned} \alpha _{\text {p}}=(1-\chi d)\left[ \alpha _{\text {p}}^o+\left( \alpha _{\text {p}}^m-\alpha _{\text {p}}^o\right) \frac{\omega _{\text {p}}}{R+\omega _{\text {p}}}\right] , \end{aligned}$$

(37)

in which $\chi$ is a scaling parameter which can take any value between 0 and 1: if $\chi$ = 0, there is no influence of damage on inelastic hardening; if $\chi$ is strictly positive, inelastic hardening decreases as damage increases, which means that the rate of inelastic deformation increases with the amount of damage accumulated. $\alpha _{\text {p}}^o$ is the plastic yielding threshold; $\alpha _{\text {p}}^m$ is the maximum value of the hardening function; R determines the plastic hardening rate.

The plastic hardening variable $\omega _{\text {p}}$ is defined as the generalized shear strain:

$$\begin{aligned} {\dot{\omega }}_{\text {p}}= & {} \sqrt{\frac{2}{3}\dot{\varvec{e}}^{p}:\dot{\varvec{e}}^{p}} \end{aligned}$$

(38)

$$\begin{aligned} \varvec{e}^p= & {} \varvec{\epsilon }^p-\frac{1}{3}\left( \varvec{\epsilon }^p:\varvec{\delta }\right)\,\, \varvec{\delta } \end{aligned}$$

(39)

A damage coupled plastic potential is adopted, as follows (Shao et al. 2006):

$$\begin{aligned} g(\varvec{\sigma },d)=qh(\theta )-(1-\chi d)\eta (p-e), \end{aligned}$$

(40)

where $\eta$ is a material parameter, controlling the boundary of the compressive dilation zone. The increment of plastic strain is calculated as follows:

$$\begin{aligned} \dot{\varvec{\epsilon }}^{p}={\dot{\lambda }} \frac{\partial g}{\partial {\varvec{\sigma }}} , \end{aligned}$$

(41)

in which ${\dot{\lambda }}$ is the plastic multiplier. According to the plasticity consistency rule, ${\dot{\lambda }}$ is a positive scalar, and ${\dot{\lambda }}f_{\text {p}}(\varvec{\sigma },d,\varvec{\epsilon }^p)=0$. Substituting Eq. (41) into Eqs. (38, 39), we have:

$$\begin{aligned} {\dot{\omega }}_{\text {p}}={\dot{\lambda }}\sqrt{\frac{2}{3}\bigg \{\frac{\partial g}{\partial {\varvec{\sigma }}}:\frac{\partial g}{\partial {\varvec{\sigma }}}-\frac{1}{3}\bigg [\text {tr}\left( \frac{\partial g}{\partial {\varvec{\sigma }}}\right) \bigg ]^2\bigg \}}. \end{aligned}$$

(42)

When the plastic yield criterion is exceeded ($f_{\text {p}} > 0$), the plastic function $\alpha _{\text {p}}$ is first updated by using the consistency rule applied to the plastic yield function $f_{\text {p}}$, given in Eq. (34). Then, the plastic hardening variable $\omega _{\text {p}}$ is obtained from Eq. (37) using the updated $\alpha _{\text {p}}$. The plastic multiplier ${\dot{\lambda }}$ is then calculated from Eqs. (40) and (42), with the updated $\omega _{\text {p}}$. Substituting ${\dot{\lambda }}$ into Eq. (41), the plastic strain $\varvec{\epsilon }^{p}$ is obtained for the current load step. The resolution algorithm of the DWCPD model is presented in Fig. 10.

4 DWCPD Model Calibration

We used the stress–strain curves obtained during the confined cyclic axial loading tests presented in Sect. 2 to calibrate the proposed discrete wing crack elastoplastic damage (DWCPD) model. Reloading was done after unloading, when the differential stress was reduced to 0 MPa. The same confined cyclic loading tests were performed more than ten times, and the repeatability of the test was confirmed. Figure 11 shows the obtained stress–strain curves.

When the differential stress is less than 35 MPa (yielding point), the specimen deforms elastically. Hence, we first calibrated the elastic parameters $E_{\text {o}}$ and $\nu _{\text {o}}$ by using the linear portion of the first loading cycle, for stresses lower than 35 MPa. Using data from all the subsequent cycles, we calibrated the yield parameters ($K_{{\text {Ic}}}$, $K_{{\text {IIc}}}$, $\alpha _{\text {p}}^o$, e) and the friction parameters ($\mu$ and c) so as to match the hardening portion of the stress–strain curve after the yield point. Then, the parameters controlling the ultimate state ($\sigma _{{\text {Ic}}}$, $\sigma _{{\text {IIc}}}$, and $\alpha _{\text {p}}^m$) were calibrated from the maximum stress in each cycle. The stiffness of the specimen in each cycle was calculated from the damage parameters $K_{{\text {Ic}}}$, $K_{{\text {IIc}}}$, $\sigma _{{\text {Ic}}}$, and $\sigma _{{\text {IIc}}}$, and compared to the stiffness measured from the unloading part of the experimental curves, for verification. Lastly, we calibrated the plasticity parameters $\chi$ and $\eta$ by trial and error, to find the best fit with the residual strain after each cycle and with the ratio between axial strain and lateral strain in the experimental stress–strain curve. The calibrated model parameters are given in Table 2.

According to Fig. 11, the yielding, hardening, and stiffness degradation of salt rock in the cyclic loading test are captured by the DWCPD model. Upon loading or reloading, cracks propagate only after the differential stress reaches the maximum differential stress ever reached in the loading history. During unloading, the magnitude of the differential stress decreases, and the cracks stop propagating (Eqs. (27), (28), (30)). Based on Eq. (23), the REV stiffness depends on crack density, which does not evolve upon unloading, leading to linear unloading paths shown in Fig. 11, i.e., the hysteresis is not captured by the DWCPD model.

The evolution of damage during the cyclic loading tests is shown in Fig. 12. The damage tensor is projected on the three directions of space, in which direction 3 is the loading axis and directions 1 and 2 are the lateral directions. The axial damage component is noted $\varOmega _3$: this is the damage that represents an equivalent crack plane normal to the loading axis. $\varOmega _1$ and $\varOmega _2$ are the lateral damage components, i.e., the equivalent crack planes that contain the loading axis, as shown in Fig. 13. Note that since the experiment is axisymmetric, the evolution curves of $\varOmega _1$ and $\varOmega _2$ overlap. The total damage $\varvec{\varOmega }$ presented in Fig. 12a is the sum of the main crack damage $\varvec{\varOmega }_{\text {m}}$ (Fig. 12b) and of the wing crack damage $\varvec{\varOmega }_{\text {w}}$ (Fig. 12c).

The evolutions of $\varOmega _1$ and $\varOmega _3$ differ, which implies that the specimen exhibits an anisotropic behavior after damage initiation (damage-induced anisotropy). Results shown in Fig. 12 indicate that damage propagates in two phases, as explained in Fig. 14. In Stage 1, under low differential stress (i.e., under 10 MPa), the main crack damage components remain constant, which means that the main cracks keep their initial radius $a_{{\text {mo}}}$. Main cracks cannot slip, because of the cohesion and the friction at salt crystal faces. By contrast, wing cracks start propagating in Mode I when the differential stress is only a few MPa. This means that the shear stresses that accumulate at the faces of the main crack lead to the accumulation of tensile stress at the faces of the wing cracks and trigger the initiation of wing cracks. Since the REV is subjected to a compression in direction 3, tensile wing crack propagation mostly leads to lateral damage ($\varOmega _{w1}$ and $\varOmega _{w2}$). Note that $\varOmega _{w3}$ is not zero, since it is calculated as the projection of the 74 wing crack density tensors on direction 3. In Stage 2, with the increase of differential stress, shear stresses at the faces of the main cracks reach the Mode II crack propagation threshold. Main crack tangential displacement jumps are noted. Main cracks start to propagate in Mode II, and main crack planes with a normal vector close to the direction perpendicular to the loading direction tend to propagate faster. Main crack slipping induces additional wing crack tensile opening, predominantly in the loading direction. As a result, in Stage 2, $\varOmega _{m3}$ increases faster than $\varOmega _{m1}$ and $\varOmega _{m2}$ and $\varOmega _{w3}$ develops faster than $\varOmega _{w1}$ and $\varOmega _{w2}$ (see Fig. 12b, c). Tensile damage is not observed in the main cracks.

5 Sensitivity Analyses

5.1 Influence of the Friction Coefficient and of the Cohesion at Main Crack Faces

Main cracks only slip when the magnitude of the shear stress exceeds $c +\mu \sigma ^m_{\text {n}}$. Here, we present a sensitivity analysis of the friction coefficient $\mu$ and of the cohesion c, which both control the amplitude of the tangential displacement jumps. Triaxial compression tests are simulated with the same confinement pressure as in the calibration simulations (1 MPa). The elastic, damage, and plastic parameters are those listed in Table 2. When the axial strain reaches 0.01, we start unloading until the differential stress reduces to 0 MPa.

For the calibrated cohesion $c = 4$ MPa, we perform simulations with $\mu$ equal to 0, 0.2, and 0.4. Figure 15 shows that a larger friction coefficient leads to larger specimen (REV) strength, because the friction on the faces of the main cracks restricts the propagation of the main cracks. With a smaller friction coefficient, the main cracks undergo larger tangential displacement jumps, hence larger plastic strain $\epsilon ^p$, which explains the larger residual strains at lower friction. In specimens with non-zero friction coefficients, crack propagation mainly occurs on the main cracks with orientation close to the axial loading axis (Eqs. (3) and (28)). Figure 16 shows that the damage rate is larger for both the main and wing cracks when the friction coefficient is smaller. As in Sect. 4, the evolution of damage presents two stages, independently of the value of $\mu$. In Stage 1, wing cracks propagate in Mode I because of the loading applied at the external boundaries of the specimen, and the main cracks do not slip. Therefore, the evolution of damage is independent of the value of the friction coefficient. In Stage 2, the main cracks propagate in Mode II and wing cracks rapidly propagate in Mode I. Stage 2 starts at a differential stress of 8 MPa for $\mu =0$, 12 MPa for $\mu =0.2$ and 15 MPa for $\mu =0.4$. Hence, a larger friction coefficient delays the propagation of the main cracks, which results in smaller total damage at the end of the unloading phase. For example, when the axial strain reaches 0.01, the total axial damage of the specimen with $\mu =0$ is 0.71, while the axial damage of the specimen with $\mu =0.4$ is only 0.48.

As shown in Fig. 16b, the difference in the final axial main crack damage between the case $\mu$ = 0 ($\varOmega _{m3}$ = 0.43) and the case $\mu$ = 0.2 ($\varOmega _{m3}$ = 0.38) is 0.05, and the difference in the final axial main crack damage between the case $\mu$ = 0.2 ($\varOmega _{m3}$ = 0.38) and the case $\mu$ = 0.4 ($\varOmega _{m3}$ = 0.30) is 0.08. With the increase of $\mu$, the effect of $\mu$ on $\varOmega _{m3}$ increases. This is because the propagation of the main cracks is controlled by both cohesion and friction, and therefore slipping is predominantly hindered by the cohesion parameter when the friction parameter is small. As a result, the final main crack damage is not very sensitive to $\mu$ when $\mu$ is small.

For the calibrated friction parameter $\mu = 0.15$, we perform simulations with c equal to 0 MPa, 8 MPa, and 16 MPa (Fig. 17). According to Fig. 18, the higher the cohesion, the later is the development of damage. This was expected, because a higher cohesion requires a higher stress to break the inter-crystalline bonds. When cohesion is 0 MPa or 8 MPa, the evolution of damage is smooth. With the increase of differential stress, the resistance to the tangential displacement of the main cracks is only provided by friction, and the damage curves start to overlay (i.e., the black line and the red line in Fig. 18 overlap when the differential stress reaches 30 MPa). For a cohesion of 16 MPa, both the main crack damage and wing crack damage accumulate by steps, suggesting a stick-slip mechanism. This is because when the shear stress at the crack faces exceeds cohesion, inter-crystalline bonds are suddenly broken: a sudden increase of the main cracks’ length occurs, which leads to the rapid propagation of wing cracks and a rapid increase of strain (Fig. 17). With a high cohesion (c = 16 MPa), main crack slipping is hindered and salt rock strength is increased.

5.2 Influence of the Confinement

We now investigate the sensitivity of deformation and damage to the confining pressure. The constitutive parameters are those obtained after calibration, as listed in Table 2. Triaxial loading–unloading cycles are simulated with a confinement pressure equal to 0 MPa, 5 MPa, and 10 MPa respectively. When the axial strain of the rock reaches 0.01, unloading begins, until the differential stress gets to 0. Results are presented in Figs. 19 and 20.

According to Fig. 19, under a confining pressure of 5 MPa, the stress of the specimen at 0.01 axial strain is 42.5 MPa, versus 38 MPa without confinement. The residual strain is almost insensitive to the confinement, although we note that the lateral residual strains increase when the confinement decreases. This was expected, since the lateral confinement restricts the lateral strains. When the confinement is low, wing cracks initiate at lower differential stress, and both wing cracks and main cracks exhibit a greater propagation rate after initiation. For instance, damage initiates at a differential stress of 0 MPa if the confining pressure is 0, 3 MPa if the confining pressure is 5 MPa and 9 MPa if the confining pressure is 10 MPa. The final wing crack damage in the loading direction is 0.26 under no confinement, 0.21 at 5 MPa confinement, and 0.19 under 10 MPa confinement. The main cracks start to propagate at a differential stress of 10MPa if the confinement is 0 MPa. When the confinement is 10 MPa, main cracks start propagating at a differential stress of 13 MPa. At the same differential stress, the main crack damage in the loading direction increases with the confining pressure. Visually, the damage evolution curve of the axial damage in the absence of confinement remains on the left side of the other damage evolution curves. Wing cracks propagate in Mode I, which means that wing cracks propagate if tensile stress develops at their faces. In the lateral direction, the second term of Eq. (11) is negative and increases in magnitude with the confining pressure. As a result, under high confinement, the lateral component of the forces that are applied in the direction normal to the wing cracks decreases. Because the tensile forces normal to the wing cracks decrease, fewer wing cracks propagate in Mode I under high confinement. In other words, a high confinement impedes the initiation of wing cracks. As expected, simulation results indicate that in Stage 1, the initiation of wing cracks is sensitive to the confinement, with a delayed occurrence of damage at high confinement. Here, the highest differential stress increases with the confining pressure. Under high confinement, the initiation of wing cracks is delayed. The accumulation rate of damage decreases with the confining pressure in the simulated tests. In Stage 2, a high confinement prevents the main cracks from slipping. Thus, under low confinement, the main cracks propagate earlier and faster, which accelerates the propagation of the connected wing cracks. A larger confinement stress induces more slipping and less opening of the main cracks. In all cases, the main crack damage exceeds the wing crack damage when the axial strain reaches 0.01.

Table 1 Deformation modes of main cracks

5.3 Damage Evolution with Different Initial Crack Distributions

We now study the effect of the initial crack distribution in the specimen on the response of the specimen to the loading–unloading cycles. Constitutive parameters are those listed in Table 2. We first simulate a triaxial extension test, in which the axial tensile stress is incrementally increased up to 3 MPa (in direction 3). Then, we simulate the unloading path from a 3 MPa axial stress to a 0 MPa axial stress. Finally, we simulate a uniaxial compression test by incrementally applying a 0.01 axial strain. The loading path is presented in Fig. 21 and the stress vs. strain curve is shown in Fig. 22 (O-A-B-C-D). During the triaxial extension (OA), damage accumulates in the specimen. Elastic unloading is represented by A-B. The response to the subsequent compressive loading (B-C-D) is compared to the response of a specimen that is not subjected to triaxial extension prior to the compression (O-C’-D’). As expected, the total accumulated damage obtained in the pre-damaged (deformed) specimen is larger than that in the undeformed specimen, and this difference is due to the larger main crack density developed in the pre-damaged specimen. The strength of the pre-damaged specimen is also lower than that of the undeformed specimen, which is consistent with observations and models reported in (Hoek et al. 1966; Hawkes and Mellor 1970).

During the triaxial extension phase (O-A), the main cracks propagate in Mode I, predominantly in the loading direction (direction 3). Slight slipping is observed in the main cracks close to the lateral direction. During the uniaxial unloading phase (A-B), cracks do not propagate. During the uniaxial compression phase (B-C), the main cracks only propagate in Mode II. The main cracks are now longer than the initial main cracks of the undeformed specimen.

Table 2 DWCPD model parameters, calibrated against the cyclic triaxial test

Fig. 1

Simplified crack patterns for the main cracks and wing cracks

Fig. 2

Schematic diagram of the cyclic loading tests (adapted after Ding 2019). The diameter of the cylinder specimen was 19.75 mm, and its length was 42.67 mm. The bulk porosity of the specimen was 5.6%. The specimen was deformed at room temperature, at a confining pressure of 1 MPa, and was kept dry during the cyclic loading tests. The axial strain rate was $3\times 10^{-6}$$\hbox {s}^{-1}$. Drawing not to scale

Fig. 3

Stress–strain curve obtained during the confined cyclic triaxial tests. Eight cycles were performed in the triaxial tests. The microscopic images were acquired at the end of each cycle, noted as red triangles. In the first cycle, the loading and unloading curves nearly fully overly

Fig. 4

Microstructure of experimentally deformed, granular salt rock after 7.3% axial strain (adapted after Ding et al. 2017). The red color indicates the presence of boundary cracks

Fig. 5

Schematic of the mechanisms of the main crack and the wing cracks. $\sigma ^m_{\text {n}}$ is the normal stress that is applied on the faces of the main crack (compression stress), and $\sigma ^m_{\text {t}}$ is the tensor of tangential stresses that are applied on the faces of the main crack (shear stresses). $\sigma ^m_{\text {l}}$ is the net tangential stress that is applied on the faces of the main crack in the direction $\varvec{l}$. Note: the sketch gives a 2D view, but the proposed model is in 3D

Fig. 6

The mechanisms of the main crack propagation. Gray region: no slipping. Blue region: slipping. Mechanism 1: pure Mode I. Mechanism 3: modes I and II. Mechanism 4: pure Mode II. Mechanisms 2 and 5: no propagation. $\mu$ is the friction coefficient and c is the cohesion of the main crack faces

Fig. 7

Schematic of the mechanisms at the faces of the wing cracks. T is the tensile force that triggers the opening of the wing crack. $\varvec{\sigma }$ is the macroscopic stress. The projection of the macroscopic stress on the direction normal to the wing crack is calculated as $\varvec{\sigma }:\left( \overrightarrow{l}\otimes \overrightarrow{l}\right)$

Fig. 8

The hyperbolic hardening model of crack toughness used in the DWCPD model

Fig. 9

Yield surface represented in $p-q-\alpha _{\text {p}}$ space. In this plot, the cohesion is set to 4 MPa, and the material parameter $m_\theta$ is 0. $\alpha _{\text {p}}$ increases with the development of plasticity

Fig. 10

Resolution algorithm of the DWCPD model

Fig. 11

Stress–strain curve obtained during the confined cyclic triaxial tests: experimental results vs. DWCPD model predictions (calibration simulations)

Fig. 12

Evolution of damage during the triaxial cyclic tests (calibration of the DWCPD model)

Fig. 13

Visual definition of the damage tensor. All crack families are projected onto the three orthogonal directions of space, direction 3 being the loading direction. The components of the damage tensor can be understood as three equivalent crack planes orthogonal to the three directions of space

Fig. 14

Damage propagation process: (1) wing crack tensile opening; (2) main crack slipping, inducing additional wing crack opening. The blue arrows indicate the loading direction

Fig. 15

Stress–strain curves showing the influence of the friction coefficient $\mu$ at main crack faces under a confinement pressure 1 MPa, for a cohesion of 4 MPa (calibrated value). A larger friction coefficient $\mu$ enhances the strength of specimen

Fig. 16

Damage evolution curves showing the influence of the friction coefficient $\mu$ at main crack faces under a confinement pressure 1 MPa, for a cohesion of 4 MPa (calibrated value). The decrease of friction coefficient enhances the increasing rate of damage induced by both main cracks and wing cracks

With the increase of compressive axial stress, thw main cracks propagate in both the undeformed and the pre-damaged specimen, and at the end of the test, the average main crack length is larger in the pre-damaged specimen. The difference between B-C and O-C’ in Fig. 23b is in fact due to the formation of Mode I main crack planes orthogonal to the loading axis during the triaxial extension loading phase (OA), applied to create “pre-damage”. In the pre-damaged specimen, very large compressive axial stress is needed to generate a tangential stress component large enough to trigger the slipping of the main crack planes that are nearly orthogonal to the loading direction 3. This is because the toughness of the main cracks increases with the main crack radius (Eq. (29)). The growth rate of the radius of the main cracks in the pre-damaged specimen is slower than that in the undeformed specimen. As a result, when compressive axial stress increases, O-C’ gets closer to B-C in Fig. 23b, but the main crack damage in the pre-damaged specimen is always larger than that in the undeformed specimen. Since the development of wing cracks is controlled by the main cracks, the propagation of wing cracks is delayed whenever main crack propagation is delayed.

During phase O-A-B, only the tensile cracks propagate. Wing cracks do not propagate. Stage 1 starts after point B is reached. During Stage 1, the main cracks do not propagate and wing cracks propagate. We observe that wing cracks propagate faster in pre-damaged specimens (Fig. 23c). This is because main cracks are longer in the pre-damaged specimens (Eqs. (10), (11), and (30)). In Stage 2, the propagation of wing cracks is dominated by the propagation of main cracks, and the difference of wing cracks radius between the pre-damaged and undeformed specimens decreases.

6 Conclusion

Cyclic axial loading tests were performed under a confining pressure of 1 MPa on synthetic salt rock generated by thermal consolidation. The stress–strain curves and the microstructure images taken at key stages of the cycles revealed the formation of a complex system of main and wing microcracks, the orientation of which was loading dependent. We formulated a discrete wing crack elastoplastic damage (DWCPD) model to interpret the mechanisms that control the coupled evolution of crack families in salt rock under confined cyclic loading. The macroscopic stress–strain relationship is coupled to the evolution law of damage accumulated by the main microcracks and associated wing cracks. Wing cracks propagate in Mode I due to shear stress that accumulates at the faces of main cracks. The expression of the REV Gibbs free energy is given as a function of the displacement jumps of the main cracks and of the wing cracks. A plastic potential, coupled to the damage induced by the microcracks, is introduced to account for the development of irreversible strains. A frictional cohesive model is proposed for the main cracks, which propagate in both Mode I and Mode II. We calibrated the proposed model against the stress–strain curves of the cyclic loading–unloading cycles performed in the laboratory and showed that the DWCPD model can successfully capture the stiffness degradation, strength reduction and irreversible strain accumulation.

Sensitivity analyses indicate that rock strength decreases when the friction coefficient or the cohesion of the faces of the main cracks decreases, when the confining pressure decreases or when the specimen contains a greater volume fraction of cracks prior to loading. Larger inelastic deformation is observed for lower friction or lower confinement. With a larger cohesion, damage development is delayed and exhibits a stick-slip evolution. In the example case treated in this paper, the initial cracks did not seem to influence the final irreversible strains accumulated, because the initial cracks that had developed in triaxial extension had closed under the compression loading phase. Damage accumulated at a higher rate in specimens that were damaged prior to compression than in the ones that were not.

Interestingly, the simulations showed that microcracks occur following two stages: (1) wing cracks initiate and main cracks do not propagate; (2) wing cracks and main cracks then propagate simultaneously. Higher friction at the crack faces leads to higher strength. At higher confinement, the initiation of wing cracks is delayed, which results in an increase of strength. Another important outcome of this research work is the demonstration that salt rock develops damage-induced anisotropy. This is an important finding, because the majority of the constitutive models of salt rock used in geotechnical engineering and in the mining industry assume that microcrack propagation and healing lead to isotropic stiffness changes.

Fig. 17

Stress–strain curves showing the influence of the cohesion c at main crack faces under a confinement pressure 1 MPa, for a friction coefficient of 0.15 (calibrated value). When the cohesion is larger than 8 MPa, the strength of the specimen is enhanced by cohesion

Fig. 18

Damage evolution curves showing the influence of the cohesion c at the main crack faces under a confinement pressure 1 MPa, for a friction coefficient of 0.15 (calibrated value). Larger cohesion reduces the increasing rate of damage induced by the main cracks and postpones the initiation of wing cracks. When the cohesion is small (i.e., less than 8 MPa), the propagation of microcracks is less sensitive to cohesion

Fig. 19

Stress–strain curves showing the influence of the confinement p, for a cohesion of 4 MPa and a friction coefficient of 0.15 (calibrated value). Larger confinement enhances the strength of the specimen

Fig. 20

Damage evolution curves showing the influence of the confinement p, for a cohesion of 4 MPa and a friction coefficient of 0.15 (calibrated value). The increase of confinement reduces the increasing rate of damage induced by both the main cracks and wing cracks. The propagation of wing cracks is more sensitive to the confinement of the specimen than the propagation of main cracks

Fig. 21

Stress paths simulated to study the influence of pre-existing cracks. Compression stress is counted positive. The initial condition O is the isotropic compression (zero differential stress in the loading direction). OA represents the triaxial extension phase with a maximum tensile differential stress of 3 MPa. AB is the unloading phase. BC is the triaxial compression phase with a maximum axial strain of 0.01. CD is the unloading phase

Fig. 22

Stress–strain curve: pre-damaged (deformed) vs. undeformed (non-pre-damaged) salt rock. The strength of the pre-damaged specimen is lower than that of the undeformed specimen

Fig. 23

Damage evolution: pre-damaged (deformed) vs. undeformed (non-pre-damaged) salt rock. Main cracks propagate during the triaxial extension phase (O-A). In Stage 1, the wing cracks in pre-damaged specimen propagate faster. In Stage 2, the difference of wing cracks radius in pre-damaged specimen and undeformed specimen decreases