Introduction

Global climate change continues to influence our world’s eco-system, water cycle and soil condition, crop yield, and other aspects of the natural environment in addition to social and economic activities (Fischer et al. 2012; Panda et al. 2013; Zhang 2013; Wang et al. 2018). Research on global climate change has grown particularly intense in recent years as the scientific community—and indeed, the public has grown increasingly aware of these effects. (Warner et al. 2009; Wu et al. 2010). Precipitation is an essential part of the hydrological cycle. Abnormal changes in precipitation contribute to a host of environmental problems (Djaman et al. 2016). Precipitation tends to rise in the tropical and high-altitude zones across the globe while decreasing in subtropical zones (Alexander et al. 2006; Frich et al. 2002). These changing trends vary by region (Mihailović et al. 2015). In China, study has revealed inconsistent trends at the regional scale due to the various analysis approaches and study periods to investigate them (Fan et al. 2012; Ip et al. 2011). Consequently, there is an urgent necessity for trend analysis methods that function independent of the study periods.

Within lengthy time series datasets, precipitation may change non-monotonically (Khaliq et al. 2007; Rahmani et al. 2015) or monotonically, however, with wide variations in amplitude across different periods (Ruggieri 2013). These phenomena reflect the existence of change points in such datasets (Chen et al. 2016; Fealy and Sweeney 2005). Traditional approaches to change-point detection assume that the change point is identical locations (or timing) and quantity of change points in the data across multiple time series; it is not flexible enough to apply for longer time series (Jamali et al. 2015). Moreover, when change points are recognized, at present, existing approaches cannot contain the necessary indices to verify the reliability and practicability of the recognized change points (Chen et al. 2016; Fealy and Sweeney 2005; Fu et al. 2015). Because change-point detection is mainly used to analyze data of lengthy time series in economy, environment, ecology, management, and demography, as well as meteorological research, its approach must meet new requirements for flexibility and simplicity.

Trend analysis approaches are primarily comprised of parametric or nonparametric trend test (Burn and Elnur 2002; Wang et al. 2014; Xu et al. 2004; Zenklusen Mutter et al. 2010). Parametric approaches are simple but require data series which follow normal distribution. The least squares method is a popular such approach, in which the best fit is a trend line with the minimized sum of squared residuals and the significance of linear fitting is considered the significance of the trend (Crujeiras and Van Keilegom 2010; Wang et al. 2014). Nonparametric approaches, conversely, do not require the data series to follow normal distribution. The most commonly used is a calculation process that combines the Mann-Kendall trend test with the Sen’s method (Kendall 1948; Mann 1945; Sen 1968). This approach is more reliable in terms of significance test results than the least squares method and is widely applied for meteorology, hydrology, agriculture, ecology, and environment (Burn and Elnur 2002; Wang et al. 2015, 2017; Xu et al. 2004). The present study focuses on a novel nonparametric approach for analyzing precipitation trends over lengthy time series.

Most of the trend analysis that has been conducted has not considered the existence of a change point in the time series analysis (Suhaila and Yusop 2018), also according to a previous study that different methods often give different numbers and locations of change points (Sharma et al. 2016); however, the identification of change points in the previous studies only consider the location and number of change points; the trend of each segmentation between adjacent change points cannot be assessed jointly in the time series; in our study, trend tests can be used as a management tool with proper measures to evade climate change impacts (Nouri et al. 2017). We try to propose an optimized non-parametric method including the automatic identification of change points and calculation of segmentation trends for each station, combined with the trend approach and change point detection which are popular hot topics in hydrology climate and ecology fields (Razmi et al. 2017). Therefore, the combination of identifying change points and calculating segmentations trends is our innovation.

This study proposes a change-point detection approach that automatically identifies the characteristics of change points (locations and timing) and calculates the trend characteristics of multiple segments. The approach involves detecting the locations and timing of change points using the maximum likelihood approach, and assessing trends analysis and significance in the data in each segment using the Mann-Kendall trend test which is also compared with the ordinary least squares (OLS) method. Notably, we need to do a normal distribution test before we use OLS linear regression. The proposed approach was applied to a region scale using the number of change points, standard deviation, timing of change points, minimum and maximum trend for segmentations, and generalization trend across the entire study period as the index. The results presented here may provide a workable reference for regional water resource management and adaptation to extreme climate, as well as technical support for time series data analysis in other domains of social sustainability.

Study area and data sources

Hebei Province in northern China (113.45–119.83° E, 36.05–42.58° N) includes 11 cities with 188,800 m2 in total area. It features complex and varied landforms and is the only Chinese province encompassed with plateaus, mountains, hills, plains, lakes, and coasts altogether. The terrain declines from northwest to southeast.

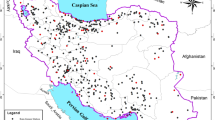
The study area consists of three landform units, Bashang Plateau, Yanshan Mountains and Taihang Mountains, and Hebei Plain respectively. Hebei has a temperate continental monsoon climate characterized by four distinctive seasons in most areas, with greater precipitation in the southeast than in the northwest. Nineteen meteorological stations are provided data for this study; they represent arable land, woodland, and grassland cover (Fig. 1). These stations are evenly distributed across the province and effectively represent the climatic and spatial patterns of Hebei.

Fig. 1
figure 1

Study area

Full size image

The series of daily precipitation values (mm) over the 19 stations during the period 1961–2014 were sourced from the China Meteorological Administration (http://data.cma.cn/en). The discontinuities with series of daily precipitation can lead to misinterpretations of the studied climate. In order to avoid errors and obtain homogeneous climate time series, non-natural irregularities in climate data series must be detected and removed prior to its use (Ribeiro et al. 2016). From March 2011 to June 2012, the China Meteorological Administration carried out the construction of ground basic meteorological data. Repeated quality testing and control were carried out on the continuous observation data in the monthly ground report data files of national stations from 1951 to the present, which corrected a large number of wrong data, and made up for the digital missing data, so that the data quality has been significantly improved. So, we can analyze the data directly with no need to do extra homogeneity assessment. Several stations with missing values were excluded to ensure the integrity and continuity of the data series across the entire study period. MODIS Land Cover product data with a 500-m spatial resolution for the year 2013 were adopted (available online from the United States Geological Survey website). The land cover in the study area was classified into six categories: water, grassland, woodland, arable land, built-up land, and unused land, pursuant to the classification standards (Liu et al. 2003). The spatial distribution of these land cover types is shown in Fig. 1.

Methodology

Multiple change-point detection approach

A change-detection approach identifies the time node where the data element in a lengthy time series changes abruptly. It also allows the researcher to divide time series data into discrete segments. In traditional detection, the locations and quantity of change points may be identical across multiple time series (Jamali et al. 2015). Although the fitting with the least squares method is popular in the present research on the detection of multiple change points, it is prone to error due to the heavy-tailed distribution of the data series (Zou et al. 2014). Segmentation at arbitrary change point also fails to reveal optimal points in terms of their locations and quantity. However, the distribution of the data in a lengthy time series within individual segmentations is typically unknown. This type of parametric method can sustain model misspecifications. If the data with time series have no parametric assumption, we consider the determined change point based on the independent data\( {\left\{{\mathrm{X}}_i\right\}}_{i=1}^n \):

$$ {X}_i\sim {F}_k(x)\kern1.5em {\tau}_{k-1}\le i\le {\tau}_k-1,k=1,.\dots, {K}_n+1,\kern1.5em i=1;\dots, n $$
(1)

where Kn is the true number or quantity of change points; the locations or date (for time series data) of the change points with the convention of τ0=1 and \( {\tau}_{K_n+1} \)=n + 1, Fk denotes cumulative distribution function (CDF) for the segment k satisfyingFk ≠ Fk + 1; the number of change points can be allowed to alter according to the sample size n.

We assume that Z1, …, Zn are mutually independent and following the same distributionF0, and let \( {\overset{\wedge }{F}}_n \) denote empirical CDF of sample, then \( n\overset{\wedge }{F_n}(u) \)~binomial(n, F0(u)). If we consider the sample as the binary data with a probability of success\( \overset{\wedge }{F_n}(u) \), in the context for formula (1), the joint-likelihood for the candidate set for change points (\( {\tau}_1^{\hbox{'}}<\cdots <{\tau}_L^{\hbox{'}} \)) can be written as follow:

$$ {\xi}_u\left({\tau}_1^{\hbox{'}},\dots, {\tau}_L^{\hbox{'}}\right)=\sum \limits_{k=0}^L\left({\tau}_{k+1}^{\hbox{'}}-{\tau}_k^{\hbox{'}}\right)\left\{{\overset{\wedge }{F}}_{\tau_k^{\hbox{'}}}^{\tau_{k+1}^{\hbox{'}}}(u)\log \left({\overset{\wedge }{F}}_{\tau_k^{\hbox{'}}}^{\tau_{k+1}^{\hbox{'}}}(u)\right)+\left(1-{\overset{\wedge }{F}}_{\tau_k^{\hbox{'}}}^{\tau_{k+1}^{\hbox{'}}}(u)\right)\log \left(1-{\overset{\wedge }{F}}_{\tau_k^{\hbox{'}}}^{\tau_{k+1}^{\hbox{'}}}(u)\right)\right\} $$
(2)

where \( {\overset{\wedge }{F}}_{\tau_k^{\hbox{'}}}^{\tau_{k+1}^{\hbox{'}}} \)denotes the empirical CDF of subsample time series \( \left\{{X}_{\tau_k^{\hbox{'}}},{X}_{\tau_{k+1}^{\hbox{'}}-1}\right\} \) with \( {\tau}_0^{\hbox{'}}=1 \) and \( {\tau}_{L+1}^{\hbox{'}}=n+1 \). To estimate change points, we maximize the formula (1) in an integrated form as follow:

$$ {R}_n\left({\tau}_1^{\hbox{'}},\cdots, {\tau}_L^{\hbox{'}}\right)={\int}_{-\infty}^{\infty}\xi \left({\tau}_1^{\hbox{'}},\dots, {\tau}_L^{\hbox{'}}\right) dw(u) $$
(3)

where w(.) denotes the positive weight function; thus, Rn can be finite, and the integral is used to combine all the information acrossu.

The log-likelihood function formula (2) is essentially related to two-sample data goodness of fit statistic test depending on nonparametric likelihood ratio (Einmahl and McKeague 2003); in order to conduct a balance or stopgap between the number of change points and the likelihood, we employ the Schwarz’s Bayesian information criterion (BIC) by considering the penalty for largeL; we identify the value of L by minimizing L as follows:

$$ {BIC}_L=-\max {R}_n\left({\tau}_1^{\hbox{'}},\cdots, {\tau}_L^{\hbox{'}}\right)+L{\zeta}_n $$
(4)

where ζn represents the proper sequence going to infinity. The BIC has been used in ζn = log n to determine the number of change points and to show its consistency (Yao and Au 1989).

An efficient nonparametric maximum likelihood approach was adopted in this study to detect multiple change points. The proposed approach does not assume that the data series has any specific parameter structure or distribution characteristics. Therefore, it is suitable for the detection of any changes in data distribution. The number of optimal change points is determined by BIC, and locations of the points can be estimated with the dynamic programming algorithm and maximum likelihood function. This approach has been performed well in previous studies on the recognition of multiple change points (Zou et al. 2014). The number of change points detected at each station is P (P > 0). Using the location of each change point, the total annual precipitation data series during the period 1961–2014 is divided into P + 1 segments.

Trend analysis approach

The Mann-Kendall (MK) trend analysis is a nonparametric test method (Kendall 1948; Mann 1945; Haktanir and Citakoglu 2014; Haktanir and Citakoglu 2015) which does not require the data series to be normally distributed. MK is a proven and effective approach to analyze monotonous change in data series (Burn and Elnur 2002; Xu et al. 2004; Ay and Kisi 2015). The null hypothesis H0 states that the data series xk(k = 1, 2, 3⋯n) are independent from one another and have the same distribution; the alternative hypothesis H1 states that there is a monotonic trend in the data series. The MK test statistics are calculated as follows:

$$ S=\sum \limits_{i=1}^{n-1}\sum \limits_{i=j+1}^n\operatorname{sgn}\left({x}_j-{x}_i\right) $$
(5)

where xj represents the sequential data values, n is the length of the dataset, and sgn is calculated as follows:

$$ \operatorname{sgn}\left({x}_j-{x}_i\right)=\left\{\begin{array}{c}1\\ {}0\\ {}-1\end{array}\begin{array}{c}\\ {}\\ {}\end{array}\right.{\displaystyle \begin{array}{c} if\\ {} if\\ {} if\end{array}}{\displaystyle \begin{array}{c}{x}_j\\ {}{x}_j\\ {}{x}_j\end{array}}{\displaystyle \begin{array}{c}>\\ {}=\\ {}<\end{array}}{\displaystyle \begin{array}{c}{x}_i\\ {}{x}_i\\ {}{x}_i\end{array}} $$
(6)

According to Mann (1945) and Kendall (1948), when n ≥ 8, the test statistics S is approximately normally distributed with the mean and variance as follows:

$$ {\displaystyle \begin{array}{l}E(S)=0\\ {}V(S)=\frac{n\left(n-1\right)\left(2n+5\right)-\sum \limits_{m=1}^n{t}_mm\left(m-1\right)\left(2m+5\right)}{18}\end{array}} $$
(7)

where tmis the extent m. The standardized test statistics Z are calculated as follows:

$$ Z=\left\{\begin{array}{c}\frac{S-1}{\sqrt{V(S)}}\kern0.5em S>0\kern0.5em \\ {}\begin{array}{c}\end{array}0\begin{array}{ccc}\begin{array}{cc}& \end{array}& S=0& \end{array}\\ {}\frac{S+1}{\sqrt{V(S)}}\begin{array}{ccc}& S<0& \end{array}\end{array}\right. $$
(8)

|Zα| = 1.65, 1.96, and 2.58, which correspond to the critical values at the significance level P = 0.1, 0.05, and 0.01, respectively. If |Z| > |Zα|, the null hypothesis H0 is rejected; P = 0.05 and 0.01 were considered in the present research.

To analyze the time series variable trend, we used the robust estimator for the amplitude of trend slopes proposed by Sen (1968):

$$ \mathrm{slope}= Median\left(\frac{x_j-{x}_i}{j-i}\right)\kern0.5em \left(1\le i<j\le n\right) $$
(9)

where slope is the monotonic increase or decrease rate (i.e. the linear slope) of the entire data series xk(k = 1, 2, 3⋯n) or any segmentation xw(w = i, i + 1, 3 + 2⋯j). If it is positive, the series monotonically increases; if it is negative, the series monotonically decreases. Median indicates that the function takes the median value. Sen’s trend calculation was performed on the entire series and the segmentations (divided by the results of change-point detection) of annual precipitation data at the stations during the period 1961–2014, and conducted significance tests on the Sen’s trend results using the MK approach.

The ordinary least squares (OLS) linear regression analysis is used to derive relationships between variables for time series data that is believed to be uniformly applicable across the study area (Foody 2003). The OLS technique can quantitatively explore the effects of a collection of independent variables on one dependent variable and OLS also can extract change trends of the time series data (Yang et al. 2016). However, if the data do not satisfy some of assumptions, then results can be misleading, especially, outliers violate the assumption of normally distributed residuals in the least-squares regression. Therefore, it is important to assess whether the time series data at each station conform to the law of normal distribution before the OLS is used; here, we adopt the Q-Q plot and parametric test (such as coefficient of Skewness, coefficient of Kurtosis, and P value (Roozbeh and Arashi 2016) to determine the normality of time series data. The U-statistics was constructed based on coefficient of skewness and coefficient of kurtosis respectively, and P values were calculated by the K-S test (Liu and Zhang 2016). then USkewness , UKurtosis, and P values are applied for testing. At least two of the three indicators can prove the normal distribution (USkewness < U0.05 = 1.96,UKurtosis < U0.05 = 1.96, P > 0.05) (Liu and Zhang 2016); the goodness of fit between the precipitation dataset and the uniform distribution on (0, 1) at each station are also revealed through Q-Q plots and histogram in our study. The OLS fitting formula is as follows:

$$ {\hat{y}}_i=a+{bx}_i $$
(10)
$$ b=\frac{\sum \limits_{i=1}^n\left({x}_i-\overline{x}\right)\left({y}_i-\overline{y}\right)}{\sum \limits_{i=1}^n{\left({x}_i-\overline{x}\right)}^2} $$
(11)
$$ a=\overline{y}-b\overline{x} $$
(12)

where yis the dependent variable, xis the independent variable , awhich represents the intercept and bwhich expresses the slope of the relationship between the two variables.

Spatial characteristics

With multiple change-point detection, the number and locations (or dates) of change points at the 19 stations were identified and the series were divided into different segmentations. The quantity of change points reflected the varying degrees of change in precipitation during the study period. This variable was compared against the standard deviation at each station to spatially assess the changes over the time series from different aspects. The location (or date) of each change point marked the year in which precipitation sustained an abrupt change in practice; this information supported engineers in developing appropriate strategies in response to such change. The Hovmöller map was used to illustrate the occurrence of change points at each station in each year (Hovmöller 1949; Wang et al. 2015). Different segmentations of the series have different amplitudes or trends of change.

As discussed above, nonparametric MK tests and Sen’s trend analysis are applied to each segmentation to determine their respective trend. Spatial comparison was performed on maximum trend, minimum trend, and generalization trend over the entire study period for each station. The automatic segmentation-based trend analysis and generalization trend analysis were compared against each other. Trends in all the segmentations and the entire period were depicted as overlapping on the same spatial-temporal diagram to make clear the magnitude of various changes at each station.

Results and discussion

Variability characteristics of annual precipitation

In this study, annual precipitation variability was characterized by the number of change points and the standard deviation. The number of change points at each station during the period 1961–2014 is shown in Fig. 2. The maximum number (4) occurred at three stations: Zhangjiakou, Weichang, and Langfang. This revealed that the precipitation at these stations underwent abrupt changes of multiple times in five time segments of the study period. The minimum number of change points (1) occurred at the five stations: Fengning, Huailai, Shijiazhuang, Xingtai, and Huanghua, indicating that precipitation at these stations was relatively stable or underwent only one abrupt change during the study period. The standard deviation for annual precipitation at each station from 1961 to 2014 is shown in Fig. 3. Its spatial distribution is more representative than that shown in Fig. 2; that is, the deviation gradually decreased from more than 190 mm in the southeast to less than 70 mm in the northwest. This might be characteristically the higher precipitation in the southeastern regions and thereby the higher inter-annual change than that in the northwestern regions. The inconsistency between Figs. 2 and 3 in terms of spatial distribution was primarily attributable to the fact that the change points in Fig. 2 represent the precipitation variability across several time sections, while the standard deviation shown in Fig. 3 represents the variability across years. The number of change points and the standard deviation depicted the variability of precipitation on different time scales. Both, however, could reveal extreme climate events or abnormalities related to climate change.

Fig. 2
figure 2

The number of change points for annual precipitation at each station

Full size image
Fig. 3
figure 3

Standard deviation for annual precipitation at each station

Full size image

The characteristics of change-point date

To illustrate the dates and locations of change points over different stations, the Hovmöller map was used to depict temporal-spatial characteristics (Fig. 4). The red marks on the map indicated the occurrence of abrupt change points. Change points were generally obvious around 1974, 1981, and 1998 and occurred in a few stations before 1974 and after 2000. This suggested that precipitation changed at a relatively stable pace during the years 1961–1974 and 2000–2014, but changed abruptly in 1974–2000 during a period in which meteorological disasters were likely to occur. Identical dates in the change points were observed at some adjacent stations due to the proximity effect of local meteorological conditions in terms of precipitation. Figure 4 also shows that the change points were concentrated mostly within Zhangjiakou, Weichang, and Langfang. The Hovmöller map was also applied to the temporal-spatial analysis of other elements as it revealed “hot-spot years,” sites or areas of interest, and the continuity of changing characteristics in terms of a given area or time.

Fig. 4
figure 4

Hovmöller map for timing of change points at each station

Full size image

Characteristics of trends

To determine the effect of our multiple change-point detection, temporal-spatial comparison was established between the data in the segmentations divided by the multiple change points and the data over the entire time series; this allowed a clear comparison among minimum trends for segmentations (Fig. 5), maximum trends for segmentations (Fig. 6), and the generalization trend (Fig. 7) at each station. In addition, significance level is shown with the Z value of the MK test (Table 1).

Fig. 5
figure 5

minimum trends for segmentations at each station

Full size image
Fig. 6
figure 6

Maximum trends for segmentations at each station

Full size image
Fig. 7
figure 7

Generalization trend at each station

Full size image
Table 1 The Mann-Kendall trend test at each station F means that significance level of trend is greater than 0.05, T means that significance level of trend is less than 0.05
Full size table

Table 1 reflected that the significance level between generalization trend and segmentation trend has some differences (T means P is less than 0.05, F means P is greater than 0.05). For generalization trend, there are no stations with a P value less than 0.05. However, four stations (Weichang, Zunhua, Qinhuangdao, Langfang) with a P value less than 0.05 for different segmentations were observed which means only the use of generalization trend may possibly mask abrupt change.

Figure 5 shows where the minimum trend for segmentations decreased at all stations. The most obvious decreased in amplitude or trend occurred at Zunhua (− 211.60 mm/year), Weichang (− 99.80 mm/year), Qinhuangdao (− 70.38 mm/year), and Leting (− 55.85 mm/year) stations. In effect, to determine the most abrupt decrease rate in the trend of a given variant, it was feasible to derive the minimum trend indicator from the segmentation-based trend analysis as part of the multiple change-point detection process.

Figure 6 illustrates where the minimum trend for segmentations increased at all stations other than Leting, and most obviously at Qinglong (43.26 mm/year), Nangong (− 37.00 mm/year), and Raoyang (27.23 mm/year). Again, deriving the maximum trend indicator from the segmentation –based trend analysis as part of multiple change-point detection appeared to reveal the most abrupt increase rate in the trend of a variant.

Decreasing generalization trends are shown in Fig.7 over the unsegmented long time data series at all stations other than Weichang, Weixian, and Nangong. The amplitude of any increase or decrease was insignificant at any of 19 stations. The greatest amplitude of increase occurred at Weichang station (0.32 mm/year), and the greatest amplitude of decrease occurred at Zunhua (− 2.56 mm/year), Leting (− 2.5 mm/year), Qinglong (− 2.27), and Qinhuangdao (− 2.26). The absolute change was less than 3 mm/year at all stations. The generalization-based trend analysis effectively smoothened the trend of abrupt changes in specific time sections.

Generalization trends over full time series and for different segmentations are shown in Fig. 8; change points occurred at all 19 stations. There was one change point at Fengning, Huailai, Huanghua, Shijiazhuang, and Xingtai stations, and four (i.e., the maximum) at Weichang, Zhangjiakou, and Langfang. As shown in Fig. 8, the segmentation trends at all stations other than Leting and Qinhuangdao increased and decreased alternatively. The generalization trends at all stations other than Huailai, Tangshan, and Raoyang fell between the minimum and maximum trends on multiple segmentations. This revealed that generalization trends covered the trends characterized by abrupt changes in specific time sections among multiple segmentations. Such a change might be abrupt at a certain time even if the generalization trend was mild.

Fig. 8
figure 8

Change trend for segmentations and generalization at each station

Full size image

To compare MK trend tests and Sen’s trend analysis, we use the OLS linear regression method to calculate the trends. Table 2 presents the results of the normal distribution test at each station in the study. T represents accept the hypothesis of the normal distribution and F is refuse the hypothesis of normal distribution. We adopt the three parameters USkewness, UKurtosis, and P values to assess the normality of time series data, in order to ensure the performance of the assessing results. It is shown that there are two or three test parameters proving normality of time series data at each station; if there is only parameter showing the normality, we think that the time series data do not conform to normal distribution. There are six stations which do not conform to normal distribution, if the OLS method is conducted, the results of fitting or calculating change slope may be wrong. We also used Q-Q plots and histogram to test the normality of time series data. Figures 9 and 10 show consistent results with Table 2; this indicates that the test results of the three methods including parameters, Q-Q plots, and histogram are consistent and effective, and there are Shijiazhuang, Xingtai, Qinhuangdao, Langfang, Raoyang, and Huanghua which do not conform to the normal distribution.

Table 2 The table of normal distribution test at each station
Full size table
Fig. 9
figure 9figure 9

Q-Q plots to present the fitting degree of the precipitation dataset relative to the uniform distribution on (0, 1) at each station

Full size image
Fig. 10
figure 10

Histograms with normal curves at each station

Full size image

Table 3 presents change trends by using the OLS method; the values of P indicate determination of the linear trends at the significance level of 0.05. There is no station with P less than 0.05 which keep pace with the generalization trend by the Mann-Kendall trend test. However, for the amplitude of change slope, there is only Weichang station with increasing trend (0.33 mm/year)) based on the OLS method, which shows consistency with the result of Sen’s trend (0.32 mm/year) analysis, Zunhua (− 2.92 mm/year), Leting (− 2.36 mm/year), and Qinglong (− 2.40 mm/year) have approximate values comparing to the trend slopes calculated by Sen’s trend analysis, respectively. The absolute change was less than 3 mm/year at all stations whose results are the same as those in Fig. 7 and the slopes in the two kinds of methods are inconsistent in most stations. The Mann-Kendall Sen trend and the linear regression trend are summarized in Table 4; there no one station with a significant trend (p < 0.05), The Sen slope method does not need the data to be a normal distribution and trends of OLS failure to pass the significance level test; therefore, we can draw the conclusion that the result of MK trend tests have a better confidence degree which indicates a further application.

Table 3 The result of linear regression at each station
Full size table
Table 4 A summary of the results of the Mann-Kendall test and linear regression trend test
Full size table

Summary and conclusion

Multiple change-point detection and segmentation-based trend analysis are crucial techniques for the recognition of climate abnormalities and the monitoring and evaluation of environmental impact within the context of global climate change, as well as in research on the spatial-temporal characteristics of other subjects. Hebei Province, one of the major grain-producing regions in China, was served as the focus of the present study. The annual precipitation data at 19 meteorological stations in the study area during the period 1961–2014 were assessed. The nonparametric maximum likelihood approach was applied and the number of change points at each station was optimized based on BIC. The lengthy time series was segmented based on the identified change points. MK trend tests and Sen’s amplitude analysis were conducted for segmentations at each station and validated by comparing with basic ordinary least squares (OLS) regression analysis based on generalization trends. The proposed approach represents an effective combination of nonparametric approaches including the maximum likelihood, MK trend tests, Sen’s trend analysis, and basic ordinary least squares (OLS) regression analysis. This approach enabled flexible and efficient multiple change-point detection and research on multi-segment trend characteristics. As reported above, the characteristics of the temporal-spatial pattern were revealed using the number of change points, standard deviation, timing of change points, minimum and maximum trends for segmentations, and generalization trends over the entire study period.

The standard deviation of annual precipitation can represent the variability of precipitation across several years, and the number of change points can represent the variability across several time segments. Change points in the dataset were generally obvious around 1974, 1981, and 1998, and at few stations in the study area before 1974 and after 2000; precipitation changes were relatively stable during the periods 1961–1974 and 2000–2014. The minimum trend for segmentations decreased at all stations but most significantly at Zunhua (− 211.60 mm/year), Weichang (− 99.80 mm/year), Qinhuangdao (− 70.38 mm/yea), and Leting (− 55.85 mm/year). The maximum trend for segmentations increased at all stations other than Leting, and most significantly at Qinglong (43.26 mm/year), Nangong (− 37.00 mm/year), and Raoyang (27.23 mm/year). The generalization trends were characterized by absolute change below 3 mm/year at all stations, and fell between the minimum and maximum trends on multiple segmentations at all but three stations. It also covered the trends characterized by abrupt changes in specific time sections among the segmented series.

The result derived from the proposed approach can better characterize the trend of climate variables over certain parts. The proposed approach represents a reference tool for regional water resource management and novel strategies to combat the effects of climate change. This approach can yield even more meaningful results if applied to the time series analysis on larger spatial scales and across more disciplines, such as quantitative evaluations of economic management practices, forest protection initiatives, and environmental and social development.