Introduction

Dams are mainly built in Saudi Arabia for flood protection and groundwater recharge. Many regions in Saudi Arabia are subjected to short but intense thunderstorms (Wheater 1996). Flood protection depends on dams to regulate the outflow through a flood channel that transfers floodwater away from populated areas. Therefore, reservoir routing is an essential technique needed to safely and economically design flood channels (Wheater 2002).

Horn (1987) introduced a simple graphical procedure to calculate the peak outflow discharge as a function of the inflow, storage, and outlet apparatus characteristics. The technique is based on two dimensionless inflow hydrograph and the solution of the routing equation with the reservoir storage expressed as an exponential function of the outflow. The procedure introduced an attenuation ratio as the ratio between the peak inflow and peak outflow. The attenuation ratio is a function of a “routing number” that encompasses the peak inflow, the time to peak, the storage characteristics, and the outlet device characteristics. A graph illustrates the relationship between the attenuation ratio and the routing number is presented. The procedure is simple and can be used to calculate the peak outflow discharge and the time to peak of the outflow hydrograph. However, the complete outflow hydrograph is not possible to be deduced by this procedure. An example for the design of small detention basin equipped with orifice outlet was given in Horn (1987).

Hager and Sinniger (1985) presented a graphical method to calculate the peak outflow and maximum reservoir level. The method incorporates a storage factor and a shape factor. The storage factor includes parameter representing peak inflow, time to peak, reservoir characteristics, and spillway characteristics. A power expression for the reservoir storage ranges between 1.7 and 2.7, which is suitable for Swiss lakes. The outflow hydrograph can be constructed using interpolation from the provided graphs. The method is suitted for large dams on rivers.

Fiorentinti and Orlandini (2013) presented numerical solution for the reservoir routing equation. They introduced three methods to handle the case where stored water is released through pipe outlet. This case of transition from free surface flow to pressurized flow causes distortion in the shape of the outflow hydrograph. They concluded that the fourth-order Runge–Kutta method with a simple back-stepping procedure constitutes robust efficient solution. However, their work did not consider the case of outflow from the dam spillway.

Fenton (1992) suggested that numerical solution for the reservoir routing equation is preferred than traditional method which involves the need to establish relation between the storage, the outflow, and the stage of reservoir. After comparing different numerical schemes, Fenton concluded that any simple scheme offers accurate solution and no need to use the traditional method (modified plus method).

Yevdjevich (1959) introduced analytical solution of the reservoir routing equation. The storage-outflow discharge relation is expressed in a power formula. Tables are prepared for the analytical solution for special cases. It was stated by the author that the analytical solution for the general case with time dependent inflow is difficult and only special cases can be handled.

To numerically solve the reservoir routing equation, a relation between the elevation or reservoir’s water depth and the reservoir surface area is needed. Mohammadzadah-Habili et al. (2009) introduced a simple mathematical equation to relate the dimensionless area with the dimensionless depth. The relation is logarithmic with an exponent they named “reservoir coefficient” N.

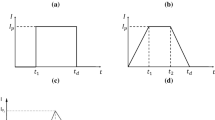
The common practice of the design of dams in Saudi Arabia considers the erratic characteristics of rainfall. Dry years are common while wet years or seasons do not follow any specific pattern (Jha et al. 2012). In Saudi Arabia, as all arid region countries, no river exists, only watersheds producing flash floods due to thunderstorms. Therefore, dam’s storage is designed for 10 or 25 years return period for economic reasons. The position of the spillway crest is equal to the reservoir height corresponding to the runoff volume for 5 to 10 years return period. The spillway crest length is designed for the peak runoff discharge of the 100 years return period for safety reasons. Figure 1a shows a typical dam components and reservoir storage zonation. The storage zones are as follows. The dead storage is located in the bottom of the reservoir below the dam outlet device (this zone contains also the sediments that are carried by the flood; Elfeki et al. 2014). Live storage is located between the top of the dam outlet device and the spillway crest, and the surcharge storage is located above the spillway crest up to the flood level. Figure 1b shows the procedure followed to estimate the design level of the spillway crest. For the design x-years flood, the volume of the hydrograph is estimated. From the estimated volume, the crest elevation is evaluated from the elevation–storage curve of the reservoir as shown in the figure.

Fig. 1
figure 1

a A typical dam reservoir and its storage components. b Estimation of the design elevation of the spillway based on the dam capacity

Full size image

To the best of the author knowledge, reservoir routing studies in arid regions do not exist specially in Saudi Arabia. The aims of this paper are first how to implement reservoir routing studies in arid regions for flood protection schemes. Second, proposing a systematic methodology that combines the mass conservation equation of the dam reservoir, the discharge equation of the dam outlet devices, and a dimensionless depth–volume equation to calculate the outflow hydrograph downstream of the dam for a given inflow hydrograph. Third, comparison of the proposed methodology with analytical solution of a specific example in the published literature and with traditional (modified puls) method to evaluate the methodology. Fourth, application of the methodology on a real case study in Saudi Arabia.

Theoretical background and methodology

The mass conservation equation in a dam reservoir is given by

$$ \frac{dS(t)}{dt}=I(t)-O(t) $$
(1)

where

I(t):

is the inflow hydrograph upstream of the dam (Fig. 2).

O(t):

is the outflow hydrograph downstream of the dam (Fig. 2; that passes through the dam outlet or spillway or both).

S(t):

is the dam reservoir storage.

Fig. 2
figure 2

Typical inflow and out flow hydrographs from a dam at the outlet of a catchment

Full size image

In case the outflow is over a spillway, the equation of spillway is given by

$$ O(t)= CB{\left[h(t)-P\right]}^{1.5}\kern0.5em \mathrm{if}\ h(t)>P $$
(2)
$$ O(t)=0\kern7em \mathrm{if}\ h(t)\le P $$
(3)

where

C :

is the spillway coefficient of discharge.

B :

is the spillway crest length.

P :

is the height of the spillway crest from the reservoir bottom.

h(t):

is the water depth upstream of the spillway above the bottom of the reservoir.

The aforementioned parameters are presented graphically in Fig. 3.

Fig. 3
figure 3

Spillway parameters used in Eq. 2: H is the head over the spillway, h is the water depth above the reservoir bottom, and P is the spillway height

Full size image

However, in case the outflow is through a multiple orifices or pipes, the outflow is given by

$$ O(t)=n{C}_da{\left[h(t)-\Delta z\right]}^{0.5}\kern0.5em \mathrm{if}\kern.3em h(t)>\Delta z $$
(4)
$$ O(t)=0\kern9em \mathrm{if}\ h(t)\le \Delta z $$
(5)

where

C d :

is the orifice/pipe coefficient of discharge.

a :

is the cross-sectional area of an orifice/pipe.

n :

is the number of orifices/pipes.

Δz :

is the height of the orifice/pipe from the reservoir bottom.

The storage term in the equation (Eq. 1), S(t), needs to be evaluated. Several methods are proposed in the literature such as Mohammadzadah-Habili et al. (2009), Michalec (2015), and Rahmanian and Banihashemi (2012). In the proposed methodology, the formula given by Mohammadzadah-Habili et al. (2009) is used, which reads

$$ S(h)={S}_{\mathrm{max}}{\left({e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}-1\right)}^{1/N} $$
(6)

where

S(h):

is the storage as a function of height above the reservoir bottom at the dam site.

S max :

is the maximum storage in the reservoir.

h max :

is the maximum height in the reservoir that corresponds to the maximum storage.

N :

is called the reservoir coefficient; it is a fitting parameter of the equation to the reservoir storage (capacity)–height curve obtained from ground survey data or digital elevation model (DEM).

Since, the reservoir surface area, A(h), is related to the storage by the following formula (Fenton 1992):

$$ A(h)=\frac{dS(h)}{dh} $$
(7)

Therefore, the reservoir surface area can be derived by differentiating Eq. 6 to read

$$ A(h)=\frac{S_{\mathrm{max}}\left(\ln 2\right)}{Nh_{\mathrm{max}}}{e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}{\left({e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}-1\right)}^{\left(1-N\right)/N} $$
(8)

Consequently, substituting h = hmax, S(hmax) = Smax, and A(hmax) = Amax in Eq. 6, the reservoir coefficient, N, is equal to

$$ N=2\left(\ln 2\right)\frac{S_{\mathrm{max}}}{A_{\mathrm{max}}{h}_{\mathrm{max}}} $$
(9)

The reservoir coefficient, N, is related to what is called reservoir shape factor, M, via the relation (Mohammadzadah-Habili et al. 2009)

$$ N=1.0751{M}^{-0.9063} $$
(10)

The value of M can be used to classify the reservoir type according to Borland and Miller (1958) as shown in Table 1.

Table 1 Classification of reservoirs (Borland and Miller 1958)
Full size table

The storage term in Eq. 1 can be expressed as

$$ \frac{dS(t)}{dt}=\frac{dS}{dh}.\frac{dh}{dt}=A(h)\frac{dh}{dt} $$
(11)

Substituting Eq. 8 into Eq. 11, one may obtain

$$ \frac{dS(t)}{dt}=\left[\frac{S_{\mathrm{max}}\left(\ln 2\right)}{Nh_{\mathrm{max}}}{e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}{\left({e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}-1\right)}^{\left(1-N\right)/N}\right]\frac{dh}{dt} $$
(12)

Then, substituting Eqs. 2, 4, and 12 into Eq. 1, the following general expression for the case of outflow from both spillway and orifices or pipes can be deduced.

$$ \frac{dh}{dt}=\frac{I(t)-\left[ CB{\left(h(t)-P\right)}^{1.5}+{nC}_da{\left(h(t)-\Delta z\right)}^{0.5}\right]}{\left[\frac{S_{\mathrm{max}}\left(\ln 2\right)}{Nh_{\mathrm{max}}}{e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}{\left({e}^{\left(\ln 2\right)\left(h/{h}_{\mathrm{max}}\right)}-1\right)}^{\left(1-N\right)/N}\right]} $$
(13)

Equation 13 is an ordinary diferential equation which can be solved numerically for the given inflow hydrograph, the spillway characteristics (C, B, and P), orifice or pipe characteristics (n, a, C d , and Δz), and reservoir characteristics defined by Smax, hmax, and N. Analytical solution of the equation is not possible.

Once Eq. 13 is solved for a given inflow hydrograph, the function of h(t) is obtained and consequently substituting in Eq. 2 or 4 or the summation of both according to the outlet device of the dam, one may get the outflow hydrograph, O(t).

The inflow hydrograph, I(t), can either be obtained from the hydrological study of the dam catchment using software like HEC-HMS (2015) or can be modeled by the following expression (Williams and Hann 1972);

$$ I(t)={I}_{\mathrm{max}}{\left[\left(\frac{t}{t_p}\right)\exp \left(1-\frac{t}{t_p}\right)\right]}^K $$
(14)

where

Imax is the maximum inflow.

t p is the time to peak of the inflow hydrograph.

K is the shape factor of the hydrograph that is evaluated by the formula.

$$ K=6.5\left(\frac{I_{\mathrm{max}}{t}_p}{V}\right) $$
(15)

where

V is the volume of the inflow hydrograph; for the SCS unit hydrograph, the value of K is 3.77.

Another hydrograph model that is presented in Fenton (1992) for the case with no base flow is given by

$$ I(t)={P}_0{t}^s\exp \left(- ft\right) $$
(16)

where

P0, s, and f are constants defining the storm hydrograph.

One could find the analogy between Williams and Haan’s equation and Eq. 16. The corresponding terms are

$$ {\displaystyle \begin{array}{l}{P}_0={I}_{\mathrm{max}}\frac{e^K}{t_p^K},\\ {}s=K,\\ {}f=K/{t}_p\end{array}} $$
(17)

Yevdjevich (1959) has introduced analytical solution of the reservoir routing equation under some simple cases of inflow hydrograph and reservoir characteristics. In his solution, the inflow is expressed as Eq. 16, and the reservoir and the spillway characteristics are expressed as power laws as follows,

$$ {\displaystyle \begin{array}{l}S(h)={ah}^m,\\ {}A(h)={amh}^{m-1},\mathrm{and}\\ {}O(h)={bh}^m\end{array}} $$
(18)

where

a and b are constants, and the exponent m is the same for both storage and spillway.

Under these assumptions, the storage function is introduced as

$$ {\displaystyle \begin{array}{l}O(h)= cS(h),\mathrm{and}\\ {}c=b/a\end{array}} $$
(19)

The analytical solution by Yevdjevich (1959) using integration factor method under the above assumptions and for s as an integer can be written as Fenton (1992)

$$ O(t)={I}_0+{e}^{- ct}\left[{O}_0-{I}_0+\frac{s!{cP}_0}{{\left(f-c\right)}^{s+1}}\right]-\frac{s!{cP}_0}{{\left(f-c\right)}^{s+1}}{e}^{- ft}\left[1+\left(f-c\right)t+\dots +\frac{{\left[\left(f-c\right)t\right]}^s}{s!}\right] $$
(20)

where

I 0 :

is the base inflow, and

O 0 :

is the base outflow.

Equation 20 is going to be used to test the proposed methodology as will be explained later in the coming sections.

Since Eq. 13 cannot be solved analytically, its finite difference formulation using forward Euler scheme in case of spillway only as an outflow device is given as

$$ h\left(t+\Delta t\right)=h(t)+\frac{I(t)-\left[ CB{\left(h(t)-P\right)}^{1.5}\right]}{\left[\frac{S_{\mathrm{max}}\left(\ln 2\right)}{Nh_{\mathrm{max}}}{e}^{\left(\ln 2\right)\left(h(t)/{h}_{\mathrm{max}}\right)}{\left({e}^{\left(\ln 2\right)\left(h(t)/{h}_{\mathrm{max}}\right)}-1\right)}^{\left(1-N\right)/N}\right]}\Delta t $$
(21)

where

Δt:

is the time step in computation.

h(t + Δt):

is the water head above the spillway crest at time t + Δt.

h(t):

is the water head above the spillway crest at time t.

The outflow hydrograph is calculated by

$$ O\left(t+\Delta t\right)\Big)= CB{\left[h\left(t+\Delta t\right)\Big)-P\right]}^{1.5} $$
(22)

where

O(t + Δt):

is the outflow discharge at time t + Δt.

O(t):

is the outflow discharge at time t.

The traditional (modified puls or reservoir indicator) method

For computational purposes, Eq. 1 is written in a finite difference form (Chow et al. 1988) as

$$ \frac{S\left(t+\Delta t\right)-S(t)}{\Delta t}=\frac{I\left(t+\Delta t\right)+I(t)}{2}-\frac{O\left(t+\Delta t\right)+O(t)}{2} $$
(23)

Equation 23 can be rearranged in a way to provide the unknown terms in one side of the equation and the know terms on the other side to read

$$ I\left(t+\Delta t\right)+I(t)+\left(\frac{2S(t)}{\Delta t}-O(t)\right)=\frac{2S\left(t+\Delta t\right)}{\Delta t}+O\left(t+\Delta t\right) $$
(24)

In this equation, only unknown terms for any time interval are the terms on the right hand side. In order to evaluate the outflow O(t + ∆t), a storage indication curve (storage–outflow) relating O(t + ∆t) and 2S(t + ∆t)/∆t + O(t + ∆t) is required. At any reservoir elevation, the storage is known from topographic data and the outflow can be calculated from the spillway governing equation. Hence, a relation between the outflow O(t) and (2S/∆t + O(t)) is obtained in a tabular form or graphically. In routing the flow through time step (t + ∆t), the left and side of Eq. 24 is evaluated to give the value of the right hand side of the equation then, from the former established relation, by interpolation within the table or regression of the graphical relation, the outflow O(t + ∆t) is obtained. Several other solutions are proposed (Fread and Hsu 1993; Li et al. 2009). However, these solutions do not take into account the case when the reservoir is empty.

In the current analysis, a focus is made on the difference between two cases of reservoir routing. The first case is when the reservoir is full and a flood arrived at the dam reservoir. In this case, the flood will be considered as surcharge storage over the water in the reservoir and it can be routed over the spillway to the downstream part of the dam. The second case is when the reservoir is empty and a flood arrived at the dam reservoir. In this case, the reservoir is filled with flood water first until the reservoir is filled up to the crest and then overflow occurs over the spillway to the downstream side. Figure 4 shows a sketch illustrating the difference between the two aforementioned cases. In a mathematical form, the storage in the dam reservoir is calculated from the inflow hydrograph as

$$ S\left(\tau \right)=\underset{0}{\overset{\tau }{\int }}I(t) dt\le {S}_{DC} $$
(25)

where

τ :

is the time required until the reservoir is getting full.

S(τ):

is the reservoir storage at time τ.

S DC :

is the dam reservoir capacity.

Fig. 4
figure 4

Comparison between reservoir routing cases. a When the reservoir is full. b When the reservoir is empty

Full size image

In case the reservoir is empty, the floodwater has to fill out the reservoir before overflow occurs. The time needed to fill out the reservoir is called τ as shown in Eq. 25. Therefore, once the volume of the flood water reaches the reservoir dam capacity, S DC , the spillway is flooded and water is discharged to the downstream end of the dam.

Testing the proposed methodology

To test the proposed methodology, since there is no complete reference example in textbooks in hydrology and hydraulic engineering, the authors used the numerical example that is presented in Fenton (1992). The data for this example is displayed in Fenton (1992) paper (Table 1). This example is made for a simple dam reservoir case (based on Eqs. 18 and 19) to test it with the analytical solution (Eq. 20) under the assumptions given by Yevdjevich (1959). In order to apply the proposed methodology to the test example, a fitting of the depth–volume power law formula (Eq. 16) has to be performed with the proposed depth–volume equation (Eq. 6). The results of the fitting process are displayed in Fig. 5. The key fitting parameter, reservoir coefficient, N equals to 0.925.

Fig. 5
figure 5

Fitting the dimensionless depth–volume equation to the power law formula

Full size image

Figure 6 shows the reservoir routing for the aforementioned example for different time steps of 60, 120, 180, and 300 s, respectively. The figure shows the outflow hydrograph based on various methods, namely, the proposed methodology using first- and second-order Euler finite difference method (Eq. 21 for first order, a similar formulation can be made for the second order), the modified puls method (Eq. 24), and the analytical method presented by Eq. 20. Evaluation of the methods is made based on the estimation of the root mean square error (RMSE) for the outflow hydrograph with the time span of 6000 s presented in Table 2. The RMSE is mathematically expressed as

$$ \mathrm{RMSE}=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left[{\widehat{O}}_i-{O}_i\right]}^2} $$
(26)

where

O i :

is the outflow hydrograph calculated by the analytical solution (Eq. 20).

\( {\widehat{O}}_i \) :

is the outflow hydrograph estimated numerically by the various methods.

n :

is the number of ordinates on the hydrograph.

Fig. 6
figure 6

Comparison of the various methods (first- and second-order Euler finite difference method, the modified puls method, and the analytical method) for reservoir routing on the example given by Fenton (1992). a Δt = 60 s. b Δt = 120 s. c Δt = 180 s. d Δt = 300 s

Full size image
Table 2 RMSE of the various methods with analytical solution as a reference
Full size table

The results show that the minimum RMSE is for the second-order Euler method for time step 300 s that is used in the example given by Fenton (1992). There is no significant difference between the first- and second-order Euler methods for solving the proposed method. Fenton (1992) also supported this conclusion where he even used higher order Runge–Kutta methods. The proposed methodology slightly produces better results in terms of RMSE. In the current analysis, investigation of the time step is made via using different values of time steps of 60, 120, and 180 s, respectively. It is obvious from Table 2 that the RMSE decreases with decreasing the time step.

Real case study (AL-Ulb dam in Riyadh Region)

Hanifa watershed is located in Riyadh administrative region, Kingdom of Saudi Arabia, as shown in Fig. 7. The watershed area is about 890 km2 and extends between longitude 46° 25′ and 46° 35′ and latitude 24° 45′ and 24° 54′. Al-Ulb dam is constructed on Hanifa watershed in the year 1975. It is located at the historical district of Ad-Dir’iyah adjacent to the capital Riyadh at longitude 46° 31′ 53″ and latitude 24° 46′ 28″. It is a concrete dam and is constructed for flood protection and groundwater recharge. Table 3 shows the characteristics of the dam and its spillway, and Fig. 8 shows images of the dam.

Fig. 7
figure 7

Catchment area and stream network of Al-Ulb dam in Riyadh Region

Full size image
Table 3 Al-Ulb dam and spillway characteristics
Full size table
Fig. 8
figure 8

Images of Al-Ulb dam in Riyadh Region, left image: upstream of the dam during the dry season showing empty reservoir and upstream face of the spillway; right image: flow over the spillway during a recent flood on November 25, 2015 and downstream channel flow

Full size image

Figure 9 illustrates fitting the dimensionless depth–volume equation to reservoir data at different heights of the reservoir. Table 4 shows that RMSE for reservoir height 25 m is minimum at a reservoir coefficient N equals 0.3812. By observing Fig. 9, the fitting for height 25 m shows very good agreement with the data for the range of the dam height, which is 7.5 m and a maximum water head of about 1.5 m that is a total of 9 m. Figure 10 illustrates a comparison of Al-Ulb dam spillway routing for both cases of full and empty reservoir at different values of reservoir coefficient N. The figure shows that the outflow hydrograph with reservoir coefficient N equals 0.3812 gives the closest results with the traditional method. Table 5 shows that the RMSE for the outflow hydrograph at different values for the reservoir coefficient N using the traditional method as a reference. The minimum value of the RMSE is for N value of 0.3812, which confirms the findings of Fig. 9 and Table 4. Figure 11 illustrates a comparison of Al-Ulb dam spillway routing for both cases of full and empty reservoir at different return periods. Table 6 shows a summary of the results regarding the attenuation ratio, Op/Ip, where Op is the peak outflow, and Ip is the peak inflow to the reservoir. The table shows that the attenuation ratio is almost constant at an average value of 65% in case the reservoir is full. However, in case of empty reservoir, an attenuation of 50% is reached for return periods more than 10 years. Since with low flows (i.e., less than 10 years return periods), most of the incoming flood is stored in the dam reservoir and small amount is released leading to less attenuation ratio. These results suggest that the design of reservoir in arid region should consider an empty reservoir routing, which leads to economic design of the downstream flood channel. While in rivers, a full reservoir routing is recommended for safety as presented in all textbooks.

Fig. 9
figure 9

Fitting the dimensionless depth–volume equation to reservoir data generated at different heights of the reservoir

Full size image
Table 4 The reservoir coefficient, N, for different maximum height of the reservoir and the corresponding RMSE for fitting to the reservoir equation
Full size table
Fig. 10
figure 10

Comparison between reservoir routing on Al-Ulb dam spillway: a in case the reservoir is full and b in case the reservoir is empty for different values of reservoir coefficient, N

Full size image
Table 5 RMSE for the outflow hydrographs at different values of reservoir coefficient, N using the traditional method as a reference
Full size table
Fig. 11
figure 11

Reservoir routing for different return periods: a 5 years, b 10 years, c 25 years, d 50 years, and e 100 years under the case of full reservoir (left column) and the case of empty reservoir (right column)

Full size image
Table 6 Summary of the reservoir routing results for peak outflow, Op
Full size table

The comparison in Fig. 10 is intended to show the sensitivity of the results to the exponent N in order to highlight the importance of seeking the best fit for the exponent N. Figure 9 shows that the best N is obtained by having almost exact fitting to the data by choosing the representative maximum height of the reservoir (h max in Eq. 9). However, the traditional modified puls method cannot handle the empty reservoir case in a straightforward way unless some numerical manipulations have to be made. On the other hand, since there is no other method to check the performance of the traditional modified puls method, therefore the proposed method could be used to check that performance.

Some reservoir characteristics in the Kingdom of Saudi Arabia

To generalize this study, eight proposed dam locations have been selected representing eight regions of the Kingdom of Saudi Arabia. Figure 12 illustrates the locations of these regions. A dimensionless relationship between height and the storage of the reservoirs in the eight regions has been established. The relationship is set up based on the ratio of the height at the watershed outlet to the maximum height of the watershed and the corresponding ratio of the reservoir storage volume at a certain height to the maximum storage of the reservoir. Figure 13 illustrates these relationships for different regions in the kingdom. The figure shows the relationship based on both the actual data of the reservoirs and the relationship based on Eq. 6. Notice that the value of the reservoir coefficient N given in the figure is based on Eq. 9. Table 7 shows the values used to prepare Fig. 13. The values of the reservoir coefficient N range between 0.39 and 0.68. The smallest value of the reservoir coefficient N (N = 0.39) corresponds to the highest value of the reservoir shape factor M (M = 3.06) which indicates reservoir of type II (Table 1), while the rest of the reservoirs are of type III.

Fig. 12
figure 12

Locations of some proposed dams in Saudi Arabia (revised from Elfeki et al. 2014)

Full size image
Fig. 13
figure 13

Dimensionless volume–depth relationship for different regions of the Kingdom

Full size image
Table 7 Physical characteristics of some reservoirs in different regions in Saudi Arabia
Full size table

Conclusions

This paper presents a methodology for reservoir routing in general and for arid region in particular. The proposed reservoir routing model is solved numerically using first- and second-order Euler finite difference schemes and shows pretty good agreement when compared with analytical solution of a specific example in the published literature and with the traditional (modified puls) method (RMSE is 0.673, 0.668, and 0.94 m3/s respectively for the time step of 300 s). The results also show that the RMSE decreases with decreasing the value of the time step. There is no significant difference between first- and second-order Euler methods for solving the proposed method. Fenton (1992) also supported this conclusion, where he even used higher order Runge–Kutta methods.

The implementation of the methodology and the parameters selection has been illustrated on a real case study (AL-Ulb dam in Riyadh). The effect of dam condition wether the reservoir is full or empty is considered. The estimated reservoir coefficient N is 0.381, and the corresponding relative RMSE is 0.073. The estimated RMSE of the outflow hydrograph is 12.75 and 12.90 m3/s for the case of reservoir is full and empty respectively when considering modified puls method hydrograph as the reference case. The attenuation ratio on average is 65% in case the reservoir is full. However, in case of empty reservoir, an attenuation of 50% is reached for return periods more than 10 years. These results suggest that the design of reservoir in arid region should consider an empty reservoir routing, which leads to economic design of the downstream flood channel. While in rivers, a full reservoir routing is recommended for safety reasons.

For further application of the proposed methodology, a priori analysis of eight proposed dam locations in different provinces in the Kingdom of Saudi Arabia is performed. The values of the reservoir coefficient N range between 0.39 and 0.68. The smallest value of the reservoir coefficient N (N = 0.39) corresponds to the highest value of the reservoir shape factor M (M = 3.06) which indicates reservoir of type II (Hill), while the rest of the reservoirs are of type III (Flood Plain Foothill).