Introduction

An engineering rock mass is usually in a triaxial stress state. With the increase of rock engineering at great depths, geo-stress will increase greatly. In China, many large-scale rock engineering works, such as the Jinping I and II Hydropower Project and the Xiangjiaba Hydropower Project, are being or will be constructed in the coming decade. In these hydropower projects, many high dams are located on batholiths of hard rock. For example, the arch dam (305-m height) of the Jinping I Hydropower Project is the highest in the world and is located in hard marble and greenschist (Lin et al. 2014). Due to the action of higher geo-stress, hard rocks can also exhibit obvious creep deformation characteristics (Yang et al. 2006). Therefore, it has become increasingly important to investigate the creep behavior of hard rocks under all kinds of stress states, in order to ensure the long-term stability and safety of high dams in key hydropower projects.

Laboratory testing is the main method to obtain the creep deformation behaviors of hard rocks. Therefore, in the past several decades, extensive laboratory investigations have been carried out on the creep behavior of hard rocks under uniaxial or triaxial compression. Uniaxial compression creep experiments have been carried out on tuff at room temperature (Ma and Daemen 2006) and at elevated temperature (Yang and Daemen 1997), and these studies analyzed the influence of stress and temperature levels on the transient, steady-state, and accelerating creep behaviors of tuff. Fujii et al. (1999) carried out creep tests on granite under confining pressure and on dry and wet sandstone and analyzed the dependency of the strain values at distinctive points on creep stress, confining pressure, and water pressure. In accordance with the triaxial creep experimental results for hard marble and greenschist from Jinping I Hydropower station, Yang et al. (2006) investigated the variance of axial and lateral strains of hard rock with time under different confining pressures and discussed the microscopic creep failure mechanism of hard rocks. According to their triaxial creep experimental results for sandstone from the Xiangjiaba Hydropower Project, Yang and Jiang (2010) gave a detailed analysis of the tertiary creep mechanical behavior of sandstone. Yang et al. (2014) analyzed quantitatively the influence of pore pressure and axial deviatoric stress on the creep mechanical behavior of saturated red sandstone. Using triaxial creep tests on the grouting materials, Nadimi and Shahriar (2014) predicted long-term creep parameter and defined time-dependent characteristics of the bonding material. In addition, Jiao et al. (2013a; b) conducted a long-term creep observation of engineering rock mass and obtained the relationship between displacements of rock mass with time. These long-term creep monitoring results for rock mass are very significant to predict unstable failure and ensure the stability of rock engineering.

The above creep experimental results provide a better foundation for the construction of creep models. In recent years, some progress on creep models for rock material has been reported (Cristescu and Hunche 1998). According to stepwise triaxial creep experimental results of granite, Maranini and Yamaguchi (2001) developed a nonassociated elastic–viscoplastic model, which can be used to describe the behavior of granite in a general stress–strain–time relationship. By considering the subcritical crack growth due to stress corrosion cracking and the interaction effects between cracks as the main mechanism of creep failure, Miura et al. (2003) presented a micromechanics-based model for predicting the creep failure of hard rock under compression. In order to describe anisotropic damage creep deformation in brittle rocks, Shao et al. (2006) proposed a new constitutive model based on relevant results from micromechanics theory. Based on uniaxial creep experimental results of granite at various temperatures, Chen et al. (2014) propose a damage creep model of rock, which can better describe the influence of temperature on the time-dependent deformation of granite.

The Jinping II Hydropower Project is located in the upriver of the Yalong River in Sichuan Province, southwestern China. As described by Wu et al. (2010), Jinping II consists mainly of three auxiliary tunnels and a sluice dam on the west side of the Jinping Mountain, four headrace tunnels through the mountain, and an underground powerhouse complex on the east side of the mountain. The total installed capacity is 4800 MW. Four headrace tunnels with a diameter of 12–13 m and a total length of 16.67 km are constructed at depths of 1500–2000 m, and the maximum buried depth is up to 2525 m. The average principal stress of the rock mass ranges from 35 to 50 MPa, and the maximum principal stress extends to 60 MPa, according to the measured geo-stress data and back analysis of the geo-stress field (Jiang et al. 2010). The main stratum of underground tunnels is mainly Triassic marble. The uniaxial compressive strength of marble in the project region ranges from 80 to 120 MPa (Li et al. 2012a; b), which indicates that it is a kind of hard rock material. Therefore, the experimental and theoretical studies of the short-term and creep mechanical behavior of marble under higher geo-stress are very significant for the long-term stability of Jinping II Hydropower Project (Aliha 2013; Xiong et al. 2014).

By proposing a new incrementally cyclic loading–unloading pressure test method, Qiu et al. (2014) analyzed experimentally the pre-peak unloading damage evolution characteristics of marble from the Jinping II Hydropower Project. The results demonstrated that the pre-peak damage and deformation characteristics of marble specimens could be easily quantified by irreversible strains. Li et al. (2013) carried out conventional triaxial compression and reducing confining pressure tests for marble specimens and analyzed the influence of two loading paths on the short-term strength and deformation behaviors of the marble. By carrying out triaxial compression loading–unloading tests for marble specimens under different confining pressure and unloading rates, Huang and Li (2014) found that the magnitudes of the initial confining pressure and unloading rate significantly influence rock failure modes and strain energy conversion (accumulation, dissipation, and release) during unloading. Based on the triaxial creep results of marble under the loading condition, Chen et al. (2013) put forward a time-dependent damage constitutive model in terms of fractional calculus theory. However, very few experimental studies have been reported regarding the triaxial creep behaviors of deep marble under cyclic loading. Furthermore, a visco-elasto-plastic creep model to describe the creep deformation characteristics of marble under cyclic loading has not been constructed to date.

In this paper, to better understand the triaxial mechanical behavior of deep engineering rock mass, short-term and creep tests were conducted for marble located at the Jinping II Hydropower Project of China under triaxial cyclic loading. Based on the short-term triaxial experimental results for marble, the elastic, plastic, and strength behaviors of marble are first analyzed. Then, in accordance with the results of triaxial creep experimental results on marble, the instant elastic and plastic strains, and the visco-elastic and visco-plastic strains of marble are all obtained. At the same time, the influence of deviatoric stress on the creep deformation behavior is also analyzed in detail. This emphasis of this research is on modeling the triaxial creep deformation of marble using Burgers creep model, to construct a visco-elasto-plastic creep model of rock material and to validate the suitability of the visco-elasto-plastic creep model using the experimental results of marble creep under cyclic loading.

Marble material and testing methodology

Marble material

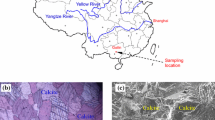
The marble located in no. 3 test branch tunnel of an auxiliary cave in the Jinping II Hydropower Project was chosen for testing. This marble is buried at a depth of about 2270 m. According to X-ray diffraction (XRD), the marble material consists mainly of carbonate minerals (calcite), together with small quantities of quartz and amorphous solids. The marble has a crystalline and blocky structure (Fig. 1), which is macroscopically very homogeneous with an average unit weight of about 2710 kg/m3.

Fig. 1
figure 1

Microscropic images of Jinping deep-buried marble. a SEM photograph. b Thin section image

Full size image

In accordance with the method suggested by the International Society for Rock Mechanics (ISRM) (Fairhurst and Hudson 1999), the length to diameter ratio of tested specimens should be in the range of 2.0–3.0 in order to minimize the influence of the end friction effects on the results. Therefore, all tested marble specimens are cylindrical 50 mm in diameter and 100 mm long. A length to diameter ratio of 2.0 ensures a uniform stress state within the samples. The short-term mechanical behaviors of specimens under triaxial compression tests were determined according to the method suggested by the ISRM (Fairhurst and Hudson 1999), and the creep mechanical behaviors were also determined in accordance with the method suggested by the ISRM (Aydan et al. 2014).

Testing equipment

The short-term and creep triaxial experiments for marble specimens were all carried out on rock servo-controlled triaxial equipment. The equipment included a loading system, constant-stability pressure equipment, a hydraulic pressure transfer system, a pressure chamber, a hydraulic pressure system, and an automatic data collection system. The most important part of this equipment is the self-equilibrium triaxial pressure chamber system, which is made up of three high-precision pumps controlling axial pressure (P1), confining pressure (P2), and pore pressure (P3). The maximum capacity of P2 and P3 is 60 MPa. However, the maximum capacity of P1 can reach 400 MPa for a normal cylindrical specimen with a diameter of 50 mm. Due to the auto-compensation system, the axial pressure generated by P1 pump is entirely transmitted as deviatoric stress.

The testing equipment can be used to perform all controlled tests, and the data acquisition and analysis by computer and automatized operations ensure that the tests are analyzed safely, timely, and precisely. The data can be collected automatically, following digitized computer configuration. This equipment can be used to perform hydrostatic pressure tests, conventional triaxial compression tests under drained or undrained conditions, triaxial seepage tests, triaxial creep tests, and chemical corrosion tests, etc.

When testing, the axial displacement is measured with two linear variable differential transformers (LVDTs), which are fixed between the bottom and top surfaces of the specimen inside the triaxial cell. The circumferential deformation is measured using a circumferential strain sensor wrapped tightly around the central region of the specimen. Considering the influence of temperature on long-term creep deformation, the creep tests were carried out at room temperature (25 ± 2 C).

Testing procedure

Short-term and creep experiments under cyclic loading condition were carried out on the marble specimens. The short-term cyclic loading experiment (Fig. 2a) consisted of the following steps. The confining pressure was first applied to a desired value at a constant rate of 0.5 MPa/s, which ensured that the specimen was under uniform hydrostatic stress. The deviatoric stress was then loaded to the surface of the specimen at a constant axial stress control rate of 0.127 MPa/s until the first stress level. After that, the deviatoric stress was unloaded at a constant axial stress control rate of 0.254 MPa/s until zero from the first stress level. The preceding steps were repeated until the seventh stress level. After the seventh stress level, the deviatoric stress was loaded to the surface of the specimen at a constant axial stress control rate of 0.127 MPa/s until failure took place.

Fig. 2
figure 2

Two experimental procedures used in the present study. a Short-term cyclic. Loading. b Creep cyclic loading

Full size image

The procedure for the triaxial creep experiments under cyclic loading condition (Fig. 2b) was as follows. First, the confining pressure of 35 MPa was applied to the specimen at a rate of 0.5 MPa/s. Next, keeping the confining pressure constant, the axial deviatoric stress was stepwise increased until the first stress level at a rate of 0.127 MPa/s. At the first stress level, the specimen was allowed to creep for a time interval of about 72 h, during which the axial deformation was continuously monitored. The deviatoric stress was then unloaded to zero from the first stress level at a constant axial stress control rate of 0.254 MPa/s. At the zero stress level, the specimen was crept for about 24 h. The preceding steps were repeated until the fifth stress level. Finally, at the fifth stress level, the deviatoric stress was maintained until creep failure took place.

Short-term mechanical behavior of marble

In order to investigate the short-term mechanical behavior of marble specimens, cyclic loading experiments under conventional triaxial compression were first conducted on three marble specimens in accordance with the short-term cyclic loading procedure shown in Fig. 2a. For the short-term experiments, the confirming method of each cyclic stress level can be described as follows.

By analyzing the volumetric strain and crack volumetric strain of brittle granite, Martin and Chandler (1994) found that when the axial stress was lower than σ ci (crack initiation stress, about 40 % peak strength), the rock specimens were considered to be at the stage of elastic deformation and the plastic strain (or damage) at this time was negligible, which could be ignored. Therefore, according to the previous results, taking into account the greater hardness of the tested marble, the stress of about 50 % peak strength was selected as the first stress level of marble under triaxial cyclic loading. The stress level was then increased by intervals of 10 MPa until it approached the peak strength in order to avoid the influence of fatigue damage caused by multi-loading and unloading.

Figure 3 shows the short-term cyclic loading experimental results for marble with different confining pressures, namely 20, 35, and 50 MPa. The figure shows that the initial unloading value is a little greater than the yielding strength of marble, even though the unloading curve does not coincide with the loading curve, but the area of the plastic loop is small, which indicates that the plastic strain is small for the first stress level. With the increase of stress level, the area of the plastic loop increases gradually. Moreover, when the axial stress is greater than the unloading value of the last cyclic increment step during the loading process, the stress–strain curve goes up along the original monotonic loading path. Therefore, the tested marble has a good memory of deformation. From Fig. 3d, we can see the influence of confining pressure on the short-term failure modes of marble. At the confining pressure of 20 and 35 MPa, deep-buried marble specimens all take on a single shear failure behavior. Furthermore, with the increase of confining pressure, the angle of shear failure decreases. However, at highest confining pressure of 50 MPa, the specimen shows a drum shape, resulting from obvious volumetric dilatancy.

Fig. 3
figure 3

Short-term experimental results of marble under triaxial cyclic loading

Full size image

Short-term elastic and plastic behavior

In accordance with Fig. 3, we are able to analyze in detail the short-term elastic and plastic characteristics of marble, which are presented in Fig. 4.

Fig. 4
figure 4

Relationship between the Young’s modulus and axial deviatoric stress of marble

Full size image

Figure 4a shows the relationship between the elastic modulus (E E) and axial deviatoric stress of marble. The value of E E is defined by the ratio of axial deviatoric stress to the elastic strain. From Fig. 4a, it can be seen that for the same confining pressure, the elastic modulus of marble remains basically constant at the lower axial deviatoric stress level but decreases slowly after yielding strength. For example, at the confining pressure of 35 MPa, the elastic modulus of marble varies only slightly from 57.73 to 57.44 GPa when the axial deviatoric stress is increased from 120 to 150 MPa, whereas the elastic modulus decreases gradually from 57.44 to 38.49 GPa when the axial deviatoric stress is increased from 150 to 180 MPa. The gradual reduction of elastic modulus results from the irreversible internal damage to the marble material.

Figure 4b shows the relationship between the plastic modulus (E P) and axial deviatoric stress of marble. The value of E P is defined by the ratio of axial deviatoric stress to the plastic strain. From Fig. 4b, it is very clear that for the same confining pressure, the plastic modulus of marble remains basically constant at the lower axial deviatoric stress level but decreases rapidly after yielding strength. The reducing rate of plastic modulus of marble with the increase of axial deviatoric stress is obviously higher than the elastic modulus. For example, at the confining pressure of 35 MPa, the plastic modulus of marble varies only slightly from 344.86 to 363.76 GPa when the axial deviatoric stress is increased from 120 to 140 MPa, whereas the plastic modulus decreases gradually from 363.76 to 38.23 GPa when the axial deviatoric stress is increased from 140 to 180 MPa, which results from the rapid increase of the plastic deformation of marble during the loading.

Figure 5 presents the relationship between axial deviatoric stress and plastic strain of marble under different confining pressures. In Fig. 5, it can be seen that with the increase of plastic strain of marble, the axial deviatoric stress also increases nonlinearly and the increasing rate tends to a stable value. The plastic deformation behavior of marble can be better expressed by the interface model proposed by Dafalias and Popov (1975), as shown in Fig. 5a. In accordance with Fig. 5a, the stress–plastic strain curve can be separated into three regions: the first is the elastic part, which indicates that the plastic strain equals to zero in this region, and thus, the plastic modulus tends to infinity. The second region is when the stress is higher than the initial yielding value σ 0, and the stress increases nonlinearly, but the rate of increase decreases step by step with the increase of plastic deformation, which means that the plastic modulus decreases gradually. The third region is where the stress–plastic strain curve tends to a stable boundary XX’, which indicates that the plastic modulus tends to a constant.

Fig. 5
figure 5

Comparison on the relationship between the axial deviatoric stress and plastic strain of marble obtained by experiment and interface model

Full size image

In order to present the characteristics of an interface model, Dafalias and Popov (1975) assumed that the plastic modulus is a function of δ and δ in (in Fig. 5a), which can be expressed by Eq. (1).

$$ {E}_P={E}_0+h\left(\frac{\delta }{\delta_{\mathrm{in}}-\delta}\right) $$
(1)

where δ and δ in have the same dimension of stress, which are defined by a particular state A 1 in the plastic flow process, h is a parameter reflecting the shape and size of specimens obtained by experiment, E 0 means the steady value of plastic modulus, which is equal to the slope of the linear boundary in the interface model, δ means the distance between the particular state A 1 and the corresponding state on linear boundary XX’, and δ in is the initial value. δ in is discrete because it occurs instantly and remains constant during the loading process. In particular, the parameters δ and δ in are always nonnegative.

Transfer Eq. (1) into a relationship between σ and ε p, and the function of linear boundary XX’ can be expressed as follows:

$$ \sigma ={\sigma}_1+{E}_0\cdot {\varepsilon}_p $$
(2)

Therefore, δ can be represented by stress (σ) and plastic strain (ε p) during the loading process before peak strength

$$ \delta =\frac{\sigma_1+{E}_0\cdot {\varepsilon}_{\mathrm{p}}-\sigma }{\sqrt{1+{E_0}^2}} $$
(3)

By substituting Eq. (3) into Eq. (1), we derive a plastic constitutive equation, which is expressed by Eq. (4):

$$ \frac{d\sigma }{d{\varepsilon}_{\mathrm{p}}}={E}_0+h\left(\frac{\sigma_1+{E}_0\cdot {\varepsilon}_{\mathrm{p}}-\sigma }{\delta_{\mathrm{in}}\sqrt{1+{E_0}^2}-{\sigma}_1-{E}_0\cdot {\varepsilon}_{\mathrm{p}}+\sigma}\right) $$
(4)

When the parameters h, E 0, and σ 1 are given, the increment method was often adopted in the past, which approximate this differential equation to a finite difference equation. By calculating every plastic strain increment (∆ε p) and the corresponding increment of stress (∆σ), the σ–ε p curve of cyclic loading tests can be obtained approximately. If the elastic deformation of material complies with Hooke’s law, the complete σ–ε curve can also be obtained.

In the present research, where the parameters h, E 0, and σ 1 were unknown, the increment method was used by directly solving the differential equation Eq. (4) according to the initial conditions: ε p = 0 and σ = σ 0, which can produce the following multiple equations:

$$ \sigma ={\sigma}_1+{E}_0{\varepsilon}_{\mathrm{p}}+\left({\sigma}_0-{\sigma}_1\right)\sqrt{1+{E_0}^2}\cdot f\left[g\left({\varepsilon}_{\mathrm{p}}\right)\right] $$
(5)
$$ g\left({\varepsilon}_{\mathrm{p}}\right)=- \exp \left(A+B{\varepsilon}_{\mathrm{p}}\right) $$
(6)
$$ {f}^{-1}\left[g\left({\varepsilon}_{\mathrm{p}}\right)\right]=g\left({\varepsilon}_{\mathrm{p}}\right)\cdot \exp \left[g\left({\varepsilon}_{\mathrm{p}}\right)\right] $$
(7)

where f −1(x) reflects the inverse function of f(x) and the parameters A and B in Eqs. (6) and(7) relate only to the basic parameters h, E 0, σ 1, and σ 0. It is clear that Eqs. (5)–(7) are too complicated to solve. Therefore, keeping the form of Eq. (5) unchanged, Eqs. (5)–(7) can be simplified to Eq. (8).

$$ \sigma =a+b{\varepsilon}_{\mathrm{p}}+c \exp \left(d\cdot {\varepsilon}_{\mathrm{p}}\right) $$
(8)

where a, b, c, and d are all the parameters relating to the mechanical characteristics of material. By analyzing the plastic strain of marble under short-term cyclic loading (Fig. 5) in accordance with Eq. (8), the nonlinear least square method (NLSM) was adopted to simulate the values of parameters a, b, c, and d. Table 1 lists the interface model parameters of marble under different confining pressures, and the correlation coefficient (R) is also given in this table. The simulated curve of interface model was compared with the experimental results, as shown in Fig. 5. The figure shows that the interface model proposed by Dafalias and Popov (1975) agrees very well with the experimental result for marble.

Table 1 Interface model parameters of marble under different confining pressures
Full size table

Short-term peak strength behavior

From Fig. 3, it can be seen that the short-term peak strength of marble specimens increases with the increase of confining pressure. Figure 6 further depicts the relationship between the short-term peak strength (σ S) of marble and the confining pressure (σ 3). From Fig. 6, it is clear that the peak strengths of marble are 180.85, 220.98, and 234.98 MPa for the confining pressures of 20, 35, and 50 MPa, respectively. Based on the short-term strength data, the linear Mohr–Coulomb criterion (i.e., Eq. (9)) can be used to obtain the short-term triaxial strength parameters of the marble material tested.

Fig. 6
figure 6

Comparison between experimental peak strength of marble and Mohr–Coulomb criterion

Full size image
$$ {\sigma}_{\mathrm{S}}=149.12+1.804{\sigma}_3=\frac{2C \cos \phi +{\sigma}_3\left(1+ \sin \phi \right)}{1- \sin \phi } $$
(9)

According to Eq. (9), the cohesion C and the internal friction angle Φ of marble material can be obtained, which are 55.51 MPa and 16.7°, respectively. In general, from Fig. 6, it can be seen that the peak strength of marble under higher stress increases with the confining pressure, which can be well described by the linear Mohr–Coulomb criterion.

Experimental analysis of creep mechanical behavior

In accordance with the testing procedure shown in Fig. 2b, we obtained cyclic loading creep test results of marble with different axial deviatoric stresses at σ 3 = 35 MPa, as shown in Fig. 7. In the creep test, the first deviatoric stress level was designed as approximately 60 % of the corresponding short-term strength, which ensured that the specimens produced primary and steady-state creep from the beginning of the first deviatoric stress level, in order to provide more experimental data on delayed damage and failure in the models.

Fig. 7
figure 7

Cyclic loading creep test results of marble with different axial deviatoric stresses at σ3 = 35 MPa

Full size image

Relationship between axial strain and time

From Fig. 7, it can be seen that at the first deviatoric stress of 110 MPa, the creep strain of the marble specimen during loading was 0.94 × 10−3. When the load was increased to the second deviatoric stress of 120 MPa, compared with that at the first stress level, the creep strain of marble showed a slight increase and reached 1.00 × 10−3. With the increase of axial load, the deviatoric stress applied to the specimen reached 130 MPa. At 130 MPa, the creep strain of the specimen was about 1.03 × 10−3. At the fourth deviatoric stress of 140 MPa, the creep strain of the specimen increased rapidly to 3.35 × 10−3, which amounted of 34.6 % of total strain, and showed that the creep effect was dominant in rock deformation at this deviatoric stress. However, at the final deviatoric stress of 145 MPa, the creep strain of the specimen was largest, at 4.23 × 10−3. Therefore, the contribution of the creep effect on rock deformation will increase with the increase of the axial deviatoric stress.

By calculating the slope of strain curves versus time, as shown in Fig. 7, the relationship between stain rate and time during the entire loading creep deformation of marble can be obtained. The results showed that the creep rate of marble depends on the deviatoric stress. For lower values of the deviatoric stress, the loading creep rates all demonstrated two stages, a primary creep stage with decreasing strain rate and a steady creep stage at constant strain rate. For the final deviatoric stress level of 145 MPa, creep failure of the marble specimens did not take place.

For many rock engineering applications, it is vital to know when a steady state is reached and the magnitude of the steady creep rate. The steady-state creep rate can be confirmed by calculating the average slope of axial strain versus time curve at the steady-state creep stage. Based on the triaxial loading creep results of marble with different deviatoric stresses, we can analyze the influence of deviatoric stress on the steady-state creep rates of the tested marble and the results are shown in Fig. 8.

Fig. 8
figure 8

Relationship between axial deviatoric stress and steady-state creep rate of marble

Full size image

From Fig. 8, it is clear that with the increase of axial deviatoric stress, the steady-state creep rate of marble increases nonlinearly for the same confining pressure. The steady-state creep rate of marble is 1.8 × 10−6/h, 2.9 × 10−6/h, and 5.5 × 10−6/h for the axial deviatoric stress of 110, 120, and 130 MPa, respectively. However, when the axial deviatoric stress is increased to 140 and 145 MPa, the steady-state creep rate of marble reaches 16.4 × 10−6/h and 31.1 × 10−6/h, respectively. In general, the relationship between axial deviatoric stress and steady-state creep rate can be better expressed in the following equation:

$$ {\sigma}_1-{\sigma}_3=A+B{\dot{\varepsilon}}_{cs}+C \exp \left(D\cdot {\dot{\varepsilon}}_{cs}\right) $$
(10)

where A, B, C, and D are all constants. The fitting line using Eq. (10) is also plotted in Fig. 8, where the constants A, B, C, and D are 133.83 MPa, 0.36 × 106 MPa h, −50.64 MPa h, and −0.41 × 106 h, respectively. In Fig. 8, the value of R is 0.995, a higher correlation coefficient.

Knowledge of the long-term strength of rock is very important for the evaluation of the stability and safety of rock engineering. Previous results (Liu 1994) have testified that the stress when the steady-state creep rate equals to zero can be regarded as the long-term strength of rock material. Thus, in accordance with Eq. (10), we can predict the long-term strength of the tested marble by substituting \( {\dot{\varepsilon}}_{\mathrm{cs}} \) = 0; i.e., the long-term strength of the tested marble at σ 3 = 35 MPa was about 83.19 MPa, which is expressed in the form of the deviatoric stress.

Analysis of creep deformation behavior

Based on the creep test results of marble under triaxial cyclic loading, the instant elastic and plastic strains, and the visco-elastic and visco-plastic strains of marble can be separated successfully. Figure 9 presents a typical sketch of visco-elasto-plastic creep curve of rock. In Fig. 9, the total strain (ε T) of rock is the sum of the instant strain (ε m) and creep strain (ε c). The instant strain (ε m) of rock consists of the instant elastic strain (ε me) and instant plastic strain (ε mp), whereas the creep strain (ε c) of rock is the sum of the visco-elastic strain (ε ce) and visco-plastic strain (ε cp). The strain (ε ∞1) of rock after the unloading creep for 24 h consists of the instant plastic strain (ε mp) and creep strain (ε c). The above relationships among all kinds of strains of rock can be expressed as follows:

Fig. 9
figure 9

A typical sketch of visco-elasto-plastic creep curve of rock

Full size image
$$ {\varepsilon}_{\mathrm{T}}={\varepsilon}_{\mathrm{m}}+{\varepsilon}_{\mathrm{c}} $$
(11)
$$ {\varepsilon}_{\mathrm{m}}={\varepsilon}_{\mathrm{m}\mathrm{e}}+{\varepsilon}_{\mathrm{m}\mathrm{p}} $$
(12)
$$ {\varepsilon}_{\mathrm{c}}={\varepsilon}_{\mathrm{c}\mathrm{e}}+{\varepsilon}_{cp} $$
(13)
$$ {\varepsilon}_{\infty 1}={\varepsilon}_{mp}+{\varepsilon}_c $$
(14)

Table 2 lists the measured visco-elasto-plastic strain data of marble under triaxial cyclic loading. It should be noted that both the visco-elastic strain (ε ce) and visco-plastic strain (ε cp) increase with the increase of time, as shown in Fig. 9. Therefore, the values for the ε ce and ε cp of marble after loading creep ends are listed in Table 2. According to Table 2, we can conclude that the percentage of instant strain to total strain decreases from 76.1 to 65.4 % with the increase of deviatoric stress, which indicates that the fluidly of marble will heighten. Moreover, it is very clear that the four strains (i.e., ε me, ε mp, ε ce, and ε cp) of marble have the same magnitude, which cannot be neglected in modeling the creep mechanical behavior of rock. In the following, we will investigate the influence of axial deviatoric stress on the instant strain and creep strain of marble, as shown in Fig. 10.

Table 2 Measured visco-elasto-plastic strain data of marble under triaxial cyclic loading (σ 3 = 35 MPa)
Full size table
Fig. 10
figure 10

Instant strains and visco strains of marble with different axial deviatoric stresses

Full size image

From Fig. 10a, it is clear that the elastic strains (including instant elastic strain and visco-elastic strain) of marble all increase with the increase of axial deviatoric stress, which can be better expressed in a linear relationship, i.e., σ 1–σ 3 = b 1 + k 1·ε e. For instant elastic strain, the values of b 1 and k 1· are 39.5 MPa and 28.43 GPa, respectively, whereas for visco-elastic strain, the values of b 1 and k 1· are 103.43 MPa and 92.65 GPa, respectively. Moreover, the instant elastic strain of marble is higher than the visco-elastic strain at the same deviatoric stress.

However, in accordance with Fig. 10b, the instant plastic strain and visco-plastic strain of marble increase nonlinearly with the axial deviatoric stress, which can also be well described by the interface model, i.e., Eq. (8). The relationship between the axial deviatoric stress and instant plastic strain can be expressed by σ 1–σ 3 = 143.02 + 0.64ε mp − 47.23 exp (−0.64ε mp), whereas the relationship between the axial deviatoric stress and visco-plastic strain can be expressed by σ 1–σ 3 = 143.02 + 4.65ε cp − 1.2 × 106 exp (−14ε cp). Moreover from Fig. 10b, the visco-plastic strain of marble is much greater than the visco-elastic strain for the same deviatoric stress, because the visco-plastic deformation makes a great contribution to the creep deformation of rock material.

Modeling of creep mechanical behavior

On the basis of the results of triaxial creep experiments on marble under cyclic loading presented in the previous section, we model the creep mechanical behavior of marble in this section. First, Burgers creep model under three-dimensional stress state is derived to evaluate the creep behavior of marble under cyclic loading. A visco-elasto-plastic creep model of rock material is then constructed to better describe the unloading creep behavior of marble.

Burgers visco-elastic model and parameter identification

In Fig. 7, it can be seen that not only the tested marble has distinct visco-elastic deformation characteristics, but also the steady-state creep rate of marble is greater than zero under all the deviatoric stresses. Therefore, Burgers visco-elastic model (Fig. 11), which is connected in series by an elastic component (Hookean body), a visco-elastic component (Newton body), and a Kelvin model, is first chosen to model the creep deformation behavior of marble.

Fig. 11
figure 11

Burgers visco-elastic model under one-dimensional stress state

Full size image

The stress tensor σ ij at a certain point can be decomposed into the partial stress tensor (S ij ) and the spherical stress tensor (σ m). Similarly, the strain tensor ε ij at a certain point can be decomposed into the partial strain tensor (e ij ) and the spherical strain tensor (ε m). These parameters have a specific relationship under an elastic state, which can be expressed as follows:

$$ \left\{\begin{array}{c}\hfill {\sigma}_{\mathrm{m}}=3K{\varepsilon}_{\mathrm{m}}\hfill \\ {}\hfill {S}_{ij}=2G{e}_{ij}\hfill \end{array}\right. $$
(15)

In classical fluid mechanics, there are the following three hypotheses (Sun 1999): (1) the creep deformation of rock material results from the partial stress tensor, but the spherical stress tensor does not cause the creep; i.e., no volume flow occurs during the creep deformation; (2) rock is a kind of isotropic material, and the short-term stress–strain curve and creep curve in the tensile and compressive stress states are very similar; and (3) the Poisson’s ratio of rock material is not dependent on time during the creep deformation. Based on the above hypotheses, we can derive the Burgers creep model in the three-dimensional stress state, which is described as follows.

For the Hookean body (H)

$$ \left\{\begin{array}{c}\hfill {S}_H=2{G}_1{e}_H\hfill \\ {}\hfill {\sigma}_H=3K{\varepsilon}_H\hfill \end{array}\right. $$
(16)

For the Kelvin model (K)

$$ \left\{\begin{array}{c}\hfill {S}_K=2{G}_2{e}_K+2{\eta}_1{\dot{e}}_K\hfill \\ {}\hfill {\sigma}_K=3K{\varepsilon}_K\hfill \end{array}\right. $$
(17)

For the Newton body (N)

$$ \left\{\begin{array}{c}\hfill {S}_N=2{\eta}_2{\dot{e}}_N\hfill \\ {}\hfill {\sigma}_N=3K{\varepsilon}_N\hfill \end{array}\right. $$
(18)

According to the definition of the components connected in series, we can obtain the following equation.

$$ \left\{\begin{array}{c}\hfill {S}_{ij}={S}_H={S}_K={S}_N\hfill \\ {}\hfill {e}_{ij}={e}_H+{e}_K+{e}_N\hfill \end{array}\right. $$
(19)

The subscripts H, K, and N in Eqs. (16)–(19) represent different model components. G and K are the shear modulus and the bulk modulus of rock material, respectively, which are all related to the elastic modulus of Poisson’s ratio of rock material, i.e.,

$$ \left\{\begin{array}{c}\hfill G=\frac{E}{2\left(1+\mu \right)}\hfill \\ {}\hfill K=\frac{E}{3\left(1-2\mu \right)}\hfill \end{array}\right. $$
(20)

By substituting Eqs. (16)–(18) into Eq. (19) and carrying out an integral for the linear differential equation on the partial strain tensor (e ij ), we can obtain the following equation by keeping the initial axial strain equal to zero and the partial stress tensor (S ij ) as constant:

$$ {e}_{ij}=\frac{1}{2{G}_1}{S}_{ij}+\frac{1}{2{G}_2}\left[1- \exp \left(-\frac{G_2}{\eta_1}t\right)\right]{S}_{ij}+\frac{t}{2{\eta}_2}{S}_{ij} $$
(21)

For the conventional triaxial stress state, we can obtain the following equations:

$$ \left\{\begin{array}{c}\hfill {\sigma}_2={\sigma}_3\hfill \\ {}\hfill {\sigma}_{\mathrm{m}}=\frac{1}{3}\left({\sigma}_1+2{\sigma}_3\right)\hfill \\ {}\hfill {S}_{11}={\sigma}_1-{\sigma}_{\mathrm{m}}\hfill \\ {}\hfill {e}_{11}={\varepsilon}_1-{\varepsilon}_{\mathrm{m}}\hfill \end{array}\right. $$
(22)

If the parameter σ 0 is used to represent the deviatoric stress (σ 1–σ 3), then substituting Eq. (22) into Eq. (21), the Burgers creep equation for rock under conventional triaxial loading condition can be expressed as follows:

$$ {\varepsilon}_1=\frac{1}{9K}\left({\sigma}_0+3{\sigma}_3\right)+\frac{\sigma_0}{3{G}_1}+\frac{\sigma_0}{3{G}_2}\left[1- \exp \left(-\frac{G_2}{\eta_1}t\right)\right]+\frac{\sigma_0}{3{\eta}_2}t $$
(23)

When the rock specimen is unloaded at t = t 1 until the axial deviatoric stress is reduced to 0 (i.e., σ 0 = 0), the Burgers creep equation under loading condition can be derived, as expressed by Eq. (24).

$$ {\varepsilon}_1=\frac{\sigma_3}{3K}+\frac{\sigma_0}{3{G}_2}\left[1- \exp \left(-\frac{G_2}{\eta_1}{t}_1\right)\right]\cdot \exp \left[\frac{G_2}{\eta_1}\left({t}_1-t\right)\right]+\frac{\sigma_0}{3{\eta}_2}{t}_1 $$
(24)

In accordance with Fig. 7 and Eq. (23), the creep parameters (K, G 1, G 2, η 1, η 2) for Burgers model can be identified by the following methods. First, the elastic modulus E and Poisson’s ratio μ are confirmed by the short-term experimental curves of marble at the stage of elastic deformation (Fig. 3). Then, according to Eq. (20), we can obtain the shear modulus (G) and bulk modulus (K) of marble. Thus, on the basis of the instant strain (ε m) of marble, the instant shear modulus G 1 can be confirmed by the following equation:

$$ {\varepsilon}_{\mathrm{m}}=\frac{1}{9K}\left({\sigma}_0+3{\sigma}_3\right)+\frac{\sigma_0}{3{G}_1}\Rightarrow {G}_1=\frac{\sigma_0}{3\left({\varepsilon}_{\mathrm{m}}-\frac{\sigma_0+3{\sigma}_3}{9K}\right)} $$
(25)

The creep parameter η 2 can be confirmed by the steady-state creep rate of marble, i.e.,

$$ {\dot{\varepsilon}}_{\mathrm{cs}}=\frac{\sigma_0}{3{\eta}_2}\Rightarrow {\eta}_2=\frac{\sigma_0}{3{\dot{\varepsilon}}_{\mathrm{cs}}} $$
(26)

After obtaining the parameters K, G 1, and η 2, the creep parameters G 2 and η 1 can be obtained by the nonlinear least square method (NLSM) (Yang and Cheng 2011). In the present study, the square of the correlation coefficient (R 2) and the sum of the least error square (Q) are simultaneously chosen as discrimination criteria to evaluate the creep model parameters obtained by NLSM. It needs to be noted that R 2 tends to 1.0 and Q approaches zero, which means that the theoretical model agrees better with the experimental data. Therefore, for a given creep model and experimental data, we can always obtain a maximum R 2 and a minimum Q.

Table 3 lists Burgers visco-elastic creep model parameters of marble under different axial deviatoric stresses. From Table 3, it can be seen that the elastic parameters E and Poisson’s ratio μ vary slightly with the increase of deviatoric stress and the average values of E and μ are 54.96 GPa and 0.19, respectively. Thus, the parameters G and K are not distinctly dependent on deviatoric stress and the average values of G and K are 23.10 and 29.85 GPa, respectively. However, the parameters G 1 and η 2 decrease with the increase of deviatoric stress, whereas the parameters G 2 and η 1 have no marked relationship with the deviatoric stress.

Table 3 Burgers visco-elastic creep model parameters of marble under different axial deviatoric stresses
Full size table

By adopting the parameters listed in Table 3, Eqs. (23) and (24) can be used to model the results of creep experiments for marble under cyclic loading. Figure 12 presents the comparison between Burgers creep model curves with various deviatoric stresses and the experimental results of marble. The figure shows that Burgers creep model curves agree very well with the experimental results of marble under the loading condition, but the theoretical values obtained by Burgers creep model are distinctly lower than the experimental values of marble under the unloading condition. The reason can be explained as follows. Burgers creep model not only cannot separate the instant elastic and instant plastic deformation, but also cannot take into account the visco-plastic deformation of rock material.

Fig. 12
figure 12

Comparison between Burgers creep model curves with the experimental result of marble under different axial deviatoric stresses (σ3 = 35 MPa)

Full size image

Visco-elasto-plastic creep model

In order to better describe the creep behavior of marble material under the unloading condition, by adopting the fundamental hypothesis of visco-plastic mechanics, a visco-elasto-plastic model of rock material can be proposed, as shown in Fig. 13. Here, σ a and σ b are respectively the elastic stress threshold and visco-elastic stress threshold. In the visco-elasto-plastic creep model, the instant elastic strain (ε me), instant plastic strain (ε mp), visco-elastic strain (ε ce), and visco-plastic strain (ε cp) are all taken into account. Next, we derive in detail the visco-elasto-plastic creep equation of rock material under three-dimensional stress state.

Fig. 13
figure 13

Proposed visco-elasto-plastic model of rock

Full size image

Based on the flow rule of plastic mechanics, the relationship between the plastic strain increment and the axial stress can be expressed as follows:

$$ d{\varepsilon}_{ij}^p=d\lambda \frac{\partial g}{\partial {\sigma}_{ij}} $$
(27)

where dλ is a nonnegative scalar function throughout the entire plastic loading history, which is the plastic viscosity coefficient of the material. The vector length or magnitude of the plastic strain increment is confirmed by dλ. The g represents the potential surface, and the gradient vector ∂g/∂σ ij decides the direction of the vector of plastic strain increment.

During the creep experiments on marble, the stress tensor σ ij was a constant. From Fig. 9, it can be seen that the plastic strain increment of marble decreases gradually with time and tends to a stable value, as shown in Fig. 10. By comparing Fig. 9 with Fig. 10, we can see that the plastic viscosity coefficient also coincides with the interface model. Therefore, dλ can be expressed as follows:

$$ d\lambda ={\lambda}_0+k\left(\frac{\delta }{\delta_{\mathrm{in}}-\delta}\right) $$
(28)

By substituting Eq. (28) into Eq. (27), the following equation can be obtained:

$$ {\dot{\varepsilon}}_{ij}^p={\lambda}_0\frac{\partial g}{\partial {\sigma}_{ij}}+k\left(\frac{\delta }{\delta_{\mathrm{in}}-\delta}\right)\frac{\partial g}{\partial {\sigma}_{ij}} $$
(29)

According to Eqs. (4)–(8), the plastic strain of marble during creep should satisfy the following function:

$$ {\varepsilon}_{\mathrm{p}}=h\left(\sigma \right)+{\eta}_0\left(\sigma \right)\cdot t+p\left(\sigma \right)\cdot \exp \left(q\left(\sigma \right)\cdot t\right) $$
(30)

where \( h\left(\sigma \right)={h}_0\frac{\partial g}{\partial \sigma } \), \( {\eta}_0\left(\sigma \right)={\dot{\varepsilon}}_{\mathrm{cs}}\left(\sigma \right) \), \( p\left(\sigma \right)={p}_0\frac{\partial g}{\partial \sigma } \), \( q\left(\sigma \right)={q}_0\frac{\partial g}{\partial \sigma } \) (31)

For brevity, the subscripts representing the tensor are omitted. η 0 is the steady-state creep rate of marble, as shown in Fig. 9. The parameters h(σ), p(σ), and q(σ) are the functions related to the properties of marble and the stress state. During triaxial creep, the stress level is a constant. Therefore, h(σ), p(σ), and q(σ) are all constants, which can be obtained in accordance with the results of creep experiment by NLSM.

According to Eq. (30) and Fig. 9, we can construct the visco-elasto-plastic creep model of rock material under loading condition, which can be expressed by the following equation under three-dimensional stress state.

$$ \left\{\begin{array}{c}\hfill {\varepsilon}_1=\frac{1}{9K}\left({\sigma}_0+3{\sigma}_3\right)+\frac{\sigma_0-{\sigma}_a}{3{G}_1}+\frac{\sigma_0-{\sigma}_b}{3{G}_2}\left[1- \exp \left(-\frac{G_2}{\eta_1}t\right)\right]+h+{\eta}_0t+p\cdot \exp \left(q\cdot t\right)\hfill \\ {}\hfill {\sigma}_0>{\sigma}_b>{\sigma}_a\hfill \end{array}\right. $$
(32)

If η 0 = σ 0/3η 2 and h = p = 0, the constructed visco-elasto-plastic creep model equation can be degenerated Burgers creep model equation. When the rock specimen is unloaded at t = t 1 until the axial deviatoric stress is reduced to 0 (i.e., σ 0 = 0), the visco-elasto-plastic creep equation under the loading condition can be derived, as expressed by Eq. (33).

$$ {\varepsilon}_1=\frac{\sigma_3}{3K}+\frac{\sigma_0-{\sigma}_b}{3{G}_2}\left[1- \exp \left(-\frac{G_2}{\eta_1}{t}_1\right)\right]\cdot \left[ \exp \frac{G_2}{\eta_1}\left({t}_1-t\right)\right]+h+{\eta}_0{t}_1+p\cdot \exp \left(q\cdot {t}_1\right) $$
(33)

Comparison of visco-elasto-plastic creep model and experimental results

In the proposed visco-elasto-plastic creep model of rock, there are ten creep parameters, K, G 1, G 2, σ a, σ b, η 1, η 0, h, p, and q, which can be identified by the following methods. It should be noted that in the visco-elasto-plastic creep model, the instant elastic and visco-elastic parameters K, G 1, G 2, σ a, σ b, and η 2 do not depend on the deviatoric stress level, but the instant plastic and visco-plastic parameters η 0, h, p, and q are closely related to the deviatoric stress level.

First, the instant elastic parameter K can be confirmed by the average value listed in Table 3 for all the deviatoric stress levels, i.e., K = 29.85 GPa. Then, according to the linear relationship between the ε me, ε ce of marble and the deviatoric stress σ 0 (Fig. 10), the creep parameters G 1, G 2, σ a, and σ b can be identified by Eq. (34):

$$ \left\{\begin{array}{c}\hfill {\varepsilon}_{\mathrm{me}}=\frac{\sigma_0-{\sigma}_{\mathrm{a}}}{3{G}_1}+\frac{\sigma_0}{9K}\hfill \\ {}\hfill {\varepsilon}_{\mathrm{ce}}=\frac{\sigma_0-{\sigma}_{\mathrm{b}}}{3{G}_2}\hfill \end{array}\right. $$
(34)

The identified creep parameters G 1, G 2, σ a, and σ b of marble are 10.79 GPa, 65.36 GPa, 42.73 MPa, and 81.37 MPa, respectively, and are in dependent of the deviatoric stress level. The parameter η 0 equals the steady-state creep rate of marble, which increases nonlinearly with the deviatoric stress, as shown in Fig. 8.

However, the creep parameter η 1 can be identified for the unloading creep curve of marble. The creep parameter η 1 of marble under four different deviatoric stress levels are respectively 226.16, 267.87, 248.52, and 238.54 GPa h, which are slight variations from the deviatoric stresses. Therefore, the average value (i.e., 245.27 GPa h) of η 1 with different deviatoric stresses is used in the visco-elasto-plastic creep model.

After obtaining the creep parameters K, G 1, G 2, σ a, σ b, η 1, and η 0, the creep parameters h, p, and q can be obtained by using the following equations:

$$ \left\{\begin{array}{c}\hfill {\varepsilon}_{\mathrm{mp}}=h+p+\frac{\sigma_3}{3K}\hfill \\ {}\hfill {\varepsilon}_{\mathrm{cp}}={\eta}_0t+p\left[ \exp (qt)-1\right]\hfill \end{array}\right. $$
(35)

In accordance with Eq. (35), we can first identify the creep parameters p and q by NLSM, and then, the creep parameter h can be obtained.

By adopting the above method, all the visco-elasto-plastic creep model parameters of marble with various deviatoric stress levels can be calculated and the results are listed in Table 4. By adopting the parameters listed in Table 4, Eqs. (32) and (33) can be used to model the results of the creep experiments on marble under triaxial cyclic loading. Figure 14 presents the comparison between visco-elasto-plastic creep model curves with various deviatoric stresses and the experimental results for marble. From Fig. 14, it can be seen that visco-elasto-plastic creep model has good agreement with the experimental result. Next, we further illustrate the dominance of the visco-elasto-plastic creep model by comparing with Burgers creep model. It is clear that Q for visco-elasto-plastic creep model is smaller by two to three orders than that obtained by Burgers creep model, which shows that proposed visco-elasto-plastic creep model is valid.

Table 4 Visco-elasto-plastic creep model parameters of marble under different axial deviatoric stresses
Full size table
Fig. 14
figure 14

Comparison between visco-elasto-plastic creep model curves with the experimental result of marble under different axial deviatoric stresses (σ3 = 35 MPa)

Full size image

Conclusions

In this paper, the results of short-term and creep experiments on marble specimens under triaxial cyclic loading are reported. In accordance with the results of the triaxial creep experiments, Burgers and visco-elasto-plastic creep model of rock were used to evaluate the time-dependent behavior of deep-buried marble. Based on our experimental and modeling results, the following conclusions can be drawn.

1. In accordance with the short-term triaxial experimental results for marble under cyclic loading, the elastic, plastic, and strength behaviors of marble were first investigated. The results show that for the same confining pressure, the elastic modulus of marble remains constant at the lower axial deviatoric level but decreases slowly after yielding strength. However, the plastic modulus of marble reduces rapidly with the increase of axial deviatoric stress at the same confining pressure. Moreover, the elastic and plastic moduli of the tested marble are independent of the confining pressure.

2. At the same confining pressure, the axial deviatoric stress increases step by step with the increase of plastic strain of marble, but the axial deviatoric stress–plastic strain curve approaches an inclined line. The relationship between the axial deviatoric stress and the plastic deformation of marble can be described well by the interface model. The peak strength of marble under higher stress increases with the confining pressure, which can be well described in accordance with the linear Mohr–Coulomb criterion.

3. Based on the results of triaxial creep experiments on marble under cyclic loading, the instant elastic and plastic strains, and the visco-elastic and visco-plastic strains were separated successfully, which provides a better foundation for constructing a visco-elasto-plastic creep model of rock. The creep strain rate of marble under different deviatoric stresses was analyzed, and the results show that the steady-state creep rate of marble increases nonlinearly with the increase of axial deviatoric stress. A nonlinear function is proposed to describe the relationship between the steady-state creep rate and axial deviatoric stress, which can better predict the long-term strength of marble.

4. Burgers creep model under three-dimensional stress state was used to describe the creep behavior of marble under triaxial cyclic loading. The simulated results show that Burgers creep model can describe very well the creep behavior of marble under the loading condition but is not adequate to describe the creep behavior of marble under the unloading condition. Therefore, based on the fundamental hypothesis of visco-plastic mechanics, a visco-elasto-plastic creep model of rock material is proposed, which can describe the unloading creep behavior better than Burgers creep model. The creep model curve agrees very well with the experimental results, which shows the validity of the proposed visco-elasto-plastic creep model.