Introduction

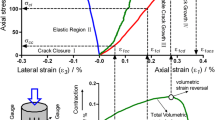
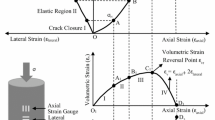
Generally, rock samples subjected to a uniaxial compression will manifest the typical mechanical responses shown in Fig. 1a. Classic works indicate that the failure process can be subdivided into five stages: (1) crack closure, (2) elastic deformation, (3) crack initiation and stable crack growth, (4) Crack damage and unstable crack growth, and (5) failure and post-peak behavior (Bieniawski 1967a, b; Brace et al. 1966; Lajtai and Lajtai 1974; Martin 1993; Xue et al. 2013). For a clearer presentation, the post-peak region is not depicted in Fig. 1a. There exist three stress thresholds prior to failure, i.e., the crack closure stress σ cc , crack initiation stress σ ci , and crack damage stress σ cd . There is no doubt that if we could construct a quantitative relationship between the uniaxial compressive strength σ ucs and any one of these three stress thresholds, the failure of rock samples could be predicted in advance.

Fig. 1
figure 1

Illustration of phase transition of a system. a Typical stress–strain diagram showing different stages of crack development under uniaxial compression test. b The bifurcation evolution process of the renormalization group theory

Full size image

It is well accepted that the macroscopic failure process of laboratory-scale rock samples is usually accompanied by accumulated micro-structural damage. In most cases, the cracks appear to be completely random in the beginning. However, as the applied load increases, additional cracks will develop and coalesce around the potential macroscopic fracture plane. When the rock sample can no longer bear the external load, ruptures may eventually occur. Numerous studies have indicated that as the stress magnitude gradually approaches the stress threshold σ cd , crack propagation and interaction appear unstable and crack growth will not be terminated, even if the stress remains constant at σ cd (Bieniawski 1967a, b; Brace et al. 1966; Eberhardt et al. 1997, 1998, 1999; Lajtai and Lajtai 1974; Martin and Chandler 1994). Conversely, when the external load is less than σ cd , crack growth is stable. Furthermore, it has also been found that when the external load approaches the stress threshold σ cd , some physical properties, such as acoustic emissions, permeability, wave velocity, and resistivity, generate significant responses (Chen and Lin 2004; Schulze et al. 2001; Souley et al. 2001; Sun et al. 2014).

It appears that the stress threshold σ cd is a very special threshold. Therefore, we will attempt to establish a theoretical quantitative correlation between the crack damage stress threshold and uniaxial compressive strength. From Fig. 1b, it appears that rock samples usually suffer a phase transition from a stable to unstable state at σ cd , which is equivalent to the critical point in renormalization group (RG) theory. The so-called critical point is a term describing a singular point at which different phases or states coexist. In the field of geology and geophysics, numerous studies have reported on the phase transition of a system (Abdusalam 2001; Allegre et al. 1982; Borri-Brunetto et al. 2004; Carpinteri et al. 2001, 2002, 2012; Chen et al. 2002; Hansen et al. 1997; Iwashita and Nakanishi 2005; Madden 1983; Matsuba 2002; Meng et al. 2009; Saleur et al. 1996; Smalley et al. 1985). Therefore, the RG method is introduced in the present study to reveal the theoretical quantitative correlation between σ cd and σ ucs .

The structure of the present study is as follows. In second section, a detailed mathematical derivation of the theoretical solution of σ cd /σ ucs is described based on RG theory. Experimental findings and the discussion are presented in the third section. Finally, concluding remarks are presented in the fourth section.

Theoretical study of the relationship between the crack damage stress threshold and uniaxial compressive strength

The model of two-dimensional RG theory

It is well accepted that as the applied load gradually increases, cracks will develop and coalesce around the potential macroscopic fracture plane. Essentially, only when the crack density of the potential macroscopic fracture plane approaches a certain level will macroscopic fracture occurs. Therefore, the forming process of the macroscopic fracture plane is simplified and considered as a two-dimensional fracture process in the present work, and two-dimensional RG theory is introduced to describe the failure process of the rock samples (see Fig. 2). Thus, the macroscopic fracture plane can be renormalized into many cells and different order blocks. Here, only the first three order blocks are shown. For example, the first-order block comprises four cells, while the second-order block consists of four first-order blocks. Similarly, the third-order block is composed of four second-order blocks. In fact, the same combination can be continued to an infinite scale. Furthermore, there exist five possible states for each of the different order blocks, i.e., B4U0, B3U1, B2U2, B1U3, and B0U4 (see Fig. 2d). The uppercase letter “B” denotes that the cells or blocks have been broken (colored box), which is followed by the digit corresponding to the number of broken cells or blocks. The uppercase letter “U” means that the cells or blocks have not been broken (white box), and the following digit corresponds to the number of unbroken cells or blocks. The corresponding probabilities of the five possible states are listed in column B of Table 1, where p 1 means the broken probability of each cell.

Fig. 2
figure 2

Illustration of the two-dimensional RG model of macroscopic fracture plane. a Rock sample with two macroscopic fracture planes after failure under a uniaxial compression test. b Sketch showing two macroscopic fracture planes. c The two-dimensional RG model. d The five possible states for each block

Full size image
Table 1 Various probabilities for cells or blocks
Full size table

Methodology of two-dimensional RG theory

As suggested by Smalley et al. (1985), it is assumed that the strength of each individual cell is σ cell , which obeys a Weibull distribution and depends on the number of microcracks in the cells. When an external load is applied to a rock sample, it is assumed that each cell of the rock will be subjected to a corresponding local stress. When the strength of the cell σ cell is less than its local stress, the cell will fail, and its broken probability is p α , which can be expressed as follows:

$$ {p}_{\alpha }=p\left({\sigma}_{cell}<\alpha \sigma \right)=1- \exp \left[-{\left(\alpha \frac{\sigma }{\sigma_0}\right)}^m\right], $$
(1)

where α is a coefficient, σ 0 is a reference strength of the cell, and m is a shape parameter that can be used to evaluate the discreteness of material strength. As suggested by Tang et al. (2000) and Wong et al. (2006), the larger the shape parameter m, the more homogeneous the material. When α is equal to 1, namely

$$ {p}_1=p\left({\sigma}_{cell}<\sigma \right)=1- \exp \left[-{\left(\frac{\sigma }{\sigma_0}\right)}^m\right]. $$
(2)

By substituting Eq. (2) into Eq. (1), the following expression can be obtained:

$$ {p}_{\alpha }=1-{\left(1-{p}_1\right)}^{\alpha^m}. $$
(3)

It is worth noting that the broken cells will inevitably affect neighboring unbroken cells owing to the stress transfer. To evaluate the influence of the broken cells on their neighboring unbroken cells, a conditional probability p m,n is introduced, which can be expressed as follows:

$$ {p}_{m,n}=\frac{p\left( n\sigma <{\sigma}_{cell}< m\sigma \right)}{p\left({\sigma}_{cell}> n\sigma \right)}=\frac{p_m-{p}_n}{1-{p}_n}, $$
(4)

where p m and p n can be calculated using Eq. (3). Essentially, the conditional probability p m,n is a probability that an unbroken cell with local stress nσ will fail when subjected to an additional stress (m − n)σ from a broken cell. At that moment, the overall local stress of the unbroken cell will increase to mσ. The conditional probabilities and overall broken probabilities of the five possible states are listed in columns C and D of Table 1, respectively.

Furthermore, some assumptions were made in this paper, as suggested in Smalley et al. (1985), namely:

  1. (1)

    A r + 1 -th order block will not be regarded as a broken state unless all the r -th order blocks that compose this r + 1 -th order block are broken.

  2. (2)

    The stress from a r -th order block, which belongs to a r + 1 -th order block, will be transferred uniformly to other r -th order blocks that belong to the same r + 1 -th order block.

Taking the first-order block with four cells as an example, its overall failure probability p 1 (2) can be expressed as follows:

$$ {p_1}^{(2)}={p}_{{\mathrm{b}}_4{\mathrm{u}}_0}+{p}_{{\mathrm{b}}_3{\mathrm{u}}_1}+{p}_{{\mathrm{b}}_2{\mathrm{u}}_2}+{p}_{{\mathrm{b}}_1{\mathrm{u}}_3}, $$
(5)

where \( {p}_{{\mathrm{b}}_4{\mathrm{u}}_0},{p}_{{\mathrm{b}}_3{\mathrm{u}}_1},{p}_{{\mathrm{b}}_2{\mathrm{u}}_2} \), and \( {p}_{{\mathrm{b}}_1{\mathrm{u}}_3} \) are the overall failure probabilities of the different states of a cell, which can be obtained as shown in column D of Table 1.

Expanding Eq. (5) gives the following:

$$ \begin{array}{c}{p_1}^{(2)}={p}_1^4+{C}_4^3{p}_1^3\left(1-{p}_1\right){p}_{4,1}+{C}_4^2{p}_1^2{\left(1-{p}_1\right)}^2\left[{p}_{2,1}^2+{C}_2^1{p}_{2,1}\left(1-{p}_{2,1}\right){p}_{4,2}\right]\\ {}+{C}_4^1{p}_1{\left(1-{p}_1\right)}^3\left\{\begin{array}{c}{p}_{4/3,1}^3+{C}_3^2{p}_{4/3,1}^2\left(1-{p}_{4/3,1}\right){p}_{4,4/3}+\\ {}{C}_3^1{p}_{4/3,1}{\left(1-{p}_{4/3,1}\right)}^2\left[{p}_{2,4/3}^2+{C}_2^1{p}_{2,4/3}\left(1-{p}_{2,4/3}\right){p}_{4,2}\right]\end{array}\right\}\end{array}. $$
(6)

For higher-order blocks, Eq. (6) can also be extended to an iteration equation between p 1 (n + 1) and p 1 (n), where n is the order of the block. It can be expressed in the following form:

$$ \begin{array}{c}{p_1}^{\left(n+1\right)}={\left({p}_1^{(n)}\right)}^4+{C}_4^3{\left({p}_1^{(n)}\right)}^3\left(1-{p}_1^{(n)}\right){p_{4,1}}^{(n)}\\ {}+{C}_4^2{\left({p}_1^{(n)}\right)}^2{\left(1-{p}_1^{(n)}\right)}^2\left[{\left({p_{2,1}}^{(n)}\right)}^2+{C}_2^1{p_{2,1}}^{(n)}\left(1-{p_{2,1}}^{(n)}\right){p_{4,2}}^{(n)}\right]\\ {}+{C}_4^1{p}_1^{(n)}{\left(1-{p}_1^{(n)}\right)}^3\left\{\begin{array}{c}{\left({p_{4/3,1}}^{(n)}\right)}^3+{C}_3^2{\left({p_{4/3,1}}^{(n)}\right)}^2\left(1-{p_{4/3,1}}^{(n)}\right){p_{4,4/3}}^{(n)}\\ {}+{C}_3^1{p_{4/3,1}}^{(n)}{\left(1-{p_{4/3,1}}^{(n)}\right)}^2\left[{\left({p_{2,4/3}}^{(n)}\right)}^2+{C}_2^1{p_{2,4/3}}^{(n)}\left(1-{p_{2,4/3}}^{(n)}\right){p_{4,2}}^{(n)}\right]\end{array}\right\}.\end{array} $$
(7)

Based on Eq. (7), a iteration dependent relationship between p 1 (n + 1) and p 1 (n) is obtained, which is shown in Fig. 3. It can be seen that there are three points where p 1 (n + 1) is equal to p 1 (n) for each shape parameter m. Among the three points, 0 and 1 mean completely stable and completely unstable states, respectively, while the critical point p* is a phase transition point, i.e., unstable fixed points, where the state changes from stable to unstable. It appears that the critical point p* is equivalent to the concept of the stress threshold σ cd .

Fig. 3
figure 3

Relationship between P n+1 and P n and the illustration of critical point p* for the two-dimensional RG model

Full size image

Theoretical relationship between σ cd and σ ucs

The broken probability of a cell can also be written as (Qin et al. 2006)follows:

$$ p=1- \exp \left[-{\left(\frac{\varepsilon }{\varepsilon_0}\right)}^m\right], $$
(8)

where ε 0 is a reference strain of the cell.

Then, by substituting p* into Eq. (8),

$$ \frac{\varepsilon_{cd}}{\varepsilon_0}={\left[- \ln \left(1-{p}^{\ast}\right)\right]}^{\frac{1}{m}}, $$
(9)

where ε cd is the strain of the rock sample at σ cd .

Furthermore, numerous studies have been performed to investigate the mechanical responses of rock samples (Chen et al. 2006; Li et al. 2012). Based on the statistics damage theory and Hooke’s law, Chen et al. (2006) derived a constitutive formula as follows:

$$ \sigma = E\varepsilon {e}^{-{\left(\frac{\varepsilon }{\varepsilon_0}\right)}^m}, $$
(10)

which could be used to describe the stress–strain curves of uniaxial compression tests.

It is well known that the first order derivative of Eq. (10) is equal to zero at the peak strength, i.e.

$$ \frac{\mathit{\partial \sigma }}{\mathit{\partial \varepsilon }}=E{e}^{-{\left(\frac{\varepsilon }{\varepsilon_0}\right)}^m}\left[1-m{\left(\varepsilon /{\varepsilon}_0\right)}^m\right]=0. $$
(11)

Rearranging Eq. (11) gives

$$ \frac{\varepsilon_{ucs}}{\varepsilon_0}={\left(\frac{1}{m}\right)}^{m^{-1}}, $$
(12)

where ε ucs is the strain of the rock sample at the peak strength.

Then, calculating the ratio of Eq. (9) and Eq. (12) gives

$$ \frac{\varepsilon_{ucs}}{\varepsilon_{cd}}={\left[-m \ln \left(1-{p}^{\ast}\right)\right]}^{-\left(\frac{1}{m}\right)}. $$
(13)

Substitution of Eq. (9) into Eq. (10) yields

$$ {\sigma}_{cd}=E{\varepsilon}_{cd}\left(1-{p}^{\ast}\right). $$
(14)

Substitution of Eq. (12) into Eq. (10) yields

$$ {\sigma}_{ucs}=E{\varepsilon}_{ucs}{e}^{-\left(1 / m\right)}. $$
(15)

The ratio of Eq. (14) to Eq. (15) is

$$ \frac{\sigma_{cd}}{\sigma_{ucs}}=\frac{\varepsilon_{cd}}{\varepsilon_{ucs}}\left(1-{p}^{\ast}\right){e}^{\frac{1}{m}}. $$
(16)

Then, substituting Eq. (13) into Eq. (16) gives

$$ \frac{\sigma_{cd}}{\sigma_{ucs}}={\left[-m \ln \left(1-{p}^{\ast}\right)\right]}^{\frac{1}{m}}\left(1-{p}^{\ast}\right){e}^{\frac{1}{m}}. $$
(17)

Thus, the theoretical quantitative relationship between the crack damage stress threshold and the peak strength is eventually established. It is found that p* and the ratio of σ cd /σ ucs gradually decreases as the shape parameter m increases and the ratio of σ cd /σ ucs gradually tends towards a constant horizontal asymptote that is approximately 0.82 (see Table 2).

Table 2 Chart of theoretical solution based on two-dimensional RG method
Full size table

Experimental findings and discussion

Experimental findings

Many previous studies have investigated the stress threshold σ cd or ratio of σ cd /σ ucs for different rock types, such as igneous rocks [involving granite (Cai et al. 2004; Chang and Lee 2004; Diederichs et al. 2004; Eberhardt et al. 1997, 1998, 1999; Hidalgo and Nordlund 2013; Liang et al. 2012; Lin et al. 2009; Takarli et al. 2008), gabbro (Hidalgo and Nordlund 2013), diabase (Hidalgo and Nordlund 2013), diorite (Andersson et al. 2009; Chen et al. 2012; Hidalgo and Nordlund 2013), and norite (Hidalgo and Nordlund 2013)], metamorphic rocks [involving marble (Chang and Lee 2004; Huang et al. 2012), quartzite (Cai et al. 2004; Hidalgo and Nordlund 2013), and gneiss (Hidalgo and Nordlund 2013)], and sedimentary rocks [involving sandstone (Cai et al. 2004; Gatelier et al. 2002; Jiang et al. 2005; Xu et al. 2012), limestone (Eslami et al. 2012; Hidalgo and Nordlund 2013; Palchik and Hatzor 2002), dolomite (Cai et al. 2004; Hatzor et al. 1997; Palchik and Hatzor 2002), coal (Ranjith et al. 2010), clay shale (Amann et al. 2011), and rock salt (Liang et al. 2011)]. The data of σ cd or σ cd /σ ucs in the above literature have been given directly in the form of tables or pictures, thus greatly aiding our study. Recently, Xue et al. (2013) analyzed 251 sets of test data on different rock types and found that the average values of σ cd /σ ucs for the low-porosity igneous, metamorphic, and sedimentary rocks were ~0.78 (±0.09), ~0.85 (±0.09), and ~0.78 (±0.11), respectively (see Fig. 4). Meanwhile, the corresponding overall average of σ cd /σ ucs from the different rock types is equal to ~0.80 (±0.10), which appears approximately consistent with the theoretical solution.

Fig. 4
figure 4

Values of σ cd /σ ucs for different rock types: a igneous rock, b metamorphic rock, and c sedimentary rock (modified after Xue et al. (2013))

Full size image

Discussion

Both the experimental results for low-porosity rock samples and the theoretical solutions (σ cd /σ ucs ) are shown in Fig. 5. It is obvious that the distribution range of experimental results is wider than that of the RG solutions, which may be attributed to the following reasons:

Fig. 5
figure 5

Comparison between the theoretical solutions of σ cd /σ ucs and the experimental results of σ cd /σ ucs for low-porosity rocks. The seven solid triangles indicate the theoretical solutions of σ cd /σ ucs based on values of the shape parameter m from 1 to 7. The horizontal solid line is the overall average of the experimental results of σ cd /σ ucs , excluding data with values less than 0.6, as shown in Fig. 4

Full size image

Firstly, it has been found that the theoretical solution of σ cd /σ ucs varies with shape parameter m, which is used to evaluate the discreteness of the material’s strength. However, Fig. 5 illustrates only the theoretical solutions based on values of parameter m from 1 to 7, and it is possible that the actual values of parameter m for the rock samples were outside this range. Therefore, it is necessary to conduct further studies to determine the actual shape parameter m of a rock sample in order that we can perform a strict comparison between the experimental results and theoretical solutions based on the same m value. This work is ongoing, in which the estimation of the shape parameter m relies on the method developed by Katz and Reches (2002).

Secondly, during the derivation process of the theoretical solution, it was assumed that the stress from broken blocks was transferred equally to the adjacent unbroken blocks, which may be an oversimplification of the real failure process. It may be more realistic that the stress be assigned according to the distance between the broken and unbroken blocks. In addition, other assumptions might also affect the theoretical solutions, for example, the choice of a two-dimensional RG model rather than a three-dimensional model. Therefore, we will attempt to conduct a more intensive theoretical study in future work.

In view of the above, Eq. (17) might be only an approximate theoretical relationship between σ cd and σ ucs . Nevertheless, it could be speculated that the ratio of σ cd /σ ucs might be an intrinsic property of low-porosity rocks, which could be considered as a reliable indicator for predicting the failure of laboratory-scale rock samples.

Conclusions

The present study investigated the relationship between the crack damage stress threshold and uniaxial compressive strength, based on experimental results and theoretical analysis. The following conclusions can be drawn:

  1. (a)

    Based on uniaxial compression tests, it is determined that the overall average and standard deviation of σ cd /σ ucs of low-porosity rock samples is ~0.80 (±0.10).

  2. (b)

    Based on the two-dimensional RG method, we eventually established the theoretical solution of σ cd /σ ucs . It was found that as the shape parameter m increases, the ratio σ cd /σ ucs gradually decreases and tends towards a horizontal asymptote that is almost consistent with the overall average of experiment results, i.e., ~0.80.

  3. (c)

    Both the experimental results and theoretical solutions imply that there exists a certain relationship between σ cd and σ ucs . The normalized quantity, σ cd /σ ucs , might be an intrinsic property of low-porosity rocks, which could be regarded as a potential indicator for predicting the failure of laboratory-scale rock samples.