Introduction

Earthquake is one of the most destroying natural disasters (Chattopadhyay and Chattopadhyay 2009; Shahri et al. 2011; Rafi et al. 2013; Deif et al. 2013). The seismic waves that spread out from the earthquake source to the entire Earth are usually measured at the ground surface by a seismometer which consists of three translational components. Translational components involve two horizontal in x and y axis and one vertical in z axis in Cartesian coordinate. However, a complete representation of the ground motion induced by earthquakes consists not only of those three components of translational motion but also three components of rotational motion plus six components of strain. Although theoretical seismologists have pointed out the potential benefits of measurements of rotational ground motion, they were not made until quite recently. Rotational movement was seen in 1958 for the first time in tombstones, big rocks, and upper parts of chimney attributed to earth motion rotational components (Gordon et al. 1970). Earth motion rotational components are not paid attention for two reasons: first, rotational components have small range, and seismographs were not able to register. Second, rotational motions effect were considered negligible (Bouchon and Aki 1982). Newmark (1969) was perhaps the first to establish a relationship between the torsional and translational components of a ground motion based on constant velocity of wave propagation assumption. Ashtiany and Singh (1986), with an idea close to Newmark (1969), tried to produce rotational components. Based on Newmark (1969) relations, other researchers such as Ghayamghamian et al. (2009) using data collected from the Chiba dense array generated the torsional ground motion and analyzed several building models for different structural characteristics subjected to six correlated components of earthquake. Gomberg (1997) estimated the rotational components induced in the Northridge, California earthquake using classical relationships and translational records. Relationships were derived by only considering S waves and estimating the apparent wave velocity. The apparent wave velocity was calculated using the arrival of the S wave and was used to scale the velocity seismogram. Nouri et al. (2010) made a comparison between different methods of torsional ground motion evaluation.

Rotational components of the ground motion are not usually considered in seismic analysis and design of structures. Rocking ground motion is expected to influence the response of tall and slender structures and base-isolated structures (Wolf et al. 1983; Ashtiany and Singh 1986; Zembaty and Boffi 1994; Politopoulos 2010; Kalanisarokolayi et al. 2008, 2012). The effects of torsional ground motion are expected to be greatest in near-symmetric buildings (De La Llera and Chopra 1994). Hart et al. (1975) attributed the torsional response of most high-rise buildings during the 1971 San Fernando earthquake. Bycroft (1980) associated the differential longitudinal motion that he described as responsible for the collapse of bridges during the 1971 San Fernando earthquake and the 1978 Miyagi-Ken-Oki earthquake with rotational components of ground motion. Politopoulos (2010) identified the excitation of the rocking mode in a base-isolated building due to rocking excitations. Both studies were based on simplified assumptions including horizontally propagating waves in bedrock and vertically propagating shear waves.

Several instruments have been used to measure the rotational excitation. Some of these are a simple extension of the traditional inertial seismometer and are cost effective, whereas others invoke ideas from a completely different field and are expensive. Graizer (2009) reviewed the classical methods of measuring rotation. Using a GyroChip rotational sensor, Nigbor (1994) succeeded in recording rotational ground motions at a distance of 1 km from a large explosion at the Nevada Test Site (NTS). Using similar instruments, Takeo (1998, 2009) recorded rotational ground motions excited by nearby earthquakes offshore of the Izu Peninsula of Japan during an earthquake swarm in 1997 and in 1998, respectively. However, after Nigbor moved his equipment to a recording site in Borrego Mountain, Southern California, he did not record significant rotational ground motions, even with more than a decade of observations. The first application of a ring laser gyroscope as a rotational sensor applied in the field of seismology was reported by Stedman et al. (1995). Fully consistent rotational motions were recorded by a ring laser gyro installed at the fundamental station in Wettzell, Germany (Igel et al. 2005).

Lee and Liang (2008) have used Lee and Trifunac’s (1985, 1987) method to develop theories and algorithms for generating rotational motion from the corresponding available translational motions. Some researchers (Li et al. 2004) proposed an improved approach to obtain the rotational components of a seismic ground motion which included the effect of the relative contributions of the P, SV, and SH waves to calculate time histories of rotational components. In the past decade, rotational motions generated by large earthquakes in the far field have been successfully measured at sites in Germany, New Zealand, and Southern California (Igel 2007), and observations agree well with classical elasticity theory (Suryanto et al. 2006a, b). However, recent rotational measurements in the near field of earthquakes in Japan (Takeo 1998, 2009) and in Taiwan (Huang 2003; Liu et al. 2009) indicate that rotational ground motion are 10 to 100 times larger than expected from the classical theory.

Recently, site effects became an attractive topic for engineers (Abbaszadeh Shahri et al. 2011; Choobbasti et al. 2014; Janalizadeh et al. 2013; Tavakoli et al. 2014). Previous studies demonstrated that soft deposits fortify the ground’s motion; therefore, the resulting devastations on these types of layers are more severe than the stiff layers (Rezaei et al. 2013; Kutanaei et al. 2011). It is proved that amplification phenomena occur frequently on the soft deposits (MirMohammad Hosseini and Asadollahi Pajouh 2012; Kutanaei et al. 2012). The main reason is the soft deposits include trapping of seismic waves which leads to difference impedance in the lower deposits or bedrock. Effects of alluvial deposits near the ground surface which amplify strong ground motions are called "site effects." Site amplification effects reduce with the increase of geometrical age. Also, an increase of bedrock depth has a considerable effect on site amplification effects (El-Hussain et al. 2013).

Previous studies show that rotational response by earth rotation is an important index of earthquake motion. In this paper, rotational components of ground motion are obtained using both classical elasticity and elastic wave propagation theories based on SV and SH wave incidence of the earthquake. The rotational component of production technique is described, and the influences of soil type and distance from the fault on the rotational component are investigated.

Earth motion rotational component production theoretical method

This serves as an input for theoretical and numerical methods with engineering application such as HAM and HPM (Soleimani et al. 2011, 2012; Taeibi-Rahni et al. 2011) and also several numerical methods with broad engineering applications such as finite difference and RBF-DQ methods (Jalaal et al. 2011; Bararnia et al. 2012; Ganji et al. 2009). Three main approaches have been developed to incorporate rotational motions in engineering applications: first, using analytical form; second, using components of translation motion; and third, direct registration of rotational components by optical dominant technology.

Analytical method

This method does not involve model and soil local feature that can be known as a defect of this method, but depending on the source behavior, it can be used in the movement of the places close to the fault. Bouchon and Aki (1982) simulated a fallible slope with the relative displacement of 1 m analytically and calculated the strains of different points and the obtained rotational components of ground motion in various distances from the causative fault. The results showed a considerable decrease in peak rotation by increasing distance from fault. Castellani and Boffi (1989) confirmed the function of this method in the wave modeling with low frequency.

Rotational component production method from translational component

Considering theoretical relations, two general methods have been suggested to produce rotational component by translational components: (1) the extraction of rotational components through the equations of the classical elastic theory between translational motion in the board and rotation upstanding the board and (2) the extraction of rotational component based on the simultaneous use from the equations of the classical elastic and wave distribution theories. The first method was introduced by Newmark (1969), and its influence on the responses of the structure was investigated. Consequently, three methods were introduced to estimate rotational components based on translational components involving time derivation, finite difference, and geodetics.

Time derivation

Ashtiany and Singh (1986) achieved rotational components of ground motion on the basis of translational components. They stated that earthquake can produce both transverse and longitudinal waves. Longitudinal waves have no role in torsion production, but transverse waves can cause torsions in the structure using the mentioned method. They tried to produce rotational component translational accelerate register, in a point on ground surface.

$$ {\varphi}_{gkk}(t)=\frac{1}{c_j}.\frac{\partial }{\partial t}\left[{\ddot{U}}_{jj}(t)-{\ddot{U}}_{ii}(t)\right] $$
(1)

where \( {\ddot{U}}_{jj}(t) \) and \( {\ddot{U}}_{ii}(t) \) are translational components of the accelerations in ii and jj directions, c j is wave propagation velocity in jj direction, and φ gkk (t) is rotation round vertical direction on ii and jj directions.

Finite difference method

A dense array of seismic accelerometers provides a unique opportunity to characterize the spatial variability of ground motion in a small geographic region. In finite difference method, the average translational components between two points (φ gz (t)) are calculated based on their translational components.

$$ {\varphi}_{gz}(t)=\frac{1}{2}\left[\frac{{\ddot{U}}_2(t)-{\ddot{U}}_1(t)}{\varDelta y}-\frac{{\ddot{\theta}}_2(t)-{\ddot{\theta}}_1(t)}{\varDelta x}\right] $$
(2)

where \( {\ddot{U}}_1(t),{\ddot{U}}_2(t),{\ddot{\theta}}_1(t) \) and \( {\ddot{\theta}}_2(t) \) are translational acceleration at points 1 and 2 along y and x directions, respectively. Δx and Δy are the distance between two points, respectively. Chopra and Lallera (1994) investigated the effects of accidental torsion due to uncertainty in the in-plane stiffness of lateral load-resisting elements in one-story systems and rotational motion. They generate torsional components by measuring translational acceleration in the two points of a structure foundation. This method was also used by Hang (2003) to estimate translational components.

Geodetic method

The geodetic method (GM) (Spudich et al. 1995) can be considered as an extension of the work of Niazi (1986). The stations were distributed in a three-dimensional space, and the relative displacement between every two stations (with a common station called the reference station) was expressed as the displacement gradient matrix, with the assumption of being constant and the region of the array. After the stationary hypothesis and the identification of the strong-motion phase for every two stations, the spatial variability was then investigated by defining a normalizing parameter. This parameter was proportional to the separation distance and the ratio of the standard deviation of the torsional motion to the average standard deviation of the horizontal motions used in the calculation of torsional motion.

Direct registration of rotational components

Several instruments have been used to measure the rotational excitation such as laser gyroscope, tilt meter, solid state sensor, and geosensor. Graizer (2009) reviewed the classical method rotation measurement. Nigbor (1994) measured the rotational components of ground motion near a large explosion directly using commercial rotational velocity sensors in the aerospace field. This micro-electromechanical gyroscopic sensor was later deployed in the Borrego Valley in Southern California but did not record any earthquake rotational ground motion at the noise level of the sensor. Takeo (1998) suggested similar issues of sensor resolution to record the near-field rotational motion caused by small earthquakes using a similar aerospace sensor. Ring laser rotation sensors are the state-of-the-art technology for measuring rotational excitation. These sensors work on the basis of principles of optical interferometry. Ring laser gyroscopes require sophisticated facilities; their operations are complex and are not compatible with large-scale permanent networks or mobile arrays (Stedman 1995).

Generation rotational components of earthquake

Rotational components due to body waves

Seismic ground motions are a direct result of plane harmonic waves arriving at the site close to the earthquake source. It is assumed that the direction of propagation of the waves lies in the vertical (x, z) plane. As the wave passes, it induces particle displacement in the perpendicular and parallel planes to the direction of propagation. The particle displacements in the plane which are perpendicular to the direction of propagation are decomposed into in-plane and out-of-plane components due to SV and SH waves, respectively. The parameters, A S and A 0 depict amplitudes of in-plane and out-of-plane components, respectively. Incidence and reflection of the body waves will originate three rotational components of the ground motion at the free surface: φ gz , φ gx , and φ gy . The component φ gz , referred to as torsional component, is related to rotation about z axis, and the components φ gx and φ gy , referred to as the rocking components, are related to rotation about x axis and y axis, respectively.

Incidence SV wave

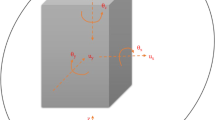
The coordinate system (x, z) and the incident and reflected rays associated with plane SV wave, reflecting off the free boundary of the elastic homogeneous and isotropic half space (Z ≤ 0), are shown in Fig. 1a. Alongside preserving generality, it is assumed here that the incident and reflected rays are in the plane of Y = 0. Amplitude of particle motion, u and w, along with the ray direction are presented by A S, A SS, and A SP. It is assumed that the ray direction demonstrated positive displacement amplitudes. A S, A SS, and A SP corresponded to incident SV wave, reflected SV wave, and reflected P wave, respectively. Considering this kind of excitation and coordination, the only definable non-zero components of motion located at Y = 0 planes are:

Fig. 1
figure 1

Propagation of a incident SV wave and b incident SH wave

Full size image

The particles of displacement u, w in the x, z directions, respectively, are given by:

$$ u=\frac{\partial {\varphi}_{\mathrm{sp}}}{\partial x}+\frac{\partial \left({\psi}_{\mathrm{SV}}+{\psi}_{\mathrm{SS}}\right)}{\partial z} $$
(3)
$$ u=\frac{\partial {\varphi}_{\mathrm{sp}}}{\partial z}+\frac{\partial \left({\psi}_{\mathrm{SV}}+{\psi}_{\mathrm{SS}}\right)}{\partial x} $$
(4)

The relation between the rotational and translational motions in a point base on the classical elasticity theory can be expressed by:

$$ {\varphi}_{gy}=\frac{1}{2}\left(\frac{\partial w}{\partial x}-\frac{\partial u}{\partial z}\right) $$
(5)

In the above equations for frequency of harmonic waves, i.e., ω, the potential functions are as follows:

$$ {\psi}_{\mathrm{S}\mathrm{V}}={A}_{\mathrm{S}} \exp i\omega \left(\frac{ \sin {\theta}_0}{\beta }x-\frac{ \sin {\theta}_0}{\beta }z-t\right) $$
(6)
$$ {\varphi}_{\mathrm{SP}}={A}_{\mathrm{SP}} \exp i\omega \left(\frac{ \sin {\theta}_1}{\alpha }x-\frac{ \sin {\theta}_1}{\alpha }z-t\right) $$
(7)
$$ {\psi}_{\mathrm{SS}}={A}_{\mathrm{SS}} \exp i\omega \left(\frac{ \sin {\theta}_0}{\beta }x-\frac{ \sin {\theta}_0}{\beta }z-t\right) $$
(8)

where α and β are the propagation velocities of P and S waves, respectively. They can be expressed as follows (Datta 2010):

$$ \alpha ={\left[\frac{E\left(1-\nu \right)}{\rho \left(1+\nu \right)\left(1-2\nu \right)}\right]}^{\frac{1}{2}} $$
(9)
$$ \beta ={\left[\frac{E}{2\rho \left(1+\nu \right)}\right]}^{\frac{1}{2}} $$
(10)

where E, ρ, and ν are the Young’s modulus, the mass density, and the Poisson ratio of the soil mass, respectively. The value of coefficients, α and β, depends on the soil properties; at the surface of the earth, their values vary in the range of 5 to 7 km s−1 and 3 to 4 km s−1, respectively (Datta 2010). According to Fig. 1, the angle of incidence (θ 0) and the angle of reflection of SV waves (θ 2) are equal. The angle of reflected P wave is denoted as θ 1. By imposing the free shear stress condition at the ground surface:

$$ {\left.{\tau}_{xz}\right|}_{z=0}={\left.\frac{\partial w}{\partial x}+\frac{\partial w}{\partial z}\right|}_{z=0}=0 $$
(11)

The rocking component can be obtained from Eqs. 3 to 11 as follows:

$$ \begin{array}{l}{\varphi}_{gy}=\frac{\partial w}{\partial x}=\frac{\partial^2{\varphi}_{\mathrm{SP}}}{\partial z\partial x}-\frac{\partial^2\left({\psi}_{\mathrm{SV}}+{\psi}_{\mathrm{SS}}\right)}{\partial {x}^2}\\ {}={\left( i\omega \right)}^2\frac{ \cos {\theta}_1}{\alpha }.\frac{ \sin {\theta}_1}{\alpha }{\varphi}_{\mathrm{SP}}-\left[\left( i\omega \frac{ \sin {\theta}_0}{\beta}\right){\psi}_{\mathrm{SV}}+{\left( i\omega \frac{ \sin {\theta}_0}{\beta}\right)}^2{\psi}_{\mathrm{SS}}\right]\end{array} $$
(12)

According to the Snell law, sin θ 0/β = sin θ 1/α, Eq. (13) can be obtained:

$$ {\varphi}_{gy}=\frac{ i\omega}{C_x}={e}^{\frac{\pi }{2}i}\left(\frac{\omega }{C_x}{R}_w{e}^{i{\theta}_w}\right)=\left(\frac{\omega }{C_x}{R}_w\right)\left({e}^{\left(\frac{\pi }{2}+{\theta}_w\right)i}\right) $$
(13)

In which C x  = β/sin θ 0, R w , and θ W are translational component and its phase. These equations can also be applied for the other rocking component φ gx .

Incidence SH waves

According to Fig. 1b, there is no mode conversion in the case of incident SH wave; hence, there is only one reflected SH wave with θ 2 = θ 0 and A 2 = A 0. The potential functions of incident and reflected waves are as follows:

$$ {V}_{\mathrm{SH}}={A}_0 \exp i\omega \left(\frac{ \sin {\theta}_0}{\beta }x-\frac{ \cos {\theta}_0}{\beta }z-t\right) $$
(14)
$$ {V}_{\mathrm{S}{\mathrm{H}}^{\prime }}={A}_1 \exp i\omega \left(\frac{ \sin {\theta}_0}{\beta }x-\frac{ \cos {\theta}_0}{\beta }z-t\right) $$
(15)

Displacement field v, which is caused by the incident and reflected waves in y direction, is as follows:

$$ v=2{V}_{\mathrm{SH}}=2{A}_0 \exp i\omega \left(\frac{ \sin {\theta}_0}{\beta }x-t\right) $$
(16)

Since u does not depend on the out-of-plane coordinate, the consideration of Eqs. (13)–(16) leads to the torsional component, φ gz :

$$ \begin{array}{l}{\varphi}_{gz}=\frac{1}{2}\left(\frac{-\partial u}{\partial y}-\frac{\partial v}{\partial x}\right)=\frac{1}{2}{\left.\frac{\partial v}{\partial x}\right|}_{Z=0}=\frac{\partial {V}_{\mathrm{SH}}}{\partial x}= i\omega \frac{ \sin {\theta}_0}{\beta}\frac{v}{2}=\frac{ i\omega}{2{C}_x}v\\ {}\Rightarrow {\varphi}_{gz}={e}^{\frac{\pi }{2}i}\left(\frac{\omega }{2{C}_x}{R}_v{e}^{i{\theta}_v}\right)=\left(\frac{\omega }{2{C}_x}{R}_v\right)\left({e}^{\left(\frac{\pi }{2}+{\theta}_v\right)i}\right)\end{array} $$
(17)

In which C x  = β/sin θ 0, R v , and θ v are translational component and its phase. It is assumed that the translational components u, v, and w of the ground motion at the free surface are available through measurements. Equations (13) and (17) could be used to define the rocking and torsional components of ground motion, respectively. These equations show that the amplitude of rotational components is related to translational component amplitude, (R w . ω/C x ) or (R v . ω/2C x ), and their phase difference is π/2. However, this is not feasible with the state-of-the-art seismology yet. Therefore, in order to apply these equations to define φ gy and φ gz , the value of incident angle θ 0 should be identified. How to determine unknown parameters is the subject of the following development.

Incidence angle of SV and SH waves

A modification of a developed approach by Li et al. (2004) was used to calculate the angle of incident waves. Using this approach while introducing (x = sin θ 0) as well as considering Snell’s law, Eqs. (16) and (17) were employed to obtain the angle of incident SV and SH waves.

$$ G=\frac{2x\sqrt{1-{K}^2{x}^2}}{K\left(1-2{x}^2\right)},\kern0.96em {\theta}_0<{\theta}_c $$
(18)
$$ G=-\frac{2x\sqrt{1-{K}^2{x}^2}}{ iK\left(1-2{x}^2\right)},\kern0.96em {\theta}_0>{\theta}_c $$
(19)

where \( G= \tan \overline{e}=w/u \) and \( G= \tan \overline{e}=w/v \) are related to rocking component in x − z and y − z plane due to SV waves, respectively; \( G= \tan \overline{e}=v/u \) is related to torsional component in x − y plane due to SH waves; K = α/β and θ = arcsin(α/β) are the incident critical angle.

Result and discussion

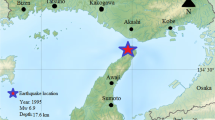
In this paper, 11 earthquakes are selected to study their relative rotational components. Characteristics of these 11 earthquakes are listed in Table 1.

Table 1 Characteristics of earthquakes
Full size table

The effects of soil type were considered in producing rocking and torsional acceleration components of earthquakes on the basis of transitional components using Eqs. (13) and (17); it was feasible by studying a wide range of average shear wave velocities from about 200 to 2,000 m/s in top 30 m of soil layers in three soil types A, C, and D (mostly close to E). As shown in Table 2, specifications of these soil types were determined in accordance with National Earthquake Hazards Reduction Program (NEHRP) Site Classification.

Table 2 NEHRP Site Classification, FEMA 450-1/2003 Edition
Full size table

In this research, the wave velocity is considered frequency dependent as shown in Fig. 2. For San Fernando earthquake, the time history of rocking component obtained by Lee and Liang (2008) and this research is also shown in the figure.

Fig. 2
figure 2

The ratio of ω/C x . a Frequency dependent. b Frequency independent

Full size image

For verification of improved approach in this research, our results are compared with the results of Lee and Liang (2008). In the mentioned work, the San Fernando earthquake is considered for calculation. This earthquake is recorded on February 9, 1971 at Pacoma dam station where its horizontal (S74W) and vertical components had a peak acceleration of 1,055 and 696 cm/s2, respectively. The peak values of rocking and torsional accelerations are obtained (0.3725 and −0.2480 rad/s2) by Lee and Liang (2008) and (−0.3833 and −0.2545 rad/s2) by our research, respectively. The differences between these results are about 3 % that are due to different wave velocity and empirical scaling. For the San Fernando earthquake, the time history of rocking component obtained by Lee and Liang (2008) and this research is also shown in Fig. 3.

Fig. 3
figure 3

Rocking component acceleration for San Fernando earthquake by a Lee and Liang (2008) and b in this research

Full size image

Torsional and rocking time histories for the near-fault and far-fault earthquake are shown in Figs. 4 and 5, respectively. As it can be seen in the figures, peak rotational acceleration for near-fault earthquakes is more than far-fault earthquakes. That is why, after passing distances because of reduction as a result of wave pass in its way, the intensity of the waves reduces. Attenuation relationship is usually a function of the magnitude of the earthquake and the distance from the source. Comparison of near-fault and far-fault earthquake records also indicates that near-fault ground motions often exhibit distinguishable pulse-like features in their acceleration time histories. Pulses which occur at the beginning of the record indicate a significant energy release in a short time. The pulse contents in acceleration time histories have also been found important for structural responses. This feature is one of the most important characteristics of near-fault ground motions. The figures also indicate that the peak rocking acceleration is more than the peak torsional acceleration.

Fig. 4
figure 4

Time history of rocking and torsional components for near-fault earthquake

Full size image
Fig. 5
figure 5

Time history of rocking and torsional components for fare-fault earthquake

Full size image

Due to problems in measurement of rotational components, we tried to establish a specific relationship between translational, torsional, and rocking component (Ghayamghamian and Nouri 2007; Suryanto et al. 2006a, b). In this part, the relation between peak torsional acceleration (PTA) and peak rocking acceleration and peak of translational acceleration of (PGA) and also the relation between peak rocking acceleration (PRA) and peak rocking acceleration have been investigated. As can be seen in Fig. 6a, b with the increase of peak translational acceleration, the peak rocking and torsional accelerations increase. In earthquakes with low peak translational acceleration, these changes are so small. The peak values of translational and rocking accelerations increase significantly with the increase of translation acceleration. In addition, Fig. 3 shows that the relation between peak translational acceleration and peak rocking and torsional accelerations and relation between peak rocking acceleration and peak torsional acceleration is precisely linear. Correlation coefficient (R 2) close to 1 indicates that values from relations are close to available data.

Fig. 6
figure 6

a Relation between peak rocking acceleration and peak torsional acceleration. b Relation between peak torsional acceleration and peak torsional acceleration. c Relation between peak rocking acceleration and peak torsional acceleration

Full size image
$$ \mathrm{PRA}=0.0020\kern0.5em \mathrm{PGA}+0.00237 $$
(20)
$$ \mathrm{PTA}=0.000142\kern0.5em \mathrm{PGA}+0.000094 $$
(21)
$$ \mathrm{PRA}=1.41884\kern0.5em \mathrm{PTA}+0.00137 $$
(22)

Equation 22 shows that the peak rocking acceleration is higher than the peak torsional acceleration. In this study, the ratio between the peak rocking acceleration and the peak torsional acceleration is 1.41884.

Figure 7 shows the effect of the near-fault and far-fault earthquakes and soil shear wave velocity on the normalized response spectra of the rocking component. By comparing the spectra of the near and far field of faulting, it is observed that the values of the normalized response spectra for almost every type of soil have a maximum value greater than its corresponding far field. According to the results of the inelastic design spectrum, in near field, rocking components for periods of less than 1 s rather than periods over 1 s and in far field for periods of less than 2 s compared to periods greater than 2 s contain considerable quantities. It shows that for far-field earthquakes, low period structures are significantly influenced by rocking components, and for near-field earthquakes, long period structures are significantly influenced by rocking components. Generally, the values of normalized response spectra reduce by an increase in shear wave velocity. But if site fundamental period is equal to rocking component period, amplification takes place and the values of the normalized response spectra for soft sites have higher amounts than hard sites.

Fig. 7
figure 7

Effect of the near-fault and far-fault earthquakes and soil shear wave velocity on the normalized response spectra of the rocking component. a Far-fault. b Near-fault

Full size image

Figure 8 shows the effect of the near-fault and far-fault earthquakes and soil shear wave velocity on the normalized response spectra of the torsional component. As can be seen in the figure, the values of torsional normalized response spectra in near field for periods of less than 0.6 s compared to periods greater than 0.7 s and in far field for periods of less than 1.5 s rather than periods longer than 1.5 s are far more. This indicates that torsional components are more important at low periods.

Fig. 8
figure 8

Effect of the near-fault and far-fault earthquakes and soil shear wave velocity on the normalized response spectra of the torsional component. a Far-fault. b Near-fault

Full size image

By comparing Figs. 7 and 8, it is observed that the values of the normalized response spectra at low periods (less than 1 s, the period of the conventional buildings) have higher amounts than at high periods. This is indicates that rotational components are more important at low periods. This behavior can be explained with the fact that the rotational components have a direct relation with derivation of one higher order of translational components, so rocking and torsional components have a more frequency content in comparison with similar horizontal components in high frequencies, and this difference in frequency content causes rotational components to become more important in loading structure with low periods.

Conclusions

Rotational components can significantly affect the behavior of structures and consequently may have structural damage and failure. Due to the high cost of rotational ground motion components recorded by the equipments which have not been developed adequately, the use of transitional components of the ground motion for generation rotational components is one of the most widely used methods. In this study, the rotational component of production technique was described, and the influences of soil type and distance from the fault on the rotational component were investigated. The results are summarized as follows:

  1. 1.

    The value of the normalized response spectra for soft soil is more than stiff soil, but for far-fault earthquake, it is less than near-fault earthquake.

  2. 2.

    The rotational components showed a direct relation with a higher order derivation of translational components, therefore, more frequency content. As a consequence, the torsional components are more important at low periods.

  3. 3.

    It was that the relation between peak acceleration values of torsional and rocking components and peak acceleration value of translational component and also the relation between peak acceleration values of rocking components and peak acceleration value torsional component acceleration are linear.

  4. 4.

    When seismic waves were propagated in the stiff soils at the same conditions between two earthquake components (i.e., in equal peak ground acceleration in vertical and horizontal direction), the shear wave velocity in the stiff soil will be higher than the soft soils; hence, lower peak acceleration was achieved in the rotational components compared to propagation in the soft soil.