Introduction

The engineering properties of rock masses are controlled by the characteristics of the discontinuities (Zadhesh et al. 2013). It is a known fact that the discontinuities have significant effect on mechanical behavior of rock masses which reduce their strength (Sharifzadeh et al. 2011; Ghazvinian et al. 2012). It has wider application in the rock excavation engineering, e.g., caverns, tunnels, slope stability, dams, and rock foundations (Verma and Singh 2009; Salari-Rad et al. 2012). The most important properties of the discontinuities are orientation, extent, planarity, asperities, roughness, and strength of wall rock. Strength, deformability, and fluid flow properties of rock joints depend on the surface roughness of joints. Roughness effects on the friction angle, dilatancy, and peak shear strength were evaluated (Patton 1966; Goodman 1975). Therefore, the accurate value of roughness is important in modeling strength, deformability, and fluid flow. The roughness, represented by the joint roughness coefficient (JRC), varies from 0 (smooth) to 20 (rough). To assign a value of JRC to the joint, the roughness profile is compared with standard roughness profile. However, it is well understood that JRC determined by visual comparison is subjective and sometimes erratic (Barton and Choubey 1977).

Many researchers have thus attempted to estimate the JRC value for a surface from the profile geometry such as fractal analysis (Den Outer et al. 1995; Huang et al. 1992; Muralha 1995) or statistics (Wu and Ali 1978; Krahn and Morgenstern 1979; Reeves 1985). The JRC value was recommended by ISRM (Brown 1981), and it has been widely used in engineering practices. Over the years, some statistical parameters having correlations with JRC have been developed (Dight and Chiu 1981; Maerz et al. 1990; Myers 1962). Tse and Cruden (1979) found that among eight different statistical parameters, Z2 (Z2 is the root mean square of the tangents of the slope angles along the profile) and structure function are strongly correlated with the values of JRC. Grasselli and Egger digitized rock joint surfaces (3D measurement) using a special optical measurement system (ATS scanner). Then, based on the results from more than 50 (CNL) direct shear tests, they developed a new constitutive criterion and estimated the JRC value by back analysis (Grasselli 2001; Grasselli and Egger 2003).

Since Mandelbrot (1983) introduced fractal geometry, some studies have been conducted to characterize the rough surfaces of rock joints by employing fractal geometry (Feder 1988; Wakabayashi and Fukushige 1992). The Fractal dimension describes the degree of variation in a curve, a surface, or a volume from its topological ideal (Charkaluk et al. 1998). There have been many methods for calculating fractal dimensions, such as divider, box counting, variogram, spectral, and roughness-length (Xie et al. 1997). With this method, less engineering judgment is required in determining the surface roughness (Jang et al. 2006). Furthermore, Lee et al. (1990) found a correlation between JRC and D such that the rougher profile with the higher JRC had a larger D value. Also, Turk et al. (1987), Seidel and Haberfield (1995), and Kulatilake et al. (1997) produced a similar trend between JRC and D as given in Table 3. Odling (1994) found a correlation between JRC and the fractal characteristics such as Hurst exponent, H (related to fractal dimension, D) and amplitude, A. Also, Jang et al. (2006) represented two new equations to estimate JRC from fractal dimensions. The fractal dimensions and intercepts of slopes were determined by plotting the length (or variogram) versus the divider span (or sampling interval) in log–log scale.

Table 1 Physical and mechanical properties of intact rock specimens
Full size table

In this study, a new equation has been proposed to estimate the JRC based on modified divider method of fractal dimension. Also, the validation of new equation was performed by actual data collected from Bakhtiary Dam site in Iran.

Description of experimental study

Geology description of the Bakhtiary Dam site

The site of Bakhtiary Dam and Hydroelectric Power project is located in Lorestan Province, in the southwest of Iran, northeast of the Tang-e-Panj railway station on the Tehran–Ahwaz railway, with the following coordinates: 48° 46′ 50″ E/32° 57′ 41″ N (see Fig. 1). The bed rock consists of limestone and marly limestone that contains nodules of siliceous limestone. The limestone also contains dolomitic material. These deposits, which were sedimented between the formations of Garau (at the bottom) and Gurpi (at the top), are marked as Bangestan Group (Kazhdomi, Sarvak, Surgah, and Ilam formations) of Cretaceous age. The limestone of the Bakhtiary Dam reservoir, which is overlying Garau formation and underlying Gurpi formation, has been considered to be Sarvak formation. This limestone has also been divided into seven units. The six units, which are within the dam area, can be considered as Sarvak formation. The units Sv2 to Sv7 have outcrops in dam site, the appurtenant structures, and the powerhouse area. Sv1 has no outcrops in this area as it is completely covered by Sv2. Also, geology longitudinal profile of the left bank of the Bakhtiary Dam site is shown in Fig. 2.

Fig. 1
figure 1

Location of Bakhtiary Dam site

Full size image
Fig. 2
figure 2

Geology longitudinal profile of the left bank of Bakhtiary Dam site

Full size image

Direct shear tests on natural rock joints

Direct shear tests on core specimens were performed with the instrumented SBEL direct shear machine DR-44, where the shear loads and shear displacement were measured with a pressure gauge and dial gauge, respectively. In general, direct shear tests were performed in accordance with ISRM (1974) suggested method for the determination of shear strength. Therefore, more than 30 direct shear tests were performed on core samples at Bakhtiary Dam site. Figure 3 shows the direct shear test setup used in this study.

Fig. 3
figure 3

Laboratory direct shear test setup

Full size image

The length of samples tested varied from 6 to 15 cm. Figure 4 shows the condition of joint surfaces after shearing. Table 1 also shows the physical and mechanical properties of intact rock specimens. Shear tests under constant normal load conditions were carried out. The normal stress of 0.52 to 3.11 MPa was applied on the rock samples. Also, surface characteristics of the test specimens such as joint roughness coefficient (JRC) and joint compressive strength (JCS) were measured. Mechanical properties of joints are given in Table 2.

Fig. 4
figure 4

Surface of natural joint after the shear test

Full size image
Table 2 Mechanical properties of rock joints
Full size table

Measurement of surface roughness

The surface roughness of rock joint was measured using a profile gauge (see Fig. 5) in shear direction of the sample and with 1 cm distance along the perpendicular direction to the shear direction (see Fig. 6) was measured. Then, the surface roughness of each sample was drawn on the white paper shown in Fig. 7. The result of drawing on the paper was scanned. Then, the result of scanning was saved in (BMP, JPG, and GIF) format. The image will be given as input data to the FDM program to be discussed in detail later.

Fig. 5
figure 5

Profile gauge tool

Full size image
Fig. 6
figure 6

The method used for measurement of surface roughness of rock joint

Full size image
Fig. 7
figure 7

The roughness profile of natural rock joint

Full size image

The concept of fractal dimension

Mandelbrot introduced the concept of fractal dimension, a concept developed much earlier in mathematics or physics (Mandelbrot 1983, 1985). Also, fractal geometry may describe irregular shapes more complex than the Euclidean geometric forms such as planes, spheres, and cylinders (Kulatilake et al. 1995). It is customary in the Euclidean space, that is, a perfectly straight line is a 1-D feature; an ideal plane is a 2-D feature; an ideal sphere is a 3-D feature (Krahn and Morgenstern 1979; Charkaluk et al. 1998; Lee et al. 1990). The fractal dimension describes the degree of variation in a curve, a surface, or a volume from its topological ideal (Charkaluk et al. 1998). There have been many methods for calculating fractal dimensions such as divider method, box counting method, variogram method, spectral method, and roughness-length method (Xie et al. 1997).

Application of the modified divider method of fractal dimension to rock joint surfaces

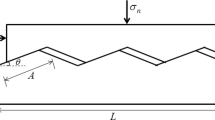
The divider methods measure the length by walking along the roughness profile with a particular divider span. In this method, the horizontal length for each divided portion is different, and it is difficult to use it in computerized work. Brown (1987) suggested a modified divider method in which it was measured by equal horizontal divider span and length in each divider span. Therefore, the modified divider method is more comfortable in processing digitized profile than the divider method. In this study, the modified divider method was used.

The number of divider spans required to cover the entire profile is counted and then multiplied by the divider span, r, to give an estimate of the profile length, L(r).

$$ L(r)= Nr $$
(1)

Where L(r), N, and r are the length of profile, the number of divider, and a divider span, respectively.

$$ N=a{r}^{-D} $$
(2)

Where a and D are a proportionality constant and the fractal dimension, respectively. By substituting Eq. 2 into Eq. 1, we obtain Eq. 3.

$$ L(r)=a{r}^{\left(1-D\right)} $$
(3)
$$ \log L(r)= \log a+\left(1-D\right) \log r $$
(4)

where log a is the intercept of the log L(r) – log r plot and the slope of the log–log plot equals 1-D, in which D is the fractal dimension. The modified divider method is shown in Fig. 8.

Fig. 8
figure 8

Modified divider method: a divider applied to profile; b log L(r) − log r plot (Jang et al. 2006)

Full size image

If the divider span is considerably shorter than feature size, then span will virtually trace the profile without bridging any peaks or valleys of the profile. Therefore, for divider spans considerably shorter than the feature size, the length L(r) will be approximately the same. On the other hand, the slope of log L(r) − log r plot will be flattened as shown in Fig. 9. When the divider span is considerably larger than the feature size, the lengths L(r) will be very close to the horizontal length of the profile and the slope of log L(r) − log r plot will be gradually flattened as shown in Fig. 9 (Kulatilake et al. 1997).

Fig. 9
figure 9

Suitable range of r for the estimation of fractal dimension with the divider method (Kulatilake et al. 1997)

Full size image

The correct slope of log L(r) − log r and, thus, the correct D can be obtained by fitting a regression line to the log L(r) − log r data in the non-flattening portion of the curve as shown in Fig. 9. This range is called crossover length in which fractal dimensions can be estimated correctly (Jang et al. 2006).

Development of the new programming code for measuring fractal dimension of roughness profiles

The surface roughness of rock joints is an important parameter influencing the mechanical and hydraulic behavior of rock masses. Several researchers have attempted to establish a suitable method for characterizing rock joint surface roughness. JRC was introduced by Barton for characterizing rock joint surface roughness. Based on various tests, Barton and Choubey (1977) developed the ten typical profiles of roughness and assigned coefficients ranging from approximately 0 to 20, from smoothest to the roughest surface, respectively, as shown in Fig. 10.

Fig. 10
figure 10

Roughness profiles and their corresponding JRC values (Barton and Choubey 1977)

Full size image

In this study, the fractal dimension of standard roughness profiles of Barton with 10 cm length was determined using the divider method. Then, a new programming code in Microsoft Visual Studio C# language was developed. The input data was the image of roughness profile with (BMP, JPG, and GIF) format, and output was the value of fractal dimension. The value of fractal dimension by FDM program was calculated using the modified divider method. Also, the quality of image for input data has been very important.

In the first step of the FDM program, the image of profile as an input data has been received. Then, based on the different values of divider spans (r), L(r) was measured. In the next step, the fractal dimension was determined from the slope log L(r) − log r plot.

A standard roughness profile (JRC range, 18–20) was chosen as an example, and then by using FDM program, the fractal dimension was obtained to be 1.015083. Figures 11 and 12 show FDM program output schema and calculation of the fractal dimension, respectively. Also, diagrammatic flowchart for the calculation of the fractal dimension by FDM program is shown in Fig. 13.

Fig. 11
figure 11

The FDM program output schema

Full size image
Fig. 12
figure 12

Plot of log(r) versus log L(r) for roughness profile (JRC range 18–20) with fractal dimension calculations

Full size image
Fig. 13
figure 13

Flowchart for calculating the fractal dimension of roughness profile

Full size image

Figure 12 shows that the quality of image was very important. Also, distribution around the regression of data to determine a value of fractal dimension was high due to the low quality of image. Selected r value had a significant effect on the value of fractal dimension so that more or less this value caused errors in the answers. Thus, in this research, r value which ranged from 0.8 to 6 mm was selected.

Results and discussion

In this study, the fractal dimension (D) value with the modified divider method was obtained. Then, by the use of statistical analysis, the new equation for the estimation of JRC was proposed.

The relationship between JRC and D

Fractal dimension (D) values with the divider method for Barton’s profiles were determined. Then, D values in this research were compared with values determined in the previous works. The results showed that the values obtained were in good agreement with the previous values. Figure 14 and Table 3 show comparison of fractal dimension D measured by different methods with the values obtained in this research.

Fig. 14
figure 14

Comparison of fractal dimension D measured by different methods with the values obtained in this research

Full size image
Table 3 Comparison of fractal dimension D measured by different methods with the values obtained in this research
Full size table

Then, non-linear regression analysis was used between the values of the fractal dimension D and JRC values. Equation 5 shows that the second-order polynomial was optimum. Also, the correlation coefficient and the standard error calculated for this equation were 0.984 and 0.941, respectively.

$$ \mathrm{JRC}=-37,580{D}^2+77,018D-39,438 $$
(5)

Where JRC and D are joint roughness coefficient and fractal dimension, respectively. The variation of the computed fractal dimension from Barton profiles with the JRC is shown in Fig. 15. Each of these points is the mean value of JRC, which was obtained from the Barton standard profiles. Based on the statistical analysis and the average values of JRC, we needed the lower and upper bound variation of JRC to improve the new equation introduced in this research. The two additional points correspond to the JRC value of 0 and 20.

Fig. 15
figure 15

Fractal dimension versus JRC range

Full size image

Application of the new equation for calculating JRC

In the first step, we collected surface roughness profile of more than 30 natural rock joints at Bakhtiary Dam site. Then, the image of roughness profile was given as input data to the FDM program. Based on the modified divider method, the FDM program measured the fractal dimensions of 30 natural rock joints.

In the next step, values of JRC were measured by the new equation in this research and Eq. 6 by Lee et al. (1990) and Eq. 7 by Wakabayashi and Fukushige (1992). Then, the values of the new equation of JRC were compared with the values of JRC calculated by Lee, Wakabayashi, and Fukushige. Figure 16 shows JRC measured by using Eqs. 5, 6, and 7.

Fig. 16
figure 16

JRC measured by using Eqs. 5, 6, and 7

Full size image
$$ \mathrm{JRC}=-0.87804+37.7844\left(\frac{D-1}{0.015}\right)-16.9304{\left(\frac{D-1}{0.015}\right)}^2 $$
(6)
$$ \mathrm{JRC}=\sqrt{\frac{D-1}{4.413\times {10}^{-5}}} $$
(7)

Figure 16 shows that the JRC measurement of 30 natural rock joints by the new equation is in good agreement with Eqs. 6 and 7.

Estimation of shear strength by Barton’s criterion using the new equation and comparison with the measured shear strength

Barton suggested the following empirical criterion for the shear strength of rock joint (Barton 1971, 1973, 1976; Barton and Bandis 1990):

$$ \tau ={\sigma}_n\kern0.5em \tan \left[\mathrm{JRC}\kern0.5em { \log}_{10}\left(\frac{\mathrm{JCS}}{\sigma_n}\right)+{\phi}_r\right] $$
(8)

Where τ, σ n , ∅ r , JCS, and JRC are shear strength, normal stress, residual friction angle, joint compressive strength, and joint roughness coefficient, respectively. For unweathered rock fractures, the residual friction angle (∅ r ) is equal to basic friction angle (∅ b ), which can be obtained from shear tests on flat unweather rock surfaces.

In this study, more than 30 direct shear tests were performed on core samples at the Bakhtiary Dam site. The range of shear strength was obtained to be from 0.29 to 2.74 MPa. Also, the shear strength was estimated by Barton's criterion using the new equation of JRC, Lee et al. (1990) and Wakabayashi and Fukushige (1992).

We employed standard descriptive measures of goodness-of-fit to evaluate the accuracy of shear strength calculated from empirical equations. Root-mean-squared error is:

$$ \begin{array}{cc}\hfill \mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n{\left({\tau}_{m_i}-{\tau}_{m_i}^{\prime}\right)}^2}}\hfill & \hfill, \kern1em i=1,2,\dots, n\hfill \end{array} $$
(9)

It represents overall error weighted by the square of deviations, where n is number of data i, \( {\tau}_{m_i} \) and \( {\tau}_{m_i}^{\prime } \) are measured value of shear strength and the estimated value of shear strength by empirical equations, respectively. Mean Absolute Relative Prediction Error (MARPE) is:

$$ \begin{array}{l}\\ {}\begin{array}{cc}\hfill \mathrm{MAPRE}=\frac{1}{n}{\displaystyle \sum_{i=1}^n\left|\frac{\tau_{m_i}-{\tau}_{m_i}^{\prime }}{\tau_{m_i}}\right|}\hfill & \hfill, \kern1em i=1,2,\dots, n\hfill \end{array}\end{array} $$
(10)

It also represents the overall error, but it is less sensitive than RMSE. We evaluated the accuracy of estimated values of shear strength with the measured values by empirical Eqs. 9 and 10. In this study, the best empirical equation of JRC was suggested, based on the above equations and the value of RMSE and MARPE equations, which was close to zero.

Then, the results of laboratory tests were compared with different empirical equations. Finally, the best estimated empirical equation was suggested using Eqs. 9 and 10. The list of the empirical equations for JRC, which was suggested to estimate the shear strength, is given in Table 4. Also, the laboratory shear strength values, compared with the values given by empirical equations, are shown in Fig. 17.

Table 4 The list of the empirical equations for JRC to estimate the shear strength at the Bakhtiary Dam site
Full size table
Fig. 17
figure 17

Comparison between shear strength estimated by Barton's criterion using JRC equations and that measured by direct shear test

Full size image

The best estimated empirical equation for JRC, with RMSE = 0.161 and MARPE = 0.089, is Eq. 5, that was developed in this study.

Figure 17 shows that the shear strength estimated by Barton's criterion using the new equation of JRC, as represented in this research, is well correlated with the measured data of shear test as compared with Eqs. 6 and 7.

Conclusions

Based on the studies carried out to investigate the rock joint roughness, it can be concluded that the joint roughness, in general, varies randomly with the direction. Also, the calculation of fractal dimension D from the roughness profiles of natural joints is difficult. Therefore, the new relationship obtained between JRC and D seems to capture well the roughness coefficient of natural rock joints.

The new programming code was developed. The input data was the image of roughness profile, and the output was the value of fractal dimension. The value of fractal dimension by FDM program was calculated using the modified divider method. The advantage of this program is simplicity and its high speed in assessing the JRC, especially for experienced engineers.

In order to verify the fractal dimension D, the fractal dimension calculated in this research was compared with previous research works such as Turk et al. (1987), Lee et al. (1990), Seidel and Haberfield (1995), Kulatilake et al. (1997), and Jang et al. (2006). It showed a very good trend compared to the above cases.

A new equation was introduced to estimate the joint roughness coefficient (JRC). For the verification of this equation, the results of previous works were compared with it. They showed a good agreement.

The shear strength of discontinuities was estimated by Barton's criterion using the new equation of JRC in this research and Lee et al. (1990) and Wakabayashi and Fukushige (1992) formulation. Then, the results were compared with those of 30 laboratory direct shear tests on natural rock joints. Finally, by using statistical analyses (RMSE and MARPE), the results showed that this new equation was well correlated with the measured data of shear tests as compared with the previous works.