Introduction

When granular material becomes saturated, the in situ stresses, which have the role of confining pressure, suddenly decrease. And then, the particle's breakage may happen and cracks may develop in the grains. Breakage of particles bonds accompanies the stress reduction (Soroush and Aghaeiaraei 2005). As a consequence of this phenomenon, rearrangement of the broken particles will happen and collapse settlement will occur (Terzaghi 1960; Feda 1995; Alonso and Oldecop 2000; Hunter 2002; Soroush and Aghaeiaraei 2005). Nevertheless, the rate of strains will decrease after flooding (Marachi et al. 1969; Marsal 1973; Alonso and Oldecop 2000; Asadzadeh and Soroush 2009; Oshtaghi and Mahinroosta 2010).

The results of a significant number of laboratory tests indicated that collapse settlement degrades the strength parameters and deformation modulus of soils (Asadzadeh and Soroush 2009; Oshtaghi and Mahinroosta 2010; Alonso 2003; Soroush and Aghaeiaraei 2009; Kakoli and Hanna 2011; Haeri et al. 2012; Kim et al. 2012). This decrease is due to the weakening of particles leading to their breakage (Marsal 1967) and lubrication effects of water, which acts on the grain-to-grain contacts (Farmer and Attewell 1973; Touileb et al. 2000).

Collapse settlement is also important in central clay core of rockfill dams. Significant settlement in the upstream shells of such dams commonly occurs when the reservoir is filled. This can be 1–2 % of the height of dam (Naylor 1997). Also, it can be considerably more than the mentioned value in the cases that the quality of rockfill material is not so good (Baumann 1958; Naylor 1997). Collapse settlement may also be important in inundated road embankments or in reclaimed lands, where buildings are to be constructed. Nevertheless, the degree of importance of this phenomenon for rockfill dams is higher than embankments (Naylor 1997; Soriano and Sánchez 1999).

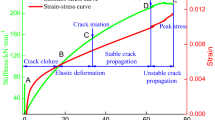
Figure 1 shows hypothetical stress and strain path for dry gravel in direct shear test. According to this figure, collapse factor, C, and the value of collapse settlement, ΔH C, can be efficiently used in studying the collapse phenomenon (Oshtaghi and Mahinroosta 2010).

Fig. 1
figure 1

a Shear stress versus horizontal displacement and b vertical displacement versus horizontal displacement of gravel specimens during collapse settlement test (Oshtaghi and Mahinroosta 2010)

Full size image

Collapse settlement factor can be used to model the stress reduction when the rockfill or the gravel material is saturated. Therefore, this factor which is also called coefficient of stress release, CSR, can be used to calculate the stress of the gravel in the saturated condition. By multiplying the stress of the material in the dry condition to the coefficient of stress release, the collapsed stress can be achieved. Thus, the collapse settlement factor can be obtained using Eq. (1) (Oshtaghi and Mahinroosta 2010):

$$ \mathrm{CSR}=\frac{{{\tau_{\mathrm{c}}}}}{{{\tau_{\mathrm{t}}}}}. $$
(1)

In Eq. (1), τ c is the collapse shear stress at the end of the impounding stage, when the collapse is completed, and τ t shows dry shear stress of the specimen before the impounding stage.

CSR is related to the relaxation coefficient, “a”, which was, firstly, introduced by Justo (1991) with the following equation:

$$ \mathrm{CSR}=1-a $$
(2)

where,

$$ a=\frac{{{\tau_{\mathrm{c}}}+{\tau_{\mathrm{t}}}}}{{{\tau_{\mathrm{t}}}}}. $$
(3)

There is a broad range of affecting parameters on the collapse settlement phenomenon such as initial water content, normal stress, shear stress level, sand soil content, clay content, relative density, number of impounding stages, etc. (Hunter 2002; Soroush and Aghaeiaraei 2005; Oshtaghi and Mahinroosta 2010). Contributing this wide range of parameters in this phenomenon makes it difficult to easily predict the value of the collapse settlement. Thus, in dire need of an inventive solution to predict this complicated function is completely obvious. High performance of artificial neural networks, a branch of artificial intelligence, and representing a precise solution for intricate situations have made it highly in demand in predicting several complicated problems. Artificial neural networks (ANNs) are broadly applied to a wide range of engineering and science complicated problems (Yang and Rosenbaum 2002; Neaupane and Adhikari 2006; Juang and Elton 1997; Yasrebi and Emami 2008; Monjezi et al. 2009; Hasanzadehshooiili et al. 2012a, b).

In this study, in order to predict the collapse settlement and the coefficient of stress release, an artificial neural network model is developed and the most affective parameters on these collapse parameters were gained by means of sensitivity analysis. Also, the effect of input parameters is investigated and results are compared by basic concepts in soil mechanics.

Artificial neural network method

ANN is a branch of artificial intelligence, which its ability to calculate logic functions is firstly introduced by McCulloch and Pitts (1988). In this method, the accuracy of the model strongly depends on the database. The larger database results in the more accurate prediction (Maulenkamp and Grima 1999; Habibagahi and Taherian 2001; Khandelwal and Singh 2006; Monjezi et al. 2009). Indeed, an ANN model predicts values of desired outputs using some input parameters. To show the ability of ANN in the pattern recognition, Rosenblatt (1988) built a perceptron network. Multilayer perceptron (MLP), which is known as the best type of ANNs, is made up of three types of layers (input–hidden–output). It is documented that this type of neural networks can accurately approximate any type of the continuous function (Hornik 1989; Funahashi 1989). ANNs do not need any prior knowledge about the nature of relationships between the input/output variables, which is one of the benefits of ANNs in comparison to the most of the empirical and statistical methods (Yasrebi and Emami 2008). The number of layers depends on the complexity of the problem, which is to be solved. But, at least, one input, one output, and one hidden layer are required. Each layer contains some elements that are called neurons. These neurons are connected from one layer to the next one. But, there is not any connection between nodes of a specific layer. These nodes are connected using some links which have weight vectors. These weights are multiplied into processed information. And the sum of weighted input signals to each neuron is transformed by an activation function (Monjezi et al. 2010). To obtain the optimum model, the network has to be trained. After well training from a large number of datasets, network detects similarities and can predict the outputs while a new pattern is fed into the network (Khandelwal et al. 2004). A network has three major components that should be accurately assigned regarding the problem type, the transfer function, the learning law, and the network architecture (Simpson 1990).

Input and output parameters

In order to study the collapse settlement phenomenon and its affecting parameters, the large-scale direct shear test was considered. This test was carried out in the geotechnical laboratory of University of Zanjan using a 30 × 30 × 15-cm direct shear device. First of all, under a constant normal stress, dry gravel with a specific relative density was sheared to reach to a pre-assumed shear stress level. Then, in this level, the material was saturated. After well saturation, which was accompanied by the collapse settlement, the shearing process was continued to the failure of the gravel. For more clarifications about the actual behavior of the studied material, the shear stress and the vertical displacement variation versus the horizontal displacement are plotted in the normal stress of 3 kg/cm2, shear stress level of 50 %, and relative density of 85 % in Fig. 2 (Oshtaghi and Mahinroosta 2010).

Fig. 2
figure 2

a Shear stress and b vertical displacement versus horizontal displacement gained by large-scale direct shear test for vertical stress of 3 kg/cm2, shear stress level of 50 %, and relative density of 85 % (Oshtaghi and Mahinroosta 2010)

Full size image

As it was previously mentioned, there are lots of parameters affecting on the value of the collapse settlement. Thus, to comprehensively study the material's collapse behavior, the effect of all the concerning parameters should be considered. In this regard and relying on the literature, all the concerning parameters were sorted and were taken into account. And then, based on the material type, clean gravel (its gradation range is shown in Fig. 3), the influencing parameters were assigned. Among all the parameters with the most influence, due to the low variation in the samples' clay contents and stress paths, also, because of the constant value of the initial water content of the specimens, four parameters, which are commonly reported as the most influential parameters (Alonso and Oldecop 2000; Basma and Kallas 2004; Asadzadeh and Soroush 2009; Oshtaghi and Mahinroosta 2010), sand content, normal stress, shear stress level, and relative density, were considered as input parameters. Also, to investigate their effects on the value of the collapse settlement, using the large-scale direct shear test, the values of the collapse settlement and the coefficient of stress release were calculated as output parameters. It should be noted that in this study, the material's clay content does not significantly vary. Furthermore, the impounding stages and the initial water content of the samples remain constant.

Fig. 3
figure 3

Gradation range of studied material

Full size image

On balance, input parameters, which their range of variation is shown in Table 1, are restricted to the sand content, normal stress, shear stress level, and relative density. In this study, a database including 180 datasets is prepared using the large-scale direct shear test. Also, the collapse settlement value and the coefficient of stress release are considered as output parameters, which are to be predicted by the network as desired values. The mentioned datasets are presented in Appendix 1.

Table 1 Input and output parameters used in ANN
Full size table

Training the network

Backpropagation algorithm is widely suggested as the most efficient procedure in the training of neural networks. It has been implemented by a variety of researchers for learning procedure of their multilayer perceptron neural networks (Basma and Kallas 2004; Neaupane and Adhikari 2006; Yuan-Ping and Xiao-Yan 2007; Hasanzadehshooiili et al. 2012a, b). In this technique, in the forward pass, first of all, a specific value for connections between neurons is assigned. Afterward, in the backpropagation pass, the differences between predicted and measured values are calculated. Then, the error, which is calculated during forward pass, is backpropagated through the network to update the weights. The controlling parameter for this mechanism is a predefined threshold for the differences (Demuth et al. 1996; Yang and Rosenbaum 2002).

In order to build the model, at first, datasets were arranged and normalized in a scale of 0–1 using Eq. (4). Then, 90 % of datasets were considered as training datasets. The remaining was kept as the test datasets.

$$ \mathrm{Scaled}\ \mathrm{value} = {{{\left( {\mathrm{unscaled}\ \mathrm{value}-\min } \right)}} \left/ {{\left( {\max\ \mathrm{value}-\min\ \mathrm{value}} \right)}} \right.}. $$
(4)

After a large number of trials on different networks, the nonlinear tangent sigmoid function, TANSIG, showing the minimum error was considered as the transfer function for all the layers. Figure 4 shows the nonlinear TANSIG transfer function. Also, its formula is presented in Eq. (5) (Demuth et al. 1996).

Fig. 4
figure 4

Tan-sigmoid transfer function (Demuth et al. 1996)

Full size image
$$ f=\frac{{{e^{{{e_{\mathrm{x}}}}}}-{e^{{-{e_{\mathrm{x}}}}}}}}{{{e^{{{e_{\mathrm{x}}}}}}+{e^{{-{e_{\mathrm{x}}}}}}}} $$
(5)

where e x is the weighted sum of the inputs for a processing unit.

As an important point, during the training process, two main phenomena should be considered: overfitting and underfitting. Overfitting, which makes the network memorize the outputs, occurs when a significant number of epochs are used during the training process. Also, if there is insufficient number of epochs used to train the network, the results will be underfitted and will lead to the model's inaccuracy (Maulenkamp and Grima 1999).

Network architecture

The best architectures of neural networks are gained by means of modeling a variety of one and two hidden layer neural networks and comparing their values of root mean square error (RMSE) and mean absolute error (MAE) (Hornik 1991; Pearson et al. 1995; Monjezi and Dehghani 2008).

RMSE and MAE are calculated using Eq. (6) and Eq. (7), respectively:

$$ \mathrm{RMSE}=\sqrt{{\frac{{\sum {{{{\left( {{O_i}-{T_i}} \right)}}^2}} }}{N}}} $$
(6)
$$ \mathrm{MAE}=\left| {\sum {\left( {{T_i}-{O_i}} \right)} } \right| $$
(7)

where O i and T i represents the predicted and the measured outputs, respectively. Also, N is the number of data pairs. As shown in Table 2 for CSR, a network with the architecture of 4–6–2 having the minimum value of RMSE is the optimum one. Also, it can be seen that the topology 4–9–2 has the minimum RMSE for ΔH and therefore is the optimum model.

Table 2 Results of comparison between some of the built models
Full size table

For the optimum models gained for CSR and ΔH, MAE was equal to 0.013 and 0.062 mm, respectively. Also, for better understanding of the network, schematic architecture of the optimum network for ΔH is shown in Fig. 5.

Fig. 5
figure 5

Architecture of optimum model for predicting the value of ΔH

Full size image

Model performance

By comparing predicted and measured values of the collapse settlement and the coefficient of stress release, the performance of constructed models can be easily evaluated. Figures 6 and 7 show the normalized measured and predicted values of both the collapse settlement and the stress release coefficient for 4–6–2 and 4–9–2 model architecture in a single diagram, respectively.

Fig. 6
figure 6

Comparison between measured and predicted CSR and ΔH for testing datasets for 4–6–2 architecture

Full size image
Fig. 7
figure 7

Comparison between measured and predicted CSR and ΔH for testing datasets for 4–9–2 architecture

Full size image

Also, achieving a considerable high value for the coefficient of determination for both models shows the good performance of models. As it can be seen in Figs. 8 and 9, for CSR and ΔH models, R 2 is equal to 0.9806 and 0.9828, respectively. To show the reasonable correlation between measured and predicted values of CSR and ΔH, the line y = x is depicted in addition to the datasets. Also, for CSR optimum model, MAE is equal to 0.013 and for ΔH optimum model, MAE is equal to 0.062.

Fig. 8
figure 8

Correlation between measured and predicted CSR for optimum model (4–6–2)

Full size image
Fig. 9
figure 9

Correlation between measured and predicted ΔH for optimum model (4–9–2)

Full size image

Sensitivity analysis

In order to attain the most affective factors on the CSR and ΔH, the cosine amplitude method (CAM), is considered (Yang and Zhang 1997; Monjezi et al. 2009). The expressed similarity relation between the target function and the input parameters is used to obtain by this method. In this method, all of data pairs are expressed in the common X-space. They would form a data array X defined as Eq. (8) (Yong-Hun and Chung-In 2004; Khandelwal and Singh 2006; Monjezi et al. 2010):

$$ X=\left\{ {{x_1},{x_2},{x_3},{x_4},\ldots,{x_i},\ldots {x_n}} \right\} $$
(8)

where each element, x i , is a vector of the length of m and is shown in Eq. (9).

$$ {x_i}=\left\{ {{x_{i1 }},{x_{i2 }},{x_{3i }},\ldots {x_{im }}} \right\}. $$
(9)

Thus, each of the datasets can be considered as a point in the m-dimensional space, where each point requires m-coordinates to be fully described (Monjezi et al. 2010). The strength of the relationship between x i and x j is given by Eq. (10).

$$ {r_{ij }}=\frac{{\sum\limits_{k=1}^m {{x_{ik }}{x_{jk }}} }}{{\sum\limits_{k=1}^m {x_{ik}^2} \sum\limits_{k=1}^m {x_{jk}^2} }}. $$
(10)

Regarding this mentioned formula, the strength of the relationship between CSR and input parameters also ΔH and input parameters is shown in Figs. 10 and 11, respectively.

Fig. 10
figure 10

Sensitivity analysis carried out between CSR and input parameters

Full size image
Fig. 11
figure 11

Sensitivity analysis carried out between ΔH and input parameters

Full size image

The results show that sand content is the most influential factor on the collapse settlement value, ΔH. Also, the normal stress is the most sensitive parameter affecting on the CSR.

Geotechnical interpretation of the network prediction

To well peruse the collapse settlement phenomenon and to ensure the accuracy of trends of predicted outputs, variation of predictions with inputs was studied. In order to study input-predicted output behavior, the mean and standard deviation of each input parameter were calculated using the following equations:

$$ X=\frac{{\sum {{x_i}} }}{N} $$
(11)
$$ \delta =\sqrt{{\frac{{\sum {{{{\left( {{x_i}-X} \right)}}^2}} }}{N}}} $$
(12)

where x i and N are input parameters and number of datasets, respectively. Also, in these formulas, X and δ, represent the mean and standard deviation of each input parameter for the studied range. Mean and standard deviation of each normalized input parameter are presented in Table 3. To gain the trend of the predicted collapse settlement and the coefficient of stress release with each of inputs, the values of X − δ, X − δ / 2, X, X + δ / 2, and X + δ are calculated for each input. Then, the desired outputs are predicted using their optimum models. Table 4 illustrates the mentioned procedure for assessing input-predicted output behavior. In this table, variation of the input X 1 on the collapse parameters is investigated.

Table 3 The mean and standard deviation of input parameters
Full size table
Table 4 Parameters used to gain the variation of predicted outputs with inputs
Full size table

Where, the index “i; i = 1, … 4” present the mean of i-th input data. For both optimum models, this table is built for all four inputs, separately. Finally, the behavior of the predicted coefficient of stress release and the collapse settlement with change in the value of sand content, normal stress, shear stress level, and relative density is, separately, depicted in Figs. 12 and 13, respectively.

Fig. 12
figure 12

Variation of coefficient of stress release with input parameters

Full size image
Fig. 13
figure 13

Variation of ΔH with input parameters

Full size image

As it can be seen in Figs. 12 and 13, results obtained from the network are efficiently in a good agreement with their real status. In Fig. 12, on one hand, the coefficient of stress release is increased with the increase in the amount of the normal stress and the relative density. On the other hand, it decreases with the increase in the amount of the sand content and the shear stress level.

Also, from Fig. 13, it is clear that the collapse settlement has a direct relationship with the sand content, normal stress, and shear stress level. And, it has an inverse relationship with the relative density.

As a matter of fact, the normal stress with imposing more breakage, the sand content with increasing the inter-grain displacement, and stresses and the relative density with increasing the weight of compacted soil in the shear box cause these behaviors, which are plotted in Figs. 12 and 13.

The dependency of the collapse phenomenon to the confining pressure has been observed experimentally and numerically by some researchers (Naderian and Williams 1997; Alizade 2009; Oshtaghi and Mahinroosta 2010; Poorjafar and Mahinroosta 2011). In fact, with increasing the normal stress, the larger amount of collapse settlement occurs, which its trend agrees with the results inferred from Figs. 12b and 13b.

Increasing the relative density in the media results in the better and stiffer contact between soil particles, which leads to fall in the collapse settlement and rise in the stress release coefficient. Also, higher shear stresses induce more micro and possibly macro cracks in rock particles. This facilitates the penetration of water into the cracks, resulting in the breakage and more degradation of the strength and the deformation modulus (Soroush and Aghaeiaraei 2005).

Conclusion

In this study, a new ANN was developed to predict the collapse settlement value and the coefficient of stress release in gravel materials using 180 datasets which were obtained by means of the large-scale direct shear test. Neglecting the parameters with the low variation and those which were constant in this study, four variables were considered as input parameters. Using the sand content, SC, the normal stress, σ n , the shear stress level, SL, and the relative density, Dr, as input parameters, a feedforward backpropagation method was used to train the datasets. After some trials and based on the comparing the values of RMSE, for different built models, a network with the architecture of 4–6–2 was found as the optimum network in predicting the value of the coefficient of stress release. For this mentioned network, RMSE and the coefficient of determination, R 2, were equal to 0.0171 and 0.981, respectively. Also, an MLP network with the topology 4–9–2 was realized to be the optimum network in predicting the value of the collapse settlement. For this network, the value of the root mean square error and the coefficient of determination were equal to 0.082 and 0.983, respectively. Furthermore, by finding the strength of the relationships between input and output parameters, based on the CAM method, the SC was introduced as the most important parameter and the Dr was the least affective parameter on the collapse settlement value, ΔH. Also, it was observed that the σ n is the most effective parameter on the coefficient of stress release, whereas the SL was found as the parameter with the least effect on the CSR. Finally, the geotechnical interpretation of the designed network was taken into account. It was shown that all trends in input–output connections are in a good agreement with the basic laws of soil mechanics. Thus, it is shown that besides the well prediction of collapse parameters, the developed ANN is well behaved with the geotechnical engineering considerations.