Passenger routing for periodic timetable optimization

Abstract

The task of periodic timetabling is to determine trip arrival and departure times in a public transport system such that travel and transfer times are minimized. This paper investigates periodic timetabling models with integrated passenger routing. We show that different routing models can have a huge influence on the quality of the entire system: Whatever metric is applied, the performance ratios of timetables w.r.t. different routing models can be arbitrarily large. Computations on a real-world instance for the city of Wuppertal substantiate the theoretical findings. These results indicate the existence of untapped optimization potentials that can be used to improve the efficiency of public transport systems by integrating passenger routing.

1 Introduction

Public transit passengers choose their routes not only to minimize travel time. They also take additional (dis)utilities like transfers, fares, and robust connections into account. This is reflected in the literature on routing models for public transport, which takes a very detailed point of view, see, e. g., the survey article of Fu et al. (2012). It has been shown that such models can deduce “correct” routes with high probability, see van der Hurk et al. (2013). Planning an attractive public transport system therefore requires a consideration of human behavior, as well as an assessment of line plans and timetables.

The integration of passenger behavior into network design, line planning, and timetabling models is a major challenge in public transit optimization. It is farthest advanced in the area of line planning: Integrated line planning and passenger routing models have been proposed by Schöbel and Scholl (2006), Borndörfer et al. (2007), and Borndörfer and Karbstein (2012), the last reference reports also on successful computations.

Timetable optimization has been extensively studied with respect to fixed passenger routings based on path lengths in the network, see, e.g., Liebchen (2006), Lindner (2000), and Nachtigall (1998). More sensitivity w.r.t. passenger behavior is provided by iterative timetabling approaches, which can also deal with practical requirements such as delays and disruptions, see, e.g., Sels et al. (2016). The full integration of passenger routing into timetable optimization models has been taken up only recently. Schmidt (2012) studies its complexity for aperiodic timetabling. She develops an exact solution approach for the case where the first and last train of each passenger path are fixed, see also Schmidt and Schöbel (2014). The only approaches to integrated passenger routing and periodic timetabling that we are aware of are the Master thesis of Lübbe (2009) and the article of Siebert and Goerigk (2013). Lübbe proposes an integrated quadratic model and linearizes it to obtain an integer linear programming model. His computations indicate a potential for travel time improvements but he could only deal with very small instances. Siebert and Goerigk provide worst case error analyses and compare an integrated integer programming model with an iterated approach.

As a next step towards the development of integrated timetabling and passenger routing methods this paper investigates the impact of routing decisions on the timetable. We focus on travel time, transfer time, and capacities as factors determining the passenger routes, and we employ simple routing models, that are amenable to a theoretical analysis. We do not consider the impact of delays or disruptions, i.e., we study the “planned” case. In this context, the following questions arise: Do different assumptions on passenger behavior matter at all? How does routing influence the optimal timetable? How can we measure differences in terms of the performance of the timetable? How important is the choice of the objective function w.r.t. the performance of the timetable?

To shed some light on these questions, we propose a family of integrated periodic timetabling and passenger routing models that differ in their routing approach. More precisely, we consider a fixed passenger routing, a routing on shortest paths w.r.t. the timetable (to be optimized), and two routings that take line capacities into account. We evaluate them in terms of the total and the maximum travel time system optimum, which is obtained by a simultaneous optimization of all passenger paths. Comparing these objectives gives an indication of the significance of different routing schemes. Evaluating optimal solutions using a different routing model gives an indication of the robustness of a timetable w.r.t. different routing schemes. It will turn out that the worst case ratio in all these performance comparisons is infinite, in some cases even regardless of the timetable, in others depending on parameters such as the number of origin-destination pairs or the number of nodes in the network. A computational test of our model on a real-world instance for the city of Wuppertal shows that such effects can indeed play a role in practice. These results question appropriateness of fixed passenger routing models and pinpoint a potential for the development of methods that can take human behavior better into account. They also suggest the existence of untapped optimization potentials for possibly substantial improvements of the quality of public transit systems.

The paper is structured as follows. Section 2 proposes an integer programming model for integrated timetabling and passenger routing that can be used with different routing schemes and objectives. Section 3 analyzes the ratios between optimal solutions for different routings, Sect. 4 evaluates optimal solutions using alternative routings, and Sect. 5 investigates the ratios between different objectives from a theoretical point. Section 6 gives a computational study with data for the city of Wuppertal. Section 7 concludes.

2 Notation

Most models in the literature about periodic timetabling are based on the periodic event scheduling problem (PESP) developed by Serafini and Ukovich (1989). We consider the following extension w.r.t. passenger routings. Let $N=(V,A)$ be a directed graph, the event-activity network. The nodes V are called events and represent arrivals and departures of lines at their stations, i.e., $V = V_{{\text{arr}}}\cup V_{{\text{dep}}}$. The arcs $A\subseteq V \times V$ are called activities and model driving between stations, waiting at stations, and possible transfers between lines at stations, i.e., $A=A_{{\text{drive}}}\cup A_{{\text{dwell}}}\cup A_{{\text{trans}}}$. Further, we are given lower and upper time bounds $\ell _a, u_a\in \mathbb {Q}_{\ge 0}$, respectively, for the duration of activity $a\in A$. Passengers can start and end their trips in $V_{{\text{dep}}}$ and $V_{{\text{arr}}}$, respectively. The passenger demand is given in terms of an origin-destination matrix (OD matrix) $(d_{st})\in \mathbb {Q}_{\ge 0}^{V_{{\text{dep}}}\times V_{{\text{arr}}}}$ specifying for each pair of arrival and departure nodes $(s,t)\in V_{{\text{dep}}}\times V_{{\text{arr}}}$ the number of passengers that want to travel from s to t. Let $\mathcal {D}=\{(s,t)\in V_{{\text{dep}}}\times V_{{\text{arr}}}: d_{st}>0\}$ be the set of all OD pairs. For an OD pair (s, t), let $\mathcal {P}_{st}$ be the set of (s, t)-paths in N and let $\mathcal {P}:=\bigcup _{(s,t)\in \mathcal {D}}\mathcal {P}_{st}$ be the set of all passenger paths.

A periodic timetable $\pi :V\rightarrow \mathbb {Q}$ determines arrival and departure times at all arrival and departure nodes, respectively, that are assumed to repeat periodically w.r.t. a period time $T\in \mathbb {N}$. Given $x\in \mathbb {Q}$, we define the modulo operator by $[x]_T:=\min \{x+zT: x + zT \ge 0, z\in \mathbb {Z}\}$. We call a timetable feasible if the periodic interval constraints

$$\begin{aligned}{}[\pi _w-\pi _v-\ell _a]_T \in [0,u_a-\ell _a]\quad \forall \,a=(v,w)\in A \end{aligned}$$

are satisfied. We assume w.l.o.g. that $\ell _a<T$ and $u_a-\ell _a<T$ for all $a\in A$. For a feasible timetable $\pi$, the time duration of activity $a\in A$ is given by $x_a:=\ell _a + [\pi _w-\pi _v-\ell _a]_T$, and the time duration or travel time of a passenger path $p\in \mathcal {P}$ is $x_p:=\sum _{a\in p} x_a$.

A passenger routing model M restricts the passenger paths to subsets $\mathcal {P}_{st}^{M}\subseteq \mathcal {P}_{st}$, $(s,t)\in \mathcal {D}$, $\mathcal {P}^{M}:=\bigcup _{(s,t)\in \mathcal {D}}\mathcal {P}_{st}^{M}$, and limits the number of passengers traveling on activity $a\in A$ by a capacity $\kappa _a^{M}\ge 0$. We introduce timetable variables $\pi _v$ for the timing of event $v\in V$, duration variables $x_a$ for the length of activity $a\in A$, and passenger variables $y_p$ for the fraction of passengers that travel on path $p\in \mathcal {P}^{M}$. The domain of the passenger routing variables $y_p$ is denoted by $Q^{M}$. Let finally $f(x,y)\rightarrow \mathbb {Q}$ be an objective function depending on the passenger routing variables and the duration variables. Then we can state the following mixed-integer non-linear program with congruence relations for the generic integrated passenger routing and timetabling problem:

$$\begin{aligned} (M ^{f} )\quad \text{min}& \quad \quad f(x,y) \nonumber \\ \text{s.t.}&\quad \quad [\pi _w-\pi _v-\ell _a]_T\le u_a-\ell _a \quad \forall \,a=(v,w) \in A \end{aligned}$$

(1)

$$\begin{aligned}[\pi _w-\pi _v-\ell _a]_T + \ell _a= x_a \quad \forall \,a=(v,w) \in A \end{aligned}$$

(2)

$$\begin{aligned}\sum _{p\in \mathcal {P}_{st}^{M}}y_p=1\quad\forall \,(s,t) \in \mathcal {D} \end{aligned}$$

(3)

$$\begin{aligned}\sum _{(s,t)\in \mathcal {D}}\sum _{p\in \mathcal {P}_{st}^{M}:a\in p}d_{st}\,y_p\le \kappa _a^{M}\quad\forall \,a \in A \end{aligned}$$

(4)

$$\begin{aligned}\pi _v< T\quad\forall \,v \in V \end{aligned}$$

(5)

$$\begin{aligned}\pi _v\ge 0\quad\forall \,v \in V \end{aligned}$$

(6)

$$\begin{aligned}y_p\in Q^{M}\quad\forall \,p\in \mathcal {P}^{M} . \end{aligned}$$

(7)

The model $(M ^{f} )$ minimizes f among all feasible timetables using the passenger routing model $M$. Constraints (1) guarantee a feasible periodic timetable. Equations (2) set the duration variables, which are convenient to define the objective function. Constraints (3) and (4) enforce a passenger flow that does not exceed the capacity.

We remark that conditions (1) and (2) can be formulated in terms of linear constraints, using additional integer periodic offset variables for each activity, see, e.g., Liebchen (2006). An alternative linearization, which we use for our computations in Sect. 6, is obtained by transforming the event-activity network into a time-expanded event-activity network, see, e.g., Kinder (2008).

Objectives. We consider two objectives that account in different ways for the travel time of the passengers induced by a timetable. Let (x, y) be a feasible solution of (1)–(7) for some routing model $M$.

• Our first objective is to minimize the total weighted travel time of all passengers:

  $$\begin{aligned} f^{{\text{sum}}}(x,y):= \sum _{(s,t)\in \mathcal {D}}\sum _{p\in \mathcal {P}_{st}^{M}}\sum _{a\in p} d_{st}\,x_a\,y_p. \end{aligned}$$

• The second objective is to minimize the maximum weighted travel time among all passengers, i.e.,

  $$\begin{aligned} f^{\max }(x,y):= \max _{(s,t)\in \mathcal {D}}\sum _{p\in \mathcal {P}_{st}^{M}}\sum _{a\in p} d_{st}\,x_a\,y_p. \end{aligned}$$

The objective $f^{\max }$ can be linearized with an auxiliary variable $z^{\max }\in \mathbb {Q}$, representing the maximum weighted travel time among all OD pairs via the constraints

$$\begin{aligned} \sum _{p\in \mathcal {P}_{st}^{M}}\sum _{a\in p} d_{st}\,x_a\,y_p \le z^{\max }\quad \forall \,(s,t)\in \mathcal {D}\end{aligned}$$

and setting $f^{\max }(x,y):= z^{\max }$.

In the remainder of the paper, it will be convenient to abbreviate models $(M ^{f^{\max }})$ and $(M ^{f^{{\text{sum}}}})$ as $(M ^{\max })$ and $(M ^{{\text{sum}}})$, respectively.

Routing models. We define four passenger routing models by specifying the set of passenger paths and the capacity constraints. The first two, the lower-bound routing model (${\text{LBR}}$) and the shortest path routing model (${\text{SPR}}$), are uncapacitated, such that demands can be routed independently of each other, the other two, the capacitated multi-path routing model (${\kappa }\text{-}{{\text{MPR}}}$) and the capacitated unsplittable path routing model (${\kappa }\text{-}{{\text{UPR}}}$), involve bounds on the maximum passenger flow on an activity.

• The lower-bound routing model (${\text{LBR}}$) arises from the assumption that passengers choose their travel paths according to lower bounds on the travel time. For our objectives, this results in a routing that is independent of the timetable. The detailed settings are:

  • $\mathcal {P}_{st}^{M}=\mathrm {arg\,min}\left\{ \sum _{a\in p} \ell _a: p\in \mathcal {P}_{st}\right\}$ for all $(s,t)\in \mathcal {D}$, i.e., for each OD pair only the shortest path w.r.t. the lower bounds on the activities is considered.

  • $\kappa _a^{M}=\infty$ for all $a\in A$, i.e., the routing model is uncapacitated

  • $Q^{M}=\mathbb {Q}_{\ge 0}$, i.e., the passenger flow is non-negative.

• The shortest path routing model (${\text{SPR}}$) arises from the assumption that passengers choose shortest travel paths according to the travel times induced by the timetable. Like in the $({\text{LBR}})$, the routing also ignores capacity restrictions. It includes the following detailed settings:

  • $\mathcal {P}^{M} = \mathcal {P}$, i.e., all paths are allowed,

  • $\kappa _a^{M}=\infty$ for all $a\in A$, i.e., the routing model is uncapacitated,

  • $Q^{M}=\mathbb {Q}_{\ge 0}$, i.e., the passenger flow is non-negative.

• The capacitated multi-path routing model (${\kappa }\text{-}{{\text{MPR}}}$) extends the shortest path routing model by capacity constraints. The detailed settings are:

  • $\mathcal {P}^{M} = \mathcal {P}$, i.e., all paths are allowed,

  • $\kappa ^{M} \le \infty$, i.e., activity capacities may be bounded,

  • $Q^{M}=\mathbb {Q}_{\ge 0}$, i.e., the passenger flow is non-negative.

• The capacitated unsplittable path routing model (${\kappa }\text{-}{{\text{UPR}}}$) extends the shortest path routing model by capacity constraints and the assumption that all passengers of one OD pair $(s,t)\in \mathcal {D}$ travel on the same (s, t)-path. The detailed settings are:

  • $\mathcal {P}^{M} = \mathcal {P}$, i.e., all paths are allowed,

  • $\kappa ^{M} \le \infty$, i.e., activity capacities may be bounded,

  • $Q^{M}=\{0,1\}$, i.e., for each OD pair exactly one path is chosen.

For the lower-bound routing model (${\text{LBR}}$), $\mathcal {P}_{st}^{M}$ contains exactly one path for each OD pair if all shortest paths are unique, which we will (w.l.o.g.) assume in the sequel. Then this routing model is a fixed path routing model. All other routing models interact with the timetable.

Comparing routings and objectives. For a problem $(M ^{f} )$ and an instance I, denote by ${\text{feas}}(M ^{f};I)$ and ${\text{opt}}(M ^{f};I)$ the set of values of time duration variables x and passenger variables y that give rise to feasible and optimal solutions, respectively. From now on, we assume w.l.o.g. that $(M ^{f} )$ is always feasible for I. Let $v(M ^{f};I)$ be the optimal objective value, i.e., $v(M ^{f};I)=f(x^*,y^*)$ for all $(x^*,y^*)\in {\text{opt}}(M ^{f};I)$. To evaluate optimal solutions w.r.t. different objectives, we denote by

$$\begin{aligned} v(M ^{f};I)|^{\max }_{}:=\sup \left\{ f^{\max }(x^*,y^*): (x^*,y^*)\in {\text{opt}}(M ^{f};I)\right\} \end{aligned}$$

the (worst) maximum weighted travel time among all OD pairs for any optimal solution of instance I of model $M ^{f}$, and by

$$\begin{aligned} v(M ^{f};I)|^{{\text{sum}}}_{}:= \sup \left\{ f^{{\text{sum}}}(x^*,y^*): (x^*,y^*)\in {\text{opt}}(M ^{f};I) \right\} \end{aligned}$$

the (worst) total weighted travel time for any optimal solution of instance I of model $M ^{f}$. Let $M _1$ and $M _2$ be two routing models, then we denote for an instance I by

$$\begin{aligned} v(M _{1}^{{\text{sum}}};I)|^{}_{M _{2}}:= \max \{ \min \{f^{{\text{sum}}}(x^*,y) :(x^*,y)\in {\text{feas}}(M ^{{\text{sum}}}_{2};I) \}\\ : (x^*,.) \in {\text{opt}}(M ^{{\text{sum}}}_{1};I) \} \end{aligned}$$

the (worst) minimum total weighted travel time achieved by an $M _2$-routing for a timetable that was optimized w.r.t. an $M _1$-routing. Note that these definitions imply

$$\begin{aligned} v(M ^{\max };I) = v(M ^{\max };I)|^{\max }_{}{} \le v(M ^{{\text{sum}}};I)|^{\max }_{} \\ v(M ^{{\text{sum}}};I) = v(M ^{{\text{sum}}};I)|^{{\text{sum}}}_{} \le v(M ^{\max };I)|^{{\text{sum}}}_{}\nonumber \end{aligned}$$

(8)

for any instance I of any routing model $M$. Furthermore, the definitions of the routing models yield

$$\begin{aligned}&v({\text{SPR}} ^{{\text{sum}}};I) \le v({\text{LBR}} ^{{\text{sum}}};I) \end{aligned}$$

(9)

$$\begin{aligned}&v({\text{SPR}} ^{\max };I) \le v({\text{LBR}} ^{\max };I)\end{aligned}$$

(10)

$$\begin{aligned}&v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I) \le v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)\end{aligned}$$

(11)

$$\begin{aligned}&v({\kappa }\text{-}{{\text{MPR}}} ^{\max };I) \le v({\kappa }\text{-}{{\text{UPR}}} ^{\max };I)\end{aligned}$$

(12)

$$\begin{aligned}&v({\text{SPR}} ^{{\text{sum}}};I) = v({\text{SPR}} ^{{\text{sum}}};I)|^{}_{{\text{SPR}}} \le v({\text{LBR}} ^{{\text{sum}}};I)|^{}_{{\text{SPR}}}\end{aligned}$$

(13)

$$\begin{aligned}&v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I) = v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)|^{}_{{\kappa }\text{-}{{\text{MPR}}}} \le v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)|^{}_{{\kappa }\text{-}{{\text{MPR}}}} . \end{aligned}$$

(14)

We will show in the following sections that there are instances such that the inequalities (8) and (9)–(14) are strict. For a more precise quantification, we will study the following performance gaps

$$\begin{aligned} \sup _{I} \frac{v(M _1^{f_1};I)|^{{{\text{sum}}}}_{}}{v(M _2^{f_2};I)|^{{\text{sum}}}_{}}, \quad \sup _{I} \frac{v(M _1^{f_1};I)|^{{\max }}_{}}{v(M _2^{f_2};I)|^{{\max }}_{}}, \quad \text{and} \quad \sup _{I} \frac{v(M _1^{{\text{sum}}};I)|^{}_{M _2}}{v(M _2^{{\text{sum}}};I)} \end{aligned}$$

(15)

of models $M _1^{f_1}$ and $M _2^{f_2}$, where the supremum is taken over all instances I.

We will show that there are instances such that the gaps (15) can be arbitrarily large. To this purpose, we construct timetabling instances based on a directed graph in the following fashion: We associate the nodes with stations and the arcs with driving activities of lines. For all transfer activities, the lower time bound is set to zero and the upper time bound is set to $T\in \mathbb {N}$. The lower and the upper time bound of all line dwell activities at each station is set to zero. For each line driving activity the lower time bound is set to the upper time bound. Hence, these timetable problems reduce to determining for each line the departure time at the first station.

3 Comparing routing models: integrated optimization

We study in this section the impact of the routing model on the value of the optimal solution.

Theorem 1

$$\begin{aligned} \sup _{I} \frac{v({\text{LBR}} ^{{\text{sum}}};I)}{v({\text{SPR}} ^{{\text{sum}}};I)} =\infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 1. D has $2k+2$ nodes and $2k+1+k+1=3k+2$ arcs, $k\in \mathbb {N}$; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as described in Sect. 2.

We associate $k+2$ lines with the arcs of D. There is one line from s to t (dotted arc) with a driving time of T and no intermediate stations. There is a second line (solid arcs) from s to t with $2k$ intermediate stations. The driving time between the stops of this line is alternatingly $\epsilon :=\frac{T-1}{2k+1}$ and T. Between every two stations, for which the driving time of the second line is T, there is another line with a driving time of only $\epsilon$ (dashed arcs). There is only one passenger that wants to travel from s to t.

First consider model $({\text{LBR}} ^{{\text{sum}}})$. The passenger is routed along the unique shortest (s, t)-path, which uses all upper arcs, with a total length of $(2k+1)\epsilon =T-1$, if the transfer times at all stations would be zero. However, there is no feasible timetable for this instance such that the transfer time at every station in this path is zero. In fact, in any solution of $({\text{LBR}} ^{{\text{sum}}})$, the transfer times at stations 2 and 3 sum up to

$$\begin{aligned} T-\epsilon \end{aligned}$$

as for every following pair of stations along this path. Hence, the travel time for this path is in total $T-1 + k(T-\epsilon )$ and $v({\text{LBR}} ^{{\text{sum}}};I)=T-1 + k(T-\epsilon )$. In an optimal solution to $({\text{SPR}} ^{{\text{sum}}})$ the passenger travels on the bottom line with a travel time of T for any timetable and, hence, $v({\text{SPR}} ^{{\text{sum}}};I)=T$. We can conclude that

$$\begin{aligned} \frac{v({\text{LBR}} ^{{\text{sum}}};I)}{v({\text{SPR}} ^{{\text{sum}}};I)} = \frac{T-1 + k(T-\epsilon )}{T} = k+ \frac{(T-1)(1 - \frac{k}{2k+1})}{T} \quad \mathop{\longrightarrow }\limits_{k\rightarrow \infty }^{}\quad \infty . \end{aligned}$$

$\square$

Fig. 1

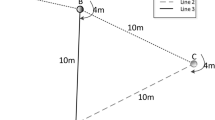
Instance for Theorem 1

Theorem 2

$$\begin{aligned} \sup _{I} \frac{v({\text{LBR}} ^{\max };I)}{v({\text{SPR}} ^{\max };I)} =\infty . \end{aligned}$$

Proof

The theorem directly follows from the proof of Theorem 1, because the example instance contains only a single OD pair. In this case the maximum weighted travel time is equal to the total travel time.$\square$

Fig. 2

Instance for Theorem 3. All bold arcs in this graph have a capacity of $\kappa$, the thinner arcs have a capacity of 1

Theorem 3

$$\begin{aligned} \sup _{I} \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)}{v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)} =\infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 2. The graph D has $6n+5$ nodes, where $n\ge 3$ is an odd number; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as defined in Sect. 2.

We set the passenger demand to $d_{st}=\bar{d}$, where $1<\bar{d}\le n$; all other demands are set to zero. The instance contains $2n+4$ lines. $2n+2$ lines are represented by the dotted arcs $(s,u_1)$ and $(u_{2n+1},t)$, which have a capacity of $\bar{d}\le \kappa \le n$, and by the arcs $\{(s,u_i):2\le i \le 2n, i\text{ is even}\}$ and $\{(u_i,t):2\le i \le 2n, i\text{ is even}\}$, with a capacity of only 1. Then there is one line (dashed arcs) starting in $u_1$ and ending in $v_{2n+1}$ and the last line (solid arcs) is from $v_1$ to $w_{2n+1}$. The dashed and the solid line also have a capacity of $\kappa$. All transfer and dwell activities have infinite capacity.

The duration of all driving activities of the dotted lines and the activities corresponding to $(u_i,v_i)$ and $(v_i,w_i)$, $1\le i \le 2n+1$, is $\epsilon >0$. The duration of the remaining driving activities are as follows:

• $\circ$ $(v_{i},u_{i+1}), i=1+4\,j, j\ge 0, i<2n+1$ have a duration of $2\epsilon +T$,

• $\circ$ $(w_{i},v_{i+1}), i=4+4\,j, j\ge 0, i<2n+1$ have a duration of $2\epsilon +5$,

• $\circ$ $(v_{i},u_{i+1}), i=2+4\,j, j\ge 0, i<2n+1$ have a duration of $\epsilon +T$,

• $\circ$ $(w_{i},v_{i+1}), i=3+4\,j, j\ge 0, i<2n+1$ have a duration of $\epsilon +T$,

• $\circ$ $(v_{i},u_{i+1}), i=3+4\,j, j\ge 0, i<2n+1$ have a duration of $2\epsilon$,

• $\circ$ $(w_{i},v_{i+1}), i=2+4\,j, j\ge 0, i<2n+1$ have a duration of $2\epsilon$,

• $\circ$ $(v_{i},u_{i+1}), i=4+4\,j, j\ge 0, i<2n+1$ have a duration of $\epsilon$,

• $\circ$ $(w_{i},v_{i+1}), i=1+4\,j, j\ge 0, i<2n+1$ have a duration of $\epsilon$.

First consider problem $({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}})$. Since the passengers have to travel on a single path, the passengers that want to go from s to t can only take lines with a capacity of at least $\bar{d}$. Hence, they need to travel along a path from $u_1$ to $w_{2n+1}$ using the dashed and the solid line. If the transfer times are zero, then a shortest $(u_1,w_{2n+1})$-path has a travel time of $5n\epsilon +2\epsilon$ and uses only driving activities with a duration of $\epsilon$ or $2\epsilon$. These values can indeed be achieved by setting the departure time of the dashed line at node $u_1$ to 0 and the departure time of the solid line at node $v_1$ to $\epsilon$. The departure times of lines $(s,u_1)$ and $(w_{2n+1},t)$ can be set accordingly to get also 0 transfer times in $u_1$ and $w_{2n+1}$. The minimum total weighted travel time (achieved for this timetable) is then

$$\begin{aligned} v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)&=\bar{d}(5n\epsilon + 2\epsilon + 2\epsilon ) =\bar{d}(5n\epsilon + 4\epsilon ). \end{aligned}$$

In an optimal solution to $({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}})$, the passengers from s to t can split and travel along $\left\lceil \bar{d}\right\rceil$ paths via $(s,u_i,v_i,w_i,t)$, $2\le i \le 2n$ and i is even. The transfer time in an optimal timetable for these passenger paths at $v_i$ is zero for all even i, $2\le i\le 2n$, e.g., if the dashed line departs at $u_1$ at time 0 and the solid line departs at $v_1$ at time $2\epsilon$. The minimum total weighted travel time is therefore

$$\begin{aligned} v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)&=\bar{d}(4\epsilon )=4\bar{d}\epsilon . \end{aligned}$$

We can conclude that

$$\begin{aligned} \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)}{v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)} =\frac{\bar{d}(5n\epsilon + 4\epsilon )}{4\bar{d}\epsilon } =\frac{5n+4}{4} \quad \mathop{\longrightarrow }\limits_{n\rightarrow \infty }^{}\quad \infty . \end{aligned}$$

$\square$

Theorem 4

$$\begin{aligned} \sup _{I} \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{\max };I)}{v({\kappa }\text{-}{{\text{MPR}}} ^{\max };I)} =\infty . \end{aligned}$$

Proof

The theorem directly follows from the proof of Theorem 3, because the example instance contains only a single OD pair. In this case the maximum weighted travel time is equal to the total travel time.$\square$

4 Comparing Routing Models: Evaluating Timetables

We proved in Sect. 3 that the performance gap between the optimal solution values between the models ${\text{SPR}}$ and ${\text{LBR}}$ and, in the capacitated case, between the models ${\kappa }\text{-}{{\text{MPR}}}$ and ${\kappa }\text{-}{{\text{UPR}}}$ can be arbitrarily large. We now want to investigate the impact of the routing decisions further by evaluating the quality of timetables that are optimal for ${\text{LBR}}$ and ${\kappa }\text{-}{{\text{UPR}}}$. The idea is to fix these timetables and route the passengers again using the models ${\text{SPR}}$ and ${\kappa }\text{-}{{\text{MPR}}}$. We compare the resulting total weighted travel times with optimal solutions for ${\text{SPR}}$ and ${\kappa }\text{-}{{\text{MPR}}}$, respectively. The resulting change in the objective value is an indication of the robustness of an optimal timetable against modifications of the routing model. This consideration arises in iterative timetabling approaches. Our results show that if the initial timetable or routing is chosen poorly, it may happen that one cannot improve it by alternatingly reoptimizing the timetable and the passenger routes.

Fig. 3

Instance for Theorem 5

Theorem 5

$$\begin{aligned} \sup _{I} \frac{v({\text{LBR}} ^{{\text{sum}}};I)|^{{}}_{{\text{SPR}}}}{v({\text{SPR}} ^{{\text{sum}}};I)} = \infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 3. D has $2m$ nodes and $3m-1$ arcs, $m\in \mathbb {N}$; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as described in Sect. 2.

We associate $m+1$ lines with the arcs of D. There are $m-1$ lines visiting the nodes $(s_i,t_{i-1},s_{i-2},s_{i-1})$ for each $2\le i\le m$, with $s_{m}=t_0$ and one line from $s_{m-1}$ to $s_{m}$. The driving time between the stops of these lines is always $\epsilon =\frac{T}{m}$. The last line is from $s_0$ to $s_{m}$ and has a driving time of $T+1$. We set the passenger demand to $d_{s_it_i}=1$ for all $0\le i \le m-1$; all other demands are set to zero.

First consider model $({\text{LBR}} ^{{\text{sum}}})$. For a passenger that wants to travel from $s_i$ to $t_i$ for $i>0$ there is only a single $s_i,t_i$-path containing a transfer at station $s_{i+1}$. The passenger from $s_0$ to $t_0$ is routed along the shortest $s_0,t_0$ path (w.r.t. zero transfer time), which is along the stations $\{s_1,\ldots ,s_{m-1}\}$. The lines visiting station $s_i$, $2\le i \le m$ are constructed in such a way that for any timetable the transfer times for the $(s_0,t_0)$-passenger and $(s_{i-1},t_{i-1})$-passenger sum up to $T-4\epsilon$. Hence, the total transfer time for all passengers is $(m-1)(T-4\epsilon )$ in any timetable. Hence, if we synchronize the lines along this path for the passenger traveling from $s_0$ to $t_0$, we obtain an optimal timetable for model $({\text{LBR}} ^{{\text{sum}}})$. Given this timetable, the optimal travel time with ${\text{SPR}}$ for the $(s_0,t_0)$-passenger is $m\epsilon =T$ and for each $(s_{i},t_{i})$-passenger, $i>0$, it is $2\epsilon + T-4\epsilon =T-2\epsilon$. We can conclude that

$$\begin{aligned} v({\text{LBR}} ^{{\text{sum}}};I)|^{}_{{\text{SPR}}} \ge T + (m-1)(T-2\epsilon ) = m\,T - 2m\epsilon +2\epsilon . \end{aligned}$$

If the timetable synchronizes the lines for the $(s_{i},t_{i})$-passengers, $i>0$, we obtain for each of these passengers a travel time of $2\epsilon$ and the passenger from $s_0$ to $t_0$ can use the alternative route with a travel of $T+1$. Hence,

$$\begin{aligned} v({\text{SPR}} ^{{\text{sum}}};I) \le T + 1 + (m-1)2\epsilon = T + 1 + 2m\epsilon -2\epsilon . \end{aligned}$$

And we can conclude

$$\begin{aligned} \frac{v({\text{LBR}} ^{{\text{sum}}};I)|^{}_{{\text{SPR}}}}{v({\text{SPR}} ^{{\text{sum}}};I)}&\ge \frac{m\,T - 2m\epsilon +2\epsilon }{T + 1 + 2m\epsilon -2\epsilon } \\&=\frac{m\,T - 2T +2\frac{T}{m}}{3T + 1 -2\frac{T}{m}} \quad \mathop{\longrightarrow }\limits_{m\rightarrow \infty }^{}\quad \infty . \end{aligned}$$

$\square$

Theorem 6

$$\begin{aligned} \sup _{I} \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)|^{{}}_{{\kappa }\text{-}{{\text{MPR}}}}}{v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)} = \infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 4; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as described in Sect. 2.

This instance contains $2\bar{d}+2$ lines, $\bar{d}\ge 2$: $2\bar{d}$ lines are represented by the dotted arcs $\{(s_0,s_i)\}_{1\le i\le \bar{d}}$ and $\{(w_i,t)\}_{1\le i\le \bar{d}}$. Then there is one line (dashed arcs) starting in $s_1$ and ending in $w_{\bar{d}}$ and the last line (solid arcs) is from $v_1$ to $v_{\bar{d}}$.

The duration of all driving activities is $\epsilon >0$ except for the activity corresponding to the arc $(v_{{\bar{d}}-1},v_{\bar{d}})$ that has a duration of $2\epsilon$. All transfer and dwell activities have infinite capacity. All driving activities have a capacity of $\kappa =\bar{d}$. We set the passenger demand to $d_{s_it}=1$ for each $1\le i\le \bar{d}-1$, and we set $d_{s_0t}=\bar{d}$; all other demands are set to zero.

First consider problem $({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}})$. For any timetable, the passenger that wants to go from $s_i$ to t, $1\le i\le \bar{d}-1$, travels along paths that must start with the arc $(s_i,v_i)$. Hence, each of these arcs has only $\bar{d}-1$ capacity left and cannot be used any more by the $\bar{d}$ passengers that want to go from $s_0$ to t. These passengers have to travel via the path $(s_0,s_{\bar{d}},v_{\bar{d}},w_{\bar{d}},t)$ since it is the only $(s_0,t)$-path with sufficient capacity that is left. These passengers block the arc $(v_{\bar{d}},w_{\bar{d}})$, such that all passengers that want to go from $s_i$ to t, $1\le i\le \bar{d}-1$, must transfer at some node $v_i$, $1 \le i \le \bar{d}-1$ (different from $v_{\bar{d}}$). The dashed and the solid line are constructed in such a way that the sum of the transfer times at nodes $v_{\bar{d}-1}$ and $v_{\bar{d}}$ is at least $T-\epsilon$. Moreover, the transfer times at nodes $v_i$, $1\le i\le \bar{d}-1$, are all identical. Hence, there is a minimum total transfer time of all passengers of at least $(\bar{d}-1)(T-\epsilon )$, while the minimum total driving time is at least $(\bar{d}-1) 3\epsilon + \bar{d}\cdot 4\epsilon$. If the passengers from $s_i$ to t travel along the paths $(s_i,v_i,w_i,t)$, these values can indeed be achieved by synchronizing the solid and the dashed line at node $v_{\bar{d}}$, namely, the solid line can depart at $v_1$ at time 0 and the dashed line can depart at $s_1$ also at 0. Hence, the minimum total travel time with ${\kappa }\text{-}{{\text{UPR}}}$ (achieved for this timetable) is

$$\begin{aligned} v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)=(\bar{d}-1)(T-\epsilon ) + (\bar{d}-1) 3\epsilon + \bar{d}\cdot 4\epsilon =6\bar{d}\epsilon -2\epsilon +\bar{d}T-T. \end{aligned}$$

Given this timetable, the passengers traveling from $s_0$ to t cannot improve their traveling time by splitting up and therefore

$$\begin{aligned} v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)|^{}_{{\kappa }\text{-}{{\text{MPR}}}}&\ge v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I). \end{aligned}$$

In an optimal solution to $({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}})$, the passengers from $s_0$ to t can split and travel along $\bar{d}-1$ paths via $v_i$, $1\le i\le \bar{d}-1$. The transfer time in an optimal timetable for these passenger paths at $v_i$ is zero for all $1\le i\le \bar{d}$ if the solid line departs at $v_1$ at time $\epsilon$ and the dashed line departs at $s_1$ at time 0. The total travel time for the optimal ${\kappa }\text{-}{{\text{MPR}}}$-timetable is therefore

$$\begin{aligned} v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)&=(\bar{d}-1) 3\epsilon + \bar{d}\cdot 4\epsilon = 7\bar{d}\epsilon -3\epsilon . \end{aligned}$$

We set $\epsilon :=\frac{1}{\bar{d}}$ and can conclude that

$$\begin{aligned} \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)|^{}_{{\kappa }\text{-}{{\text{MPR}}}}}{v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)}&\ge \frac{v({\kappa }\text{-}{{\text{UPR}}} ^{{\text{sum}}};I)}{v({\kappa }\text{-}{{\text{MPR}}} ^{{\text{sum}}};I)} \\&=\frac{6\bar{d}\epsilon -2\epsilon +\bar{d}T-T}{7\bar{d}\epsilon -3\epsilon } \\&=\frac{6-\frac{2}{\bar{d}}+\bar{d}T-T}{7-\frac{3}{\bar{d}}} \quad \mathop{\longrightarrow }\limits_{\bar{d}\rightarrow \infty }^{}\quad \infty . \end{aligned}$$

$\square$

Fig. 4

Instance for Theorem 6. All arcs in this graph have a capacity of k

5 Comparing Objectives

In this section we compare the impact of the objective function. We show that if one optimizes w.r.t. the total travel time, there can be individuals that must take very long trips. On the other hand, if the longest travel time is minimized, the total travel time can be large.

Fig. 5

Instance for Theorem 7

Theorem 7

Let $M \in \{{\text{SPR}},{\text{LBR}}, {\kappa }\text{-}{{\text{MPR}}}, {\kappa }\text{-}{{\text{UPR}}} \}$ be a routing model, then

$$\begin{aligned} \sup _{I} \frac{v(M ^{{\text{sum}}};I)|^{\max }_{}}{v(M ^{\max };I)} =\infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 5. D has $3m$ nodes and $4m-2$ arcs, $m\in \mathbb {N}$; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as described in Sect. 2.

All activities have infinite capacity. We associate two lines with the arcs of D. There is one line (dashed arcs) from $s_1$ to $v_{m}$ with a driving time of $\epsilon =\frac{T+1}{m}$, $T\in \mathbb {N}$, on each driving activity. The second line (solid arcs) starts in $v_1$ and ends in $t_{m}$. The duration for each driving activity of this line equals $\epsilon$ except for the second last arc from $t_{m-1}$ to $v_{m}$ that has a driving time of T. We set the passenger demand for each OD pair $(s_i,t_i)$, $1\le i \le m$, to one; all other demands are set to zero.

For each OD pair $(s_i,t_i)\in \mathcal {D}$, $1\le i \le m$, there exists only a single path from $s_i$ to $t_i$ via the node $v_i$. Hence, the passenger routes are fixed and independent of the routing model $M$; the driving time for each OD pair is $2\epsilon$ for any feasible timetable. The dashed and the solid line are constructed in such a way that the transfer times at nodes $v_i$, $1\le i\le m-1$, are all identical. Moreover, if the two lines are synchronized at node $v_m$, then the transfer times at nodes $v_i$, $1\le i\le m-1$, are all equal to $\epsilon$. This would yield a total transfer time of $(m-1)\epsilon = T-\frac{T+1}{m}+1$. If a timetable synchronizes the lines at the nodes $v_i$, $1\le i\le m-1$, on the other hand, the transfer time at node $v_m$ is $T-\epsilon = T-\frac{T+1}{m}$.

First consider problem $(M ^{{\text{sum}}})$. In an optimal solution, the departure time of the dashed line in $s_1$ is 0 and the solid line departs in $v_1$ at $\epsilon$, such that the two lines are synchronized at the nodes $v_i$, $1\le i\le m-1$. The resulting transfer time for the pair $(s_m,t_m)$ at $v_m$ equals $T-\epsilon$. Hence, this OD pair yields the maximum travel time of $T+\epsilon$ among all OD pairs for this timetable.

In an optimal solution to problem $(M ^{\max })$, the lines are synchronized at node $v_m$ by setting the departure time of the dashed line at $s_1$ to 0 and the departure time of the solid line at $v_1$ to $2\,\epsilon$. The resulting transfer time for each OD pair $(s_i,t_i)$ at $v_i$ with $1\le i\le m-1$ is $\epsilon$ and for the pair $(s_m,t_m)$ the transfer time at $v_m$ is zero. The travel time for all OD pairs $(s_i,t_i)$ with $1\le i\le m-1$ is $3\,\epsilon$, which gives the maximum travel time. We can conclude that

$$\begin{aligned} \frac{v(M ^{{\text{sum}}};I)|^{\max }_{}}{v(M ^{\max };I)} =\frac{T+\epsilon }{3\epsilon } = \frac{T+\frac{T+1}{m}}{3\frac{T+1}{m}} = \frac{(m+1)T+1}{3T+3} \mathop{\longrightarrow }\limits_{m\rightarrow \infty }^{}\infty . \end{aligned}$$

$\square$

Fig. 6

Instance for Theorem 8

Theorem 8

Let $M \in \{{\text{SPR}},{\text{LBR}}, {\kappa }\text{-}{{\text{MPR}}}, {\kappa }\text{-}{{\text{UPR}}} \}$ be a routing model, then

$$\begin{aligned} \sup _{I} \frac{v(M ^{\max };I)|^{{\text{sum}}}_{}}{v(M ^{{\text{sum}}};I)} =\infty . \end{aligned}$$

Proof

Consider the directed graph D in Fig. 6. D has $3m$ nodes and $4m-2$ arcs, $m\in \mathbb {N}$; arcs corresponding to transfer and dwell activities are omitted. Based on D we construct a timetabling instance I as described in Sect. 2. All activities have infinite capacity. We associate 2 lines with the arcs of D. There is one line (dashed arcs) from $s_1$ to $t_{m}$ with a driving time of $\epsilon =\frac{1}{m}$ on each driving activity except the second last driving activity with a driving time of $2\epsilon$. The second line (solid arcs) starts in $v_1$ and ends in $v_{m}$. The driving time for each driving activity of this line equals $\epsilon$. We set the passenger demand for each OD pair $(s_i,t_i)$, $1\le i \le m$, to one and zero otherwise.

For each OD pair $(s_i,t_i)\in \mathcal {D}$, there exists only a single path from $s_i$ to $t_i$ via the node $v_i$. Hence, the passenger routes are fixed and independent of the routing model $M$. Again, both lines are constructed in such a way that the transfer times at nodes $v_i$, $1\le i\le m-1$, are all identical. And the transfer times at the nodes $v_{m-1}$ and $v_{m}$ sum up to at least $T-\epsilon$.

First consider problem $(M ^{\max })$. In an optimal solution, the dashed line departs at $s_1$ at 0 and the solid line departs at $v_1$ at $\frac{T+\epsilon }{2}$. The resulting transfer time for each OD pair $(s_i,t_i)$ at $v_i$ is $\frac{T-\epsilon }{2}$. Hence, the total travel time for this timetable is $2m\epsilon + m\frac{T-\epsilon }{2} =\tfrac{1}{2}(3m\epsilon +mT)$.

In an optimal solution to $(M ^{{\text{sum}}})$, the departure time of the dashed line at $s_1$ is 0 and the solid line departs at $v_1$ at $\epsilon$. The resulting transfer time for each OD pair $(s_i,t_i)$, $1\le i\le m-1$, at $v_i$ is zero and the transfer time at $v_m$ equals $T-\epsilon$ for the pair $(s_{m},t_{m})$. The total travel time for all passengers is therefore $2m\epsilon +T-\epsilon$.

We can conclude that

$$\begin{aligned} \frac{v(M ^{\max };I)|^{{\text{sum}}}_{}}{v(M ^{{\text{sum}}};I)} =\frac{3m\epsilon +mT}{2(2m\,\epsilon +T-\epsilon )} =\frac{3+m\,T}{4+2T-\frac{2}{m}} \quad \mathop{\longrightarrow }\limits_{m\rightarrow \infty }^{}\quad \infty . \end{aligned}$$

$\square$

We finally give a lemma that shows that there exists no instance such that the maximum weighted total travel time gap and the maximum weighted travel time gap can be both arbitrarily large since they bound each other. They are bounded by the number of OD pairs, i.e., by an input parameter of the problem instance.

Lemma 1

Let $m:=|\mathcal {D}|=|\{(s,t)\in V_{{\text{dep}}}\times V_{{\text{arr}}}: d_{st}>0\}|$ be the number of OD pairs, then we have for every instance I and every routing model $M \in \{{\text{SPR}},{\text{LBR}}, {\kappa }\text{-}{{\text{MPR}}}, {\kappa }\text{-}{{\text{UPR}}} \}$

$$\begin{aligned} \frac{v(M ^{\max };I)|^{{\text{sum}}}_{}}{v(M ^{{\text{sum}}};I)} \le m\frac{v(M ^{\max };I)}{v(M ^{{\text{sum}}};I)|^{\max }_{}} \le m\end{aligned}$$

and

$$\begin{aligned} \frac{v(M ^{{\text{sum}}};I)|^{\max }_{}}{v(M ^{\max };I)} \le m\frac{v(M ^{{\text{sum}}};I)}{v(M ^{\max };I)|^{{\text{sum}}}_{}} \le m. \end{aligned}$$

Proof

Let $(x^*,y^*)\in \mathrm {arg\,max}v(M ^{\max };I)|^{{\text{sum}}}_{}$ be an optimal solution of instance I for problem $M ^{\max }$ yielding the maximum total weighted travel time among all optimal solutions, i.e., by definition there is an OD pair $(s', t')\in \mathcal {D}$ s.t.

$$\begin{aligned} v(M ^{\max };I) = \sum _{p\in \mathcal {P}_{s' t'}}\sum _{a\in p}d_{s' t'}\, x^*_a\,y^*_p. \end{aligned}$$

Hence, we get

$$\begin{aligned} v(M ^{\max };I)|^{{\text{sum}}}_{}&= \sum _{(s,t)\in \mathcal {D}} \sum _{p\in \mathcal {P}_{st}} \sum _{a\in p} d_{st} \,x^*_a\,y^*_p\\&\le \sum _{(s,t)\in \mathcal {D}} \sum _{p\in \mathcal {P}_{s' t'}} \sum _{a\in p} d_{s' t'}\, x^*_a\,y^*_p \\&= m\sum _{p\in \mathcal {P}_{s' t'}} \sum _{a\in p} d_{s' t'}\, x^*_a\,y^*_p \\&= m\,v(M ^{\max };I). \end{aligned}$$

It is easy to see that $v(M ^{{\text{sum}}};I) \ge v(M ^{{\text{sum}}};I)|^{\max }_{}$. This implies

$$\begin{aligned} \frac{v(M ^{\max };I)|^{{\text{sum}}}_{}}{v(M ^{{\text{sum}}};I)}&\le \frac{m\,v(M ^{\max };I)}{v(M ^{{\text{sum}}};I)} \le m\frac{v(M ^{\max };I)}{v(M ^{{\text{sum}}};I)|^{\max }_{}}. \end{aligned}$$

$\square$

6 Computations

The aim of this section is to also give some computational evidence that routing decisions do indeed have a significant impact on timetabling. To this purpose, we compare the solution of an integrated timetabling and shortest path routing model $({\text{SPR}})$ with a fixed passenger routing resulting from a real-world reference timetable.

We consider a scenario from a cooperation with the public transit company of Wuppertal, the Wuppertaler Stadtwerke (WSW), which is operating the famous cableway line “Schwebebahn”. The data represents the periodic timetable of the core network of the public transport system of Wuppertal for the year 2013. The network has 158 station nodes, 229 OD nodes, and 460 directed arcs. There are 71 lines: 67 bus lines, three city train lines, and the cableway line. The lines are operated at different frequencies; their period times are 10, 15, 20, 30, or 60 min. The data also contains the connections to the regional railway system, such that we can take these important transfers into account. Here, we fixed the departure and arrival times for these lines. After some preprocessing, the data contains 45,254 OD pairs with a positive demand. In our setting, the dwell and driving times along each line are fixed s.t. the timetable affects only passengers that transfer. We can therefore remove all OD pairs for which a lower bound route is a direct connection. Furthermore, we assume that each transfer has a lower time bound of 2 min.

For the computations, we used our integer programming model $({\text{SPR}} ^{{\text{sum}}})$ that integrates a passenger routing. The passengers are represented by a path-flow in an event-activity network, in which they can travel freely. In the fixed routing case the demand of each OD pair is sent along some shortest path w.r.t. a given reference timetable, namely, the WSW timetable of 2013 (WSW2013). The objective is to minimize the total weighted travel time. The core network of Wuppertal gives rise to a time-expanded event-activity network with 86,386 events and 431,604 activities. There are 3990 binary line variables modeling the timetable. The passenger path-flow variables are dynamically added with a column generation algorithm, solving shortest path pricing problems. Our code is based on the constraint integer programming framework SCIP version 3.1.0 using Cplex 12.6 as an LP-solver. All computations were done on an Intel(R) Xeon(R) CPU E3-1245, 3.4 GHz computer (in 64 bit mode) with 8 MB cache, running Linux and 32 GB of memory. We set the time limit to 12 hours.

The WSW2013 reference timetable results in a total weighted travel time of 2,630,211.97 min and a total weighted transfer waiting time of 171,985.41 min. Fixing this routing and optimizing a classical PESP model, we could not find a timetable that improves the total weighted travel time. With the integrated timetabling and passenger routing model $({\text{SPR}})$, however, we found a timetable that yields a total weighted travel time of 2,597,571.95 min and a total weighted transfer waiting time of only 131,456.07 min. This corresponds to an improvement of 1.24 % in travel time and 23.57 % in transfer waiting time. While the first improvement is marginal, the latter is substantial, in particular, since transfer waiting time is known to be perceived beyond proportion by passengers. The solution still has an optimality gap of 12 %. Figure 7 illustrates the worsening and the improvement of the travel time for each OD pair when comparing the passenger routings arising from the reference timetable and an integrated timetable and passenger routing optimization. The figure shows that for the integrated solution the number of OD pairs where the travel time decreases is much larger than the number of OD pairs where the travel time increases compared to the reference solution.

Fig. 7

Heat maps comparing differences in travel times between timetables computed with different passenger routing models. The axes of both diagrams correspond to the OD nodes. The color of a point represents the difference in the travel time for the corresponding OD pair between the best passenger routing for WSW2013 reference timetable and the result of an integrated timetable and passenger routing optimization. Left: the redder a dot the better is the travel time for the timetable computed with the fixed routing, white means no difference or the integrated timetable is better. Right: the greener a dot the better is the travel time for the timetable computed with the shortest path routing, white means no difference or the reference timetable is better (color figure online)

Table 1 Summary of the theoretical results. Denote by $\bar{d}:=\max _{(s,t)\in \mathcal {D}}d_{st}$ the maximum demand, by $n:=|V|$ the number of events, by $m:=|\mathcal {D}|$ the number of OD pairs, and by $k:=|A_{{\text{trans}}}|$ the number of transfer activities

7 Summary

In this paper we investigated the influence of different passenger routing models on timetable optimization. The results are summarized in Table 1. In our theoretical analysis we showed that the best timetable for a fixed or lower bound routing can yield total travel times that are arbitrarily larger than those of an optimal timetable, i.e., a timetable optimized w.r.t. an integrated passenger routing. If we do not consider capacity constraints then all passengers can be assumed to use the same shortest path. If line capacities have to be fulfilled we showed that the total travel time can be arbitrarily reduced if the passengers of one OD pair are allowed to split their travel routes.

Addressing the importance of the choice of the routing approach in the optimization model, we get the following result. The routing model used in the optimization is substantial: If we take a timetable that is optimized for a lower bound routing and reroute the passengers again along the shortest paths according to this timetable, we can obtain a total travel time that is arbitrarily larger than the travel time for an optimal timetable with integrated shortest path routing. The same holds when we evaluate an optimal timetable for an unsplittable routing with a rerouting using multiple passenger paths.

Finally, we showed that the maximum travel time of a timetable minimizing the total travel time is bounded by the number of OD pairs times the maximum total travel time of a timetable that minimizes the maximum total travel time.

These results show that, no matter what comparison is done, choosing the wrong routing model can lead to arbitrarily bad results. Fixed and, especially, lower bound routings are questionable. Admittedly, the characteristics of the examples used in our proofs may usually not appear in real world instances, and it would be an interesting research direction to identify (realistic) assumptions on the problem structure under which the gaps are substantially smaller. We believe that such structures are present in real-world networks, i. e., that the difference between a lower bound routing and a shortest path routing in a subway or bus network is not arbitrarily bad. But even then, the gaps call for an improved understanding and treatment of passenger behavior. This can, on the positive side, release hitherto untapped optimization potentials. Our computational results indeed show that integrating passenger routing and timetabling can yield significant improvements: computations with data from the city of Wuppertal indicate that the total transfer waiting time can be substantially reduced by around 24 % in comparison to a real-world reference solution.